Ćwiczenie 4
Temat:
BADANIE CZWÓRNIKÓW PASYWNYCH
I. ZAGADNIENIA
1.
Wyznaczanie parametrów łańcuchowych dotyczących czwórników kształtu
„T” i „Π”
2.
Wyznaczanie parametrów impedancyjnych i admitancyjnych badanych
czwórników
3.
Określenie parametrów falowych Zc, g, a, b czwórników rezystancyjnych
i reaktancyjnych symetrycznych i niesymetrycznych
4.
Pomiar i analityczne wyznaczenie sygnałów wejściowych i wyjściowych
czwórnika w różnych stanach pracy, w tym: w stanie jałowym, w stanie
zwarcia i stanie dopasowania falowego
II. WIADOMOŚCI PODSTAWOWE
1. Klasyfikacja czwórników
Czwórnikiem (dwuwrotnikiem) nazywamy układ mający cztery zaciski, a ściśle
dwie pary uporządkowanych zacisków (rys.1.1). Dla czwórnika musi być spe-
łniony warunek
2
2
1
1
'
'
I
I
I
I
=
=
(4.1)
Jedną parę zacisków nazywamy wejściem, a drugą - wyjściem. Wielkości
związane z wejściem opatrujemy wskaźnikiem 1, a wielkości związane z
wyjściem - wskaźnikiem 2. Przeważnie do wejścia doprowadzone jest źródło
energii, a na wyjściu dołączony jest element odbiorczy
Czwórnik nazywamy symetrycznym, jeżeli przy zamianie miejscami wejścia
z wyjściem nie zmieni się rozpływ prądów i rozkład napięć w obwodzie poza
czwórnikiem, tzn. w obwodzie dołączonym do wejścia i w obwodzie dołączonym
do wyjścia.
Czwórniki dzielimy na odwracalne i nieodwracalne. Jeżeli do zacisków
wejściowych czwórnika odwracalnego doprowadzimy idealne źródło napięcia E,
które w zwartym obwodzie wyjścia wywoła prąd I, to po przeniesieniu tego
źródła do wyjścia w zwartym obwodzie wejścia też popłynie prąd I. Czwórnik,
dla którego spełniony będzie podany warunek, zwany warunkiem odwracalności,
nazywamy czwórnikiem odwracalnym.
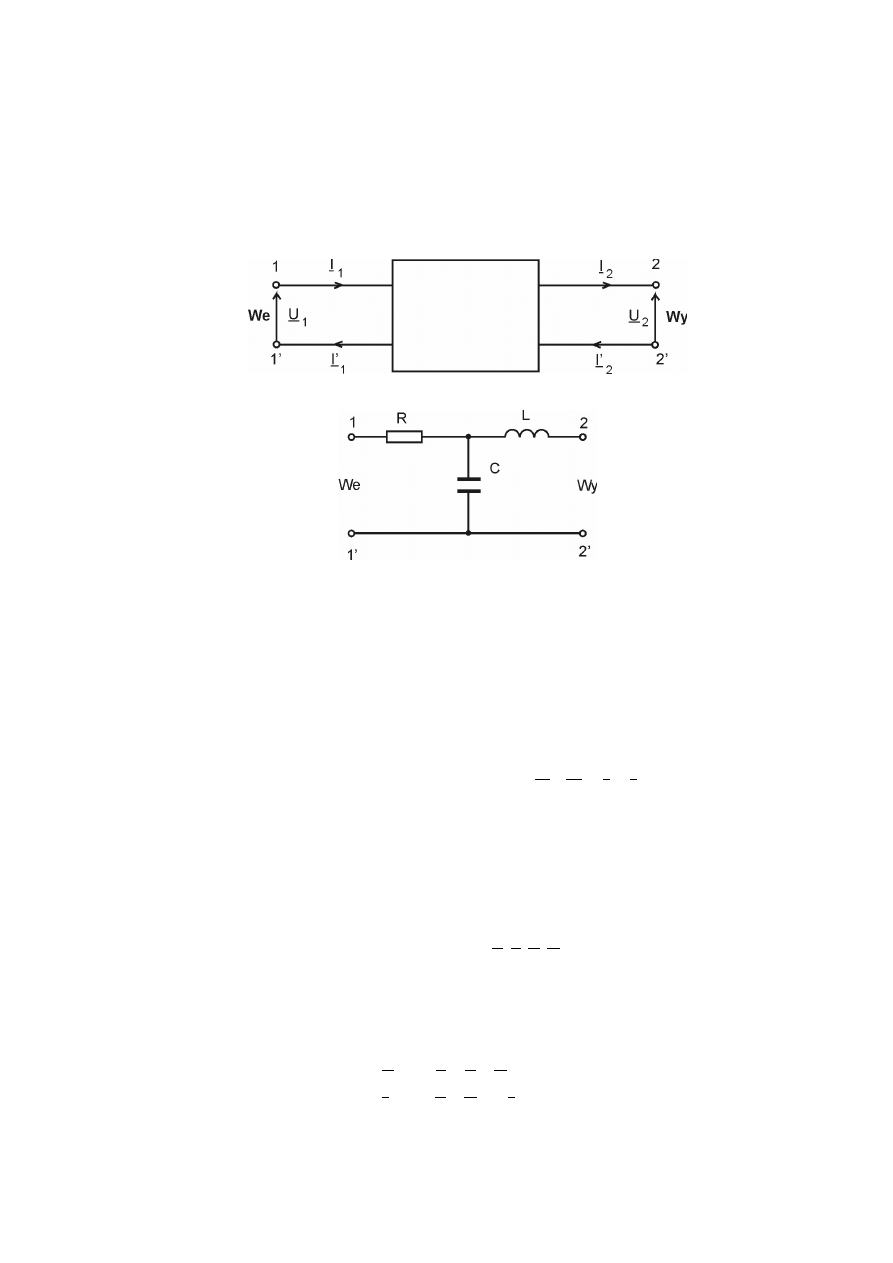
Czwórniki dzielimy na pasywne i aktywne. Czwórnik nazywamy pasywnym. Je-
żeli całkowita energia pobrana przez elementy czwórnika przy dołączeniu do jego
zacisków źródła energii, jest nieujemna, tzn. dodatnia lub równa zeru. Do chwili
dołączenia źródła do zacisków czwórnika pasywnego prąd w nim nie płynie.
Czwórnik pasywny zbudowany jest np. z rezystorów, cewek i kondensatorów
(rys. 1.2).
Rys. 4.1. Symbol graficzny czwórnika w postaci tzw. „czarnej skrzynki”
Rys. 4.2. Przykładowy schemat czwórnika pasywnego
Czwórnik, który nie spełnia warunków określonych w podanej definicji z2-
wamy czwórnikiem aktywnym. Czwórniki pasywne są z reguły odwracalne, z2-
miast czwórniki aktywne są przeważnie nieodwracalne
2. Równania czwórnika
Na rys. 4.1 wskazano cztery wielkości fizyczne (U
1,
U
2
, I
1
, I
2
) opisujące stan
elektryczny czwórnika. Wielkości te są nazywane współrzędnymi stanu czwór-
nika. Dla czwórnika liniowego są one ze sobą powiązane algebraicznymi związ-
kami liniowymi.
Parametry wchodzące do którejkolwiek z wymienionych postaci równań czwór-
nika wyznacza się na podstawie znajomości struktury czwórnika i wartości impe-
dancji lub admitancji gałęzi tworzących tę strukturę. Znajomość jednej grupy
parametrów, np. parametrów łańcuchowych
D
C
B
A
,
,
,
umożliwia wyznaczenie
wszystkich pozostałych parametrów.
Równania zostały podane w postaci macierzowej (oznaczenia przyjęte z rys. 4.1).
2.1
Równanie łańcuchowe
−
=
2
2
1
1
I
U
D
C
B
A
I
U
(4.2)
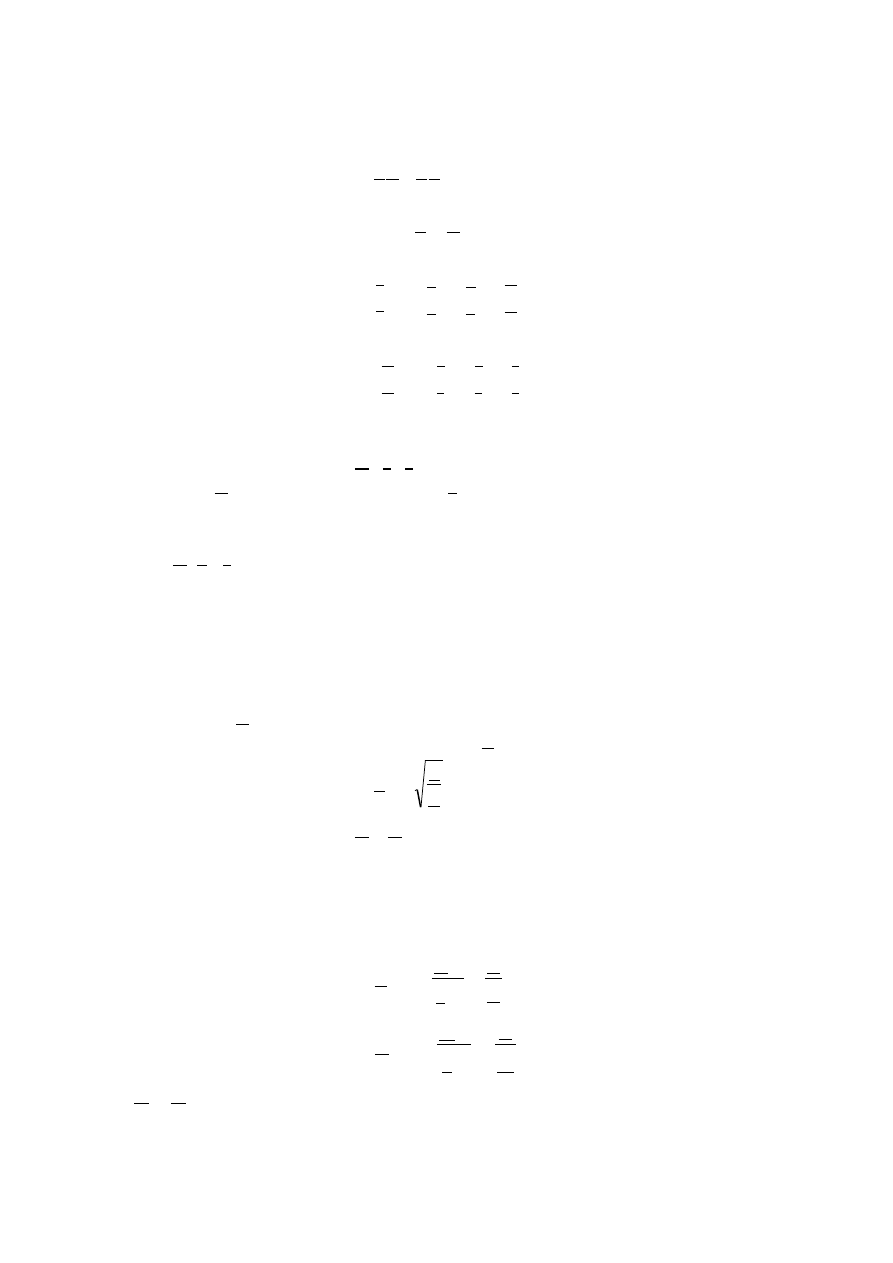
Dla czwórników pasywnych, odwracalnych słuszna jest zależność
1
=
−
C
B
D
A
(1.8)
a dla czwórników symetrycznych
D
A
=
2.2
Równanie admitancyjne
=
2
1
22
21
12
11
2
1
U
U
y
y
y
y
I
I
(4.3)
2.3
Równanie impedancyjne
=
2
1
22
21
12
11
2
1
I
I
z
z
z
z
U
U
(4.4)
Występujące w równaniach (4.2) do (4.4) macierze kwadratowe (oznaczać je
będziemy odpowiednio przez A, y, z) są nazywane, podobnie jak odpowiednie
równania, np. A – macierz łańcuchowa, , z – macierz impedancyjna. Macierze te
są nazywane macierzami charakterystycznymi czwórnika.
Spośród sześciu macierzy charakterystycznych czwórnika najczęściej stosuje się
macierze A, y i z.
Do opisu czwórników pasywnych najczęściej stosuje się postać łańcuchową.
3
Impedancja charakterystyczna czwórnika symetrycznego
Impedancją charakterystyczną lub falową czwórnika symetrycznego nazywamy
taką impedancję Z
C
, która dołączona do zacisków wyjściowych powoduje, że im-
pedancja wejściowa czwórnika też jest równa Z
C
.
C
B
Z
C
=
(4.5)
Znając parametry łańcuchowe B i C można wg wzoru (4.5) obliczyć impedancję
charakterystyczną czwórnika.
Impedancję charakterystyczną czwórnika symetrycznego można też uzależnić od
impedancji wejściowej czwórnika w stanie jałowym i w stanie zwarcia.
Skorzystamy z równań
C
A
I
U
Z
weo
=
=
10
10
(4.6)
D
B
I
U
Z
z
z
wez
=
=
1
1
(4.7)
przy A = D
A
B
Z
C
A
Z
wez
we
=
=
,
0
(4.8)
wez
we
C
Z
Z
C
B
Z
0
=
=
(4.9)
Uzależnienie impedancji charakterystycznej czwórnika od impedancji wejściowej
w stanie jałowym i impedancji wejściowej w stanie zwarcia jest dogodne, dlatego
że impedancje te można dla określonego czwórnika nie tylko obliczyć, ale rów-
nież zmierzyć.
4
Współczynnik tłumienia. Współczynnik fazowy. Współczynnik
przenoszenia czwórnika symetrycznego.
Jeżeli czwórnik symetryczny obciążymy impedancją charakterystyczną
C
Z
, to
jak mówimy czwórnik znajduje się w warunkach dopasowania falowego.
Przy obciążeniu czwórnika symetrycznego impedancją charakterystyczną,
stosunek napięć
1
U
do
2
U
jest równy stosunkowi prądów
2
1
I
do
I
i wynosi
C
B
A
+
Można inaczej powiedzieć, że przekładnia napięciowa czwórnika jest
równa przekładni prądowej.
Wprowadzimy teraz następujące oznaczenie
g
e
C
B
A
=
+
(4.10)
Wyrażenie e
g
jest liczbą zespoloną, gdyż przy zasilaniu czwórnika napięciem
sinusoidalnym, parametry łańcuchowe czwórnika
C
B
A ,
,
są zależne od impe-
dancji zespolonych gałęzi czwórnika, a więc są liczbami zespolonymi.
Wielkość g w wyrażeniu (4.10) będącą liczbą zespoloną można wyrazić w postaci
algebraicznej i nazwać współczynnikiem przenoszenia czwórnika.
g=a+jb
(4.11)
Część rzeczywistą współczynnika przenoszenia, czyli a nazywamy współczyn-
nikiem tłumienia czwórnika, a część urojoną b – współczynnikiem fazowym
czwórnika.
.]
[
ln
20
ln
20
2
1
2
1
Nep
I
I
U
U
a
=
=
(4.12)
W czwórniku symetrycznym obciążonym impedancją charakterystyczną
współczynnik tłumienia napięć jest równy współczynnikowi tłumienia
prądów.
ψ
1
-
ψ
2
=b [rad]
(4.13)
Z równania (4.13) wynika, że współczynnik fazowy czwórnika symetrycznego
jest równy różnicy faz początkowych napięć, czyli określa kąt przesunięcia z2-
ęcia na wyjściu czwórnika względem napięcia na wejściu.
O ten sam kąt przesunięte są względem siebie prądy na wejściu i wyjściu czwór-
nika.
Współczynnik fazowy mierzymy w radianach (lub stopniach kątowych), czyli
jednostkach miary kątów.
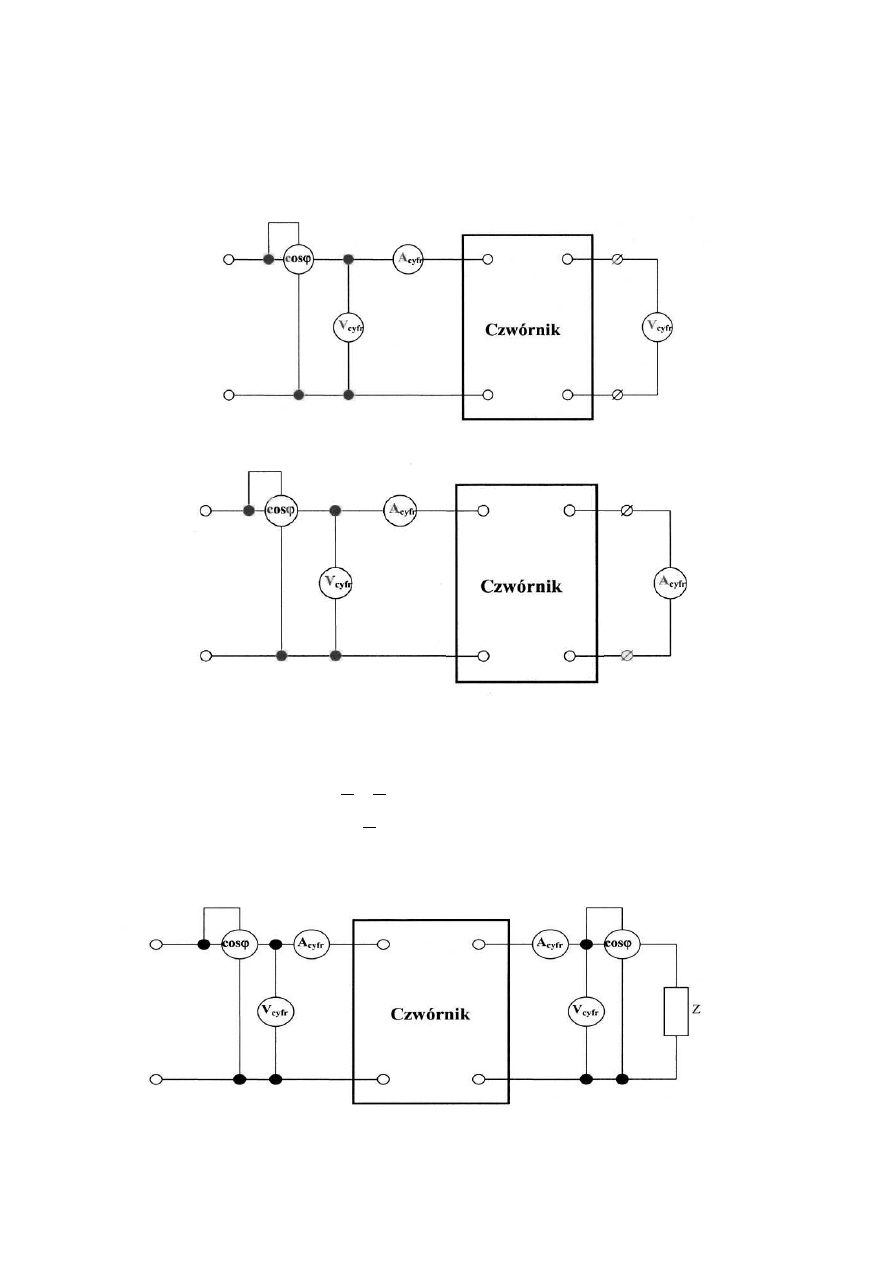
III. Pomiary
1. Badanie czwórnika w stanie jałowym
Schemat pomiarowy:
2. Badanie czwórnika w stanie zwarcia
Schemat pomiarowy:
3. Badanie czwórnika obciążonego:
3.1
impedancją falową Z
2
=Z
C
3.2
dowolną impedancją Z
2
Schemat pomiarowy:
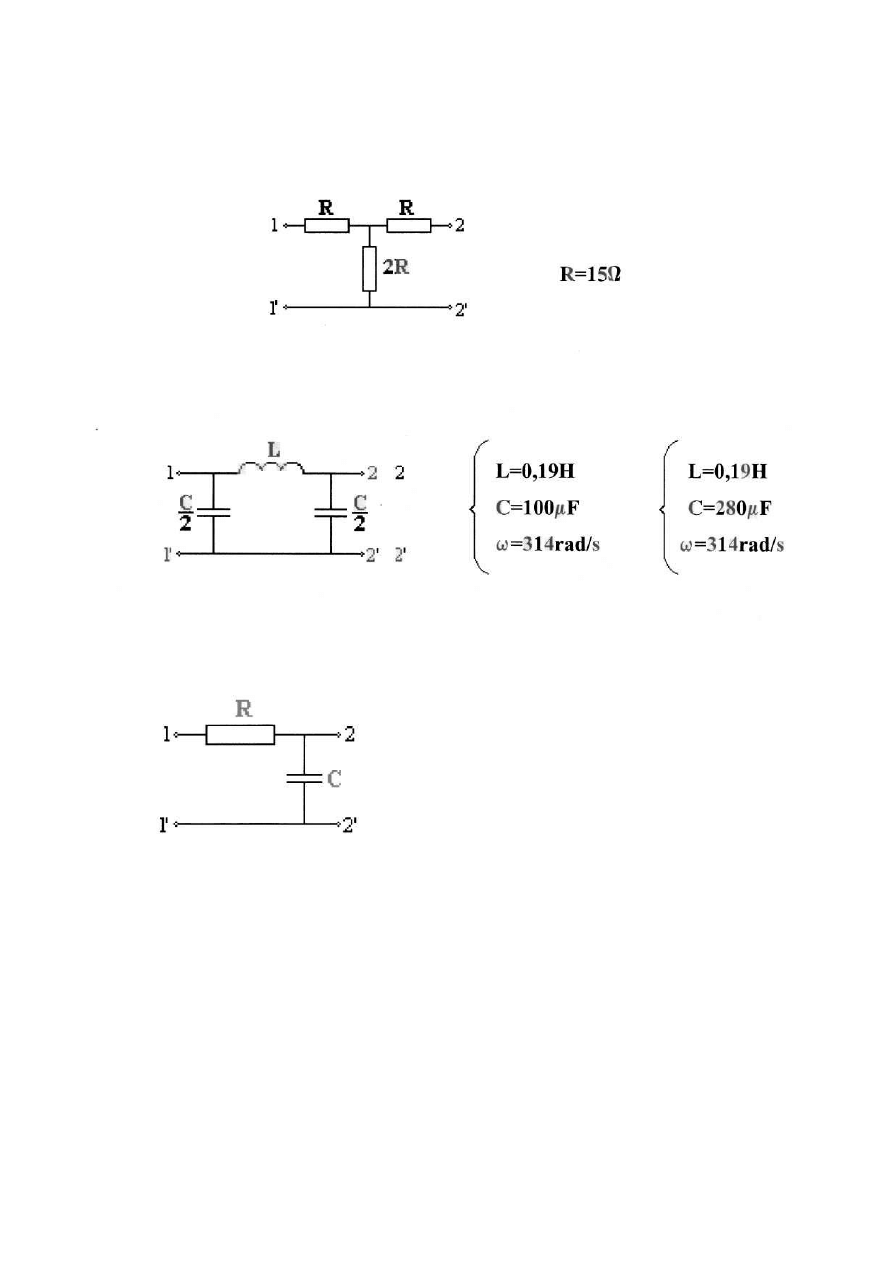
4. Schematy badanych czwórników
4.1.Czwórnik rezystancyjny kształtu „T'
4.2.Czwórnik reaktancyjny kształtu „Π " (filtr dolnoprzepustowy)
4.3.Czwórnik niesymetryczny
typu „Г”
R=33Ω,C=50μF
ω=314 rad/s
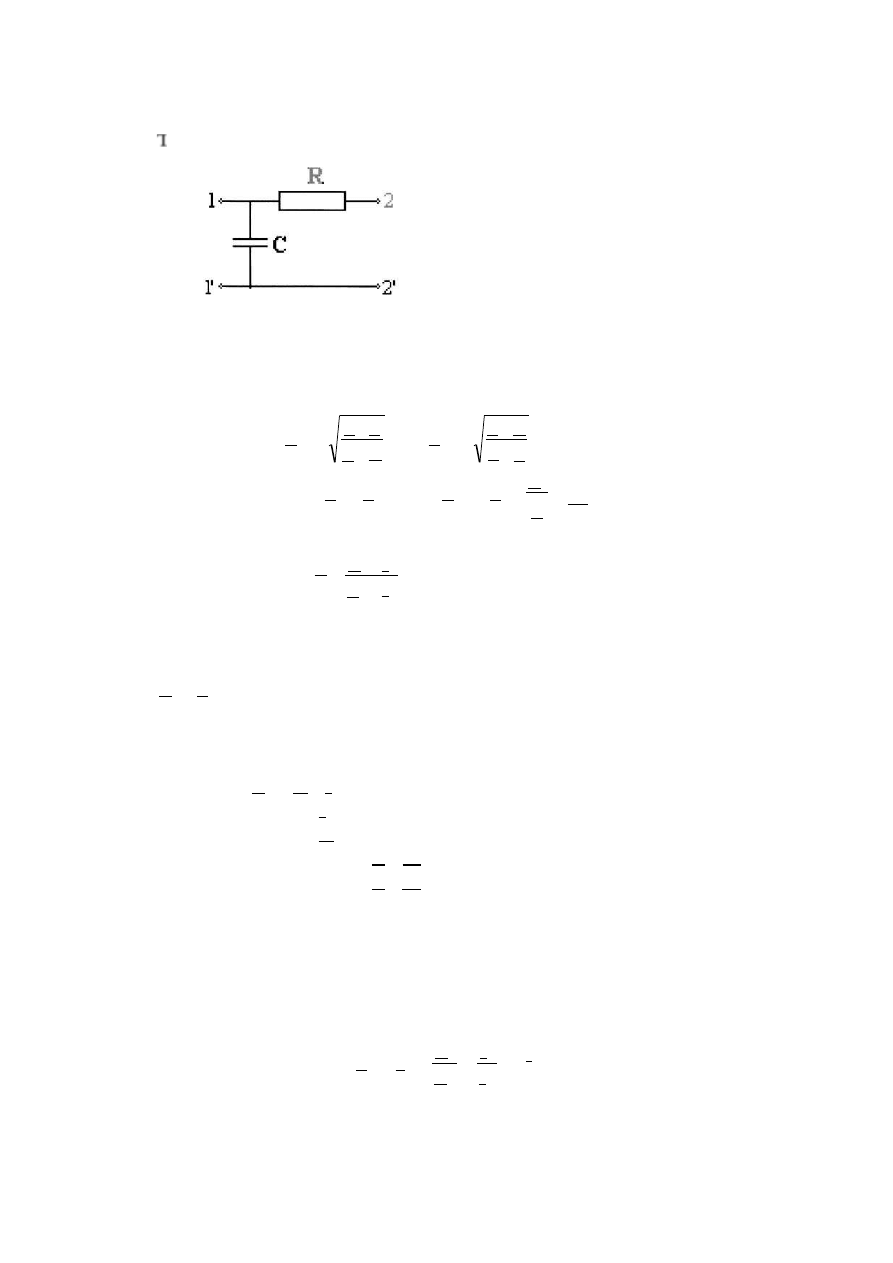
typu „ ”
R=33Ω,C=5OμF
ω=314 rad/s
UWAGA: Czwórnik niesymetryczny ma dwie impedancje falo-
we, które wyrażają zależności:
2
2
1
1
1
1
1
1
2
ln
2
1
:
,
2
2
1
I
U
I
U
g
ia
przenoszen
stala
wówczas
Z
I
U
Z
Z
to
Z
Z
Jeśeś
C
A
D
B
Z
i
D
C
B
A
Z
C
WE
C
C
C
•
•
=
=
=
=
=
•
•
=
•
•
=
(4.14)
5. Przebieg ćwiczenia
5.1. Wyznaczyć analitycznie macierz łańcuchową A na podstawie schematu
badanego czwórnika oraz jego parametry falowe
Zc , g = a + jb
5.2. Dla zadanego czwórnika wykonać pomiary według schematów 1,
2, 3 dla dwóch wartości napięcia zasilania.
5.3. Wyznaczyć na podstawie pomiarów impedancję wejściową badanego
czwórnika Z
1
= U
1
/ I
1
dla stanu:
a) jałowego;
I
2
=0;
b) zwarcia;
U
2
=0
c) dopasowania falowego
Z
2
= Z
C
d)obciążenia impedancją
Z
2
≠ Z
C
5.4. Obliczyć impedancję wejściową czwórnika dla wymienionych stanów
pracy jako funkcję jego parametrów łańcuchowych (z równań łańcucho-
wych) porównać jej wartości z wynikami, otrzymanymi w punkcie 5.3
(wyniki pomiarów i obliczeń zestawić wtabelce)
5.5. Sprawdzić, czy w stanie dopasowania falowego czwórnika symetrycz-
nego jego przekładnia napięciowa i prądowa spełnia zależność:
g
i
u
e
I
I
U
U
=
=
=
=
2
1
2
1
ϑ
ϑ
Wyznaczyć z pomiarów i obliczeń teoretycznych stałą tłumienia a.
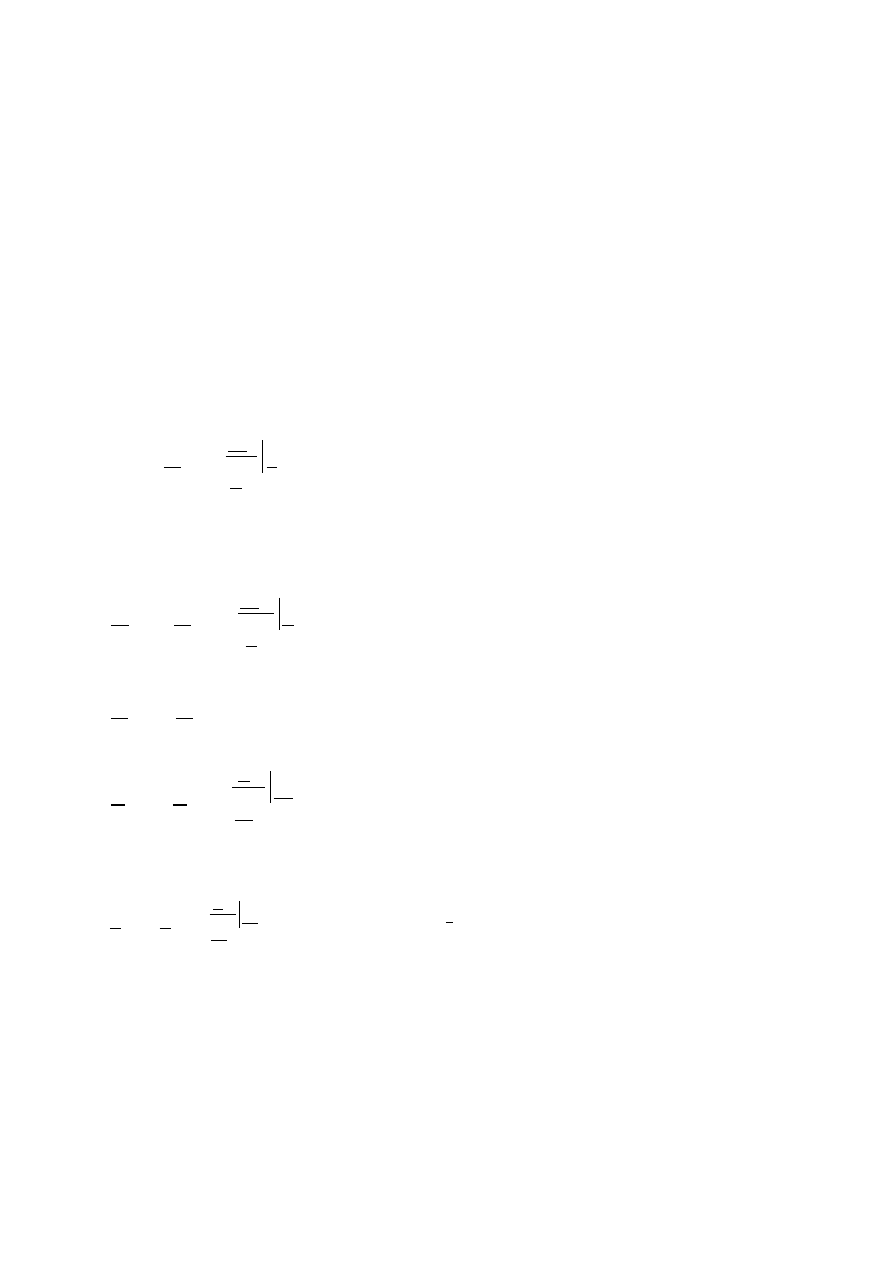
5.6 Porównać dla czwórnika reaktancyjnego pulsację ω=314rad/s z jego pul-
sacją graniczną cou obliczoną dla filtru dolnoprzepustowego na z2-
awie schematów 3.2.a) oraz 3.2.b) i ocenić czy dla a)=314rad/s wartość
stałej a jest równa zeru, czy jest różna od zera.
5.7 Dla wybranego stanu pracy badanego czwórnika wyznaczyć analitycznie
przebiegi wejściowe u
1
(t) oraz i
1
(t) wykorzystując równania łańcuchowe
(przyjąć zmierzoną wartość sygnału wyjściowego czwórnika napięcia lub
prądu za wie/kość odniesienia).
5.8. Wyznaczyć na podstawie pomiarów i na podstawie kształtu czwórnika jego
:
a)parametry impedancyjne
b)parametry admitancyjne
UWAGA:
0
2
2
1
11
=
=
I
I
U
Z
Impedancja wejściowa w stanie jałowym
zacisków wyjściowych
dla czwórnika odwracającego:
0
2
1
2
21
12
=
=
=
I
I
U
Z
Z
dla czwórnika symetrycznego:
oraz
0
2
1
1
11
22
=
=
=
U
U
I
y
y
Admitancja wejściowa czwórnika symetrycz-
nego w stanie zwarcia zacisków wejściowych
←
=
=
=
0
2
1
2
21
12
U
U
I
y
y
Zwrot prądu I
2
„ do pudełka
”
11
22
Z
Z
=