X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Grzegorz PROKOPSKI
1
Janusz KONKOL
2
Janusz Ł AKOMY
2
BADANIE STAŁ YCH MATERIAŁ OWYCH SKLEJKI
1. Wprowadzenie
Wielkościami niezbędnymi w projektowaniu są opró cz naprężeń dopuszczalnych
(obliczeniowych) ich stałe materiałowe, takie jak moduł Younga E czy liczba Poissona ν .
Znana z wytrzymałości materiałó w zależność pomiędzy stałymi materiałowymi - modułem
sprężystości poprzecznej G, modułem Younga E i wspó łczynnikiem Poissona
n
dla
materiałó w jednorodnych i izotropowych ma postać:
)
1
(
2
n
+
=
E
G
(1)
Podczas gdy moduł Younga i wspó łczynnik Poissona jest stosunkowo prosto wyznaczyć w
badaniach, to moduł sprężystości poprzecznej G jest najczęściej określany w sposó b
analityczny z zależności (1).
Określanie w badaniach modułu G ró żnego rodzaju materiałó w konstrukcyjnych było
dotychczas bardzo rzadko podejmowane. Badaniami takimi w Polsce, w odniesieniu do
kompozytó w z matrycą cementową zbrojonych włó knami, zajmował się Jaworski [1, 2].
Badania nad doświadczalnym ustaleniem wszystkich trzech stałych materiałowych zaprawy
normowej (1:1:3) na specjalnie przygotowanym stanowisku badawczym prowadzili także
Prokopski i in. [3]. W badaniach tych wykorzystano model czystego ścinania stosowany do
weryfikacji teorii płyt przedstawiony w pracy Timoshenki [4].
W przypadku materiałó w anizotropowych, takich jak sklejki, niezbędne jest niezależne
określenie wszystkich stałych materiałowych.
Zalecenia RILEM [5] precyzują metodykę badań właściwości wytrzymałościowych
sklejki. Zgodnie z tymi zaleceniami, badaniom do wyznaczenia modułu G sklejki należy
poddawać płyty kwadratowe o krawędzi l = (25÷40)g, gdzie g – grubość sklejki, natomiast
do wyznaczenia sztywności zginania belki o wymiarach 1200× 300× g [mm].
1
Dr hab. inż., prof. PRz., Wydział Budownictwa i Inżynierii Środowiska Politechniki
Rzeszowskiej
2
Mgr inż., Wydział Budownictwa i Inżynierii Środowiska Politechniki Rzeszowskiej
66
2. Cel i zakres badań
Celem badań było określenie modułu sprężystości poprzecznej G oraz moduł sprężystości
podłużnej E sklejki brzozowej.
Moduł sprężystości poprzecznej G
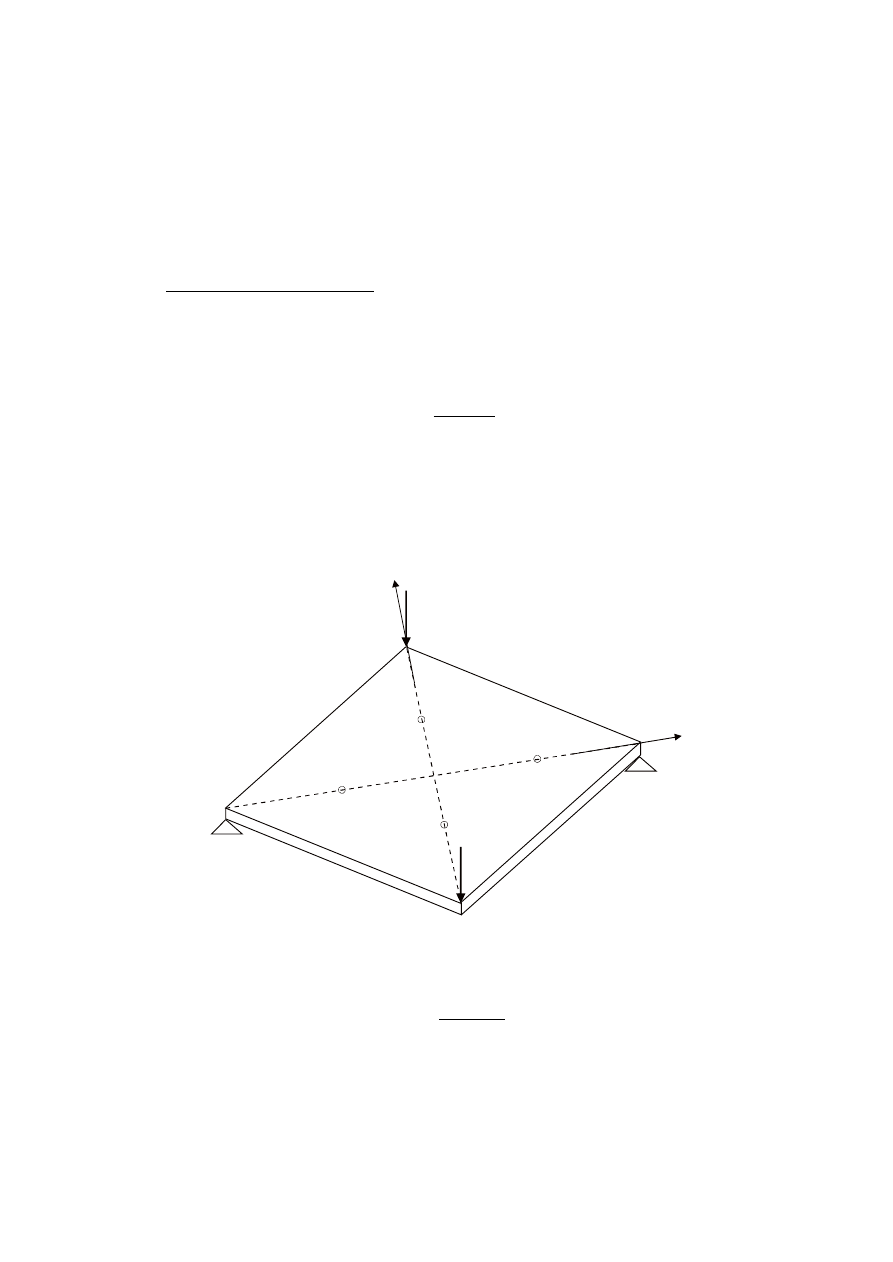
Badaniom poddano sklejkę z brzozy o grubości 10,2 mm. Płyta obcią żona była dwiema siłami w
dwó ch narożach po przeką tnej i podparta w dwó ch narożach na drugiej przeką tnej (rys. 1). Przy
takim schemacie podparcia i przy tak zadawanym obcią żeniu w płaszczyźnie płyty wystą pi stan
czystego ścinania, a odkształcona powierzchnia ma kształt paraboloidy hiperbolicznej.
Ogó lne ró wnanie ugięcia płyty ma postać:
)
2
2
(
)
1
(
2
)
,
(
y
x
D
M
y
x
w
-
-
=
n
(2)
gdzie:
w(x, y) – ugięcie płyty,
M – moment zginają cy odniesiony do jednostki długości, M=P/2,
D – sztywność płytowa obliczana według wzoru (3),
n
– wspó łczynnik Poissona,
x, y – wspó łrzędne punktó w płyty w przyjętym układzie wspó łrzędnych.
Rys. 1. Schemat obcią żenia płyty
Sztywność płytową D oblicza się według zależności:
)
2
1
(
12
3
n
-
=
Eh
D
(3)
P
P
A
B
C
D
X
Y
67
w
P
bh
l
E
D
D
×
=
3
4
3
gdzie:
E – moduł sprężystości podłużnej,
h – grubość płyty.
Podstawiają c ró wnania (1) i (3) do ró wnania (2) otrzymuje się:
)
2
2
(
3
2
3
)
,
(
y
x
Gh
P
y
x
w
-
=
(4)
Podstawiają c wspó łrzędne punktu A, x = -113 mm, y = 0 (rys. 1) do ró wnania (4), po
przekształceniach wzó r na moduł sprężystości poprzecznej przyjmuje postać:
3
2
2
3
wh
Pa
G
=
(5)
gdzie:
a – odległość punktu A od środka płyty.
W celu ustalenia zakresu pracy sprężystej płyty uzasadniony jest pomiar przemieszczenia dla
kilku stanó w obcią żenia, przy stopniowo wzrastają cej sile.
Wzó r (5) przyjmuje wó wczas postać:
w
P
h
a
G
D
D
×
=
3
2
2
3
(6)
gdzie:
D
P – przyrost siły między kolejnymi stanami obcią żenia,
D
w – przyrost przemieszczenia punktu A wywołany przyrostem siły.
Moduł sprężystości podłużnej E
Moduł sprężystości podłużnej przy zginaniu wyznaczono na podstawie pomiaru ugięcia i
przyłożonej siły w środku rozpiętości między podporami, na pró bkach mniejszych niż
podano w [5]. Wartość modułu wyznaczono ze znanej z wytrzymałości materiałó w
zależności ugięcia od przyłożonej siły (7):
(7)
gdzie:
l – rozstaw podpó r,
b – szerokość pró bki,
h – grubość pró bki,
D
P/
D
w – tangens nachylenia prostej określonej na podstawie wykresu siła – ugięcie.
Opis badań
Badania modułu G przeprowadzono na płytach ze sklejki brzozowej o wymiarach
68
360
´
360× 10,2 mm, wykonanych, na specjalnie przygotowanym stanowisku badawczym
(rys. 2). Wilgotność sklejki wynosiła około 7%.
Pomiaru siły dokonano przy pomocy siłomierzy pałą kowych typu PRL-T1 o zakresie do
2000 N, natomiast pomiaru ró żnicy przemieszczeń pomiędzy punktami A i B oraz C i D
dokonano przy użyciu zegarowego czujnika przemieszczeń , umieszczonego w specjalnej
konstrukcji, tzw. „pają k”.
Rys. 2. Stanowisko badawcze
Badanie modułu E przeprowadzono na pró bkach o wymiarach 360× 50× 10,2 mm, przy
zadawaniu obcią żenia wzdłuż i w poprzek włó kien oklein zewnętrznych. Pomiaru siły
dokonano za pomocą siłomierza pałą kowego, natomiast pomiar ugięcia wykonano przy
użyciu przyrzą du do pomiaru ugięć bezwzględnych, tzw. „Yoke” (rys. 3).
Zastosowany do pomiaró w system pomiarowy GOELAB został przystosowany do
precyzyjnego pomiaru wielkości fizycznych (takich jak przemieszczenie) i przetwarzania ich
na sygnał elektryczny. Program dołą czony do systemu GEOLAB umożliwia dowolną
kalibrację zastosowanych czujnikó w, np. w przypadku siłomierzy pałą kowych
przeskalowanie przemieszczenia na siłę. Pomiaró w dokonywano co ustalony okres
pró bkowania (w badaniach przyjęto okres pró bkowania co 1 sekundę), a wyniki zapisywane
były w zbiorze tekstowym w komputerze.
Wyniki badań
Otrzymane wyniki badań posłużyły do określenia zależności obcią żenie-
przemieszczenie punktu przyłożenia jednego z ramion „pają ka” (rys. 2) dla modułu G lub
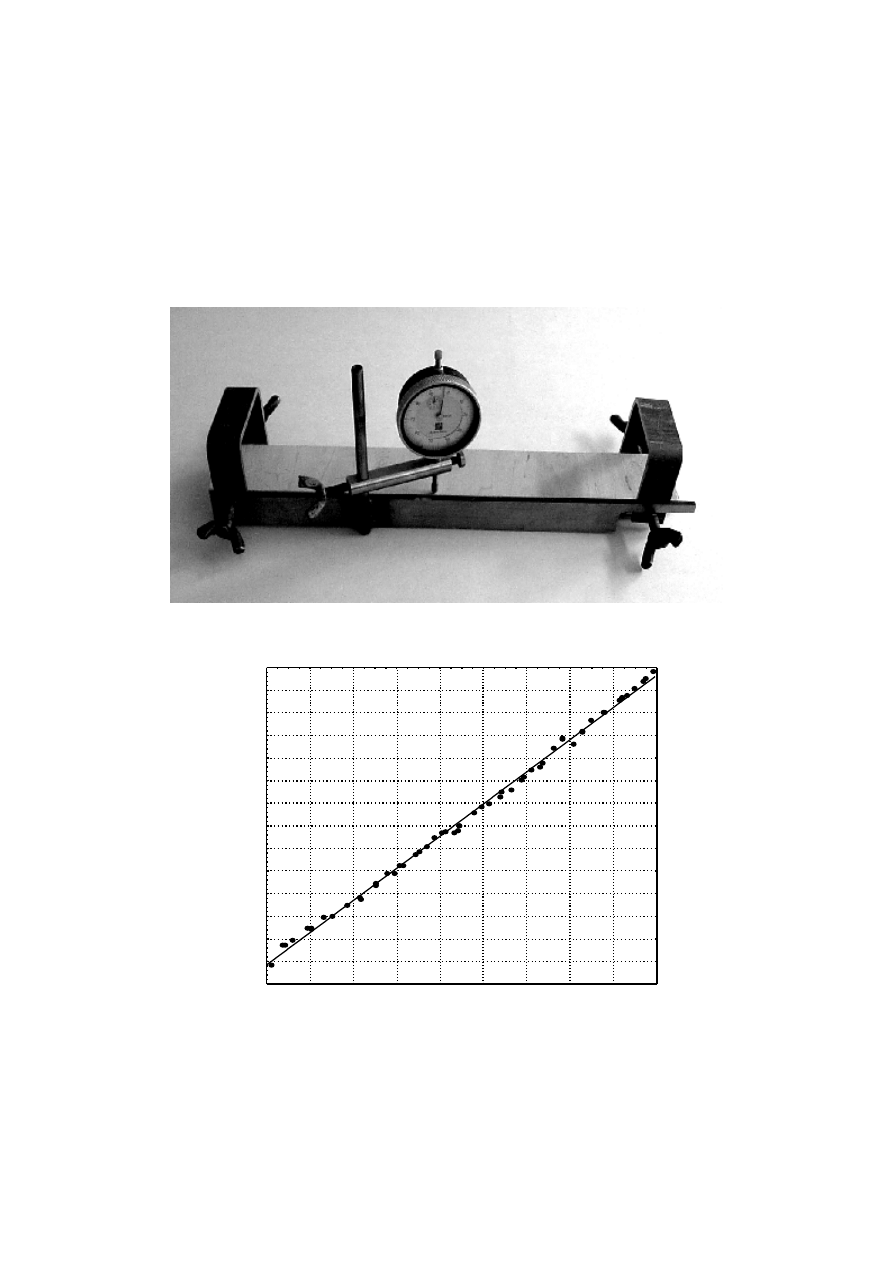
69
ugięcia w środku rozpiętości pró bki dla modułu Younga. Z zależności tych wyznaczono
sprężysty zakres pracy badanych elementó w i obliczono tangens nachylenia prostych
(
D
P/
D
w). Wyniki badań każdej z pró bek sklejki zostały użyte do obliczenia modułu
sprężystości poprzecznej G, zgodnie z zależnością (6) oraz modułu E według zależności (7).
Wyniki badań podano w tablicach 1-3.
Rys. 3. Przyrzą d do pomiaru ugięć bezwzględnych „Yoke”
Ugi
ę cie, mm
S
iła
,
N
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
Rys. 4. Zależność ugięcia od siły dla modułu G (pró bka 1)
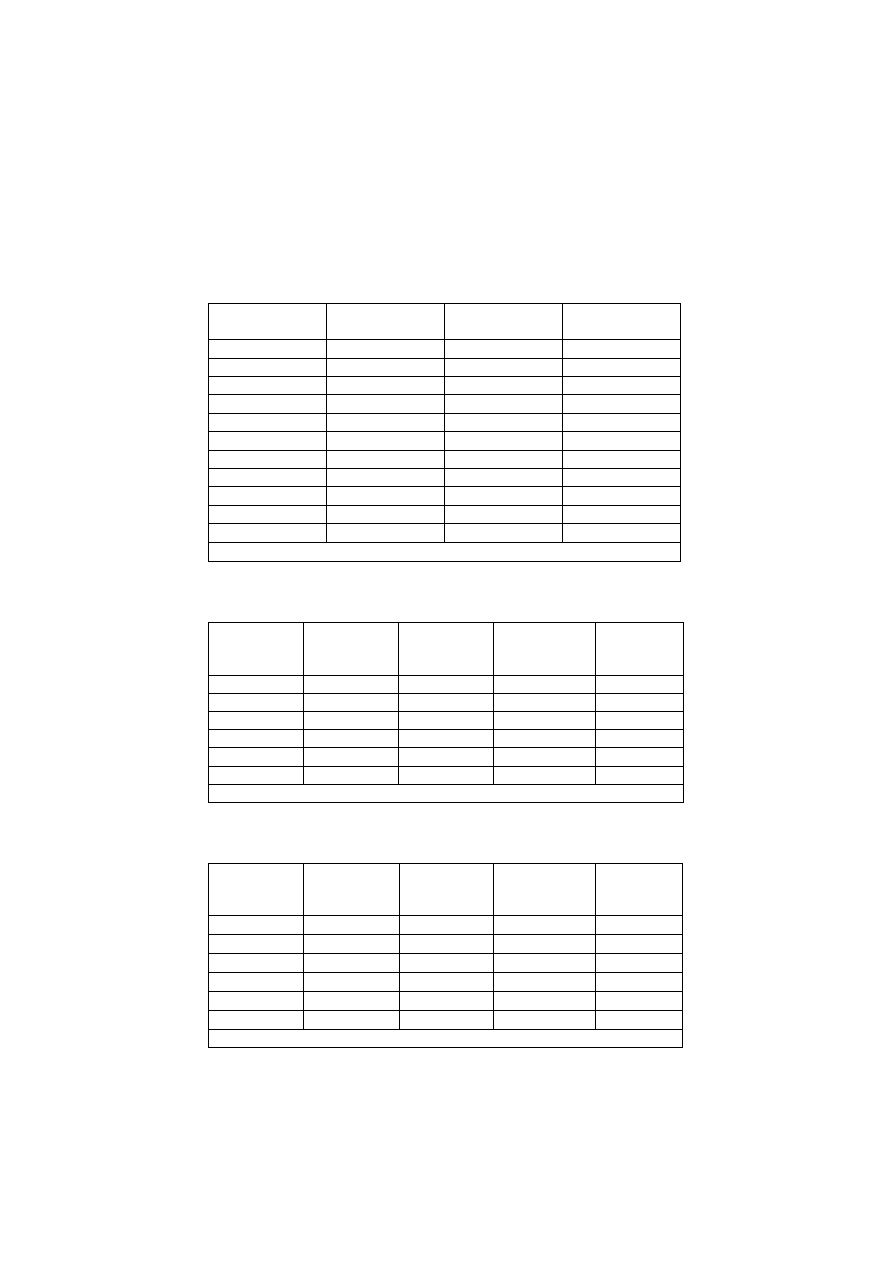
70
W tablicach 1-3 podano wyniki dla wszystkich pró bek oraz wartości średnie modułu
sprężystości poprzecznej i podłużnej wraz z odchyleniem standardowym średniej. Dla każdej
wartości
D
P/
D
w podano odpowiadają cy im wspó łczynnik korelacji R.
Tablica 1. Wyniki badań modułu G
Nr pró bki
D
P/
D
w
Wspó łczynnik
korelacji R
Moduł G
GPa
1
55,00
0,997
0,978
2
55,00
0,999
0,978
3
55,30
0,998
0,984
4
54,30
0,999
0,966
5
55,70
0,997
0,991
6
58,30
0,998
1,037
7
57,10
0,999
1,016
8
55,20
0,999
0,982
9
53,00
0,997
0,943
10
51,90
0,998
0,923
11
55,30
0,997
0,984
0,980 ± 0,01
Tablica 2. Wyniki badań modułu E – zginanie wzdłuż włó kien oklein zewnętrznych
Nr pró bki
Szerokość
pró bki
mm
D
P/
D
w
Wspó łczynnik
korelacji R
Moduł E
GPa
1
51,3
66,3
0,996
9,52
2
51,3
65,8
0,999
9,44
3
51,5
67,9
0,996
9,71
4
51,5
63,1
0,999
9,02
5
50,7
67,2
0,998
9,76
6
50,7
68,3
0,999
9,92
9,56± 0,13
Tablica 3. Wyniki badań modułu E – zginanie w poprzek włó kien oklein zewnętrznych
Nr pró bki
Szerokość
pró bki
mm
D
P/
D
w
Wspó łczynnik
korelacji R
Moduł E
GPa
1
50,8
49,9
0,998
7,23
2
50,8
50,2
0,997
7,28
3
50,5
52,3
0,997
7,63
4
50,5
51,3
0,998
7,48
5
50,7
49,2
0,996
7,15
6
50,7
53,3
0,998
7,74
7,42± 0,10
71
Wartości wspó łczynnikó w zmienności wynoszą ce dla modułu G 3,1%, zaś dla modułu E
3,3%, świadczą o dużej dokładności badań .
3. Wnioski
Przeprowadzone badania wykazały pełną przydatność zastosowanych metod do określania
modułu sprężystości poprzecznej G oraz podłużnej E sklejek. Otrzymane wyniki mieszczą
się w granicach wartości podawanych w literaturze, m.in. [6].
Zastosowana do pomiaró w technika komputerowa umożliwiła precyzyjny pomiar
badanych wielkości, co byłoby trudne lub nawet niemożliwe przy użyciu tradycyjnych
metod badawczych.
Literatura
[1] JAWORSKI J., Fiberconcrete in the pure shear deformation. Report of Technical
University of Cracow, 1983.
[2] JAWORSKI J., Slow crack growth in cement pastes and mortars. Report No Fo 7813.
Swedish Cement and Concrete Research Institute, Stockholm, 1978.
[3] PROKOPSKI G., KONKOL J., Ł AKOMY J., Metody określania stałych materiałowych
kompozytó w cementowych. 5
th
Int. Scientific Conference “ Current Issues of Civil
Engineering”, Rzeszó w, Sept. 25-26, 2000.
[4] TIMOSHENKO S., WOINOWSKY-KREIGER S., Teoria płyt i powłok. Arkady,
Warszawa 1962.
[5] RILEM Final Recommendation TT-2. Testing methods for plywood in structural grades
for use in load-bearing structures. Materials and Structures, nr 79, 1981.
[6] Poradnik inżyniera i technika budowlanego. Tom 2, cz. II, Arkady, Warszawa 1969.
INVESTIGATIONS OF THE MATERIAL’
S CONSTANTS FOR
PLYWOOD
Summary
The results of the shear modulus and Young’s modulus investigations have been shown.
Modulus G has been performed in accordance with RILEM recommendations. Modulus
E has been determined by using special equipment for direct deflection measurement.
It has been found that used methods are useful for the material’s constants
determination for plywood.