Zastosowania pochodnej

Badanie monotoniczności funkcji

Twierdzenie. Niech f będzie funkcją określoną i
różniczkowalną w przedziale E. Wówczas:

- jeżeli

0

)

(

'



x

f

dla każdego

E

x



, to funkcja f jest w

przedziale E rosnąca,

- jeżeli

0

)

(

'



x

f

dla każdego

E

x



, to funkcja f jest w

przedziale E malejąca.

Przykład 1. Zbadać monotoniczność funkcji

5

24

9

2

)

(

2

3









x

x

x

x

f

.

Rozwiązanie. Dziedzina:

R

x



.

Pochodna:

24

18

6

)

(

'

2







x

x

x

f

Rozwiążmy nierówność:

0

)

(

'



x

f

:

0

24

18

6

2







x

x

0

4

3

2







x

x

5

,

25

)

4

(

1

4

3

4

2

2























ac

b

,

4

2

5

3

2

1



















a

b

x

,

1

2

5

3

2

2

















a

b

x

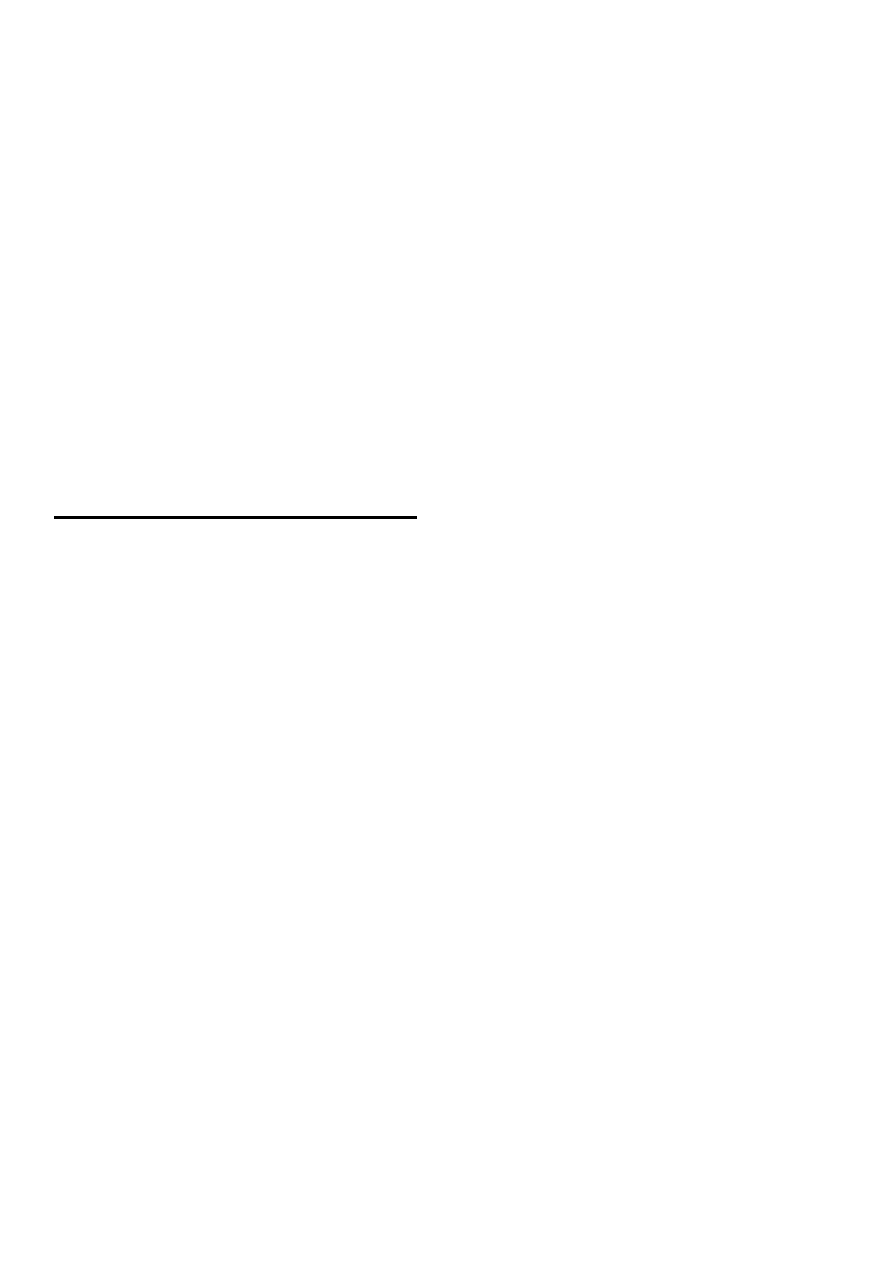
Wykresem pochodnej jest parabola z ramionami do góry,
zatem:

0

)

(

'



x

f

gdy

)

;

1

(

)

4

;

(











x

oraz

0

)

(

'



x

f

gdy

)

1

;

4

(





x

.

Odpowiedź. Funkcja jest rosnąca w przedziale

)

4

;

(





oraz w przedziale

)

;

1

(



. Funkcja jest malejąca w

przedziale

)

1

;

4

(



.

Pojęcie ekstremum funkcji

0

x

- punkt należący do dziedziny funkcji f .

Mówimy, że funkcja f ma w punkcie

0

x

maksimum, gdy

istnieje otoczenie U punktu

0

x

zawarte w dziedzinie

funkcji f i takie, że dla każdego

U

x



różnego od

0

x

jest:

)

(

)

(

0

x

f

x

f



Mówimy, że funkcja f ma w punkcie

0

x

minimum, gdy

istnieje otoczenie U punktu

0

x

zawarte w dziedzinie

funkcji f i takie, że dla każdego

U

x



różnego od

0

x

jest:

)

(

)

(

0

x

f

x

f



Mówimy, że w funkcja f ma w punkcie

0

x

ekstremum,

gdy ma w tym punkcie maksimum lub minimum.

Wyznaczanie ekstremów funkcji

Twierdzenie. Jeżeli funkcja f jest różniczkowalna w
pewnym otoczeniu punktu

0

x

i pochodna tej funkcji jest:

- równa zero w punkcie

0

x

- dodatnia w pewnym lewostronnym sąsiedztwie p-tu

0

x

- ujemna w pewnym prawostronnym sąsiedztwie p-tu

0

x

to funkcja f ma w punkcie

0

x

maksimum.

Twierdzenie. Jeżeli funkcja f jest różniczkowalna w
pewnym otoczeniu punktu

0

x

i pochodna tej funkcji jest:

- równa zero w punkcie

0

x

- ujemna w pewnym lewostronnym sąsiedztwie p-tu

0

x

- dodatnia w pewnym prawostronnym sąsiedztwie p-tu

0

x

to funkcja f ma w punkcie

0

x

minimum.

Przykład 2. Wyznaczyć ekstrema funkcji

2

1

4

)

(

x

x

x

f





Rozwiązanie. Dziedzina:

R

x



.

Pochodna:

















2

2

2

2

)

1

(

)'

1

(

4

)

1

(

)'

4

(

)

(

'

x

x

x

x

x

x

f

2

2

2

2

2

2

2

)

1

(

8

4

4

)

1

(

2

4

)

1

(

4

x

x

x

x

x

x

x





















2

2

2

)

1

(

4

4

x

x







Rozwiążmy równanie:

0

)

(

'



x

f

, czyli

0

4

4

2





x

1

2



x

1

1





x

,

1

2



x

Mianownik pochodnej jest dodatni, zaś wykresem licznika
pochodnej jest parabola z ramionami do dołu, zatem:

0

)

(

'



x

f

gdy

)

;

1

(

)

1

;

(











x

oraz

0

)

(

'



x

f

gdy

)

1

;

1

(





x

.

Wyniki obliczeń możemy zilustrować w tabeli:

x





…

1



…

1

…



)

(

' x

f

–

0

+

0

–

)

(x

f

mal.

min.

ros.

max.

mal.

Odpowiedź. W punkcie

1





x

funkcja ma minimum, zaś

w punkcie

1



x

funkcja ma maksimum.

Przykład 3. Wyznaczyć ekstrema funkcji

x

e

x

f

x



)

(

Rozwiązanie. Dziedzina:

0



x

.

Pochodna:

2

2

2

)

1

(

)'

(

)'

(

)

(

'

x

x

e

x

e

xe

x

x

e

x

e

x

f

x

x

x

x

x

















Rozwiążmy równanie:

0

)

(

'



x

f

. Ponieważ dla każdego

x

jest:

0



x

e

, zatem:

0

1





x

1



x

Stąd (z uwzględnieniem dziedziny):

0

)

(

'



x

f

gdy

)

1

;

0

(

)

0

;

(







x

oraz

0

)

(

'



x

f

gdy

)

;

1

(





x

.

Wyniki obliczeń możemy zilustrować w tabeli:

x





…

0

…

1

…



)

(

' x

f

–



–

0

+

)

(x

f

mal.



mal.

min.

ros.

Odpowiedź. W punkcie

1



x

funkcja ma minimum.

Reguła de l’Hospitala. Jeżeli:

1. Funkcje f i g są różniczkowalne w pewnym
sąsiedztwie punktu

0

x

2.

0

)

(

lim

)

(

lim









x

g

x

f

c

x

c

x

lub











)

(

lim

)

(

lim

x

g

x

f

c

x

c

x

3. Istnieje granica

)

(

'

)

(

'

lim

x

g

x

f

c

x



to

)

(

)

(

lim

x

g

x

f

c

x



=

)

(

'

)

(

'

lim

x

g

x

f

c

x



Uwaga: c może oznaczać liczbę lub



lub





Przykład 4.

4

11

2

1

3

lim

0

0

4

6

lim

2

2

2

3

2



























x

x

x

x

x

x

H

x

Przykład 5.

8

1

cos

3

5

sin

lim

0

0

sin

3

5

cos

lim

0

0



























x

x

e

x

x

x

e

x

x

H

x

x

Przykład 6.





























































2

2

lim

2

lim

1

lim

2

x

x

H

x

x

H

x

x

e

x

e

x

e