2011

1

RÓWNIANIA MAXWELLA
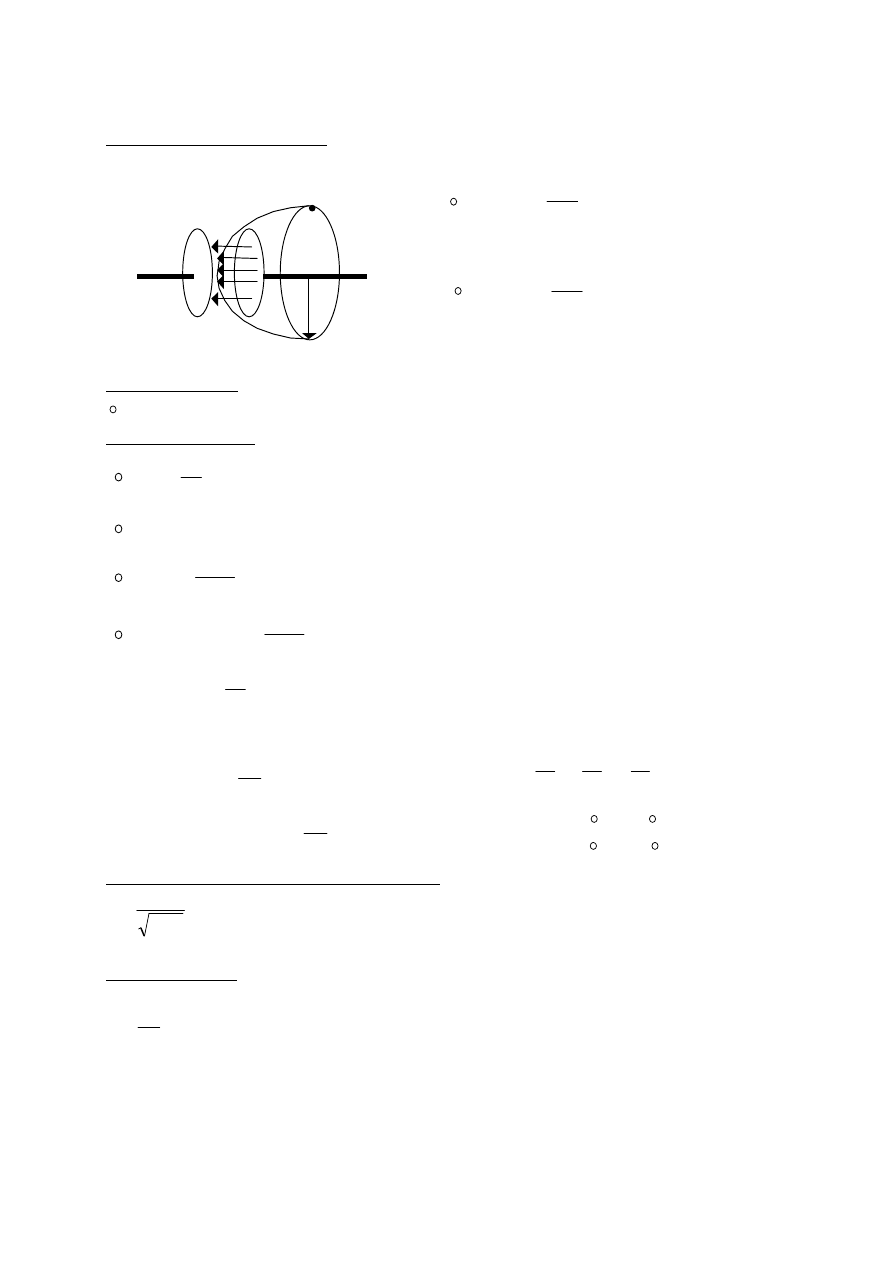
Indukowane pole magnetyczne - W kondensatorze (cylindrycznym) powstaje tam pole
magnetyczne wytworzone przez zmieniające się pole elektryczne.

S

S'

E

i

i

r

P

Prąd przesunięcia

∫

+

=

)

(

d

0

I

I

P

µ

l

B

r

r

Równania Maxwella

Fale elektromagnetyczne

–

prędkość w próżni

0

0

1

ε

µ

=

c

Wektor Poyntinga

B

E

S

r

r

r

×

=

0

1

µ

E i B - chwilowe wartości pola elektromagnetycznego w rozpatrywanym punkcie.

∫

=

t

E

d

d

d

0

0

φ

ε

µ

l

B

r

r

prawo Ampera po modyfikacji ma
postać

∫

+

=

I

t

E

0

0

0

d

d

d

µ

φ

ε

µ

l

B

r

r

Pole magnetyczne jest wytwarzane
przez przepływ prądu i/lub przez
zmieniające się pole elektryczne.

∫

∫

∫

∫

=

Φ

=

•

=

Φ

=

Φ

=

•

=

Φ

s

d

B

d

S

B

s

d

E

d

S

E

B

B

E

E

r

r

r

r

r

r

r

r

k

z

j

y

i

x

r

r

r

r

∂

∂

+

∂

∂

+

∂

∂

=

∇

)

(

0

0

0

0

0

P

E

B

I

I

t

I

l

d

B

t

l

d

E

s

d

B

q

s

d

E

+

=













∂

Φ

∂

+

=

∂

Φ

∂

−

=

=

=

∫

∫

∫

∫

µ

ε

µ

ε

r

r

r

r

r

r

r

r















∂

∂

+

=

×

∇

=

∂

∂

−

=

×

∇

=

=

•

∇

=

=

•

∇

=

t

E

J

B

B

rot

t

B

E

E

rot

B

B

div

E

E

div

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

0

0

0

0

ε

µ

ε

ρ

E – natężęnie pola elektrycznego
B – indukcja magnetyczna

ρ

- gęstość ładunku

ε

0

– przenikalność dielektryczna

µ

0

– przenikalność magnetyczna

J – gęstość prądu
I – natężenie prądu
I

p

– prąd przesunięcia

ds – element powierzchni
dl – element przewodnika

Φ

B

– strumień pola magnetycznego

Φ

E

– strumień pola elektrycznego

∇

∇

∇

∇

- operator Nabla

2011

2

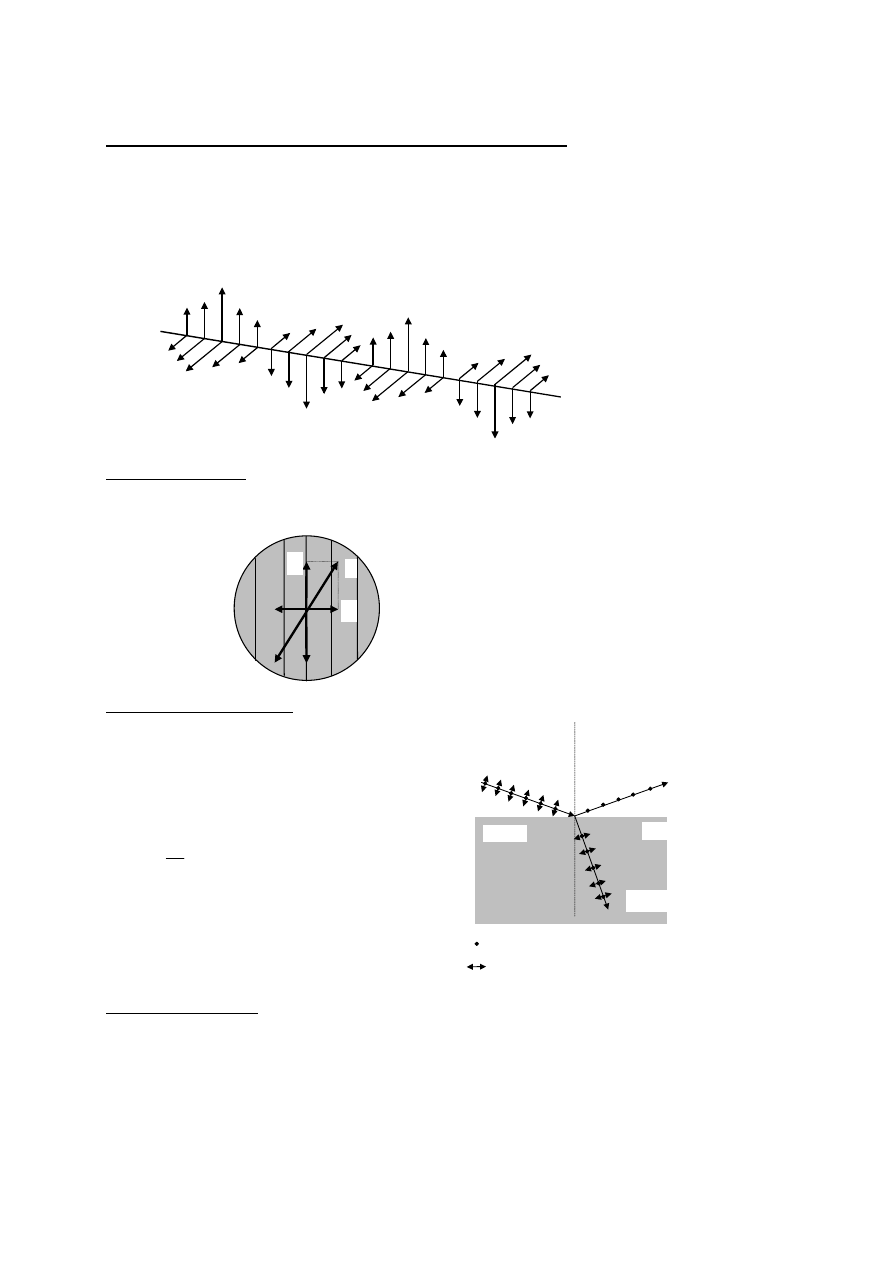
Polaryzacja - Fala elektromagnetyczna jest falą poprzeczną.
W fali poprzecznej, spolaryzowanej liniowo, należy określić dwa kierunki:

•

kierunek drgania (np. wektora

E),

•

kierunek rozchodzenia się fali.

(Zauważmy, że w fali podłużnej te dwa kierunki się pokrywają.)

Płytki polaryzujące
Płytka przepuszcza tylko te fale, dla których kierunki drgań wektora elektrycznego są
równoległe do kierunku polaryzacji, a pochłania te fale, w których są one prostopadłe.

E

y

E

E

x

θ

Polaryzacja przez odbicie

α

α

β

padające światło
niespolaryzowane

fala odbita

fala załamana

składowa

π

składowa

σ

powietrze

szkło

n = 1.5

Załamanie podwójne

•

promień

o przechodzi przez kryształ z jednakową prędkością we wszystkich kierunkach

tzn. ma jeden współczynnik załamania

n

0

tak jak izotropowe ciało stałe.

•

promień

e ma prędkość w krysztale zależna od kierunku tzn. prędkość zmienia się od

v

0

do

v

e

a współczynnik załamania od

n

o

do

n

e

. Dla kalcytu

n

e

= 1.658,

n

o

= 1.486.

E

y

= Ecos

θ

E

x

= Esin

θ

B

E

α

+

β

= 90°

β

α

sin

sin

2

1

n

n

=

α

α

α

cos

)

90

sin(

sin

2

2

1

n

n

n

=

−

=

o

n

n

n

tg

=

=

1

2

α

prawo Brewstera

2011

3

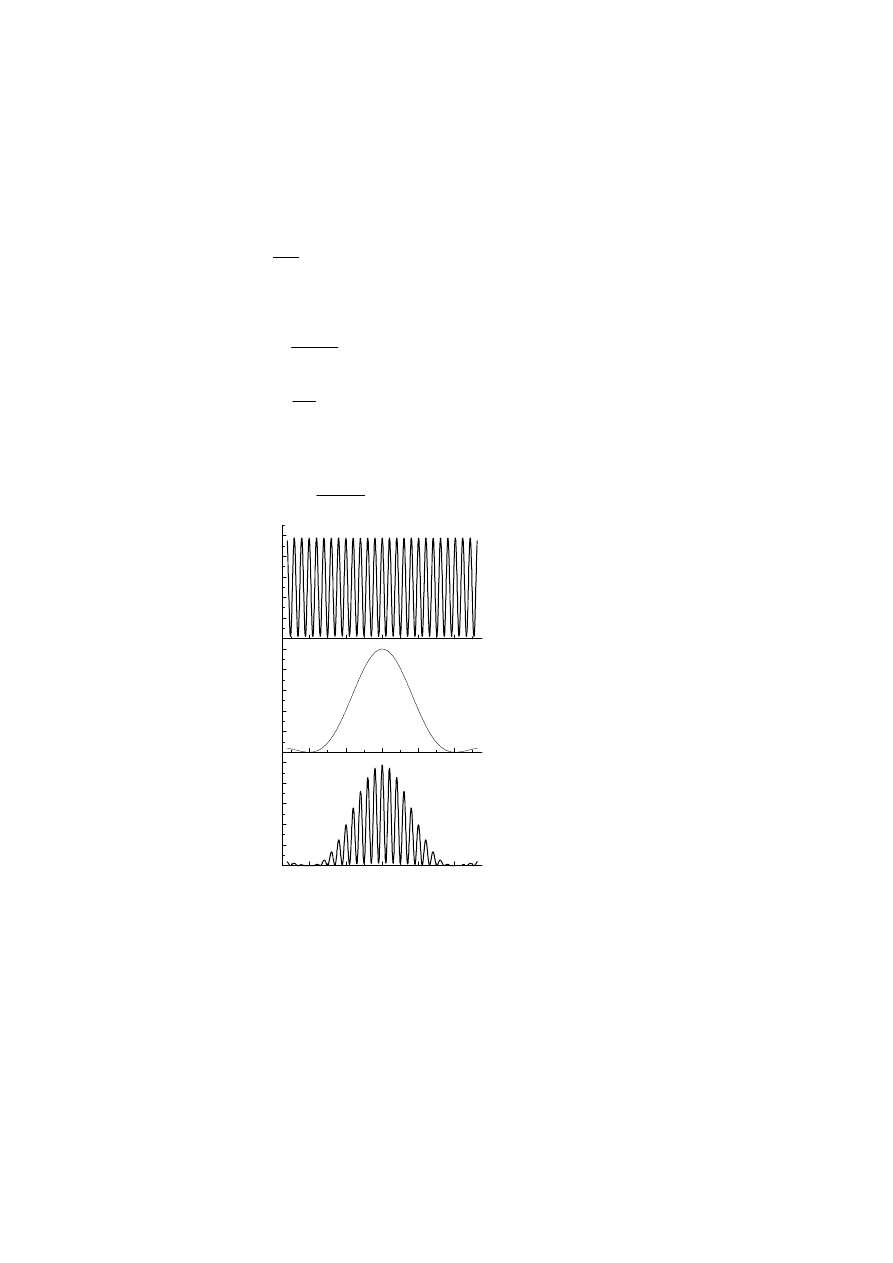
Dyfrakcja i interferencja

1.

Obraz interferencyjny dla dwóch szczelin

gdzie

d - odległość między szczelinami.

2.

Natężenie fali ugiętej na szczelinie

gdzie

a - szerokość szczeliny.

3. Sumaryczny efekt

Siatka dyfrakcyjna
Maksima główne - warunek

dsin

θθθθ

= m

λλλλ

,

m = 0, 1, 2, (maksima)

gdzie m - rząd widma, a d - odległość między szczelinami (

stała siatki dyfrakcyjnej

).

0.0

0.2

0.4

0.6

0.8

1.0

w

z

g

l

ę

d

n

e

n

a

t

ę

ż

e

n

ie

0.0

0.2

0.4

0.6

0.8

1.0

w

z

g

l

ę

d

n

e

n

a

t

ę

ż

e

n

ie

0.0

0.2

0.4

0.6

0.8

1.0

10

10

5

5

θ

(deg)

a = 5

λ

w

z

g

l

ę

d

n

e

n

a

t

ę

ż

e

n

ie

β

θ

2

int

,

int

,

cos

m

I

I

=

θ

λ

π

β

sin

d

=

2

,

,

sin













=

α

α

θ

dyf

m

dyf

I

I

θ

λ

π

α

sin

a

=

2

2

sin

)

(cos













=

α

α

β

θ

m

I

I

2011

4

TERMODYNAMIKA

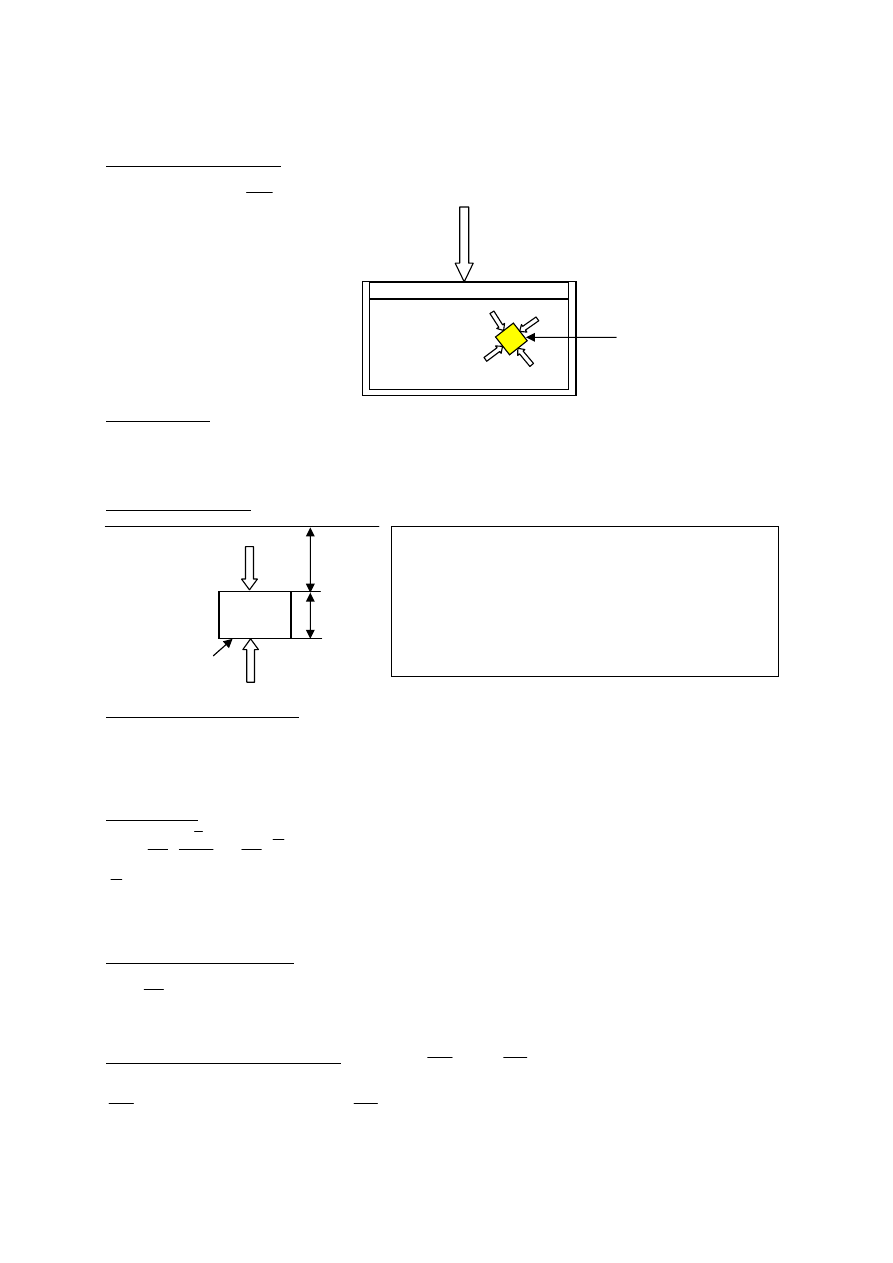
Ciśnienie i hydrostatyka

Ciśnienie

A

F

P

∆

∆

=

∆

F – siła działająca na powierzchnię o polu ∆A

Prawo Pascala

gh

P

P

ρ

+

=

0

P

0

– ciśnienie zewnętrzne przyłożone do górnej powierzchni,

ρ

– gęstość, h – odległość od

górnej powierzchni.

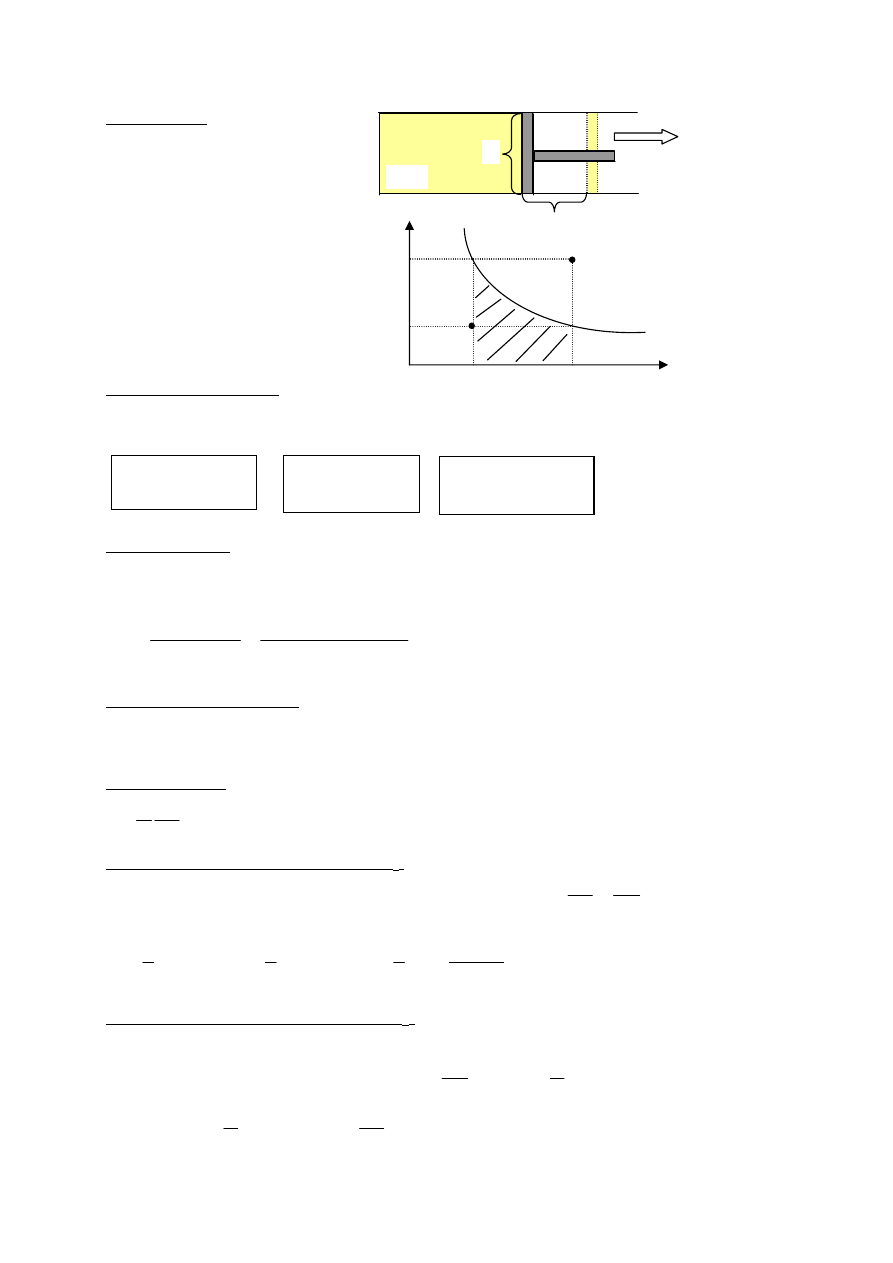
Prawo Archimedesa









Prawo gazów doskonałych
PV = NkT

lub PV=nRT

dla n – moli gazu

P – ciśnienie gazu, N – liczba cząstek gazu w objętości V
T – temperatura bezwzględna, k – stała fizyczna.

Temperatura

k

E

k

v

m

k

T













=













=

3

2

2

3

2

2

k

E - jest średnią energia kinetyczna przypadającą na jedna cząsteczkę,

2/3k – jest współczynnikiem proporcjonalności, k – stała Boltzmana k=1,38 x 10

-23

J/K.

Równanie van der Wasala

RT

b

v

v

a

p

=

−

+

)

)(

(

2

a, b – wyznacza się doświadczalnie.

Prawo przewodnictwa cieplnego

dx

dT

kA

dt

dQ

−

=

dt

dQ

- szybkość przepływu ciepła,

dx

dT

- gradient temperatury,

k – współczynnik proporcjonalności zwany przewodnictwem cieplnym

F

w górę

F

w dół

Pole A

h

l

Tłok

∆

F

∆

F

∆

F

∆

F

F

0

∆

A - powierzchnia

ściany sześcianu

F

w

= F

w górę

- F

w dół

= (

ρ

gl)A = m

c

g

m

c

=

ρ

lA jest masą cieczy wypartej przez blok,

F

w

– siła wyporu.

F

w

= m

c

g

2011

5

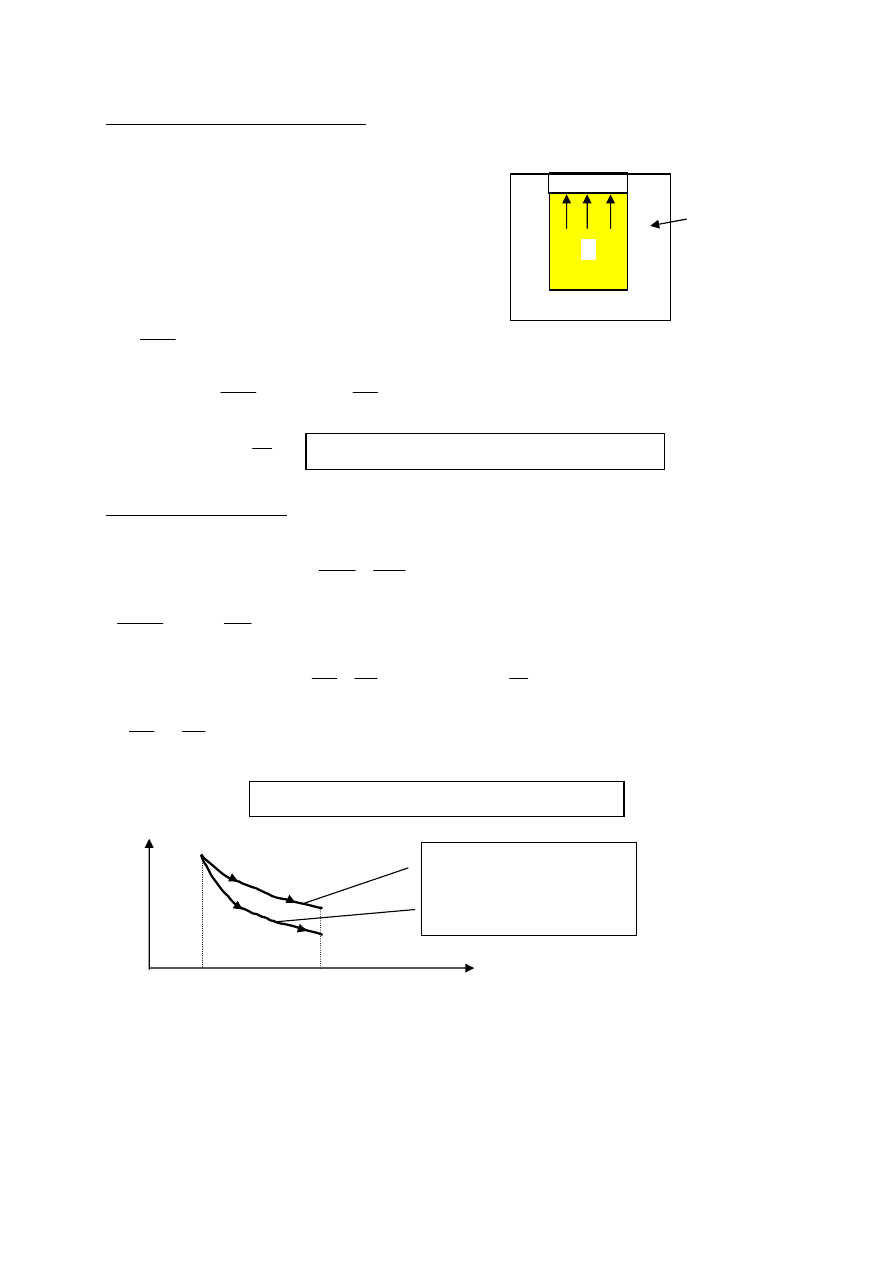
Ciepło i praca
Praca wykonana przez gaz

∫

=

=

=

=

1

0

V

V

pdV

W

pdV

pAds

Fds

dW

W – pole powierzchni pod krzywą.






I zasada termodynamiki

dW

dU

dQ

W

Q

U

U

p

k

+

=

−

=

−

=

+

Liczba Avogadra
m

H

= 1,673 x 10

-24

g atomu wodoru

N

0

- liczbą atomów w molu wodoru atomowego (M = 1,008 g)

mol

atomów

atom

g

mol

g

atom

g

m

mol

g

M

N

H

/

10

02

,

6

/

10

673

,

1

/

008

,

1

/

/

23

24

0

⋅

=

⋅

=

=

−

Prawo gazów doskonałych
PV = N

0

kT= RT

(dla 1 mola gazu doskonałego)

R = N

0

k = (6,02·10

23

)(1,38·10

-23

) = 8,31 J/(mol K) = 1,99 cal/(mol K)

Ciepło właściwe

dT

dQ

m

c

1

=

)

(

2

1

T

f

c

cdT

m

Q

T

T

=

=

∫

Ciepło właściwe przy stałej objętości (c

v

)

dV = 0 i

PdV

dQ

dU

−

=

stąd dQ = dU,

dT

dU

dT

dQ

c

v

=

=

dla 1 mola jednoatomowego gazu doskonałego (z zasady ekwipatrycji energii)

K

mol

cal

R

c

k

N

c

kT

N

U

v

v

⋅

=

=

⇒

=

=

3

2

3

2

3

2

3

0

0

Ciepło właściwe przy stałym ciśnieniu (c

p

)

i

dT

c

dU

v

=

PdV

dQ

dU

−

=

R

c

c

R

c

dT

dQ

c

dT

P

R

P

dT

c

dQ

dT

P

R

dV

i

P

RT

V

RT

PV

PdV

dT

c

dQ

v

p

v

p

v

v

=

−

⇒

+

=

=













+

=

=

=

⇒

=

+

=

ds

p, V

0

A

B

p

p

0

p

1

A

V

0

V

1

V

Ciepło pobrane
przez układ

Wzrost energii
wewnętrznej

Praca wykonana
przez układ

2011

6

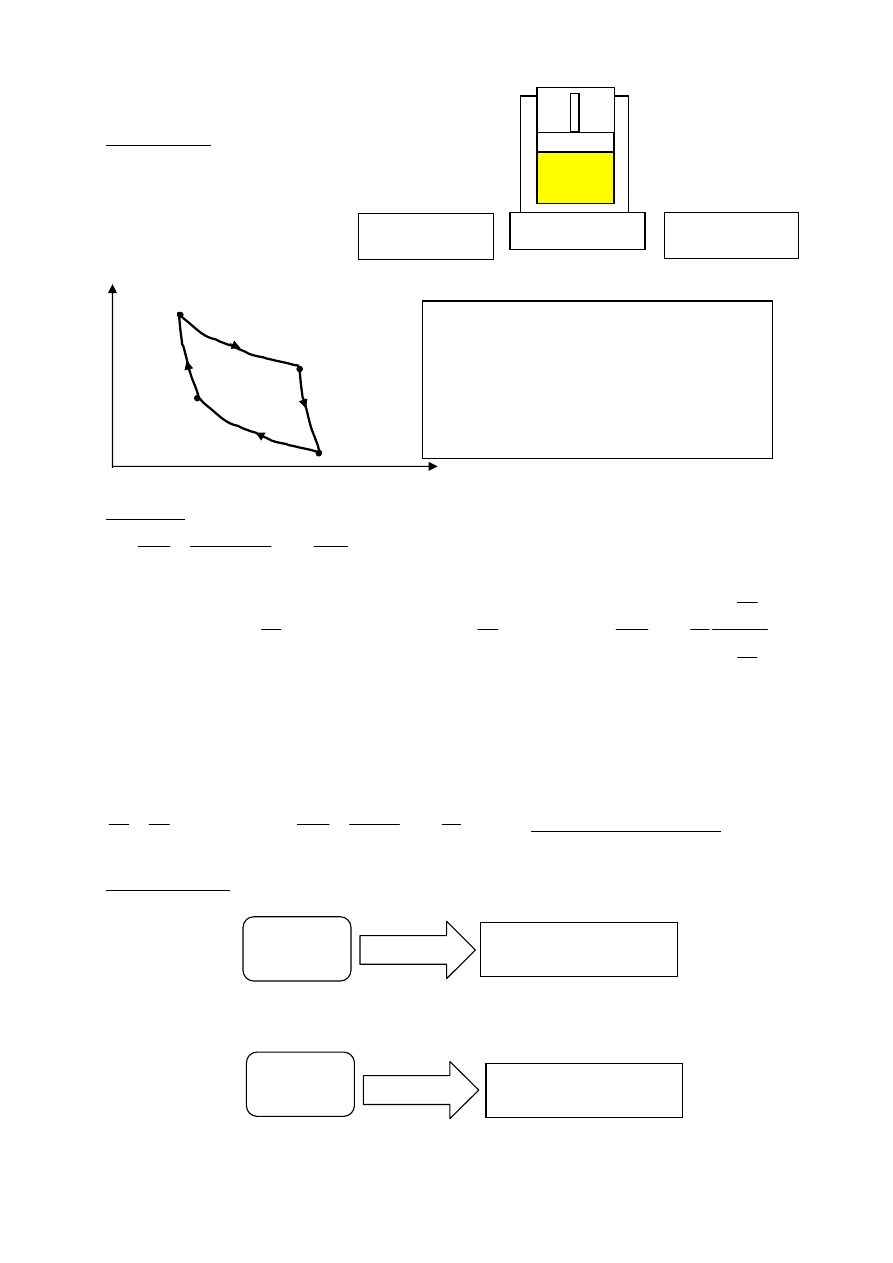
Rozprężanie izotermiczne T = const

∫

=

∆

=

∆

=

=

=

+

=

+

=

2

1

0

V

V

PdV

W

Q

dW

PdV

dQ

wtedy

dU

i

PdV

dU

dW

dU

dQ

podstawiamy

1

2

ln

2

1

2

1

V

V

NkT

W

Q

V

dV

NkT

dV

V

NkT

W

Q

V

NkT

P

V

V

V

V

=

∆

=

∆

=













=

∆

=

∆

=

∫

∫

Rozprężanie adiabtyczne

0

0

0

=

+

=

+

=

+

=

PdV

dT

c

PdV

dU

dQ

i

dW

dU

dQ

v

K

PV

K

PV

K

P

V

P

dP

V

dV

c

c

gdzie

P

dP

V

dV

VdP

c

PdV

c

R

c

c

ale

dP

R

V

c

PdV

R

R

c

PdV

R

VdP

R

PdV

c

VdP

PdV

RdT

v

p

v

p

v

p

v

v

v

=

=

=

+

=

+

=

=

+

=

+

+

=

=

+













+

=

+













+

+

=

∫

∫

γ

γ

γ

γ

γ

γ

ln

)

ln(

ln

ln

ln

0

0

0

0

0

γ

γ

2

2

1

1

V

P

V

P

=

Tłok

V

T

T

T

Termostat

Rozprężanie
izotermiczne

Izotermiczne rozprężanie gazu doskonałego

Adiabatyczne rozprężanie gazu doskonałego

p

0

V

1

V

V

2

)

(

)

(

adiabata

const

PV

izoterma

const

PV

=

=

γ

lnK - stała całkowania

2011

7

Silnik Carnota


(

∆

Q

1

–

∆

Q

2

) =

∆

W

Sprawność

1

2

1

2

1

1

1

Q

Q

Q

Q

Q

Q

W

∆

∆

−

=

∆

∆

−

∆

=

∆

∆

=

η

a

b

V

V

NkT

W

Q

ln

1

1

=

∆

=

∆

d

c

V

V

NkT

W

Q

ln

2

2

=

∆

=

∆

























−

=

∆

∆

=

a

b

d

c

V

V

V

V

T

T

Q

W

ln

ln

1

1

2

1

η

b

b

a

a

V

P

V

P

=

- rozprężanie izotermiczne

γ

γ

c

c

b

b

V

P

V

P

=

- rozprężanie adiabatyczne

c

c

c

c

V

P

V

P

=

- sprężanie izotermiczne

γ

γ

d

d

d

d

V

P

V

P

=

- sprężanie adiabatyczne

d

c

a

b

V

V

V

V

=

1

2

1

2

1

1

1

T

T

T

T

T

Q

W

−

=

−

=

∆

∆

=

η

sprawność silnika Carnota

Perpetum mobile
I rodzaju




II rodzaju

Izolator

Zbiornik ciepła T

1

(źródło ciepła)

Zbiornik ciepła T

2

(chłodnicą)

T

1

> T

2

p

0

T

1

=const

V

T

2

=const

a

b

c

d

ab - rozprężanie izotermiczne,

∆

Q

1

ze źródła

ciepła (unoszenie tłoka, silnik na źródle)
bc - rozprężanie adiabatyczne (unoszenie
tłoka, silnik na izolatorze)
cd - sprężanie izotermiczne,

∆

Q

2

z chłodnicy

da - sprężanie adiabatyczne

T

2

< T

1

Układ
zamknięty

∆

W

Ciągły wypływ energii
z naczynia

T

2

T

1

Obniżanie

∆

W

Ciągły wypływ energii
mechanicznej

T

2

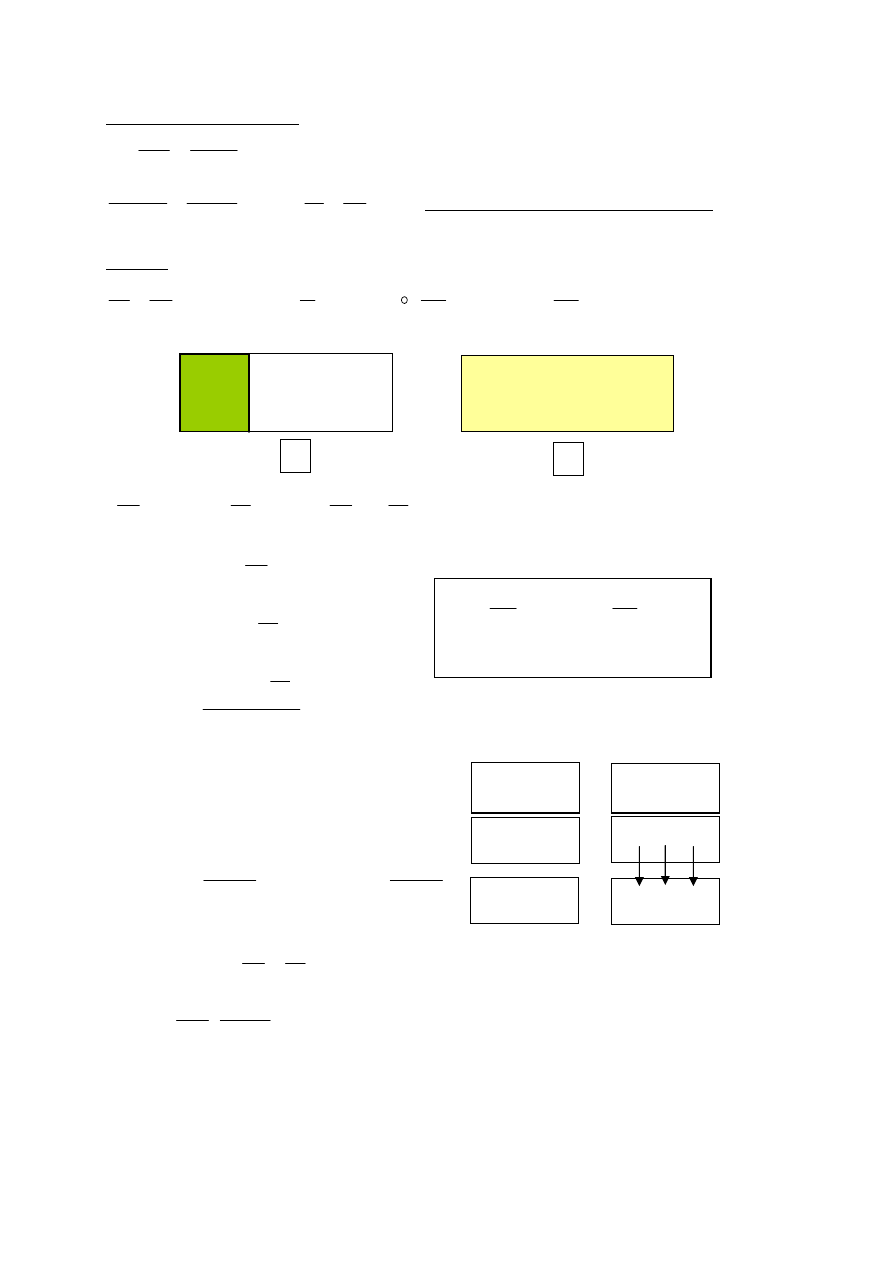
2011

8

Sprawność silnika Carnota

1

2

1

1

T

T

T

Q

W

−

=

∆

=

η

i

∆

W = Q

1

–Q

2

2

1

2

1

1

2

1

1

2

1

Q

Q

T

T

czyli

T

T

T

Q

Q

Q

=

−

=

−

tzw. termodynamiczna skala temperatur

Entropia

2

2

1

1

T

Q

T

Q

=

0

lub

0

=

=

∫

∑

T

dQ

T

Q

2

1

2

1

S

S

T

dQ

−

=

∫

S = k · lnp

∆

S = S

1

-S

2

= k

⋅

lnp

2

- k

⋅

lnp

1

k – stała Boltzmana.

1

2

1

2

V

V

p

p

cząząst

jedna

=













N

V

V

p

p













=













1

2

1

2

T

V

V

NkT

S

V

V

Nk

S

p

p

k

S













⋅

=

∆













⋅

=

∆













⋅

=

∆

1

2

1

2

1

2

ln

ln

ln

T

1

-dT

1

oraz T

2

-dT

2

,

dQ

1

= -mcdT

1

i dQ

2

= +mcdT

2

,

c - ciepło właściwe na jednostkę masy,
dQ

1

= -dQ

2

,

dT

1

= -dT

2

= dT













−

=

=

−

=

1

2

2

2

1

1

1

1

T

T

mcdT

dS

entropii

zmiana

wypadkowa

czyli

T

mcdT

dS

oraz

T

mcdT

dS













−

=

2

1

2

1

T

T

dS

mc

T

T

dT

V

2

-V

1

V

2

rozprężony gaz

V

1

1

2

T

1

T

2

T

2

+dT

T

1

-dT

Warunki
początkowe

Chwilę
później

T

dQ

dS

T

Q

S

=

∆

=

∆

lub

dQ - ciepło dostarczane do układu
podczas procesu odwracalnego

2011

9

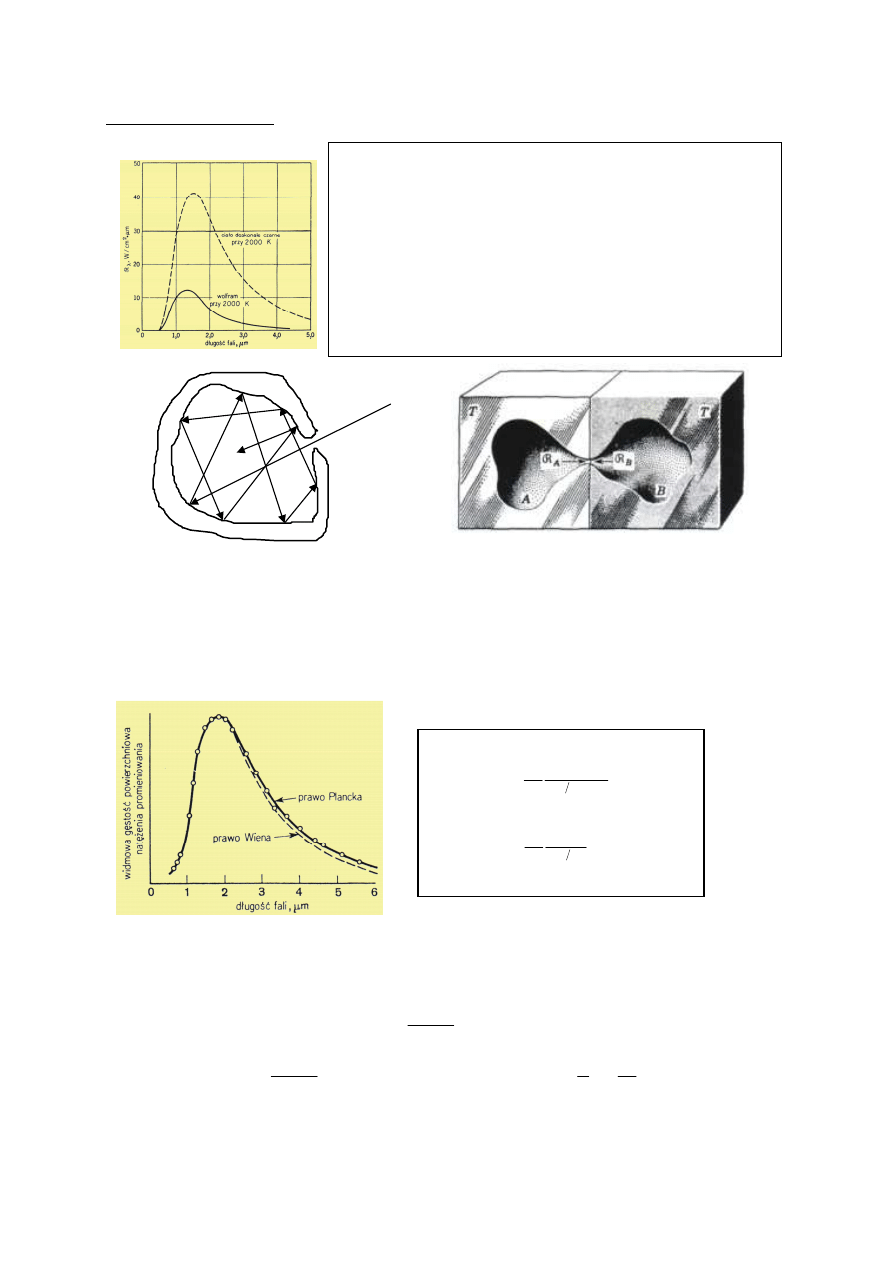
Ciało doskonale czarne

1. Promieniowanie wychodzące z wnętrza bloków - prawo Stefana

4

T

R

C

σ

=

σ

- stała Stefana-Boltzmana

2. Emisja energetyczna promieniowania zewnętrznej powierzchni ciała - ciało szare -

4

T

e

R

C

σ

=

e - zdolność emisyjna, wielkość zależy od substancji i od temperatury.

Zjawisko fotoelektryczne

e

W

e

h

V

eV

W

h

eV

m

m

W

h

E

h

W

E

W

h

h

h

h

K

K

−

=

⇒

+

=

⇒

=

=

−

=

=

+

=

ν

ν

υ

υ

ν

ν

ν

2

2

2

max

2

max

max

0

max

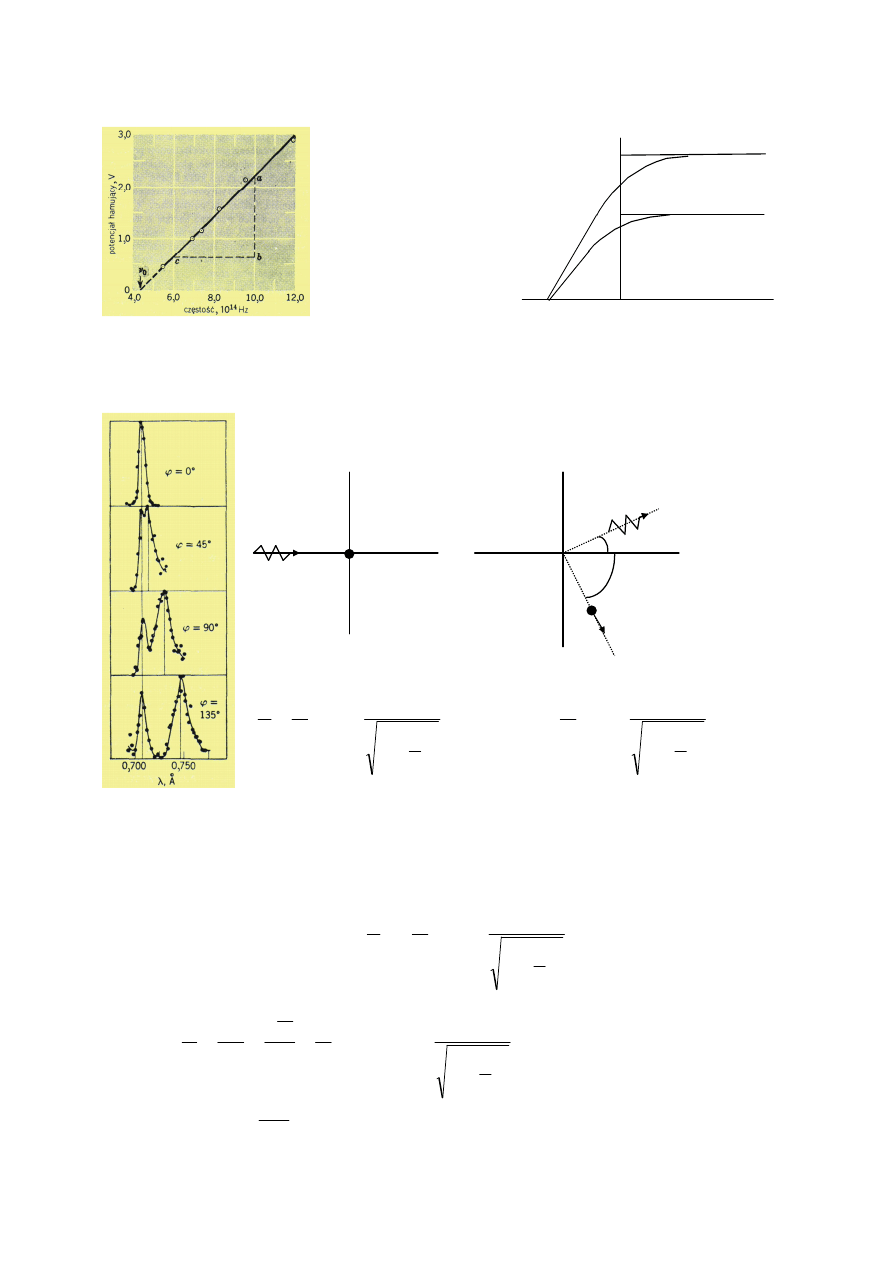
Prawo Plancka

1

1

2

5

1

−

=

T

c

e

c

R

λ

λ

λ

Prawo Wiena

T

c

e

c

R

λ

λ

λ

2

1

5

1

=

∫

∞

=

0

λ

λ

d

R

R

R

λ

- widmowa zdolność emisyjna promieniowania

R

λ

d

λ

- szybkość, z jaką jednostkowy obszar powierzchni

wypromieniowuje energię odpowiadającą długościom fal
zawartym w przedziale

λ

,

λ

+d

λ

.

R - całkowitą emisja energetyczna promieniowania
(powierzchnię pod wykresem).

2011

10

I

a

I

b

+

-

V

h

V

Efekt Comptona

Przesunięcie Comptona zależy tylko od kąta rozproszenia (gdzie m

0

jest masą spoczynkową

elektronu).

foton

foton

λ

'

λ

elektron

elektron

v=0

v

ϕ

θ

θ

υ

υ

ϕ

λ

θ

υ

υ

ϕ

λ

λ

sin

1

sin

'

0

cos

1

cos

'

2

0

2

0













−

−

=













−

+

=

c

m

h

c

m

h

h

(

)

2

0

2

2

0

2

0

1

'

'

'

1

1

1

'

'













−

=

=

=

=

=





























−













−

+

=

−

+

=

c

m

p

h

c

c

h

c

h

c

E

p

c

c

m

c

h

c

h

c

m

m

h

h

υ

υ

λ

λ

ν

υ

λ

λ

ν

ν

(

)

(

)

ϕ

λ

λ

λ

cos

1

'

0

−

=

−

=

∆

c

m

h