www.etrapez.pl 

Strona 1 

 

 
 

 

 
 

KURS 

FUNKCJE WIELU ZMIENNYCH 

 

Lekcja 5 

Dziedzina funkcji 

 
 

ZADANIE DOMOWE 

 

 

 

 

 

www.etrapez.pl 

Strona 2 

 

Częśd 1: TEST 

Zaznacz poprawną odpowiedź (tylko jedna jest prawdziwa). 

Pytanie 1 

Co to jest dziedzina funkcji? 

a)  Zbiór wartości, które osiąga funkcja 
b)  Zbiór argumentów, dla których funkcja nie osiąga żadnej wartości 
c)  Zbiór wartości, które nie zostają osiągnięte dla żadnego argumentu 
d)  Zbiór argumentów, dla których funkcja osiąga jakąś wartośd 

Pytanie 2 

Jakie podstawowe założenia do dziedziny wymienione zostały podczas Lekcji? 

a)  Dzielenie, pierwiastek, logarytm, arcsinx i arccosx 
b)  Dzielenie, pierwiastek, logarytm, arcsinx, arccosx, arctgx, arcctgx 
c)  Dzielenie, pierwiastek, logarytm, arcsinx, arccosx, funkcja wykładnicza 
d)  Dzielenie, pierwiastek, logarytm, tgx, ctgx, arcsinx i arccosx 

Pytanie 3 





1

ln

sin

2

1

z

x

x

x











 

Jakie założenia do dziedziny należałoby wypisad przy powyższej funkcji? 

a) 

1 0

0

x

x



 





 

b) 

1

0

0

x

x



 





 

 

c) 

1

0

1 0

0

x

x

x



 



 





 

 

d) 

1

0

1 0

1

2 1

x

x

x



 



 

    

 

 

www.etrapez.pl 

Strona 3 

 

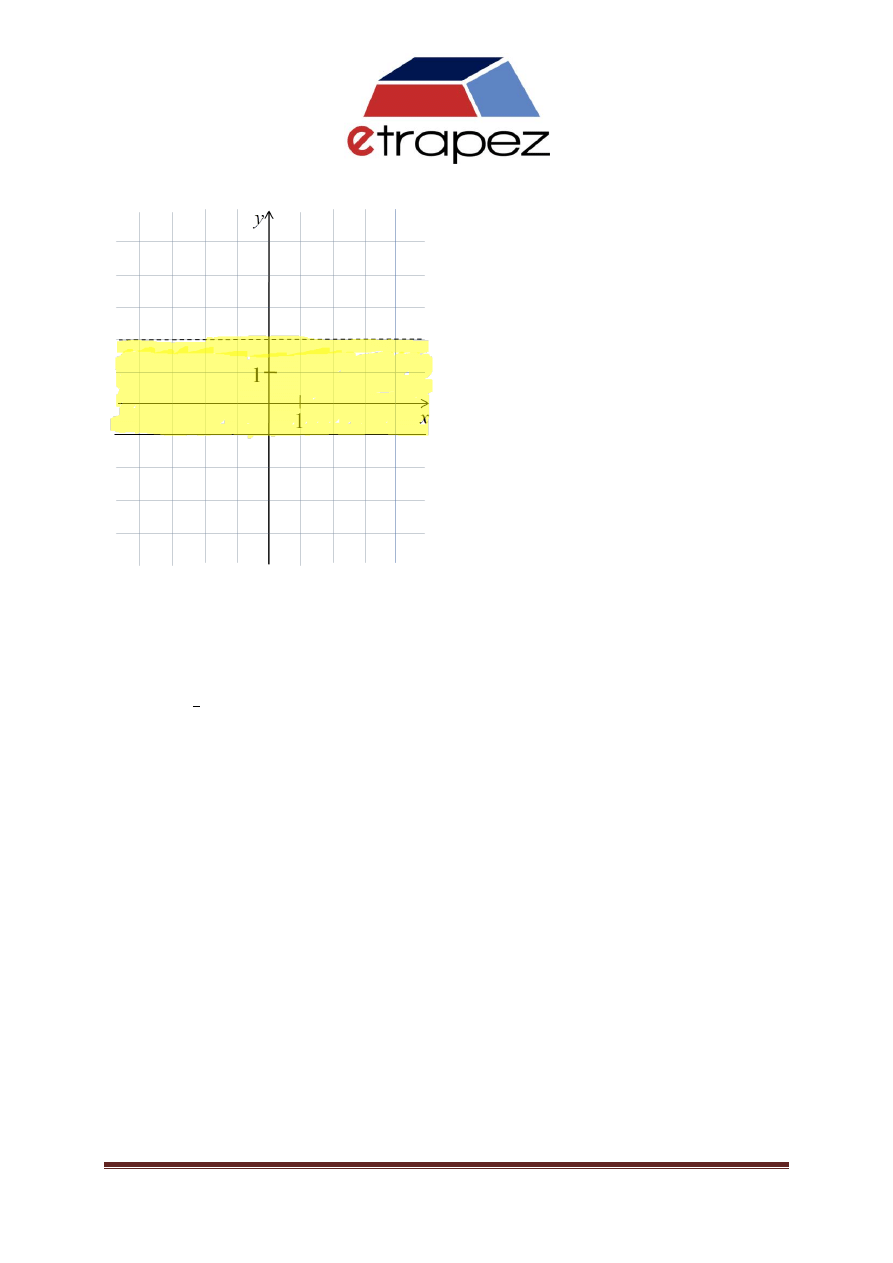
Pytanie 4 

 

Jakie punkt nie należy do dziedziny, której  obszar na płaszczyźnie wygląda jak wyżej? 

a) 

 

0, 2

 

b) 





10000, 1



 

c) 





3
4

0,1

 

d) 





567, 0



 

Pytanie 5 

1

y

x

  

 

Jak zaznaczyd powyższy obszar na płaszczyźnie?

 

a)  Narysowad linię ciągłą prostą 

1

y

x

  

 i zaznaczyd obszar leżący pod nią 

b)  Narysowad linię przerywaną prostą 

1

y

x

  

 i zaznaczyd obszar leżący pod nią 

c)  Narysowad linię ciągłą prostą 

1

y

x

  

 i zaznaczyd obszar leżący nad nią 

d)  Narysowad linię przerywaną prostą 

1

y

x

  

 i zaznaczyd obszar leżący nad nią 

 

 

 

www.etrapez.pl 

Strona 4 

 

Pytanie 6 







1

3

0

x

y



 

 

Na jakie nierówności trzeba rozłożyd powyższą? 

a) 



 



1 0

3

0

1 0

3

0

x

y

x

y

          

 

b) 



 



1 0

3

0

1 0

3

0

x

y

x

y

          

 

c) 



 



1 0

3

0

1 0

3

0

x

y

x

y

          

 

d) 



 



1 0

3

0

1 0

3

0

x

y

x

y

          

 

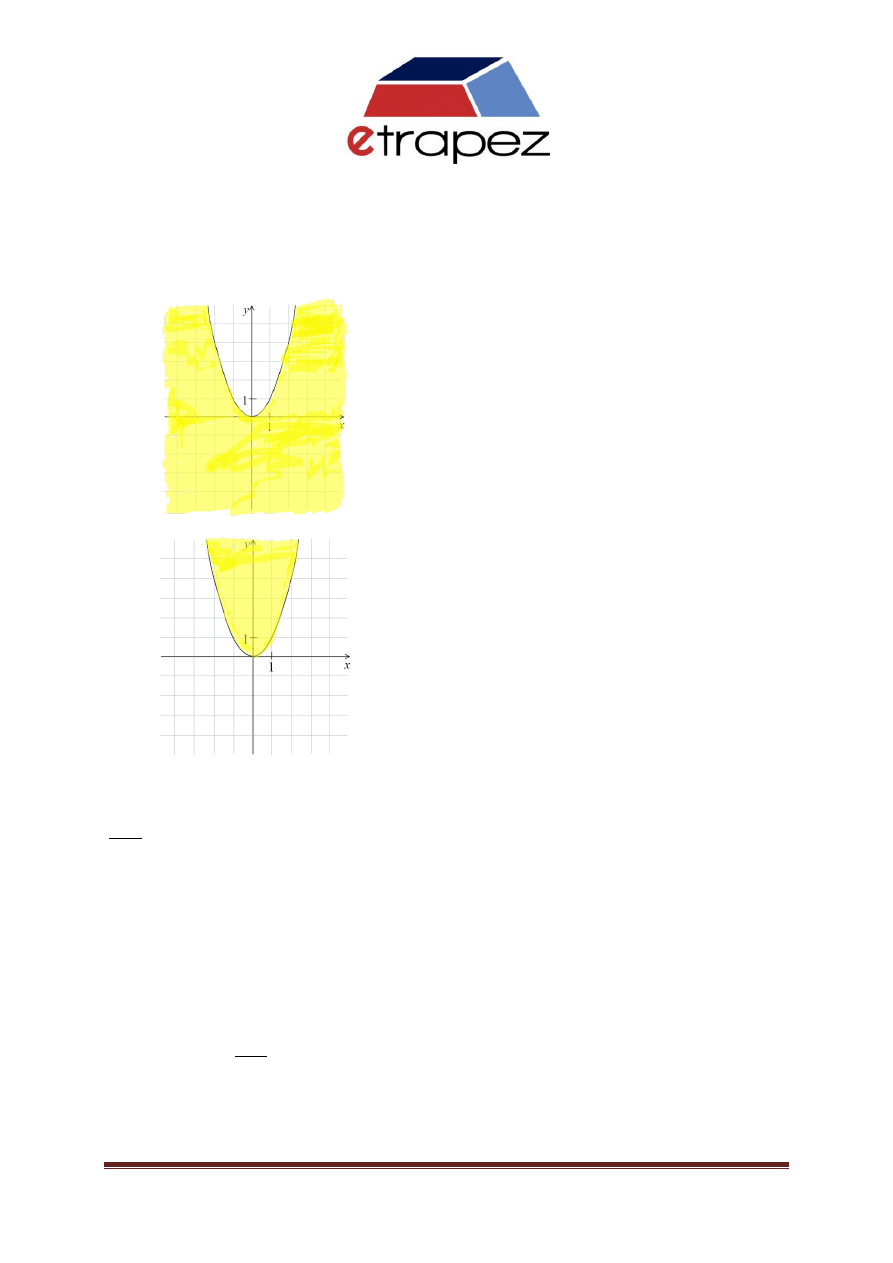
Pytanie 7 



 



2

2

1

1

4

x

y









 

Jak narysowad na płaszczyźnie powyższy obszar?

 

a)  Narysowad wnętrze okręgu o środku w punkcie 

 

1,1

 i promieniu 2 

b)  Narysowad wszystkie punkty na zewnątrz okręgu o środku w punkcie 

 

1,1

 i 

promieniu 2 

c)  Narysowad wnętrze okręgu o środku w punkcie 





1, 1

 

 i promieniu 2 

d)  Narysowad wszystkie punkty na zewnątrz okręgu o środku w punkcie 





1, 1

 

 i 

promieniu 2 

 

 

 

www.etrapez.pl 

Strona 5 

 

Pytanie 8 

2

y

x



 

Jak zaznaczyd powyższy obszar na płaszczyźnie? 

a) 

 

b) 

 

Pytanie 9 

1

1

y

x

 



 

Jak rozwiązad powyższą nierównośd? 

a)  Zamienid ją na nierównośd: 





1

1

y x

  

  

b)  Pomnożyd obie strony nierówności przez 

1

x



  

c)  Pomnożyd obie strony nierówności przez  1



 

d)  Przenieśd  1



 na lewą stronę nierówności, sprowadzid do wspólnego mianownika i 

dodad do 

1

y

x



 , a potem zamienid dzielenie na mnożenie 

 

 

 

www.etrapez.pl 

Strona 6 

 

Pytanie 10 

1

1

x

y

   

 

Jak rozwiązad powyższą nierównośd? 

a)  Rozwiązując osobno nierówności  1 x y

  

 i 

1

x

y

 

 , a potem biorąc ich częśd 

wspólną 

b)  Rozwiązując osobno nierówności  1 x y

  

 i 

1

x

y

 

 , a potem biorąc ich sumę 

c)  Rozwiązując osobno nierówności  1 x

 

 i 

1

y



 , a potem biorąc ich częśd wspólną 

d)  Rozwiązując osobno nierówności  1 x

 

 i 

1

y



 , a potem biorąc ich sumę 

 

 

 

www.etrapez.pl 

Strona 7 

 

Częśd 2: ZADANIA 

Wyznacz i narysuj w układzie współrzędnych dziedziny funkcji: 

1) 





ln 2

8

1

z

x

y



 



 

2) 





2

ln

1

z

y

x



 

 

3) 





2

2

2

2

3

log

25

16

z

x

y

x

y













 

4) 

1

2

2

1

z

y

x

y











 

5) 

u

xy

xy





 

6) 

arccos

y

z

x



 

KONIEC