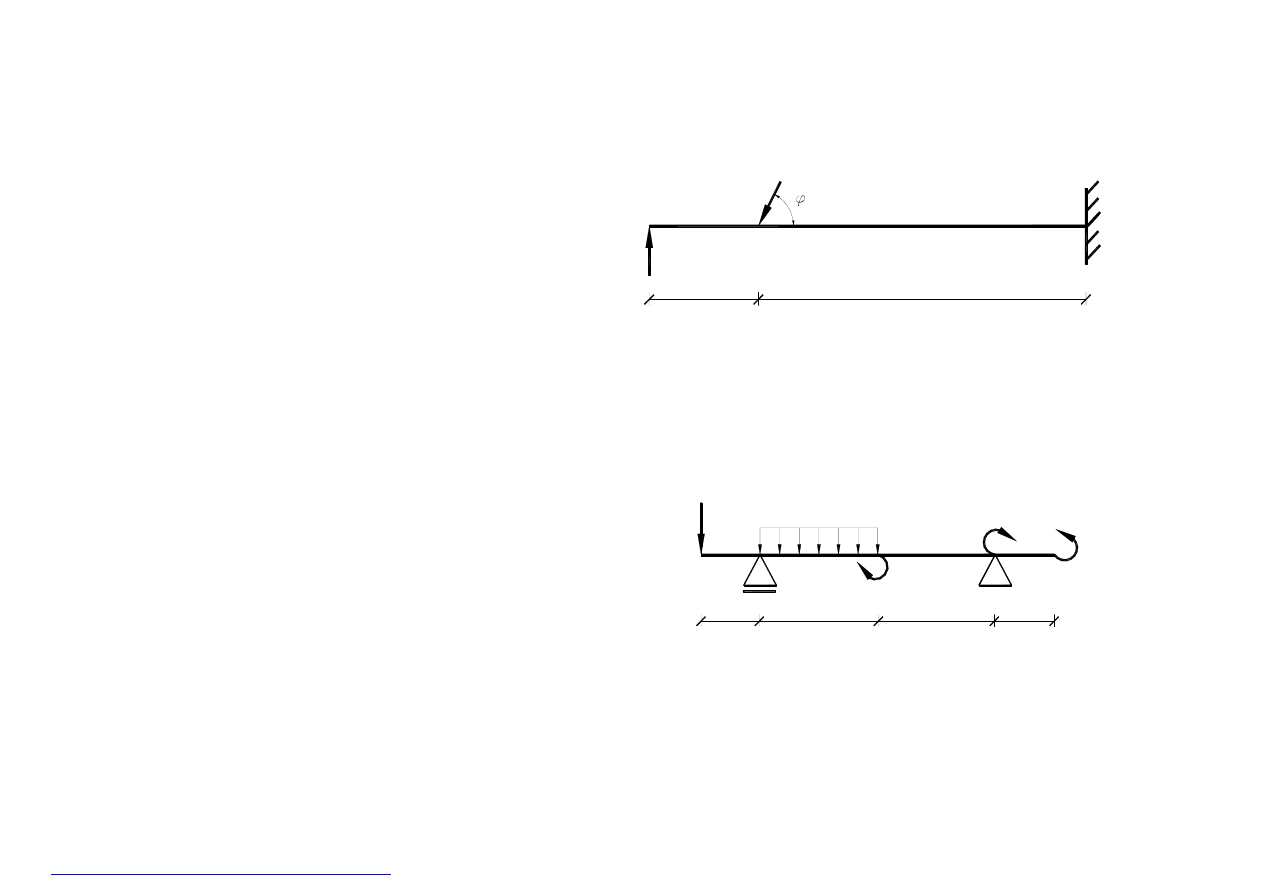
Zadanie 3. Belki statycznie wyznaczalne.

Dla belek statycznie wyznaczalnych przedstawionych

na rysunkach

−

rys.A

,

rys.B

, wyznaczyć:

1. składowe reakcji podpór,

2. zapisać funkcje sił przekrojowych,

3. sporządzić wykresy :

• momentów zginających M(x),

• sił poprzecznych Q(x),

• sił podłużnych N(x).

1.5m

15KN

0.5m

18KN

rys.A. Belka wspornikowa

4KN

8KNm

3KNm

4KN/m

3KNm

1.0 m

2.0 m

2.0 m

1.0 m

rys.B. Belka wolnopodparta

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

1/10

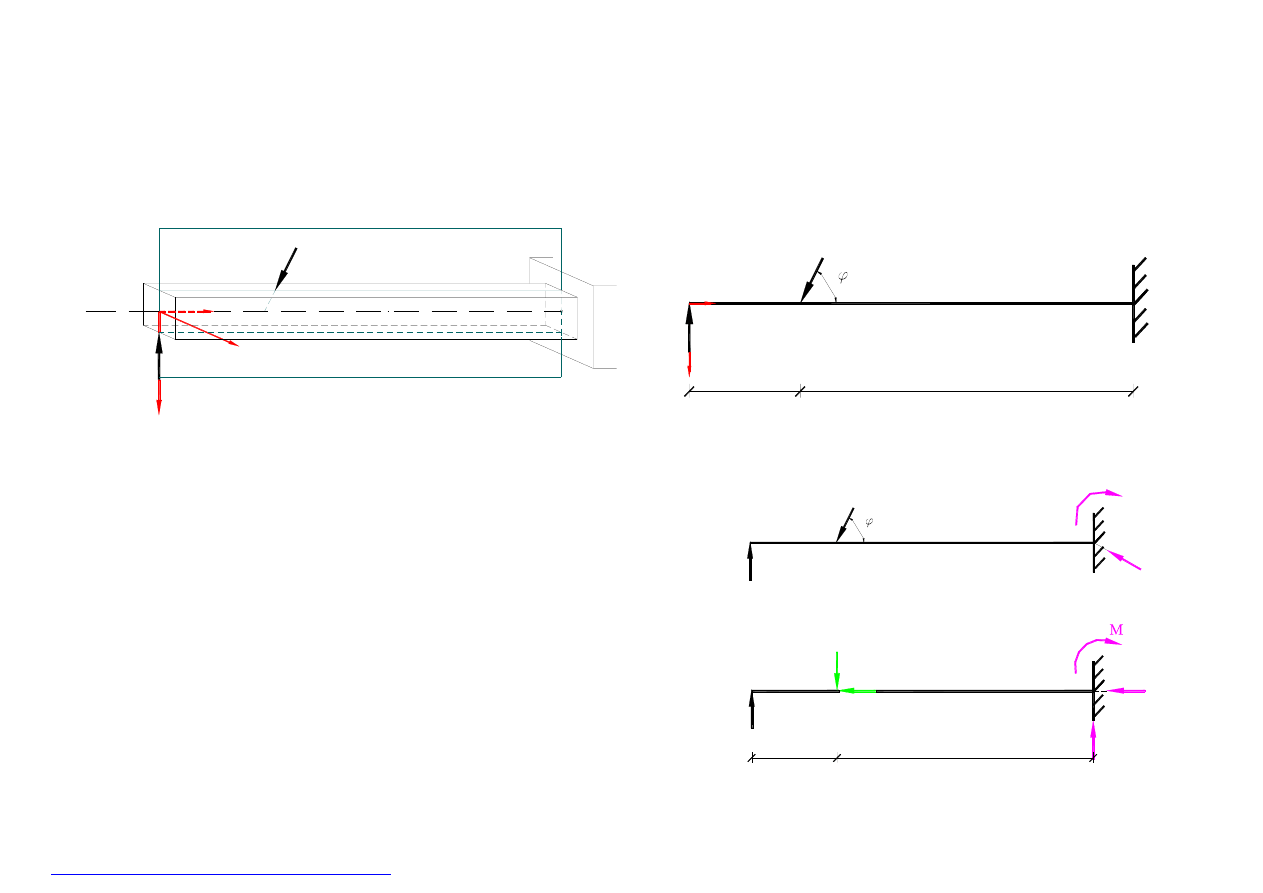
A. Belka wspornikowa

Na

rys.1

przedstawiona jest belka w aksonometrii o przekroju prostokątnym, utwierdzona jednym końcem w ścianie, obciążona w płaszczyźnie xz.

Na

rys.2

przedstawiony jest schemst statyczny belki z oznaczonymi punktami charakterystycznymi belki – punkt podporowy A oraz punkty przyłożenia

obciążenia: B, C. Do dalszych obliczeń przyjęty jest prawoskrętny układ osi współrzędnych x, y, z.

X

Z

Y

płaszczyzna obciążenia

15KN

18KN

oś pręta

1.5m

0.5m

C

B

A

= 53.13°

18KN

15KN

Z

X

rys.1. Belka wspornikowa – rysunek w aksonometrii

rys.2. Belka wspornikowa – schemat statyczny

1A. Wyznaczenie reakcji

:

1A.1.Usuwamy myślowo podporę (utwierdzenie) i zastępujemy jej działanie

poszukiwanymi

reakcjami

przyjmując dowolnie ich zwroty -

rys.3

1A.2.W celu ułatwienia obliczeń siły o kierunkach ukośnych zastepujemy ich

składowymi równoległymi do osi przyjętego układu współrzędnych -

rys.4

Składowa pozioma: 15

∗ cosϕ = 15 ∗ cos 53.13° = 9 KN

Składowa pionowa: 15

∗ sinϕ = 15 ∗ sin 53.13° = 12KN

A

C

B

R

A

M

A

18KN

15KN

rys.3.

18KN

0.5m

1.5m

C

B

12KN

9KN

A

V

A

H

A

A

rys.4

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

2/10

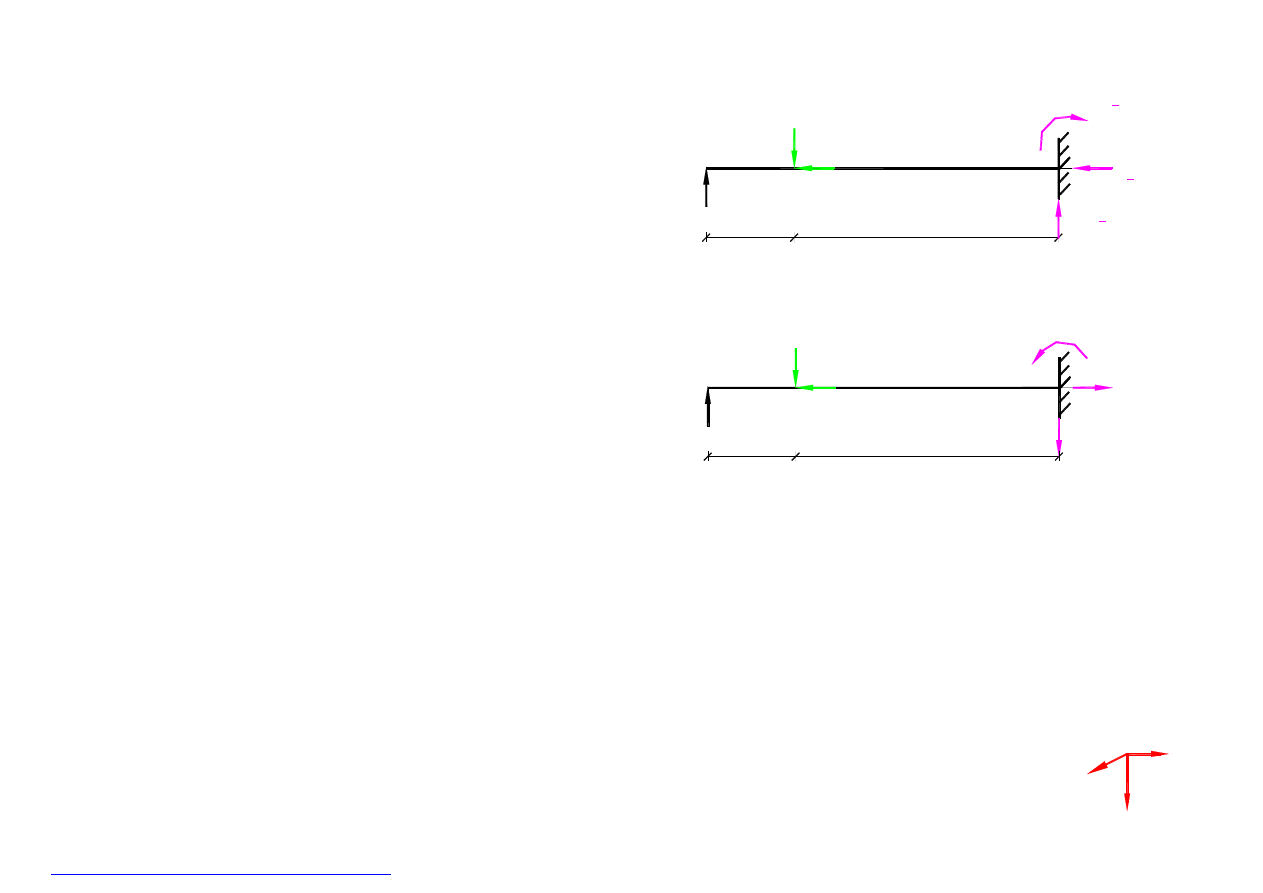
1A.3. Układając równania równowagi przyjmuje się zwykle jako dodatnie siły

poziome zwrócone w prawo, siły pionowe zwrócone w góre, a momenty
sił zwrócone zgodnie z ruchem wskazówek zegara.

Jeżeli przyjety zwrot reakcji jest zgodny z rzeczywistym, to w wyniku
obliczeń otrzymujemy dodatnią wartość tej siły. Jeżeli przyjety zwrot
reakcji jest niezgodny z rzeczywistym, to w wyniku obliczeń
otrzymujemy ujemną wartość tej siły.

Ustawiamy odpowiednie trzy równania równowagi z których
wyznaczamy niewiadome reakcje (

rys.5 )

:

1.

Σ X = 0 –9 – H

A

= 0 H

A

= –9 KN

2.

Σ Z = 0 18 –12 + V

A

= 0 V

A

= –6 KN

3.

Σ M

A

=0 18

∗2–12∗1.5+ M

A

= 0 M

A

= –18 KNm

Zmieniam zwroty reakcji tak , aby ich wartości były dodatnie –

rys.6

Sprawdzenie (

rys.6 )

:

Σ M

B

=0 18

∗0.5 + 6∗1.5 – 18 =

0

A

C

0.5m

B

1.5m

H

A

= 9KN

M

A

= 18KNm

V

A

= 6KN

9KN

12KN

18KN

rys.5

9KN

B

C

0.5m

18KN

V

A

= 6KN

H

A

= 9KN

1.5m

A

12KN

M

A

= 18KNm

rys.6

2A. Wyznaczenie funkcji sił przekrojowych M(x), Q(x), N(x) w poszczególnych przedziałach osi belki.

Wartość momentu zginającego M(x) w rozpatrywanym przekroju pręta (belki) równa się sumie algebraicznej momentów wszystkich sił zewnętrznych
działajacych na układ z lewej lub prawej strony danego przekroju względem jego środka ciężkości.

Wartość siły poprzecznej Q(x) w rozpatrywanym przekroju pręta (belki) równa się sumie algebraicznej składowych prostopadłych do osi preta
wszystkich sił działających z lewej lub prawej strony danego przekroju.

Wartość siły podłużnej N(x) w rozpatrywanym przekroju pręta (belki) równa się sumie algebraicznej składowych równoległych do osi preta
wszystkich sił działających z lewej lub prawej strony danego przekroju.

Przy znakowaniu siły przekrojowych M(x), Q(x), N(x) posługujemy się prawoskrętnym układem osi współrzędnych –

rys.7

.

Dla przekroju o normalnej zewnętrznej dodatniej (

strona lewa

-

rys.8

), za dodatnie będziemy uważali te siły przekrojowe, których

wektory mają zwroty zgodne ze zwrotem odpowiedniej osi układu współrzędnych. Dla przekroju o normalnej zewnetrznej
ujemnej (

strona prawa

–

rys.9

) za dodatnie będziemy uważali te siły przekrojowe, których wektory mają zwroty przeciwne do

zwrotu odpowiedniej osi układu współrzędnych.

X

Z

Y

rys.7

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

3/10

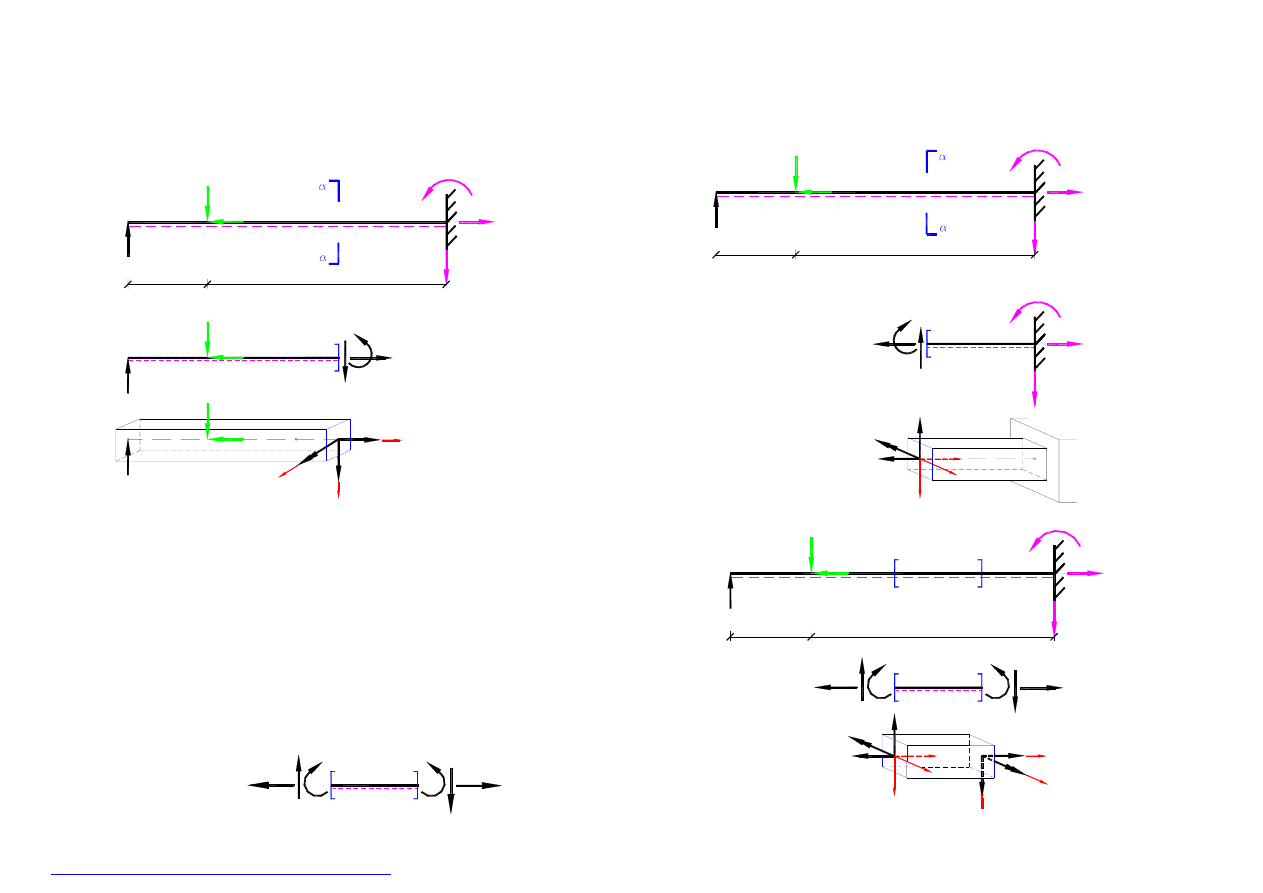
Na rysunku –

rys.8

pokazane są dodatnie wektory M, Q, N

dla przekroju o dodatniej normalnej zewnętrznej,
przy prawoskrętnym układzie współrzednych –

strona lewa

Na rysunku –

rys.9

pokazane są dodatnie wektory M, Q, N

dla przekroju o ujemnej normalnej zewnętrznej,
przy prawoskrętnym układzie współrzednych –

strona prawa

1.5m

0.5m

V

A

= 6KN

9KN

18KN

C

B

12KN

H

A

= 9KN

M

A

= 18KNm

A

N

Q

M

Y

Q

Z

M

N

X

rys.8

1.5m

0.5m

V

A

= 6KN

N

N

M

Z

Y

X

Q

M

Q

9KN

18KN

C

B

12KN

H

A

= 9KN

M

A

= 18KNm

A

A

M

A

= 18KNm

H

A

= 9KN

V

A

= 6KN

rys.9

Na rysunkach -

rys.10

,

rys.11

przedstawiony jest wycięty na dowolnym odcinku

element belki dwoma przekrojami, oraz pokazano dodatnie wektory M, Q, N,
przy prawoskrętnym układzie współrzednych. Możemy również powiedzieć, że
za dodatnie momenty zginajace przyjmuje się takie, które przy zginaniu prętów
(belek) wywołują rozciąganie ich włókien dolnych tzw. spodów ( na rysunkach
spody zaznaczone są

przerywaną kreską

----

); przy takim założeniu momenty sił

tworzą dodatnie momenty zginajace, jeżeli na lewo od

przekroju

mają zwrot

zgodny z ruchem wskazówek zegara, a na prawo od

przekroju

mają zwrot

przeciwny do ruchu wskazówek zegara.

N

Q

M

M

Q

N

rys10

M

A

= 18KNm

H

A

= 9KN

V

A

= 6KN

12KN

B

C

0.5m

18KN

1.5m

9KN

A

N

M

Q

M

Z

N

Z

Y

X

Q

M

Q

M

N

Y

X

Q

N

rys.11

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

4/10

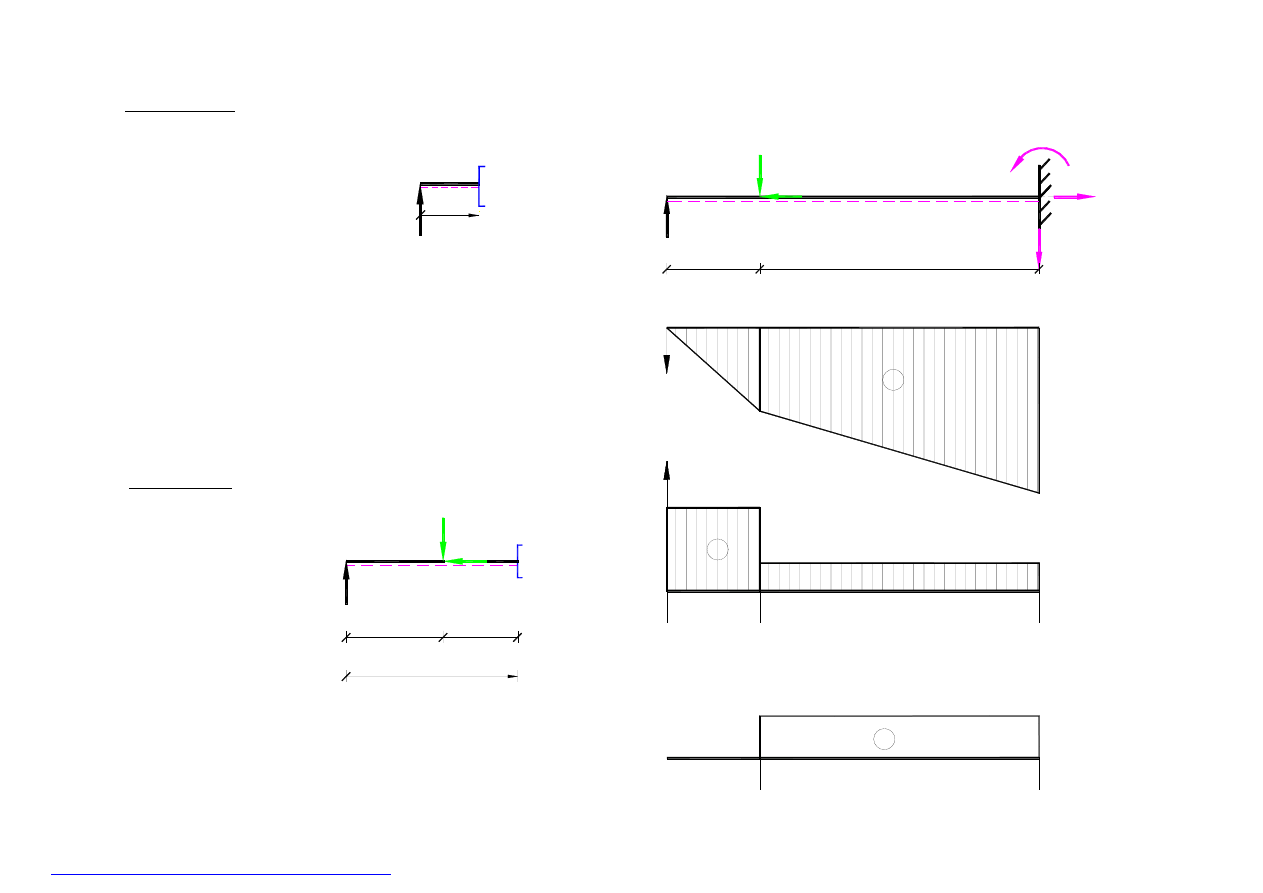
2A.1. Przedział C-B -

rys.12

0

≤ x ≤ 0.5

M(x) = + 18x

M(x=0) = 0

M(x=0.5) = + 9 KNm

0

≤ x < 0.5

Q = + 18 KN

N = 0

2A.2. Przedział B-A -

rys13

0.5

≤ x ≤ 2.0

M(x) = +18x –12(x-0.5)

M(x=0.5) = + 9 KNm

M(x=2.0) = + 18 KNm

0.5

< x ≤ 2.0

Q = + 6 KN

N = + 9 KN

18KN

C

x

rys.12

18KN

0.5

12KN

C

B

9KN

X

x-0.5

rys.13

3A. Wykresy momentów zginających M(x),

sił poprzecznych Q(x), sił podłużnych N(x) –

rys.14

B

12KN

C

18KN

0.5m

V

A

= 6KN

H

A

= 9KN

M

A

= 18KNm

9KN

1.5m

A

M(x)

[KNm]

+9.0

+1

8.

0

Q(x)

[KN]

+18

.0

+18

.0

+6.

0

+6.

0

N(x)

[KN]

+

+

+

+9.

0

+9.

0

rys.14

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

5/10

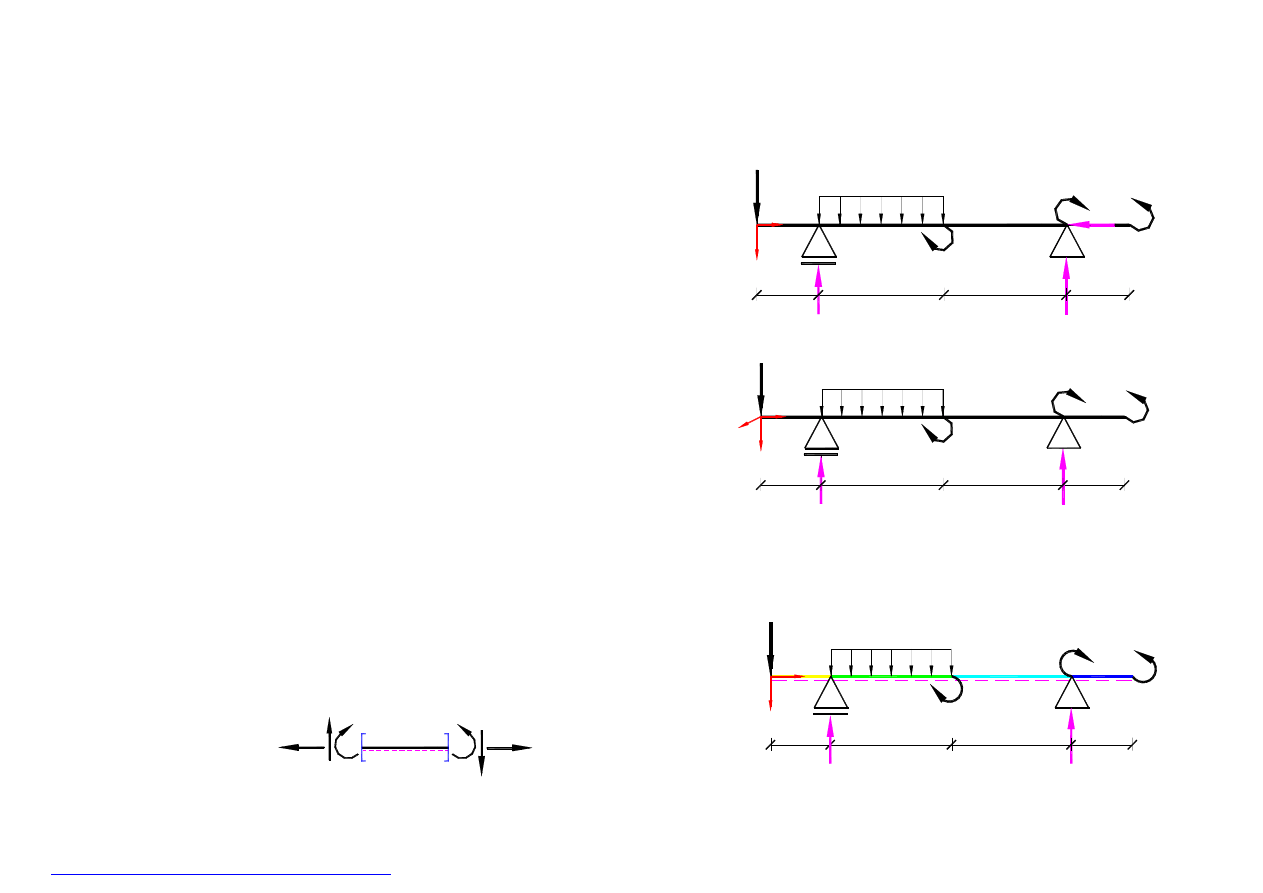
B. Belka wolnopodparta

1.B. Wyznaczenie reakcji

:

W pierwszej kolejności

oznaczamy punkty charakterystyczne belki –

punkty podporowe B, D oraz punkty przyłożenia obciążenia : A, C, E

-

rys.15

. Znakowanie sił zewnętrznych zgodne z p.1A.3. ze strony 3.

Dane obciążenie ciągłe równomiernie rozłożone przedstawione
w postaci prostokąta, zastępujemy siłą skupioną zaczepioną w środku
ciężkości prostakąta.

1.

Σ

X = 0 –

H

D

= 0

H

D

= 0

2.

Σ

M

D

=0 – 4

∗5 +

R

B

∗4 – 4∗2∗3 + 8 + 3 – 3

= 0

R

B

= 9 KN

3.

Σ

M

B

=0 – 4

∗1 + 4∗2∗1 + 8 –

V

D

∗4 + 3 – 3

= 0

V

D

= 3 KN

Sprawdzenie

rys.16

:

Σ Z = 0 – 4 +

9

– 4

∗2 +

3

=

0

A

3KNm

E

R

B

1.0 m

Z

4KN

X

B

2.0 m

4KN/m

3KNm

2.0 m

8KNm

C

V

D

1.0 m

D

H

D

rys.15

4KN/m

2.0 m

9 KN

B

X

4KN

A

8KNm

C

D

E

3 KN

Z

2.0 m

1.0 m

1.0 m

3KNm

3KNm

Y

rys.16

2.B. Wyznaczenie funkcji sił przekrojowych M(x), Q(x), N(x) w poszczególnych przedziałach osi belki

2B.1.Wyrażnie podkreślamy

spody

belki za pomocą linii przerywanej -

rys.17

Dodatnie wartości sił przekrojowych przedstawione są na rysunku -

rys 10

znajdującym się na stronie 4 . Dla wygody ryunek ten jest pokazany jeszcze
raz poniżej.

N

Q

M

M

Q

N

rys. 10

ze strony 4.

8KNm

2.0 m

1.0 m

R

B

= 9 KN

4KN

A

Z

4KN/m

B

C

1.0 m

2.0 m

V

D

= 3KN

3KNm

3KNm

D

E

X

rys.17

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

6/10

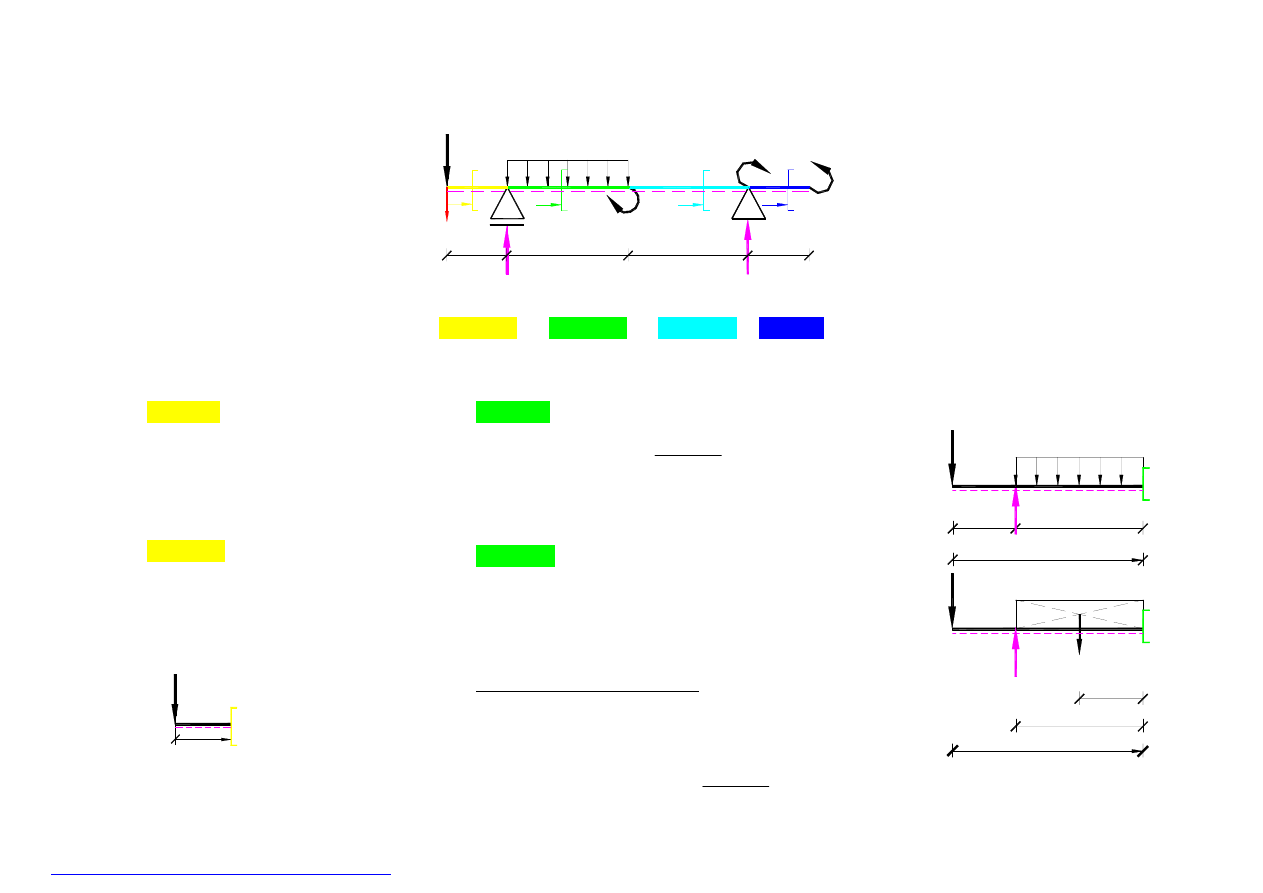
2B.2. Na rysunku –

rys.18

przedstawione są wszystkie przedziały belki idąc od lewej strony.

x

x

x

x

A

B

C

D

E

4KN/m

4KN

8KNm

R

B

= 9 KN

V

D

= 3KN

3KNm

3KNm

Z

1.0 m

2.0 m

2.0 m

1.0 m

rys.18

0

< x < 1 1 < x < 3 3 < x < 5

5

< x <

_______________________________________________________________________________________________________________________________

2B.3. Przedział A-B –

rys.19

0

≤ x ≤ 1

M(x) = – 4x

M(x=0) = 0

M(x=1) = – 4 KNm

0

< x < 1

Q = – 4 KN

4KN

x

A

rys.19

2B.4. Przedział B-C –

rys.20

1

≤ x < 3

2

)

3

x

(

M

4

)

1

x

(

M

2

)

1

x

(

4

)

1

x

(

9

x

4

)

x

(

M

2

−

=

=

−

=

=

−

−

−

+

−

=

1 < x

≤ 3

3

)

3

x

(

Q

5

)

1

x

(

Q

)

1

x

(

4

9

4

)

x

(

Q

−

=

=

+

=

=

−

−

+

−

=

Obiczenie extremum momentu

m

25

.

2

x

0

)

1

x

(

4

9

4

)

x

(

Q

=

=

−

−

+

−

=

KNm

875

.

0

2

)

1

x

(

4

)

1

x

(

9

x

4

)

25

.

2

x

(

M

2

−

=

−

−

−

+

−

=

=

M

extr.

= – 0.875 KNm

4(

x

-1)

B

A

x

4KN

9KN

9KN

x

4KN

A

B

1

x

- 1

4KN/m

x

- 1

0.5(

x

- 1)

rys.20

_

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

7/10

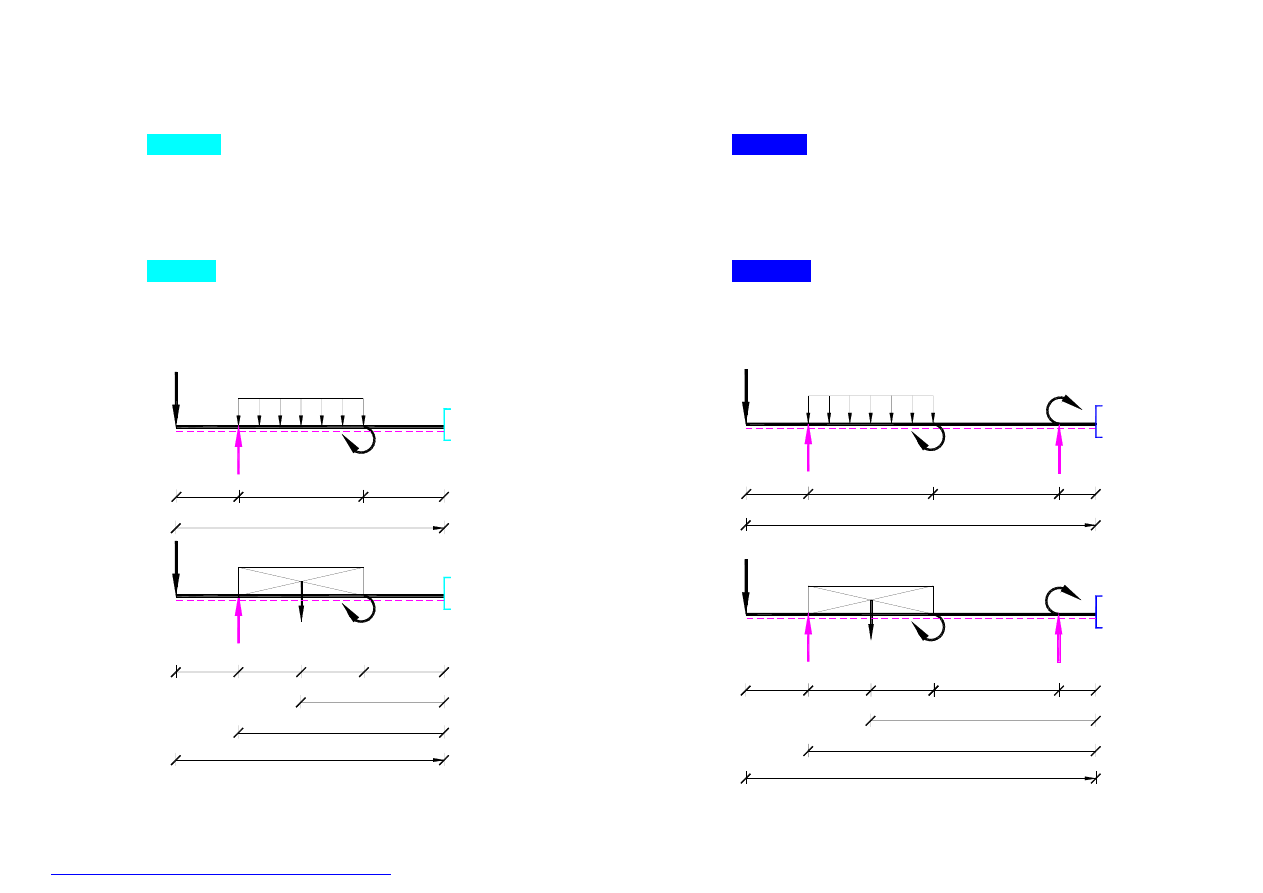
2B.5. Przedział C-D –

rys.21

3 < x < 5

0

)

5

x

(

M

6

)

3

x

(

M

8

)

2

x

(

2

*

4

)

1

x

(

9

x

4

)

x

(

M

=

=

+

=

=

+

−

−

−

+

−

=

3

≤ x <5

3

2

*

4

9

4

Q

−

=

−

+

−

=

9KN

4*2=8KN

4KN

A

B

1

9KN

4KN

A

B

2

C

8KNm

C

8KNm

x

- 3

4KN/m

x

x

x

- 3

x

- 2

x

- 1

1

1

1

rys.21

2B.6. Przedział D-E –

rys.22

5 < x < 6

3

)

6

x

(

M

3

)

5

x

(

M

3

)

5

x

(

3

8

)

2

x

(

2

*

4

)

1

x

(

9

x

4

)

x

(

M

=

=

=

=

+

−

+

+

−

−

−

+

−

=

5 < x

≤ 6

0

3

2

*

4

9

4

Q

=

+

−

+

−

=

1

4*2=8KN

4KN/m

1

1

9KN

A

B

4KN

4KN

9KN

A

B

2

x

- 5

1

C

8KNm

C

8KNm

x

x

2

2

x

- 5

3KN

3KN

D

3KNm

3KNm

D

x

- 2

x

- 1

rys.22

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

8/10

2B.7. W celu uproszczenia obliczeń przy wyznaczaniu powyższych równań, postępujemy tak, aby ilość członów składowych wywodzacych się od

obciążeń zewnętrznych była jak najmniejsza. W naszym przykładzie opłaca się to uczynić już w przedziale C-D i D-E. Zmieniamy położenie
osi x-ów, zakładamy początek osi x-ów w punkcie E przyjmując dodatni zwrot tej osi w lewo. Aby odróżnic tę oś od poprzedniej, oznaczamy ją
przez x

1

. Dodatnie wartości sił przekrojowych przyjmujemy tak jak w punkcie 2A strony: 3 i 4, zgodnie z przedstawionym jeszcze raz poniżej

rysunkiem

rys. 10

ze str. 4:

N

Q

M

M

Q

N

rys. 10

ze str. 4

2B.8. Przedział E-D –

rys.23

0

< x

1

< 1

M(x

1

) = + 3

M(x

1

=0) = + 3 KNm

M(x

1

=1) = + 3 KNm

Q = 0

E

x

1

3KNm

rys.23

2B.9. Przedział D-C –

rys.24

1

< x

1

< 3

M(x

1

) = + 3 – 3 + 3(x

1

– 1)

M(x

1

=1) = 0

M(x

1

=3) = + 6 KNm

1

< x

1

< 3

Q = 3 KN

x

1

3KNm

3KNm

3KN

x

1

- 1

D

1

E

rys.24

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

9/10

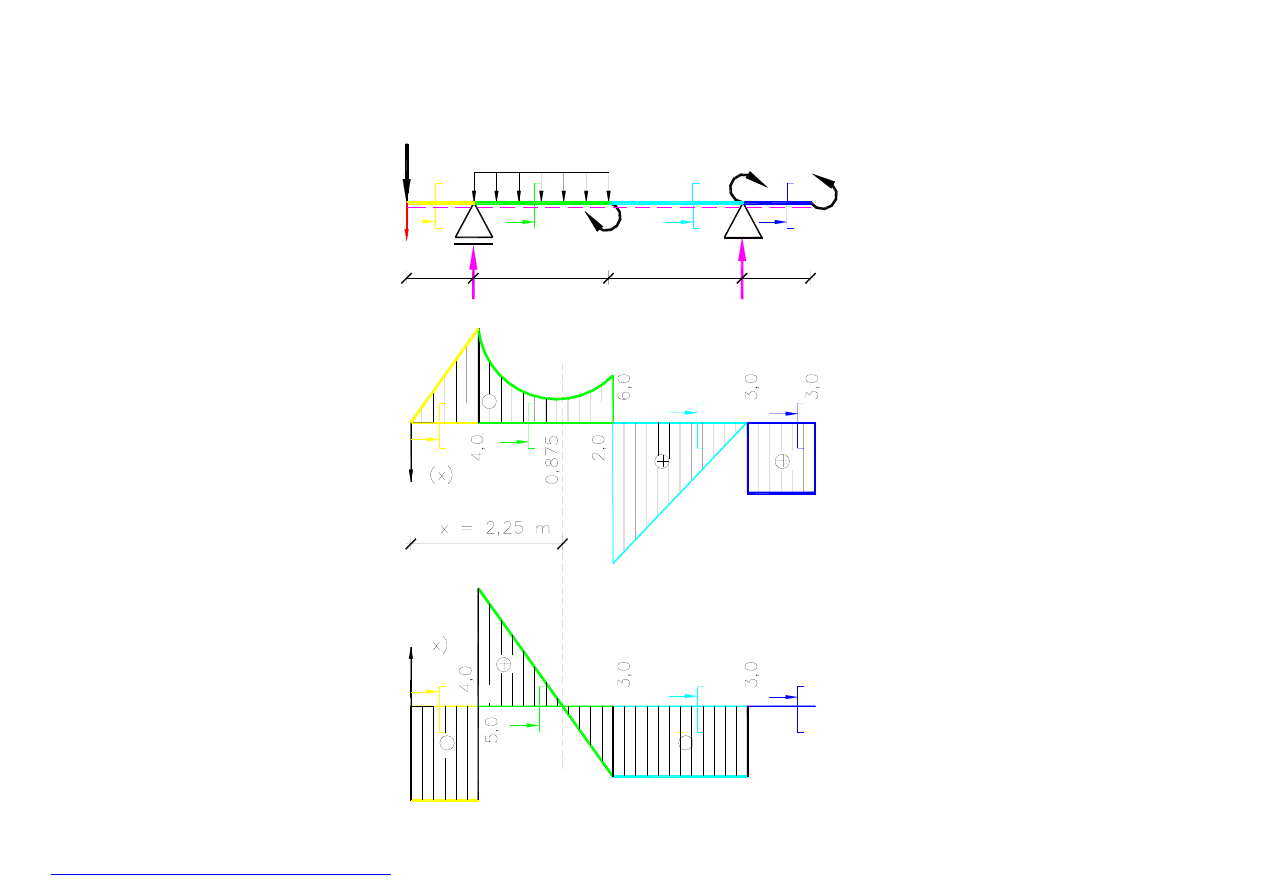
3B. Wykresy momentów zginających M(x) i sił poprzecznych Q(x) –

rys.25

A

C

D

E

M

-

B

-

+

-

x

x

x

x

A

B

C

D

E

4KN/m

4KN

8KNm

R

B

= 9 KN

V

D

= 3KN

3KNm

3KNm

+

+

-

-

Q(

A

B

C

-

-

D

E

+

-

x

x

x

x

x

x

x

x

-

Z

1.0 m

2.0 m

2.0 m

1.0 m

rys.25

________________________________________________________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

10/10