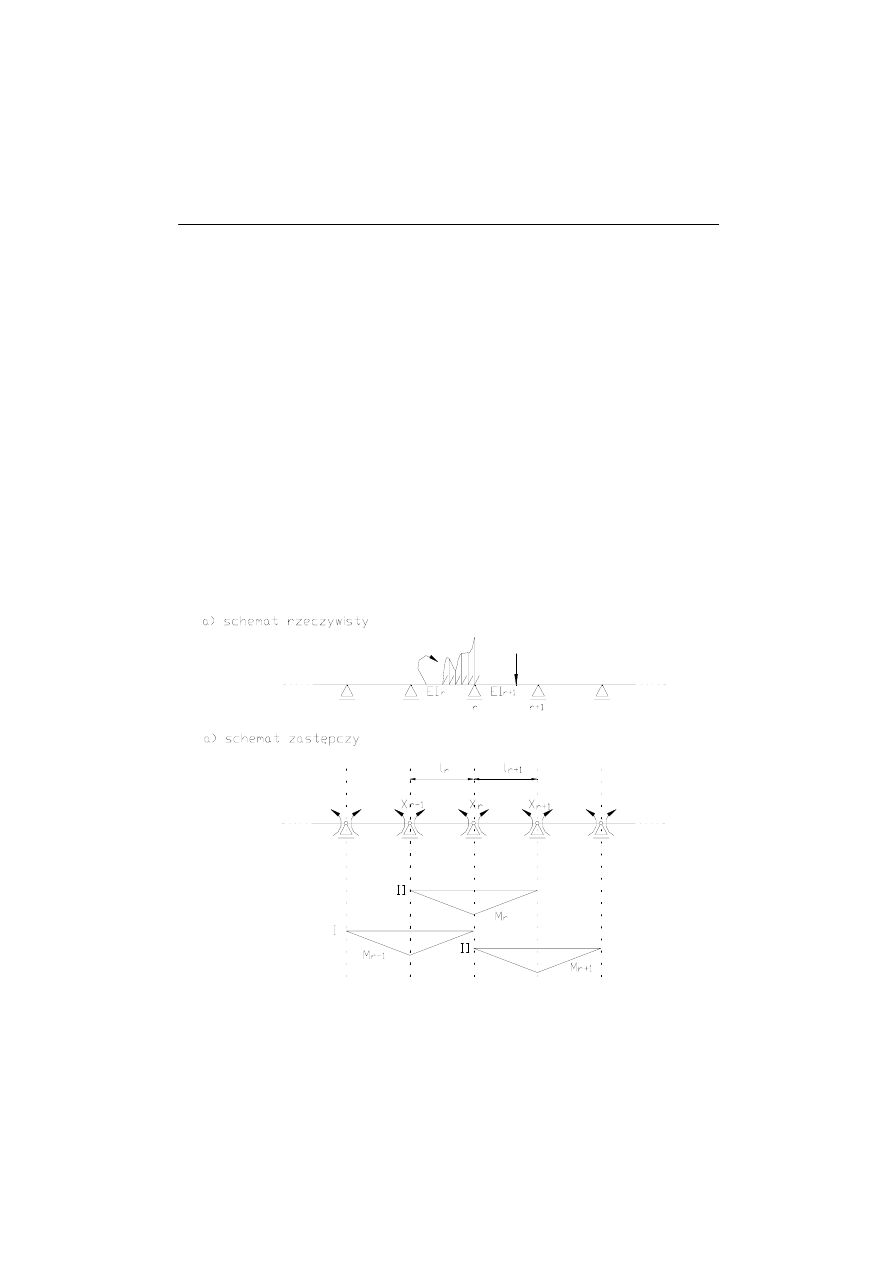
W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

R

OZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

1

Olga Kopacz, Adam Łodygowski, Wojciech Pawłowski,

Michał Płotkowiak, Krzysztof Tymper

Konsultacje naukowe: prof. dr hab. J

ERZY

R

AKOWSKI

Poznań 2002/2003

MECHANIKA BUDOWLI 10

ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH

STSTYCZNIE NIEWYZNACZALNYCH.

1.1. Metoda trzech momentów.

Do rozwiązywania wieloprzęsłowych belek statycznie

niewyznaczalnych stosowana jest szczególna postać metody sił, zwana
metodą trzech momentów.

Rozważmy dowolnie obciążoną wieloprzęsłową belkę statycznie

niewyznaczalną (rys.1.1a). Schemat zastępczy ( podstawowy ) statycznie
wyznaczalny może być w tej metodzie przyjęty dowolnie, wprowadzając
przeguby w miejscu podpór

Rys.1.1

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

R

OZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

2

i przyjmując niewiadome w postaci momentów podporowych (rys.1.1b)
Wówczas otrzymamy macierz podatności w postaci pasmowej!!!

Rozważmy następnie dwa sąsiednie, dowolnie wybrane przęsła

belki (r)
oraz (r-1). Dla przegubu r warunek geometryczny należy zapisać jako
wzajemny kąt obrotu równy zeru:

0

)

1

,

(

)

,

1

(

=

∆

+

∆

=

∆

+

∆

=

∆

+

−

r

r

r

r

r

r

p

r

l

r

r

(1.1)

gdzie:

−

∆

l

r

to kąt obrotu przekroju belki jednoprzęsłowej r obciążonej na

podporach momentami

r

r

X

X

,

1

−

oraz obciążeniem zewnętrznym,

−

∆

p

r

to kąt obrotu przekroju belki jednoprzęsłowej 1

+

r

obciążonej na

podporach momentami

1

,

+

r

r

X

X

oraz obciążeniem zewnętrznym.

Wprowadźmy równanie kanoniczne dla

tego

r

−

punktu:

0

...

1

,

1

1

,

1

=

∆

+

+

+

+

+

+

−

−

rp

r

r

r

r

rr

r

r

r

X

X

X

δ

δ

δ

(1.2)

gdzie (patrz rys.1.1b):

∫

=

⋅

⋅

⋅

⋅

⋅

=

⋅

=

−

−

r

r

r

r

r

r

r

r

EI

l

l

EI

ds

EI

M

M

6

1

3

1

1

2

1

1

1

,

1

δ

∫

=

⋅

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

⋅

=

⋅

=

+

+

1

3

2

1

2

1

1

1

3

2

1

2

1

1

1

1

,

r

r

r

r

r

r

r

r

l

EI

l

EI

ds

EI

M

M

δ









+

=

+

+

1

1

3

1

r

r

r

r

EI

l

EI

l

∫

+

+

+

+

+

+

=

⋅

⋅

⋅

⋅

⋅

=

⋅

=

1

1

1

1

1

,

1

6

1

3

1

1

2

1

1

r

r

r

r

r

r

r

r

EI

l

l

EI

ds

EI

M

M

δ

∫

=

⋅

=

+

−

+

−

0

1

1

1

,

1

ds

EI

M

M

r

r

r

r

δ

(1.3)

Podstawiając do równania (1.2) wyznaczone wartości (1.3)

otrzymujemy:

0

...

3

1

1

1

1

1

1

1

=

∆

+

+

+









+

+

+

+

+

+

+

−

rp

r

r

r

r

r

r

r

r

r

r

r

X

EI

l

X

EI

l

EI

l

X

EI

l

(1.3)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

R

OZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

3

a po uporządkowaniu równanie, zwane równaniem trzech momentów,
przyjmuje postać:

(

)

0

6

...

2

0

1

1

1

1

=

∆

+

+

′

⋅

+

′

+

′

⋅

+

′

+

+

+

−

rp

r

r

r

r

r

r

r

EI

l

X

l

l

X

X

l

(1.4)

przy czym:

r

r

r

EI

EI

l

l

0

⋅

=

′

a ,

0

EI -sztywność porównawcza

A co z warunkami brzegowymi?

Załóżmy, że nasza belka jest belką podpartą z lewej strony

(rys.1.2a).

Moment w punkcie "0" równy jest
zeru! mamy zatem już warunek
brzegowy!(x

0

=0!). Gdyby zaś nasza

belka była z jednej strony
utwierdzona (rys.1.2b) należałoby ją
rozszerzyć o jedno przęsło, i w celu
wyznaczenia warunków brzegowych
założyć że: 0

0

=

l

. Jeżeli zaś znamy

obciążenie jakie występuje po
zewnętrznej stronie przęsła jak na
rysunku (rys.1.2c), możemy
wyznaczyć wykres momentów co
umożliwia nam wyznaczenie

0

X i

rozpisanie równania dla dwóch
sąsiednich

przęseł z czego otrzymamy szukane warunki brzegowe.

1.2. Linie wpływu dla belek wieloprzęsłowych.

Wyznaczając w układach statycznie niewyznaczalnych linie

wpływu wielkości statycznych, klasyczną metodą sił, wyznacza się
najpierw linie wpływu nadliczbowych, co w dalszej kolejności umożliwi
nam wyznaczenie linii wszystkich innych wielkości.

Wróćmy do naszego przykładu. Przypuśćmy, że po naszej belce

porusza się poziomo siła P (rys.1.3). Ponieważ belka jest statycznie
niewyznaczalna, na nic zdadzą się próby rozwiązania jej, przy pomocy
równań równowagi. W takim przypadku należałoby rozwiązać układ

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

R

OZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

4

równań liniowych (1.4 ), co pozwoli nam na wyznaczenie wielkości

r

X .

Jeżeli mamy:

[ ] [ ] [ ]

P

X

A

=

⋅

to w celu wyznaczenia linii wpływu

wystarczy macierz

[ ]

P pomnożyć przez macierz

podatności odwróconą:

[ ] [ ] [ ]

1

−

⋅

=

A

P

X

Zastanówmy się teraz jak określić

rp

∆

gdy

mamy do czynienia z ruchomym obciążeniem.
Spójrzmy na rysunek obok (rys.1.3). Z naszej
belki wycięliśmy jedno przęsło (r-1,r) po
którym jeździ siła P (teraz już w układzie

lokalnym!) Oczywiście efektem jej działania jest wystąpienie sił
wewnętrznych (momentów, tnących...) Spójrz na rysunek 1.1. Stosując
tw. Maxwella wiemy, że

pr

rp

∆

=

∆

, czyli jest to ugięcie belki wywołane

działaniem jednostkowego momentu przyłożonego do podpory „ r ”.
Ugięcie to jest niezerowe tylko dla dwóch przęseł (r-1,r) i (r,r+1) p
wspólnym węźle „ r ”.

Wyznaczamy linię ugięcia od zadanego
momentu. Mamy zatem:

)

(

)

(

2

2

x

M

dx

x

d

EI

−

=

⋅ δ

(1.6)

u nas:

x

l

x

M

r

⋅

=

1

)

(

po podstawieniu i dwukrotnym scałkowaniu otrzymujemy:





 →



⋅

−

=

⋅

cakujemy

r

x

l

dx

x

d

EI

1

)

(

2

2

δ





 →



+

⋅

−

=

⋅

cakujemy

r

C

l

x

dx

x

d

EI

2

)

(

2

δ

D

x

C

l

x

x

EI

r

+

⋅

+

⋅

−

=

⋅

6

)

(

3

δ

z warunków brzegowych:

0

)

0

(

=

=

x

δ

i

0

)

(

=

=

r

l

x

δ

możemy

wyznaczyć szukane

C

D, . Linia ugięcia od założonego przez nas

momentu jedynkowego równa jest szukanej wartości

P

r,

∆

i wynosi:

(

)

3

2

6

)

(

ξ

ξ

δ

−

−

=

r

EI

l

x

gdzie:

r

l

x

=

ξ

(1.7)

Rys.1.3

δ

Rys.1.4

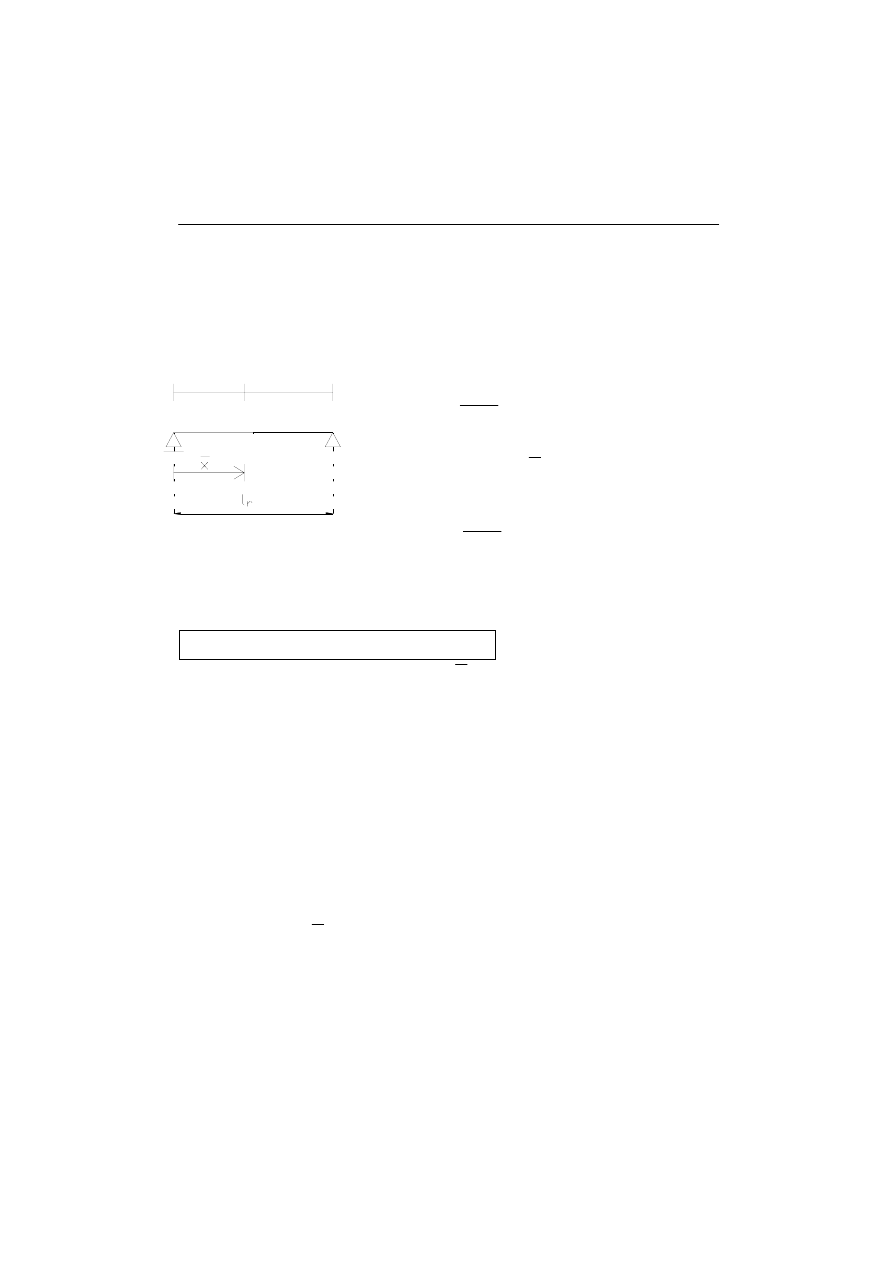
W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

R

OZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

5

Wiemy też, że: 0

,

1

≠

∆

−

P

r

i

1

,

,

1

−

−

∆

=

∆

r

P

P

r

(

−

∆

−

1

,r

P

to

przemieszczenie pionowe pod siłą P wywołane działaniem momentu
skupionego

1

−

r

X

). Jeżeli więc, do równania wyżej (1.7) zgodnie z

rysunkiem (rys.1.5) za

ξ

podstawimy

ξ

−

1

to otrzymamy gotowe

rozwiązanie:

(

)

ξ

ξ

ξ

δ

2

3

6

)

(

2

3

2

+

−

=

r

EI

l

x

(1.8)

Wprowadźmy pewną funkcje

⇒

−

=

3

)

(

ξ

ξ

ξ

ω

.

ξ

ξ

ξ

ξ

ω

2

3

)

(

2

+

−

=

,po

podstawieniu mamy:

)

(

6

6

2

0

ξ

ω

⋅

=

r

r

EI

l

EI

)

(

ξ

ω

⋅

′

⋅

⇒

r

r

l

l

W układzie równań kanonicznych, w przypadku, gdy
wędrująca siła porusza się w obrębie przęsła (r-1,r)
tylko dwa równania mają niezerowe prawe strony, a
mianowicie:

(

)

mp

m

m

m

m

m

m

m

C

l

X

l

l

X

X

l

=

′

⋅

+

′

+

′

⋅

+

′

+

+

+

−

1

1

1

1

2

(1.9)

dla 1

−

=

r

m

)

(

,

1

ξ

ω

⋅

′

⋅

−

=

−

r

r

p

r

l

l

C

oraz

dla

r

m

=

)

(

,

ξ

ω

⋅

′

⋅

−

=

r

r

p

r

l

l

C

Rozwiązując otrzymany układ równań względem niewiadomych

n

X

X

X

,...,

,

2

1

otrzymamy:

( )

+

⋅

+

+

⋅

+

+

⋅

+

⋅

=

−

−

P

r

r

k

kP

kk

P

k

P

k

k

C

C

C

C

X

,

1

1

,

2

2

1

1

...

...

β

β

β

β

ξ

...

...

,

1

1

,

+

+

⋅

+

⋅

+

+

P

r

r

k

rP

kr

C

C

β

β

(1.10
)

przy czym, współczynniki

kj

β

są wyrazami macierzy odwrotnej dla

układu równań (1,9), tzn. są to elementy macierzy odwrotnej, w stosunku
do macierzy podatności, i:

( )

( )

ξ

ω

ξ

′

⋅

−

=

−

r

r

P

r

l

l

C

,

1

,

( )

( )

ξ

ω

ξ

′

⋅

−

=

r

r

P

r

l

l

C

,

(dla obciążenia siłą

skupioną P=1).

Rys.1.5

1−ζ

ζ

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

R

OZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

6

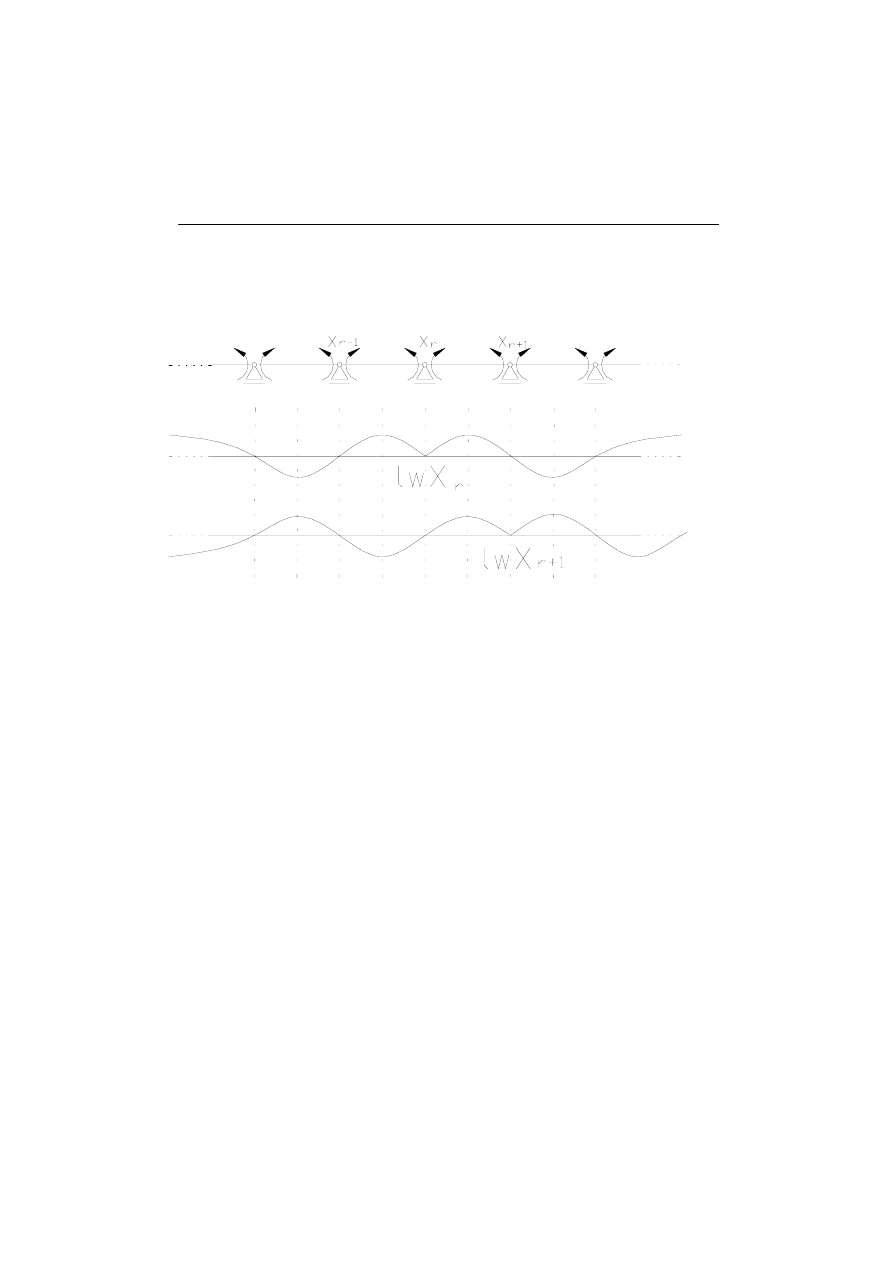
Rysunek poniżej pokazuje nam linie wpływu nadliczbowych

(rys.1.6).

Rys.1.6