Zadanie 4
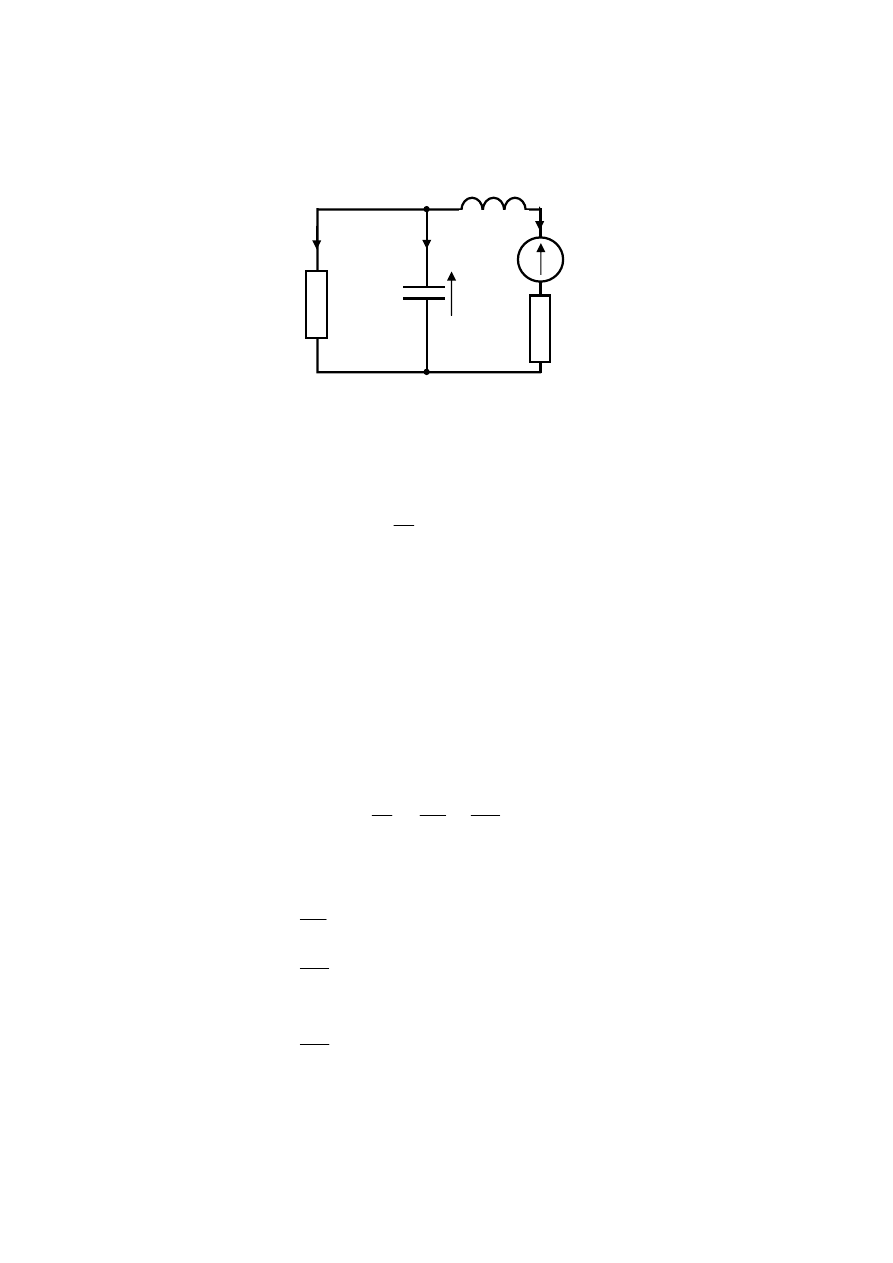
Wyznacz opis stanowy obwodu przedstawionego na rys.4.1.
L
i
L
i
R
Rys.4.1
Rozwiązanie
Opis stanowy układu liniowego ma postać:
(4.1)
gdzie:
(4.2)
jest macierzą stanu,
(4.3)
jest wektorem stanu, jego składowe
n
,
i
x
i
K
1
;
=
to zmienne stanu, n jest rzędem obwodu a
(4.4)
to wektor źródłowy. Wektor
(4.5)
jest wektorem pochodnych zmiennych stanu. Zależność (4.1) przedstawia n równań
następującej postaci :
( )
( )
( )
t
b
x
a
x
a
x
a
t
x
t
b
x
a
x
a
x
a
t
x
t
b
x
a
x
a
x
a
t
x
n
n
nn
n
n
n
n
n
n
n
+
+
+
+
=
+
+
+
+
=
+
+
+
+
=
K
M
K
K
2
2
1
1
2
2
2
22
1
21
2
1
1
2
12
1
11
1
d
d
d
d
d
d
(4.6)
Cechą charakterystyczną równań (4.6) jest to, że po lewej stronie każdego równania
występuje pochodna zmiennej stanu, w każdym równaniu innej, po prawej stronie mogą
C
e
u
C
i
C
R
2
R
1
( )
t
t
b
Ax
x
+
=
d
d
[ ]
n
n
ij
a
×
=
A
[
]
T
1
n
x
x K
=
x
( )
( )
[
]
T
1
t
b
t
b
n
K
=
b
T
1
d
d
d
d
d
d
=
t
x
t
x
t
n
K
x
2
występować wszystkie zmienne stanu z odpowiednimi współczynnikami oraz elementy
wektora źródłowego.
Obwód z rys.4.1 jest układem drugiego rzędu. Jako zmienne stanu przyjęte zostają: napięcie
na kondensatorze
( )
t
C
u
oraz prąd płynący przez cewkę
( )
t
i
L
. W przypadku prostych
obwodów, takich jak przedstawiony na rys.4.1, równania stanu można sformułować
posługując się prawami Kirchhoffa oraz zależnościami elementarnymi.
Prądowe prawo Kirchoffa dla każdego z dwóch węzłów obwodu ma postać:
0
=
+
+
L
C
R
i
i
i
Wielkość
( )
t
i
L
jest zmienną stanu,
( )
t
C
i
- pochodną zmiennej stanu. Z równania należy
zatem wyeliminować tylko prąd
( )
t
i
R
zastępując go wyrażeniem zależnym wyłącznie od
zmiennych stanu oraz ewentualnie prądu
( )
t
i
C
. Podstawiając:
2
R
u
i
C
R
=
otrzymuje się zależność, która nie zawiera żadnych wielkości obwodowych poza zmiennymi
stanu oraz pochodną jednej z nich. Jest to zatem równanie stanu w nieuporządkowanej jeszcze
formie.
0
d
d
0
2
=
+
+
⇒
=
+
+
L
C
C
L
C
R
i
t
u
C
R
u
i
i
i
Wynikiem uporządkowania ostatniego równania zgodnie z formatem zależności (4.6) jest
pierwsze z równań stanu:
C
i
CR
u
t
u
L
C
C
−
−
=
2
d
d
W celu wyznaczenia drugiego równania stanu sformułowane zostaje napięciowe prawo
Kirchhoffa dla prawego oczka obwodu z rys.4.1.
0
d
d
1
=
−
−
−
R
i
e
t
i
L
u
L
L
C
Jest to równanie stanu, które wymaga uporządkowania zgodnie z zależnością (4.6).
L
e
i
L
R
L
u
t
i
L
C
L
−
−
=
1
d
d
Poszukiwany opis stanowy to:
L
e
i
L
R
L
u
t
i
C
i
CR
u
t
u
L
C
L
L
C
C
−
−
=
−
−
=
1
2
d
d
d
d
lub w postaci macierzowej:
3
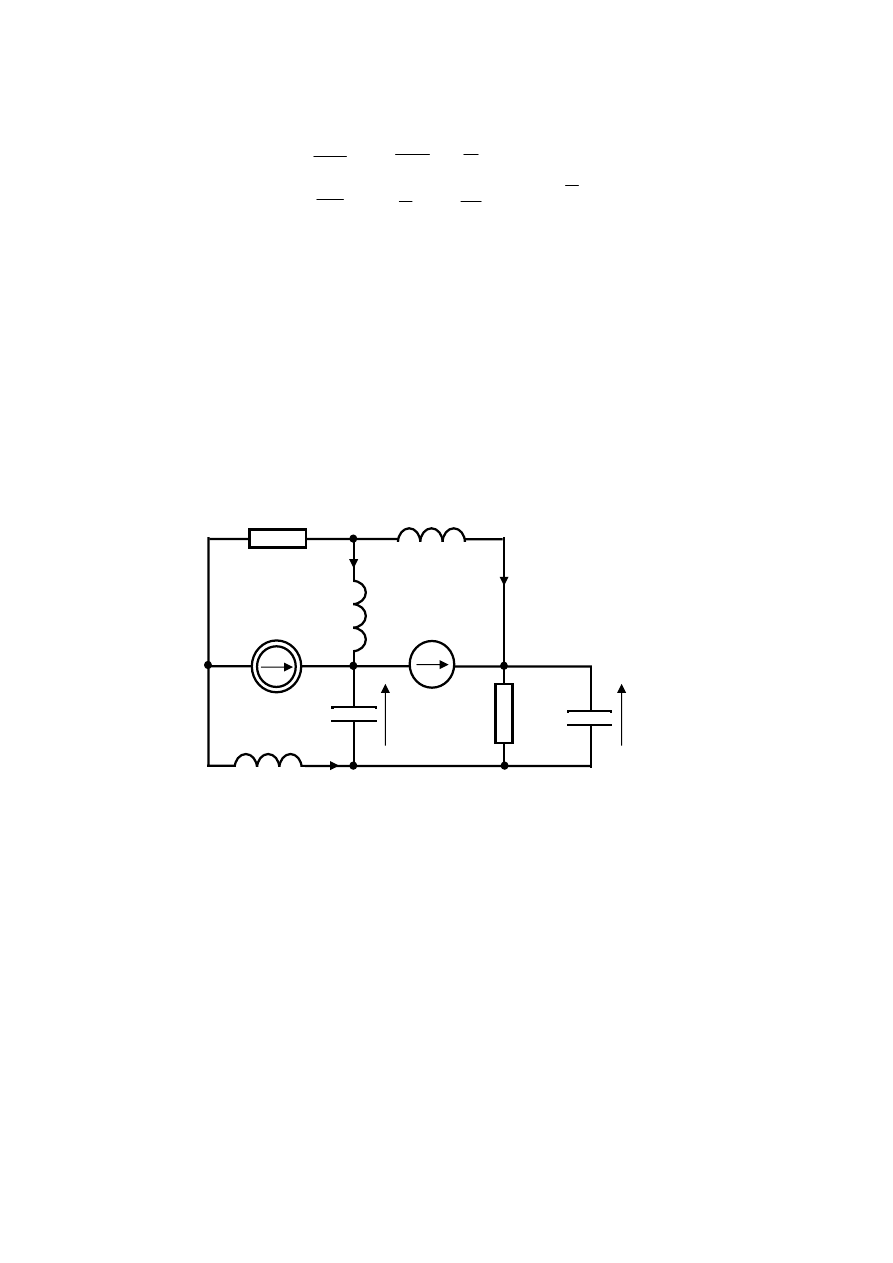
Zadanie 5
rzedstawiony jest obwód dynamiczny zawierający cewki i kondensatory.
Rozwiązanie
jest najmniejszą liczbą warunków początkowych niezbędnych do
Rys.5.1
Dla obwodów zawierających niezależne źr
ęciowe i prądowe oraz elementy R, L i C
(5.1)
dzie: n jest rzędem obwodu, n
L
ie, n
C
– liczbą kondensatoró
ierwszym przybliżeniem rzędu
Na rys.5.1 p
Wyznacz rząd tego obwodu.
Rząd obwodu
jednoznacznego określenia stanu obwodu w dowolnej chwili.
ódła napi
(bez źródeł sterowanych) rząd obwodu jest równy liczbie cewek i kondensatorów obecnych w
obwodzie pomniejszonej o liczbę pętli CE (pętli zawierających wyłącznie kondensatory oraz
idealne źródła napięciowe) oraz liczbę przekrojów LJ (przekrojów zawierających wyłącznie
gałęzie z cewkami oraz idealnymi źródłami prądowymi).
g
w w
– liczbą cewek w obwodz
CE
LJ
C
L
−
+
−
−
−
=
L
e
i
u
L
R
L
C
CR
t
i
t
L
C
L
C
0
1
d
d
d
1
2
u
1
1
d
n
n
n
n
n
L
7
−
−
+
=
u
j
9
C
i
7
L
5
3
e
8
R
2
C
4
L
6
u
3
i
i
6
5
4
R
1
obwodzie, n
LJ
– liczbą przekrojów LJ a n
CE
– liczbą pętli CE.
Przedstawiony obwód zawiera 2 kondensatory oraz 3 cewki. P
obwodu jest liczba 5 (suma cewek i kondensatorów. Rząd obwodu ulega jednak obniżeniu o
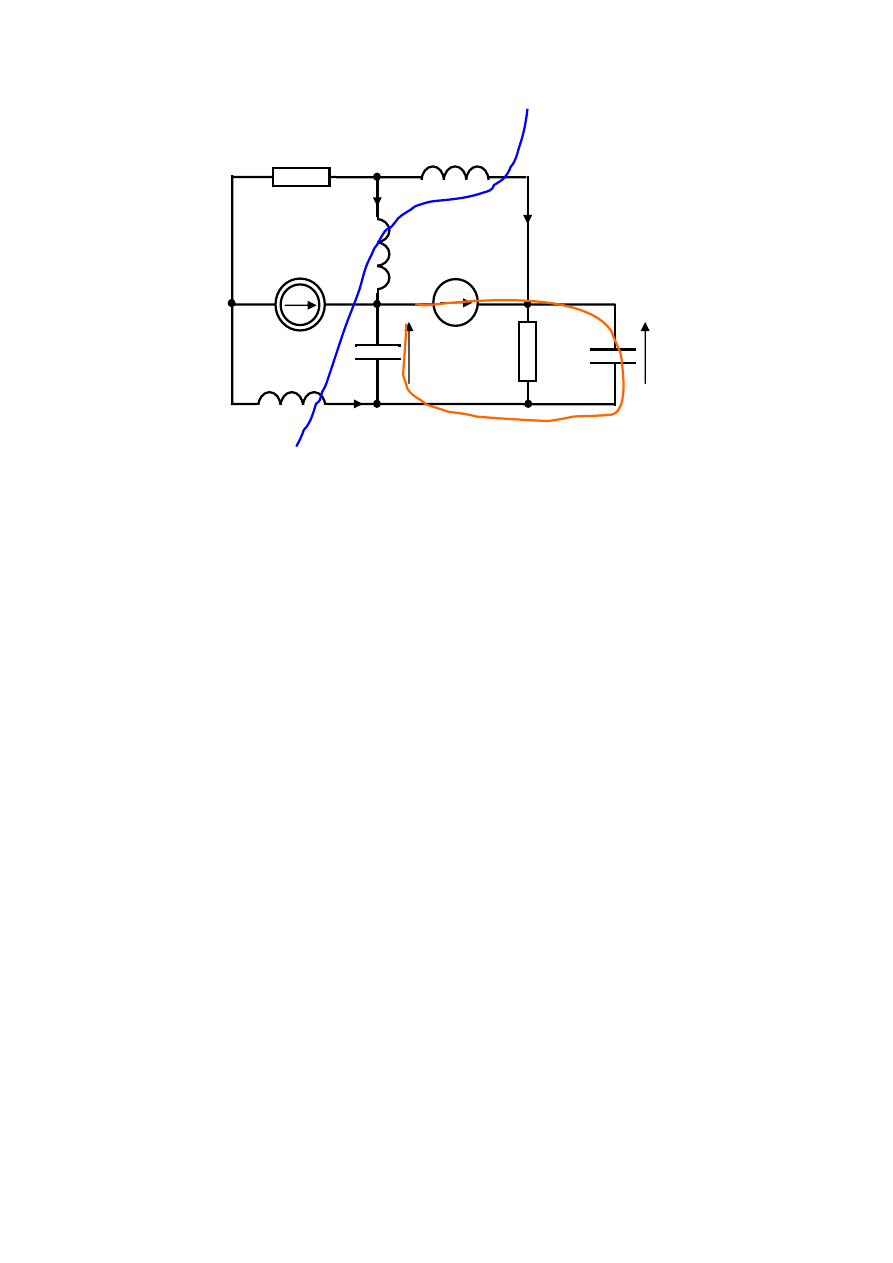
liczbę pętli CE oraz liczbę przekrojów LJ. Na rys.5.2 przedstawione zostały znalezione pętle
CE oraz przekroje LJ.
4
u
j
C
e
L
R
R
C
L
L
u
i
i
i
1
7
6
7
6
9
8
3
4
3
2
5
4
5
Rys.5.2. Znalezione w obwodzie pętle CE oraz przekroje LJ.
W obwodzie jest jedna pętla CE, oznaczona kolorem czerwonym na rys.5.2 oraz jeden
oraz dla przekroju LJ – prą
Pierwsze równanie pozwala na wyznaczen
ęć na kondensatorach u
3
lub u
4
adanie 6
rzedstawiony jest obwód dynamiczny zawierający cewki i kondensatory.
przekrój LJ oznaczony na niebiesko na rys.5.2. Można sformułować zatem dwa równania. Dla
pętli CE – napięciowe prawo Kirchhoffa:
dowe prawo Kirchhoffa
4
8
3
0
ie jednego z napi
7
6
9
5
=
−
+
u
e
u
0
=
+
+
+
i
i
j
i
jeżeli znamy wartość drugiego. Jeden z warunków początkowych dla napięć na
kondensatorach staje się zbyteczny a rząd obwodu obniża się o 1. Drugie równanie pozwala
na obliczenie jednego z prądów cewek: i
5,
i
6
lub i
7
gdy znamy wartości dwóch pozostałych.
Jeden z warunków początkowych dla prądów staje się niepotrzebny a rząd obwodu ulega
obniżeniu o 1. Rząd obwodu wynosi zatem 3.
Z
Na rys.6.1 p
Wyznacz opis stanowy tego obwodu. Jako zmienne stanu przyjmij prąd cewki
L
i
oraz
napięcia na kondensatorach:
1
C
u i
2
C
u
.
5
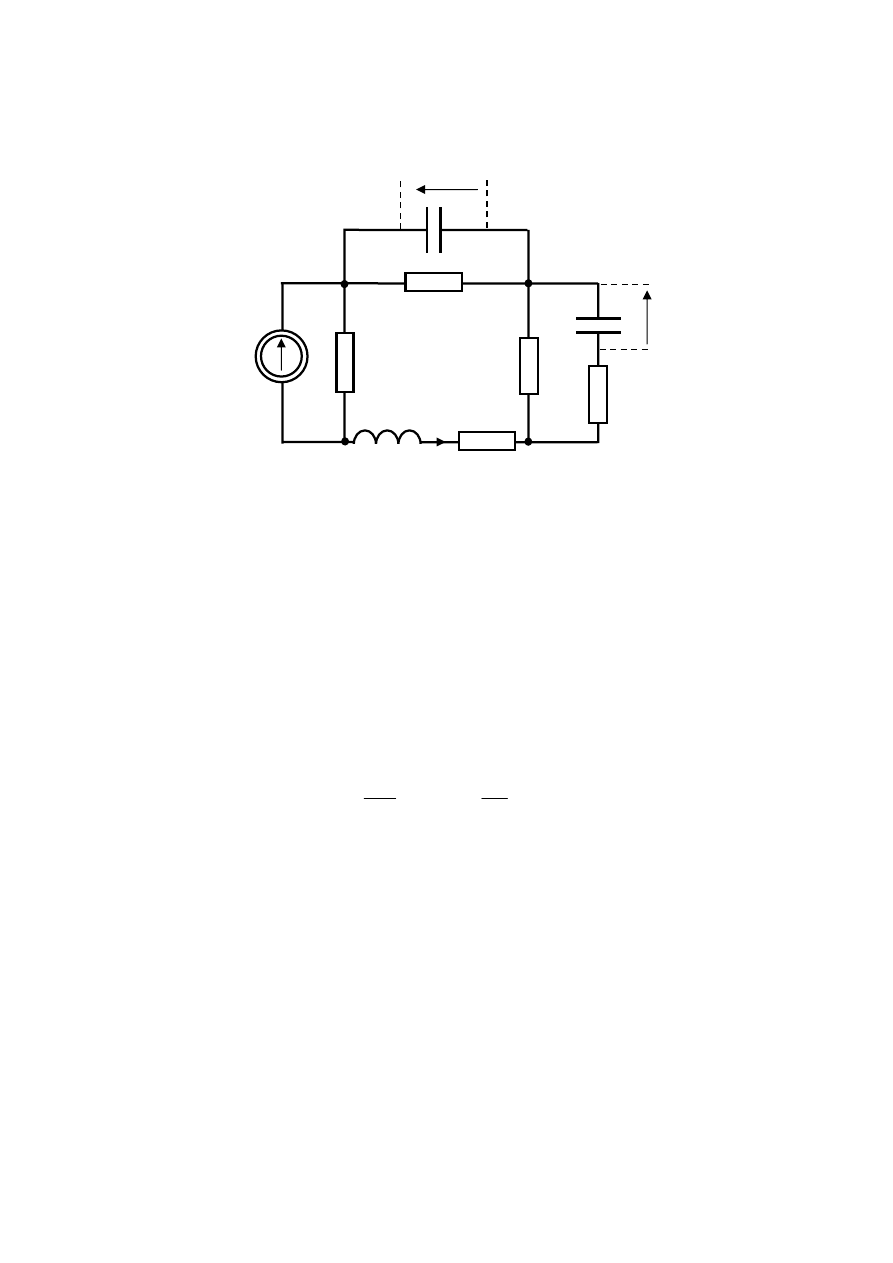
Rys.6.1
Rozwiązanie
problemu zostanie zastosowana następująca koncepcja wyznaczania opisu
a o wartościach napięć źródłowych
2.
sposób obwodu rezystancyjnego względem prądów
3.
ależności:
(6.1)
4. podzielenie równań przez C lub odpowiednio L, co kończy formułowanie równań
Realizacja punktu 1 polega na zastąpieniu kondensatorów C
1
oraz C
2
idealnymi źródłami
j
C
C
L
u
i
R
R
R
R
R
Do rozwiązania
stanowego. Kolejność postępowania jest następująca:
1. zastąpienie kondensatorów źródłami napięci
równych napięciom na kondensatorach (są to zmienne stanu) oraz zastąpieniu cewek
źródłami prądu o wartościach prądów źródłowych równych prądom płynącym przez
cewki (są to też zmienne stanu)
rozwiązanie otrzymanego w ten
kondensatorów oraz napięć na cewkach
wprowadzenie do otrzymanych równań z
stanu
napięciowymi o napięciach źródłowych:
1
C
u i
2
C
u
oraz zastąpieniu cewki L idealnym
źródłem prądowym o prądzie źródłowym
L
i
.
rowadzi to do otrzymania obwodu
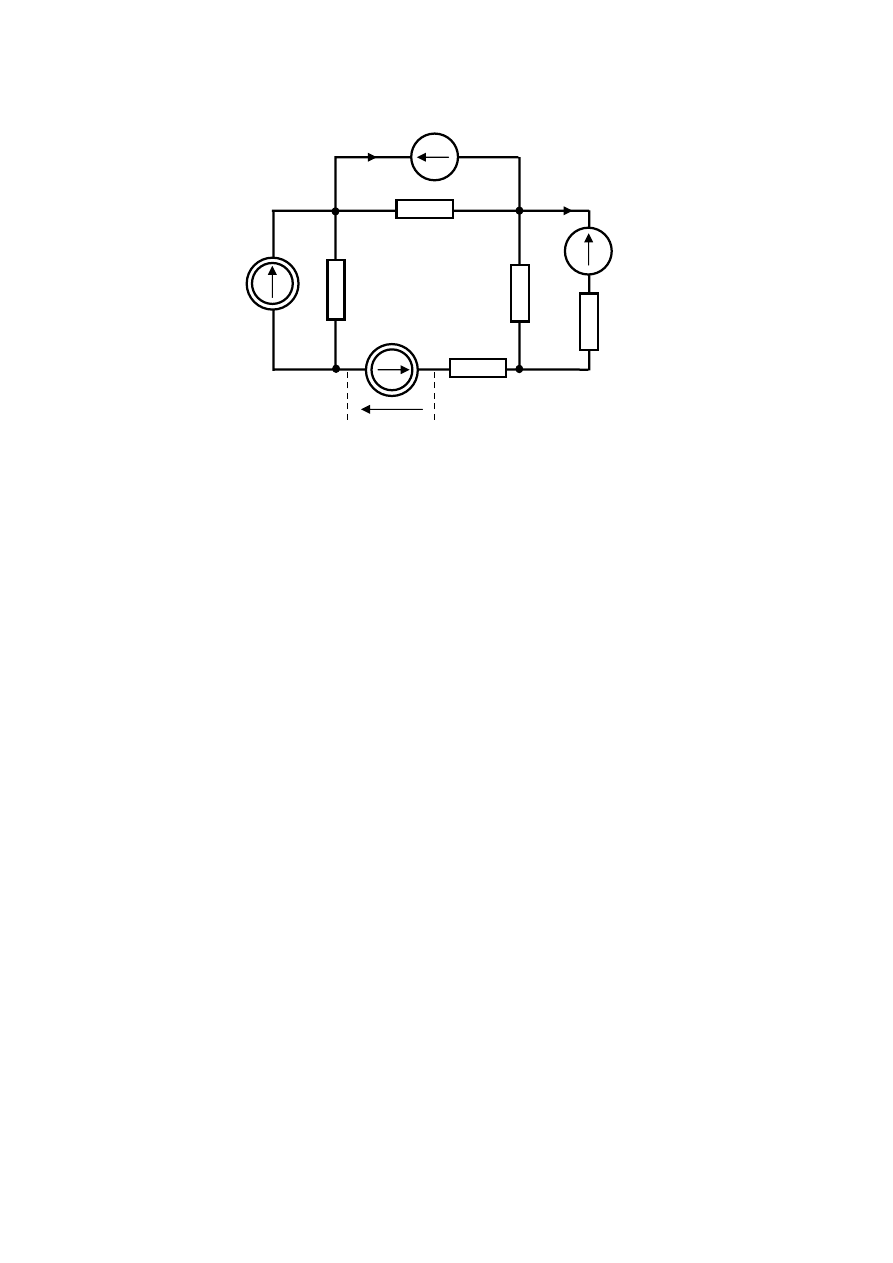
rezystancyjnego przedstawionego na rys.6.2.
Otrzymany obwód zostanie rozwiązany wzglę
P
dem prądów płynących przez źródła napięciowe
zastępujące kondensatory:
1
C
i oraz
2
C
i i napięcia panującego na zaciskach źródła prądowego
zastępującego cewkę
L
u
Zastos
ana będzie metoda superpozycji. Wyniki analiz
poszczególnych obwodów, w których obecne są kolejno różne źródła będą oznaczane
górnymi indeksami.
.
ow
u
t
L
u
t
C
i
L
L
C
C
d
d
=
=
i
u
d
d
1
2
3
L
1
C1
2
C2
4
5
6
i
u
j
u
i
R
R
R
R
R
i
u
C1
C1
C2
2
C2
1
4
L
L
5
3
Rys.6.2. Obwód rezystancyjny otrzymany po wprowadzeniu źródeł
ierwszym analizowanym obwodem będzie przedstawiony na rys.6.3. Powstał on przez
z rys.6.3 prąd płynie tylko przez opornik R
1
. Jest to prąd źródłowy j. Prądy w
(6.2)
Płynący przez opornik R
1
prąd źródła powoduje powstanie napięcia, które jest równe napięciu
(6.3)
zastępujących kondensatory oraz cewkę
P
usunięcie źródeł zastępujących kondensatory i cewkę oraz pozostawienie w obwodzie jedynie
źródła prądowego j. Usunięcie z obwodu źródeł napięciowych związane jest ze zwarciem
zacisków tych źródeł, usunięcie źródła prądowego wymaga pozostawienia jego zacisków
rozwartych.
W obwodzie
obu gałęziach, w których znajdowały się kondensatory są równe 0.
1
1
)
(
)
(
0
0
2
1
=
=
C
C
i
i
na zaciskach usuniętego źródła prądowego. Jego wartość wynika z prawa Ohma.
1)
(
1
R
j
u
L
⋅
−
=
7
i
C2
(1)
u
L
(1)
j
R
2
R
1
i
C1
(1)
R
3
R
4
R
5
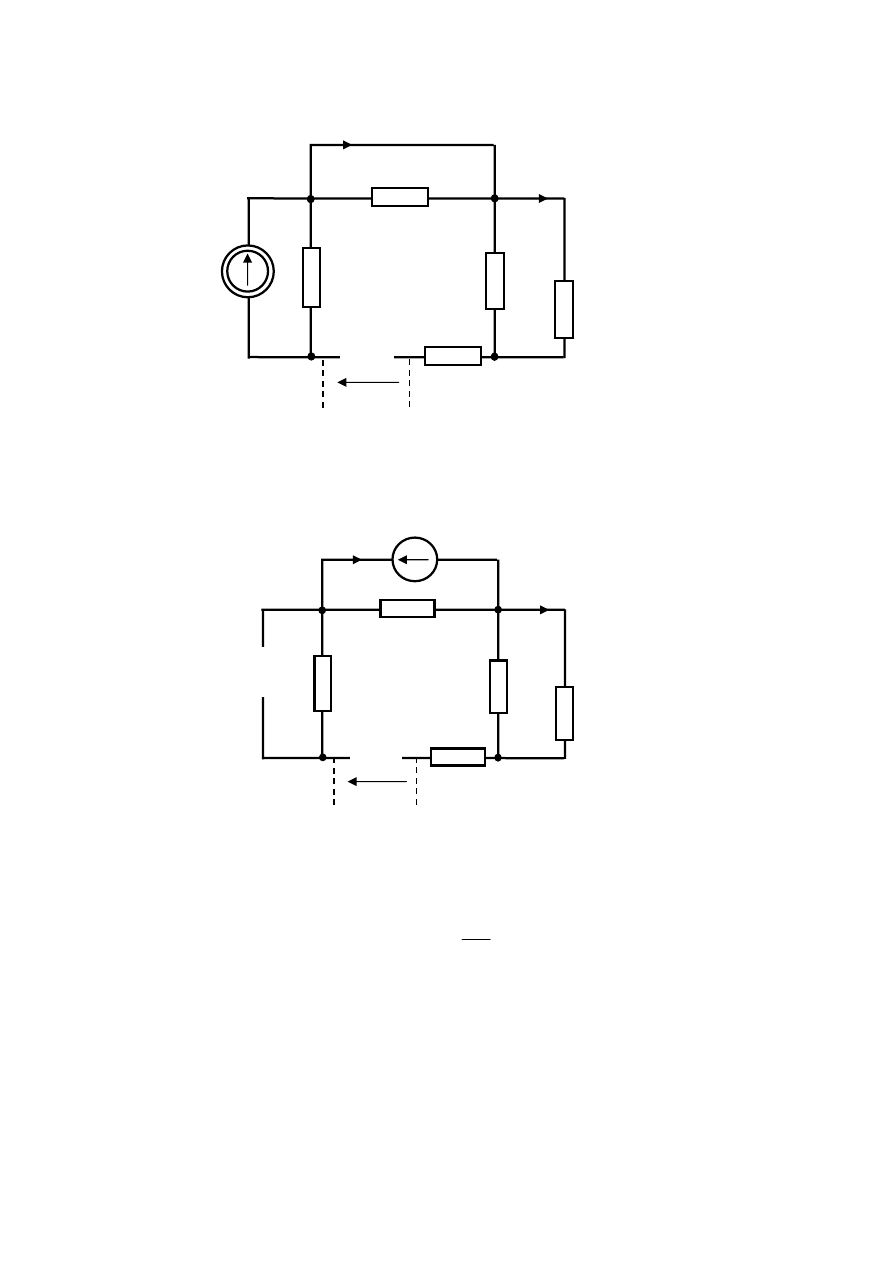
Rys.6.3. Pierwszy z analizowanych obwodów zbudowany na mocy zasady superpozycji
W drugim z analizowanych obwodów pozostawione zostanie źródło napięciowe
. Inne
źródła zostają usunięte. Otrzymany w ten sposób obwód przedstawiony jest na rys.6.4.
1
C
u
u
C1
i
C1
(2)
R
1
R
2
R
3
R
4
u
L
(2)
i
C2
(2)
R
5
Rys.6.4. Drugi z analizowanych obwodów zbudowany na mocy zasady superpozycji
W obwodzie z rys.6.4 źródło
wywołuje przepływ prądu przez opornik R
1
C
u
2
. Jego wartość
wynika z prawa Ohma.
2
1
2
1
R
u
i
C
)
(
C
−
=
(6.4)
Drugi z prądów w gałęziach z kondensatorami to
0 (6.5)
2
2
=
)
(
C
i
Ponieważ przez rezystory R
1
oraz R
4
nie płynie prąd, napięcia na ich zaciskach są równe 0.
Napięcie na rozwartych zaciskach źródła prądowego
L
i
jest równe napięciu źródłowemu
.
1
C
u
8
(6.6)
1
2
C
)
(
L
u
u
=
u
C2
i
C1
(3
)
i
C2
(3)
R
2
R
4
R
R
5
R
3
u
L
(3)
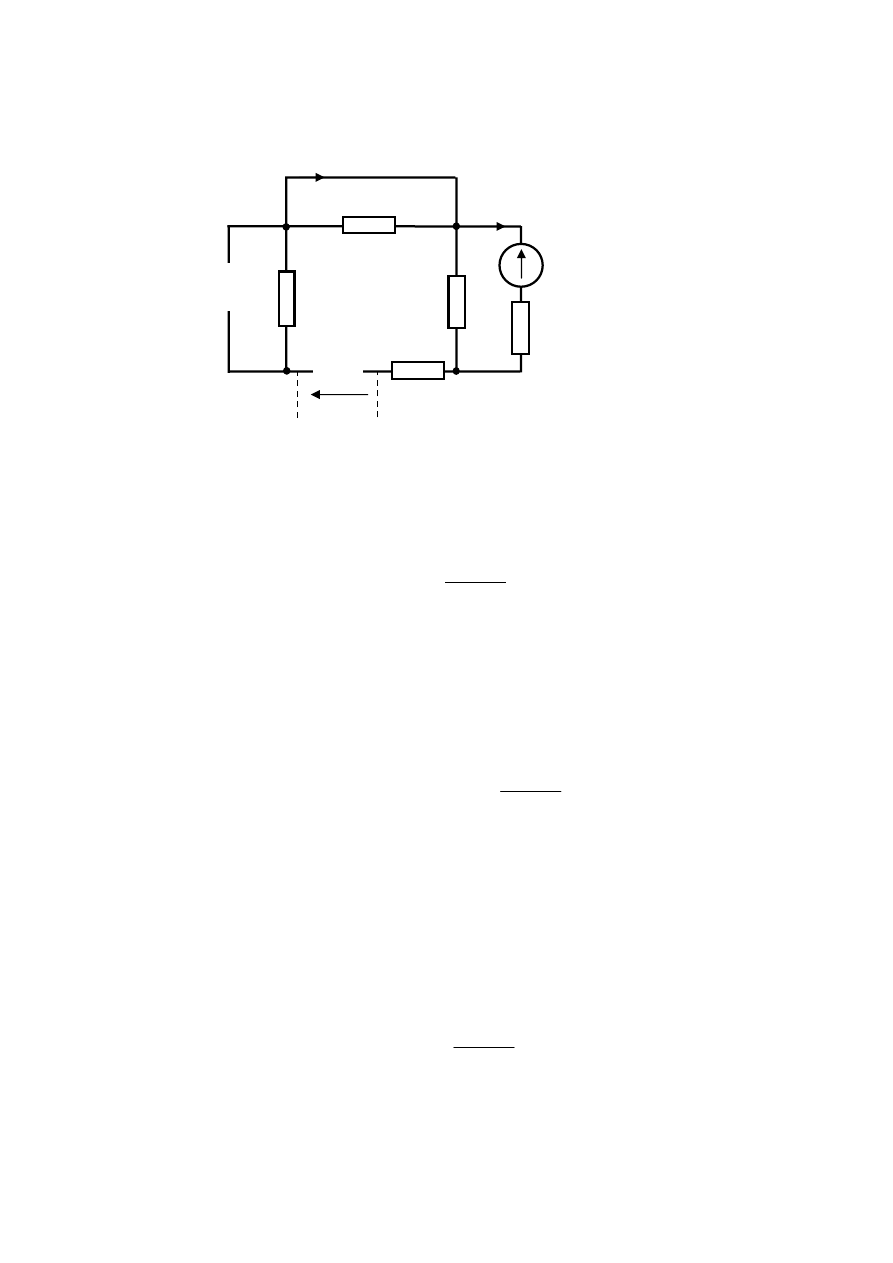
Rys.6.5. Trzeci z analizowanych obwodów zbudowany na mocy zasady superpozycji
Trzeci z analizowanych obwodów zawierający jedynie źródło
przedstawiony jest na
rys.6.5. W obwodzie z rys.6.5 źródło
wywołuje przepływ prądu przez oporniki R
2
C
u
2
C
u
4
oraz
R
5
. Jego wartość wynika z prawa Ohma.
5
4
2
3
2
R
R
u
i
C
)
(
C
+
−
=
(6.7)
Drugi z prądów w gałęziach z kondensatorami to
0 (6.8)
3
1
=
)
(
C
i
Ponieważ przez rezystory R
1
, R
2
oraz R
3
nie płynie prąd, napięcia na ich zaciskach są równe 0.
Napięcie na rozwartych zaciskach źródła prądowego
L
i
jest równe napięciu panującemu na
zaciskach rezystora R
4
. Wynosi ono:
5
4
4
2
4
3
2
3
R
R
R
u
R
i
u
C
)
(
C
)
(
L
+
=
⋅
−
=
(6.9)
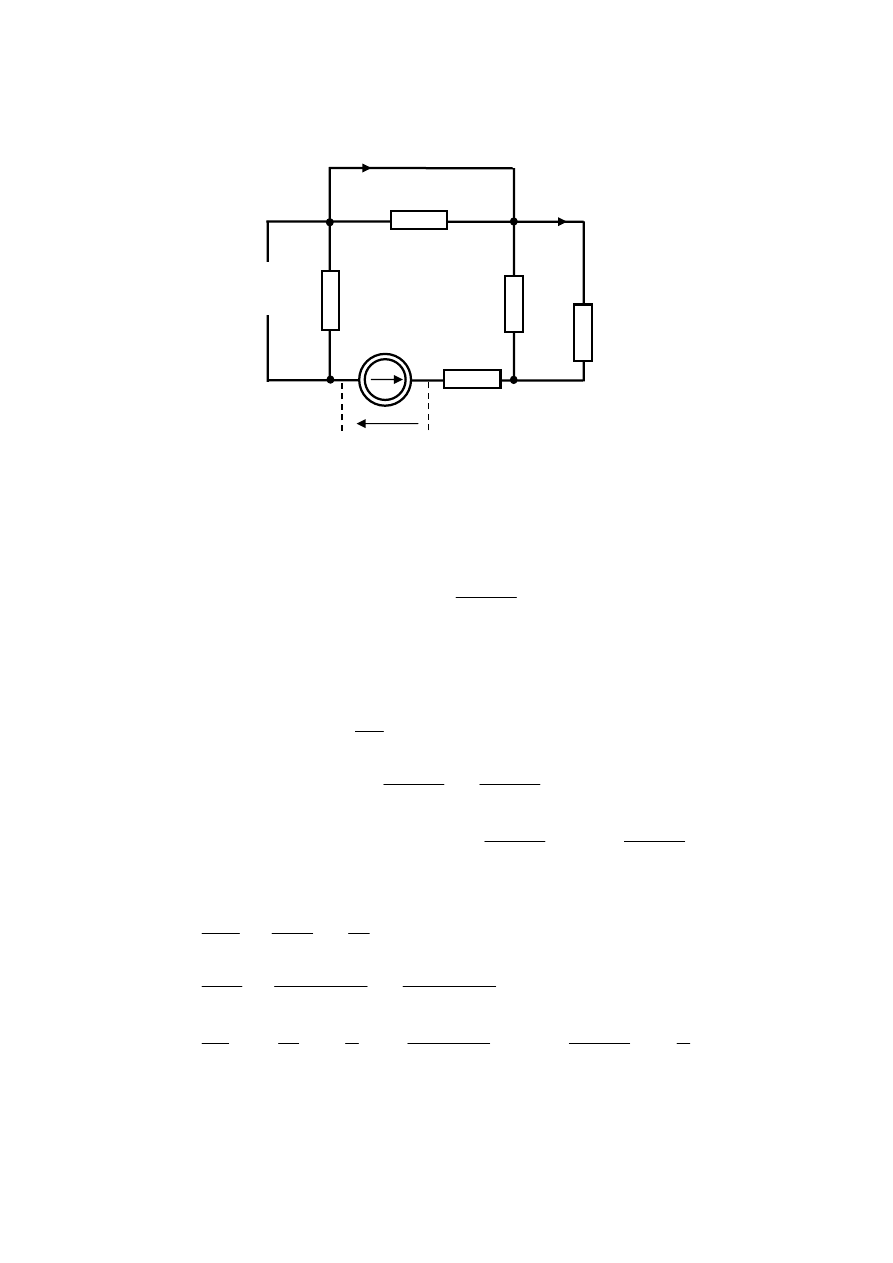
Ostatni z analizowanych obwodów zawierający jedynie źródło prądowe
L
i
przedstawiony
jest na rys.6.6. Prąd źródła
L
i
płynie przez rezystor R
3
, połączony szeregowo ze źródłem,
następnie przez równoległe połączenie oporników R
4
oraz R
5
, przez bezoporową zworę
łączącą zaciski rezystora R
2
i przez opornik R
1
. Prądy w gałęziach, w których były
umieszczone kondensatory wynoszą:
(6.10)
L
)
(
C
i
i
−
=
4
1
i na podstawie zależności obowiązującej dla dzielnika prądowego:
5
4
4
4
2
R
R
R
i
i
L
)
(
C
+
−
=
(6.11)
9
i
L
i
C1
(4)
R
1
R
2
R
3
R
4
u
L
(4)
i
C2
(4)
R
5
Rys.6.6. Czwarty z analizowanych obwodów zbudowany na mocy zasady superpozycji
Napięcie na źródle prądowym
L
i
wynosi zgodnie z napięciowym prawem Kirchhoffa:
+
+
+
−
=
1
5
4
5
4
3
4
R
R
R
R
R
R
i
u
L
)
(
L
(6.12)
Podsumowanie otrzymanych wyników analizy czterech układów dla trzech poszukiwanych
wielkości, przedstawionych przez zależności (6.2) ÷ (6.12) prowadzi do następujących
wzorów:
+
+
+
−
+
+
+
⋅
−
=
+
+
+
=
+
−
+
−
+
=
+
+
+
=
−
+
−
=
+
+
+
=
1
5
4
5
4
3
5
4
4
2
1
1
4
3
2
1
5
4
4
5
4
2
4
2
3
2
2
2
1
2
2
2
1
4
1
3
1
2
1
1
1
1
0
0
0
0
R
R
R
R
R
R
i
R
R
R
u
u
R
j
u
u
u
u
u
R
R
R
i
R
R
u
i
i
i
i
i
i
R
u
i
i
i
i
i
L
C
C
)
(
L
)
(
L
)
(
L
)
(
L
L
L
C
)
(
C
)
(
C
)
(
C
)
(
C
C
L
C
)
(
C
)
(
C
)
(
C
)
(
C
C
(6.13)
Uwzględnienie zależności (6.1) prowadzi do równań stanu:
(
)
(
)
(
)
L
R
R
R
R
R
R
i
L
R
R
R
u
L
u
L
R
j
t
i
C
R
R
R
i
C
R
R
u
t
u
C
i
R
C
u
t
u
L
C
C
L
L
C
C
L
C
C
1
1
d
d
d
d
1
d
d
1
5
4
5
4
3
5
4
4
2
1
1
2
5
4
4
2
5
4
2
2
1
2
1
1
1
+
+
+
−
+
+
+
⋅
−
=
+
−
+
−
=
−
−
=
(6.14)
Postać macierzowa tych równań to:
10
(
)
(
)
(
)
⋅
−
+
⋅
+
+
+
−
+
+
−
+
−
−
−
=
L
R
j
i
u
u
L
R
R
R
R
R
R
L
R
R
R
L
C
R
R
R
C
R
R
C
R
C
t
i
t
u
t
u
L
C
C
L
C
C
1
2
1
1
5
4
5
4
3
5
4
4
2
5
4
4
2
5
4
1
2
1
2
1
0
0
1
1
1
0
1
0
1
d
d
d
d
d
d
(6.15)
11