Kolokwium I

rok 2011/2012

Zadanie 3:

a) Sformułować twierdzenie Greena.
b) Korzystając z twierdzenia Greena obliczyć całkę









dy

y

x

dx

y

x

2

6

4









gdzie

łuk L jest łukiem zamkniętym zorientowanym ujemnie, złożonym z wykresów funkcji

2

x

2

,

0









x

y

y

.

Rozwiązanie:

a) Twierdzenie Greena

Jeżeli funkcje P i Q są funkcjami klasy C

1

wewnątrz obszaru domkniętego

2

R

D



i normalnego względem

obu osi układu współrzędnych, brzeg L obszaru

D

jest łukiem zorientowanym dodatnio oraz pole wektorowe





Q

P

F

,



jest różniczkowalne w sposób ciągły na

D

, wówczas:































L

D

dxdy

y

P

x

Q

Qdy

Pdx

.

b)

Całka

1.

Przekształcamy wzór funkcji

2

x

2







x

y

, która składa się na łuk :

2

x

2







x

y

/( )

2

2

2

2

x

x

y







0

2

2

2







y

x

x





1

1

2

2







y

x

-

powstaje równanie okręgu o środku S(-1,0) i promieniu r=1

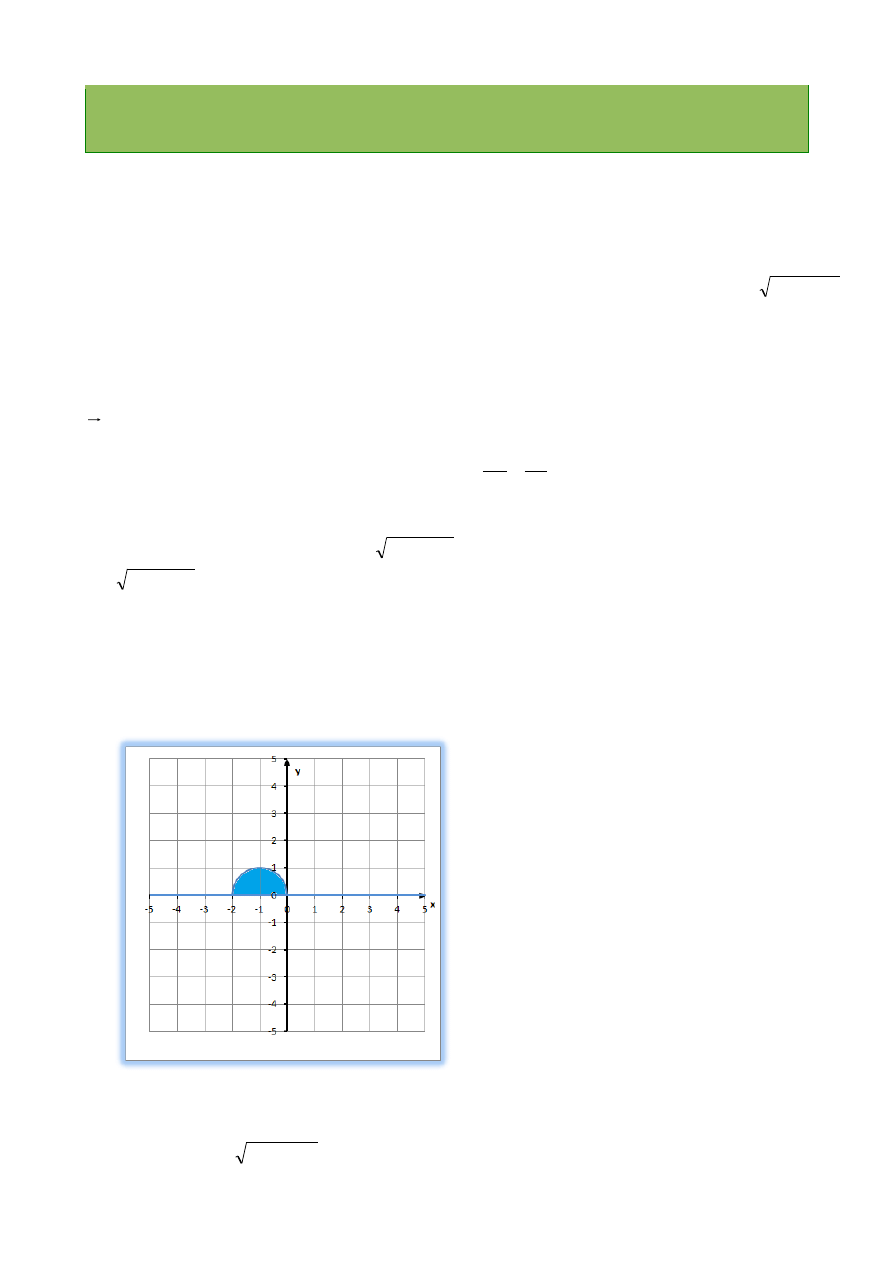
2. Rysujemy

układ współrzędnych z funkcjami tworzącymi łuk L :

3.

Określamy dziedzinę:























2

2

0

0

2

:

x

x

y

x

D

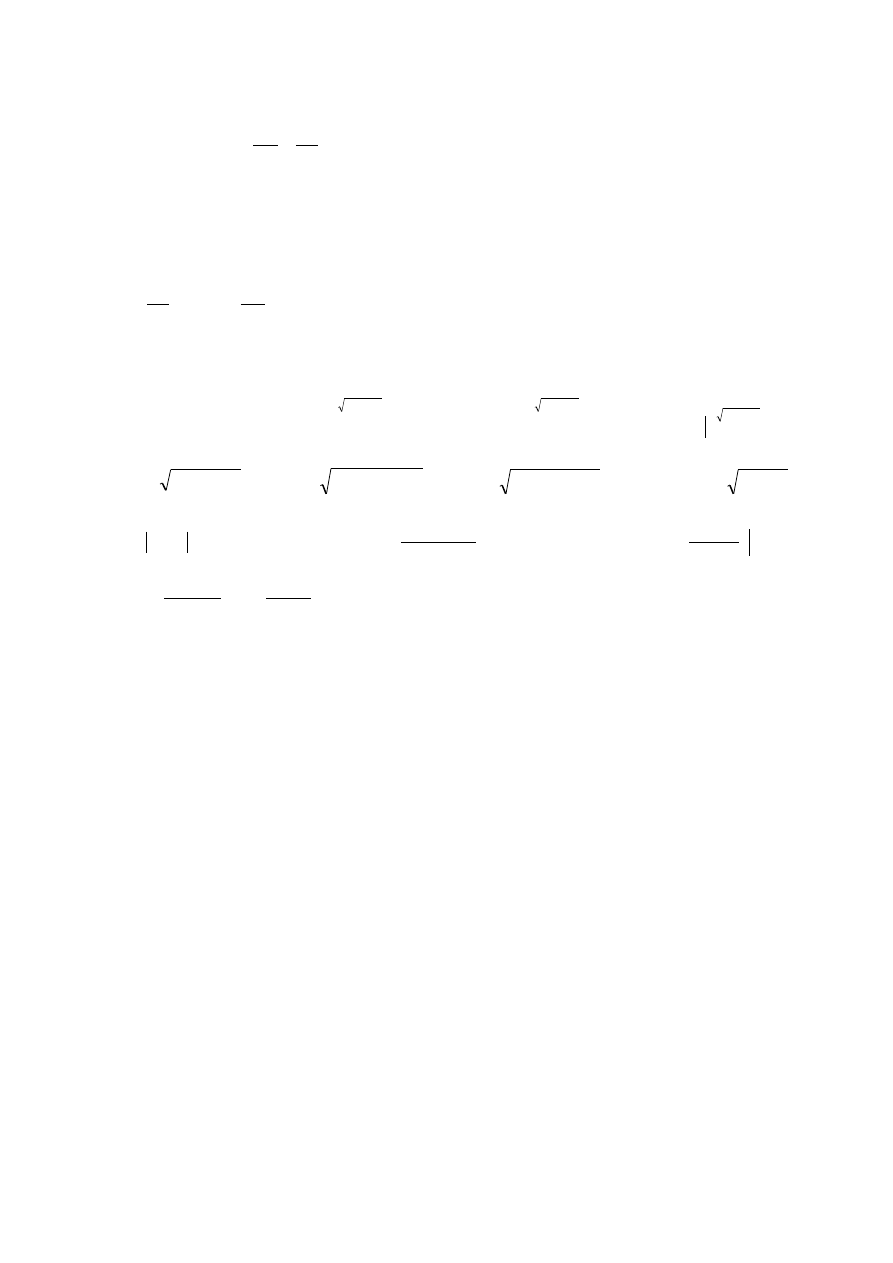
4. Korzystamy ze wzoru z twierdzenia Greena:

- funkcje

P

i

Q

są ciągłe i różniczkowalne w obszarze

D

5. Obliczamy pochodne z

P

i

Q

:

6.

Obliczamy całkę:

W drugiej linii

powyższych obliczeń skorzystano z podstawienia:

x+1 = cos t

dx = - sin t dt

Odpowiedź:





















L

dy

y

x

dx

y

x



5

2

6

4

Autor:

Agata C.

grupa

2

20.10.2013

;































L

D

dxdy

y

P

x

Q

Qdy

Pdx

y

x

Q

y

x

P

2

6

4









4









y

P

6







x

Q









 









 

 





   

   

 

 

 





 



























5

0

0

0

5

2

)

0

sin(

0

2

)

2

sin(

5

2

2

sin

5

2

cos

1

5

2

2

cos

1

10

sin

10

sin

sin

10

sin

sin

10

sin

1

cos

10

1

1

10

2

10

10

10

4

6

2

6

4

0

0

0

0

2

0

0

2

0

2

0

2

0

2

2

2

0

2

2

0

2

0

0

2

2

0

0

2

2

2

2











































 

























































































 

 



























t

t

dt

t

dt

t

dt

t

dt

t

t

dt

t

t

dt

t

t

dx

x

dx

x

x

dx

y

dydx

dydx

dy

y

x

dx

y

x

L

x

z

x

x

x

x