- 1 -

KONSTRUKCJE ALUMINIOWE

Rozwój konstrukcji aluminiowych rozpoczął się w okresie II wojny światowej, a bezpośrednią
przyczyną tego były ograniczone możliwości dostaw stali. Pojawiły się wówczas w budownictwie
różne typy konstrukcji aluminiowych, takie jak: mosty, wiadukty, kładki, konstrukcje wieżowe,
maszty, przestrzenne przekrycia prętowe, kopuły, zbiorniki, a nawet wieże wyciągowe w górnictwie.

Po wojnie rynek konstrukcji stalowych odzyskał dawną pozycję z uwagi na rozwiązania tańsze niż
aluminium. Obecnie konstrukcje aluminiowe rozwijają się w kierunku rozwiązań bardziej
zekonomizowanych.

Przełomem w technologii konstrukcji aluminiowych stało się wynalezienie przegrody termicznej
z tworzywa sztucznego (poliuretan, polamid). Jego wbudowanie w aluminiowy kształtownik
spowodowało radykalne obniżenie przewodności cieplnej przegrody.

K417845X

K518101X

- 2 -

Wszystkie profile w konstrukcjach fasad, dachów i okien są izolowane przekładką ze wzmocnionego
włóknem szklanym poliamidu.
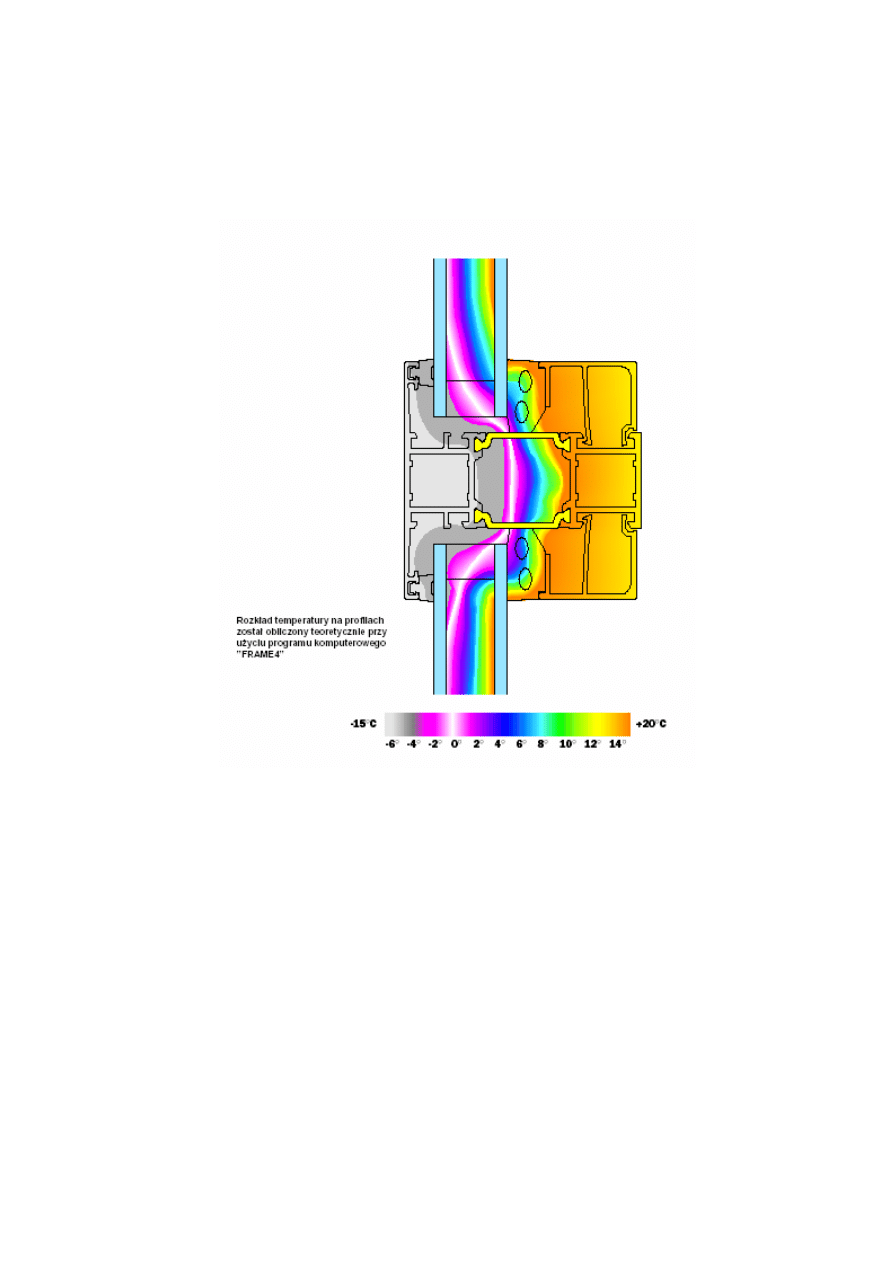
Niektóre rozwiązania posiadają ponadto izolację w postaci wkładki z tworzywa komórkowego
umieszczonej między przekładkami termicznymi. Izolacja z tworzywa komórkowego poprawia
wartość współczynnika U dla przekroju profilu o 0,3 W/m2K. Przykładowy rozkład temperatur
pokazano na rysunku poniżej.

Decydującymi o stosowaniu w budownictwie konstrukcji aluminiowych są następujące cechy:

- niski ciężar objętościowy,
- wysokie wartości wytrzymałości obliczeniowej,
- odporność na korozję atmosferyczną,
- odporność na działanie wielu czynników chemicznych.

Glin (aluminium) jest pierwiastkiem powszechnie występującym w przyrodzie, najczęściej w postaci
wodorotlenków, takich jak: boksyt, glinokrzemiany, kaoliny i glinki. Podstawową rudą do produkcji
aluminium jest boksyt, a proces technologiczny przebiega w dwóch etapach.
W pierwszym etapie rudę przetwarza się na tlenek glinu:

- metodami chemicznymi, polegającymi na rozpuszczaniu boksytu wodorotlenkiem sodowym

lub kwasem siarkowym,

- metodami termicznymi, polegającymi na spiekaniu boksytu z sodą i wapieniem w piecu

obrotowym lub na jego stapianiu z wapieniem i koksem w piecu elektrycznym.

W drugim etapie przeprowadza się elektrolizę tlenku glinu w roztopionym kriolicie, służącym jako
rozpuszczalnik.
Otrzymane w ten sposób surowe aluminium, podlega oczyszczeniu (chlorowanie, filtrowanie,
przetapianie), po czym wykonuje się wlewki w kształcie gąsek lub bloków.

- 3 -

W konstrukcjach budowlanych mają zastosowanie głównie stopy aluminium,
ponieważ charakteryzują się one znacznie lepszymi parametrami niż czyste aluminium. Do
wytwarzania elementów i konstrukcji budowlanych stosuje się stopy przeznaczone do obróbki
plastycznej o oznaczeniu PA:

- stopy aluminium z magnezem (AlMg), charakteryzujące się na ogół średnią wytrzymałością i

odpornością na korozję oraz dobrą spawalnością,

- stopy aluminium z magnezem i krzemem (AlMgSi), charakteryzujące się średnią

wytrzymałością i odpornością na korozję oraz średnią spawalnością,

- stopy aluminium z miedzią i magnezem (AlCuMg – dural, duraluminium), charakteryzujące się

dużą wytrzymałością, słabą odpornością na korozję i słabą spawalnością,

- stopy aluminium z cynkiem i magnezem (alZnMg – duralumin cynkowe), charakteryzujące się

dużą wytrzymałością, średnią odpornością na korozję i dobrą spawalnością.

Wyroby ze stopów aluminium w postaci blach, taśm, prętów, drutów, rur i kształtowników wytwarza
się metodą obróbki plastycznej (wyciskanie, walcowanie, ciągnienie) na zimno i na gorąco.


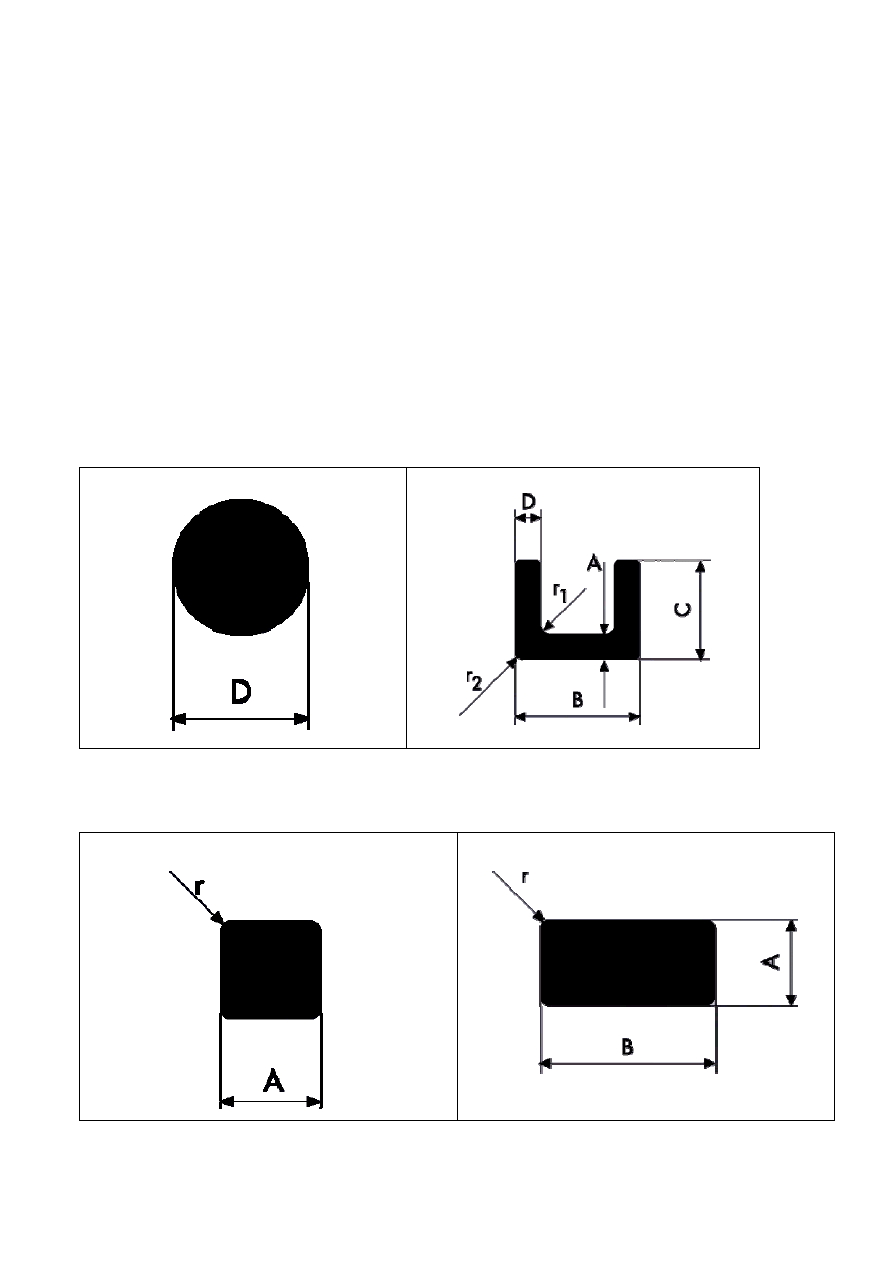
Poniżej przedstawiono wybrane profile produkowane przez firmę SAPA:

Pręty okrągłe

Ceowniki

Pręty kwadratowe

Pręty prostokątne

- 4 -

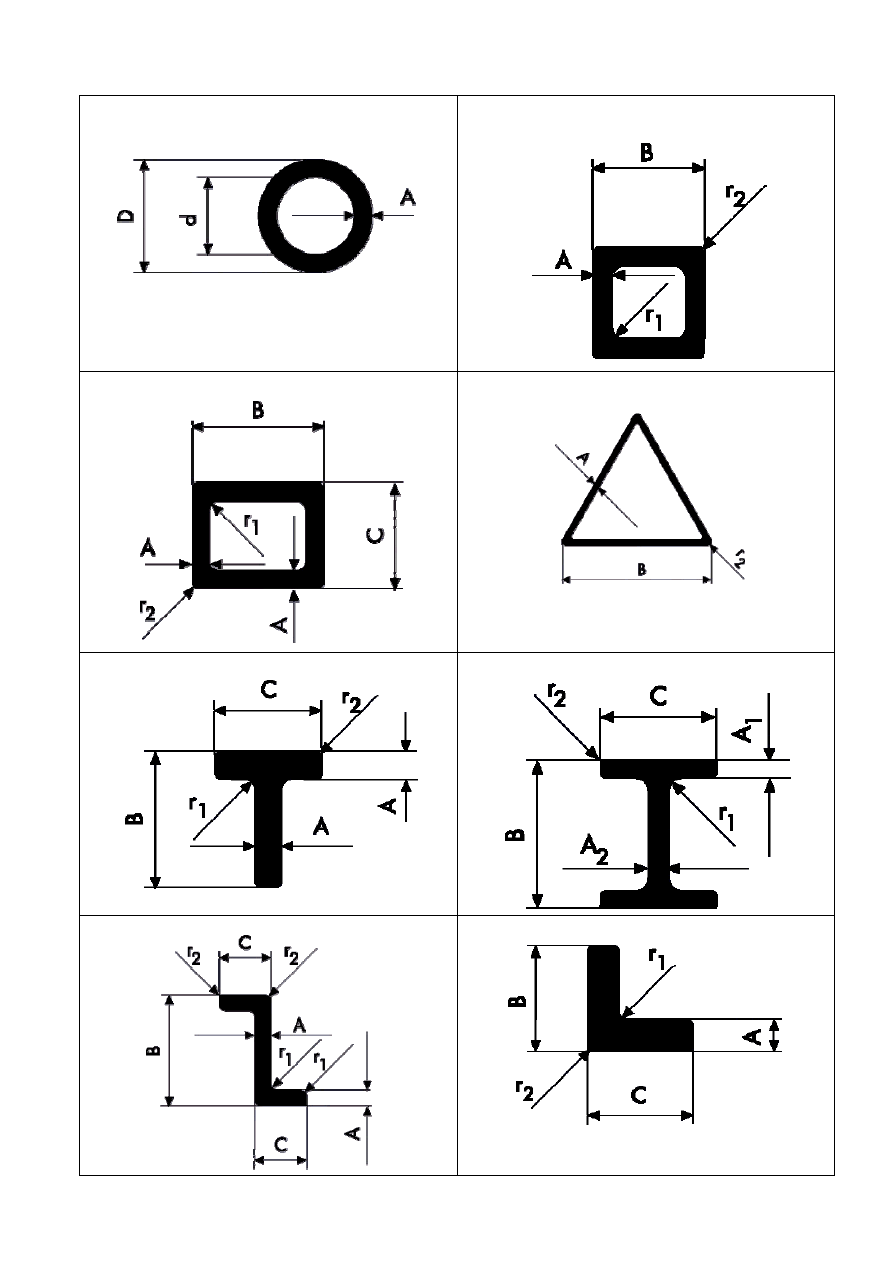
Rury okrągłe

Rury kwadartowe

Rury prostokątne

Rury trójkątne

Teowniki

Dwuteowniki

Zetowniki

Kątowniki równoramienne

- 5 -

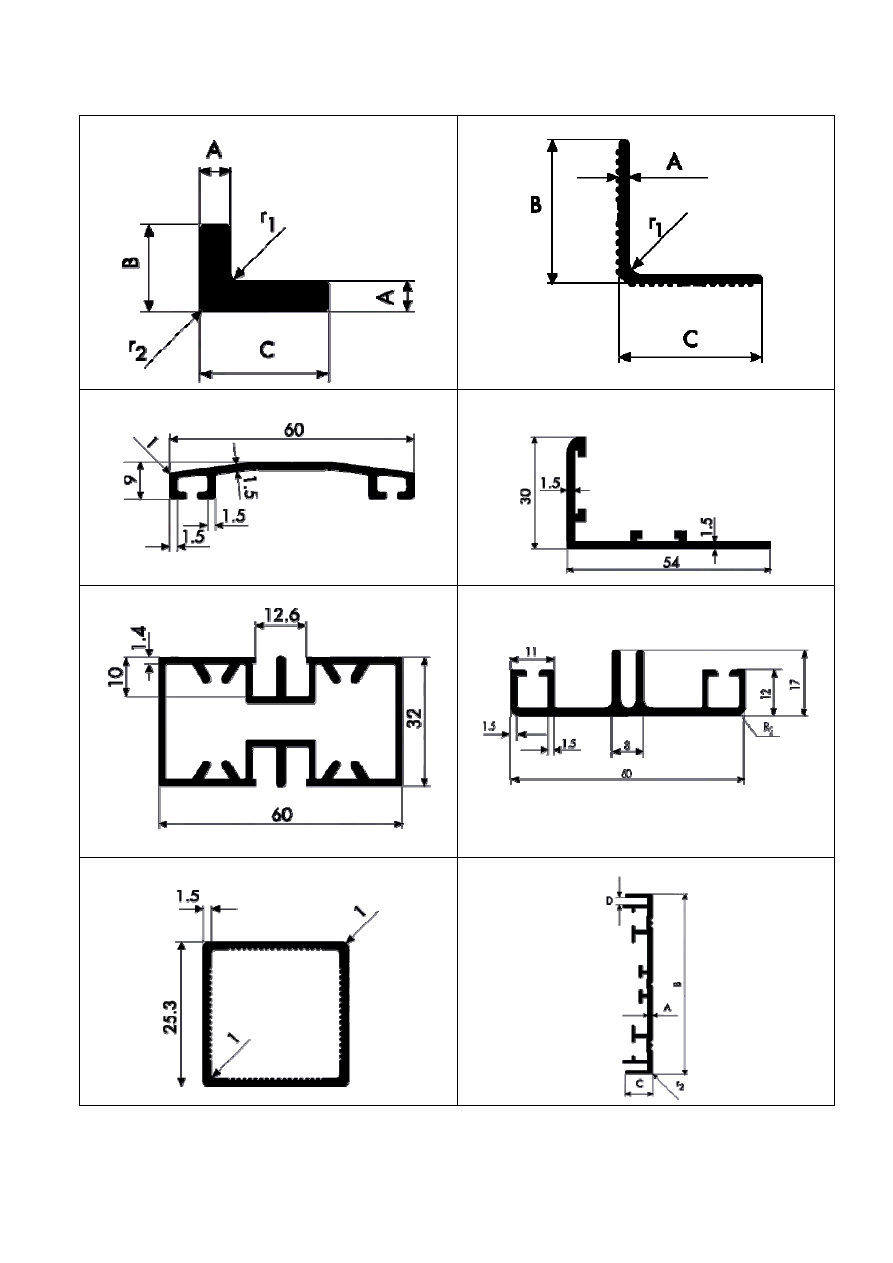
Kątowniki nierównoramienne

Kątowniki ozdobne

Profile specjalnego przeznaczenia

Profile specjalnego przeznaczenia

Profile specjalnego przeznaczenia

Profile specjalnego przeznaczenia

Profile specjalnego przeznaczenia

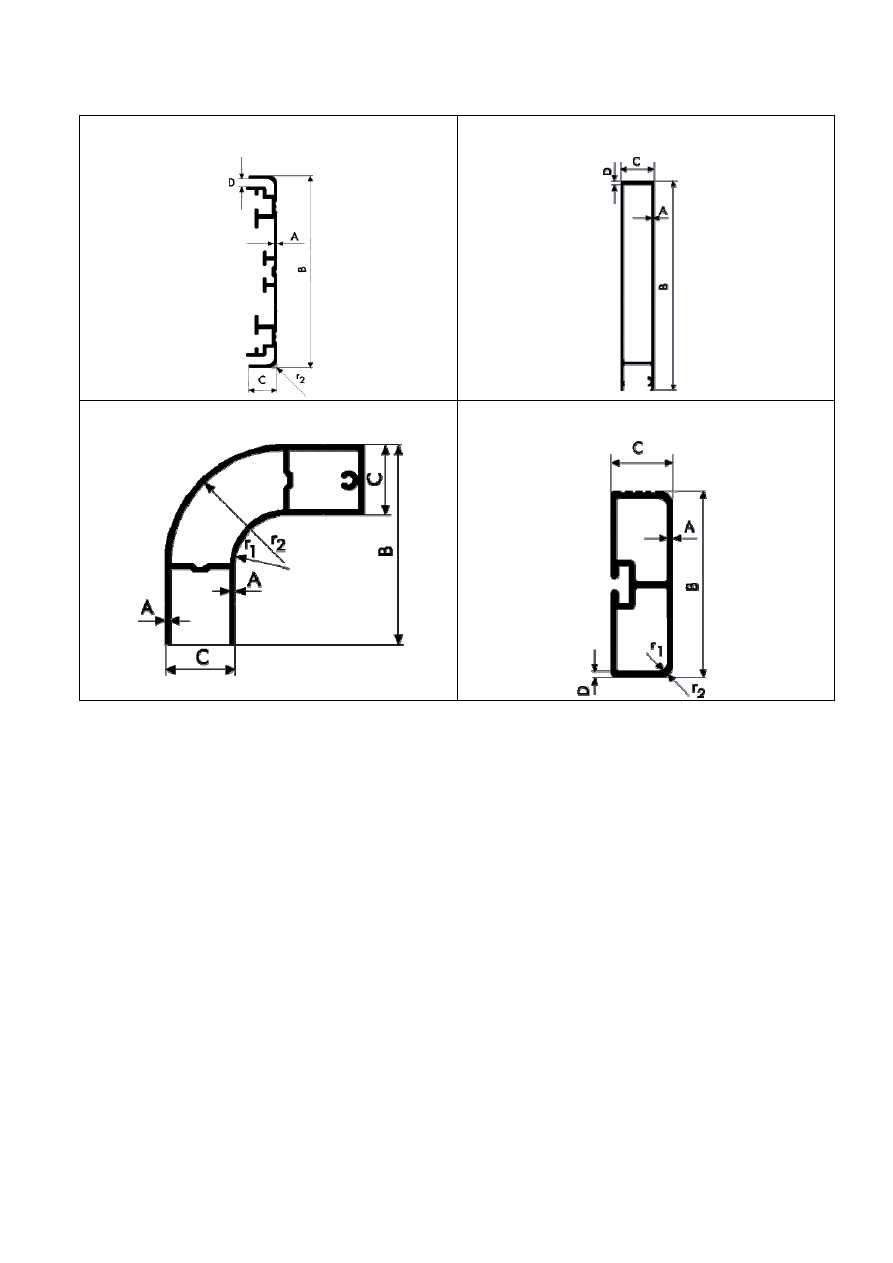
Profile kasetonowe

- 6 -

Profile kasetonowe

Profile burtowe - górne

Profile burtowe – odbojniki

Profile burtowe - odbojniki

- 7 -

Założenia do wymiarowania konstrukcji ze stopów aluminium:

Wykres σ-ε dla stopów aluminium jest zbliżony do
wykresu dla stali stopowej. Nie mają one wyraźnej
granicy plastyczności. Jako podstawę do określenia
wytrzymałości obliczeniowej przyjmuje się umowną
granicę plastyczności R

0,2

odpowiadającą trwałemu

wydłużeniu ε=0,2%.
Własności mechaniczne zależą od gatunku stopu i
postaci obróbki cieplnej.

Postać lub stan obróbki cieplnej

Oznaczenie wg PN-71/H-01706

Rekrystalizowany

r

Wyciskana

pp

Naturalnie utwardzony wydzielinowo

ta

Sztucznie utwardzony wydzielinowo

tb

Naturalnie starzony

tc

Sztucznie starzony

td

Zgnieciony:

- półtwardy
- twardy

z4
z6

Przykładowe wartości własności mechanicznych niektórych stopów aluminiowych w zależności od
stanu obróbki podano w tabeli poniżej:

Gatunek stopu - cecha

Stan obróbki

R

m

[MPa]

R

0,2

[MPa]

r, pp

90

40

PA1N

z4

120

90

r, pp

150

60

PA2N

z4

180 110

r, pp

180 80

PA11N

z4

230 140

r, pp

240 120

PA20N

z4

280 200

ta

140

80

tb

220 160

tc

120

60

PA38

td

200 140

ta

200 100

tb

280 200

PA4N

tb, R

m

32

320 260

ta

160 110

PA45

tb

250 210

- 8 -

Metoda wymiarowania
Obecnie u nas w kraju brak jest normy dotyczącej projektowania konstrukcji aluminiowych. Norma
PN-64/B-03220 Konstrukcje aluminiowe. Obliczenia statyczne i projektowanie. – bazowała na
metodzie naprężeń dopuszczalnych i już nie obowiązuje z uwagi, miedzy innymi, na brak spójności z
innymi normami dotyczącymi projektowania (np. normy obciążeń). Aktualnie opracowywana jest
nowa norma bazująca na metodzie stanów granicznych.

Na dzień dzisiejszy można obliczać konstrukcje aluminiowe na podstawie wytycznych opracowanych
przez COBPKM „Mostostal”, również w Poradniku Inżyniera i Technika Budowlanego – tom 5,
podany jest sposób obliczania elementów i ich połączeń.

Wytrzymałość obliczeniową stopów aluminium na rozciąganie f

dt

określa się jako:

1,65

R

min

f

R

0,82

m

dt

t

0,2,

=

×

analogicznie określa się wytrzymałość obliczeniową na ściskanie f

dc

.

Wprowadzając do obliczeń wartości wytrzymałości obliczeniowych należy mnożyć przez
współczynnik warunków pracy α, który wynosi:

- 9 -

Jeżeli mamy do czynienia z przekrojem osłabionym przez spawanie i zachodzi warunek A

sp

≤0,15×A

(A – przekrój elementu), to wpływ spawania można pominąć. W innym przypadku należy określić
wytrzymałość obliczeniową zredukowaną:

(

)

'

d

d

sp

d

dz

f

f

A

A

f

f

−

×

−

=

,

gdzie: A

sp

– pole części przekroju osłabionego spawaniem,

A – pole całego przekroju poprzecznego,
f

d

– wytrzymałość obliczeniowa materiału,

f

d

’

– właściwa wytrzymałość obliczeniowa materiału osłabionego spawaniem.

Powyższe odnosi się do rozciągania lub strefy rozciąganej w elemencie zginanym.

Dla stopów aluminium należy do obliczeń przyjmować następujące współczynniki:

- moduł sprężystości podłużnej E=70000 MPa,
- moduł sprężystości poprzecznej G=27000 MPa,
- współczynnik liniowej rozszerzalności cieplnej α

t

=0,000023

Projektowanie elementów konstrukcyjnych
A. Elementy rozciągane:
Elementy rozciągane oblicza się określając naprężenia normalne,

dt

n

f

A

N ≤

=

σ

- dla elementów osłabionych spawaniem należy wstawić

f

dz

,

Rozciągane kątowniki połączone jedną ścianką z blachą węzłową, na nity lub śruby, sprawdza się ze
wzoru:

dt

n

f

t

b

3

2

A

N

σ

≤

×

×

−

=

.

W powyższych wzorach występują następujące oznaczenia:

n

A - przekrój poprzeczny pręta netto,

N - siła rozciągająca w elemencie,

t

b, - odpowiednio szerokość i grubość półki.

B. Elementy ściskane:
Elementy ściskane należy obliczać z uwzględnieniem wyboczenia. W przypadku konstrukcji
aluminiowych wyboczenie jest problemem znacznie szerszym niż ma to miejsce w konstrukcjach
stalowych. Zaleca się aby smukłość prętów ściskanych nie przekraczała:

λ ≤ 180 – w przypadku obciążeń statycznych,

λ ≤ 120 – w przypadku obciążeń o charakterze dynamicznym.

Naprężenia normalne przy ściskaniu osiowym sprawdza się wg wzoru:

φ

f

σ

dc

×

≤

=

A

N

Współczynnik wyboczeniowy

φ wyznacza się w zależności od smukłości pręta λ i umownej granicy

plastyczności

R

0,2

.

Przykładowo, dla stopu PA38-td (sztucznie starzonego)

R

0,2

=140 MPa, wartości współczynnika

wyboczeniowego w zależności od smukłości

λ są następujące:

λ

0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180

φ

1,00 1,00 0,93 0,85 0,78 0,71 0,65 0,60 0,54 0,49 0,44 0,39 0,35 0,30 0,26 0,23 0,20 0,18 0,16

- 10 -

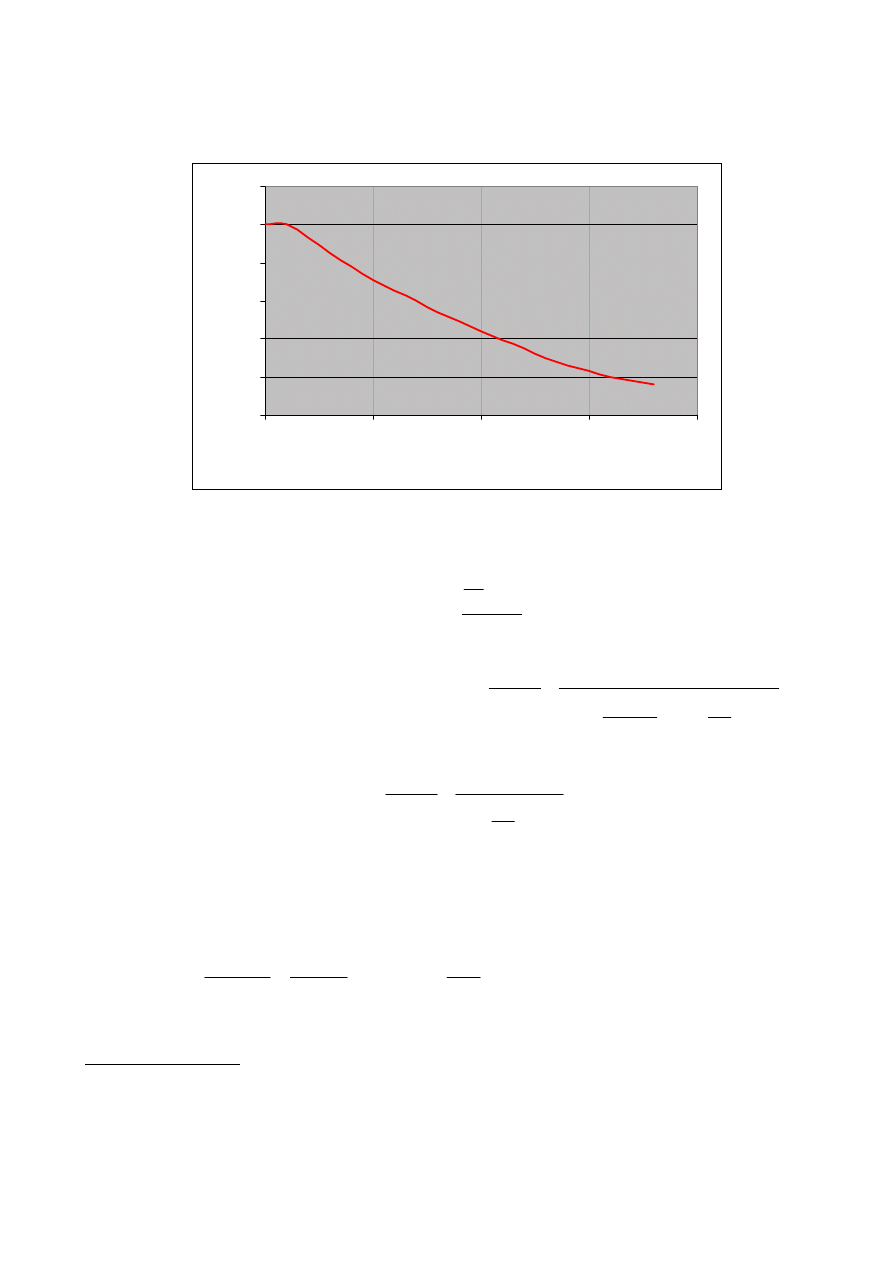
Powyższe obrazuje również przedstawiony wykres zależności współczynnika wyboczeniowego od
smukłości elementu:

0

0,2

0,4

0,6

0,8

1

1,2

0

50

100

150

200

Smukłość

Wsp. wyboczeniow

y

Nośność prętów mimośrodowo ściskanych sprawdza się w zależności od wartości stosunku momentu
zginającego w środku rozpiętości

0

M do maksymalnego momentu występującego w pręcie

max

M

,

wg następujących wzorów:

- gdy

max

,

M

5

0

M

0

×

≤

=>

1

f

σ

φ

σ

dc

g

c

≤

+

,

- gdy

max

max

,

,

M

9

0

M

M

5

0

0

×

<

<

×

=>

1

f

σ

σ

1

M

M

2

1

σ

f

φ

σ

dc

E

c

0

g

dc

c

≤

×

⎥

⎦

⎤

⎢

⎣

⎡

×

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

×

−

+

×

max

,

- gdy

max

,

M

9

0

M

0

×

≥

=>

1

f

σ

σ

1

σ

f

φ

σ

dc

E

c

g

dc

c

≤

×

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

×

gdzie:

c

σ - naprężenie od ściskania osiowego,

g

σ - naprężenie od zginania (ściskające),

φ - współczynnik wyboczeniowy dla największej smukłości pręta,

2

2

2

E

λ

431800

λ

64

1

E

π

σ

≈

×

×

=

,

, przy czym

64

1

1

,

- jest współczynnikiem niejednorodności,

λ

- smukłość w płaszczyźnie działania momentu.

C. Elementy zginane:
Elementy zginane oblicza się wg wzorów znanych z teorii sprężystości, przy czym naprężenia
normalne

σ

, styczne

τ

i zastępcze

z

σ , muszą spełniać warunki:

dt

f

σ

≤

,

dv

f

τ

≤

,

dc

z

f

σ

≤

.

Wytrzymałość obliczeniową przy zginaniu przyjmuje się dla strefy rozciąganej

dt

d

f

f

=

, a dla strefy

ściskanej

dc

d

f

f

=

.

- 11 -

Stateczność ogólną belek aluminiowych należy sprawdzać w przypadkach, gdy pas ściskany nie jest

połączony ze sztywną tarczą i gdy smukłość belki

y

y

i

l

λ

=

jest większa od wartości granicznych

1

λ

.

Stateczność sprawdza się z warunku:

dz

f

≤

σ

,

gdzie:

σ

- naprężenia ściskające,

dz

f - wytrzymałość obliczeniowa przy zwichrzeniu.

Dla wyznaczenia

dz

f , należy ustalić smukłość belki ze wzoru

yz

yz

i

l

λ

=

, w którym zastępczy promień

bezwładności oblicza się z zależności:

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

×

×

+

+

±

×

×

×

=

2

y

s

x

y

yz

h

l

I

I

152

0

25

1

W

h

I

7

1

γ

i

,

,

,

Znak „+” przyjmuje się, jeżeli obciążenie belki jest przyłożone do dolnej półki, a znak „–”, gdy do
półki górnej.
Współczynnik

(

)

6

1

0

1

γ

,

,

÷

=

w zależności od: schematu statycznego i warunków brzegowych oraz

sposobu obciążenia elementu.
Wytrzymałość obliczeniowa

dz

f , zależna od kształtu przekroju poprzecznego i smukłości granicznych.

Dodatkowym zagadnieniem jest stateczność miejscowa ścianek prętów ściskanych i ścianek
elementów zginanych. Procedury dla odpowiednich przypadków wytrzymałościowych z
uwzględnieniem stateczności miejscowej podane są, między innymi w podręczniku

„Konstrukcje

metalowe, część II”, autorstwa M. Łubińskiego i W. Żółtowskiego, wydanym przez „Arkady” – 2004.

- 12 -

KONSTRUKCJE ALUMINIOWE – UZUPEŁNIENIE Z UWAGI NA NORMY ISO I EC9.


Własności mechaniczne stopów aluminium zależą od zawartości pierwiastków stopowych.
Głównymi składnikami stopów są: miedź, krzem, mangan, cynk i magnez.

W praktyce metalurgicznej stopy aluminium dzieli się na dwie podstawowe grupy:
- stopy do przeróbki plastycznej, np. AlMg, AlMn, AlMgSi, AlZnMg i AlCuMg,
- stopy odlewnicze, np. AlMg, AlSi, AlSiMg i AlCuMgTi.

Można też spotkać się z podziałem wynikającym z obróbki termicznej:
- stopy nie ulepszone cieplnie, np. AlMg, AlMn, AlSi, AlMgMn,
- stopy ulepszonie cieplnie, np. AlCuMg, AlMgSi,AlZnMg,AlSiCu.

Norma

PN-EN 573-1/2 Aluminium i stopy aluminium. Skład chemiczny i rodzaje wyrobów

przerobionych plastycznie. Część 1: System oznaczeń numerycznych. Część 2: System oznaczeń na
podstawie symboli chemicznych. PKN – 1997. wprowadza nowe, numeryczne oznaczenia stopów
aluminium. Pierwsza z czterech cyfr w oznaczeniu jest związana z zawartością dominującego
pierwiastka
w stopie i opisuje serię stopu:

1xxx techniczne aluminium o zawartości czystego Al Powyżej 99%,
2xxx stopy aluminium z miedzią (seria 2000),

3xxx

stopy aluminium z magnezem (seria 3000),

4xxx stopy aluminium z krzemem (seria 4000),

5xxx

stopy aluminium z magnezem (seria 5000),

6xxx

stopy aluminium z magnezem i krzemem (seria 6000),

7xxx

stopy aluminium z cynkiem (seria 7000),

8xxx stopy aluminium z innymi dodatkami stopowymi (seria 8000),
9xxx stopy specjalne.

Jeżeli druga cyfra w oznaczeniu jest zerem, to oznacza ona stop oryginalny, a cyfry od 1 do 9
oznaczają kolejne modyfikacje stopu oryginalnego. Dwie ostatnie cyfry nie mają szczególnego
znaczenia i służą wyłącznie do identyfikacji różnych stopów aluminium w danej serii.
Konstrukcyjne stopy aluminium według

Eurocode 9 Projektowanie konstrukcji aluminiowych należą

do serii

3000, 5000, 6000

i

7000

.

Stopy aluminium produkowane są w szerokim zakresie stanów, związanych ściśle z przyszłym ich
zastosowaniem. Wg

PN-EN 515 Aluminium i stopy aluminium. Wyroby przerobione plastycznie.

Oznaczenia stanów. PKN-1996 występują następujące oznaczenia literowe:
F – stan wytworzony, tzn. wyciskany, walcowany itp.
O – stan wyżarzony,
H – stan umocniony zgniotem,
W – stan przesycony (opis stanu niestabilnego),
T – stan obrobiony cieplnie,
H – stan obrobiony cieplnie z dodatkowym umocnieniem.
Po oznaczeniach literowych występują oznaczenia cyfrowe opisujące stan stopu bardziej szczegółowo.

- 13 -

Wytrzymałość obliczeniowa stopów konstrukcyjnych
Rozróżnia się następujące wytrzymałości charakterystyczne i obliczeniowe przekrojów aluminiowych
w stanie nośności granicznej:

- wytrzymałość charakterystyczna

f

o

i obliczeniowa

f

do

przekrojów zginanych, ściskanych lub

rozciąganych na granicy plastyczności umownej materiału rodzimego:

,

f

f

f

s

02

02

o

γ

(

=

=

,

f

f

f

f

1

M

o

CM

o

CM

s

02

do

γ

γ

γ

γ

=

=

×

=

(

- wytrzymałość charakterystyczna

f

a

i obliczeniowa

f

da

przekrojów zginanych, ściskanych lub

rozciąganych na granicy wytrzymałości rozdzielczej przekroju lokalnie osłabionego:

,

f

f

f

s

u

u

a

γ

(

=

=

,

f

f

f

f

2

M

a

CM

a

CM

s

u

da

γ

γ

γ

γ

=

=

×

=

(

- wytrzymałość charakterystyczna

f

v

i obliczeniowa

f

dv

przy ścinaniu na granicy plastyczności

umownej materiału rodzimego:

,

3

f

f

3

f

f

1

M

o

dv

o

v

×

=

→

=

γ

- wytrzymałość charakterystyczna

f

w

i obliczeniowa

f

dw

przy ściskaniu lub rozciąganiu na granicy

wytrzymałości rozdzielczej przekroju spoiny:

.

f

f

f

f

Mw

w

dw

u

w

γ

=

→

=

Oznaczenia:
f

02

– umowna granica plastyczności,

f

u

– wytrzymałość doraźna (rozdzielcza),

γ

s

,

γ

CM

,

γ

M1

,

γ

M2

,

γ

Mw

– częściowe współczynniki bezpieczeństwa i współczynniki materiałowe.

Nośność przekrojów aluminiowych
Normalizacja obliczeń konstrukcji aluminiowych w rekomendacjach europejskich EC9 wprowadza
w sposób konsekwentny rozwiązania teorii nośności granicznej. Wyrazem takiego podejścia jest
klasyfikacja przekrojów aluminiowych (tak jak dla przekrojów stalowych).
Jednak możliwość uwzględniania plastostatyki oraz pełnej plastycznej redystrybucji naprężeń
w obliczeniach statycznie niewyznaczalnych aluminiowych konstrukcji prętowych jest dyskusyjna,
z uwagi na ograniczone własności plastyczne stopów aluminium.

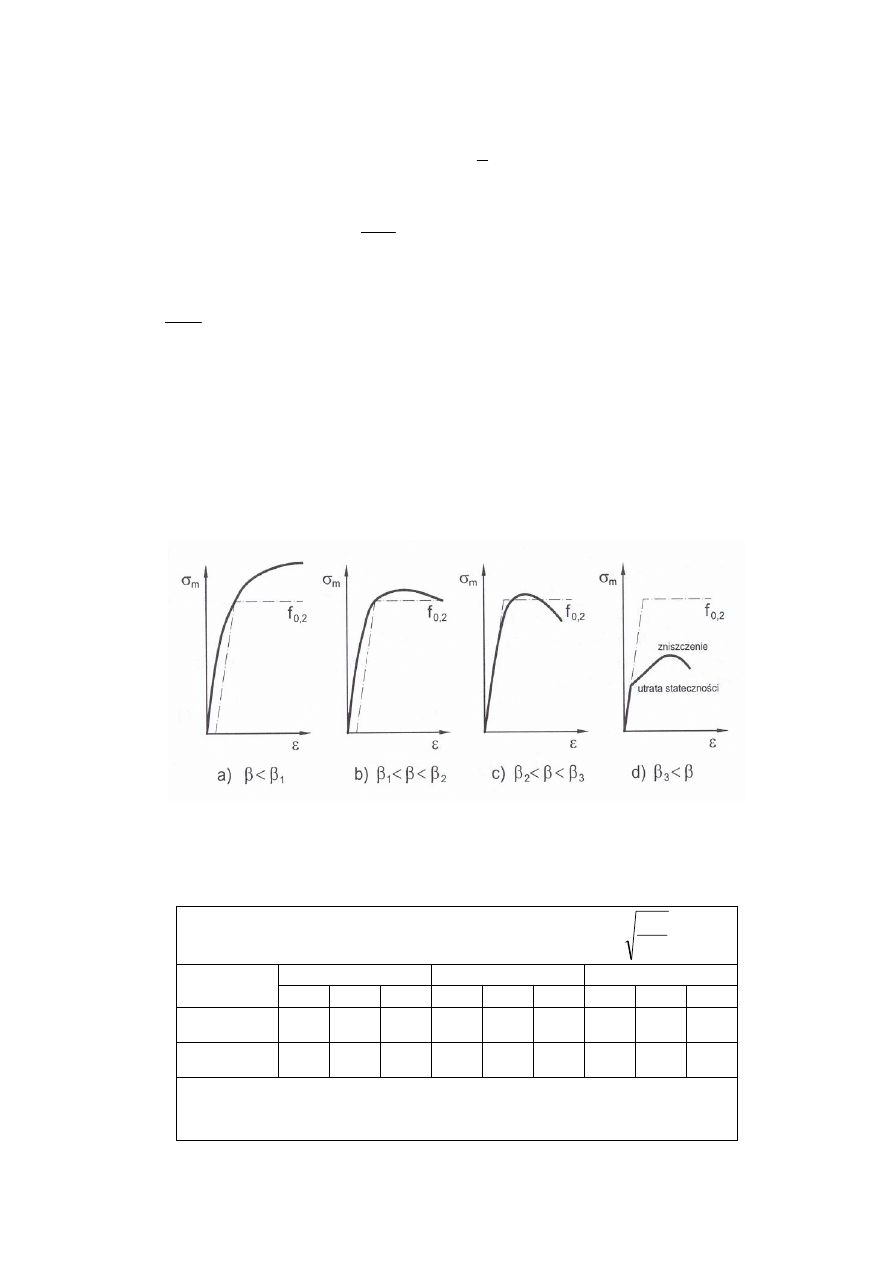
W EC9 rozróżnia się cztery klasy przekrojów aluminiowych zginanych, w zależności od podatności
ich ścianek na utratę stateczności miejscowej:

¾ Klasa 1 obejmuje przekroje, które przy zginaniu osiągają nośność uogólnionego przegubu

plastycznego oraz wykazują zdolność do obrotu wymaganą w pełnej analizie plastycznej
konstrukcji,

¾ Klasa 2 obejmuje przekroje, które przy zginaniu osiągają nośność uogólnionego przegubu

plastycznego, jednak ich zdolność do obrotu jest ograniczona,

¾ Klasa 3 obejmuje przekroje zginane, których nośność zostaje osiągnięta po uplastycznieniu

skrajnych włókien strefy ściskanej; uplastycznienie całej strefy ściskanej jest niemożliwe,
ponieważ jest ona podatna na utratę stateczności miejscowej,

¾ Klasa 4 obejmuje przekroje podatne na utratę stateczności miejscowej, które tracą nośność

przy największych naprężeniach ściskających mniejszych od granicy plastyczności.

- 14 -

Parametrem charakteryzującym podatność ścianek przekroju na utratę stateczności miejscowej jest ich
smukłość płytowa (

λ

p

wg PN lub

β wg EC9):

,

t

b

g

×

=

β

1,

dla

-

1

0,8

g

-1,

1

dla

3

,

0

7

,

0

g

≤

=

>

>

×

+

=

ψ

ψ

ψ

ψ

gdzie:

b – wysokość ścianki,

t – grubość ścianki,

ψ=

min

max

σ

σ

– stosunek naprężeń krawędziowych.

Zakwalifikowanie przekroju do jednej z czterech klas wymaga sprecyzowania kryteriów
klasyfikacyjnych. Taką rolę spełniają smukłości graniczne klas

β

i

, gdzie (

i=1,2,3),ustalone dla ścianek

opartych na trzech lub czterech krawędziach, dla których zachodzi:

4.

klasa

3,

klasa

2,

klasa

1,

klasa

3

3

2

2

1

1

→

<

→

≤

<

→

≤

<

→

≤

β

β

β

β

β

β

β

β

β

β

Powyżej pokazano zależności pomiędzy średnim naprężeniem ściskającym

σ

m

i odkształceniem

ε dla

różnych smukłości ścianek przekroju

β.

Graniczne smukłości

β

i

dla trzech klas imperfekcji ścianek

A, B i C zestawiono w tablicy poniżej:

Graniczne smukłości ścianek aluminiowych

β

i

,

o

f

250

=

ε

,

β

1

β

2

β

3

Podparcie

ścianki

A B C A B C A B C

Z krawędzią
swobodną

3

ε

2,5

ε

2

ε

4,5

ε

4

ε

3

ε

6

ε

5

ε

4

ε

na całym
obwodzie

11

ε

9

ε

7

ε

16

ε 13ε 11ε 22ε 18ε 15ε

A –

stopy ulepszone cieplnie nie spawane,

B –

stopy ulepszone cieplnie spawane lub nie ulepszone cieplnie nie spawane,

C –

stopy nie ulepszone cieplnie spawane.

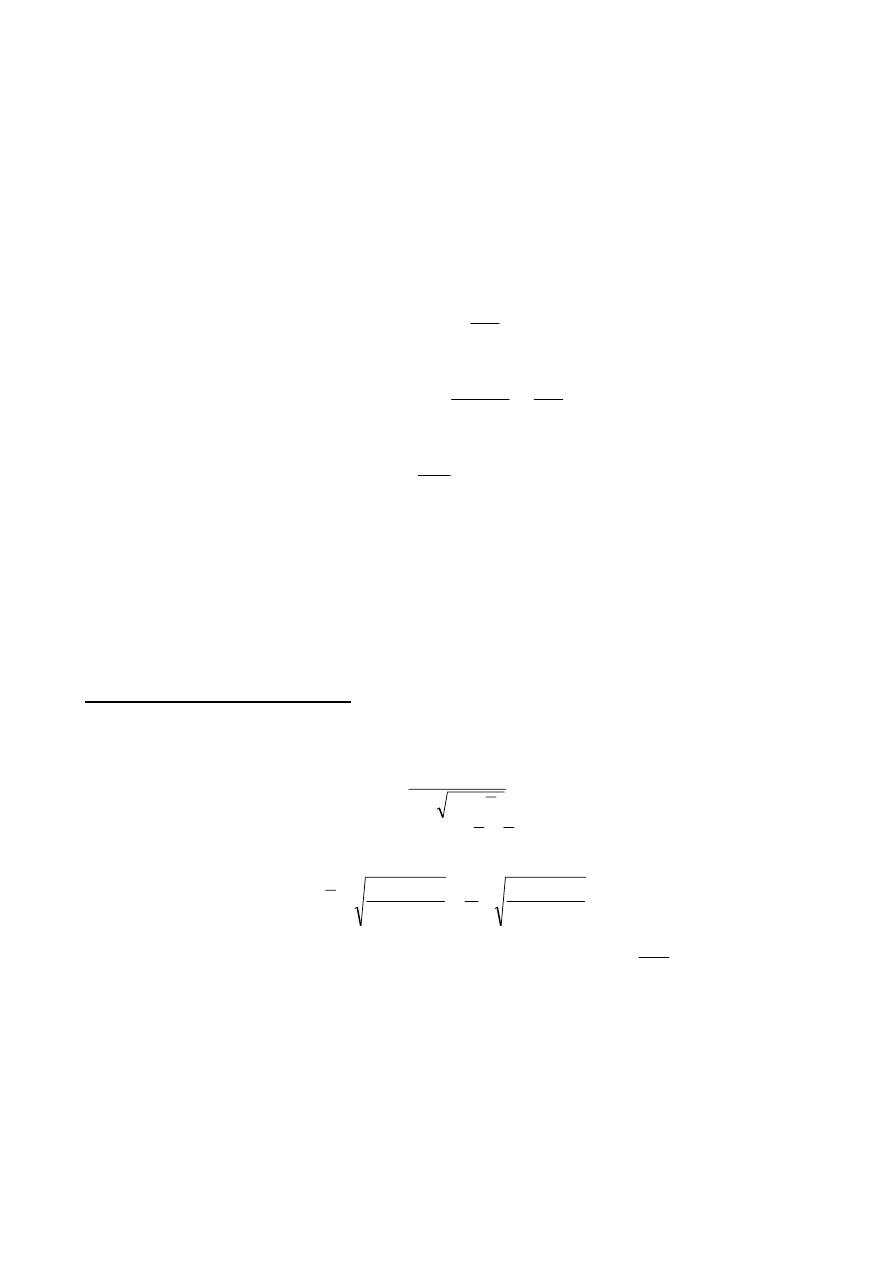
- 15 -

Nośność zginanego przekroju aluminiowego określa się jako mniejszą z dwóch wartości granicznych
M

R

=min(M

Ra

,

M

Rc

):

⎩

⎨

⎧

×

×

=

×

=

=

,

f

W

M

,

f

W

M

min

M

do

el

Rc

da

net

Ra

R

α

gdzie:
W

net

– wskaźnik zginania sprężystego netto z uwzględnieniem wszelkich osłabień przekroju,

W

el

– wskaźnik zginania sprężystego brutto,

W

eff

– wskaźnik wytrzymałości przekroju efektywnego,

α – współczynnik nośności przekroju przy zginaniu zależny od klasy przekroju:

o

dla przekrojów klasy 1 i 2:

,

W

W

el

pl

pl

=

=

α

α

o

dla przekrojów klasy 3:

,

1

W

W

1

el

pl

2

3

3

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

×

−

−

+

=

β

β

β

β

α

o

dla przekrojów klasy 4:

.

W

W

el

eff

=

α

Granica nośności ścinanych przekrojów klasy 1, 2 i 3 wynosi:

.

f

A

V

dv

v

R

×

=

Dla klasy 4 należy uwzględnić współczynnik stateczności miejscowej przy ścinaniu

φ

pv

<1:

.

f

A

V

dv

v

pv

R

×

×

=

ϕ

Nośność prętów osiowo ściskanych
Krzywe wyboczenia słupów aluminiowych ściskanych osiowo przyjęte w dokumentach ISO i EC9
bazują na modelu Younga, dotyczącym pręta ze wstępnym wygięciem. Bezwymiarową formułę
nośności, (współczynnik wyboczeniowy) opisuje wzór:

,

1

1

2

2

≤

−

+

=

λ

φ

φ

ϕ

(

)

[

]

,

1

5

,

0

2

o

λ

λ

λ

α

φ

+

−

×

+

×

=

dla smukłości względnej:

.

E

f

A

N

f

A

o

02

cr

02

×

×

×

=

×

×

=

η

π

λ

η

λ

Współczynnik

η przyjmuje wartości η=1 dla przekrojów klasy 1, 2 i 3, i

A

A

eff

=

η

dla przekrojów klasy

4.

Nośność słupa aluminiowego ściskanego osiowo zapisana jest wzorem:

,

f

k

k

A

N

do

2

1

bR

×

×

×

×

×

=

ϕ

η

gdzie:

k

1

, k

2

– ujmują odpowiednio wpływ asymetrii przekroju i wpływ spawania na nośność słupa.

- 16 -

PRZYKŁADOWE REALIZACJE

Obecny zakres stosowania konstrukcji aluminiowych, to przede wszystkim systemy fasadowe, okna,
drzwi, balustrady, konstrukcje dachowe, ogrody zimowe, ścianki działowe, czy pokrycia dachów.
W kraju bazuje się w zasadzie na trzech systemach, a mianowicie:

- „METALPLAST” Bielsko-Biała,
- „SAPA” – system szwedzki,
- „REYNAYERS” – system belgijski.

Poniżej podano kilka przykładów realizacyjnych:

Salon samochodowy Renault w Zabrzu

Centrala Powszechnego Banku Kredytowego w Warszawie

- 17 -

Browary Żywiec w Żywcu

Hotel KÄMP, Helsinki, Finlandia

- 18 -

Spektri Business Park, Finlandia

Ogród zimowy – okolice Gorzowa