1

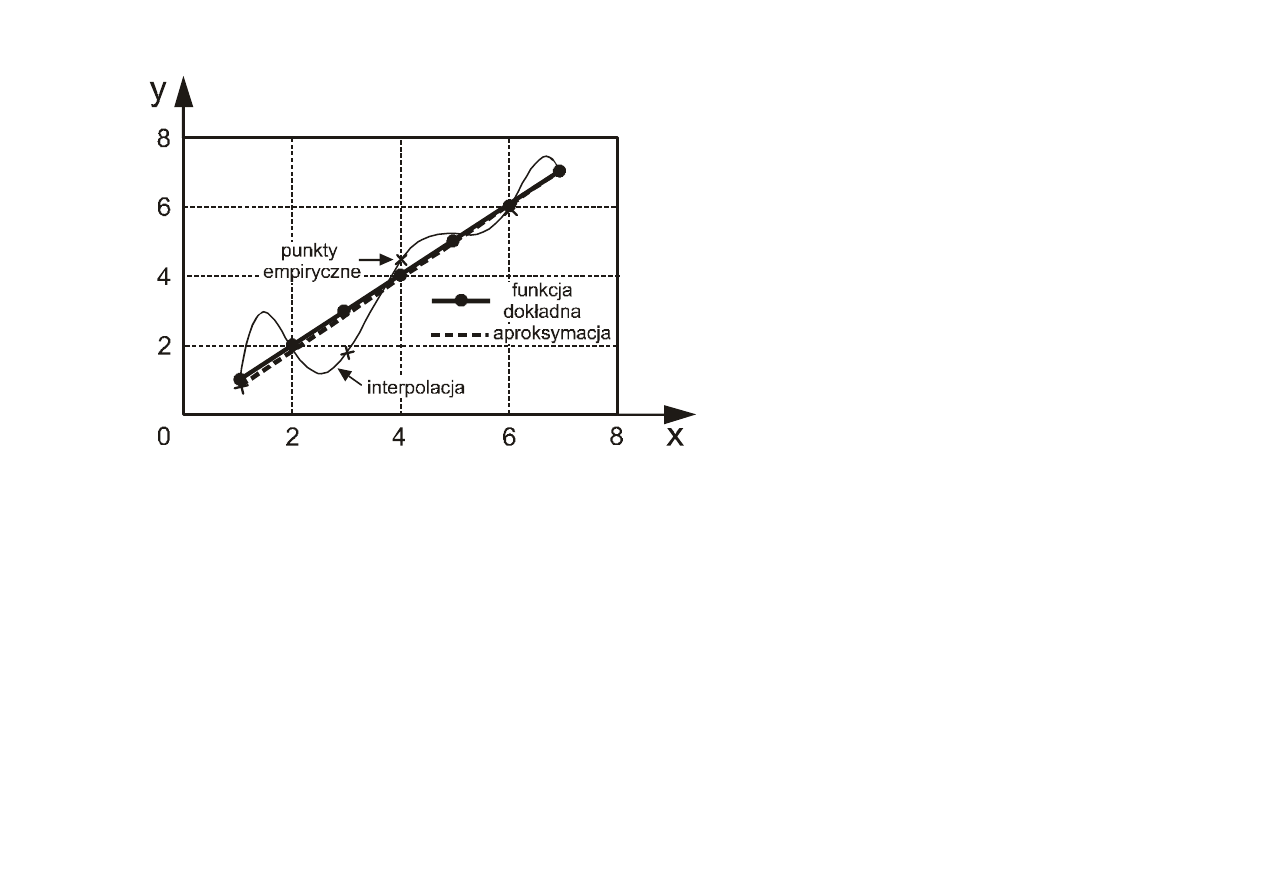
Aproksymacja funkcji na podzbiorze

dyskretnym metod

ą

najmniejszych kwadratów

2

Zakładamy,

ż

e znane s

ą

warto

ś

ci

( )

n

i

x

f

y

i

i

,

,

2

,

1

,

0

,

K

=

=

funkcji f (·) dla dyskretnych warto

ś

ci argumentu równych

b

x

x

x

a

x

n

=

<

<

<

<

=

K

2

1

0

3

B

ę

dziemy poszukiwa

ć

funkcji aproksymuj

ą

cej

( )

x

y

Φ

=

w postaci

( )

( )

( )

( )

x

c

x

c

x

c

x

m

m

ϕ

ϕ

ϕ

⋅

+

+

⋅

+

⋅

=

Φ

K

1

1

0

0

gdzie:

() ()

()

⋅

⋅

⋅

m

ϕ

ϕ

ϕ

,

,

,

1

0

K

s

ą

pewnymi funkcjami okre

ś

lonymi na danym przedziale [a, b],

m

c

c

c

,

,

,

1

0

K

s

ą

współczynnikami b

ę

d

ą

cymi liczbami rzeczywistymi.

Wielomian uogólniony

4

Jako

ść

aproksymacji

Kryterium okre

ś

laj

ą

ce jako

ść

aproksymacji – funkcja bł

ę

du F(·) definiuj

ą

ca

odległo

ść

pomi

ę

dzy funkcjami f (·) i

Φ

(·) na danym zbiorze

{

}

n

x

x

x

,

,

,

1

0

K

=

Z

z zakresu [a, b].

Przez

(

)

Φ

,

f

F

oznaczono warto

ść

funkcji bł

ę

du

W metodzie najmniejszych kwadratów, przy aproksymacji na podzbiorze dyskretnym,
funkcj

ę

bł

ę

du definiuje si

ę

jako:

(

)

( ) ( )

( )

2

/

1

2

0

0

,



























ϕ

−

=

Φ

−

=

Φ

∑

∑

=

=

n

i

m

k

i

k

k

i

i

def

x

c

x

f

x

w

f

f

F

Z

norma wyznaczana na podzbiorze dyskretnym Z

funkcja wagowa

5

6

Poszukujemy współczynników

m

c

c

c

,

,

,

1

0

K

dla których funkcja

(

)

( ) ( )

( )

2

/

1

2

0

0

,



























ϕ

−

=

Φ

−

=

Φ

∑

∑

=

=

n

i

m

k

i

k

k

i

i

def

x

c

x

f

x

w

f

f

F

Z

przyjmuje warto

ść

minimaln

ą

.

Funkcje bazowe

() ()

()

⋅

⋅

⋅

m

ϕ

ϕ

ϕ

,

,

,

1

0

K

s

ą

dane.

7

Otrzymujemy m+1 równa

ń

,

,

,

2

,

1

,

0

dla

,

0

m

k

dc

d

k

K

=

=

Ψ

z m +1 niewiadomymi

m

c

c

c

,

,

,

1

0

K

Po zró

ż

niczkowaniu funkcji

( )

( )

⋅

=

⋅

Ψ

2

F

mamy

( ) ( )

( )

∑

∑

=

=

























ϕ

⋅

−

⋅

ϕ

⋅

−

=

Ψ

n

i

m

l

i

l

l

i

i

k

k

x

c

x

f

x

dc

d

0

0

2

m

k

,

,

2

,

1

,

0

L

=

8

Układ równa

ń

przyjmuje posta

ć

:

( ) ( )

( )

0

0

0

=













⋅

−

⋅

∑

∑

=

=

m

l

i

l

l

i

n

i

i

k

x

c

x

f

x

ϕ

ϕ

gdzie:

m

k

,

,

2

,

1

,

0

L

=

a po przekształceniu:

( )

( )

( ) ( )

∑

∑

∑

=

=

=

⋅

=













⋅

⋅

n

i

i

i

k

m

l

i

l

l

n

i

i

k

x

f

x

x

c

x

0

0

0

ϕ

ϕ

ϕ

m

k

,

,

2

,

1

,

0

L

=

9

Do oblicze

ń

stosujemy nast

ę

puj

ą

c

ą

form

ę

układu równa

ń

:

( ) ( )

( ) ( )

∑

∑ ∑

=

=

=

⋅

=

⋅













⋅

n

i

i

i

k

l

m

l

n

i

i

l

i

k

x

f

x

c

x

x

0

0

0

ϕ

ϕ

ϕ

m

k

,

,

2

,

1

,

0

L

=

[ ]

kl

s

=

S

Oznaczaj

ą

c macierz współczynników układu przez

( ) ( )

m

l

k

x

x

s

n

i

i

l

i

k

kl

,

,

1

,

0

,

,

0

L

=

ϕ

⋅

ϕ

=

∑

=

10

Wektor wyrazów wolnych oznaczymy przez

[

]

T

m

t

t

t

,

,

,

1

0

L

=

t

Mo

ż

emy układ m+1 równa

ń

z m+1 niewiadomymi

zapisa

ć

jako

m

c

c

c

,

,

,

1

0

L

t

c

S

=

⋅

( ) ( )

m

k

x

f

x

t

n

i

i

i

k

k

,

,

1

,

0

,

0

L

=

⋅

ϕ

=

∑

=

Jest to układ równa

ń

nazywany układem równa

ń

normalnych

11

Funkcje bazowe

przyjmuje si

ę

jako ci

ą

g wielomianów

( ) ( )

( )

L

L

,

,

,

,

1

0

⋅

⋅

⋅

k

ϕ

ϕ

ϕ

L

L

,

,

,

,

,

1

2

0

k

x

x

x

x

=

Jako funkcje aproksymuj

ą

ce stosujemy wielomian pot

ę

gowy

( )

m

m

x

c

x

c

x

c

c

x

⋅

+

+

⋅

+

⋅

+

=

Φ

K

2

2

1

0

Wtedy

∑

=

+

=

=

n

i

l

k

i

kl

m

l

k

x

s

0

,

2

,

1

,

0

,

,

L

( )

∑

=

=

⋅

=

n

i

i

k

i

k

m

k

x

f

x

t

0

,

2

,

1

,

0

,

K

12

Przyj

ę

to oznaczenie

kl

j

s

s

=

gdzie j = k + l

Układ równa

ń

mo

ż

emy zapisa

ć

:













=

⋅

+

+

⋅

+

⋅

+

⋅

=

⋅

+

+

⋅

+

⋅

+

⋅

=

⋅

+

+

⋅

+

⋅

+

⋅

=

⋅

+

+

⋅

+

⋅

+

⋅

+

+

+

+

m

m

m

m

m

m

m

m

m

m

m

m

t

c

s

c

s

c

s

c

s

t

c

s

c

s

c

s

c

s

t

c

s

c

s

c

s

c

s

t

c

s

c

s

c

s

c

s

2

2

2

1

1

0

2

2

2

4

1

3

0

2

1

1

2

3

1

2

0

1

0

2

2

1

1

0

0

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

K

K

K

K

gdzie

∑

=

=

=

n

i

j

i

j

m

j

x

s

0

2

,

,

2

,

1

,

0

dla

,

K

13

Dla m = 1 mamy wyra

ż

enia:

∑

∑

∑

=

=

=

=

=

=

n

i

i

n

i

i

n

i

i

x

s

x

s

x

s

0

2

2

0

1

1

0

0

0

∑

∑

=

=

⋅

=

⋅

=

n

i

i

i

n

i

i

i

y

x

t

y

x

t

0

1

1

0

0

0

Dla m = 2 mamy wyra

ż

enia:

∑

∑

∑

=

=

=

⋅

=

⋅

=

⋅

=

n

i

i

i

n

i

i

i

n

i

i

i

y

x

t

y

x

t

y

x

t

0

2

2

0

1

1

0

0

0

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

=

=

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

x

s

x

s

x

s

x

s

x

s

0

4

4

0

3

3

0

2

2

0

1

1

0

0

0

14

Przykład

i

0

1

2

i

x

0

1

2

i

y

-1

0

3