KOREKCJA ZAZĘBIENIA

W kołach o zazębieniu

niekorygowanym linia środkowa

narzędzia zębatki toczy się bez

poślizgu po kole podziałowym

nacinanego koła zębatego.

Wielkość odsunięcia lub dosunięcia

narzędzia wyraża się za pomocą

współczynnika przesunięcia

zarysu x.

• Korekcja dodatnia x>0

zarys

odsuwany od materiału koła.

• Korekcja ujemna x<0

zarys

dosuwany do materiału koła.

• np. x>0:
• w zazębieniu zewnętrznym 

odsuwamy na zewnątrz koła,

• w zazębieniu wewnętrznym 

odsuwamy ku wnętrzu koła.

• Dodatnie odsunięcie narzędzia w

zazębieniu zewnętrznym w kierunku

promieniowym o wielkość +xm umożliwia:

• wykonanie koła o małej liczbie zębów bez

podcinania stopy zęba,

• uzyskanie dowolnej odległości osi kół przy

zachowaniu znormalizowanych modułów

i całkowitej liczby zębów,

• poprawienie wytrzymałości zazębienia na

złamanie i na naciski (uniknięcie pracy

zarysów w pobliżu koła zasadniczego,

gdzie ewolwenta ma mały promień

krzywizny, a więc naciski są duże).

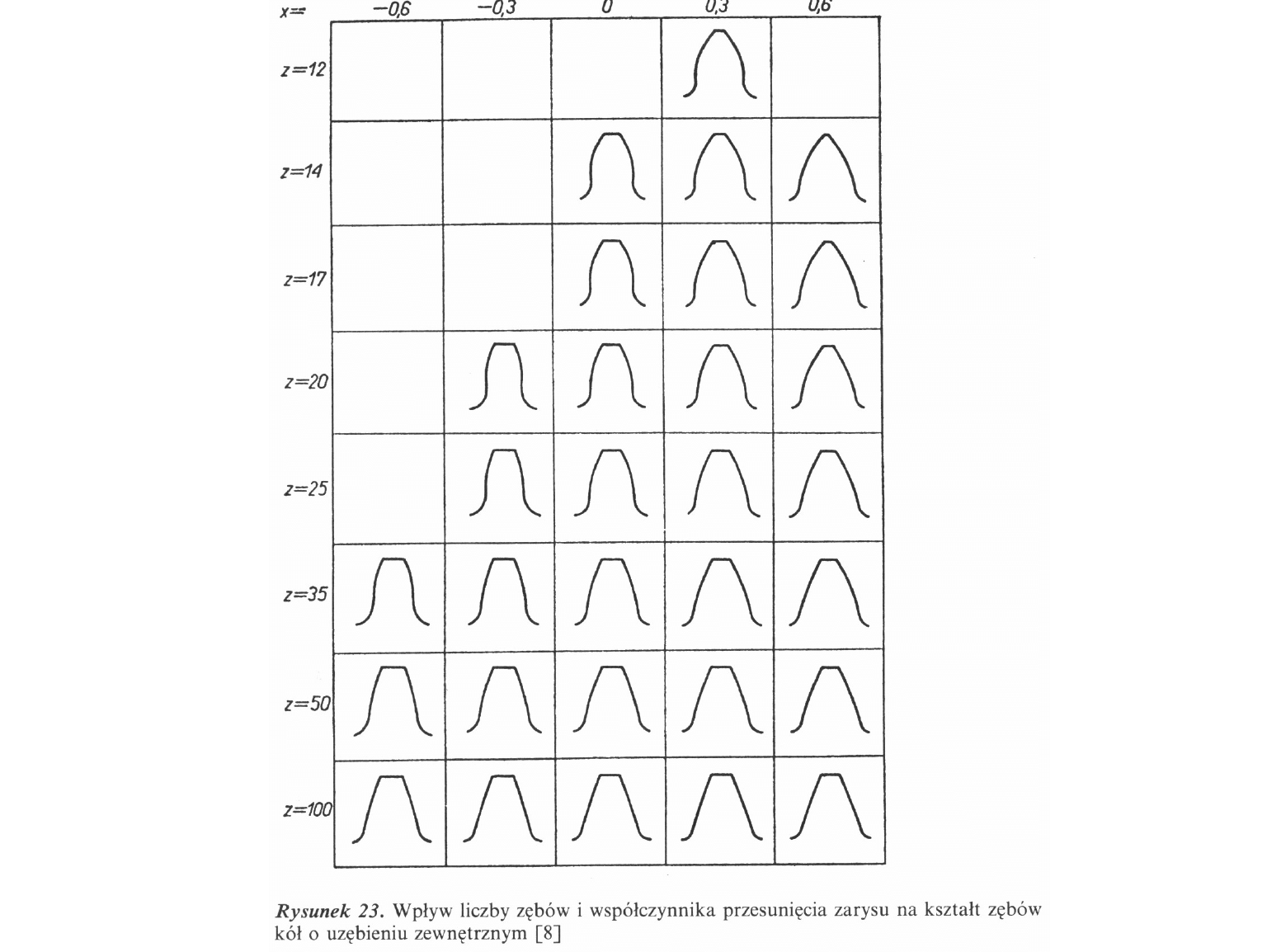
• Wpływ przesunięcia jest tym mniejszy

im większa jest liczba zębów.

• Korekcja ujemna:
• pogarsza warunki pracy,
• używana jest tylko dla uzyskania

potrzebnej odległości osi w kołach o
dużej liczbie zębów.

• Korekcja dodatnia jest

ograniczona zaostrzeniem zęba.

• Z praktyki wiadomo, że grubość zęba

na kole wierzchołkowym nie może
nie może być mniejsza niż 0,4 m, ze
względu na wykruszenie
wierzchołka.

• Rodzaje korekcji zazębienia:
• bez przesunięcia (zazębienie

niekorygowane)

• x

1

=x

2

=0

• równej sumie przesunięć (korekcja P-0)
• x

1

=-x

2

albo x

1

+x

2

=0

• dodatniej lub ujemnej sumie przesunięć

(korekcja P)

• x

1

+x

2

≠0

•

Stosując korekcję P-0 zachowuje się taką samą

odległość osi i ten sam kąt zarysu, czyli średnica

toczna pokrywa się z podziałową. Dodatnie

przesunięcie występuje dla zębnika, co pozwala na

uniknięcie podcinania, nadając zębom małego koła

korzystne kształty z punktu widzenia wytrzymałości

zmęczeniowej. Dla dużego koła występuje ujemne

przesunięcie zarysu ma mały wpływ na jego kształt.

•

Dla kół wykonanych z tego samego materiału i z

1

=z

2

stosowanie równej sumy przesunięć nie jest celowe.

•

Dla korekcji P współczynnik x

1

i x

2

dobiera się

oddzielnie, aby w optymalny sposób spełnione były

warunki wytrzymałościowe kół.

•

Korekcji P wymaga zmiany odległości osi, natomiast

przy korekcji P-0 odległość osi kół nie ulega

zmianie.

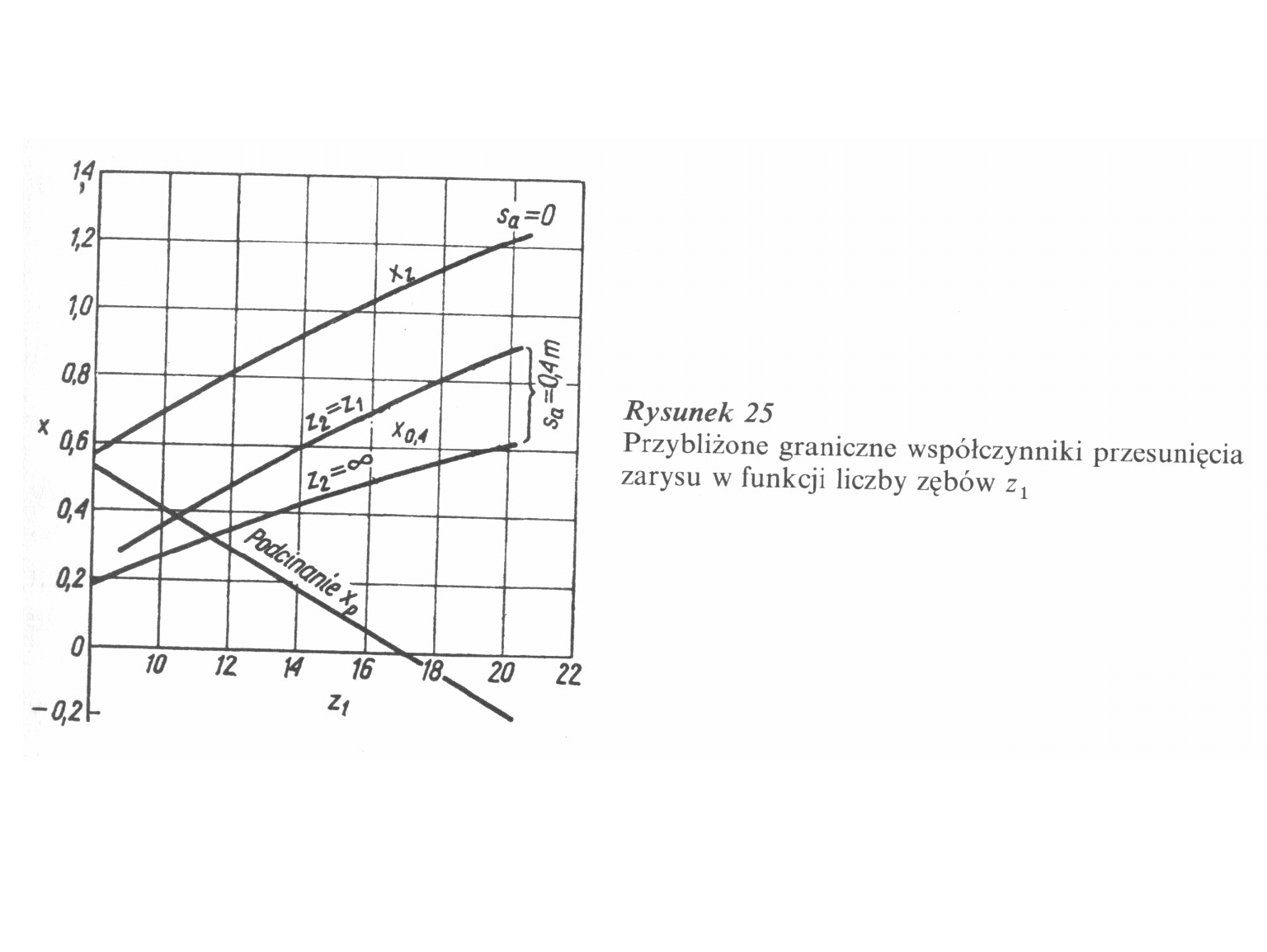
• Dla uniknięcia podcinania zęba

współczynnik przesunięcia zarysu:

/dla 

0

=20

o

, h

a0

=1/

17

17

min

z

x





• Dla uzyskania założonej odległości

osi:

• W wyniku przesunięcia zarysu zębnika

o wartość x

1

m i koła o wartość x

2

m,

odległość między kołami a

0

uległaby

zmianie i wyniosłaby:

• W celu skasowania luzu należy

przybliżyć osie kół do siebie o
wielkość ym:

m

x

x

m

z

z

m

x

x

a

p

a

)

2

1

(

2

2

1

)

2

1

(

0















m

y

x

x

a

ym

p

a

w

a

)

2

1

(

0













• Jednocześnie należy skrócić głowy

zębów w obu kołach o tą samą

wielkość, zachowując przy tym stałą

wielkość luzu wierzchołkowego:

• Jeżeli współczynnik y jest mały w

porównaniu ze współczynnikiem luzu

wierzchołkowego,

można nie skracać głowy zęba,

godząc się na zmniejszenie

rzeczywistego luzu wierzchołkowego.

)

0

(

)

2

1

(

a

w

a

m

x

x

w

a

p

a

ym













Przy obliczeniach przesunięcia osi

stosuje się przybliżone metody:

)

1

(

0

p

B

a

p

a







)

1

(

0

r

B

a

w

a







m

z

z

a

)

2

1

(

5

,

0

0





Wartości współczynników Bp i Br w

funkcji kąta zarysu na średnicy
tocznej w przekroju normalnym do
linii zęba są stabelaryzowane.

o

tg

o

inv

nw

inv

p

B

20

20







1

cos

20

cos





nw

o

r

B



W praktyce konstrukcyjnej spotyka się

dwa typy zadań:

I. Dane są:
• moduł (m),
• liczba zębów (z

1

, z

2

),

• rzeczywista odległość osi (a

w

),

• Kąt przyporu na średnicy podziałowej

(nominalny)



• Tok postępowania:
• obliczenie a

0

,

• obliczenie B

r

,

• odczyt B

p

z tablic w funkcji B

r

,

• określenie tocznego kąta zarysu



w

z

tablic w funkcji Br lub Bp, albo z
zależności:

• obliczenie x

1

+x

2

,

• obliczenie współczynnika y,





cos

0

cos

w

a

a

w









tg

inv

inv

z

z

x

x

w









2

2

1

2

1

II. Dane są:
• moduł (m),
• liczba zębów (z

1

, z

2

),

• wartość współczynników

przesunięcia zarysu
(x

1

, x

2

)

• Kąt przyporu na średnicy podziałowej

(nominalny)



• Tok postępowania:
• obliczenie a

0

,

• obliczenie B

p

• odczyt B

r

z tablic w funkcji B

p

,

• obliczenie a

w

,

• obliczenie współczynnika y,
• określenie tocznego kąta zarysu



w

z

tablic w funkcji B

r

lub B

p

, albo z

zależności podanej poprzednio







inv

tg

z

z

x

x

inv

w









2

1

2

1

2