Metody badań Tg

POLITECHNIKA ŁÓDZKA

WYDZIAŁ INŻYNIERII PROCESOWEJ I OCHRONY ŚRODOWISKA

Prof. dr hab. Maria Mucha

POLIMERY

4

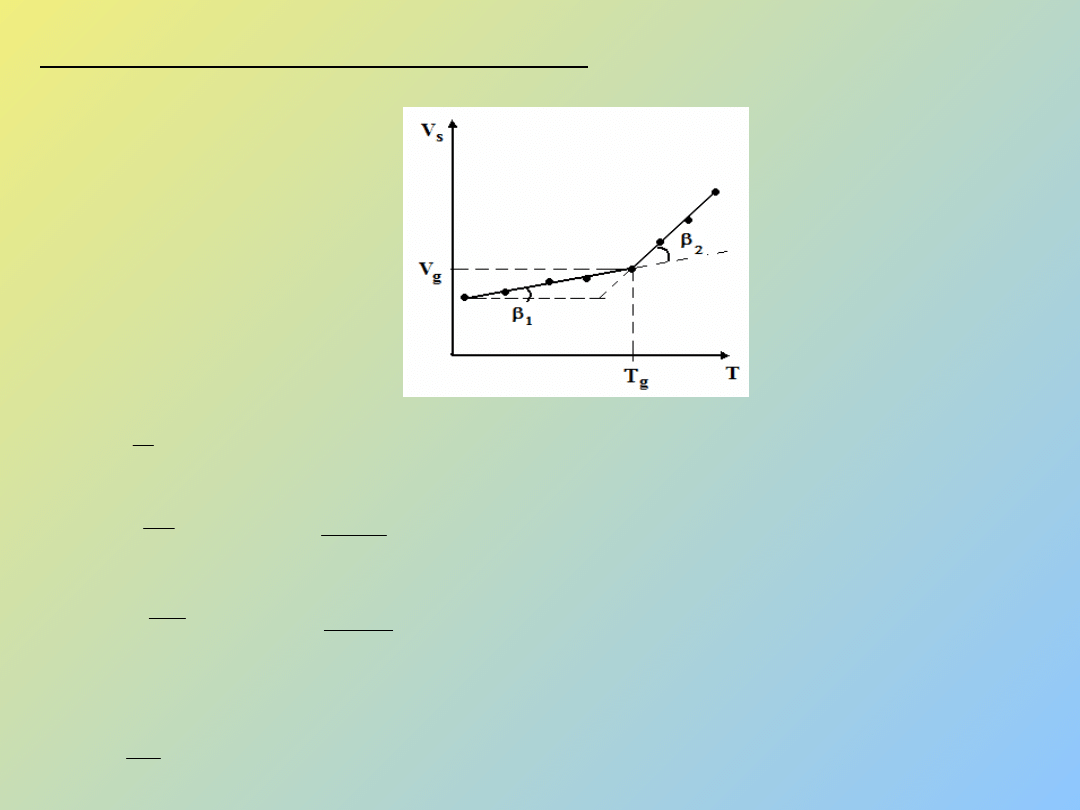
2

1. Metoda dylatometryczna (dylatometr,

termostat)

m

V

V

s



g

T

T

T

V

tg





















1



g

T

T

g

g

V

T

V



























- współczynnik rozpuszczalności objętościowej a

g

poniżej T

g

g

T

T

T

V

tg





















2



g

T

T

g

L

V

T

V



























- współczynnik rozpuszczalności objętościowej a

L

poniżej T

g

   

 

g

L













 

T

V









 

113

,

0

1











K

const

T

g



 

164

,

0

2









K

const

T

g

L



} wolne objętości Simhy Boyera

Rys. 1 Zależność objętości właściwej V

s

od temperatury T.

3

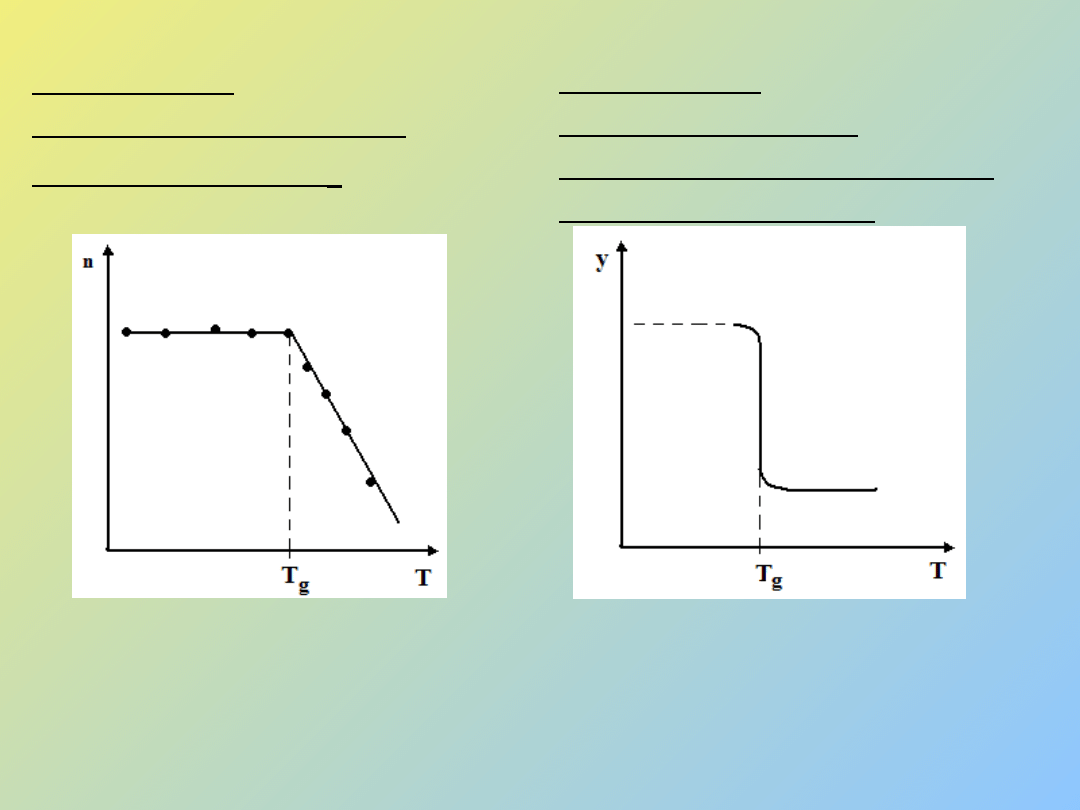
2. Metoda
refraktometryczna
(refraktometr)

Rys. 2 Zależność współczynnika
załamania światła n od
temperatury T.

3. Metoda
termooptyczna
(mikroskop, komórka
termooptyczna)

Rys. 3 Zależność natężenia światła
I przechodzącego przez próbkę od
temperatury T.

4

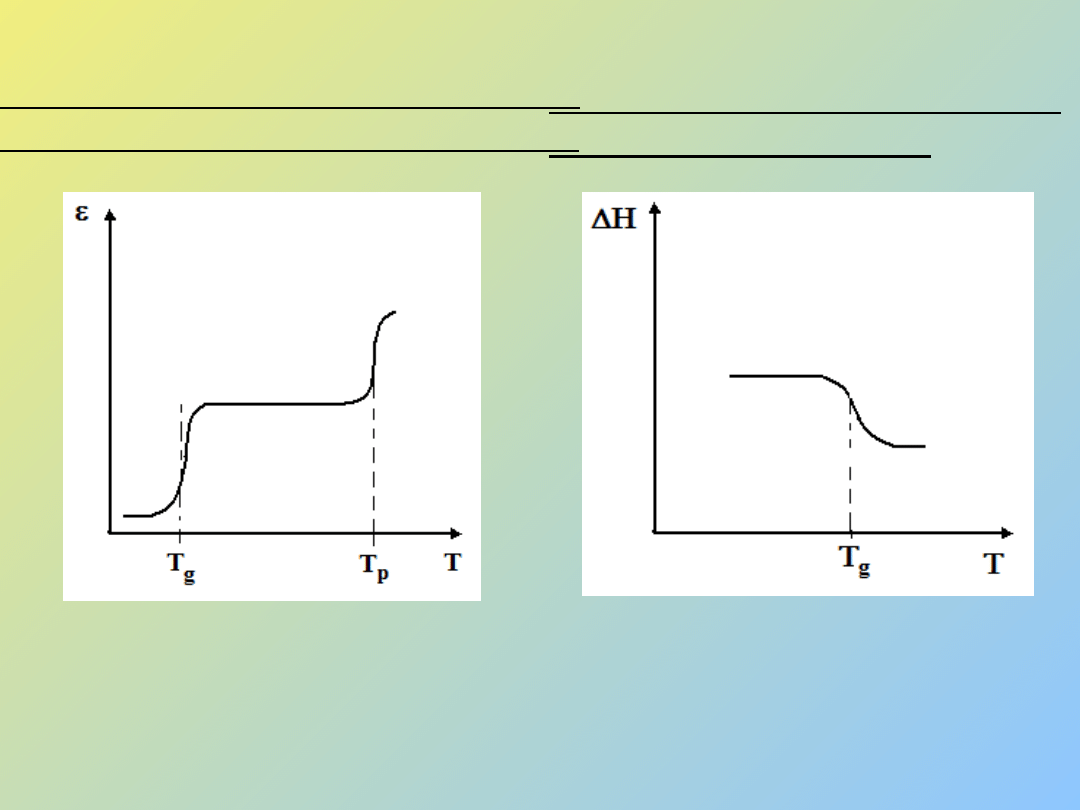
4. Metoda termomechaniczna

(komórka termomechaniczna)

Rys. 4 Zależność wydłużenia ε od temperatury T.

5. Metoda DSC lub DTA
(kalorymetr - DSC)

Rys. 5 Zależność pojemności
cieplnej od temperatury T.

5

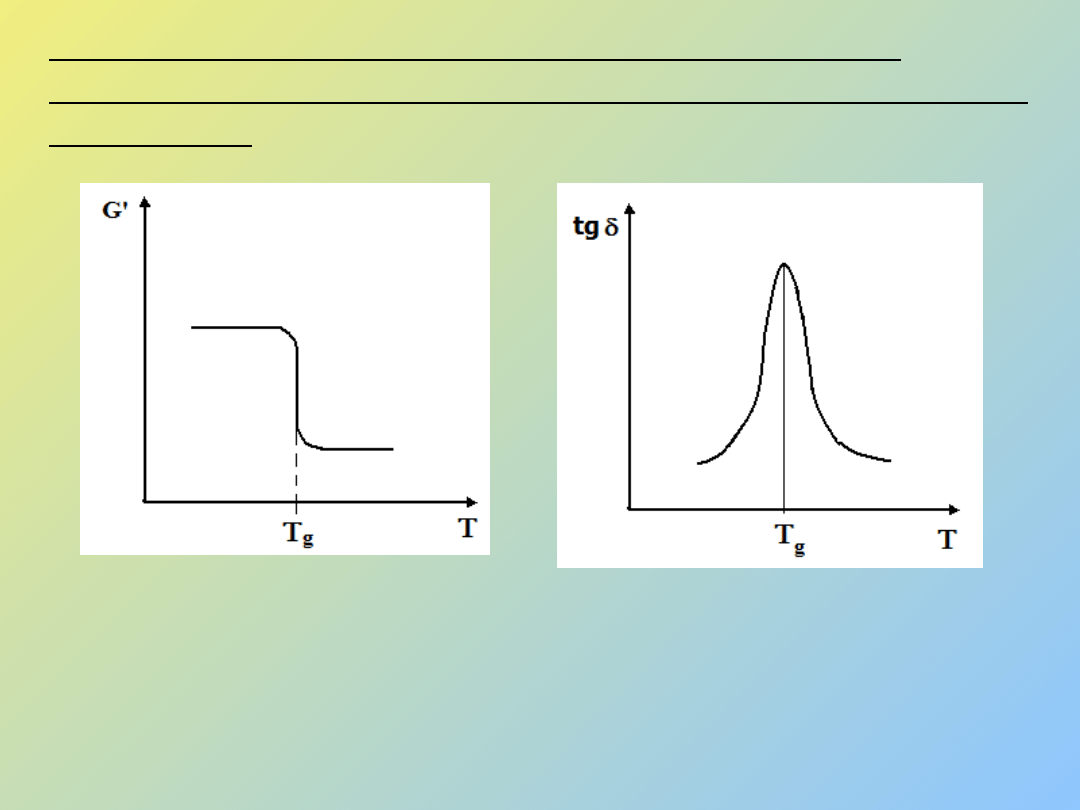
6. Moduł elastyczności (metoda stratności
mechanicznej lub dielektrycznej - aparaty DMTA
oraz DEA)

a)

b)

Rys. 6 Zależność modułu elastyczności G` lub tgδ od temperatury T.

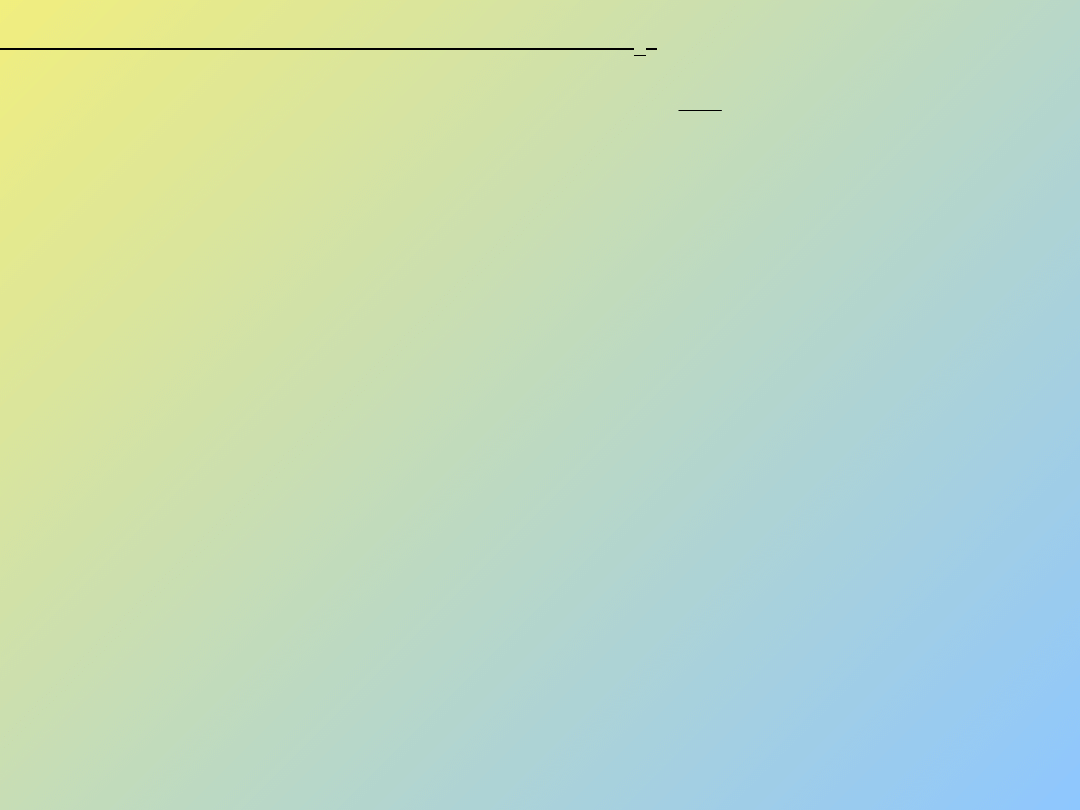
6

Podstawowe równanie termodynamiczne dla T

m

f

f

m

S

H

T







gdzie:

H

f

– ciepło topnienia,

S

f

– entropia topnienia.

gdzie:

h

1

f

H

H

H











H

h

– ciepło topnienia związane z energią potrzebną do rozsunięcia

łańcuchów, a więc do wytworzenia niezajętej przestrzeni zwanej
dziurami; wielkość H

h

jest proporcjonalna do gęstości energii kohezji ≈

(CED)

H

1

– wartość stała,





CED

k

H

H

1

1

f









gdzie:

k

1

– stała

D

R

V

f

S

S

S

S















S

V

- entropia topnienia związana ze wzrostem objętości w procesie topnienia,

którą można wyznaczyć doświadczalnie,

S

D

- entropia topnienia związana z powstaniem układu nieuporządkowanego,

S

R

- entropia izomerii rotacyjnej która jest związana ze zdolnością cząsteczki

polimeru do przyjmowania wielu konformacji podczas topnienia w wyniku
rotacji wokół wiązań łańcucha głównego tzw. wiązań szkieletowych

Wpływ parametrów energetycznych na T

g

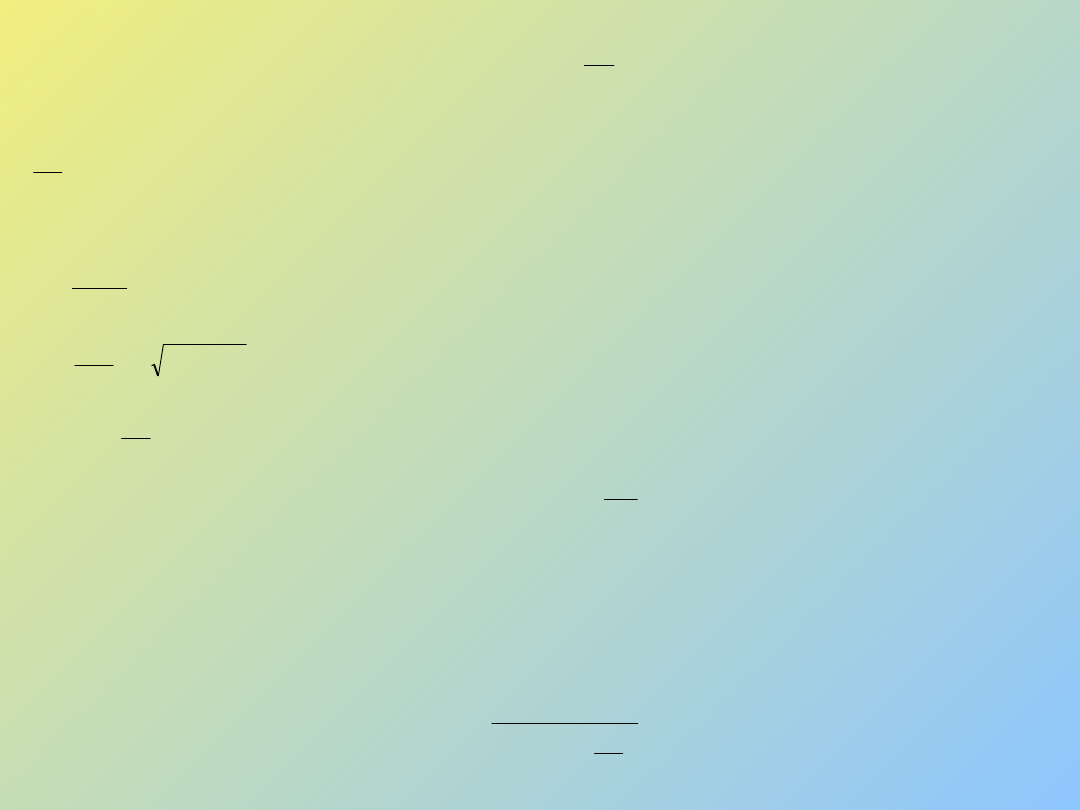
7

R

86

.

0

kT

f

ln

R

S

R

























gdzie:

kT



– parametr sztywności łańcucha,

g

log

d

ln

d

f



























2

1

g

g

4

1

2

1

g











 



kT

exp

g



–

różnica energii między konformacją trans i gauche (dodatnia),

– jest ułamkiem wiązań konformacji gauche,

– jest stałą modelu siatki,

kT

k

S

S

f



2

0









gdzie:

S

0

– stanowi sumę wartości zmian entropii niezależnych od sztywności łańcucha,

k

2

– wartość stała.

Stąd:





kT

k

S

CED

k

H

T

2

0

1

1

m













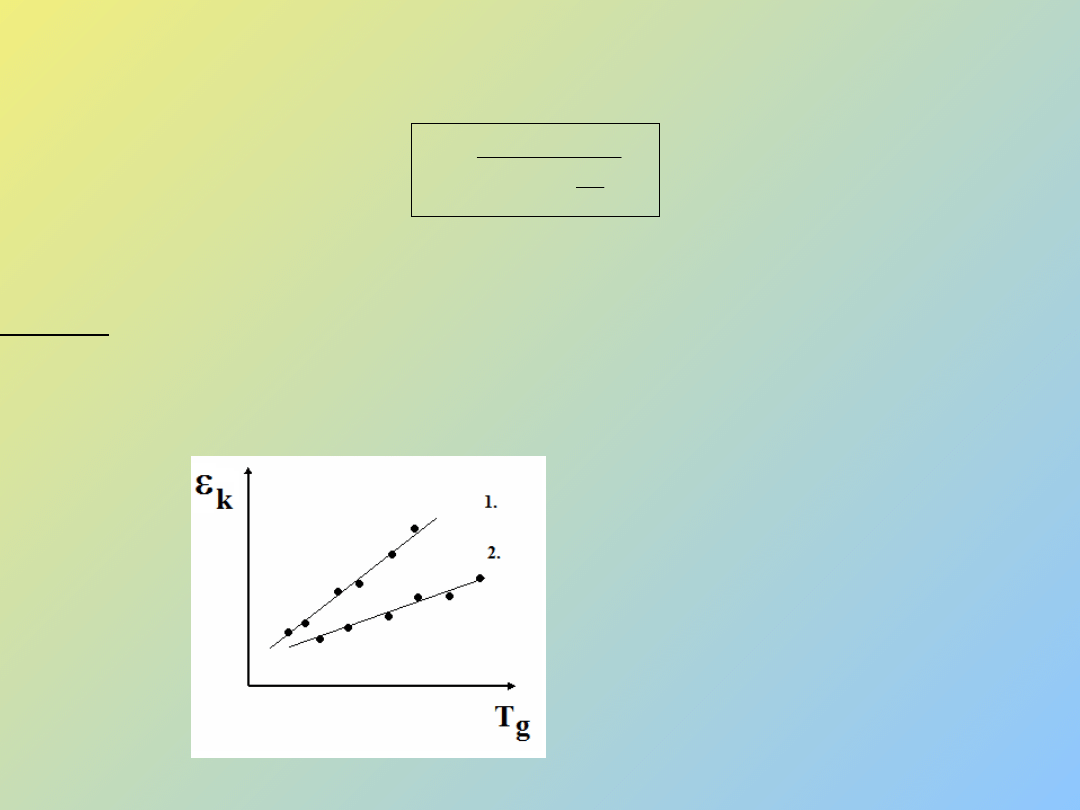
8

Ponieważ T

m

i T

g

(wg Boyer) są liniowo

zależne

Temperatura Tg zależy od CED (energii kohezji - oddziaływań

międzycząsteczkowych)

oraz od energii sztywności łańcucha (własność łańcucha polimeru) ε/kT.

b

aT

T

m

g





zatem





b

kT

k

S

CED

k

H

a

T

g















2

0

1

1

Przykład:
1. (Marei) otrzymał następującą zależność:

105

K

H

02

.

0

]

C

[

T

c

o

g





K- liczba grup funkcyjnych na 4 atomy węgla Hc – energia kohezji

2. (Mucha)

kopolimer chlorku vinylidenu z akrylonitrylem

kopolimer chlorku vinylidenu z chlorkiem vinylu

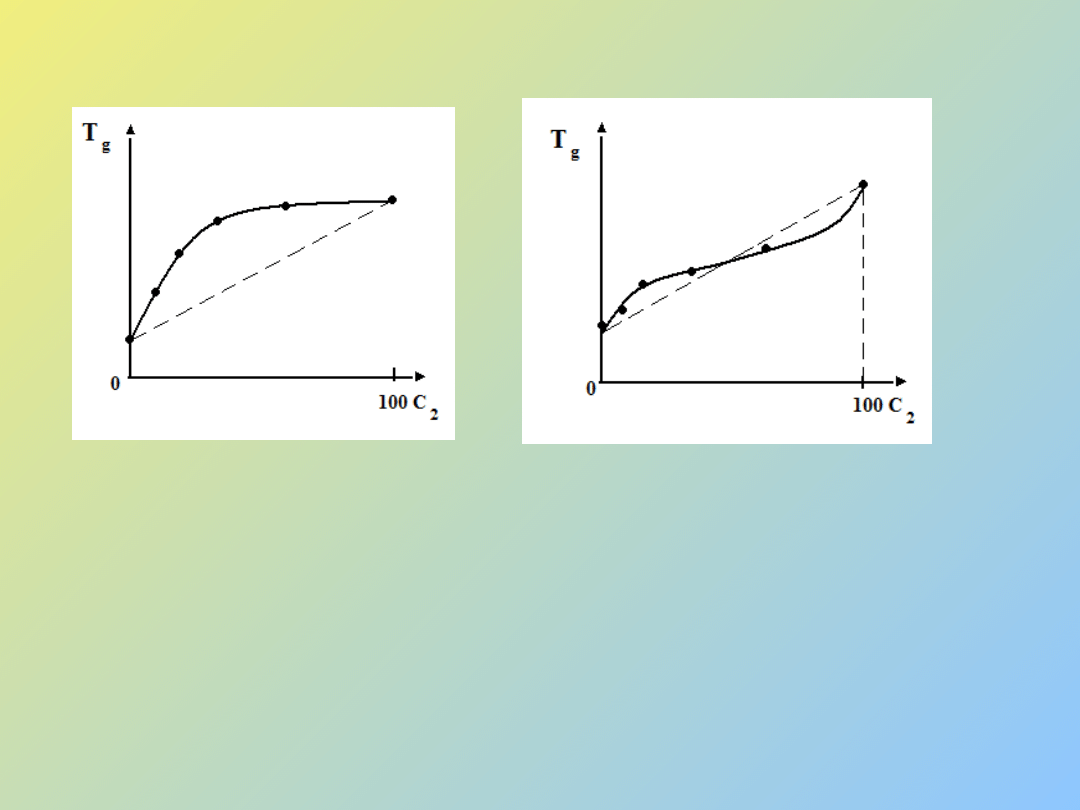
Rys. 7 Proporcjonalność energii sztywności łańcucha ε

k

i temperatury zeszklenia T

g

2

2

1

1















A

A

k

9

a)

b)

Rys. 8 Zależność temperatury zeszklenia T

g

kopolimerów chlorku vinylidenu z

akrylonitrylem
a) oraz chlorkiem winylu b) od udziału chlorku vinylidenu C

2

Równanie Gordona Taylora:









0

2

2

2

1

1

1









g

g

g

g

T

T

C

A

T

T

C

A

A

1

=Δ

1

A

2

=

2

C

1

+C

2

=1