Wykład 14

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

Dynamika układu o jednym stopniu swobody

Drgania swobodne nietłumione i tłumione

Część 1

Drgania swobodne nietłumione

3

( )

( )

( )

( )

mq t

cq t

kq t

P t

+

+

=

&&

&

1.1. Równanie ruchu

Ogólne równanie ruchu układu materialnego o jednym stopniu swobody

W drganiach swobodnych nietłumionych przyjmuje się:

c = 0 , P(t) = 0

( )

( )

0

mq t

kq t

+

=

&&

Uwagi:

1. Drgania są wzbudzane przemieszczeniem i/lub prędkością początkową.

2. W rzeczywistości przypadek braku tłumienia nie jest możliwy.

3. Jest to równanie różniczkowe liniowe zwyczajne drugiego rzędu o stałych
współczynnikach

4

1.2. Wzór Eulera

Szereg Maclaurina

( )

( )

( )

0

0

n

n

n

f

f x

x

n!

�

=

=

�

( )

( )

2

4

6

2

0

1

1

2

4

6

2

n

n

n

x

x

x

x

cosx

...

!

!

!

n !

�

=

= -

+

-

+ =

-

�

( )

(

)

3

5

7

2 1

0

1

3

5

7

2

1

n

n

n

x

x

x

x

sinx x

...

!

!

!

n

!

+

�

=

= -

+ -

+ =

-

+

�

Rozwinięcie funkcji

cos x

Rozwinięcie funkcji

sin x

Rozwinięcie funkcji

e

x

(wzór Eulera)

( )

( )

( )

( )

2

3

4

5

2

4

3

5

1

2

3

4

5

1

2

4

3

5

ix

ix

ix

ix

ix

e

ix

...

!

!

!

!

x

x

x

x

... i x

...

cosx i sinx

!

!

!

!

= + +

+

+

+

+ =

�

�

-

+

-

+

-

+

-

=

+

�

�

�

�

5

1.3. Rozwiązanie równania ruchu

Przewidywane rozwiązanie

( )

rt

q t

e

=

( )

rt

q t

re

=

&

( )

2 rt

q t

r e

=

&&

2

0

rt

rt

mr e

ke

+

=

(

)

2

0

rt

mr

k e

+

=

2

0

mr

k

+ =

12

,

k

r

i

m

=�

( )

( )

1

2

iωt

iωt

q t

e , q t

e

-

=

=

k

ω

m

=

1

2

r iω , r

iω

=

=-

 – częstość kołowa drgań własnych (częstość drgań własnych)

6

( )

( )

1

2

iωt

iωt

q t

e

cosωt i sinωt

q t

e

cosωt i sinωt

-

=

=

+

=

=

-

( )

( )

( )

( )

( )

( )

1

1

2

2

1

2

1

2

1

2

ˆq t

q t

q t

cosωt

ˆq t

q t

q t

sinωt

i

=

+

=

�

�

�

�

=

-

=

�

�

�

�

( )

q t

asinωt bcosωt

=

+

Rozwiązania równania
jednorodnego

Kombinacja rozwiązań

Całka ogólna równania
jednorodnego

a

,

b

– stałe całkowania

( )

0

0

0

0

q t

q

asinωt

bcosωt

= =

+

( )

0

0

0

0

q t

v

aωcosωt bωsinωt

= =

-

&

0

b q

=

0

v

a

ω

=

( )

0

0

v

q t

sinωt q cosωt

ω

=

+

7

( )

0

0

v

q t

sinωt q cosωt

ω

=

+

( )

(

)

q t

Acosωt φ

=

+

Dwie postaci rozwiązania
równania ruchu

( )

0

0

v

q t

Acosωtcosφ Asinωtsinφ

sinωt q cosωt

ω

=

-

=

+

0

0

v

Asinφ

ω

Acosφ q

�

=-

�

�

�

= �

v

A

q

ω

v

tgφ

ωq

�

� �

=

+

�

� �

�

� �

�

� =-

�

�

2

2

2

0

0

0

0

A

– amplituda drgań

 – kąt fazowy

8

1.4. Wielkości charakteryzujące drgania swobodne nietłumionego
układu o jednym stopniu swobody

A

– amplituda drgań [m]

 – kąt fazowy [rad]

 – częstość kołowa drgań własnych [rad/s]

 – okres drgań [s]

f – częstotliwość drgań [1/s] (

1/s = 1

Hz)

( )

(

)

q t

Acosωt φ

=

+

2π ωT

=

2π

T

ω

=

1

f

T

=

9

0

1

2

3

4

5

6

7

8

9

10

5

4

3

2

1

0

1

2

3

4

5

4.472

4.472



X1

2

 

X1

3

 

10

0

X1

1

 

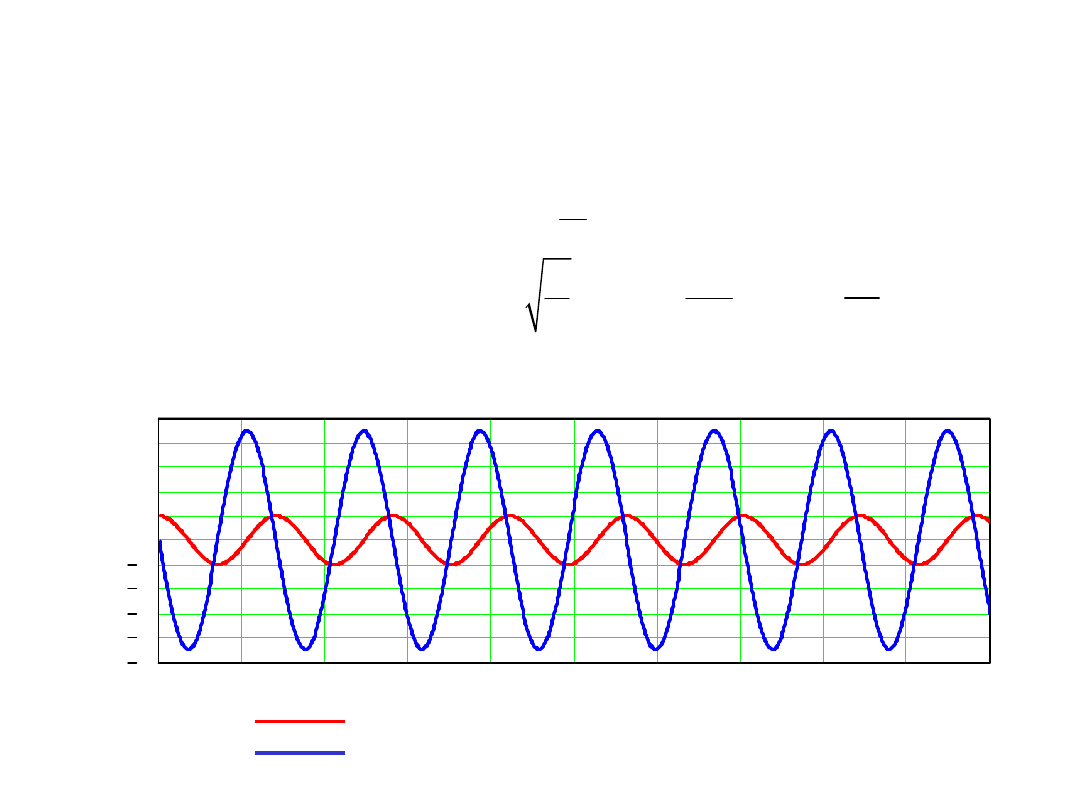
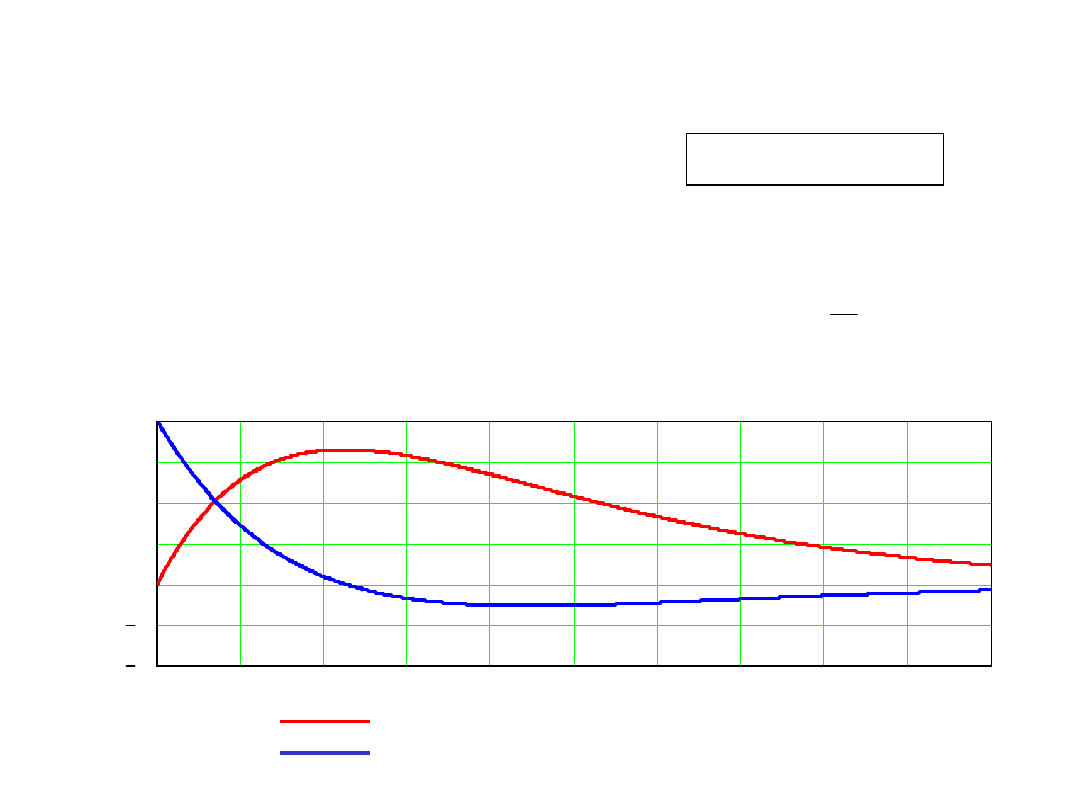
1.5. Przykład drgań swobodnych nietłumionego układu
o jednym stopniu swobody

Masa układu

Sztywność więzów sprężystych

1

m

kg

=

20

N

k

m

=

Częstość i okres drgań własnych

4 472

k

rad

ω

,

m

s

=

=

2

1405

π

T

,

s

ω

=

=

Czas
[s]

P

o

ło

że

n

ie

[m

]

P

rę

d

ko

ść

[m

/s

]

Warunki początkowe

( )

( )

0

1

0

0

q

m, q

=

=

&

Położenie
Prędkość

Część 2

Drgania swobodne tłumione

11

2.1. Rozwiązanie równania ruchu

( )

( )

( )

0

mq t

cq t

kq t

+

+

=

&&

&

Równanie ruchu układu materialnego o jednym stopniu swobody z tłumieniem
wiskotycznym

Przewidywane rozwiązanie

( )

rt

q t

e

=

( )

rt

q t

re

=

&

( )

2 rt

q t

r e

=

&&

2

0

rt

rt

rt

mr e

cre

ke

+

+

=

(

)

2

0

rt

mr

cr k e

+ +

=

2

0

mr

cr k

+ + =

2

2

1

2

2

2

2

2

c

c

k

c

c

k

r

, r

m

m

m

m

m

m

� �

� �

=-

+

-

=-

-

-

� �

� �

� �

� �

( )

1

2

1

2

rt

r t

q t

C e

C e

=

+

Rozwiązanie równania ruchu

12

2.2. Pojęcie tłumienia
krytycznego

2

0

2

kr

c

k

c c

m

m

� �

=

�

-

=

� �

� �

2

kr

c

km

=

2

2

kr

k

c

mω

ω

=

=

Definicja tłumienia
krytycznego

Definicja bezwymiarowego współczynnika tłumienia

kr

c

γ

c

=

( )

( )

( )

( )

mq t

cq t

kq t

P t

+

+

=

&&

&

( )

( )

( )

( )

2

2

P t

q tγωq t

ω q t

m

+

+

=

&&

&

( )

( )

( )

2

2

0

q tγωq t

ω q t

+

+

=

&&

&

Ogólne równanie ruchu układu o jednym stopniu swobody

Równanie ruchu niewymuszonego układu o jednym stopniu
swobody

2

2

1

2

1

1

rγω ω γ

, r

γω ω γ

=-

+

-

=-

-

-

Pierwiastki równania
charakterystycznego

13

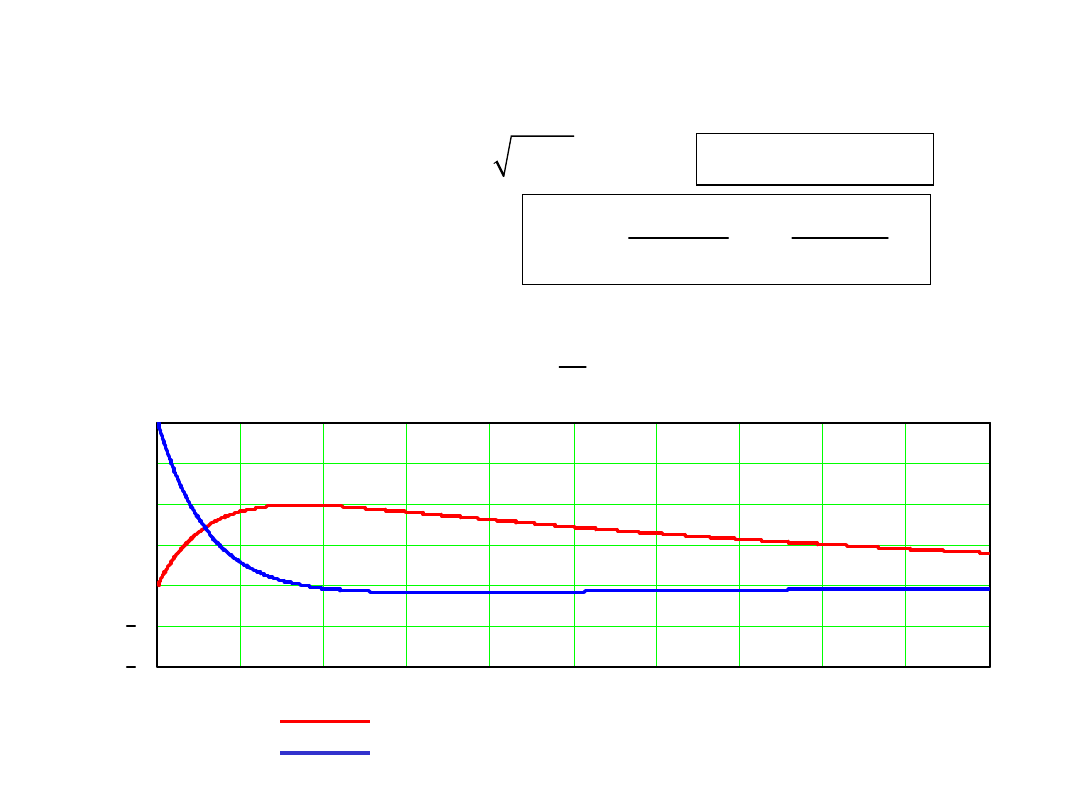
2.3. Ruch układu z krytycznym współczynnikiem
tłumienia

1

2

r rγω

= =-

kr

c c

=

1

γ=

( ) (

)

1

2

γωt

q t

C C t e

-

=

+

0

1

2

3

4

5

6

7

8

9

10

2

1

0

1

2

3

4

4

0.541



X2

2

 

X2

3

 

10

0

X2

1

 

Czas
[s]

P

o

ło

że

n

ie

[m

]

P

rę

d

ko

ść

[m

/s

]

Położenie
Prędkość

Masa układu

Sztywność więzów sprężystych

1

m

kg

=

0 2

N

k

,

m

=

Warunki początkowe

( )

( )

0

0

0

4

q

m, q

=

=

&

Przykład:

14

2.4. Ruch układu z nadkrytycznym współczynnikiem
tłumienia

2

12

1

,

rγω

γ

=-

�

-

kr

c c

>

1

γ>

( )

1

2

1

2

rt

r t

q t

C e

C e

=

+

( )

0

0

q t

q

=

( )

0

0

q t

v

=

&

( )

1

2

0

2 0

0

1 0

2

1

2

1

rt

r t

v

r q

v

rq

q t

e

e

r r

r r

-

-

=-

+

-

-

0

1

2

3

4

5

6

7

8

9

10

2

1

0

1

2

3

4

4

0.191



X2

2

 

X2

3

 

10

0

X2

1

 

Czas
[s]

P

o

ło

że

n

ie

[m

]

P

rę

d

ko

ść

[m

/s

]

Położenie
Prędkość

1

m

kg

=

0 2

N

k

,

m

=

Przykład:

2

kr

c

c

=

15

2.5. Ruch układu z podkrytycznie tłumionego

2

1

1

rγω iω

γ

=-

+

-

kr

c c

<

1

γ<

2

2

1

rγω iω

γ

=-

-

-

( )

(

)

( )

(

)

1

2

d

d

iω t

γωt

γωt

d

d

iω t

γωt

γωt

d

d

q t

e e

e

cosω t i sinω t

q t

e e

e

cosω t i sinω t

-

-

-

-

-

=

=

+

=

=

-

( )

( )

( )

( )

( )

( )

1

1

2

2

1

2

1

2

1

2

γωt

d

γωt

d

ˆq t

q t

q t

e

cosω t

ˆq t

q t

q t

e

sinω t

i

-

-

=

+

=

�

�

�

�

=

-

=

�

�

�

�

( )

(

)

1

2

γωt

d

d

q t

e

A sinω t A cosω t

-

=

+

Rozwiązania równania
jednorodnego

Kombinacja rozwiązań

Całka ogólna równania
jednorodnego

A

1

,

A

2

– stałe całkowania

2

1

d

ω

γ

ω

-

=

16

( )

(

)

1

2

γωt

d

d

q t

e

A sinω t A cosω t

-

=

+

( )

(

)

(

)

1

2

1

2

γωt

γωt

d

d

d

d

d

d

q tγωe

A sinω t A cosω t

e

Aω cosω t A ω sinω t

-

-

=-

+

+

-

&

( )

0

2

0

q

q

A

= =

( )

0

2

1

0

d

q

v

Aγω Aω

= =-

+

&

d

γωq v

A

ω

+

=

0

0

1

2

0

A

q

=

( )

γωt

d

d

d

γωq v

q t

e

sinω t q cosω t

ω

-

�

�

+

=

+

�

�

�

�

0

0

0

Warunki brzegowe

Stałe całkowania

Rozwiązanie

Wyznaczenie stałych
całkowania

17

Alternatywna postać rozwiązania

( )

(

)

γωt

d

q t

Ae

cosω t α

-

=

-

Alternatywna postać rozwiązania

A ,α

- nowe stałe całkowania

(

)

0

0

0

γωt

γωt

d

d

d

d

γωq v

Ae

cosω tcosα sinω tsinα

e

sinω t q cosω t

ω

-

-

-

�

�

+

=

+

�

�

�

�

0

0

d

γωq v

Asinα

ω

-

=

0

Acosα q

=

(

)

d

γωq v

A

q

ω

+

=

+

2

0

0

2

2

0

2

d

γωq v

tgα

qω

+

=

0

0

0

2

2

2

1

d

d

π

π

T

ω

ω

γ

=

=

-

Okres drgań w ruchu tłumionym

Gdy

0 10

γ

,

=

0 995

d

ω

,

ω

=

1005

d

T

,

T

=

18

0

1

2

3

4

5

6

7

8

9

10

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

1

1



x2 t

( )

e

b



t



e

b



t





10

0

t

Czas
[s]

P

o

ło

że

n

ie

[m

]

położenie
funkcja
wykładnicza

1

m

kg

=

20

N

k

m

=

Przykład:

0 5

Ns

c

,

m

=

0 056

γ

,

=

0

1

q

m

=

0

0

m

v

s

=

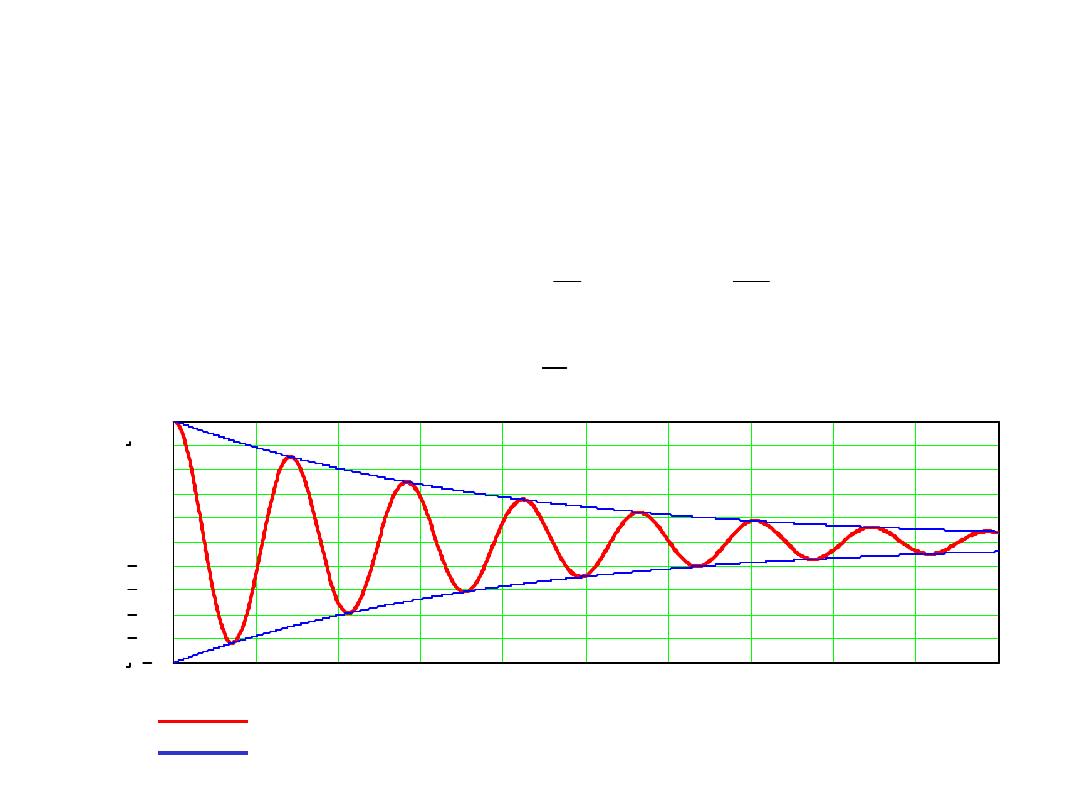
Ruch oscylacyjny nieokresowy

Ruch okresowy modulowany funkcją

( )

γωt

m

q t

Ae

-

=

( )

γωt

m

q t

Ae

-

=

19

2.6. Logarytmiczny dekrement tłumienia

1

n

n

A

Δ ln

A

+

=

( )

(

)

γωt

d

q t

Ae

cosω t α

-

=

-

( )

n

γωt

n

n

A

q t

Ae

-

=

=

(

)

(

)

1

n

d

γω t T

n

n

d

A

q t T

Ae

-

+

+

=

+

=

1

d

γωT

n

n

A

e

A

+

=

2

2

1

d

πγ

Δ γωT

γ

=

=

-

Logarytmiczny dekrement tłumienia wykorzystuje się do wyznaczania
współczynnika tłumienia na drodze doświadczalnej.

2

2

1

n

m

n m

A

mπγ

Δ

ln

A

γ

+

=

=

-

m

– liczba cykli, po których

mierzy się drugą amplitudę
drgań