Funkcjonały gęstości

elektronowej.

Metody DFT

Wykład 8



Koszt obliczeniowy ~ N

4

(N jest liczbą funkcji

bazy)

STO-3G

6-31G 6-31G* 6-31G**

H

1

2

2

5

C

5

9

15

15

C

6

H

6

36

66

102

120

Praktyka metody HF

e

-

e

-



Dokładność - ograniczona (nie uwzględnia

korelacji elektronów

).

Ruch elektronów jest

skorelowany

:

Dwa elektrony, które mają

ten sam

spin

unikają się (ten efekt jest uwzględniony
w metodzie HF przez zastosowanie
wyznacznika Slatera)

Dwa elektrony o

przeciwnym

spinie

też się unikają (ten efekt nie jest uwzględniony
w metodzie HF)

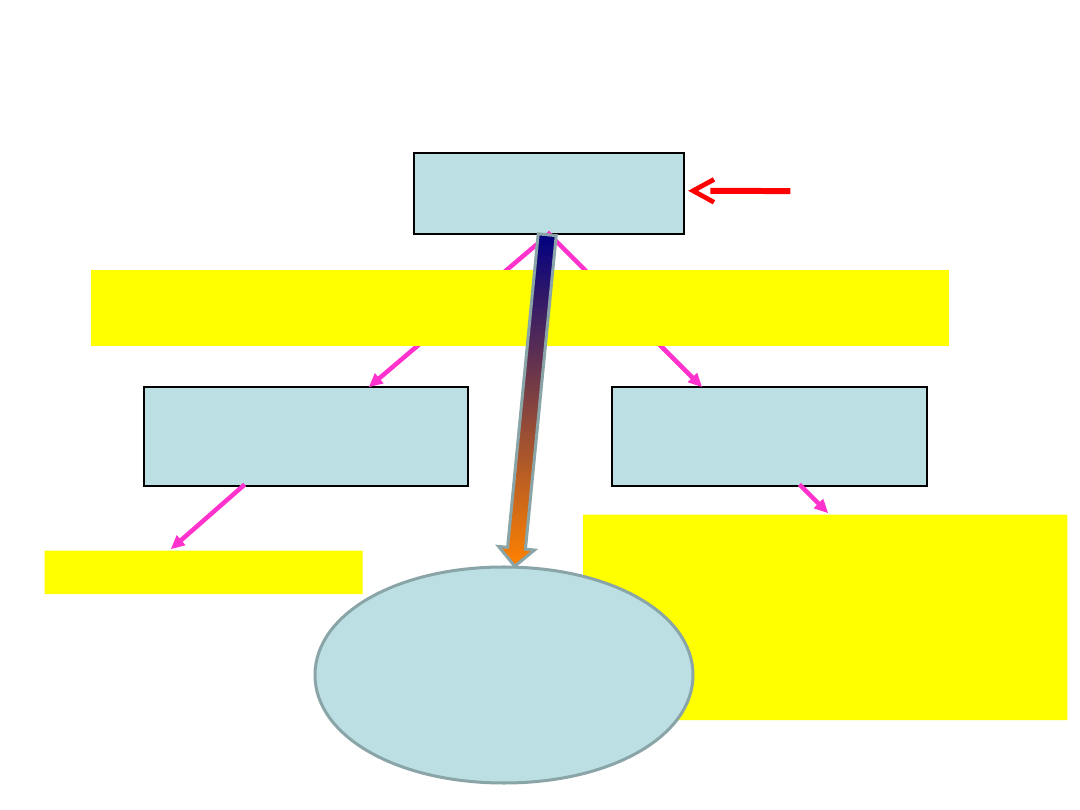
Korelacja elektronów

Metoda HF

Metody półempiryczne

Korelacyjne

metody ab initio

Metody uwzględniające

pośrednio

korelację elektronów

AM1, PM3, MNDO, itd.

•Metoda perturbacyjna Møller-

•Plesset MPn (n = 2, 3, 4…)

•Metody Configuration Interaction

Full CI, CISD, MRCI, itd.

•Metody sprzężonych klasterów

CCSD, CCSD(T), itd.

nie uwzględnia
korelacji
elektronów

Metody uwzględniające

wprost

korelację elektronów

Metody

DFT

Krótka historia metod DFT



1927

: Model Thomasa-Fermiego statystycznego rozkładu

elektronów w atomie.



1964

: Artykuł Hohenberga i Kohna udowadniający istnienie

dokładnego funkcjonału gęstości.



1965

: Równania Kohna-Shama.



lata1970-te i wczesne 80

: Przybliżenie lokalnej gęstości

LDA. Metoda DFT staje się użyteczna.



1985

: Wprowadzenie metod DFT do dynamiki molekularnej

(Car-Parrinello) (Obecnie jedna z 10 najczęściej cytowanych
publikacji).



1988

: Funkcjonały Becke i LYP. DFT zaczyna być stosowane

w chemii.



1998

: Nagroda Nobla dla Waltera Kohna w dziedzinie

chemii za rozwój metod DFT.

Walter Kohn, nagroda Nobla

1998

“Self-consistent Equations including Exchange and Correlation
Effects”
W. Kohn and L. J. Sham, Phys. Rev. 140, A1133 (1965)

Cytat z pracy Kohna i Shama :

“…

“…

nie oczekujemy

nie oczekujemy

dokładnego opisu wiązania chemicznego

dokładnego opisu wiązania chemicznego

.”

.”



Funkcja

zależy od zmiennych liczbowych. Jest to

przepis jak z

liczby

(lub z wielu liczb) otrzymać

inną

liczbę

.

y = f (x)

np. funkcja falowa zależy od współrzędnych

elektronu.

Co to jest funkcjonał?



Funkcjonał

zależy od funkcji, która z kolei

zależy od zmiennych liczbowych. Jest to przepis
jak z

funkcji

otrzymać

liczbę

.

E = F [ f (x) ]

np. energia zależy od funkcji falowej, z ta

zależy od współrzędnych elektronu.



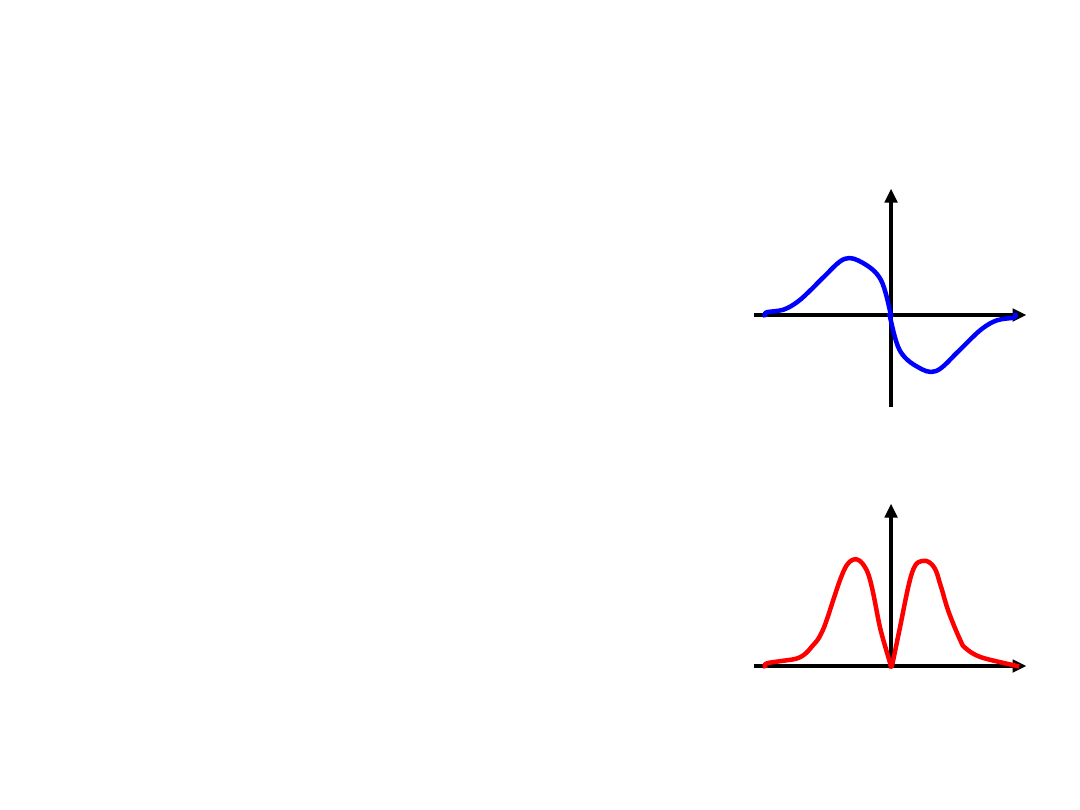
Gęstość elektronową można obliczyć jako
kwadrat funkcji falowej scałkowany po
współrzędnych N-1 elektronów.



Stopień skomplikowania funkcji falowej
wzrasta wraz z liczbą elektronów,
natomiast gęstość elektronowa zawsze
zależy od 3 współrzędnych.

Teoria funkcjonałów

gęstości

x

x







1964 Hohenberg & Kohn

●

Energia

stanu podstawowego

jest

całkowicie określona przez gęstość
elektronową

.

E = F [



(x) ]

●

Jeżeli znamy gęstość elektronową

,

możemy bezpośrednio obliczyć energię,
pomijając funkcję falową.

●

Energia E osiąga

minimum

jeżeli gęstość

elektronowa

, jest

dokładną

gęstością

stanu podstawowego.

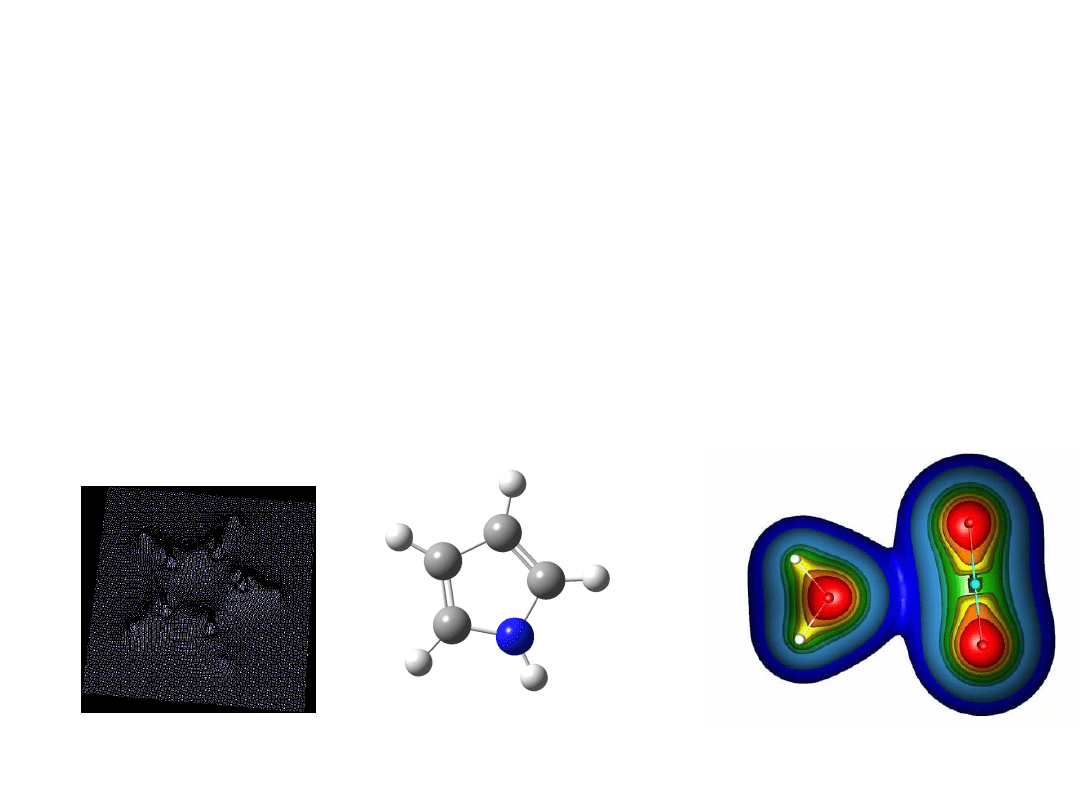
Lemat* Hohenberga-Kohna

Gęstość elektronowa (r) całkowicie definiuje

układ chemiczny. Intuicyjny dowód tego
stwierdzenia:



Całka gęstości elektronowej określa liczbę elektronów
w układzie



Szpice gęstości elektronowej określają położenia jąder
atomowych



Wysokość tych szpiców jest proporcjonalna do ładunku
jąder atomowych

*Lemat – w matematyce twierdzenie pomocnicze, którego głównym
zastosowaniem jest uproszczenie dowodów innych, bardziej istotnych
twierdzeń.

pirol

H2O + CO2

Istnieje ścisła zależność pomiędzy energią cząsteczki E a

gęstością elektronową



: E = F [



(x) ], ale nie znamy

funkcjonału F!

Głównym celem metod DFT jest znaleźć postać F[



(x)

].

Funkcjonał energii można podzielić na kilka części:

E[



] = T[



] + E

ne

[



] + J[



] + K[



]

Teoria funkcjonałów

gęstości

Energia
kinetyczna
elektronów

Energia przyciągania
jąder i elektronów

Energia odpychania
elektron - elektron

Energia wymiany

Energia odpychania
jąder atomowych jest w
przybliżeniu Borna-
Oppenheimera stała

r

r

R

r

R

d

Z

E

M

a

a

a

a

ne









)

(

)

(

]

[





'

'

)

'

(

)

(

2

1

]

[

r

r

r

r

r

r

d

d

J













Z wzorami na E

ne

[

] + J[] nie ma problemu:

Ale jak obliczyć T[

] i K[] ?

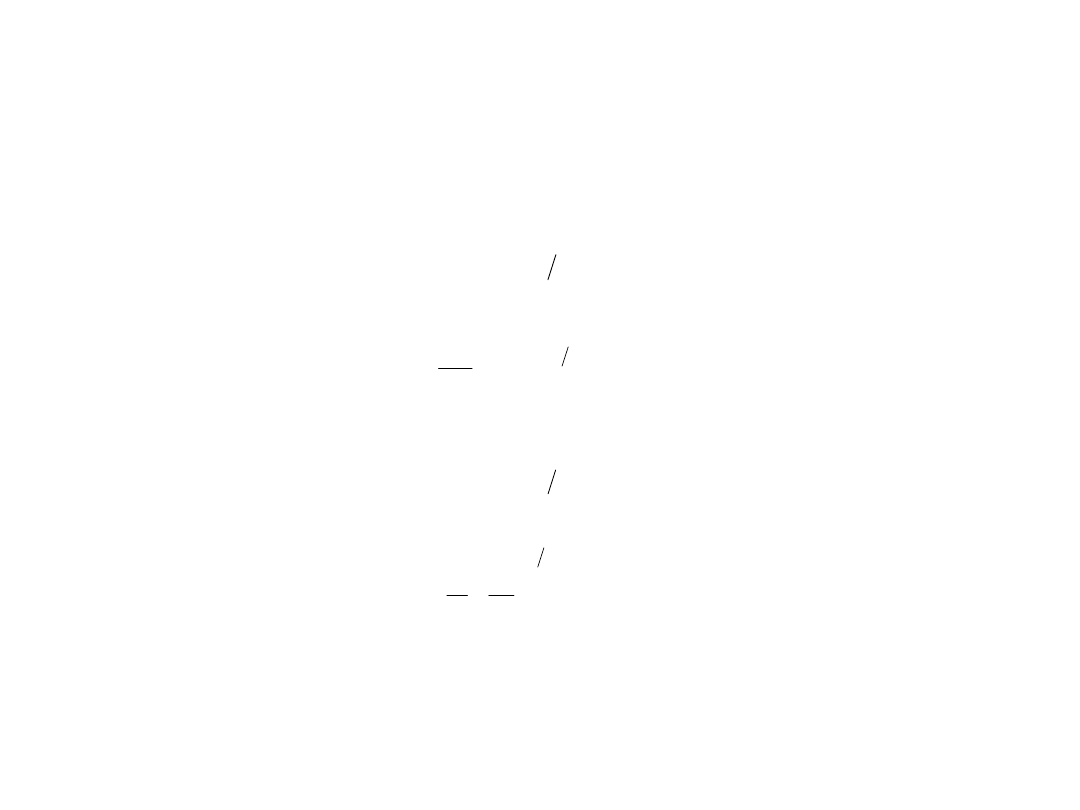
Funkcjonał energii

kinetycznej i wymiany

Wczesne próby znalezienia postaci funkcjonału energii
kinetycznej opierały się na teorii gazu elektronowego Thomasa-
Fermiego:





r

r d

C

T

F

TF

)

(

]

[

3

5





3

2

2

)

3

(

10

3





F

C

A wzór na funkcjonał wymiany został zaproponowany przez
Diraca:





r

r d

C

K

X

D

)

(

]

[

3

4





3

1

3

4

3

















X

C

Ta wczesna (nie używająca pojęcia orbitali elektronowych) teoria
funkcjonału gęstości nieźle opisywała elektrony walencyjne w
metalach, ale zupełnie nie nadawała się do opisu atomów i
cząsteczek. W tej teorii wiązanie chemiczne nie istniało!

Teoria Kohna-Shama



Głównym powodem niepowodzenia wczesnej teorii Thomasa-
Fermiego był nieodpowiedni funkcjonał energii kinetycznej, co
powodowało błąd ok. 10-20%.



Ideą metody KS jest podzielić funkcjonał energii kinetycznej na dwie
części – jedną, która może być obliczona dokładnie i drugą - małą
poprawkę.



Ceną, którą trzeba zapłacić jest ponowne wprowadzenie orbitali co
zwiększa liczbę zmiennych do 3N. Metoda KS jest podobna do
metody Hartree-Focka, stosuje takie same wzory na energię
kinetyczną, energią oddziaływania elektronów z jądrami atomowymi i
elektronów między sobą.



W metodzie KS nieco inaczej dzieli się funkcjonał energii całkowitej:

Gdzie

T

0

[]

jest energią kinetyczną nieoddziaływujących ze sobą

elektronów, które mają ten sam rozkład gęstości elektronowej (r) jak
układ rzeczywisty.

J(r)

to coulombowskie oddziaływanie elektronów

(również oddziaływanie elektronu z samym sobą), a

V

ext

(r)

to

potencjał zewnętrzny, pochodzący od jąder atomowych, a

E

XC

[]

zawiera wszystkie pozostałe składniki.

]

[

)

(

)]

(

ˆ

)

(

ˆ

[

]

[

]

[

0









XC

ext

E

d

J

V

T

E











r

r

r

r



Energia korelacyjno-wymienna jest podstawową wielkością
w DFT



Dokładna postać funkcjonału tej energii nie jest znana.
Stosowane są różne przybliżenia.



W funkcjonale

E

XC

[]

zostały

„zamiecione pod dywan”

wszystkie trudne do policzenia oddziaływania:

energia wymiany

energia korelacji elektronów

korekta energii kinetycznej

korekta energii coulombowskiej (oddziaływanie elektronu z
sobą)

Energia korelacyjno-

wymienna

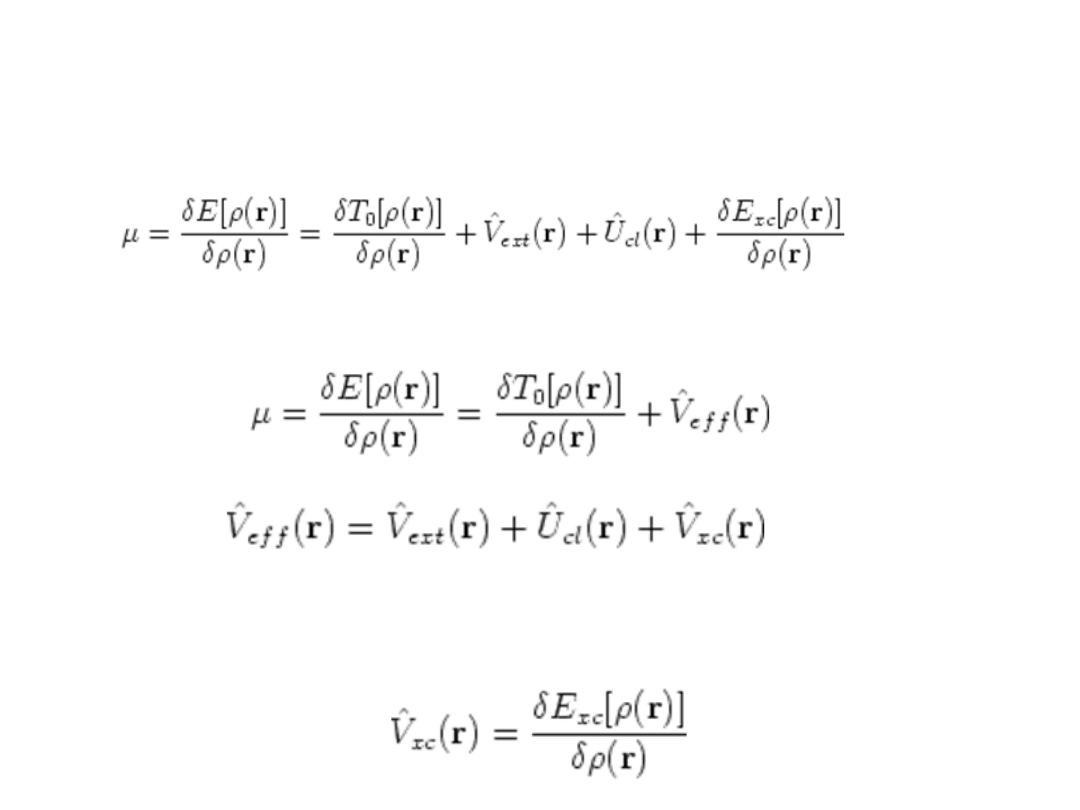
Stosując zasadę wariacyjną otrzymamy:

Potencjał efektywny

Co inaczej można

zapisać:

gdzie:

Potencjał korelacyjno-wymienny jest pochodną
funkcjonału energii korelacyjno-wymiennej:

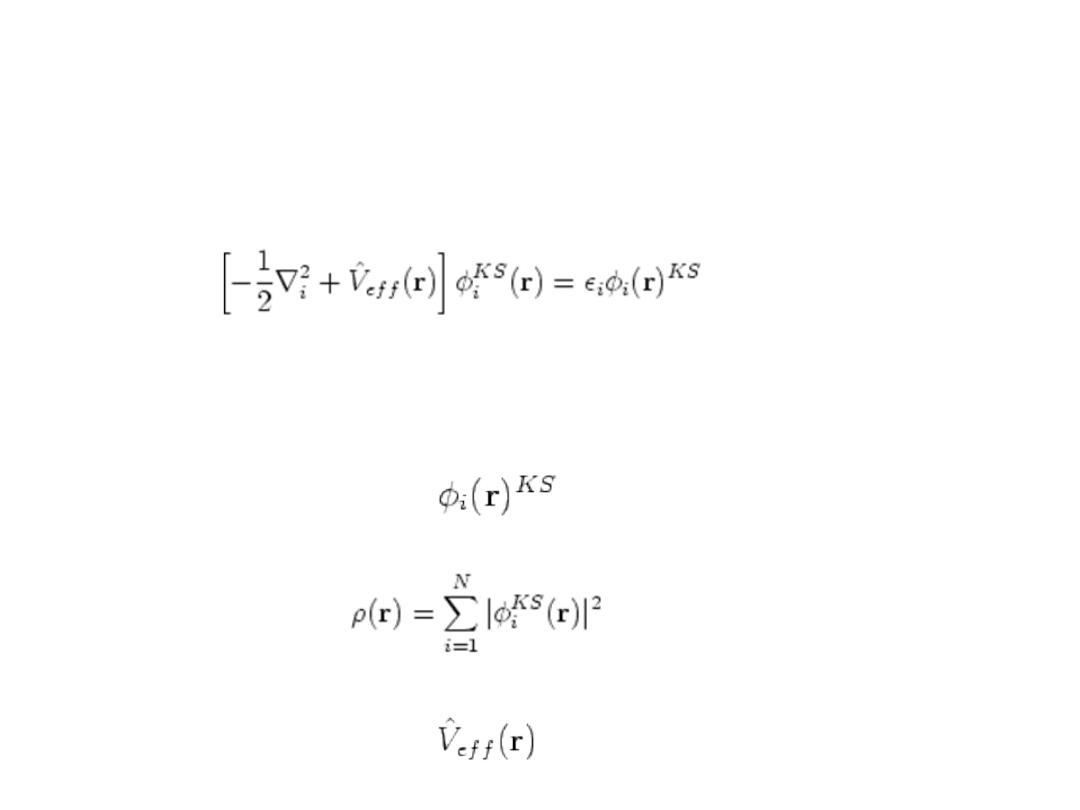
Równanie Kohna-Shama

Równania Kohna-Shama to jednoelektronowe równania
Schrödingera dla fikcyjnego układu nieoddziaływujących
elektronów w zewnętrznym polu pochodzącym od jader
atomowych

Które mogą być użyte do obliczenia gęstości elektronowej:

Tak! Te równania są podobne do równań Hartree-Focka ale są
znacznie łatwiejsze do rozwiązania, bo operator w równaniach
KS jest taki sam dla wszystkich orbitali. Rozwiązując je
otrzymujemy orbitale Kohna-Shama:

Która może być użyta do obliczenia poprawionego potencjału
efektywnego :

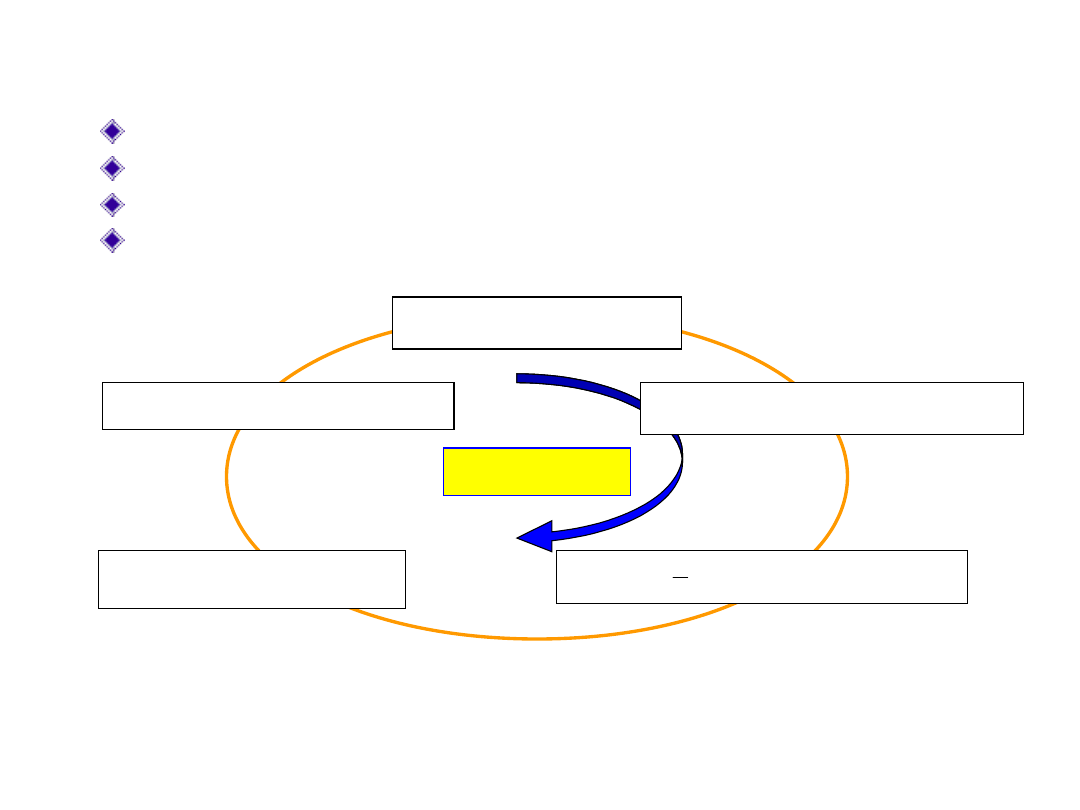
Algorytm metody KS

Aby rozwiązać równania KS musimy znać potencjał V

ef

(r)

Do V

ef

(r) niezbędna jest gęstość elektronowa (r)

Gęstość (r) można otrzymać z orbitali ψ(r)

ψ(r) są nieznane dopóki nie rozwiążemy równań KS.



The computational complexity goes like O(NlogN) , O(N^3)

cykl SCF

Zacznij od



in

(r)

oblicz V

ef

(r) =f[



(r)]

)

(

)

(

)}

(

2

1

{

R

2

r

r

r

i

i

i

ef

V

ozwiąz























F

i

E

i

blicz





2

|

)

(

|

)

(

O

r

r

użyj poprawionej



(r)

Głównym celem metody DFT jest znalezienie funkcjonału

najlepszego z możliwych. (Możliwe, że nigdy nie poznamy

dokładnego

funkcjonału…)

Proponowane są różne funkcjonały, których współczynniki są

dopasowywane tak, aby uzyskać zgodność z eksperymentem
lub wynikami zaawansowanych obliczeń ab initio.

Funkcjonały gęstości



Przybliżenie lokalnej gęstości (

ang. Local Density

Approximation

(

LDA

))

Przyjmuje się, że funkcjonał zależy wyłącznie od gęstości

elektronowej

Przykłady: LSDA (w), VWN (k)



Przybliżenie uogólnionych gradientów (

ang. Generalized

Gradient Approximation

(

GGA

))

Przyjmuje się, że funkcjonał zależy zarówno od gęstości

elektronowej jak i od gradientu tej gęstości.

Przykłady: PW86 (w), B88 (w), PW91 (k), LYP (k), BLYP

(w = wymiana, k =korelacja)



Funkcjonały

hybrydowe

•Tworzone jako kombinacja liniowa różnych funkcjonałów i

metody Hartree-Focka.

•Przykłady: HH (w), B3 (w), B3LYP

• Funkcjonały podwójnie hydrydowe

•Oprócz mieszania funkcjonałów wymiany z energią

wymiany Hartree-Fock, również miesza funkcjonał
korelacji z energią korelacji liczona metodą MP2.

•Przykłady: MC3MPW, MC3BB

• Funkcjonały Meta-GGA

•Przyjmuje się, że funkcjonały zależą od gęstości

elektronowej, jej gradientu (tak jak w GGA) i jeszcze od
energii kinetycznej.

•Przykłady: VSXC, BB95

Funkcjonały gęstości

(2)



Czas obliczeń metodami DFT jest proporcjonalny do ~ N

4

(N –

liczba funkcji bazy)

Trochę bardziej kosztowne niż metoda HF ale dokładniejsze
Nie ma sposobu na systematyczny wzrost dokładności obliczeń

(przynajmniej na razie).



Dokładność zależy wybranego funkcjonału i od typu
obliczanych układów.

•BLYP

dobry dla metali, kiepski dla związków organicznych

•B3LYP

kiepski dla metali, dobry dla związków organicznych

•MPW1K

specjalnie sparametryzowany do opisu kinetyki reakcji

(dobry dla energii i geometrii stanów przejściowych, kiepski
dla trwałych cząsteczek)



Na ogół uważa, że metoda DFT źle opisuje wiązania

wodorowe i słabe oddziaływanie (dyspersyjne) , ale niektórzy
się z tym nie zgadzają.



Należy sprawdzić funkcjonał zanim go się zacznie używać.

Przetestować metodę na małej cząsteczce dla której są dostępne

wiarygodne dane eksperymentalne lub wyniki zaawansowanych
metod ab initio.

Który funkcjonał wybrać?

Jak dokładne wyniki daje metoda DFT?

Metoda Kohna-Shama -

testy

Energie dysocjacji cząsteczek

[eV]

Cząsteczk

a

LDA

GGA

Dokł.

H

2

4.9

4.6

4.7

CH

4

20.0

18.2

18.2

NH

3

14.6

13.1

12.9

H

2

O

11.6

10.1

10.1

CO

13.0

11.7

11.2

O

2

7.6

6.2

5.2

Długość wiązania [Bohr]

Cząsteczk

a

LDA

GGA

Eksper.

H

2

2.16

2.01

2.07

CO

2.22

2.08

2.13

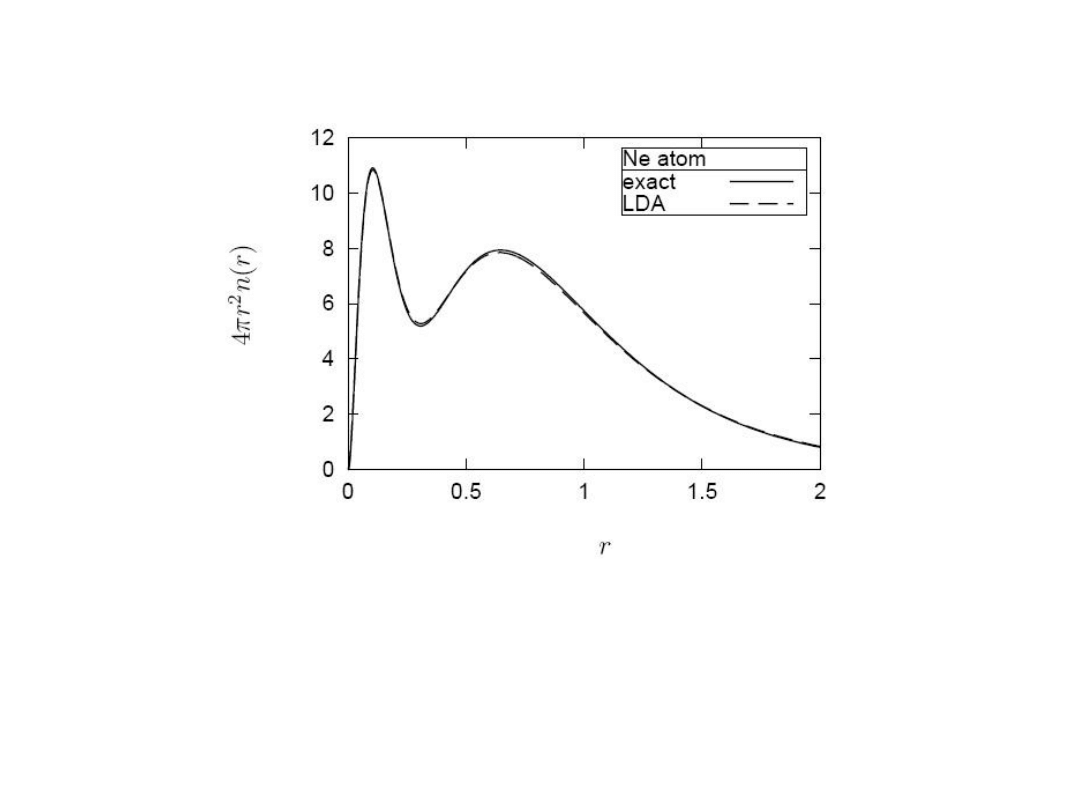
Metoda Kohna-Shama -

testy

Dokładna i obliczona z użyciem funkcjonału LDA

radialna gęstość atomu Ne.

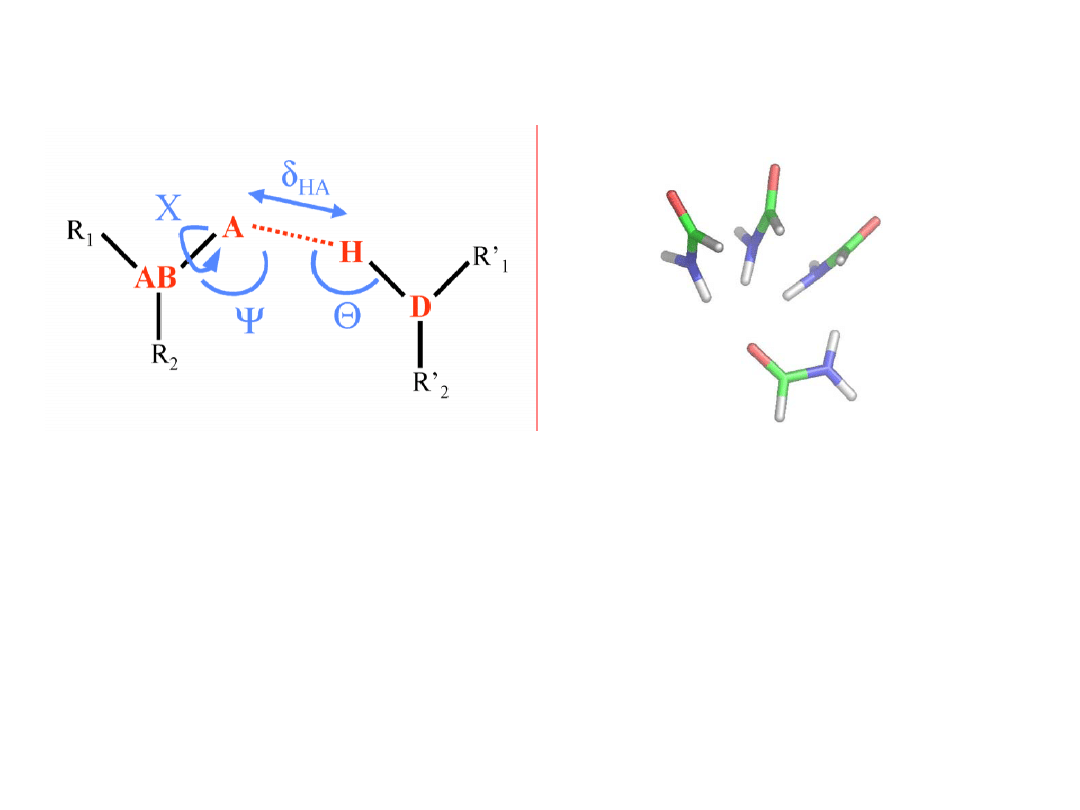
A – akceptor protonu;
D – atom donora;
H –atom wodoru;
4 parametry geometryczne
na jedno wiązanie

wodorowe.

Wiązanie wodorowe – opis

układu

Model wiązania
wodorowego
w białkach to dimery
małych amidów, np.
formamidu

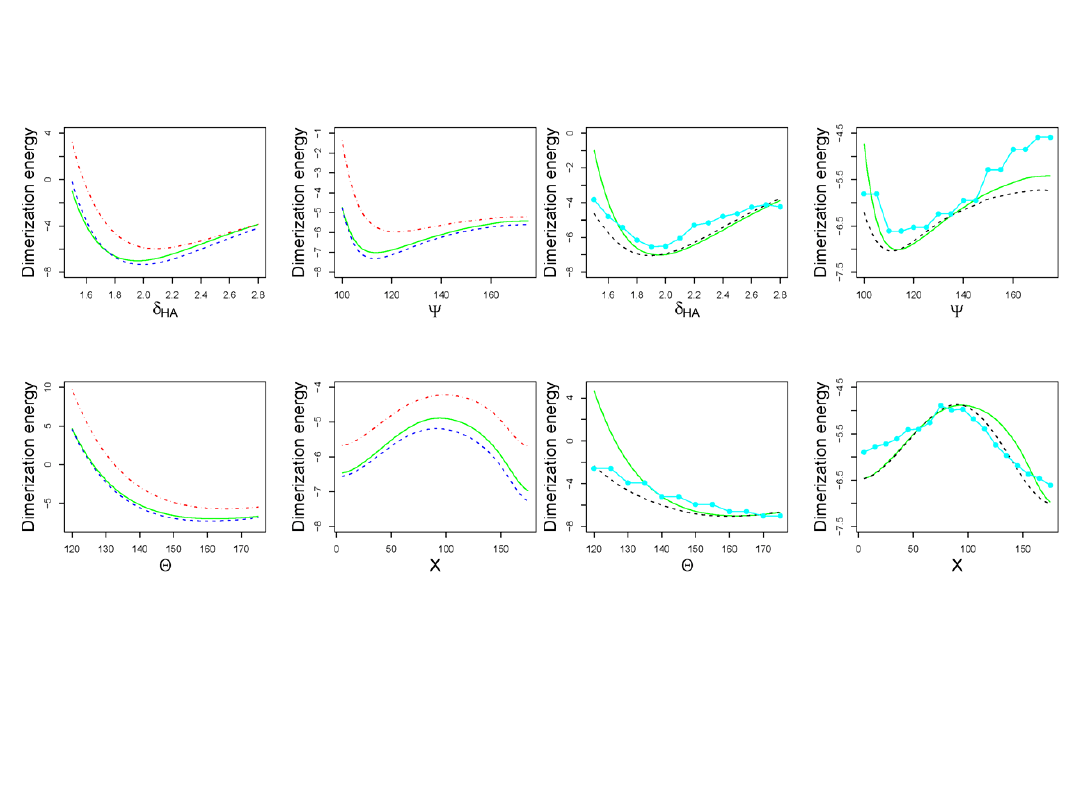
Porównanie wyników DFT

czerwone

– HF;

zielone

– DFT;

niebieskie

– HF+MP2;

czarne – DFT z dodatkową relaksacją energii;

turkusowy

– dane eksperymentalne.

Pytania

•Co to jest funkcjonał? Podać przykłady
•Jakie znasz metody obliczeniowe uwzględniające energię

korelacji elektronów? Jakie są wady i zalety każdej z nich?

•Rodzaje funkcjonałów korelacyjno-wymiennych.