Psycho-emocjonalne

uwarunkowania

istnienia systemów

autonomicznych

wg Mariana Mazura

mgr inż. Maciej Węgrzyn

http://autonom.edu.pl

Plan prezentacji

•Wprowadzenie

•Cybernetyczne parametry systemów

autonomicznych (układów samodzielnych)

•Równowaga funkcjonalna systemu

autonomicznego

•Przejście od systemów działaniowych do

systemów konfiguracyjnych

•Najmniejszy możliwy do zrealizowania

system autonomiczny typu „pattern”

•Zależność układów zdalnych od otoczenia

•Możliwość zapisu matematycznego

właściwości systemu autonomicznego

•Wnioski praktyczne

Wprowadzenie

Marian

Mazur,

twórca

polskiej

szkoły

cybernetycznej,
jest autorem oryginalnej metody postępowania

przy badaniu różnych zjawisk dotyczących

sterowania

.

Postępując w badaniu zjawisk tą

metodą należy wychodzić od założeń ogólnych

i przechodzić do rozpatrywania przypadków

szczegółowych. Metodę te nazwał

metoda

systemową

, przy czym systemy według tej

metody są kreowane ze względu na

wykonywane czynności - więc są systemami

typu „acting”. W dalszej części prezentacji

pokażemy jak ta metoda pozwala przewidzieć

przebieg zjawisk związanych z zachowaniami

społecznymi ludzi i jak dalece różni się od

innych metod.

Cybernetyczne parametry

systemów autonomicznych

(układów samodzielnych)

Systemy

autonomiczne

(S.A.,

wcześniej

zwane

układami

samodzielnymi)

–

są to systemy zdolne do sterowania sobą i zdolne do

zachowania zdolności sterowania sobą, w szczególności ludzie.

Akumulator – podsystem S.A., który przechowuje i „wydatkuje” energię.

Korelator

–

podsystem S.A., który przechowuje, przetwarza i „wydatkuje”

informacje.

Homeostat

–

podsystem S.A., który współpracując z akumulatorem i

korelatorem ma zapobiegać utracie równowagi funkcjonalnej systemu

autonomicznego.

Jeżeli

coś

musi być to

to

jest!

M. Mazur, „Cybernetyka i charakter”

Cybernetyczne parametry

systemów autonomicznych

Równowaga funkcjonalna

systemu autonomicznego

System autonomiczny (układ samodzielny) jest nazwą cybernetyczną,
określającą "coś" (pewien twór, ustrój żywy lub nawet abstrakcyjny), co
wypełnia następujące funkcje sterownicze:

steruje sobą samym i

zapobiega utracie zdolności sterowania sobą

.

Wszystkie systemy spełniające te funkcje zaliczamy do S.A., są to
organizmy żywe, w tym również i ludzie, gdyż organizm człowieka
spełnia także postulaty zawarte w definicji (a więc jest S.A.).
Aby te postulaty zrealizować, każdy proces informacyjny, określający typ
reakcji, oraz proces energetyczny (określający natężenie reakcji) musi
sprzęgać ze sobą coś, co tą czy inną drogą

utrzymuje równowagę

funkcjonalną (homeostazę) systemu

, i co wchodzi w skład tego systemu -

tym czymś jest homeostat.

Równowaga funkcjonalna

systemu autonomicznego

Każdy proces wymaga przepływu energii, ale

w procesach

informacyjnych jest to

energia sterownicza

, która służy do wskazania

różnic między stanami fizycznymi, podczas gdy w procesach
energetycznych jest to energia poświęcona na wykonanie pracy, służącej
dla przeprowadzenia transformacji jednych stanów fizycznych w drugie.
Stąd podział funkcji pomiędzy odpowiednie podsystemy.
Podział na podsystemy jest poddany rygorom ścisłej funkcjonalności -

jeden podsystem spełnia tylko jedną funkcję

,

zaś do wypełnienia jednej

funkcji służy zawsze tylko jeden podsystem

. Relacja pomiędzy zbiorem

podsystemów i zbiorem funkcji jest "relacją doskonałą". Między
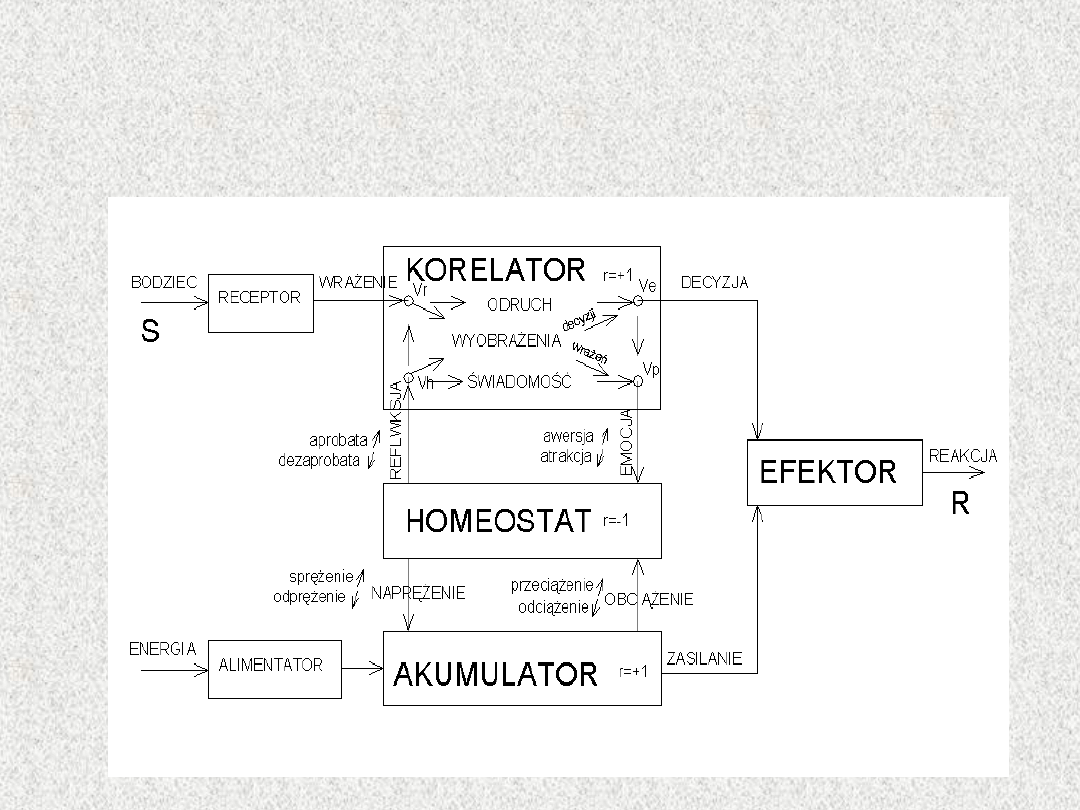
podsystemami występują sprzężenia proste i sprzężenia zwrotne. Na
rysunku przedstawiono funkcje podsystemów i sprzężenia podsystemów
w systemie autonomicznym.

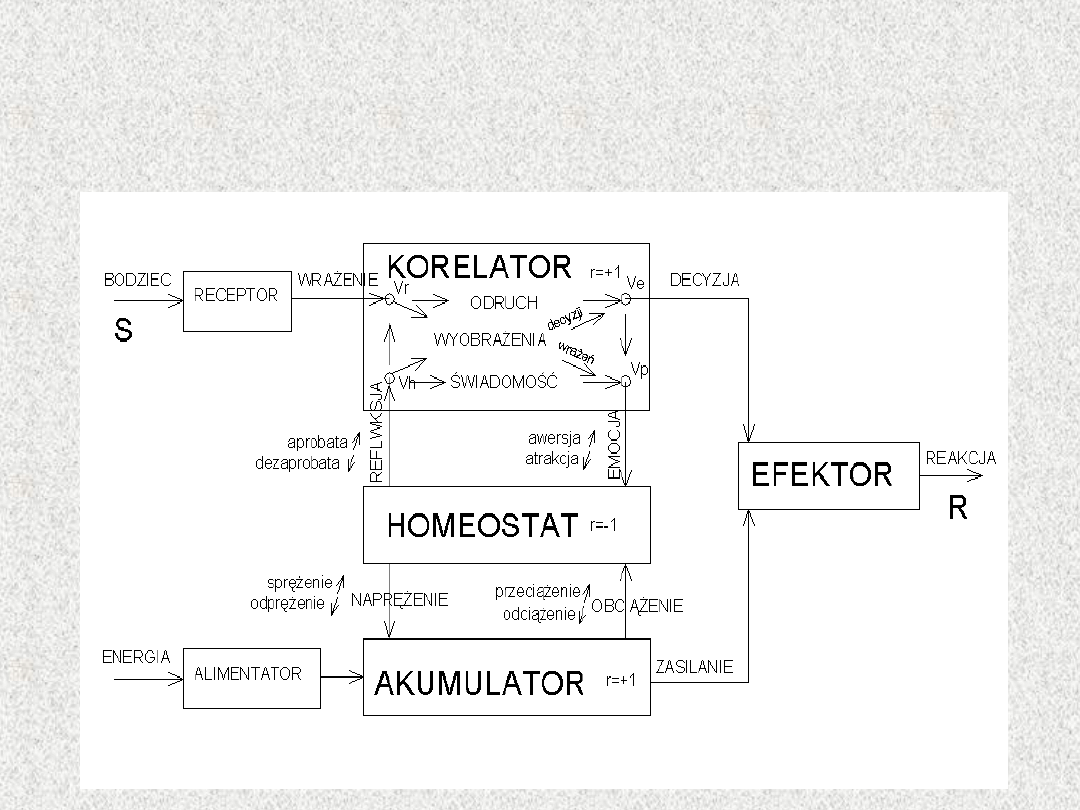
Równowaga funkcjonalna systemu

autonomicznego

Równowaga funkcjonalna

systemu autonomicznego

Reaktywność

podsystemu

jest

to

sposób

transformowania bodźców. Reaktywność

r = +1

oznacza

wierne transformowanie, zaś

r = -1

oznacza odwracanie

oddziaływań.
Zachowanie się S.A. jest rezultatem sprzężeń zwrotnych
pomiędzy reakcjami a bodźcami.

Korelator daje informacje

o sposobach modyfikacji.

Akumulator daje energię

w

pożądanej postaci.

Efektor

zasilany przez oba te

podsystemy

oddziałuje na otoczenie

, aby zdobyć

niezbędny stopień zasilania i potrzebne informacje.
Homeostaza

systemu

autonomicznego

polega

na

sprzężeniu

zwrotnym

pomiędzy

korelatorem

a

homeostatem oraz akumulatorem a homeostatem:

odwracanie oddziaływań ma przeciwdziałać zarówno
nadmiarom, jak i niedomiarom w koncentracji energii w
systemie

autonomicznym

,

w

zakresie

czułości

homeostatu.

Równowaga funkcjonalna

systemu autonomicznego

Oddziaływanie akumulatora na homeostat jest to

obciążenie

(informacja o poziomie energii w akumulatorze).
Jeżeli poziom energii rośnie, obciążenie rośnie i jest to przeciążenie.
Jeżeli obciążenie spada, jest to odciążenie.

Oddziaływania homeostatu na akumulator jest to

naprężenie

(jest to

obrona przed nadmiarem i niedomiarem energii).

Jeżeli naprężenie rośnie - jest to sprężenie. Jeżeli naprężenie spada
- jest to odprężenie.

Działanie korelatora na homeostat jest to emocja.

Jeżeli emocja rośnie, jest to awersja. Jeżeli emocja opada, jest to
atrakcja.

Działanie homeostatu na korelator jest to refleksja

.

Jeżeli refleksja rośnie, jest to aprobata. Jeżeli refleksja spada jest to
dezaprobata.
Powyższe terminy należy używać w znaczeniu, w jakim zostały
oparte

w

konwencjach

terminologicznych,

choćby

zakres

znaczeniowy nie w pełni pokrywał się z potocznym rozumieniem
użytych wyrazów.

Podział systemów na klasy

Podział systemów na klasę systemów działaniowych "acting"
i klasę systemów konfiguracyjnych "pattern" podał Alfred
Kuhn (1974).
Wyszczególniając podsystemy w systemie typu "acting"
mamy na uwadze

funkcje

przez nie wykonywane,

wyszczególniając systemy typu "pattern” mamy na uwadze

elementy oddzielne fizycznie

, na jakie możemy podzielić

system.
Rozważania na temat systemu typu "acting" nadają się do
rozwiązywania

problemów decyzyjnych

(jak coś działa).

Systemy typu „pattern" stosuje się przy rozwiązywaniu

problemów poznawczych

(co jest jakie).

Czarna skrzynka

Przez „

S

” oznaczymy oddziaływanie

wejściowe

(od ang. stimulus -

bodziec).
Przez „

R

” oznaczymy oddziaływanie

wyjściowe

(od ang. reaction -

reakcja).
Według ustaleń M. Mesarovica oddziaływania wyjściowe są zawsze

mniejsze od wejściowych:

S>R

niezależnie od rodzaju oddziaływań.

Jest to zgodne z ustaleniami M. Mazura, że „wszelkim procesom

przetwarzania energii towarzyszą straty energii do otoczenia”.
Jak widać z rysunku, aby uznać że system istnieje, dowolny

Obserwator powinien wykonać następujące czynności:

S

R

Czarna skrzynka

Pomierzyć sygnał uznany za wejściowy S
Pomierzyć sygnał uznany za wyjściowy R
Porównać wielkość sygnałów
Rozpatrzyć wszystkie możliwości :
1. Jeżeli

S>R

to może uznać, że system istnieje.

2. Jeżeli

S=R

to jeszcze nie wiadomo, czy system istnieje.

3. Jeżeli

S<R

to Obserwator pomylił wejście z wyjściem (pomylił

kierunek procesu).
Jak widać, prawdziwe jest stwierdzenie:

Systemy kreuje Obserwator!

S

R

Budowa najmniejszej czarnej

skrzynki

Jakie jest najmniejsze skupienie energii i
materii aby działało jako system?

Adam Lech

Aby mogło zadziałać "wyjście", musi być
różnica potencjałów pomiędzy wyjściem a
otoczeniem.
Przyjmijmy, że różnica ta jest w wysokości +1
ziarno energomaterii na wyjściu systemu, czyli
R=+1.
Ponieważ

wielkość

„ziarna”

zależy

od

możliwości

obserwacyjnych

Obserwatora,

„najmniejszość” systemu jest więc rzeczą
umowną - trzeba podawać, jakie „ziarna”
rozpatrujemy!

Budowa najmniejszej czarnej

skrzynki

Aby mógł nastąpić przepływ energomaterii
pomiędzy "wejściem" i "wyjściem", "wejście”
musi mieć potencjał wyższy od „wyjścia”, gdyż
pewna część energii jest zużywana na potrzeby
własne systemu.
1. Jeżeli przyjmiemy, że jest to także +1 ziarno,
to potencjał wejściowy musi być wyższy
również o +1 ziarno od "wyjścia”, czyli o +2 od
otoczenia.
A więc nie wszystkie skupienia energomaterii
powodują działanie systemu typu "czarna
skrzynka", ale tylko takie, które są +2 ziarnami
energomaterii.

Budowa najmniejszej czarnej

skrzynki

2. Jeżeli przyjmiemy, że straty są niższe, to

ziarno na wyjściu musi być jakby „mniejsze” od

ziarna na wejściu.
3. Ponieważ obserwator też powinien być

systemem, może to oznaczać, że odbierane są

sygnały o wartości energetycznej +2 ziaren.

I tylko takie będą nośnikami informacji.

Pozostałe nie spowodują zadziałania "czarnej

skrzynki".
Jednocześnie można na podstawie powyższego

rozważania określić maksymalną dopuszczalną

stratność "w" systemu - wynosi ona 0,5 i nie

jest zależna od masy systemu.

Sieci najmniejszych czarnych

skrzynek

Biorąc pod uwagę, że nośnikami energii są
kwanty

promieniowania

można

ustalić

następujące

reguły

połączenia

"czarnych

skrzynek " w sieć systemów:

E = hxv

0

≥ hxv

1

≥ hxv

2

Jeżeli straty energii są niewielkie, dużo poniżej
kwantu absorbowanego przez wejście systemu,
to na wyjściu mogą pojawić się dwa kwanty o
niższej wartości energetycznej.
Gdzie "v" to częstotliwość (gdyż kwant
kwantowi nie jest równy).
Wtedy można systemy łączyć szeregowo.

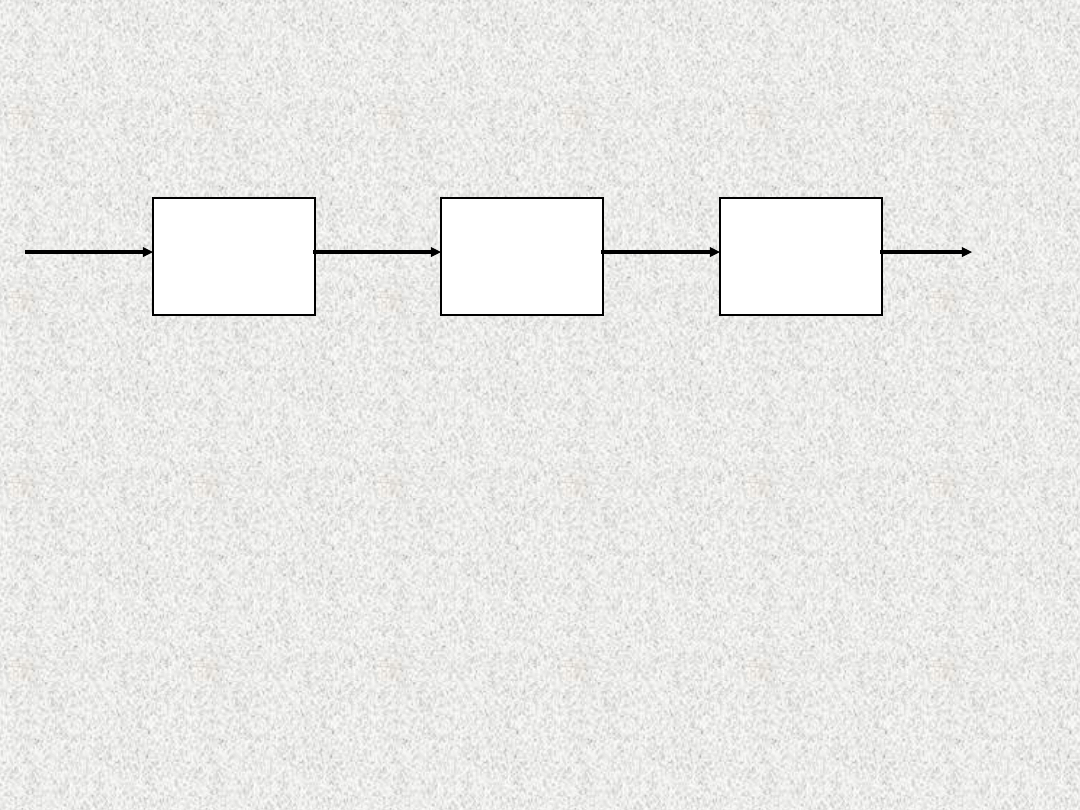
Sieci najmniejszych czarnych

skrzynek

Łączenie szeregowe systemów typu czarna
skrzynka.

S

R=S

1

R

1

=S

2

R

2

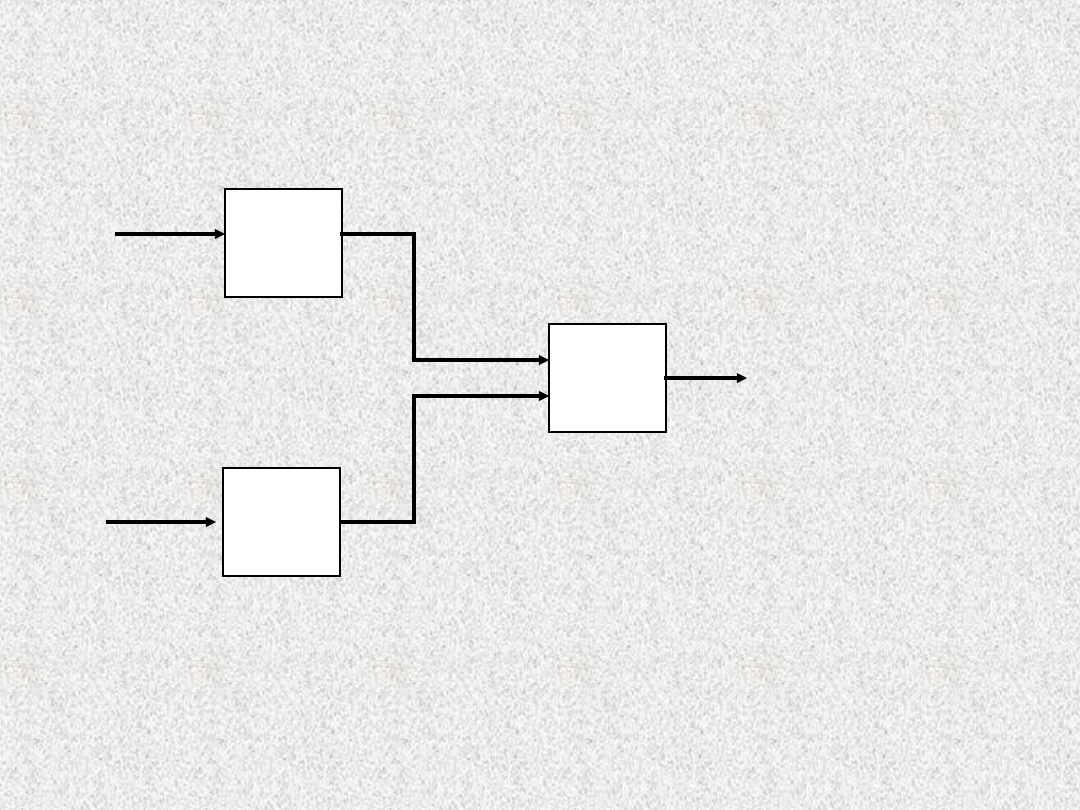
Sieci najmniejszych czarnych

skrzynek

Łączenie równoległe systemów typu czarna
skrzynka.

S

1

S

2

R

1

R

2

S

3

R

1

+ R

2

= S

3

Sieć najmniejszych czarnych

skrzynek

Szereg można włączyć do równoległego działania zawsze,

działa wtedy jako sumator zbiorów.
Sieć kombinowana wymaga przetwarzania w ostatnim

elemencie dwu kwantów o niższej wartości w jeden o wyższej

wartości:

2 hv

1

= / hv

2

/

Połączenie dwu odcinków sieci, z których jeden działa jako

szeregowy, a drugi działa jako równoległy może nastąpić, gdy:
- połączenie ma charakter "równoległy" lub szeregowo-

równoległy,
- dwa "ziarna” płynące jako sygnał z sieci szeregowej mają

energię nieco wyższą niż jedno ziarno sieci równoległej,

2hv

s

> hv

r

- sieć kombinowana ma dwa różne rodzaje "częstotliwości

wejściowej" przy czym "częstotliwość szeregowa" jest prawie

dwukrotnie niższa, niż częstotliwość "równoległa"

2v

s

= v

r

Sieć najmniejszych czarnych

skrzynek

Ilustracją takiego łączenia sieci „czarnych skrzynek” jest
działanie chlorofilu w procesie fotosyntezy:

• dwa fotony odczepiają dwa elektrony, które przenoszone są

na coraz niższe poziomy energetyczne,

• chlorofil wykazuje dwa pasma maksimum absorbcji – we

fiolecie i w czerwieni. Do tej pory nie było wiadome dlaczego
akurat te pasma są absorbowane – wystarczyłoby przecież
jedno, aby zapewnić zasilanie. Ale jedno pasmo ogranicza
możliwość budowania sieci logicznych. Albo buduje się
szeregowe albo równoległe,

• podwojony sygnał pojawia się trzy razy częściej niż

pojedynczy.

Sieć najmniejszych czarnych

skrzynek

Warunki budowy sieci przystosowanych do rozwiązywania zadań

logicznych:

• Przesyłanie sygnałów wymaga połączeń szeregowych.

Dodawanie zbiorów

– połączeń równoległych z sieci

szeregowych.

Mnożenie zbiorów

– połączeń równoległych sieci

równoległych.

• Mnożenie zbiorów, z których jeden powstał w wyniku

dodawania, a drugi w wyniku mnożenia zbiorów wymaga pracy

na dwu „częstotliwościach”, z których pierwsza jest niecałe dwa

razy niższa niż druga.

• Można udowodnić, że jest możliwość budowania „maszyny

logicznej” przeznaczonej do rozwiązywania konkretnego zadania

logicznego, ale

przy niepełnym zasilaniu wejść maszyna ta

będzie rozwiązywać inne zadanie logiczne

!

• Zapis matematyczny takiego wywodu wymaga wprowadzenia

nowych symboli.

Najmniejszy możliwy do

zrealizowania system

autonomiczny typu „pattern”

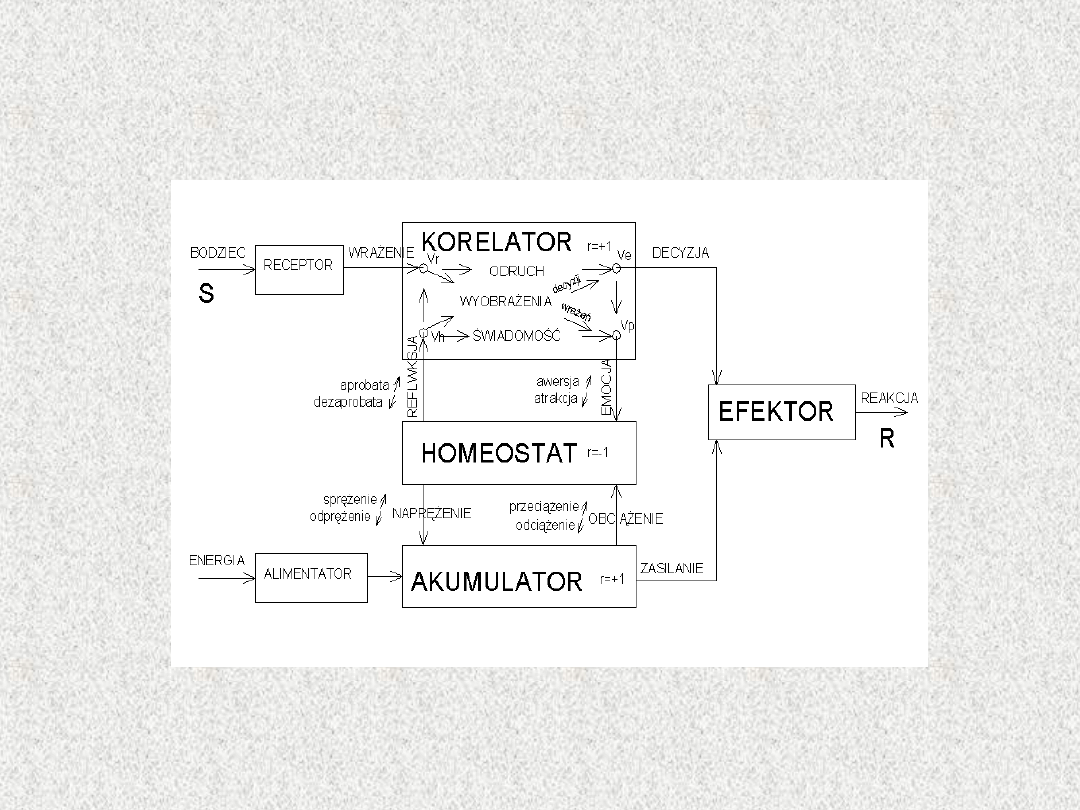
Schemat funkcjonalny systemu autonomicznego (S.A.) podał M. Mazur.
Na rysunku zaznaczono nazwy wszystkich oddziaływań pomiędzy podsystemami.

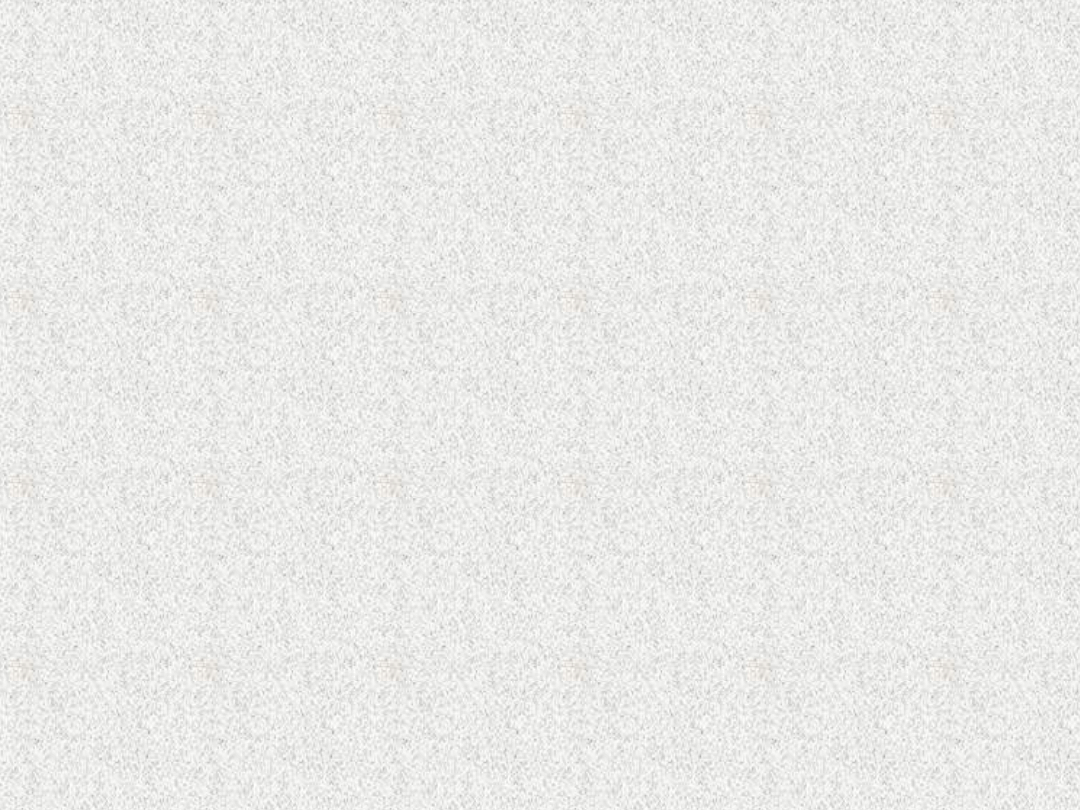
Najmniejszy możliwy do

zrealizowania system

autonomiczny typu „pattern”

Zbudowanie takiego systemu jest możliwe technicznie.
Również w takiej formie jaką podał M. Mazur.
Potrzeba do tego jednak aż 12 punktów gromadzenia energii
i 10 dróg rozpływów wewnętrznych w podsystemach oraz 4
dróg rozpływu pomiędzy podsystemami.
Powstanie takiego systemu w drodze przypadkowych
połączeń jest niezwykle mało prawdopodobne.
Powstaje jednak pytanie, czy można to samo zrobić
„oszczędniej” z użyciem mniejszej liczby elementów, gdyż
jeden element odrębny fizycznie, z jakich konstruujemy
system „patter” może w systemie „acting” spełniać więcej
niż jedną funkcję. Przy czym funkcją będzie tu wypełnianie
jakiejś czynność niezbędnej do działania systemu jako
całości, bo sposób przyporządkowania elementów systemu
”acting” polega na tym, że jeden element wypełnia tylko
jedną funkcję systemu.

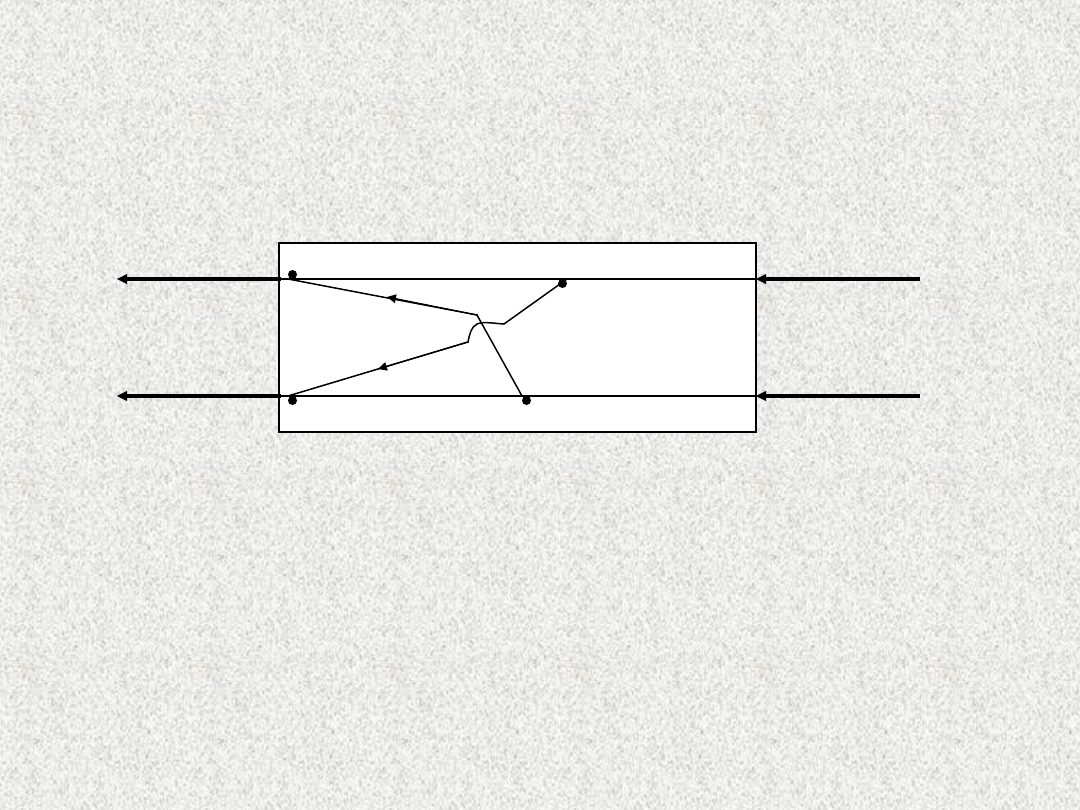
Budowa homeostatu

Wg. A. Lecha układ połączeń w homeostacie wygląda następująco.

refleksja

naprężenie

emocja

obciążenie

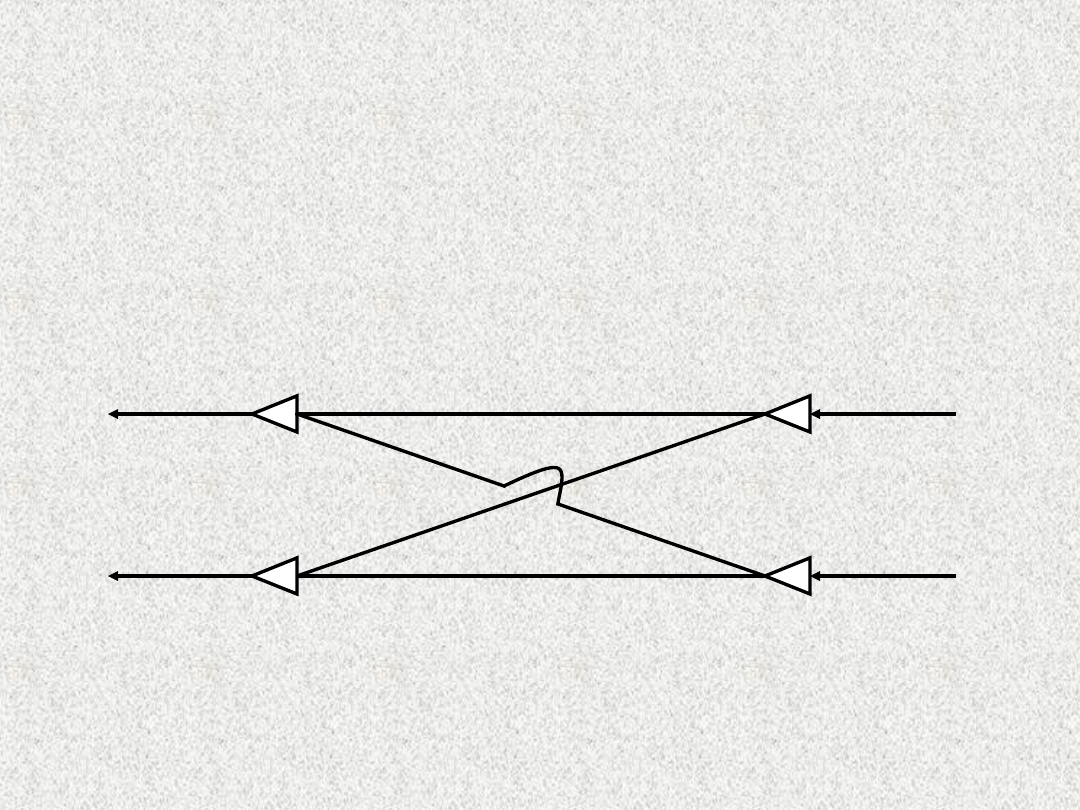
Budowa homeostatu

Biorąc pod uwagę zasadę Mazura, że każda czynność wymaga
zaznaczenia na schemacie odrębnego podsystemu, a
przesłanie sygnału jest ukierunkowane, można ten schemat
nieco zmodyfikować i podsystemy rozdzielające sygnał na
połowy oznaczyć jako diody.

Układ połączeń w homeostacie wg M. Węgrzyna

refleksja

naprężenie

emocja

obciążenie

Budowa homeostatu

Zgodnie z deklarowaną w tytule zasadą
minimalizmu przyjmijmy za poprzednim
rozdziałem, że podsystemy są
właśnie tymi najmniejszymi „czarnymi
skrzynkami”.
Dalej ze względu na właściwości przekazywania
sygnału „tylko w jedną stronę”, to znaczy od
„wejścia” do „wyjścia”, możemy przyjąć, że działają
one jak diody, ale szczególnego rodzaju, gdyż
dzielące sygnał na dwie połowy!
Otrzymamy wtedy schemat jak na poprzednim
rysunku.
Schemat ten można narysować jeszcze trochę
odmiennie, przez co wyraźnie zarysowana będzie
struktura systemu.

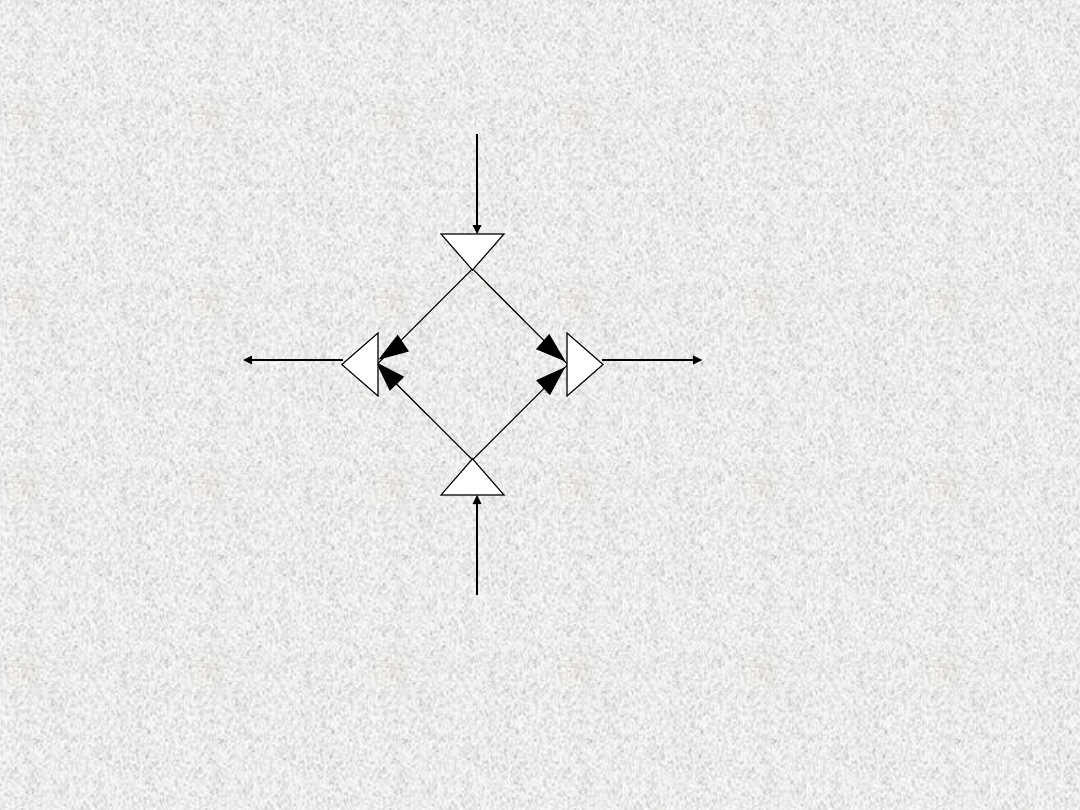
Budowa homeostatu

Struktura połączeń w
homeostacie.

Widać tutaj, że jest to struktura podobna do
mostka elektrycznego.

emocja

obciążenie

naprężenie

refleksja

Budowa homeostatu

Homeostat ma za zadanie odwracać działania

: jeżeli

oddziaływanie na homeostat rośnie, to ma on takie

działanie zmniejszać i odwrotnie.
Ze schematu wynika, że gdy na wejściu pojawią się dwa

„ziarna”, to na wyjściu będzie tylko jedno, a może też być

sytuacja, że gdy na wyjściu będzie zero „ziaren”, to na

wejściu będzie jedno „ziarno”.
Jak widać powiodło się nam skonstruowanie homeostatu –

ale czy to już wszystkie funkcje, jakie taki mały system

wypełnia?

Korelator ma za zadanie gromadzić energię korelacyjną i

przesyłać ją po ściśle określonych drogach przewodności

.

Nasz mały system również nic innego nie robi. Problem

tylko w tym, że dróg przewodności jest mało – ale to

problem liczbowy, a nie sterowniczy.

Budowa homeostatu

W korelatorze po każdym przepływie powinna wzrastać

przewodność

– ten warunek jest o tyle trudny do

uzasadnienia na poziomie „mikro”, że tutaj utrata oporności

oznaczałaby utratę „jakości” – własności tworzywa

pozwalającej na zaistnienie koncentracji ładunku. Niemniej

jest to warunek do spełnienia, jeżeli przyjąć np., że

tworzywo ma już przewodność graniczną – wtedy nasz

system niczego by się nie nauczył, ale nie popadajmy w

antropiczny punkt widzenia, jemu wystarczy to, co „wie”.

Akumulator ma magazynować energię i oddziaływać nią na

otoczenie.

A przecież nasz system też nic innego, tylko właśnie to robi.

WNIOSEK –

tak zbudowany system jest systemem

autonomicznym (S.A.), gdyż spełnia wszystkie funkcje

systemów autonomicznych.

Budowa homeostatu

Sprawa receptora i alimentatora rozwiązuje się „sama

przez się”, zresztą z teorii automatyki wynika, że

podzespoły

szeregowo

połączone

mogą

być

zastępowane przez jeden podzespół.

Natomiast

efektor może znajdować się z powodzeniem

w otoczeniu

. Sytuacja w efektorze nie wpływa na

homeostat bezpośrednio, ale poprzez obserwację

otoczenia.

Dalsza analiza możliwości działania takiego S.A.

wymaga ścisłego trzymania się ustaleń M. Mazura. Jest

to zgodne z zasadami nowoczesnej nauki, aby prawa

ogólne stosować tak długo, jak długo się da.

Zastosujemy tutaj prawo systemowe, że systemy

połączone szeregowo można przedstawić na schemacie

jako jeden system.

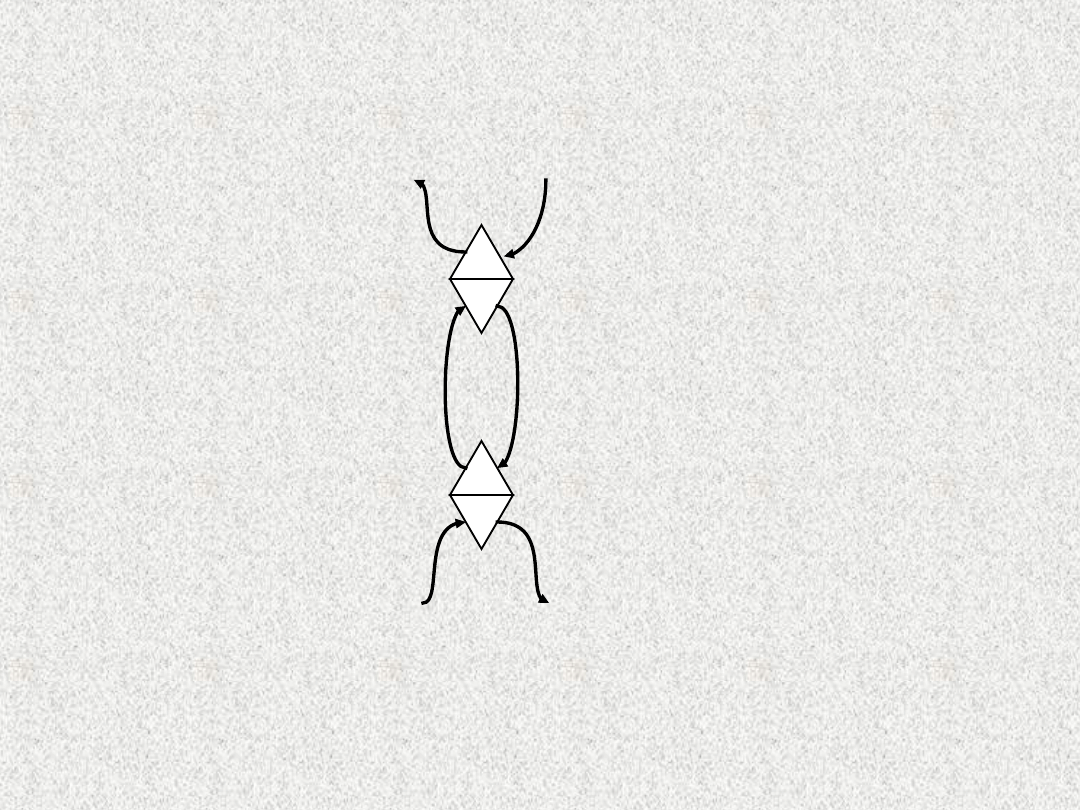
Najmniejsza struktura S.A.

Najmniejsza struktura systemu autonomicznego.

refleksja

emocja

naprężenie

obciążenie

Struktura S.A.

Jak widzimy,

systemem autonomicznym może być

taki system dwu elementowy, w którym każda część
połowę swojego zasilania przekazuje drugiej połówce
systemu

(co jest ważne np. w małżeństwie!).

Zasada ta obowiązuje niezależnie od wielkości
„ziarna”. Mogą to być stosunki – państwo a
obywatel, przyjaciele, grupy przyjaciół itd. System
utrzymuje się w równowadze przy zachowaniu
zasady „połówek”.

Połowę potrzeb my zaspakajamy kontrahentowi, a on
zaspokaja połowę naszych potrzeb. Wtedy nie ma
dominacji żadnego z elementów i system trwa w
równowadze.

Poszukiwania najmniejszego realnie

istniejącego S.A.

W świecie cząsteczek budowę analogiczną do podanej

powyżej mają wiązania pomiędzy zasadami tworzącymi

łańcuch DNA.
Wynikałoby z tego, że już DNA jest siecią najmniejszych S.A.
W świecie atomów znane mi jest tylko jedno wiązanie, tzw.

wiązanie amylowe:

=C=C=

Wiązanie to jest uważane za nietrwałe, ażeby było trwałe,

musi przebiegać bez przerwy proces obiegana wiązania

przez

chmurę

elektronową.

Ciekawostką jest, że nowo odkryte fulereny wypełniające

czarną materią przestrzenie międzygwiezdne też są oparte

na tym wiązaniu! Czyżby „pożerały” światło?
Również reakcje typu metatezy przebiegają w podobny

sposób. Badania nad sieciami takich S.A. mogą mieć

znaczenie przy opracowywaniu nowych metod pozyskiwania

substancji o właściwościach np. leczniczych do „reperacji”

łańcuchów DNA.

Zależność systemów autonomicznych

od otoczenia

Niedocenianą stroną badań nad strukturami systemów

autonomicznych jest ich

zależność od otoczenia

. Aby

powstały – wymagają one istnienia strumienia energomaterii

na tyle uporządkowanego, aby istniały co najmniej

dwuziarnowe porcje energomaterii.

Przerwanie dopływu

energomaterii powoduje rozpad struktury tych systemów

.

Oddziaływanie otoczenia oznaczone jest tu jako

emocja

(bo

tak było oznaczone na schemacie na początku rozważań),

zaś oddziaływanie systemu autonomicznego – jako

refleksja

.

Użycie akurat takich słów na oznaczenie tych oddziaływań

nie jest nadużyciem semantycznym – wskazuje na to, że

otoczenie jest w pewien sposób przyjaźnie związane z

istnieniem

systemów

autonomicznych.

Systemy

te

porządkują otoczenie na swoich wyjściach, umożliwiając

przyłączanie nowych struktur tego samego typu i tworząc w

rezultacie rodzaj struktur dyssypatywnych. Replikacja nie

jest ich zadaniem nadrzędnym – stanowi ucieczkę przed

nadmiarem nagromadzonej energomaterii, stąd wniosek, że

rozmnażanie się jest celem życia nie jest trafny. Replikacja

powoduje oznakowanie ziaren energomaterii i zapobiega ich

przyłączaniu ponownie.

Możliwości zapisu matematycznego

właściwości systemu

autonomicznego

O ile zapis matematyczny sumowania zbiorów i

iloczynu zbiorów jest ogólnie znany, to zapis

działania polegającego na dzieleniu zbioru na dwie

równe połówki jest mi nieznany i być może

wymaga wprowadzenia do matematyki, jeżeli ktoś

się na to odważy. Wtedy można by prześledzić

prawidłowości, jakie rządzą połączonymi w sieci

zbiorami.

Wydaje mi się, że obecnie używane narzędzia do

tworzenia tzw. sieci neuronowych – programów

komputerowych zdolnych do samodoskonalenia

się nie wykorzystują prawidłowości rządzących

najmniejszymi systemami autonomicznymi.

Wnioski praktyczne

Ustalenia powyższe mogą być pomocne nie tylko w

biotechnice, ale i w innych dziedzinach sterowania, w tym w

sterowaniu ludźmi, począwszy od nauczania, poprzez

marketing do wychowania obywatelskiego. Dotychczas

stosowana metoda „prób i błędów”, pomimo swej

skuteczności nie pozwala na dostrzeganie nowych

możliwości

poza

wektorem

inercji

wynikającym

z

przyzwyczajenia do starych metod. Metoda prób i błędów

jest poza tym droższa i wymaga większych nakładów na

początku, jednakże jest stosowana przez ludzi niecierpliwych

i żądnych natychmiastowego sukcesu, a kierujących się

hasłem: działajmy już choćby na oślep, a wyniki też będą

już, najwyżej się poprawi metodę jeżeli wyniki nie będą nam

odpowiadały. Wynika to ze strachu przed opóźnieniem w

stosunku do konkurencji, a strach jest powodem pozornego

przyspieszenia dynamizmu pozornego, co prowadzi do

przywiązania do metody postępowania. Dlatego m.in.

cybernetyka nie przebiła się do tej pory, jako metoda

działania

ciągle

zbyt

nowa

i

odbiegająca

od

dotychczasowych

przyzwyczajeń

w

postępowaniu

badawczym.

Literatura

•T. Dietl, „O przyszłości miniaturyzacji”, Dleta, nr

10/1999, str. 12.

•R. Klimek, J.M. Madej, A. Sieroń, „Rak – nowotwory a

choroby nowotworowe”, Kraków 2006.

•A. Kuhn, „The Logic of Social Systems: A Unified,

Deductive, System-Based Approach to Social

Science”, San Francisco 1974.

•M.

Mazur,

„Cybernetyczna

teoria

układów

samodzielnych”, Warszawa 1966.

•M. Mazur, „Cybernetyka i charakter”, Warszawa

1999.

•M. Mesarovic, „Matematyczna teoria systemów

ogólnych”, [w:] „Ogólna teoria systemów”, pod. red.

G.J. Klira, Warszawa 1976.

•A. H. Piekara, „Nowe oblicze optyki”, Warszawa

1976.

•G. Weinberg, „Myślenie systemowe”, Warszawa

1979.

•M. Węgrzyn, „Zagadnienie minimalnego autonomu.

Przejście od systemów działaniowych do systemów

konfiguracyjnych”, Problemy Genezy, nr 1-2 (215-

216), 2007, Warszawa, s. 43-50.