Seria: Informatyka
Elementy teorii
niezawodności
Wykład 4
Obiekty proste odnawialne
z niezerowym czasem
odnowy

dr hab. inż. Tadeusz Nowicki prof.

nadzw. WAT

e-mail:[e-mail], tel.

6-837118

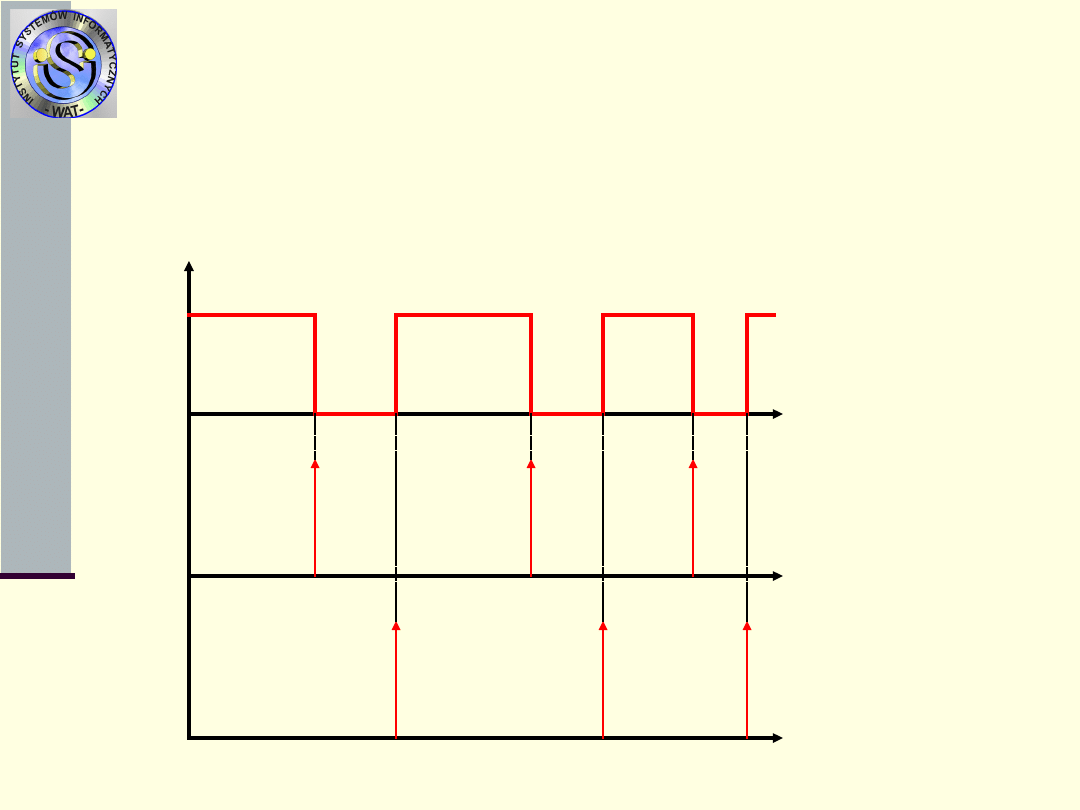
Model niezawodnościowy

Jedynymi istotnymi zdarzeniami w eksploatacji
obiektu prostego odnawialnego z niezerowa
odnową są chwile uszkodzeń i chwile odnowień,
które przy niezerowej odnowie, są chwilami
różnymi.

T

1

t

T

2

T

3

T

4

1

0



1



2



3

N

1

(

t)

N

2

(

t)

strumień
uszkodzeń

strumień
odnowień

X(

t)

Model niezawodnościowy

Naprzemienny ciąg zmiennych losowych:

T

1

, 

1

, T

2

, 

2

, T

3

, 

3

, ...

czasów poprawnej pracy i

czasów

odnów

obiektów

jest

modelem

niezawodnościowym

obiektu

prostego

odnawialnego z niezerowym czasem odnowy.
Zmienne T

i

są zmiennymi losowymi oznaczającymi

kolejne czasy poprawnej pracy obiektu określone

dystrybuantą F(t), gęstością f(t), transformatą

Laplace’a f*(s), wartością oczekiwaną 

1

oraz

odchyleniem standardowym 

1

.

Zmienne 

i

są zmiennymi losowymi oznaczającymi

kolejne

czasy

odnów

obiektu

określone

dystrybuantą G(t), gęstością g(t), transformatą

Laplace’a g*(s), wartością oczekiwaną 

2

oraz

odchyleniem standardowym 

2

.

Charakterystyki tych zmiennych losowych są

zatem

miarami niezawodnościowymi

obiektu.

Zmienna losowa 

Załóżmy, że zmienna losowa 

r

jest sumą

zmiennych losowych oznaczających czas poprawnej
r-tej pracy obiektu i czas r-tej odnowy obiektu.

Zmienne losowe 

1

, 

2

, 

3

, ... mają identyczny

rozkład
o dystrybuancie

i gęstości

zatem

r

r

r

T 

























t

0

r

dx

)

x

(

g

)

x

t

(

F

t

P

)

t

(













t

0

dx

)

x

(

g

)

x

t

(

f

)

t

(

dt

d

)

t

(

)

s

(

g

)

s

(

f

)

s

(













Miary procesu odnowień N

2

(t)

1.

Czas t

”r

do r-tej odnowy– zmienna losowa

spełniająca:

Jej dystrybuanta wyznaczana jest na podstawie

a gęstość

gdzie

r

3

2

1

"

r

...

t























)

s

(

L

)

t

(

r

1

r











)

s

(

r





- transformata
Laplace’a
dystrybuanty





)

s

(

L

)

t

(

r

1

r











)

s

(

r





- transformata
Laplace’a gęstości



 



)

s

(

g

)

s

(

f

)

s

(

)

s

(

r

r

r























)

s

(

g

)

s

(

f

s

1

)

s

(

s

1

)

s

(

r

r

r



















Miary procesu odnowień N

2

(t)

dla czasów odpowiednio dużych (t ) zmienna

losowa t

”r

dąży do rozkładu normalnego













r

,

r

N

2
2

2

1

2

1

















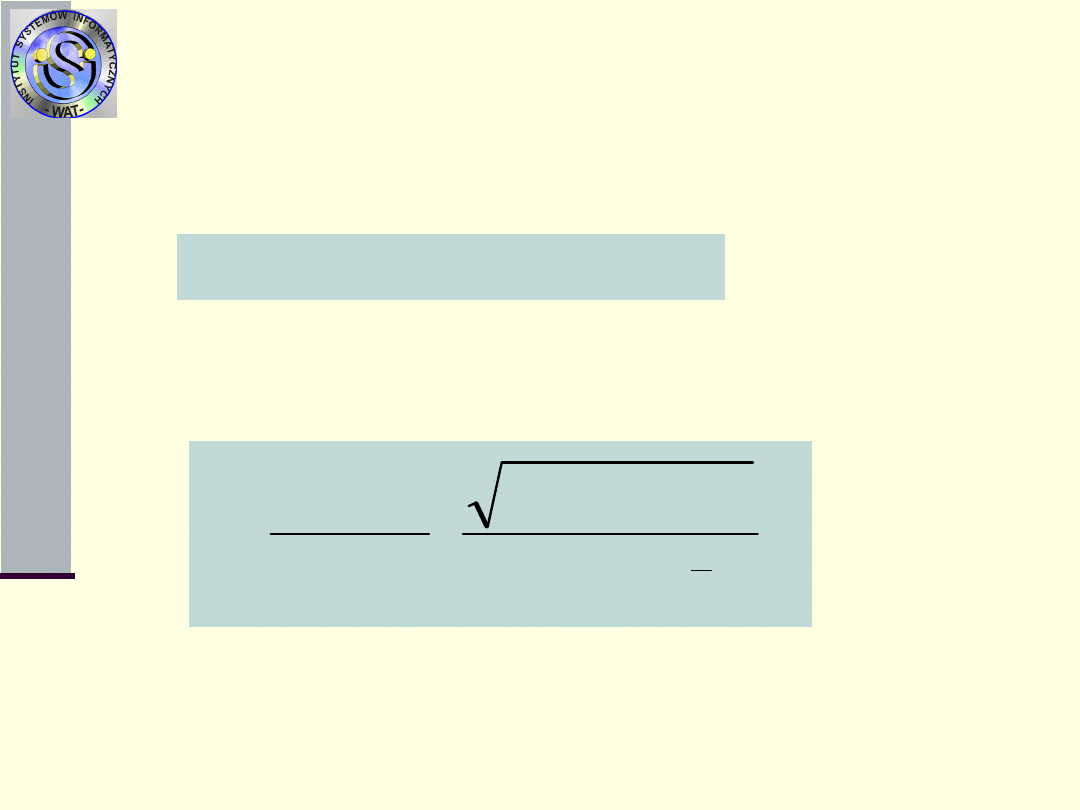
Miary procesu odnowień N

2

(t)

2.

Proces stochastyczny N

2

(t) – liczba odnowień do

chwili

t

Można pokazać, że

Można pokazać, że dla dużych t (odpowiednio
duża liczba odnowień) proces N

2

(t) dąży do

 





)

t

(

)

t

(

r

t

N

P

1

r

r

2





















t

,

t

N

2

3

2

1

2
2

2

1

2

1





































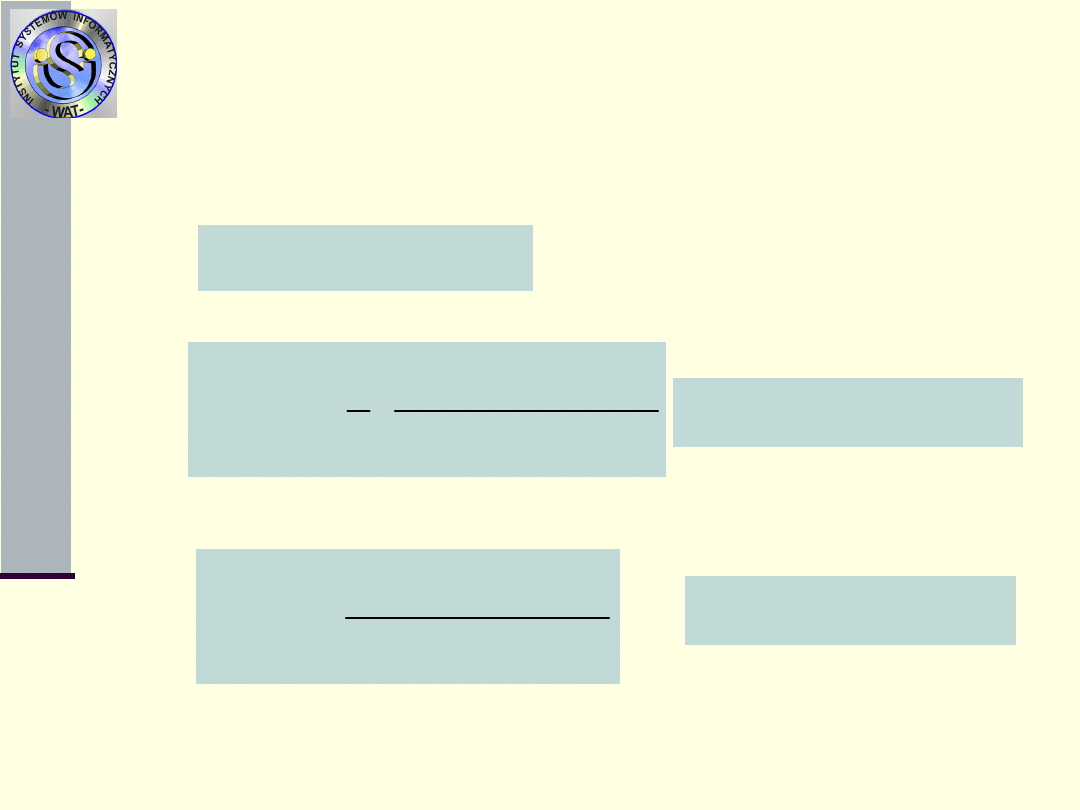
Miary procesu odnowień N

2

(t)

3.

Funkcja odnowy H

2

(t) – oczekiwana

liczba odnowień do chwili t

oraz

4.

Gęstość odnowy h

2

(t)

 





t

N

E

)

t

(

H

2

2



(s)

g

)

s

(

f

1

(s)

g

(s)

f

s

1

)

s

(

H

2





















(s)

g

)

s

(

f

1

(s)

g

(s)

f

)

s

(

h

2























)

s

(

H

L

)

t

(

H

2

1

2











)

s

(

h

L

)

t

(

h

2

1

2







Miary procesu uszkodzeń N

1

(t)

5.

Czas t

’r

do r-tego uszkodzenia– zmienna losowa

spełnia:

Jej dystrybuanta wyznaczana jest na podstawie

a gęstość

gdzie

r

3

2

1

'

r

...

T

t





















)

s

(

L

)

t

(

r

1

r











)

s

(

r





- transformata
Laplace’a
dystrybuanty





)

s

(

L

)

t

(

r

1

r











)

s

(

r





- transformata
Laplace’a gęstości





)

s

(

g

)

s

(

f

)

s

(

f

)

s

(

1

r

r





















)

s

(

g

)

s

(

f

)

s

(

f

s

1

)

s

(

s

1

)

s

(

1

r

r

r























Miary procesu uszkodzeń N

1

(t)

dla czasów odpowiednio dużych (t ) zmienna

losowa t

’r

dąży do rozkładu normalnego













r

,

r

N

2
2

2

1

2

1

















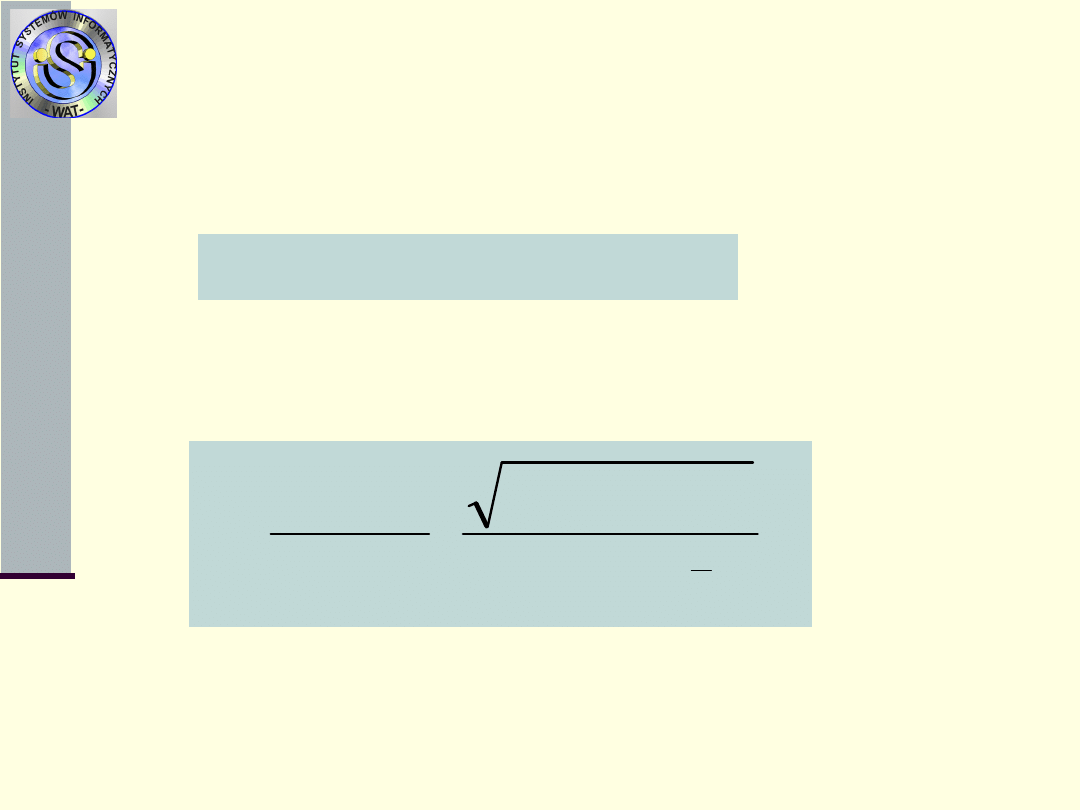
Miary procesu uszkodzeń N

1

(t)

6.

Proces stochastyczny N

1

(t) – liczba uszkodzeń

do

chwili

t

Można pokazać, że

Można pokazać, że dla dużych t (odpowiednio
duża liczba odnowień) proces N

1

(t) dąży do

 





)

t

(

)

t

(

r

t

N

P

1

r

r

1





















t

,

t

N

2

3

2

1

2
2

2

1

2

1





































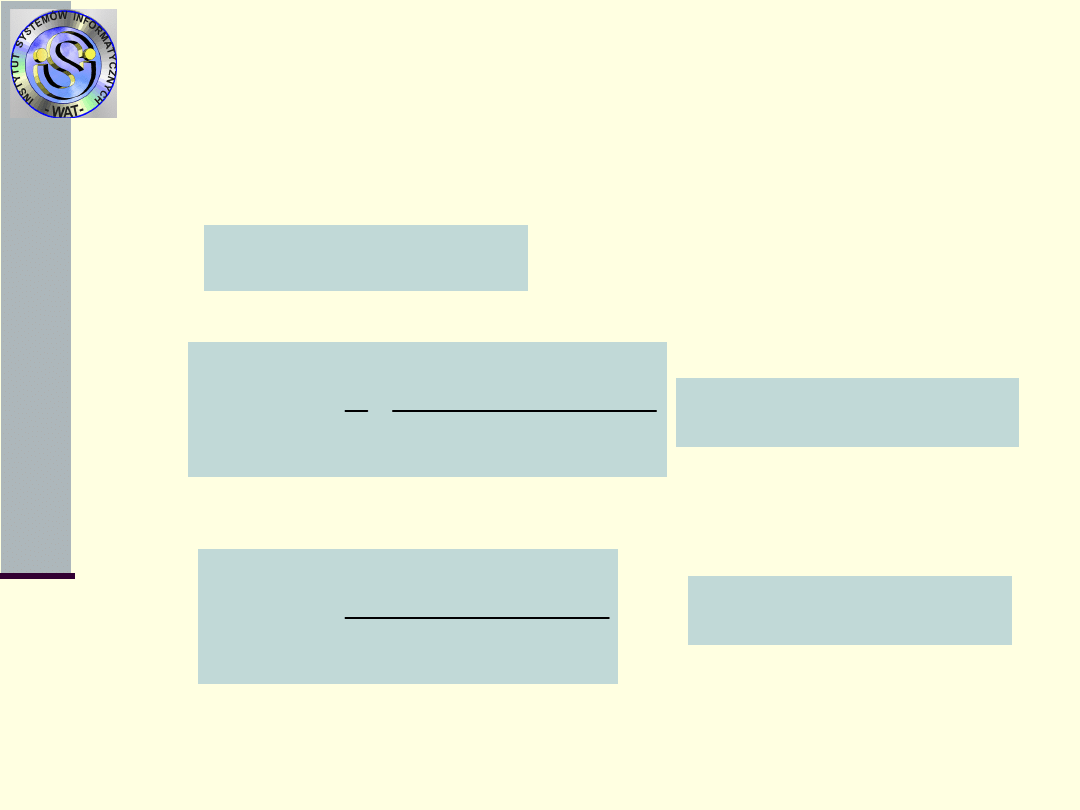
Miary procesu uszkodzeń N

1

(t)

7.

Funkcja odnowy H

1

(t) – oczekiwana

liczba uszkodzeń do chwili t

oraz

8.

Gęstość odnowy h

1

(t)

 





t

N

E

)

t

(

H

1

1



(s)

g

)

s

(

f

1

(s)

f

s

1

)

s

(

H

1

















(s)

g

)

s

(

f

1

(s)

f

)

s

(

h

1



















)

s

(

H

L

)

t

(

H

1

1

1











)

s

(

h

L

)

t

(

h

1

1

1







Miary niezawodności łączne dla
strumieni

9.

Współczynnik

gotowości

k

g

(t)

-

prawdopodobieństwo poprawnej pracy obiektu
w chwili t

Można pokazać, że

Stosując przekształcenie Laplace’a

lub

i oczywiście:





1

)

t

(

X

P

)

t

(

k

g





















t

0

2

g

du

)

u

t

(

F

1

)

u

(

h

)

t

(

F

1

)

t

(

k







(s)

g

)

s

(

f

1

(s)

f

1

s

1

)

s

(

h

1

)

s

(

f

1

s

1

)

s

(

k

2

g





























s

1

)

s

(

H

)

s

(

H

)

s

(

k

1

2

g

















)

s

(

k

L

)

t

(

k

g

1

g







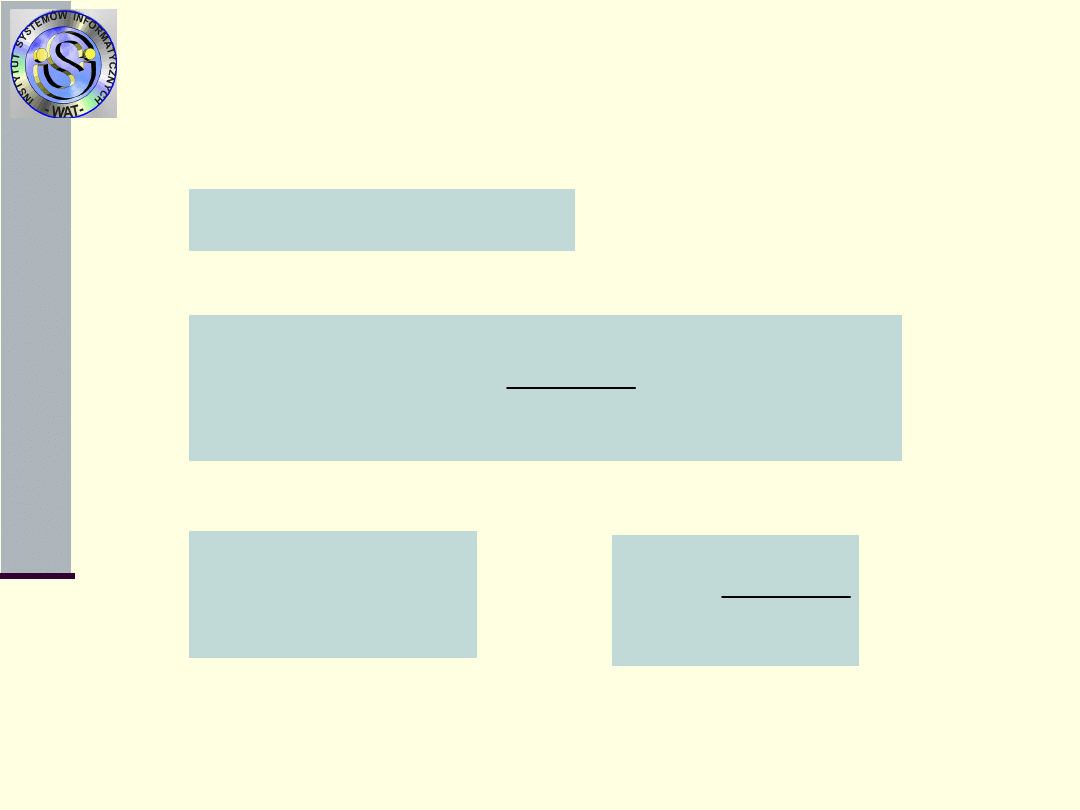
Miary niezawodności łączne dla
strumieni

Zatem

Dla dużych t otrzymujemy:

ale

zatem



























0

2

1

g

t

g

du

)

u

(

F

1

1

)

t

(

k

lim

K

1

)

t

(

H

)

t

(

H

)

t

(

k

1

2

g











1

0

du

)

u

(

F

1











2

1

1

g

K











Miary niezawodności łączne dla
strumieni

10.

P(t,t+) – prawdopodobieństwo tego, że w

przedziale (t,t+) nie będzie uszkodzenia

a dla dużych t (korzystając z tw. Smitha)
otrzymujemy charakterystykę graniczną





























t

0

2

dx

)

x

t

(

F

1

)

x

(

h

)

t

(

F

1

)

t

,

t

(

P































dy

)

y

(

R

1

)

t

,

t

(

P

lim

)

(

P

2

1

t