Metody probabilistyczne

Franciszek Mosiński

Zakład Wysokich Napięć

CZĘŚĆ II

Elementy Niezawodności i

Statystycznej Kontroli Jakości

– HISTORIA

•

Jakość jako kategoria filozoficzna

•

Pojęcie

jakości

jako

kategorii

filozoficznej

zostało

wprowadzone przez Platona (427-346 p.n.e.), który zaprzeczył
poglądom Demokryta (ur. około 460 p.n.e.), który z kolei głosił,
że istnieje tylko ilościowy, deterministyczny opis rzeczywistości.
Platon, a za nim Arystoteles twierdzili, że obiekt rzeczywisty ma
nieskończenie wiele cech.

•

Opis ilościowy polega na podporządkowaniu cechom obiektu

wyników pomiarów. Obiekty o identycznych charakterystykach
ilościowych mogą się różnić w istotny sposób. W celu
rozróżnienia Platon wprowadził pojęcie jakości jako kategorii
charakteryzującej obiekt w sposób uwzględniający również to,
czego nie można opisać ilościowo.

•

W wiekach od XVI do XVII przedstawiciele mechanicyzmu

(Galileusz, Newton, Laplace) powrócili do bezjakościowego,
deterministycznego modelu rzeczywistości.

•

Niezawodność

i

ryzyko

to

również

pojęcia

ze

starożytności, wynikające z praktyk ubezpieczania statków
morskich w starożytnym Rzymie.

•

Niezawodność

•

Prawdopodobnie

pierwszym,

który

posługiwał

się

rachunkiem

prawdopodobieństwa przy ocenie ryzyka był Jan de Witt (Holender
16251672), który posługiwał się funkcją ryzyka.

•

Pierwszym, który stosował intuicyjne współczynniki bezpieczeństwa był

Charles Augustin de Coulomb (Francuz, znany z elektrotechniki, a
jednocześnie inżynier wojskowy).

•

Odrębną gałęzią wiedzy niezawodność stała się w końcu lat 50-tych. Na

początku lat 70-tych jest to już nauka (system twierdzeń naukowych).

•

Obecnie niezawodność rozumiana jest jako niezawodność techniczna,

której jedną z podstawowych dyscyplin jest matematyczna teoria
niezawodności.

•

Niezawodność techniczną możemy podzielić na dwie kategorie:

•

niezawodność projektową R(0) dla czasu t = 0;

•

niezawodność ruchową R(t).

•

Współczesne definicje jakości i niezawodności brzmią:

•

Jakość jest to stopień w jakim obiekt/towar odpowiada wymaganiom
użytkownika/klienta.

•

Niezawodność obiektu jest to właściwość określona przez wartości istotnych
wielkości charakteryzujących zdolność obiektu do spełnienia wymagań.

•

Wielkością charakteryzującą zdolność do spełnienia wymagań może być
prawdopodobieństwo spełnienia przez obiekt stawianych mu wymagań. Czyli
niezawodność to prawdopodobieństwo sukcesu. Niezawodność obiektu to
prawdopodobieństwo, że wartości parametrów określających istotne
właściwości obiektu nie przekroczą w ciągu okresu czasu (0, t)
dopuszczalnych granic, w określonych warunkach życia obiektu.

•

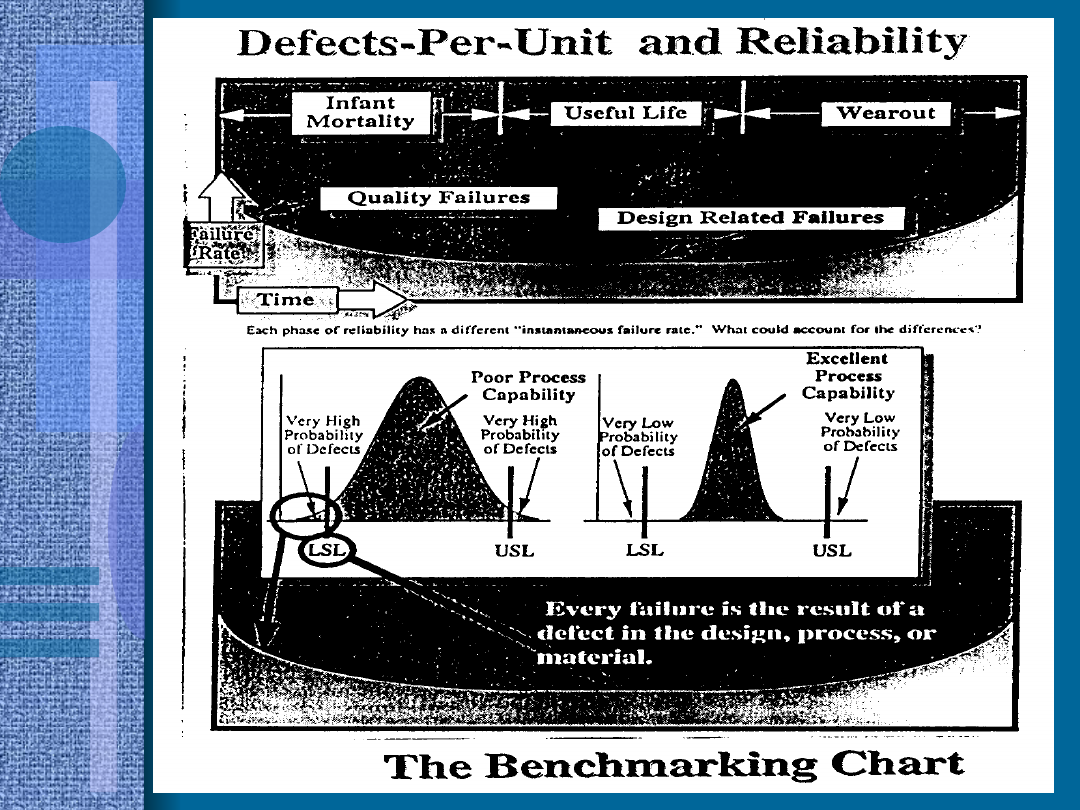
Zależność określającą jaka część obiektów, które przetrwały sprawne w przedziale
(0, t) stanie się prawdopodobnie niesprawna w przedziale (t, t + dt) nazywa się
funkcją ryzyka albo funkcją intensywności uszkodzeń. Kształt funkcji ryzyka
jest istotny pzry ocenie właściwości niezawodnościowych obiektu. Dla t = 0 wartość
początkowa R(0) jest jednocześnie niezawodnością projektową. Przykład funkcji
ryzyka pokazuje rys. 10.1. Początkowa opadająca część funkcji dotyczy okresu
początkowego gdy intensywność uszkodzeń maleje. Powszechnie nazywa się ten
fragment funkcji ryzyka śmiertelnością niemowląt. W oparciu o tę część krzywej
określa się okresy gwarancyjne. Druga, zwykle niemal płaska część funkcji to okres
normalnego użytkowania/pracy obiektu. I wreszcie część trzecia to okres starczy,
gdy następuje intensyfikacja zużycia części lub całości obiektu.

•

Rys. 10.1. Przykładowy kształt funkcji ryzyka

time

R

(t

)

•

PRAWDOPODOBIEŃSTWO SUKCESU, A STRUKTURA OBIEKTU

•

Struktura obiektu, który jest sprawny gdy co najmniej k dowolnych

spośród n jego elementów jest sprawnych, nazywa się strukturą typu k z
n co zapisuje się krótko jako k/n i nazywa się strukturą progową.

•

Jeśli: k < n to jest to struktura z redundancją (nadmiarowością);

1

.

11

)

,

,

.....

,

1

(

1

)

1

(

)

(

/

i

n

R

R

k

i

i

R

n

k

i

k

i

n

k





















g

d

z

i

e

)

,

,

.....

,

1

(

i

n

R

R



-

s

u

m

a

w

s

z

y

s

t

k

i

c

h

i

l

o

c

z

y

n

ó

w

s

t

a

n

o

w

ią

c

y

c

h

k

o

m

b

i

n

a

c

j

e

z

R

1

,

.

.

.

,

R

n

p

o

i

j

a

k

w

p

r

z

y

kł

a

d

z

i

e

,

d

l

a

n

=

4

:

4

3

2

1

4

4

)

4

,

,

....

,

1

(R

4

3

2

4

3

1

4

2

1

3

2

1

4

3

)

3

,

,

....

,

1

(R

4

3

4

2

3

2

4

1

3

1

2

1

4

2

)

2

,

,

....

,

1

(R

4

3

2

1

4

1

)

1

,

,

....

,

1

(R

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

n

i

R

R

R

R

n

R

R

R

R

R

R

R

R

R

R

R

R

R

n

R

R

R

R

R

R

R

R

R

R

R

R

R

n

R

R

R

R

R

n

R























•

k = n to jest to struktura
szeregowa;

)

2

.

11

(

1

/







n

i

ei

n

n

R

R

gdzie: R

ei

- niezawodność elementu

składowego

•

k = 1 to jest to struktura równoległa.

o

)

3

.

11

(

)

1

(

1

1

/

1











n

i

ei

n

R

R

gdzie: R

ei

- niezawodność elementu składowego

•

Układy elektryczne są zwykle strukturami typu szeregowego co oznacza, że
uszkodzenie jednego elementu składowego jest jednocześnie uszkodzeniem
całego obiektu.

•

Gdy obiekt składa się z n elementów i każdy ma taką samą niezawodność Re
i gdy obiekt jest sprawny wtedy i tylko wtedy gdy sprawne są wszystkie jego
elementy, od których zależy sprawność obiektu (struktura szeregowa) to
niezawodność obiektu wynosi:

)

4

.

11

(

/

n

e

n

n

R

R 

•

Jest to struktura niezawodnościowa szeregowa n/n, gdzie
defekt jednego elementu stanowi o defekcie obiektu.
Mówi się wówczas o teorii łańcuch lub teorii słabego
ogniwa. Z teorii tej wynikają następujące wnioski
praktyczne:

•

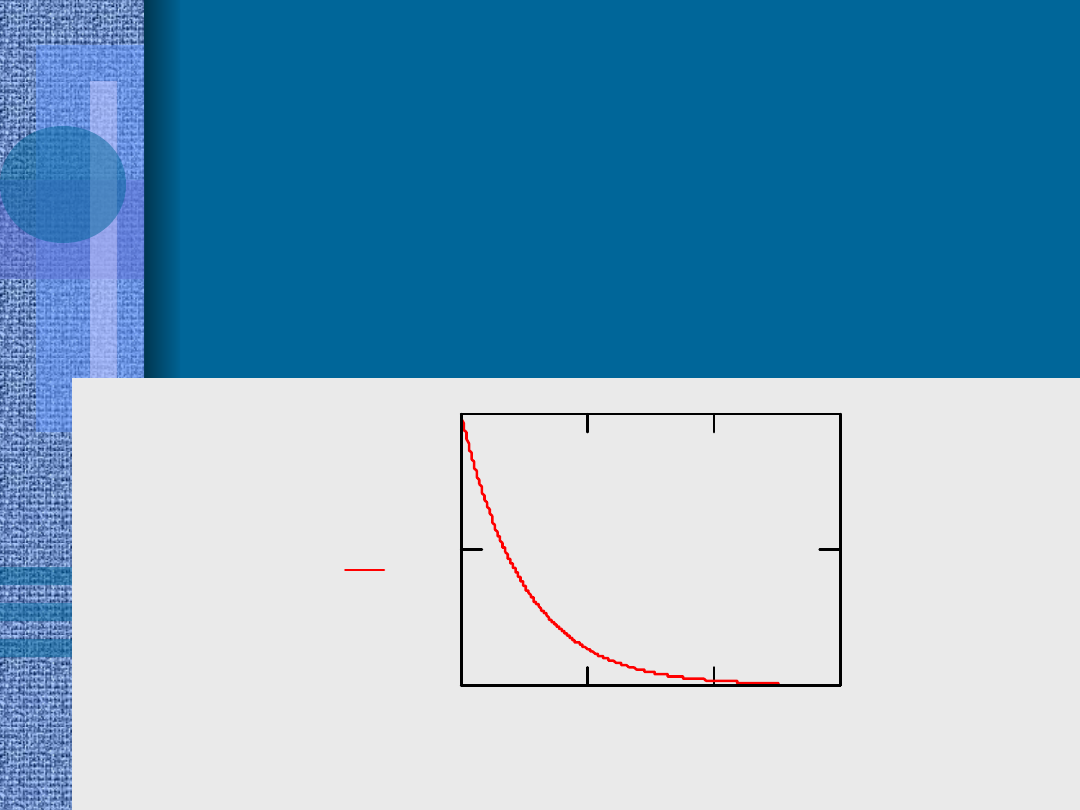
Niezawodność może zaskakująco szybko maleć gdy liczba
elementów obiektu rośnie, np. dla Re = 0.99 (obrazuje to
również rys. 10.2):

•

n 1 10 50 100 200 300

400

•

Rn/n 0.99 0.90 0.60 0.37 0.13 0.05
0.02

0

200

400

600

0

0.5

1

R( )

n

n

Rys. 10.2. Zależność niezaw

odności obiektu od liczby elem

entów

składow

ych. Przykład dla

R

e

=

0.99

•

Aby zachować niezmienną niezawodność trzeba ze wzrostem liczby
elementów zwiększać niezawodność składników. Przy stałej niezawodności
obiektu Rn/n = 0.8, o strukturze szeregowej niezawodność elementów, ze
wzrostem ich liczby, musi rosnąć:

•

n 1 10 100 1000 10000 100000
200000

•

Rn/n 0.8 0.978 0.9978 0.99978 0.999978 0.999998
0.999999

•

Z prawa iloczynu wynika, że istnieją sytuacje, w których o defekcie
(niepowodzeniu) decydują nie najmniej pewne (najbardziej zawodne)
elementy lecz najbardziej pewne (najbardziej niezawodne) jeśli jest ich
dużo! Przykładowo w obiekcie składającym się ze 100 elementów, każdy o
niezawodności Re = 0.99 i z jednego elementu o niezawodności Re101 =
0.9 wypadkowa niezawodność wynosi:

33

.

0

9

.

0

99

.

0

100

/







n

n

R

Jeśli teraz ten najgorszy element poprawić z R

e101

= 0.9 na

R

e101

= 1.0 to nadal wypadkowa niezawodność wynosi:

37

.

0

0

.

1

99

.

0

100

/







n

n

R

czyli element najgorszy decydował tylko o 4%
niezawodności.

•

Jeśli chcemy zwiększyć prawdopodobieństwo sukcesu
(niezawodność) to musimy zwracać uwagę przede
wszystkim na elementy najliczniejsze. Wystarczy w
poprzednim przykładzie zwiększyć niezawodność 100
elementów o 0.5% czyli z 0.99 do 0.995 by niezawodność
obiektu wzrosła około dwa razy:

61

.

0

0

.

1

995

.

0

100

/







n

n

R