Ścinanie

Shear

Z obliczeń statycznych otrzymujemy
wartość i rozkład siły poprzecznej na

długości belki

V

Ed

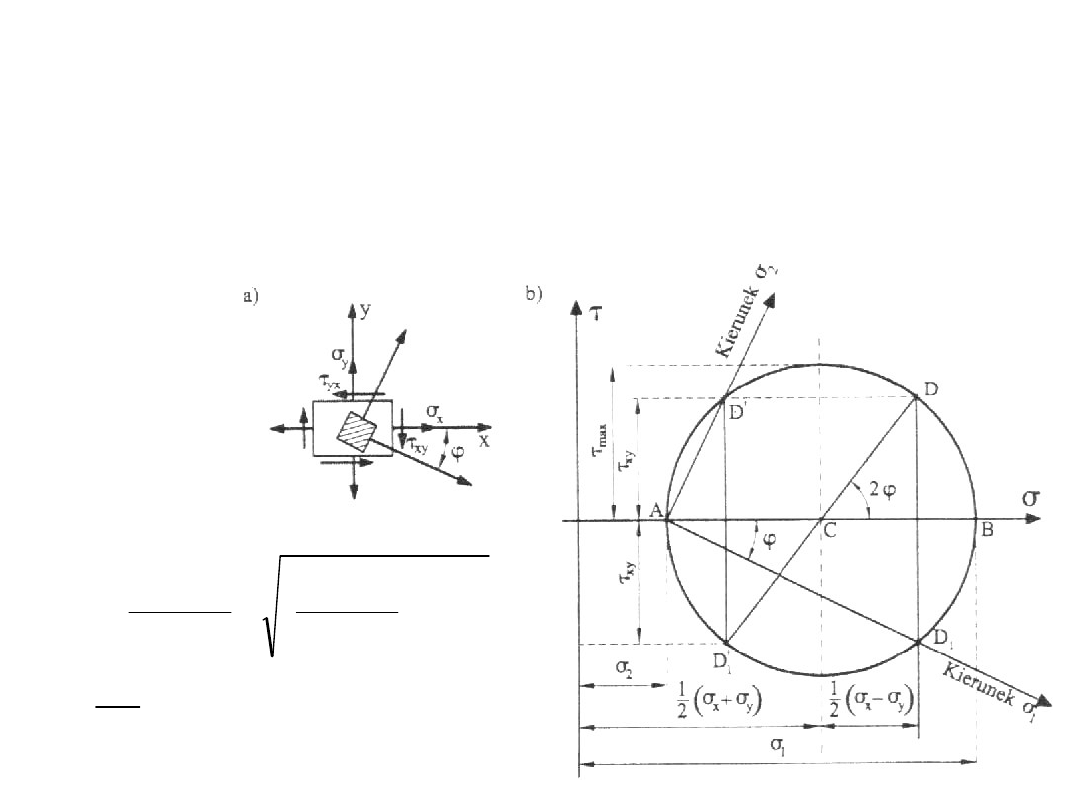
Naprężenia główne

Elementy prętowe – płaski stan odkształcenia,

naprężenia, koło Mohra

bI

VS

2

2

2

2

y

x

y

x

2

,

1







































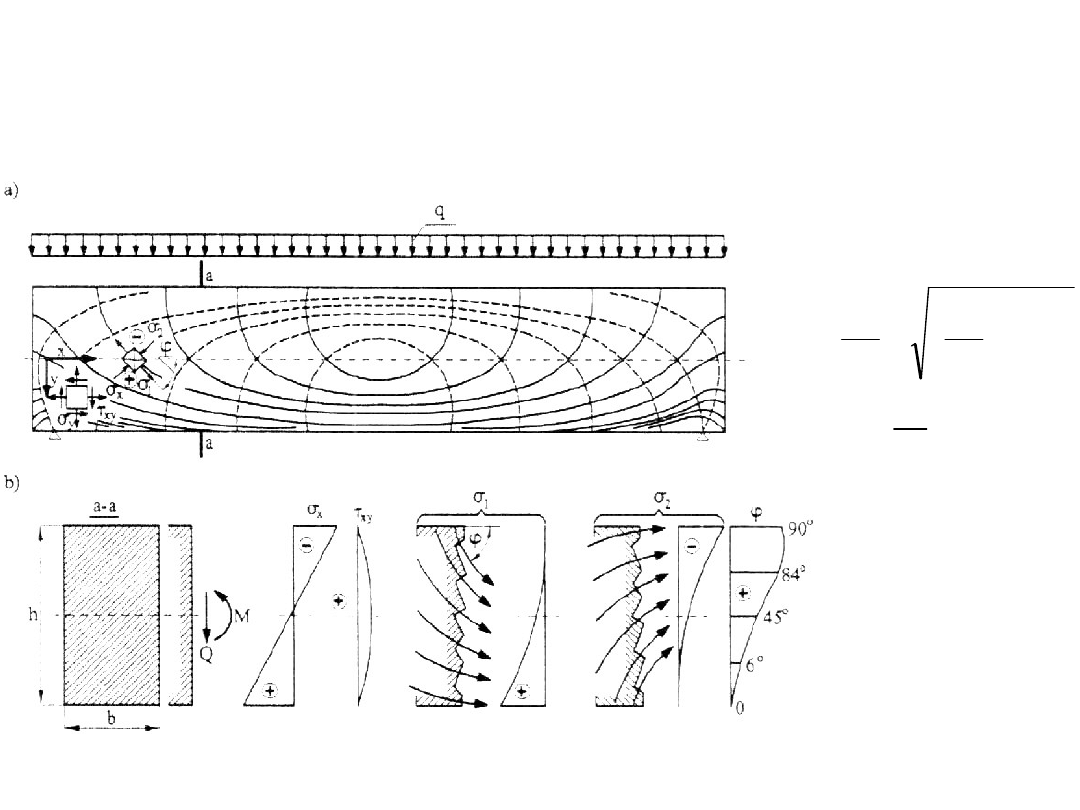
Trajektorie naprężeń głównych

























 













2

)

2

(

tg

2

2

0

2

2

x

x

2

,

1

y

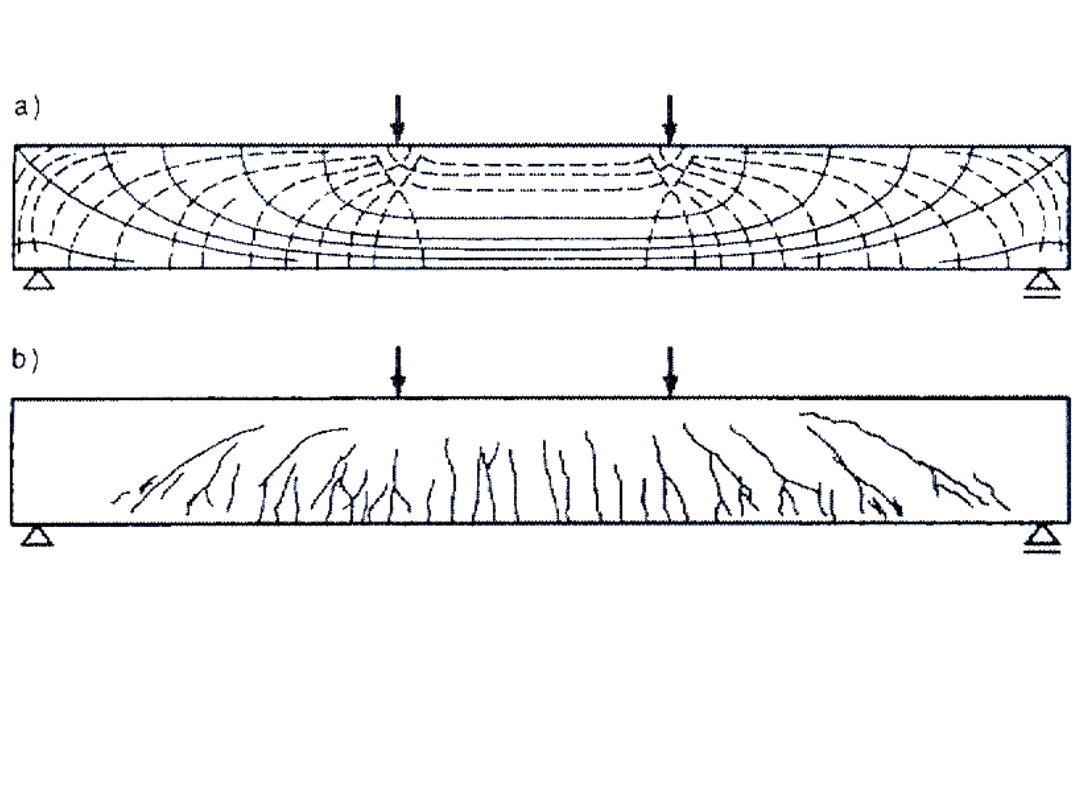
a) Trajektorie naprężeń głównych przy obciążeniu siłami

skupionymi

b) Obraz zarysowania

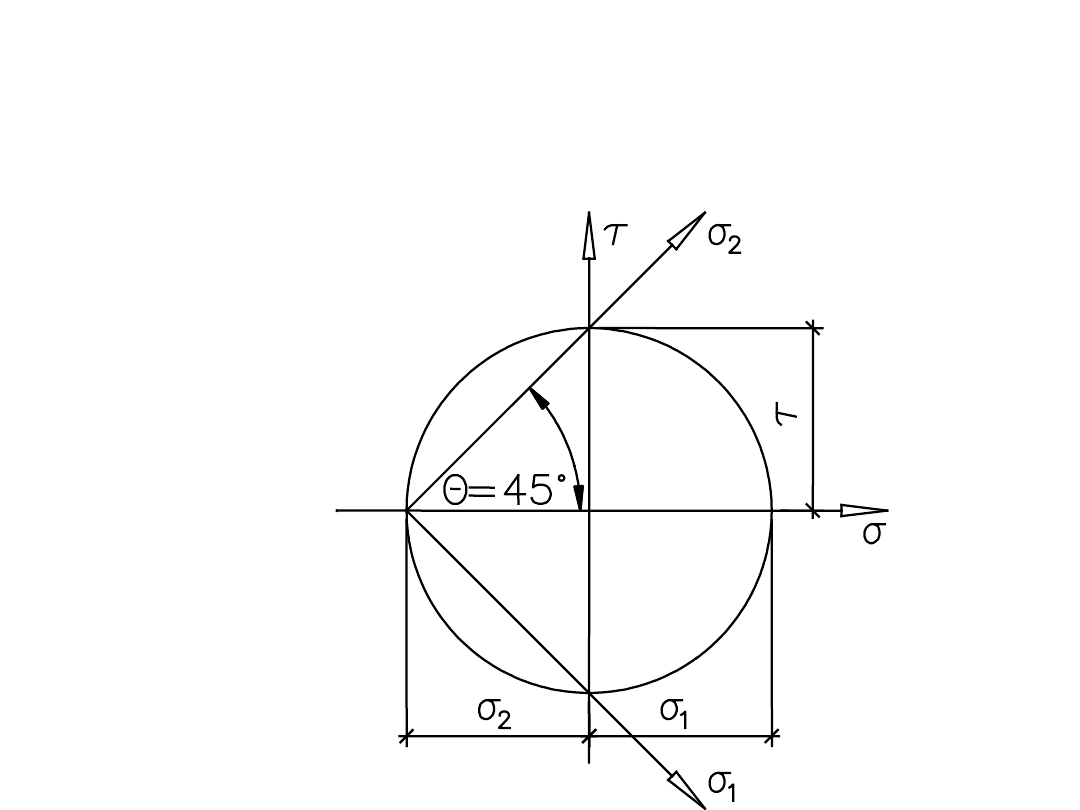
Naprężenia główne w osi obojętnej przekroju

Koło naprężeń Mohra



















2

1

x

y

0

0

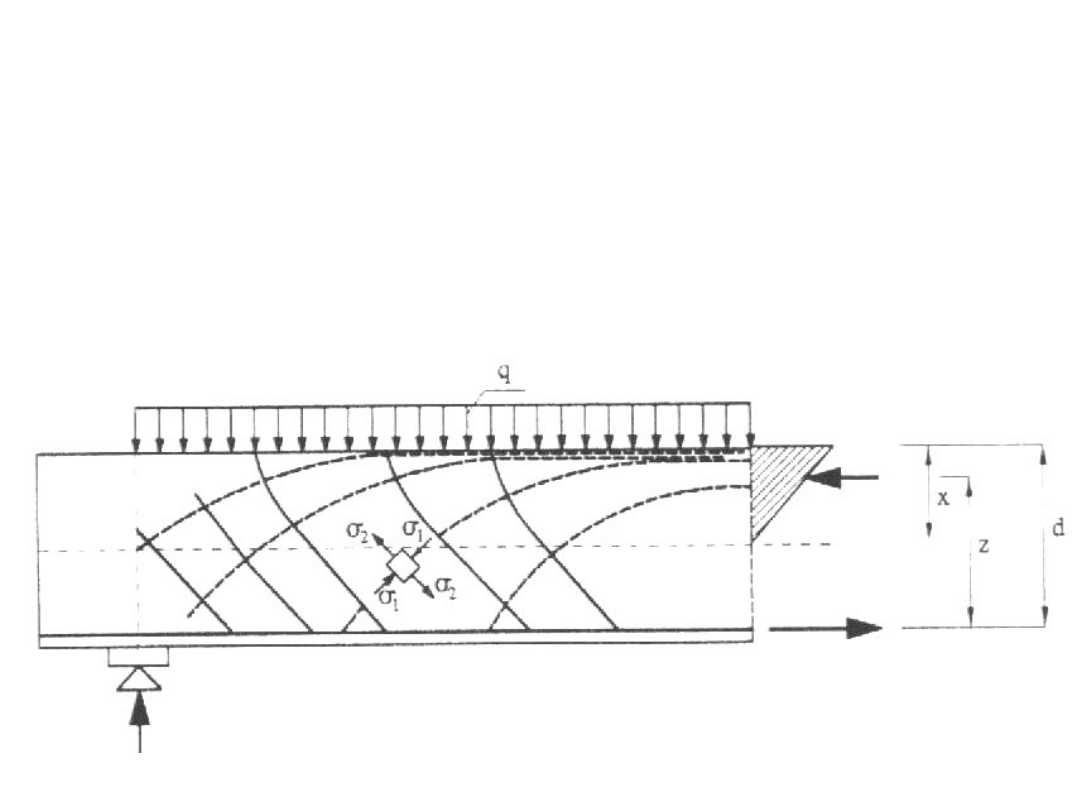
Trajektorie naprężeń

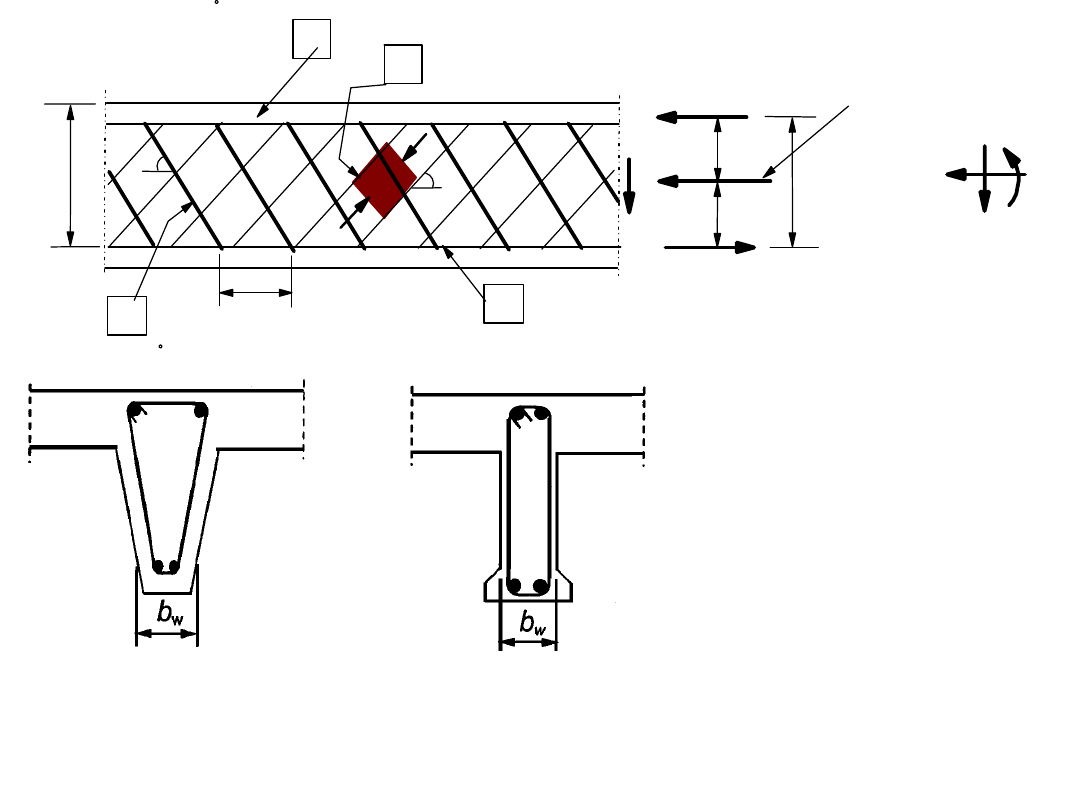
Trajektorie naprężeń po zarysowaniu
Trajektorie naprężeń w fazie II oznaczają nachylenie

krzyżulców ściskanych pod kątem 45°

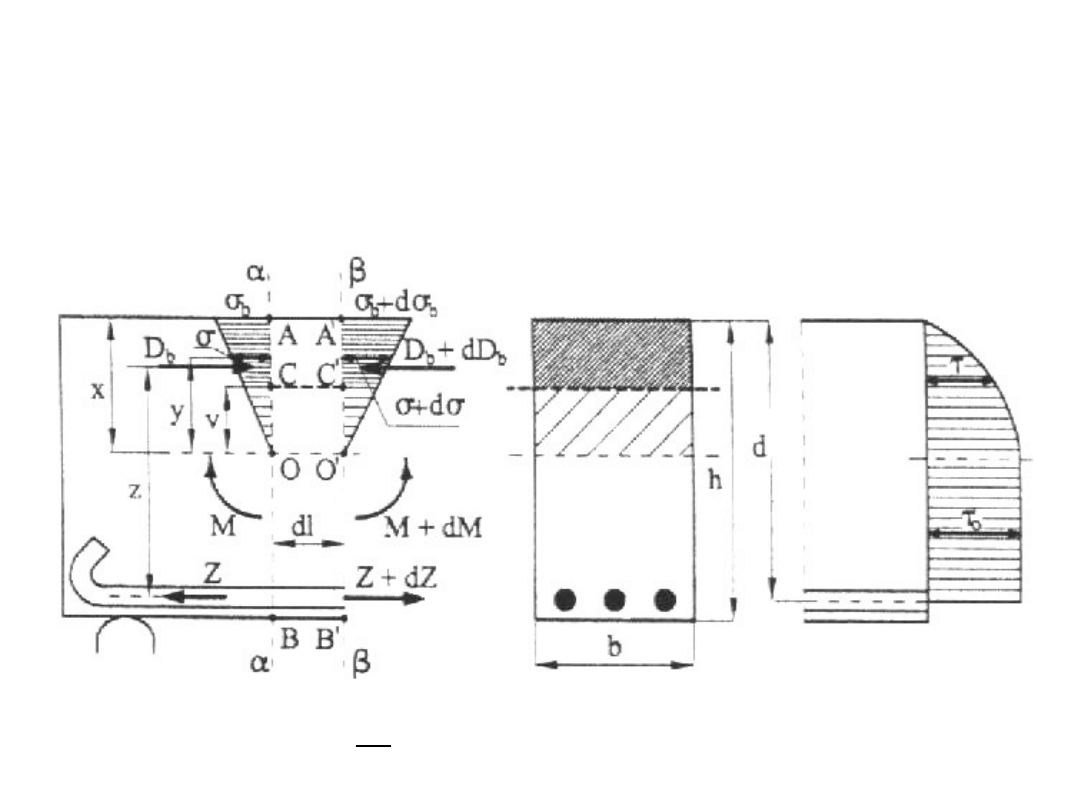
Naprężenia styczne (ścinające) – przekrój prostokątny

Naprężenia σ i τ w przekrojach oddalonych o

odcinek dl

bz

V

0





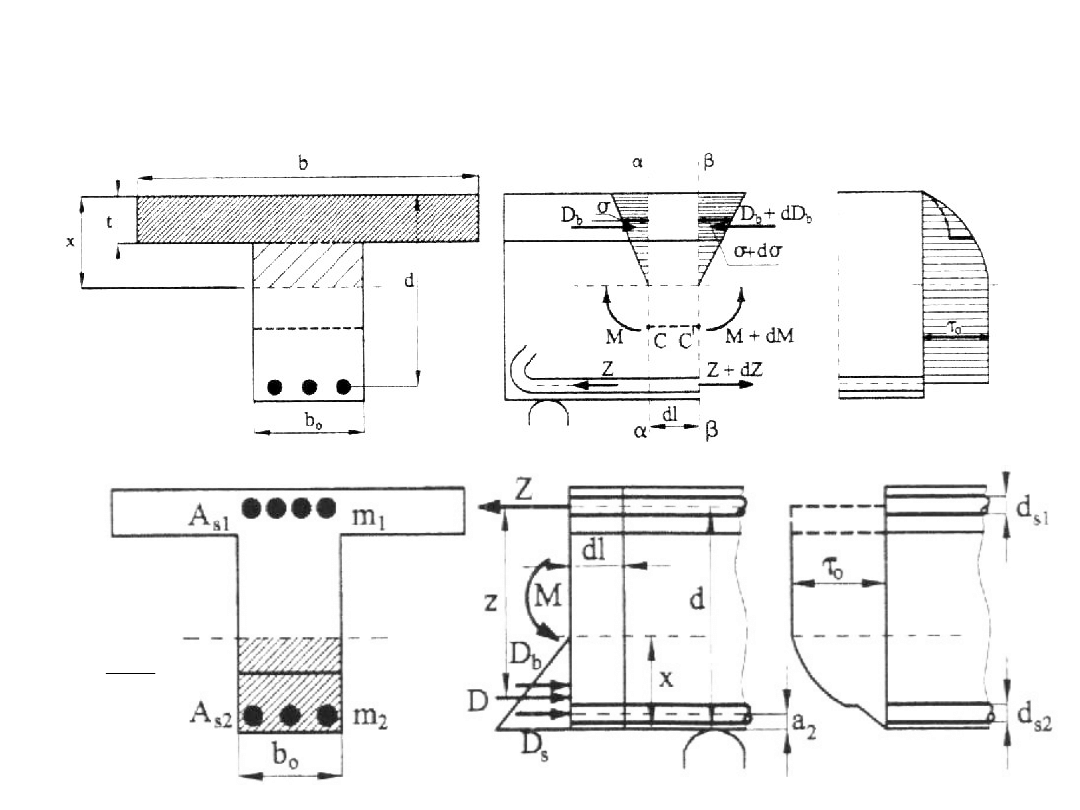
Naprężenia styczne (ścinające) – przekrój teowy

z

b

V

0

0





Ścinanie według PN-EN 1992-1-1

wrzesień 2008

Obowiązuje model kratownicowy, z
krzyżulcami ściskanymi o kącie pochylenia
względem podłużnej osi belki θ ≤ 45°
( w ograniczonym zakresie)

Stosowane symbole:

V

Rd,c

– nośność krzyżulca rozciąganego

betonowego
(bez zbrojenia poprzecznego)

V

Rd,max

– nośność krzyżulca ściskanego

betonowego

V

Rd,s

– nośność krzyżulca rozciąganego

zbrojonego,
po zarysowaniu betonu



s

d

A

V(cot



- cot







V

N

M



½ z

½ z

V

z = 0.9d

F

cd

F

td

B

C

D

A – pas ściskany
B –
krzyżulce
ściskane
C – pas
rozciągany D
– zbrojenie na
ścinanie

Rys. 6.5: Model kratownicowy i
oznaczenia

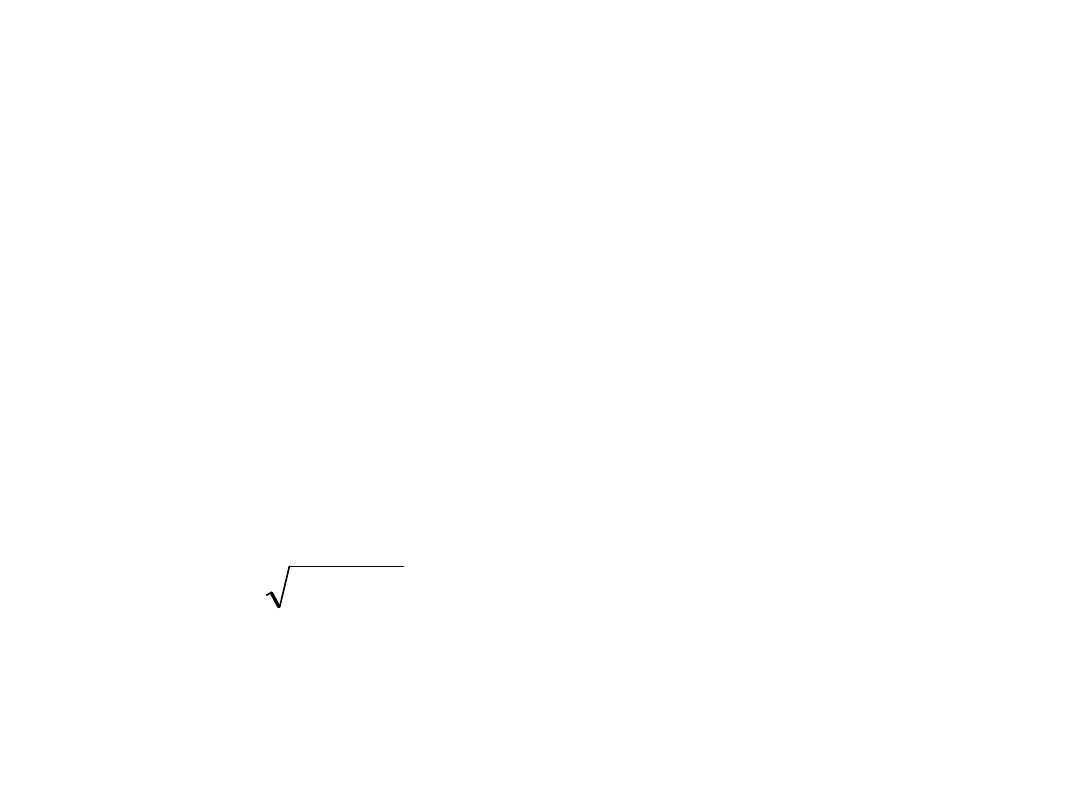
Nośność krzyżulca rozciąganego betonowego

– przed zarysowaniem

V

Rd,c

= [C

Rd,c

k(100

l

f

ck

)

1/3

+ k

1



cp

]b

w

d

V

Rd,c

≥ (

min

+ k

1



cp

)b

w

d

C

Rd,c

= 0,18 / γ

c



min

= 0,035 k

3/2

f

ck

1/2

k = 1 + d [mm]

k

1

= 0,15

σ

cp

= N

Ed

/ A

c

lecz nie więcej niż 0,2 f

cd

(MPa)

d

/

200

02

,

0





d

b

A

w

sL

L



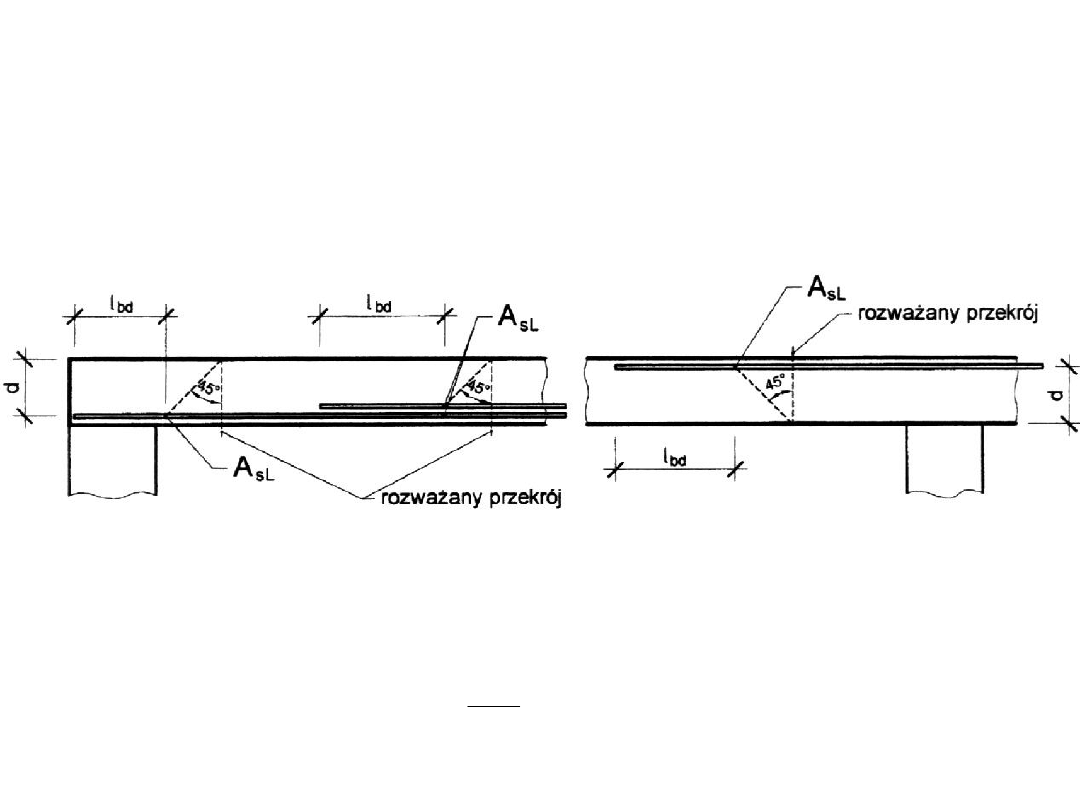
Nośność krzyżulca rozciąganego betonowego

– przed zarysowaniem

Rys. 6.3: Określanie A

sl

Zbrojenie poprzeczne nie jest obliczeniowo

wymagane, jeżeli:

V

Ed

≤ V

Rd,c

nośność betonowego krzyżulca

rozciąganego

V

Ed

≤ 0,5 b

w

d  f

cd

nośność betonowego krzyżulca
ściskanego

 = 0,6 (1 – f

ck

/250)

f

ck

[MPa]

Jeżeli obciążenie równomiernie rozłożone jest

obciążeniem dominującym, to siłę poprzeczną
oblicza się w

odległości d od podpory

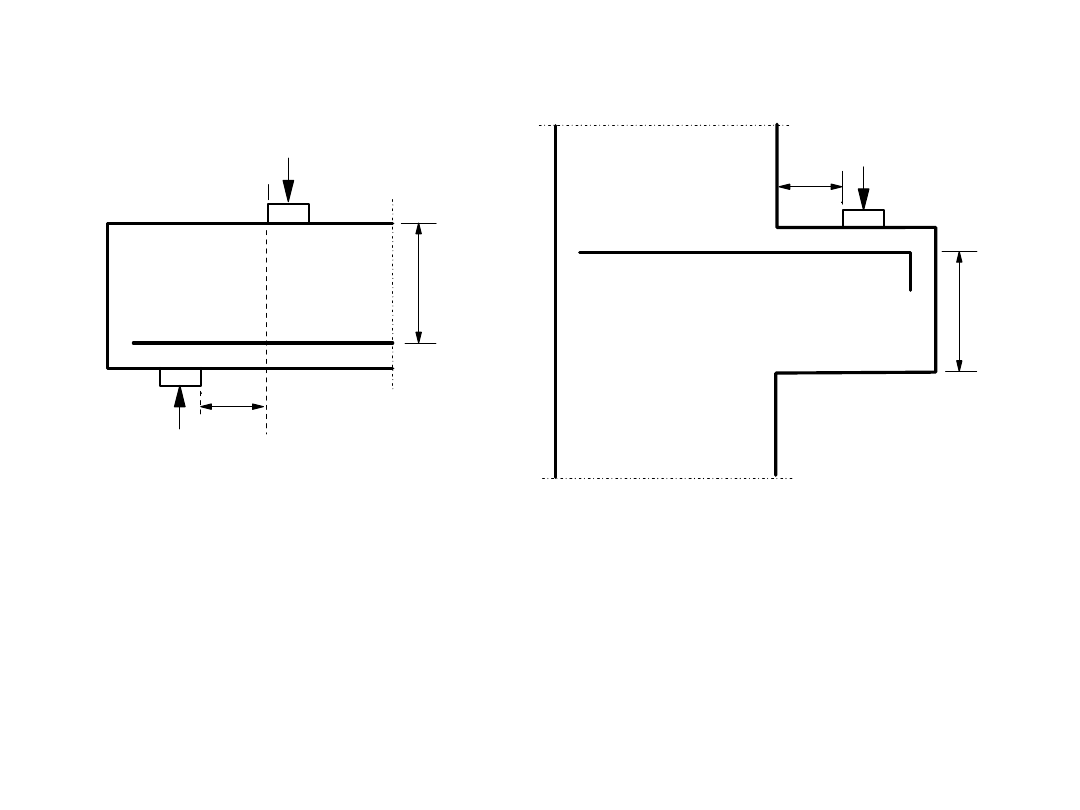
Rysunek 6.4: Obciążenia w pobliżu podpór

a

v

d

a

v

d

a) Belka z podporą

bezpośrednią b) Krótki wspornik

Jeżeli 0,5d ≤ a

v

≤ 2d, to siłę poprzeczną można

pomnożyć przez

β = a

v

/ (2d) – przy sprawdzaniu warunku V

Rd,c

Nie redukujemy siły przy sprawdzaniu warunku V

Rd,max

Można także stosować modele ST (Struts – Ties)

Elementy wymagające obliczania
zbrojenia na ścinanie
V

Ed

> V

Rd,c

Oblicza się je na podstawie modelu kratownicowego

Kąt pochylenia krzyżulca ściskanego względem
podłużnej osi belki przyjmuje się

1,0  cot(θ)  2,5 EN

1,0  cot(θ)  2,0 PN

a kąt pochylenia zbrojenia poprzecznego
α

45° ≤ α ≤ 90°



s

d

A

V(cot



- cot







V

N

M



½ z

½ z

V

z = 0.9d

F

cd

F

td

B

C

D

A – pas ściskany B – krzyżulce ściskane

C – pas rozciągany D – zbrojenie na ścinanie
(poprzeczne)

Jeżeli belka jest zbrojona pionowymi

strzemionami, to
α = 90°

cotθ

zf

s

A

V

ywd

sw

s

Rd,



V

Rd,max

= 

cw

b

w

z 

1

f

cd

/(cot+tan)



cw

= 1,0 konstrukcje

niesprężone


1

= 

= 0,6 (1 – f

ck

/250) (f

ck

w

MPa)

Jeżeli f

ywd

≤ 0,80 f

yk

, to można

przyjmować



1

= 0,6

f

ck

≤ 60 MPa



1

= 0,9 – f

ck

/200 ≥ 0,5

f

ck

> 60 MPa

Jak przyjmować kąt pochylenia krzyżulców

ściskanych?

Ze względu na strzemiona –

jak największy

V

Rd,s

= V

Ed

s =

Ze względu na krzyżulec ściskany –

tak, aby nie

przekroczyć jego nośności



cot

z

V

f

A

Ed

ywd

sw

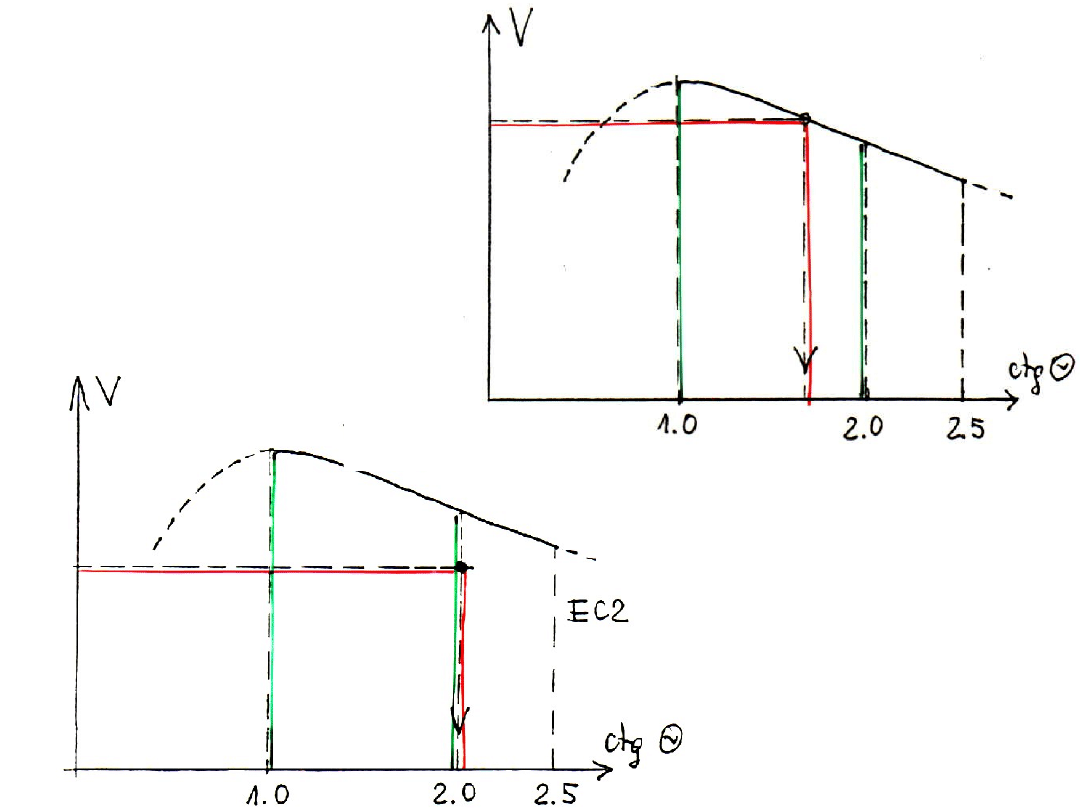
Nośność krzyżulca

ściskanego w funkcji

ctgθ

V

Ed

V

Ed

V

Rd,max

Decyzja o kącie pochylenia krzyżulca ściskanego
wpływa ponadto na zakotwienie prętów zbrojenia
podłużnego

Siłę rozciągającą

V (cotθ – cotα)
przykładamy po połowie do obu pasów kratownicy

Powoduje to

zwiększenie siły w pasie rozciąganym

,

co uwzględniamy rozsuwając wykres momentów
zginających o odcinek

a

l

= 0,5 z (cotθ – cotα)

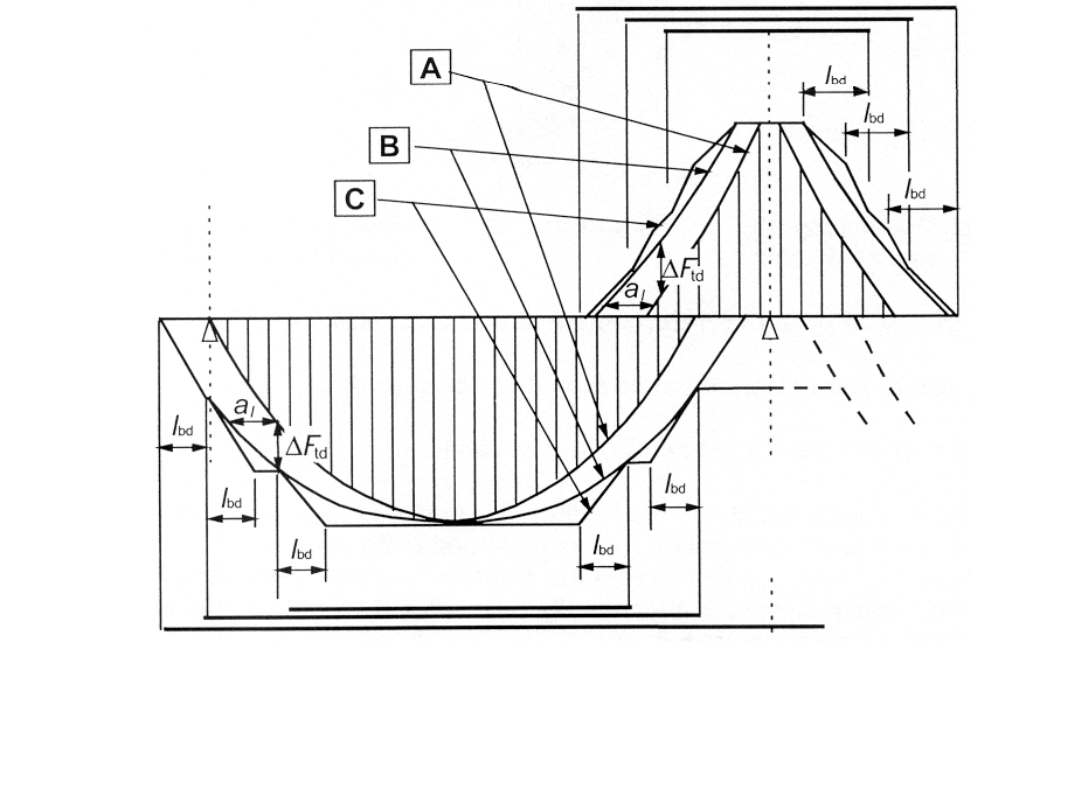
A – obwiednia siły M

Ed

/z + N

Ed

B – siła rozciągająca w zbrojeniu F

s

C – nośność zbrojenia na rozciąganie F

Rs

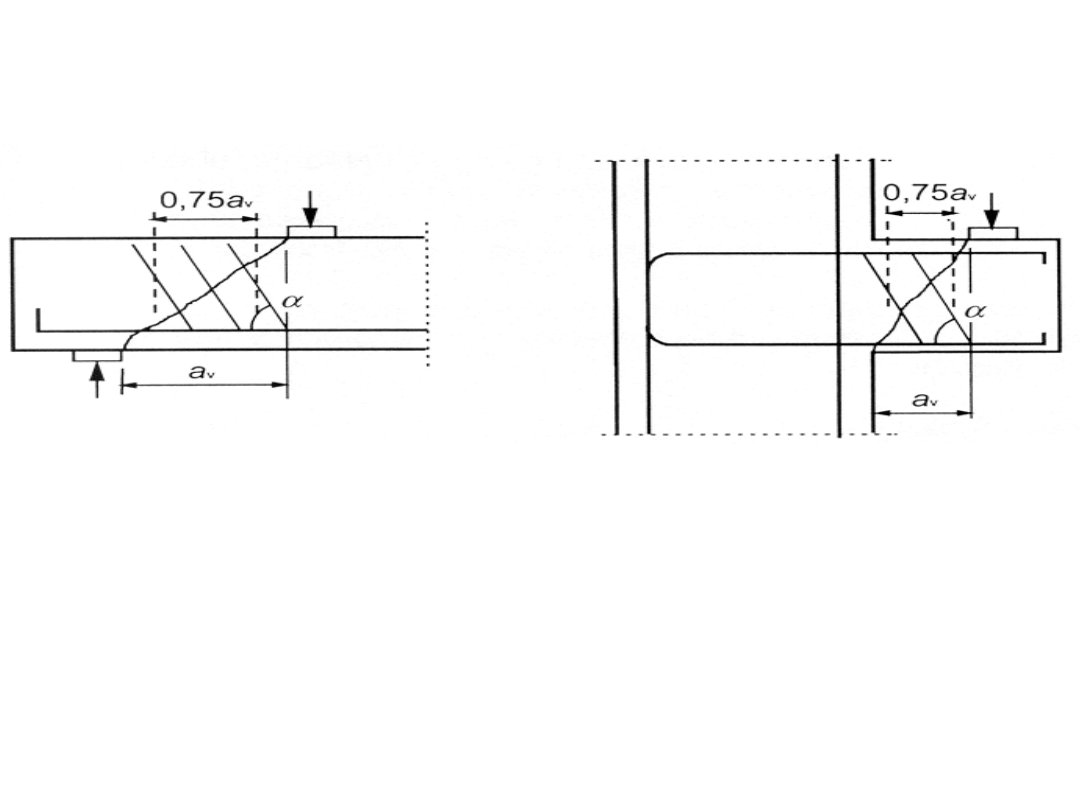
Rys. 6.6: Zbrojenie na ścinanie przy
bezpośrednim przekazywaniu obciążenia przez
ściskany krzyżulec

Jeżeli 0,5 d < a

v

< 2,0 d

V

Ed

a

v

/(2d) ≤ A

sw

f

ywd

sin α

A

sw

– oznacza pole przekroju zbrojenia na

oznaczonym
odcinku

Zmniejszenie V

Ed

można stosować tylko przy

obliczaniu zbrojenia na ścinanie.

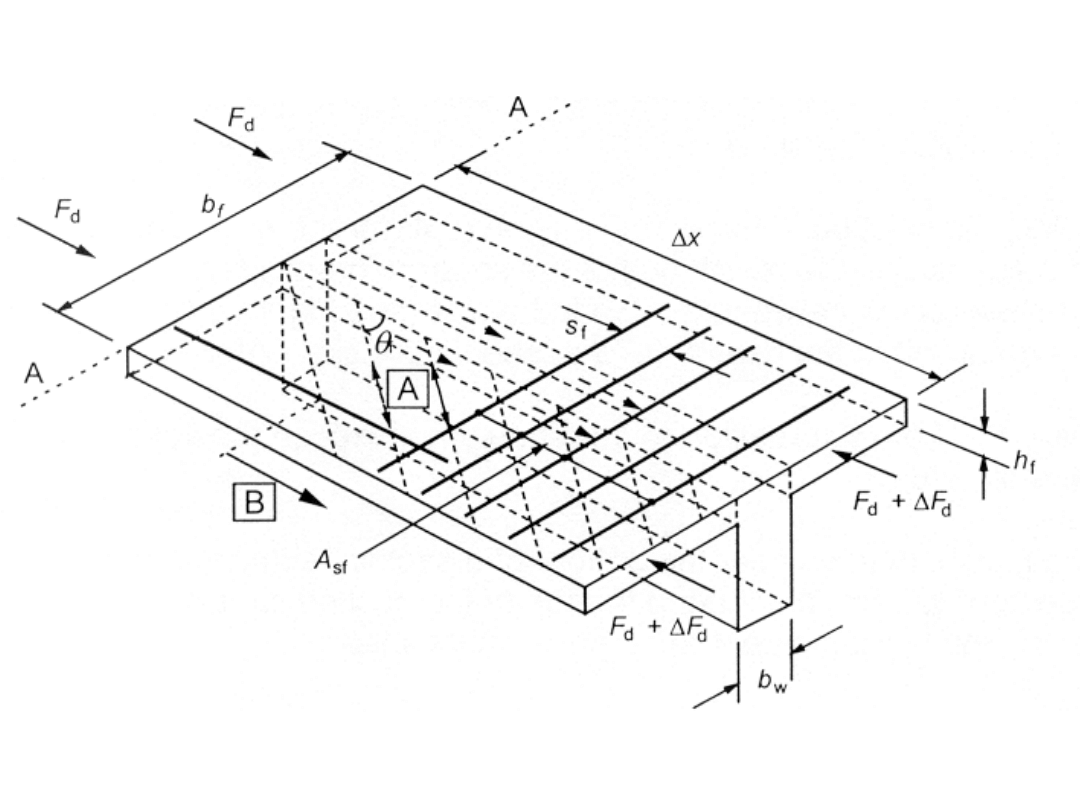
Zbrojenie między środnikiem a półkami

A – krzyżulce ściskane
B – pręt podłużny zakotwiony poza przekrojem, od
którego
poprowadzono strzałkę B

Skręcanie

Torsion

T

Ed

- moment skręcający z obliczeń

statycznych

Za modele przekrojów pełnych można
przyjmować ich cienkościenne
odpowiedniki.

Przekroje o złożonym kształcie można
dzielić na części i przypisać im momenty
skręcające proporcjonalnie do sztywności
tych części na skręcanie.

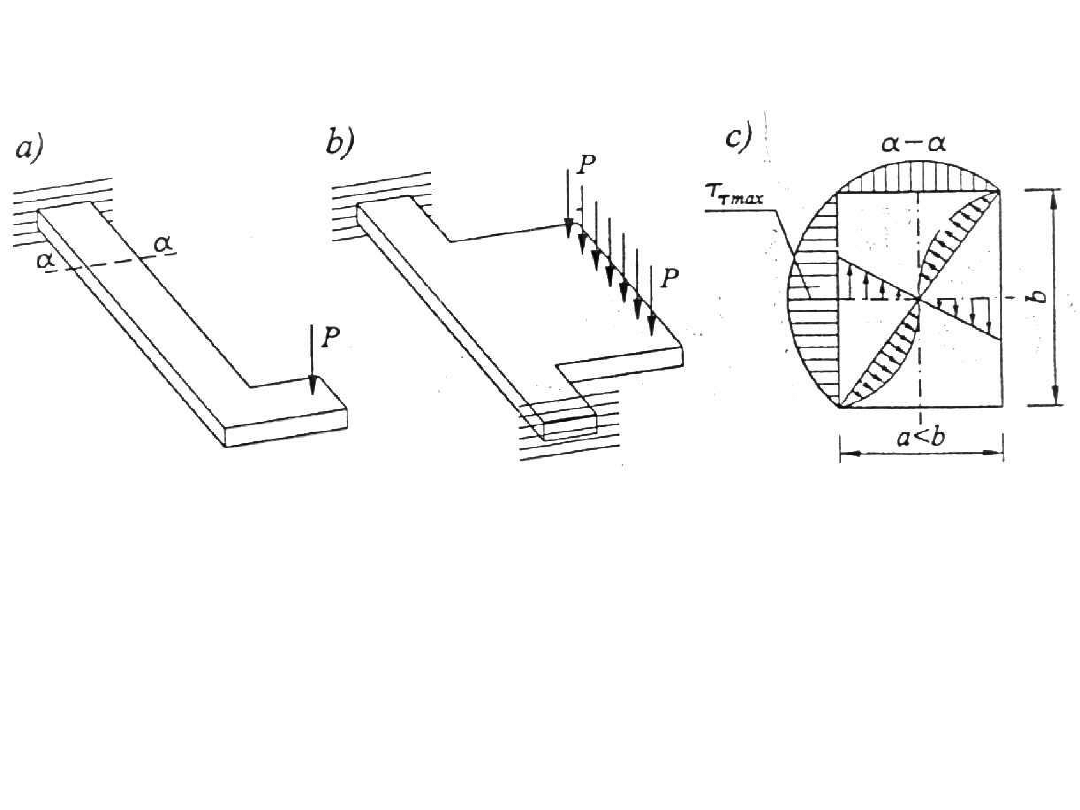
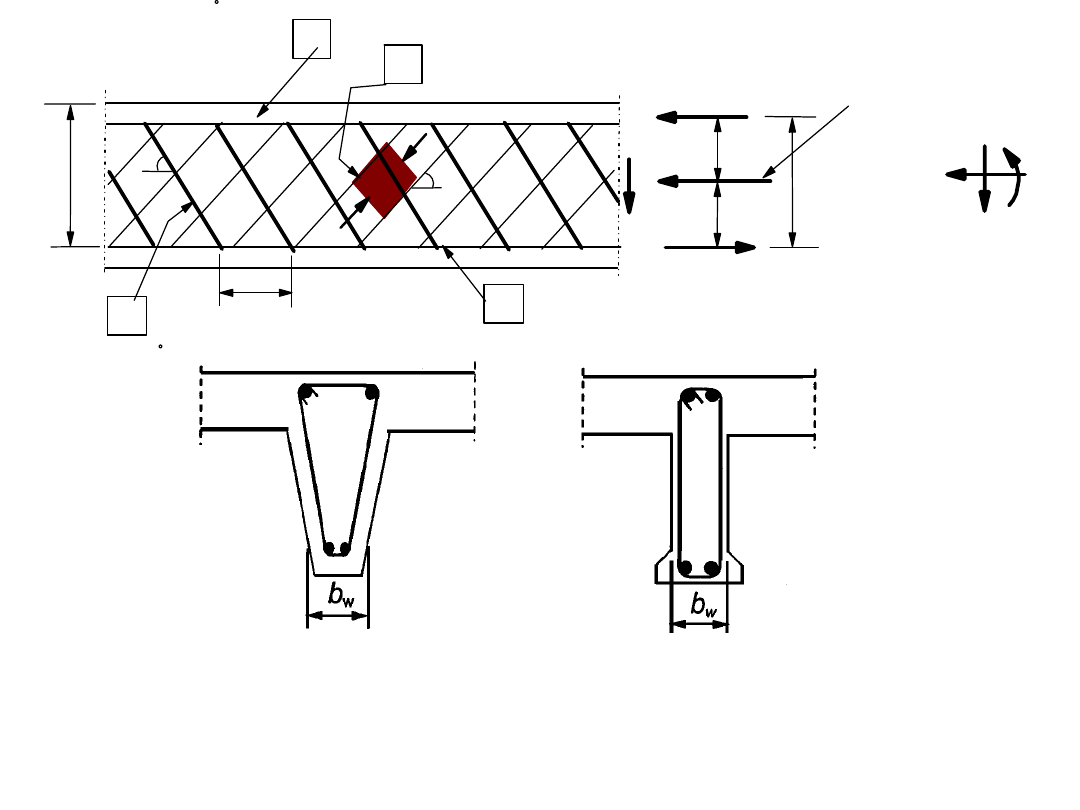
a, b – przykłady obciążenia wywołującego skręcanie

c – naprężenia styczne w przekroju, spowodowane
skręcaniem

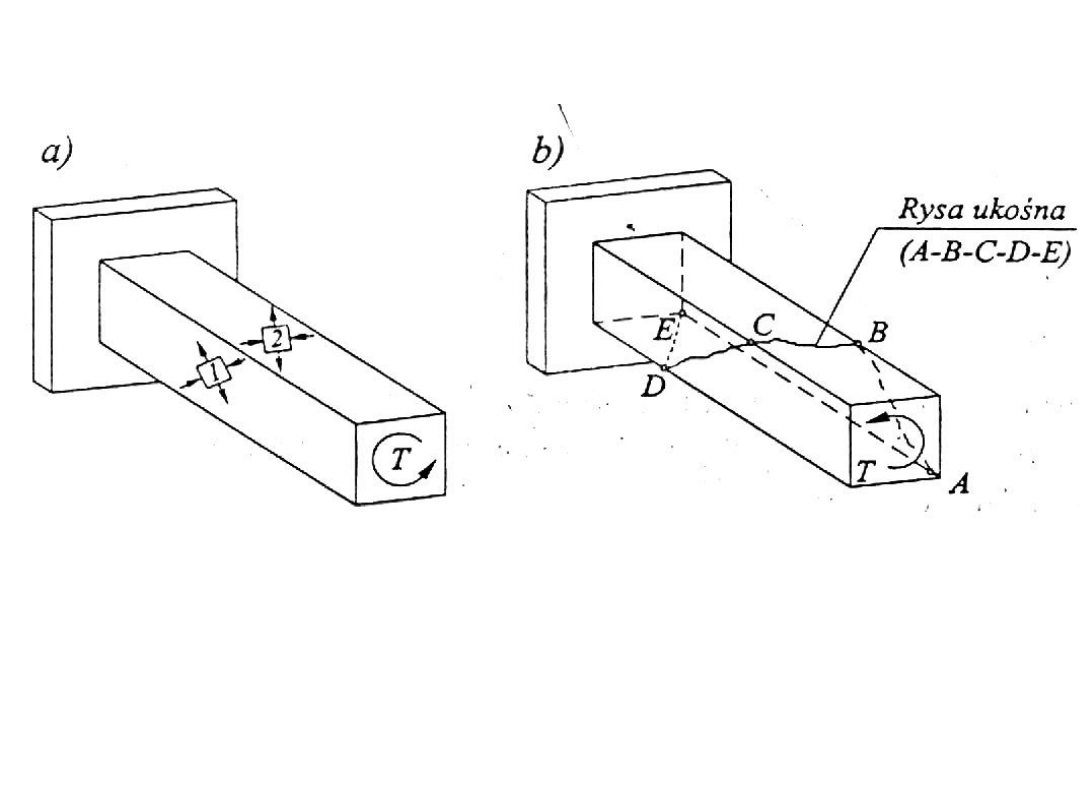
a – naprężenia główne

b – charakter zarysowania

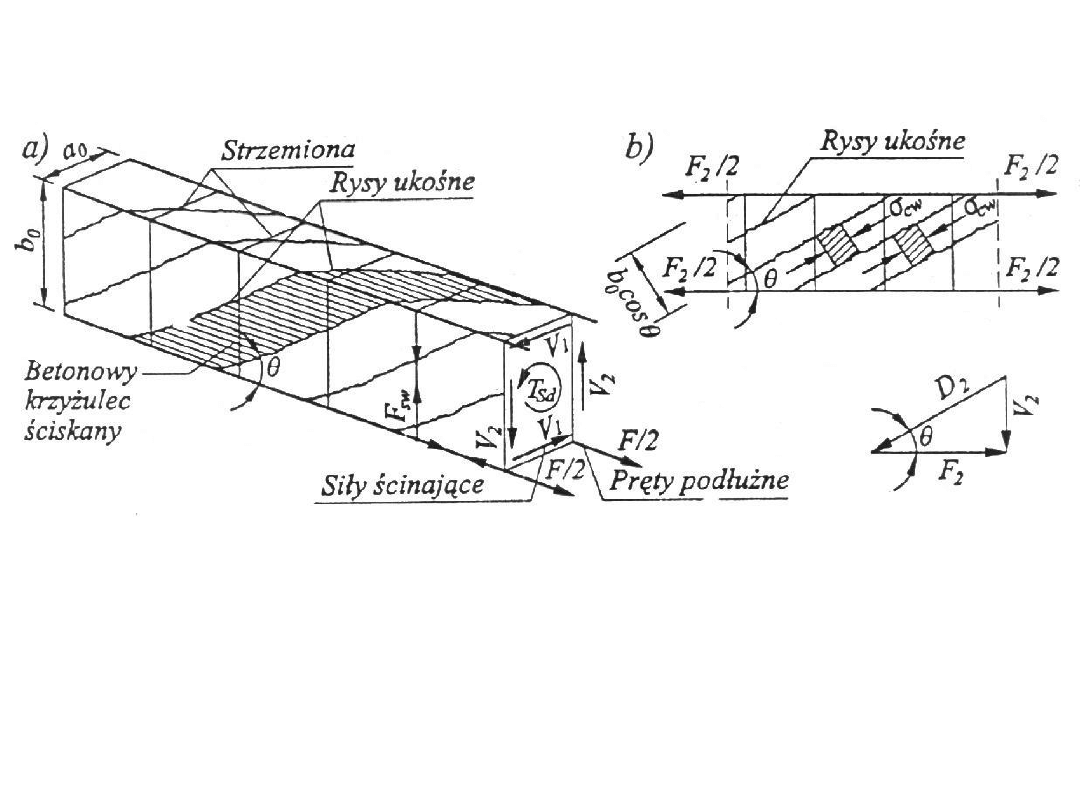
Kratownicowy model
obliczeniowy

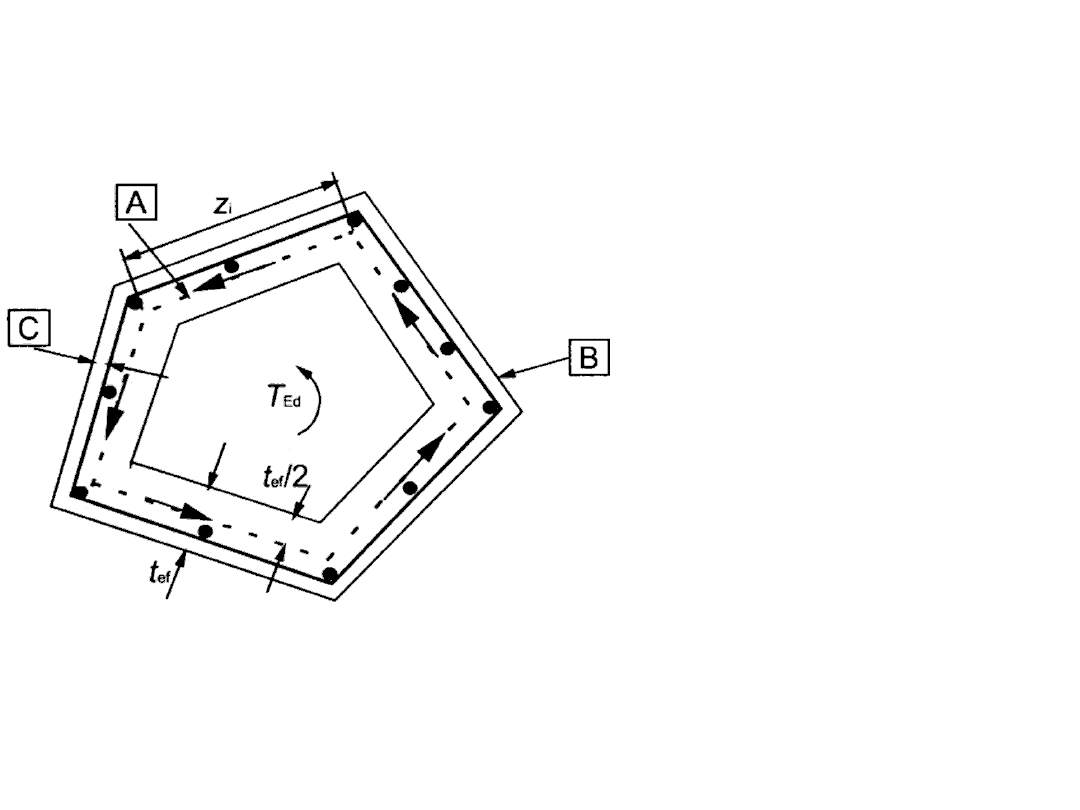
Skręcanie według PN-EN 1992-1-1

wrzesień 2008

A - linia środkowa

B – zewnętrzna krawędź

przekroju efektywnego,

obwód u,

C - otulina

Rysunek 6.11. Oznaczenia i określenia

Czyste skręcanie

W przekrojach pełnych, w przybliżeniu prostokątnych,

zbrojenie na skręcanie nie jest wymagane,

poza zbrojeniem minimalnym, jeżeli

T

Ed

≤ T

Rd,c

T

Rd,c

– skręcający moment rysujący, przy τ

t

= f

ctd

T

Rd,c

= 2 A

k

f

ctd

t

ef

A

k

– pole powierzchni wewnątrz linii środkowej

t

ef

– efektywna grubość ściany, równa A/u

A – całe pole powierzchni przekroju,

u – zewnętrzny obwód przekroju

Czyste skręcanie

Zbrojenie na skręcanie jest wymagane

, jeżeli

T

Ed

> T

Rd,c

Stosuje się strzemiona + pręty podłużne

Nośność ze względu na strzemiona

Uwaga – A

sw

oznacza pole przekroju jednego ramienia

strzemiona

Pole przekroju dodatkowego zbrojenia podłużnego





cot

s

A

f

A

2

T

sw

ywd

k

s

,

Rd





cot

A

f

2

u

T

A

k

yd

k

Ed

sl

Element jednocześnie ścinany i skręcany

W przekrojach pełnych, w przybliżeniu
prostokątnych, zbrojenie minimalne uznaje
się za wystarczające, gdy spełniony jest
warunek:

T

Ed

/ T

Rd,c

+ V

Ed

/ V

Rd,c

≤ 1,0

T

Rd,c

- skręcający moment rysujący

V

Rd,c

- siła poprzeczna określana dla ścinania

Element jednocześnie ścinany i

skręcany,

wymagane zbrojenie

Zbrojenie obliczamy niezależnie na ścinanie i

skręcanie

Sprawdzamy nośność krzyżulca ściskanego,
obciążonego ścinaniem i skręcaniem

T

Ed

/T

Rd,max

+ V

Ed

/V

Rd,max

 1,0

T

Rd,max

= 2 ν α

cw

f

cd

A

k

t

ef

sinθ cosθ

Kąt θ przyjmuje się taki sam przy ścinaniu i skręcaniu

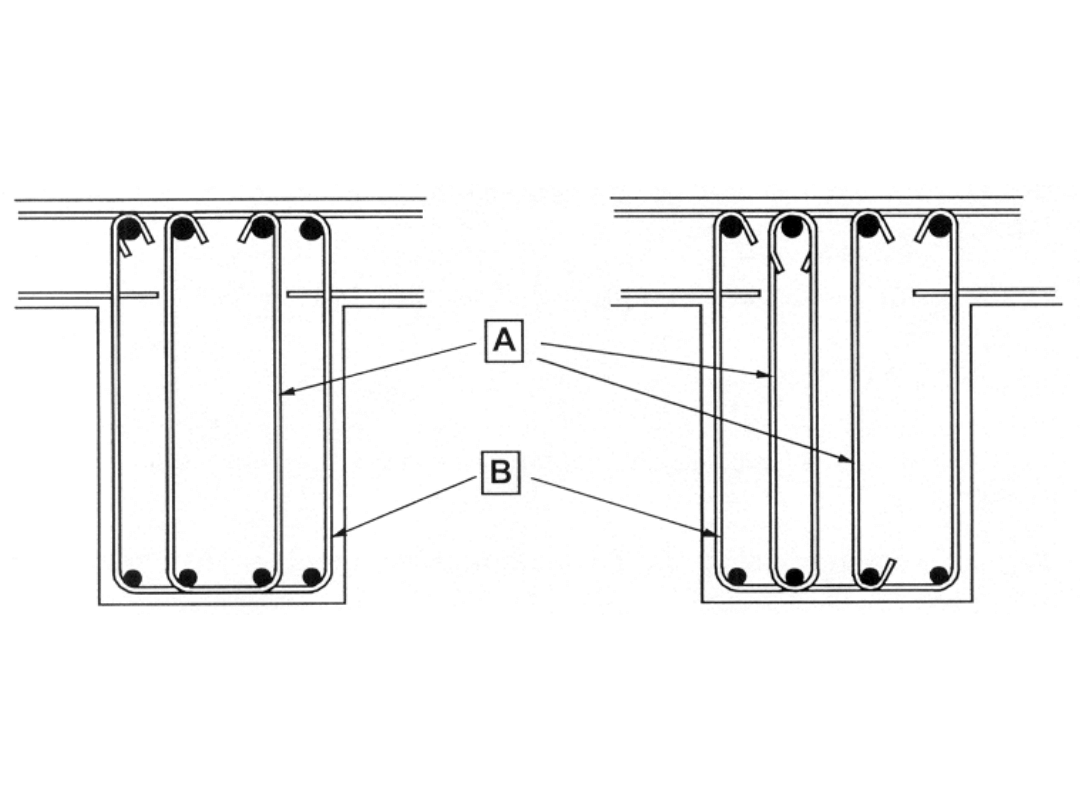
Przykłady zbrojenia na ścinanie

A - strzemiona wewnętrzne nie otaczające

B - strzemię otaczające

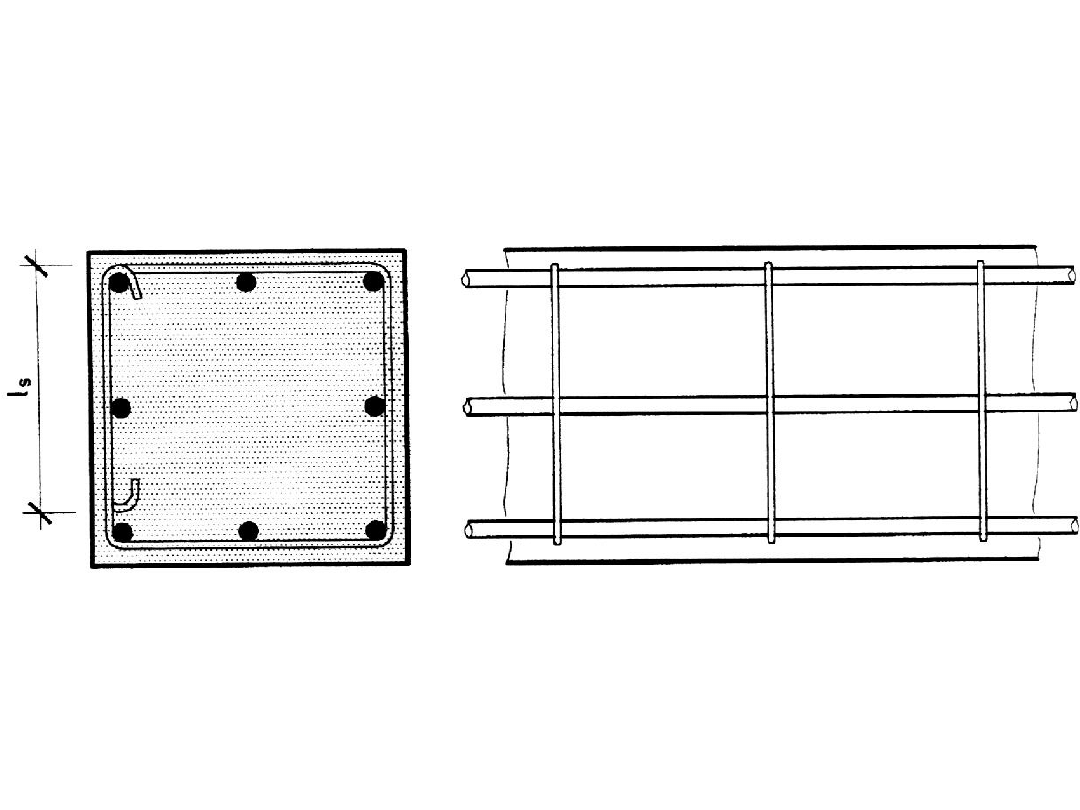
Kotwienie strzemion przenoszących

skręcanie

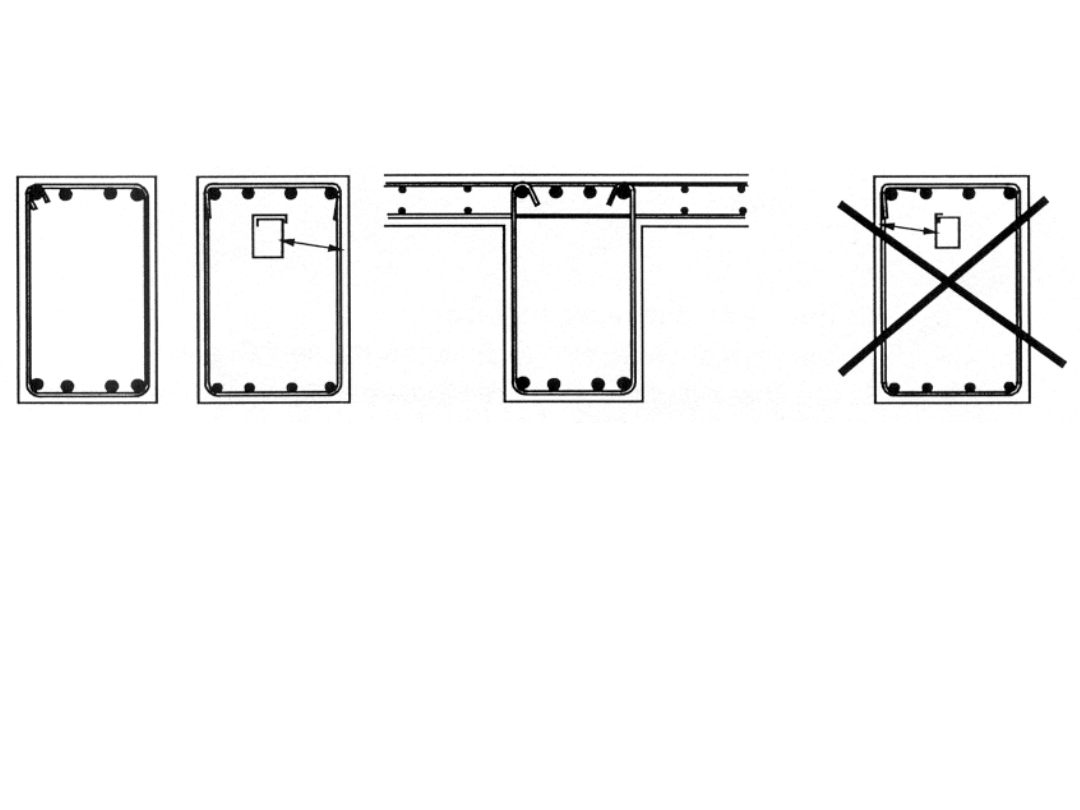
Przykłady kształtów strzemion na skręcanie

Należy przyjmować α = 90°

a1) a2) a3) b)
kształt nie

zalecany
a) kształty zalecane

Uwaga: na rysunku a2 zakład na górze powinien mieć
pełną długość wymaganą przy połączeniu na zakład

Stopień zbrojenia strzemionami pionowymi na

ścinanie

(dotyczy też skręcania)

nie może być mniejszy niż

Maksymalny rozstaw ramion strzemion powinien

spełniać warunki:
- w kierunku podłużnym

s

max

 0,75d

- w kierunku poprzecznym

s

max

 0,75d

s

max

 600mm

s

b

A

w

sw

w





yk

ck

min

,

w

f

f

08

,

0





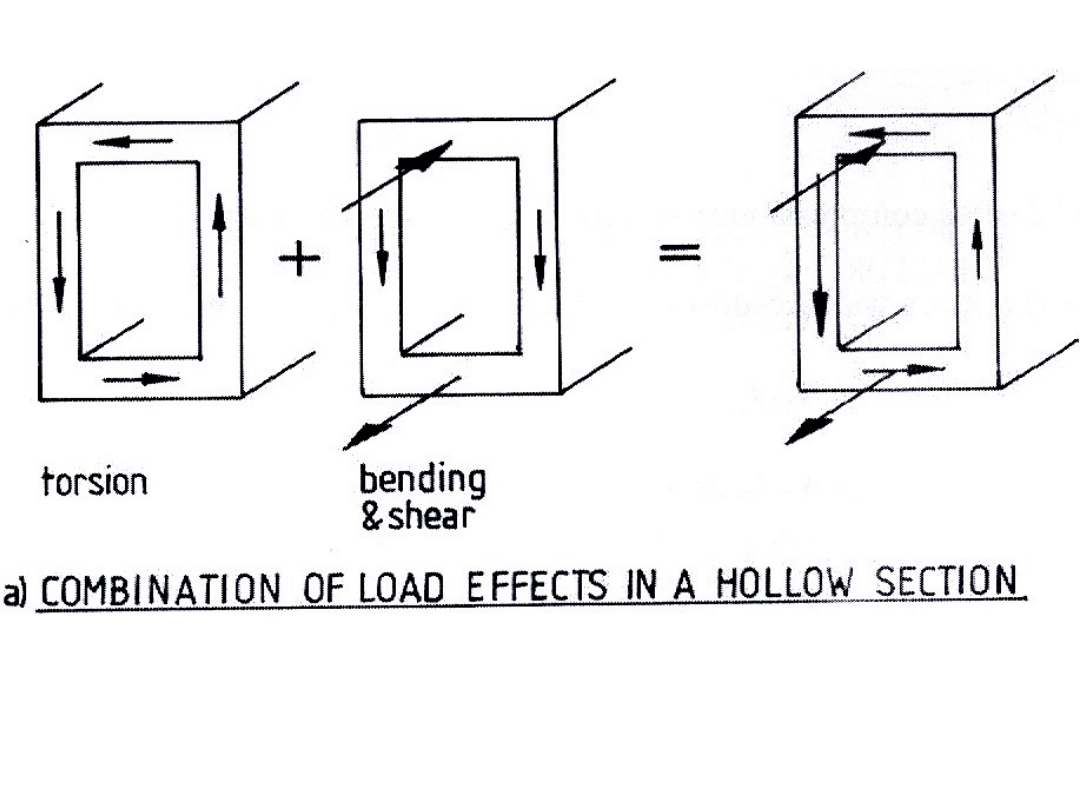
Łączne oddziaływanie ścinania, skręcania i

zginania – element wydrążony

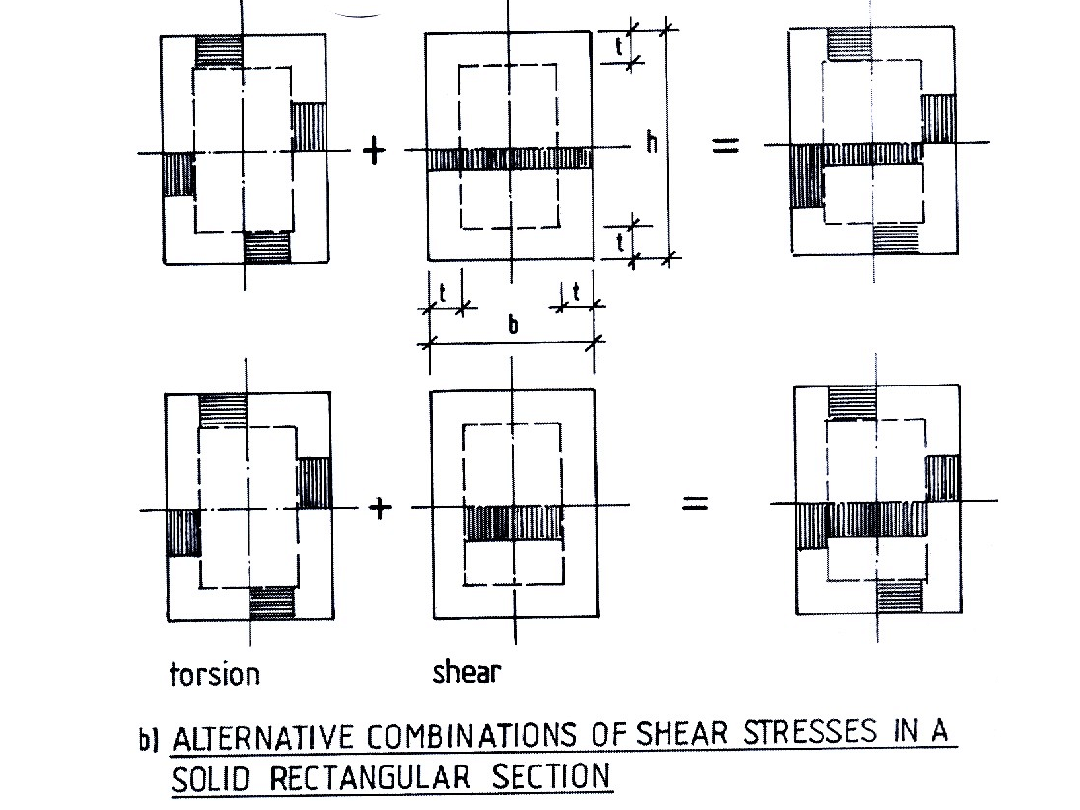
Pełny

przekrój

prostokątny

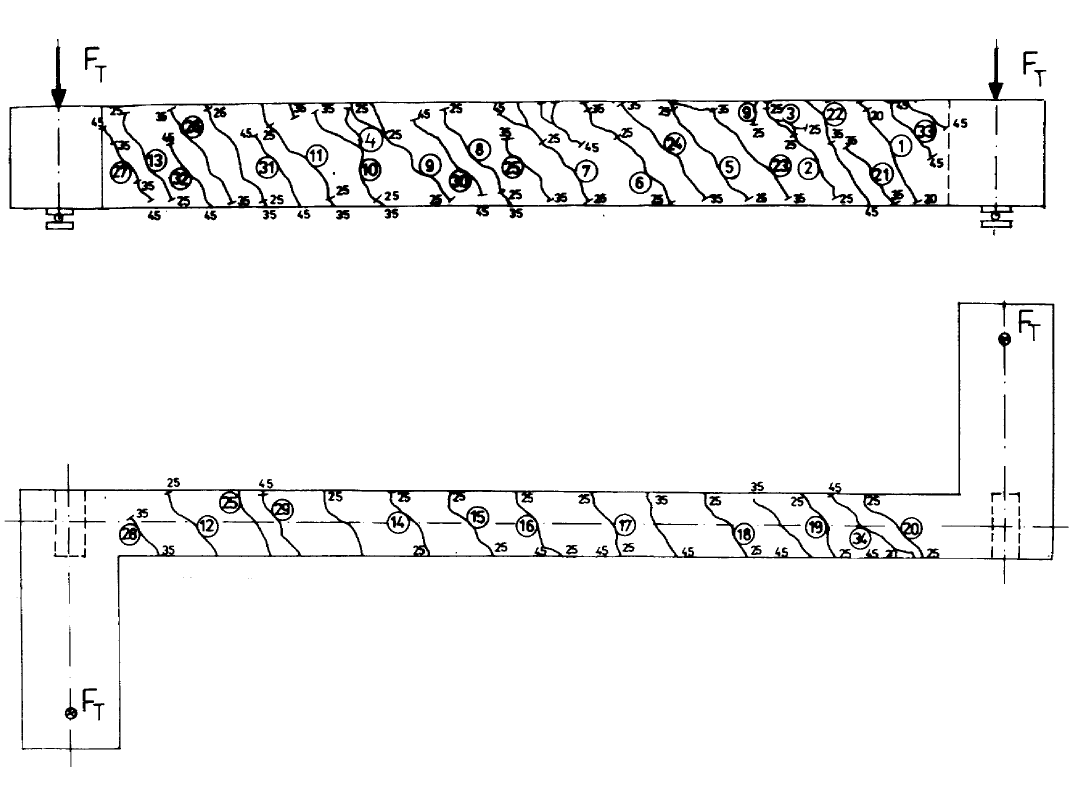
Badania dr inż. P. Bodzaka

Badania dr inż.
A. Kosińskiej
z zespołem