1

• Jeżeli istnieje

to

• Jeżeli istnieje

to

Twierdzenia o wartościach

granicznych

 

t

f

lim

t



 0

 

 

s

sf

t

f

lim

lim

s

t











0

 

t

f

lim

t 



 

 

s

sf

t

f

lim

lim

s

t

0









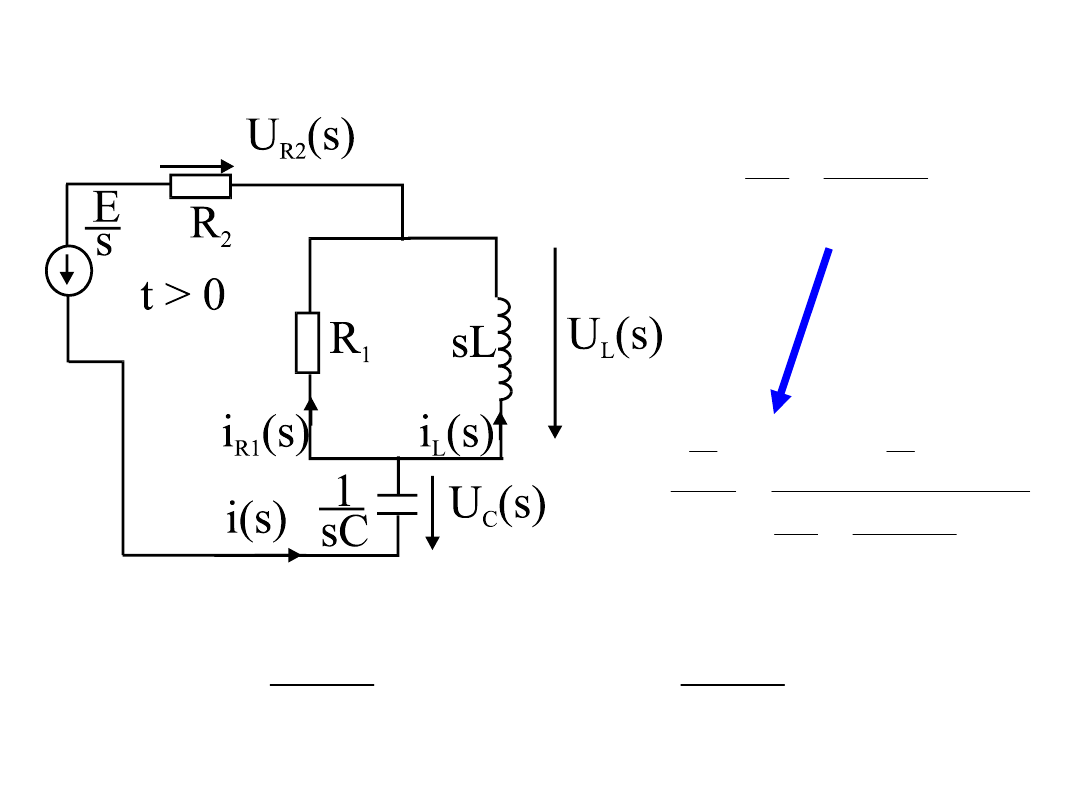
2

Twierdzenia o wartościach

granicznych

 

2

1

1

1

R

R

sL

sLR

sC

s

Z









 

 

2

1

1

1

R

R

sL

sLR

sC

s

E

s

Z

s

E

s

i











   

1

1

R

sL

R

s

i

s

i

L





   

1

1

R

sL

sL

s

i

s

i

R





3

• Obliczenie wartości początkowych prądów:

Twierdzenia o wartościach

granicznych

 

 

 

2

1

2

1

1

1

0

R

R

E

R

R

sL

sLR

sC

E

s

Z

E

s

si

i

lim

lim

lim

s

s

s































 

 





2

1

2

1

1

1

1

1

1

0

R

R

E

R

R

sL

sLR

sC

sL

R

sLE

sL

R

sL

s

si

i

lim

lim

s

s

R









































 

 





0

1

0

2

1

1

1

1

1

1







































R

R

sL

sLR

sC

sL

R

E

R

sL

R

R

s

si

i

lim

lim

s

s

L

4

• Obliczenie wartości początkowych napięć:

Twierdzenia o wartościach

granicznych

 

 

0

1

1

0

2

1

1



































R

R

sL

sLR

sC

sC

E

s

i

sC

s

U

lim

lim

s

s

C

   

 





2

1

1

2

1

1

1

1

1

1

1

1

0

0

R

R

ER

R

R

sL

sLR

sC

sL

R

sLER

sL

R

sL

R

s

si

U

U

lim

lim

s

s

L

R













































 

 

2

1

2

2

1

1

2

2

2

1

0

R

R

E

R

R

R

sL

sLR

sC

E

R

R

s

si

U

lim

lim

s

s

R

























5

• Obliczenie wartości końcowych prądów:

Twierdzenia o wartościach

granicznych

 

 

0

1

2

1

1

0

0























R

R

sL

sLR

sC

E

s

si

i

lim

lim

s

s

 

 





0

1

2

1

1

1

0

1

0

1







































R

R

sL

sLR

sC

sL

R

sLE

sL

R

sL

s

si

i

lim

lim

s

s

R

 

 





0

1

2

1

1

1

1

0

1

1

0







































R

R

sL

sLR

sC

sL

R

E

R

sL

R

R

s

si

i

lim

lim

s

s

L

6

• Obliczenie wartości końcowych napięć:

Twierdzenia o wartościach

granicznych

 

 

E

R

R

sL

sLR

sC

sC

E

s

i

sC

s

U

lim

lim

s

s

C



































2

1

1

0

0

1

1

 

 

 





0

1

2

1

1

1

1

0

1

1

0

1











































R

R

sL

sLR

sC

sL

R

sLER

sL

R

sL

R

s

si

U

U

lim

lim

s

s

L

R

 

 

0

1

2

1

1

2

0

2

0

2























R

R

sL

sLR

sC

E

R

R

s

si

U

lim

lim

s

s

R

7

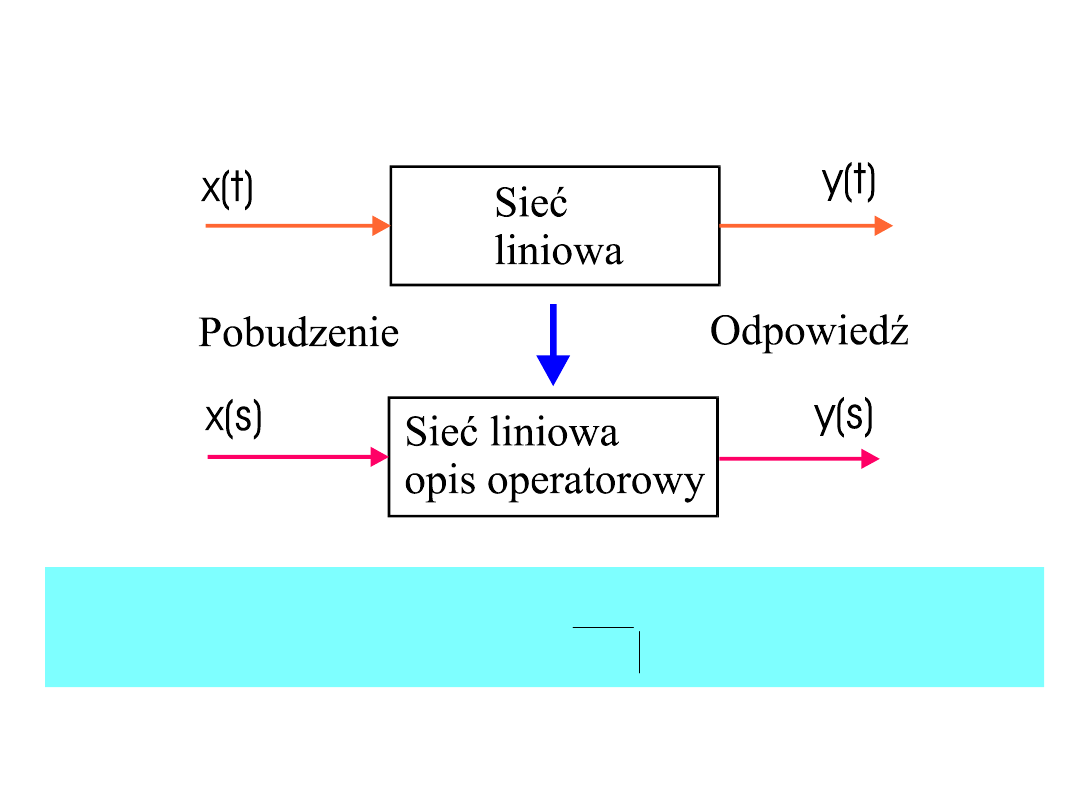
Charakterystyka sieci liniowych

• Funkcja przenoszenia:

 

 

 

pocz.

war.

zer.

przy

s

x

s

y

s

K



8

Charakterystyka sieci liniowych

• Funkcja przenoszenia K(s) umożliwia znalezienie
odpowiedzi na

dowolne pobudzenie:

 

 





   





s

x

s

K

s

y

t

y

1

1









L

L

• Wyróżnić można następujące funkcje przenoszenia
:

• Napięciowa
• Prądowa
• Napięciowo-prądowa
• Prądowo-napięciowa

 

 

 

 

0

1

2





s

i

przy

s

U

s

U

s

K

2

u

 

 

 

 

0

1

2





s

U

przy

s

i

s

i

s

K

2

i

 

 

 

 

0

1

2





s

U

przy

s

U

s

i

s

K

2

ui

 

 

 

 

0

1

2





s

i

przy

s

i

s

U

s

K

2

iu

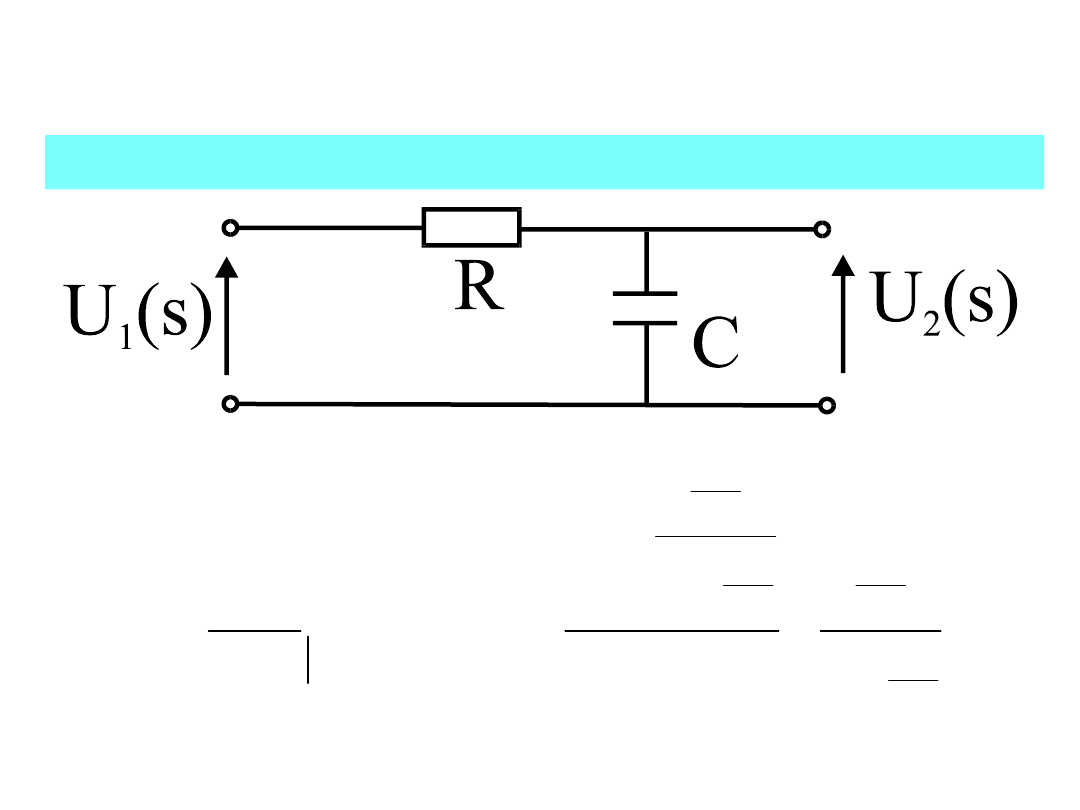
9

Charakterystyka sieci liniowych

• Obliczyć napięciową funkcję przenoszenia K(s) :

 

 

 

 

 

 

sC

R

sC

s

U

sC

R

sC

s

U

s

i

przy

s

U

s

U

s

K

2

u

1

1

1

1

0

1

1

1

2













10

Charakterystyka sieci liniowych

• Obliczyć odpowiedź na pobudzenie x(t) = E1(t).

 

   































































sC

R

E

s

E

s

E

sC

R

sC

s

x

s

K

t

y

1

1

1

1

1

1

L

L

L

 

 

t

e

E

sC

R

E

s

E

t

y

RC

t

1

1

1

1

















































L

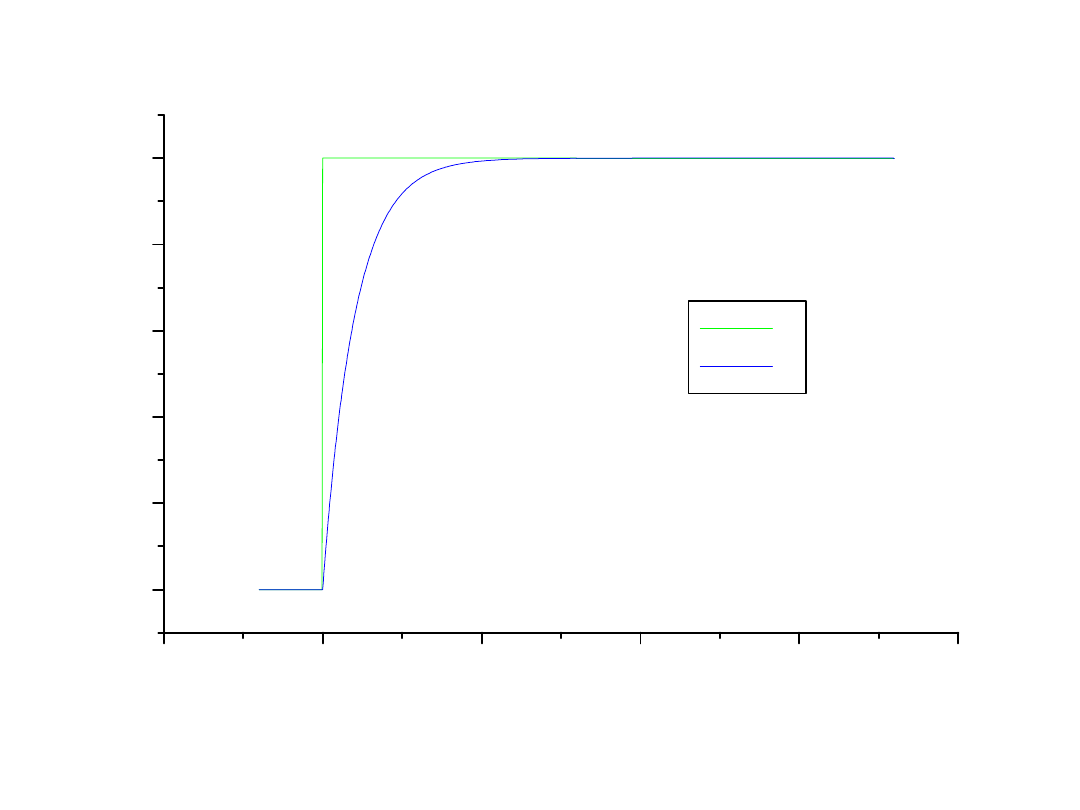
11

Charakterystyka sieci liniowych

-5

0

5

10

15

20

0

1

2

3

4

5

x
y

N

a

p

ię

ci

e

Czas

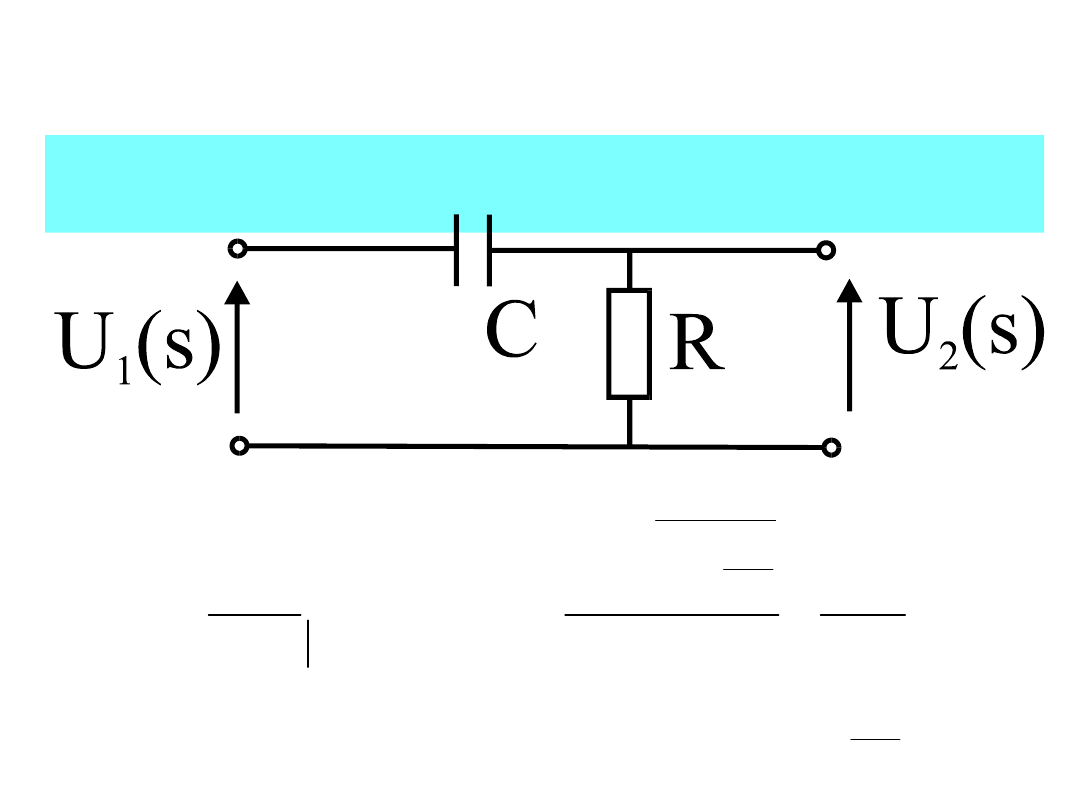
12

Charakterystyka sieci liniowych

• Odpowiedź na skok jednostkowy może
charakteryzować układ.

 

 

 

 

 

 















s

s

s

U

sC

R

R

s

U

s

i

przy

s

U

s

U

s

K

2

u

1

1

1

2

1

0

RC

1





gdzie

13

Charakterystyka sieci liniowych

• Niech przebieg pobudzający ma postać:

   

































t

i

t

dla

t

dla

,

t

,

t

x

0

0

0

1

 



 ,

t

t

1



1

1 

2

1 

2



3



3

1 

 

  



















t

t

,

t

x

1

1

1

14

 

 

  







 

t

dt

d

t

t

lim

,

t

x

lim

t

1

1

1

1

0

0



























Charakterystyka sieci liniowych

 

















0

0

0

t

dla

t

dla

t

 

 

1

1

0

0













































t

dt

dt

,

t

dt

,

t

x

Nie zależnie
od wartości
 !!!

Funkcja nosi nazwę funkcji impulsowej, funkcji
delta lub funkcji delta Diraca. Nie jest ona funkcją w
tradycyjnym znaczeniu.

 

t



15

Charakterystyka sieci liniowych

• Transformata funkcji x(t, ) ma postać:

• Transformata odpowiedzi przyjmie zatem postać:

• Odpowiedź można wyrazić w postaci:

 

 





 

 













s

e

s

t

t

,

t

x

,

s

x





























1

1

1

1

1

1

L

L

L

       





s

e

s

s

K

,

s

x

,

s

y





















1

1

 

   









 







































































t

t

s

e

t

e

t

s

e

,

s

x

s

K

,

t

y

1

1

1

1

1

1

L

L

16

Charakterystyka sieci liniowych

 

 





































t

t

e

t

e

t

,

t

y

1

1

1

 

 













 





t

t

t

e

t

dt

d

e

t

e

t

lim

,

t

y

lim







































1

1

1

1

0

0

 

 





 

 

t

e

t

dt

d

e

e

t

dt

d

,

t

y

lim

t

t

t

1

1

1

0



























Dla t > 0
otrzymamy:

 

t

e

,

t

y

lim

















0

17

Charakterystyka sieci liniowych

Dla t  0

otrzymamy:

 

 

 

 

 

t

e

t

e

t

e

t

dt

d

e

,

t

y

lim

t

t

t

t

1

1

1

0





































 

 

   

   

t

y

t

e

t

t

e

t

e

,

t

y

lim

t

t

t





































1

1

0

• Obliczenie transformaty
funkcji delta:

 

 





s

e

s

lim

t

















1

1

0

L

Z uwagi na problem
nieoznaczoności 0 / 0, stosujemy
regułę de l’Hospitala.

18

Charakterystyka sieci liniowych

 

 

s

e

lim

t

s

















1

0

L



d

d



d

d

 

 

1

0















s

se

lim

t

s

L

 

 

1



 t

L

 

 

t







1

1

L

• Obliczenie transformaty odwrotnej
funkcji K(s):

 













 

     

t

y

t

k

t

e

t

s

s

s

s

K

t































































1

1

1

1

1

L

L

L

Pobudzając układ impulsemDiraca można
wyznaczyć jego funkcję przenoszenia k(t)!!!

19

Funkcję
nazywamy

splotem lub mnożeniem splotowym.

Charakterystyka sieci liniowych -

twierdzenie Borela

• Jeżeli funkcje f

1

(t) i f

1

(t) są bezwzględnie

transformowalne, oraz chociaż jedna jest
ograniczona w każdym przedziale [0, ] dla  > 0 to:

  



   

s

f

s

f

d

t

f

f

t

2

1

0

2

1

























L

 

  



 

 

t

f

t

f

d

t

f

f

t

t

2

1

0

2

1



















20

Charakterystyka sieci liniowych

• Odpowiedź układu może być obliczona przy
wykorzystaniu

operacji splotu:

 

  



 

 

t

x

t

k

d

t

x

k

t

y

t

















0

 

  



 

 

t

k

t

x

d

t

k

x

t

y

t

















0

 

 





s

K

t

k

1



L

gdzie

• Dla
• Odpowiedź układu stanowi

   

t

t

x





 

  



 

t

k

d

t

k

t

y

t

















0

21

Charakterystyka sieci liniowych

• Dla pobudzenia
• Odpowiedź układu stanowi

   

t

t

x

1



 

  



 

t

h

d

t

k

t

y

t















0

1

 

 





s

H

t

h

1



L

gdzie

 

  



 

1

0































s

K

d

t

k

s

y

t

L

• Przy pobudzeniu impulsem Diraca:

• Przy pobudzeniu impulsem
jednostkowym:

 

  



 

 

1

1

1

0

































s

H

s

s

K

d

t

k

s

y

t

L

22

Charakterystyka sieci liniowych

Pobudzenie układu opisanego funkcją k(s) impulsem
jednostkowym jest równoważne pobudzeniu układu
opisanego funkcją h(t) impulsem Diraca.

 

  



  





















































t

t

d

t

h

d

t

k

s

y

0

0

1

L

L

 

 

1

1







s

H

s

s

K

23

• 1) Przy pobudzeniu impulsem Diraca:

Charakterystyka sieci liniowych

• Związek między odpowiedzią impulsową k(t) a
odpowiedzią

jednostkową h(t) :

 







s

s

s

K

RC

1





gdzie

     

t

t

x

t

U







1

24

Charakterystyka sieci liniowych

   

 























































s

s

s

s

K

t

k

t

y

1

1

1

1

L

L

L

     

 

 

t

U

t

e

t

t

k

t

y

t

2

1 















• 2) Przy pobudzeniu impulsem jednostkowym:

     

t

t

x

t

U

1

1





 

   

 

 

s

s

K

s

H

s

U

s

K

s

U

1

1

2









 

 





 

t

e

s

s

H

t

h

t

1

1

1

1































L

L

25

Charakterystyka sieci liniowych

   

   

t

k

t

e

t

dt

t

h

d

t

d















1

• Pojęcie pochodnej
dystrybucyjnej:

• Pochodna funkcji h(t) w zwykłym
sensie:

 

 

 



















0

h

s

sH

t

h

dt

d

L

Na mocy
własności 7

 

 

 



















0

h

s

K

t

h

dt

d

L

 

 

 

 

 

























0

h

t

t

k

t

h

dt

d

L

L

L

26

Charakterystyka sieci liniowych

 

 

 

 

 

























0

h

t

t

k

t

h

dt

d

L

L

L

     

 









0

h

t

t

k

t

h

dt

d

 

   

 









0

h

t

t

h

dt

d

t

k

 

   

 









0

h

t

dt

t

dh

dt

t

h

d

d

Jeżeli h(0

+

) = 0 wówczas wartość pochodnej

dystrybucyjnej jest równa pochodnej w
zwykłym sensie.

27

Charakterystyka sieci liniowych

• Związek między odpowiedzią y(t) i pobudzeniem
x(t) przy

znajomości h(t):

 

   

   

s

x

s

sH

s

x

s

K

s

y





 

   

 









0

h

t

dt

t

dh

dt

t

h

d

d

 

 

 



















0

h

s

sH

t

h

dt

d

L

 

 

 

t

h

s

dt

t

h

d

d

L

L















 

   

t

x

t

h

dt

d

t

y





28

Charakterystyka sieci liniowych

• Jeżeli funkcja h(t) jest dla t  0 funkcją ciągłą,

oraz funkcja x(t) ma dla t > 0 ciągłą pochodną to
można różniczkować splot:

lub jeżeli funkcja x(t) jest dla t  0 funkcją ciągłą,

oraz funkcja h(t) ma dla t > 0 ciągłą pochodną to

 

 

 

  



 

 

  



































t

'

t

d

t

x

h

x

t

h

d

t

x

h

dt

d

t

x

t

h

dt

d

t

y

0

0

0

 

 

 

  



 

 

  



































t

'

t

d

t

h

x

h

t

x

d

t

h

x

dt

d

t

h

t

x

dt

d

t

y

0

0

0

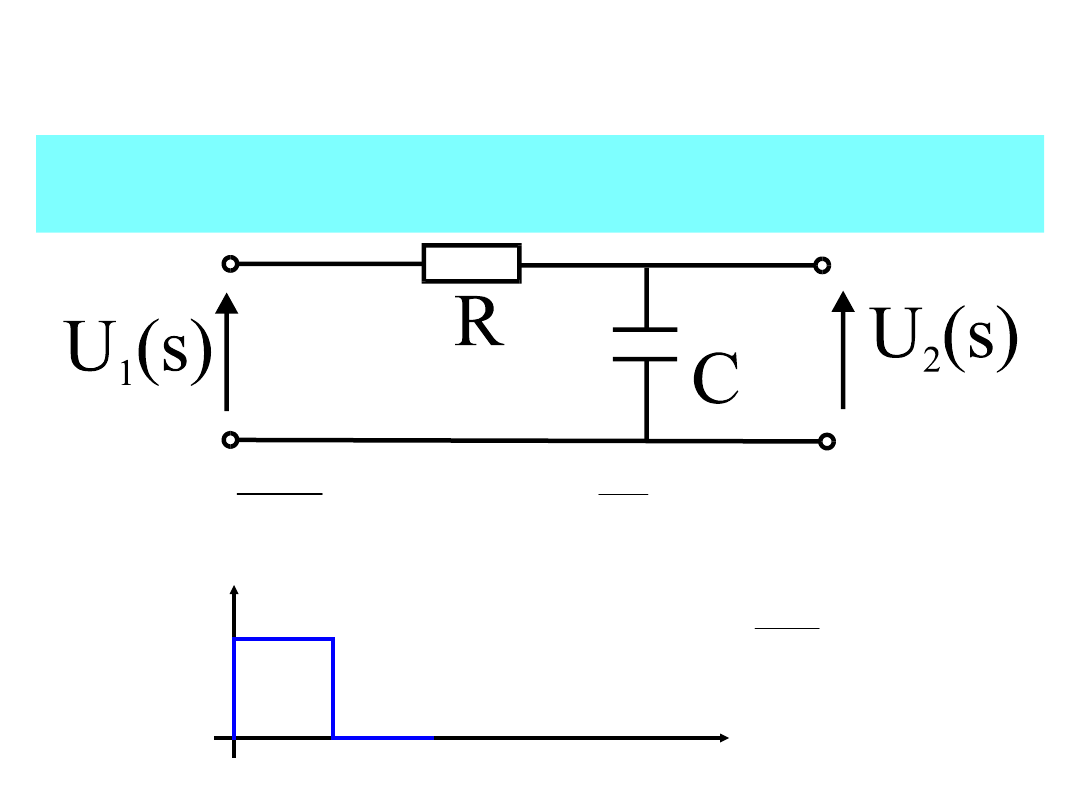
29

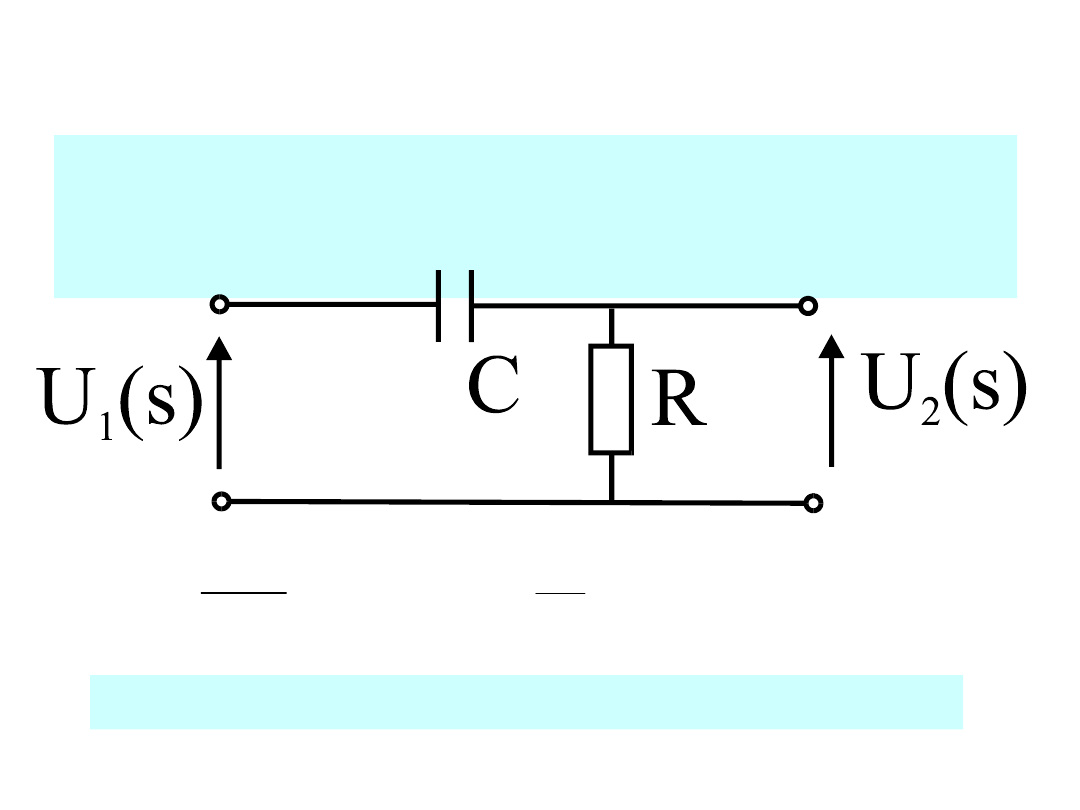
Zastosowanie splotu do sieci

liniowych

Obliczyć napięcie na wyjściu czwórnika korzystając z
operacji splotu:

RC

1





gdzie

 









s

s

K

E

T

t

U

1

(t)

 

 





 

t

e

s

s

K

t

k

t

1

1

1





































L

L

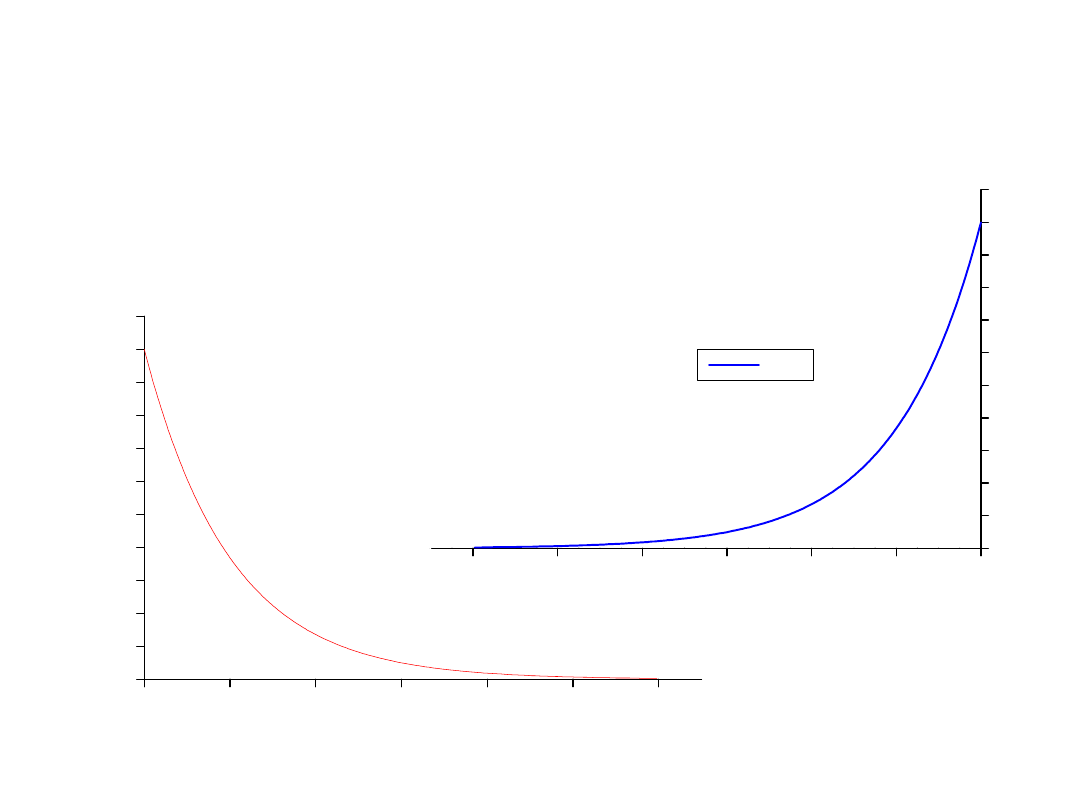
30

Zastosowanie splotu do sieci

liniowych

 

  



 

 

t

k

t

U

d

t

k

U

t

U

t

















1

0

1

2

0

1

2

3

4

5

6

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

k(



)

Czas -



-6

-5

-4

-3

-2

-1

0

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

k(-



)

Czas -



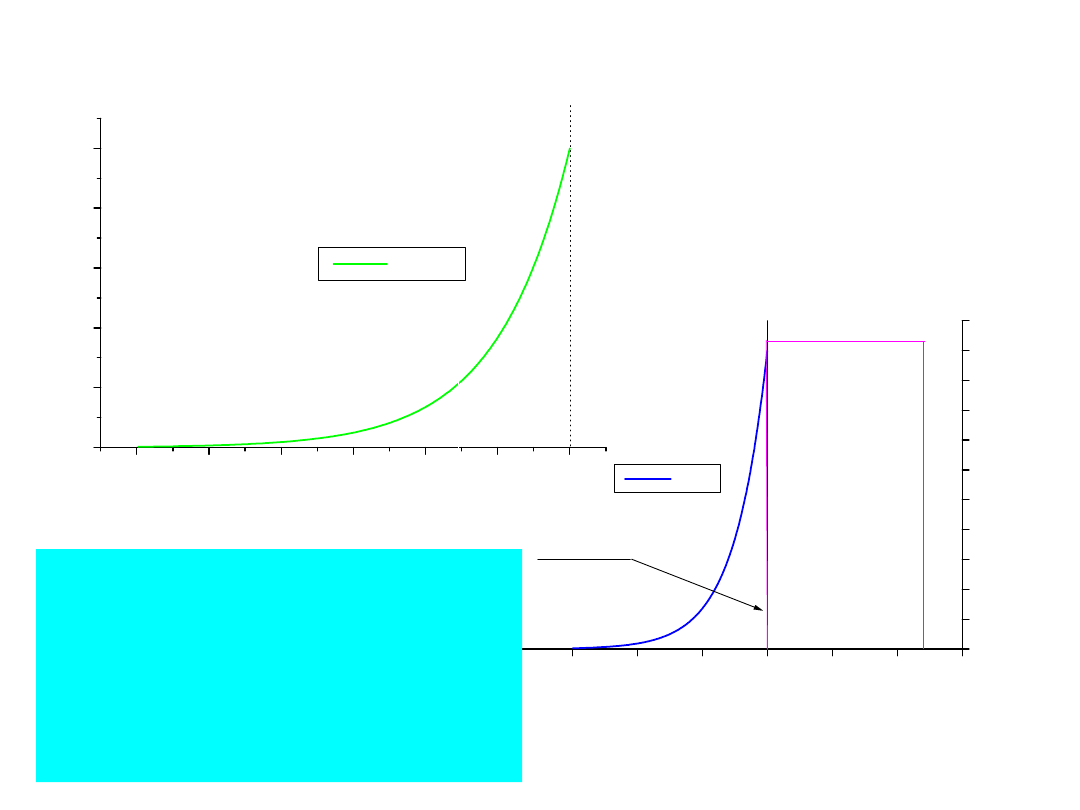
31

Zastosowanie splotu do sieci

liniowych

-4

-3

-2

-1

0

1

2

0,0

0,2

0,4

0,6

0,8

1,0

k(t -



)

Czas -



-8

-6

-4

-2

0

2

4

6

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

U

1

(



)

k(-



)

Czas -



Dla t < 0, iloczyn
podcałkowy jest równy
zeru - brak wspólnego
obszaru dla funkcji k(t-)

oraz funkcji U

1

().

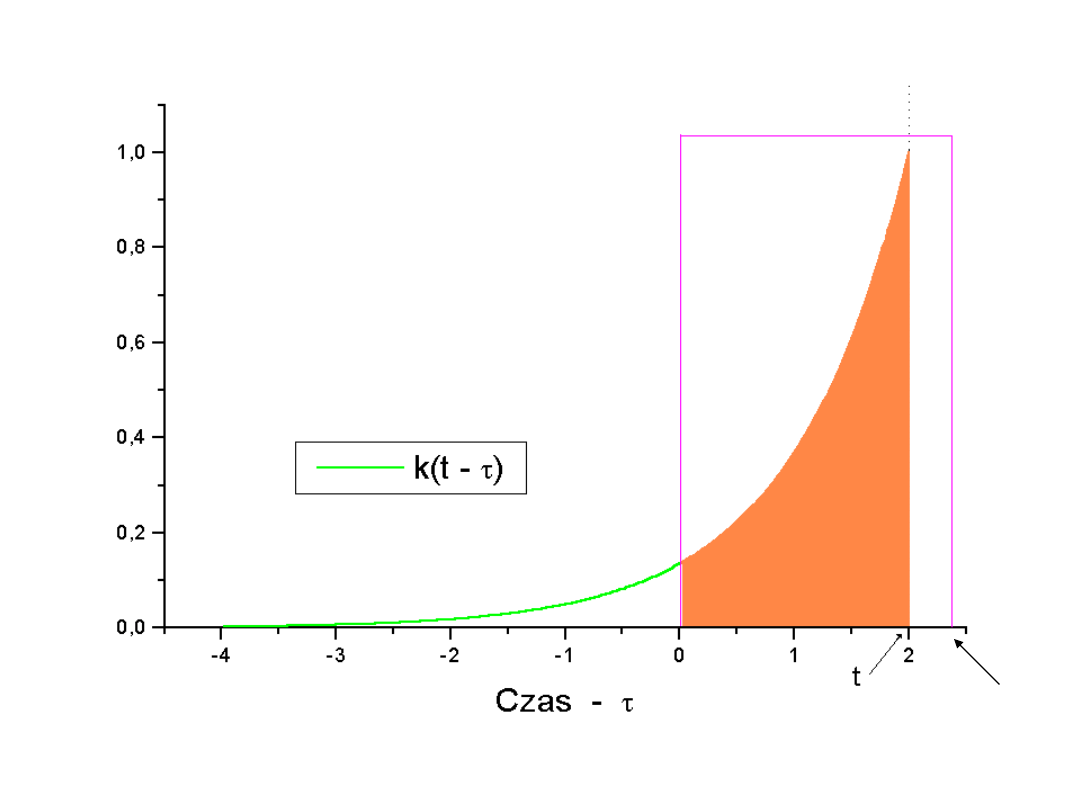
32

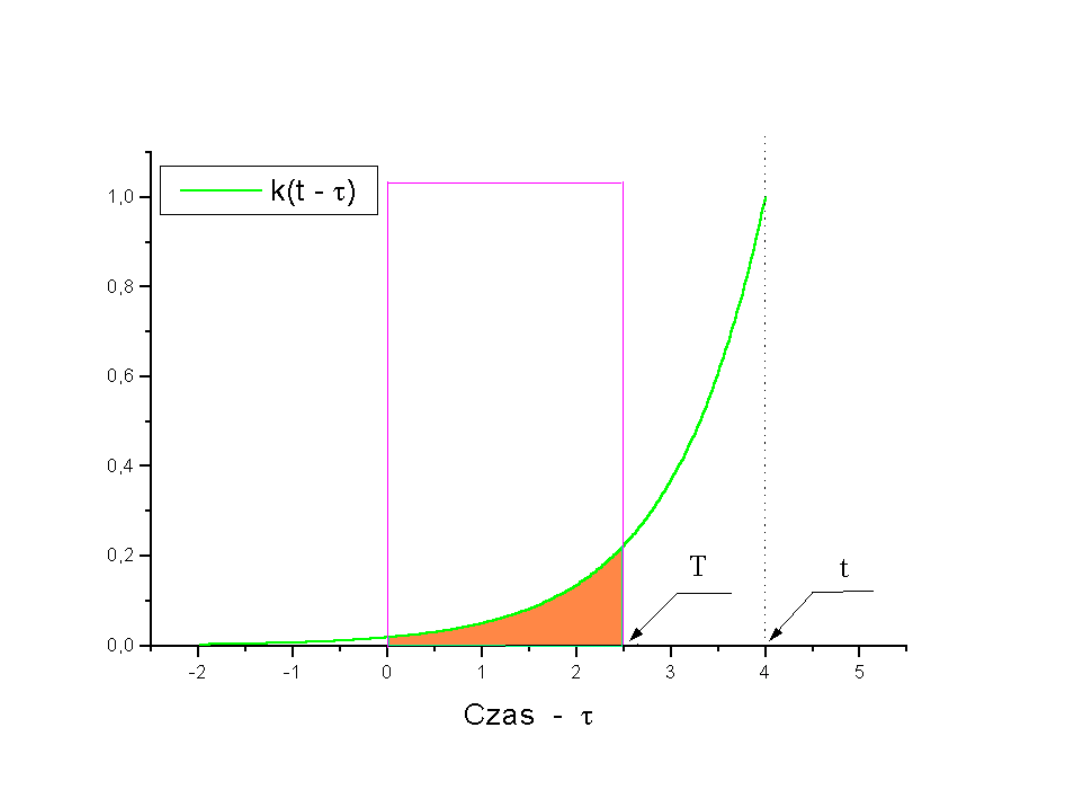
Zastosowanie splotu do sieci

liniowych

T

33

Zastosowanie splotu do sieci

liniowych

 

  



































t

t

t

d

e

E

d

t

k

U

t

U

0

0

1

2

W przedziale 0 < t < T napięcie wyjściowe można
wyrazić:

 









t

t

t

t

t

t

t

e

E

e

Ee

d

e

e

E

d

e

E

t

U















































1

0

0

0

2

34

Zastosowanie splotu do sieci

liniowych

35

Zastosowanie splotu do sieci

liniowych

 









































T

t

T

t

d

e

E

d

e

E

t

U

0

0

2

W przedziale t > T napięcie wyjściowe można
wyrazić:

 





1

0

0

2

































T

t

T

t

T

t

e

Ee

e

Ee

d

e

e

E

t

U

 











































T

t

dla

e

Ee

T

t

0

dla

e

E

0

t

dla

t

U

T

t

t

1

1

0

2

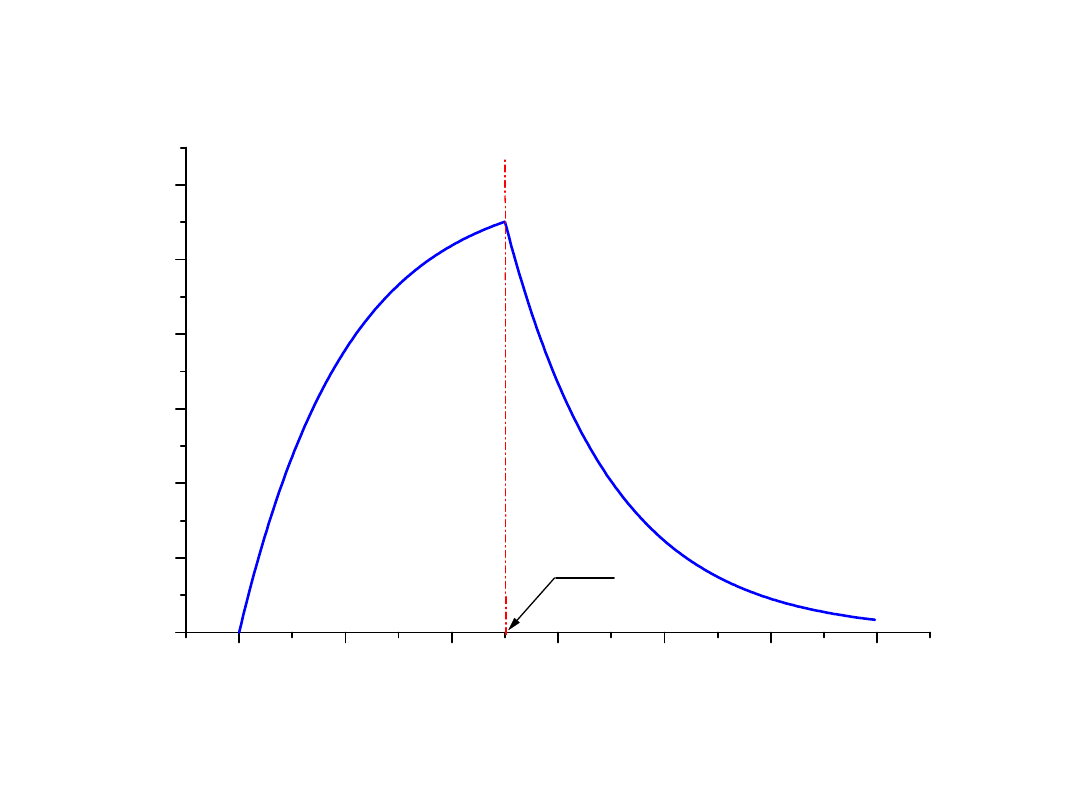
36

Zastosowanie splotu do sieci

liniowych

0

1

2

3

4

5

6

0,0

0,2

0,4

0,6

0,8

1,0

1,2

T

U

2

(t

)

Czas - t

37

Zastosowanie splotu do sieci

liniowych

 

  



 

 

t

U

t

k

d

t

U

k

t

U

t

1

0

1

2

















Przypadek
2)

0

1

2

3

4

5

6

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

1,1

k(



)

Czas -



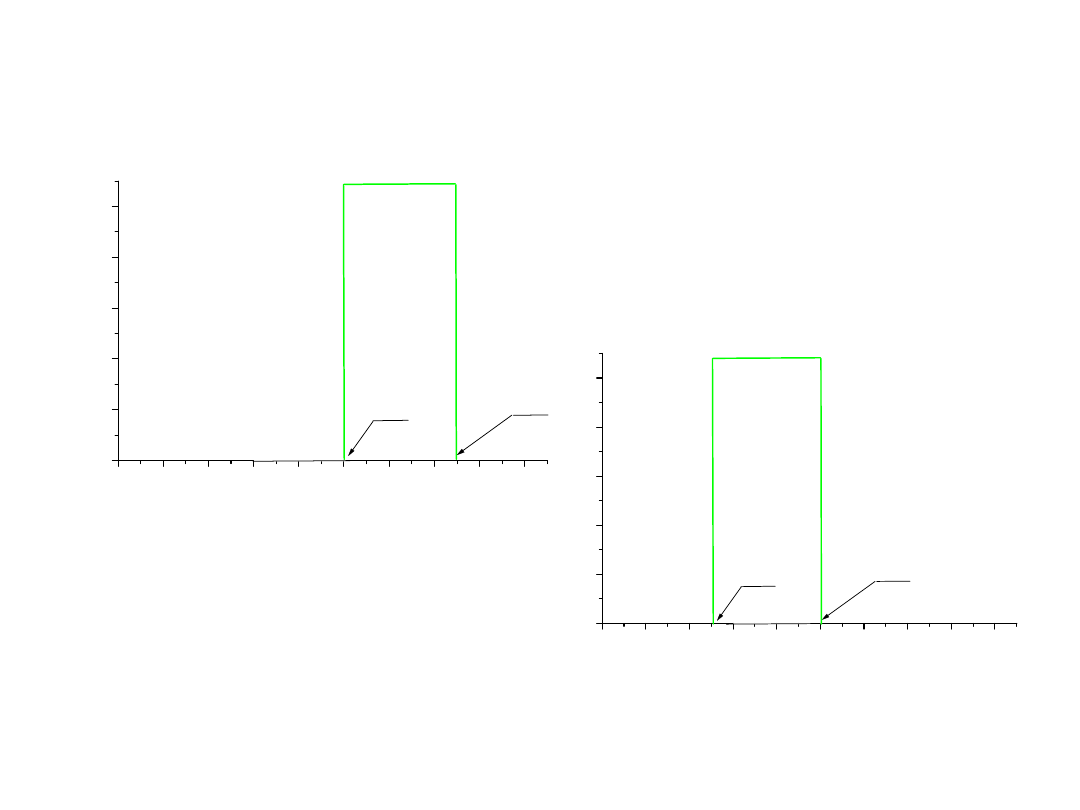
38

Zastosowanie splotu do sieci

liniowych

-5

-4

-3

-2

-1

0

1

2

3

4

0,0

0,2

0,4

0,6

0,8

1,0

T

0



-5

-4

-3

-2

-1

0

1

2

3

4

0,0

0,2

0,4

0,6

0,8

1,0

t - T

t



U

1

()

U

1

(-

)

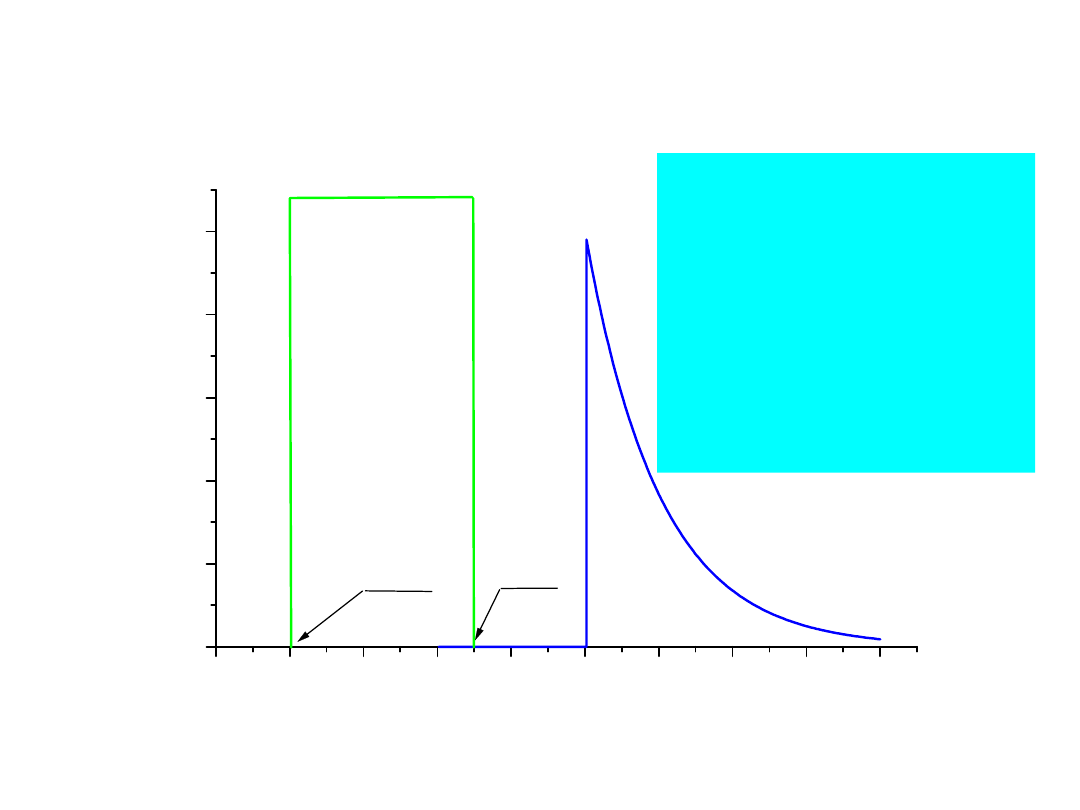
39

Zastosowanie splotu do sieci

liniowych

-5

-4

-3

-2

-1

0

1

2

3

4

0,0

0,2

0,4

0,6

0,8

1,0

t

t - T



Dla t < 0, iloczyn
podcałkowy jest
równy zeru - brak
wspólnego obszaru
dla funkcji k()

oraz funkcji U

1

(t -

).

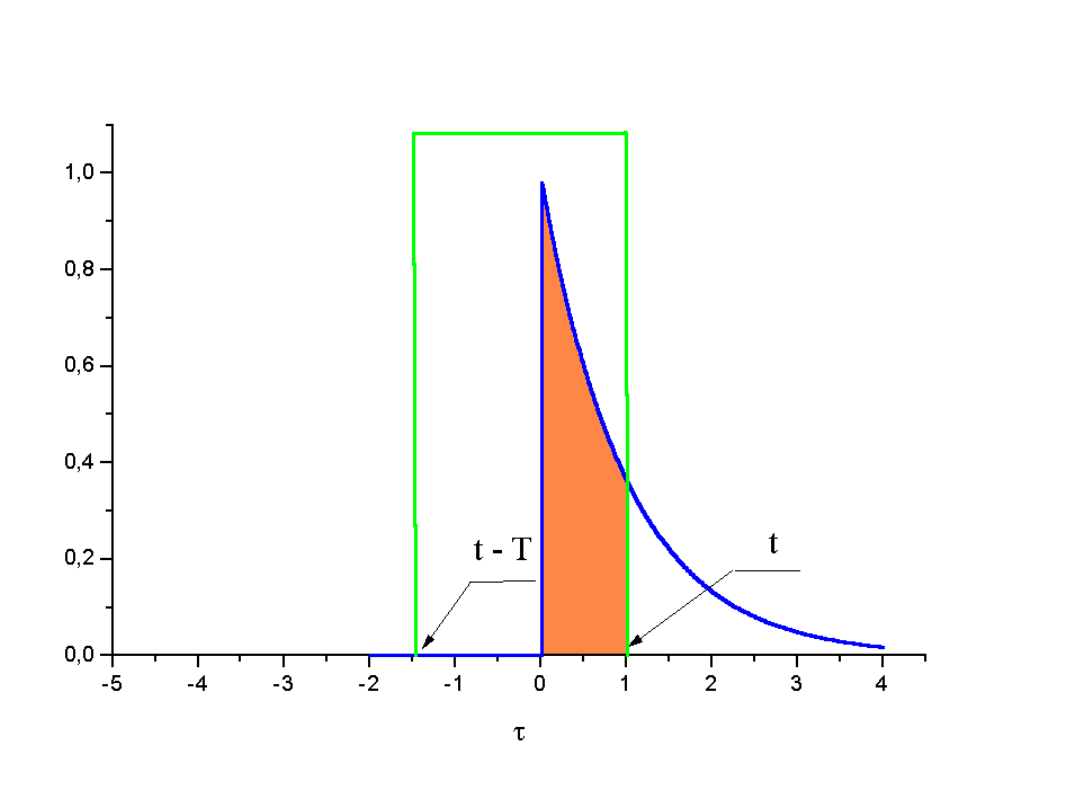
40

Zastosowanie splotu do sieci

liniowych

41

Zastosowanie splotu do sieci

liniowych

 

  



























t

t

d

e

E

d

t

U

k

t

U

0

0

1

2

W przedziale 0 < t < T napięcie wyjściowe można
wyrazić:

 





t

t

t

t

e

E

Ee

d

e

E

d

e

E

t

U









































1

0

0

0

2

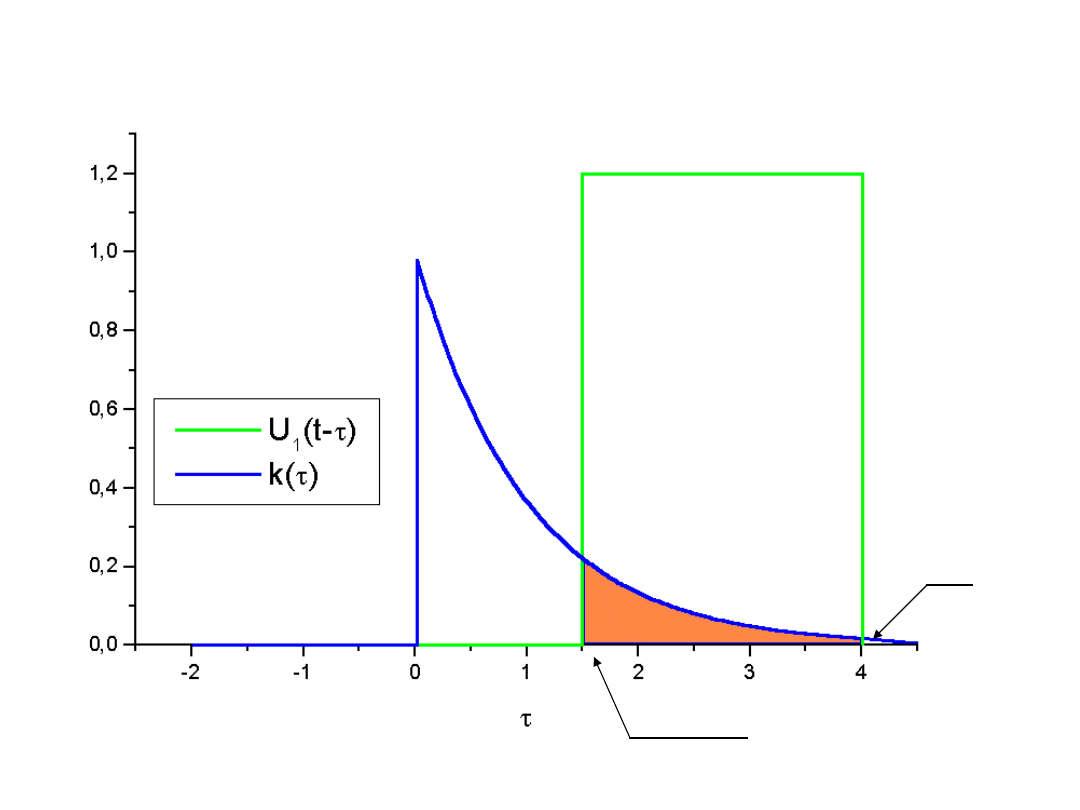
42

Zastosowanie splotu do sieci

liniowych

t

t - T

43

Zastosowanie splotu do sieci

liniowych

 





























t

T

t

t

T

t

d

e

E

d

e

E

t

U

2

W przedziale t > T napięcie wyjściowe można
wyrazić:

 





1

2

































T

t

T

t

t

t

T

t

e

Ee

Ee

d

e

E

t

U

 











































T

t

dla

e

Ee

T

t

0

dla

e

E

0

t

dla

t

U

T

t

t

1

1

0

2

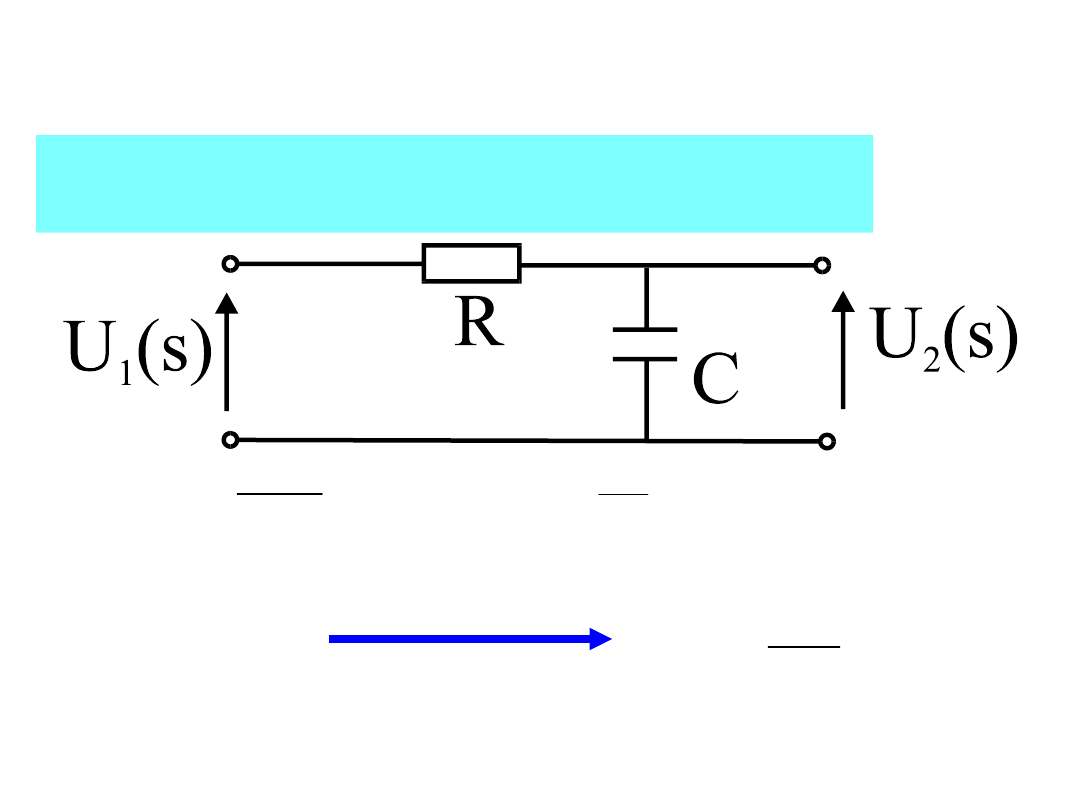
44

Zastosowanie splotu do sieci

liniowych

Obliczyć napięcie na wyjściu czwórnika przy
różnych pobudzeniach:

RC

1





gdzie

 









s

s

K

Dla  =

1,

 

1

1





s

s

K

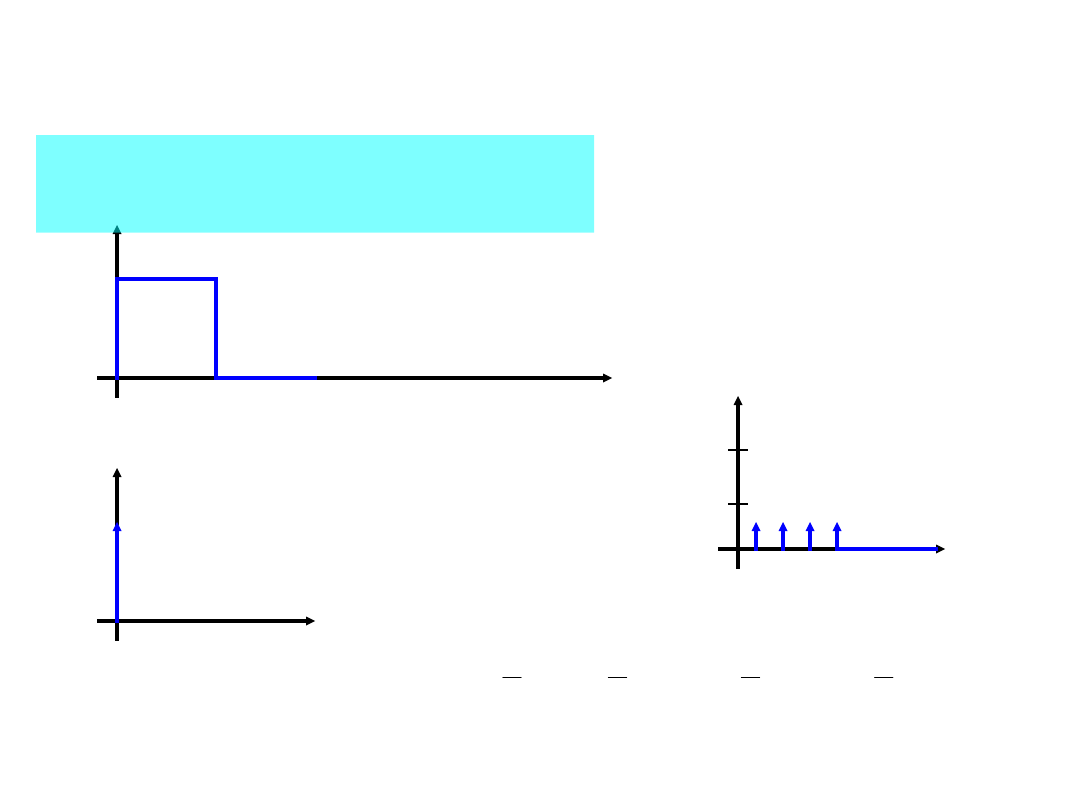
45

1

1

t

U

1a

(t)

Zastosowanie splotu do sieci

liniowych

    



1

1

1

1







t

t

t

U

a

Rozważmy nastepujące
pobudzenia:

1

0

t

U

1b

(t)

   

t

t

U

b





1

1

1

t

U

1c

(t)

 





























 















 















 





1

4

3

2

1

4

1

4

1

1

t

t

t

t

t

U

c

46

Zastosowanie splotu do sieci

liniowych

Obliczmy
odpowiedzi:

 

   















































s

e

s

s

s

U

s

K

t

U

s

a

a

1

1

1

1

1

1

2

L

L

 















































































s

s

a

e

s

s

s

e

s

s

t

U

1

1

1

1

1

1

1

1

1

2

L

L

 































1

1

1

1

1

2

s

e

s

s

e

s

t

U

s

s

a

L

    



 

 





1

1

1

1

1

1

1

2



















t

e

t

e

t

t

t

U

t

t

a

47

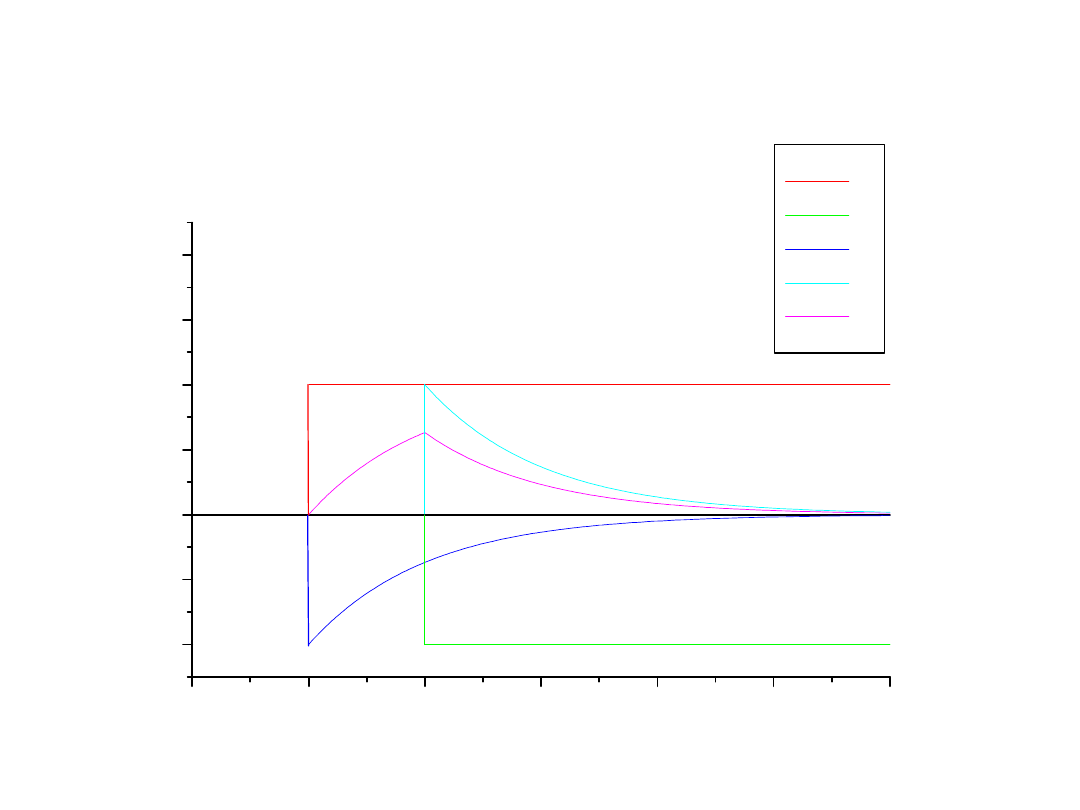
Zastosowanie splotu do sieci

liniowych

-1

0

1

2

3

4

5

-1,0

-0,5

0,0

0,5

1,0

1,5

2,0

B
C
D
E
F

P

rz

e

b

ie

g

i

n

a

p

ię

ci

a

Czas - t

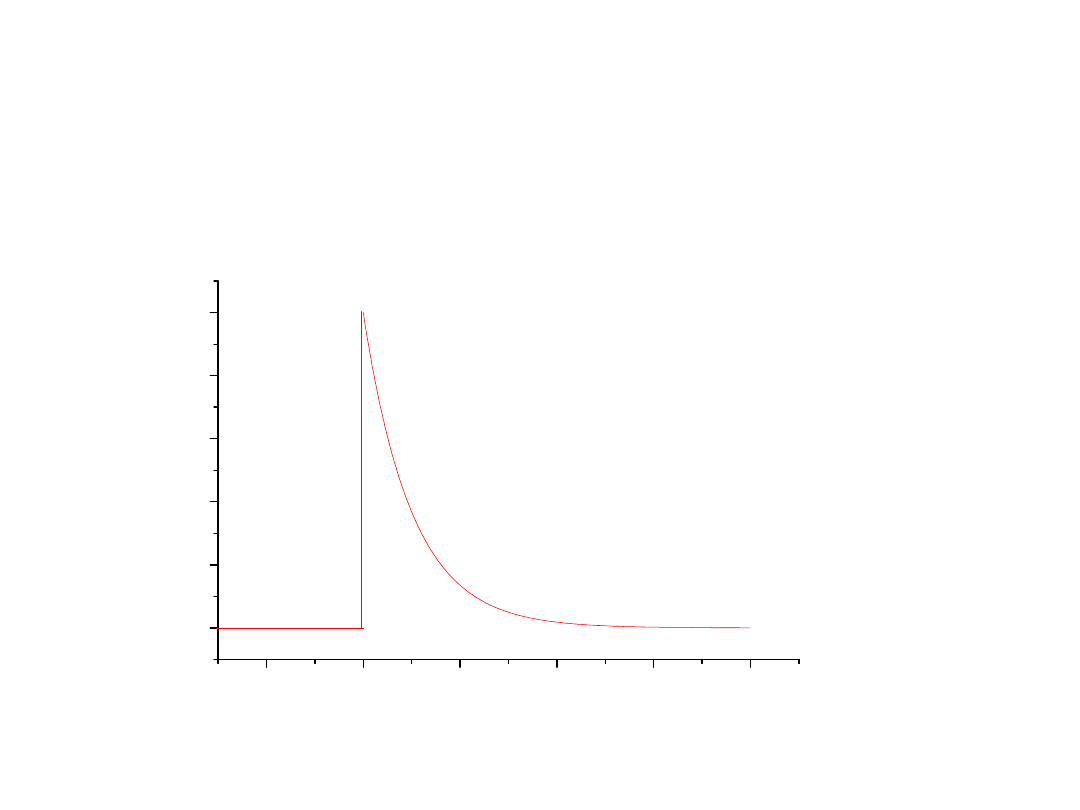
48

 

 



  

 

t

e

t

k

s

K

t

U

t

b

1

1

2













L

Zastosowanie splotu do sieci

liniowych

-2

0

2

4

6

8

0,0

0,2

0,4

0,6

0,8

1,0

k(

t)

Czas - t

49

 





























 















 















 





1

4

3

2

1

4

1

4

1

1

t

t

t

t

t

U

c

Zastosowanie splotu do sieci

liniowych

 





 





























 













 













 

















 













 













 



1

4

3

2

1

4

1

2

1

1

4

3

1

2

1

1

4

1

1

4

1

t

t

t

t

c

e

t

e

t

e

t

e

t

t

U

 

   





































































4

4

4

4

1

1

4

3

2

1

4

1

1

1

1

2

s

s

s

s

c

c

e

e

e

e

s

s

U

s

K

t

U

L

L

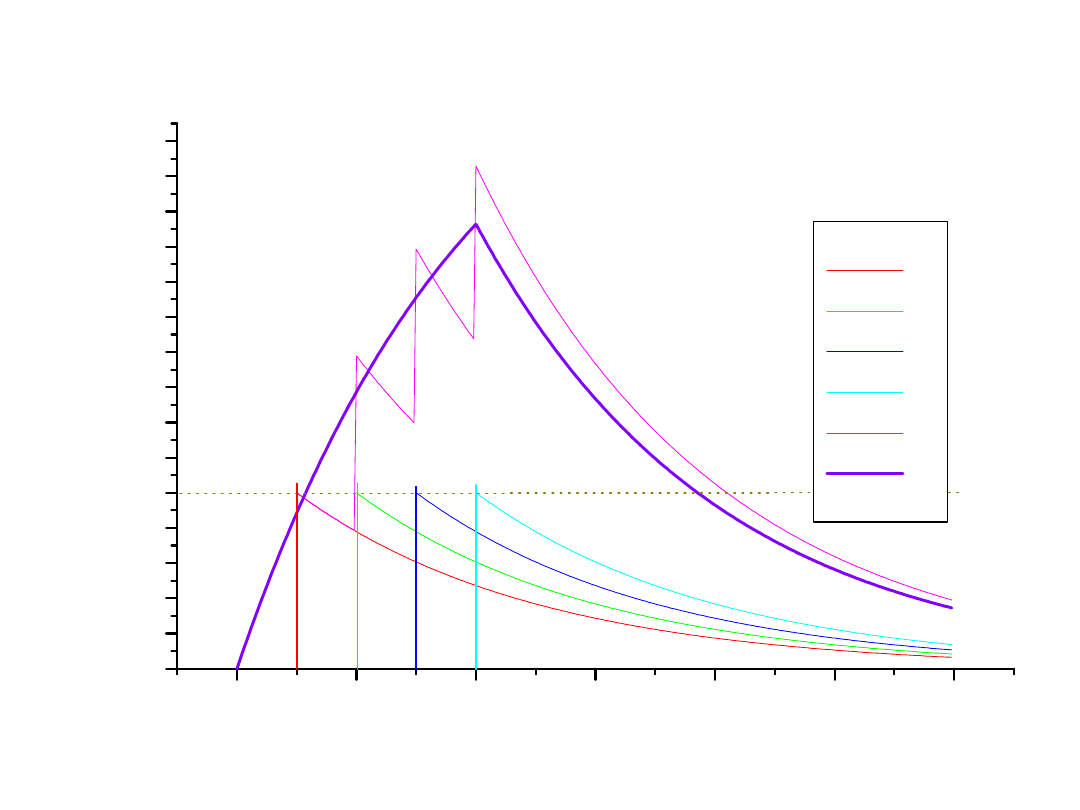
50

Zastosowanie splotu do sieci

liniowych

0,0

0,5

1,0

1,5

2,0

2,5

3,0

0,00

0,05

0,10

0,15

0,20

0,25

0,30

0,35

0,40

0,45

0,50

0,55

0,60

0,65

0,70

0,75

B
C
D
E
F
G

P

rz

e

bi

eg

i

n

ap

ię

ci

a

Czas - t