Autor: dr inż. Aleksander Karolczuk

1

Teoria maszyn

i części maszyn

Wały i osie

Autor: dr inż. Aleksander Karolczuk

2

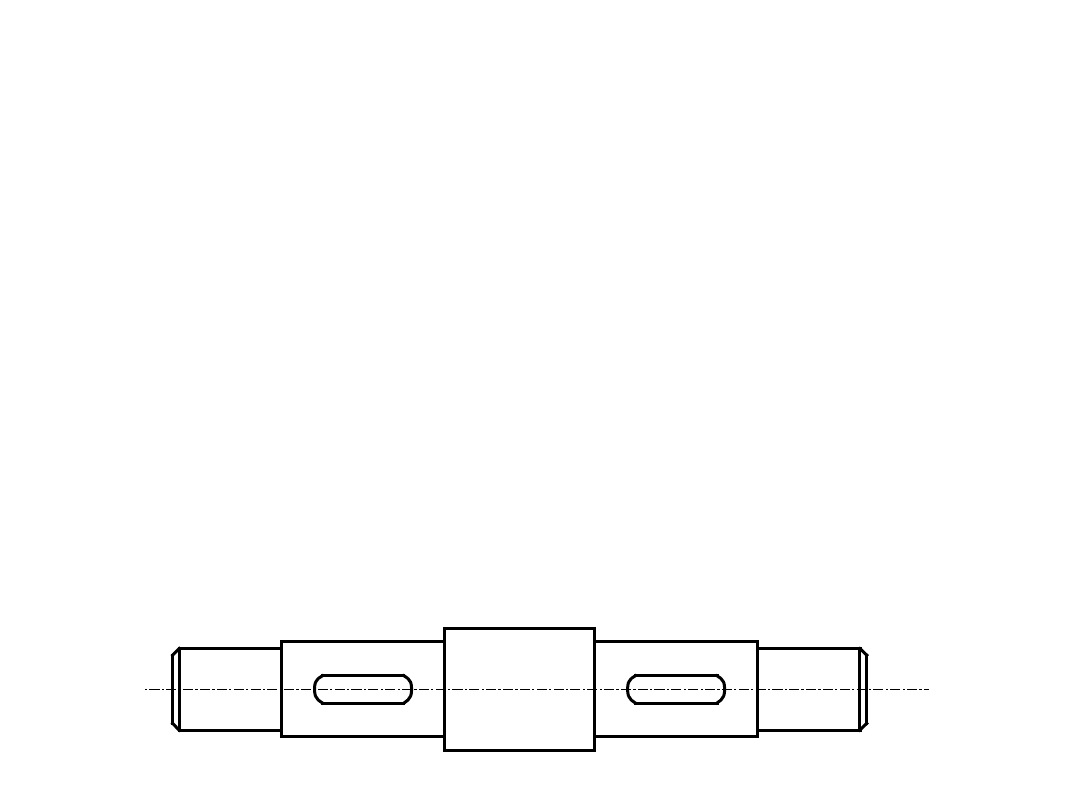
Wały i osie

• Osią lub wałem nazywamy element maszyny najczęściej

mocowany w łożyskach, na których osadzane są części
maszynowe wykonujące ruchy obrotowe lub wahadłowe.

• Wałem nazywamy część, której głównym zadaniem jest

przenoszenie momentu obrotowego. W związku z tym wał
poddawany jest skręcaniu, przy czym może jednocześnie
przenosić moment zginający oraz siły ściskające lub
rozciągające.

• Oś nie przenosi momentu obrotowego, jest obciążona

głównie momentem gnącym, służy do utrzymania w zadanym
położeniu innych elementów i przenoszenia obciążeń na
łożyska lub podpory.

• Odcinki wałów i osi służące do osadzania łożysk lub innych

elementów nazywamy czopami.

• Osie i wały mogą być gładkie lub kształtowe.

Autor: dr inż. Aleksander Karolczuk

3

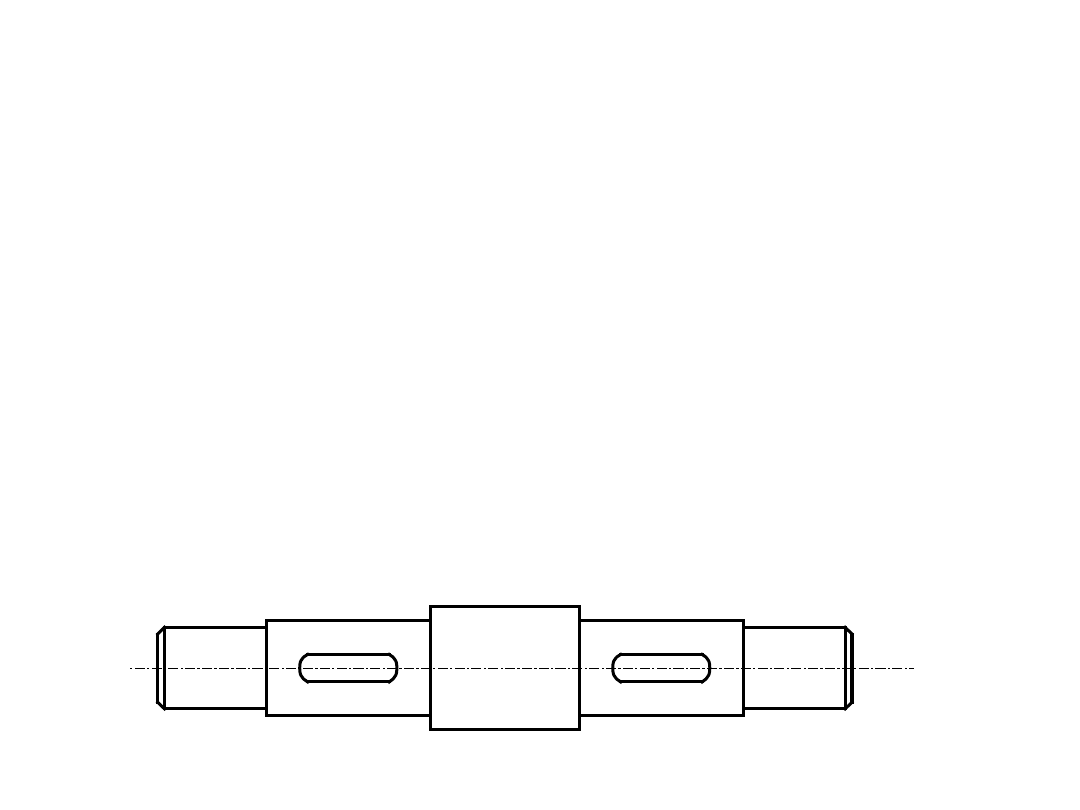
Kształtowanie wałów

• Po wyznaczeniu teoretycznego kształtu wału, wynikającego z

obliczeń wytrzymałościowych, należy określić rzeczywisty
kształt wału, uwzględniający zadania poszczególnych
powierzchni. Kształt ten powinien spełnić cztery wymagania:
1) powinien być jak najprostszy technologicznie,
2) musi zapewniać wymaganą wytrzymałość wału,
3) zróżnicowane powierzchnie muszą stworzyć dobre bazy do
ustalenia części osadzonych na wale,
4) powinien zapewniać taniość produktu.

• Wymagania te są sprzeczne
• Należy szukać optymalnego rozwiązania

Autor: dr inż. Aleksander Karolczuk

4

Kształtowanie wałów

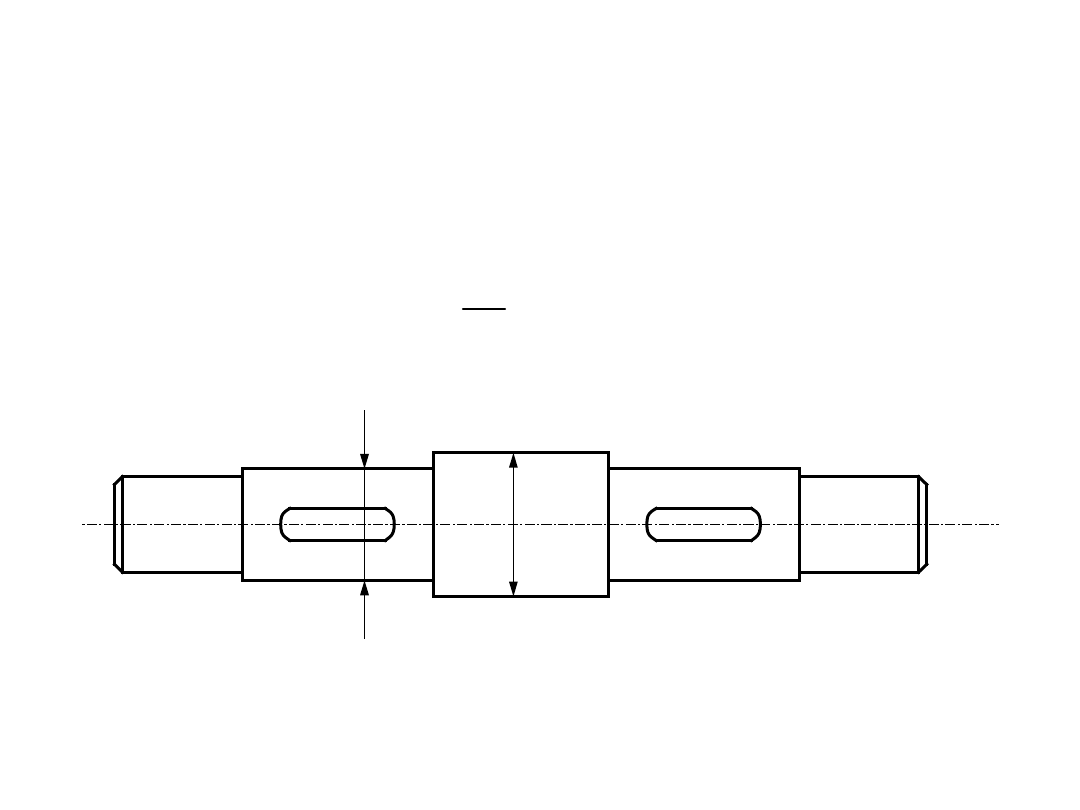
• Projektując wał, najchętniej nadajemy mu kształty składające

się z odcinków cylindrycznych. W ten sposób powstaje wał o
różnych średnicach. Każdy skok ze średnicy d na średnicę D
powoduje powstawanie karbu. Stopniowanie średnic następuje
według zasady

2

,

1



d

D

d

D

Autor: dr inż. Aleksander Karolczuk

5

Materiały stosowane na wały

• Osie i wały wykonuje się najczęściej ze stali:

1) konstrukcyjnej węglowej zwykłej jakości (St3, St4, St5), gdy
elementy są mało obciążone
2) konstrukcyjnej węglowej wyższej jakości (25, 35, 45)
3) konstrukcyjnej stopowej do ulepszania cieplnego, najczęściej
chromoniklowej, gdy wymagana jest mała średnica wału
4) konstrukcyjnej stopowej do nawęglania lub azotowania gdy
zależy nam na twardości powierzchni
5) konstrukcyjne stopowe o szczególnych własnościach, gdy
wymagane są szczególne cechy, jak żaroodporność,
nierdzewność, kwasoodporność itp.

Autor: dr inż. Aleksander Karolczuk

6

Uproszczone obliczenia wałów i osi

• Osie przenoszą głównie obciążenie zginające

)

,

(lub

32

3

g

go

go

g

x

g

g

k

k

k

d

M

W

M











gdzie M

g

- moment gnący w rozpatrywanym przekroju, W

x

– wskaźnik

wytrzymałości na zginanie, d – średnica osi (wału)

3

32

go

g

k

M

d





Średnicę osi (wału) określa wzór

Obliczoną wartość należy zwiększyć o ewentualny wymiar
głębokości rowka na wpust.

Autor: dr inż. Aleksander Karolczuk

7

Uproszczone obliczenia wałów i osi

• W niektórych przypadkach oś opieramy na podporach o małych

powierzchniach. W takim przypadku należy sprawdzić warunek
wytrzymałości na naciski powierzchniowe między czopem wału
a podporą według wzoru

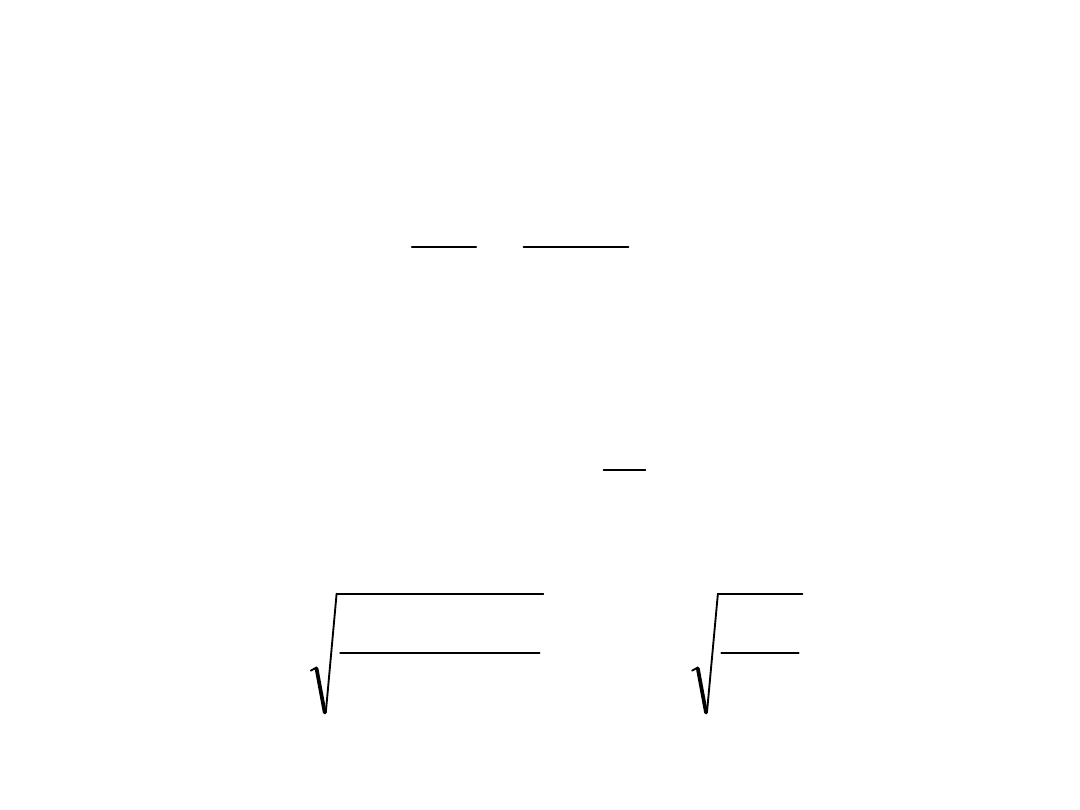
dop

p

dg

P

p





gdzie P – siła, g – grubość podpory, d –średnica czopa,
p

dop

– dopuszczalne naciski dla materiału czopa i dla materiału

podpory.

Autor: dr inż. Aleksander Karolczuk

8

Uproszczone obliczenia wałów i osi

• Długie wały wielopodporowe są jednocześnie zginane i

skręcane. Uproszczone (wstępne) obliczenia wałów polega
sprawdzeniu warunku na skręcanie

Jeśli obliczany odcinek wału przenosi moc N kW przy prędkości
obrotowej n obr/min, to moment skręcający M

s

obliczymy ze

wzoru

stąd średnica wału

so

s

o

s

k

d

M

W

M







3

16





n

N

M

s

001

,

0



3

3

252

,

0

16

001

,

0

so

so

nk

N

nk

N

d







Autor: dr inż. Aleksander Karolczuk

9

Uproszczone obliczenia wałów i osi

• Dla wałów długich należy sprawdzić dodatkowo warunek na

dopuszczalne odkształcenie skrętne

• W przypadku gdy decyduje dopuszczalny kat skręcenia (dla

małych średnic), nie warto stosować stali o dużej wytrzymałości

• Przy dużych średnicach należy stosować materiały o dużej

wytrzymałości

• Podpory należy rozmieszczać tak, aby koła pasowe, zębate lub

inne częsci zginające wał znajdowały się możliwie blisko podpór

dop

o

s

GJ

l

M









gdzie l – długość skręcanego wału, G – moduł sprężystości postaciowej
(dla stali G = 81 000 MPa), J

o

– biegunowy moment bezwładności

przekroju wału, 

dop

– dopuszczalny kąt skręcenia

32

4

d

J

o





Autor: dr inż. Aleksander Karolczuk

10

Obliczanie wytrzymałościowe wału

dwupodporowego

• Wały dwupodporowe obliczamy na zginanie i skręcanie. W

dowolnym przekroju wału panuje naprężenie normalne
wywołane zginaniem

oraz styczne wywołane skręcaniem

x

g

g

W

M





o

s

s

W

M





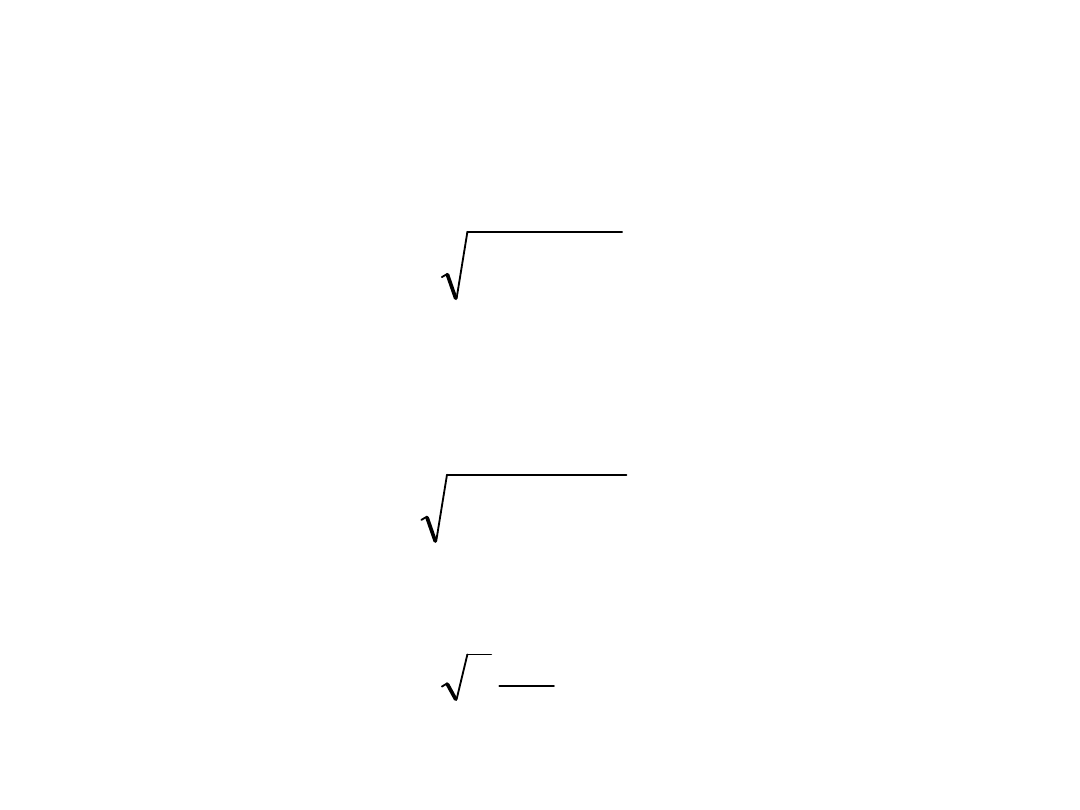
Autor: dr inż. Aleksander Karolczuk

11

Obliczanie wytrzymałościowe wału

dwupodporowego

• Naprężenia zastępcze obliczamy według hipotezy Hubera-

Misesa-Henckyego największej energii odkształcenia
postaciowego

Naprężenia gnące w wałach są z reguły obustronnie zmienne, a
naprężenia skręcające jednostronnie zmienne. Licząc według
powyższego wzoru, otrzymamy zbyt duży zapas
bezpieczeństwa. W związku z tym przyjmujemy naprężenia
zastępcze

2

2

3

s

g

z











2

'

2

)

(

s

g

z











gdzie zredukowane naprężenie

s

sj

so

s

k

k





3

'



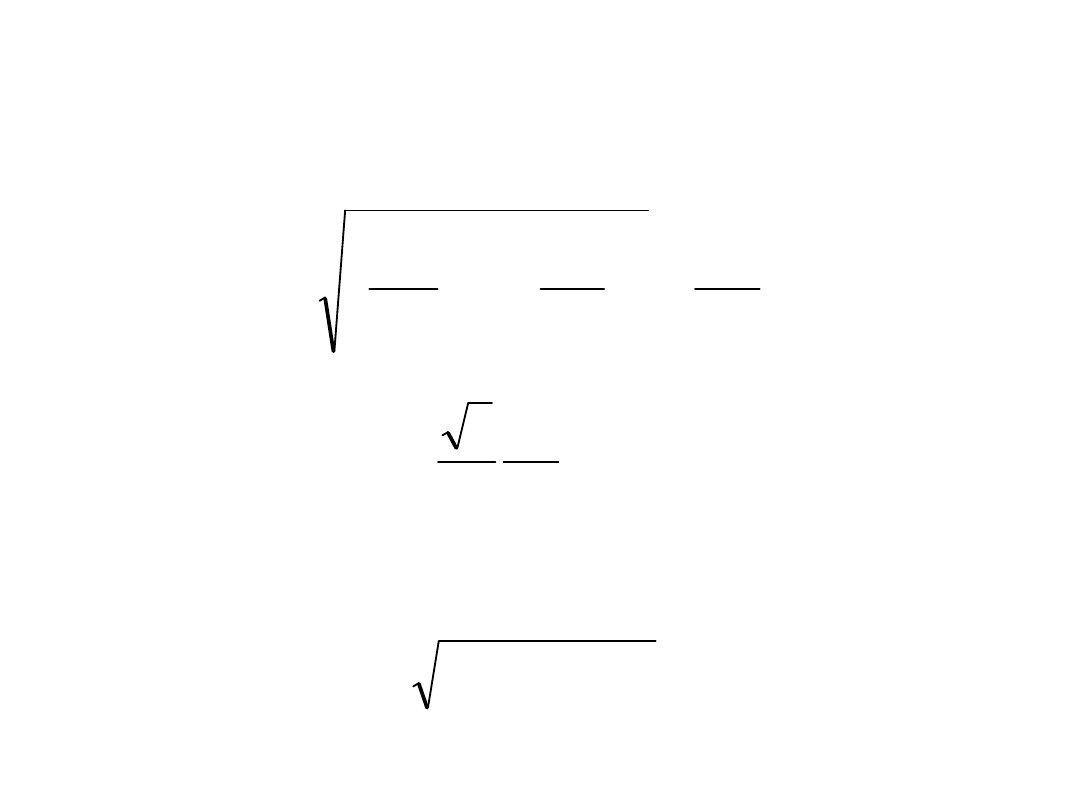
Autor: dr inż. Aleksander Karolczuk

12

Obliczanie wytrzymałościowe wału

dwupodporowego

• Przekształcając ten wzór do postaci

gdzie

możemy obliczyć moment zastępczy

s

sj

so

s

M

k

k

M

2

3

'



x

z

x

s

x

g

z

W

M

W

M

W

M































2

'

2



2

'

2

)

(

s

g

z

M

M

M





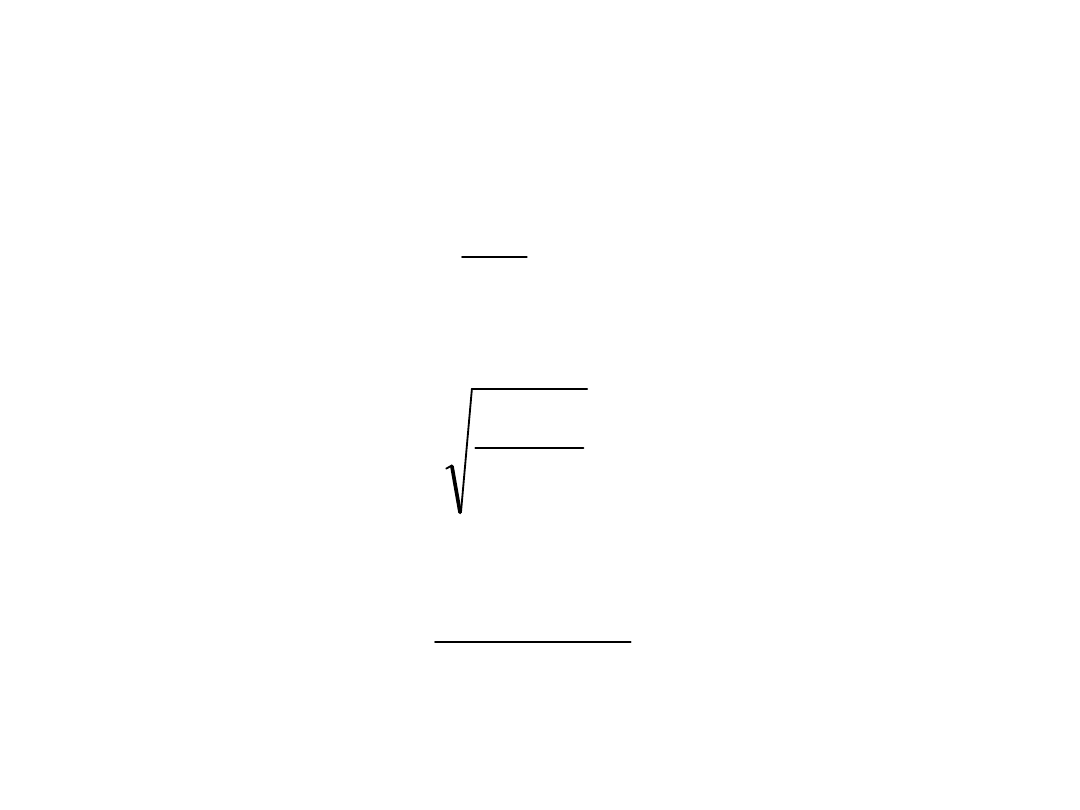
Autor: dr inż. Aleksander Karolczuk

13

Obliczanie wytrzymałościowe wału

dwupodporowego

• Warunek wytrzymałości

stąd średnica wału pełnego

Dla wału drążonego

go

x

z

z

k

W

M







3

32

go

z

k

M

d





d

d

d

W

o

x

32

)

(

4

4







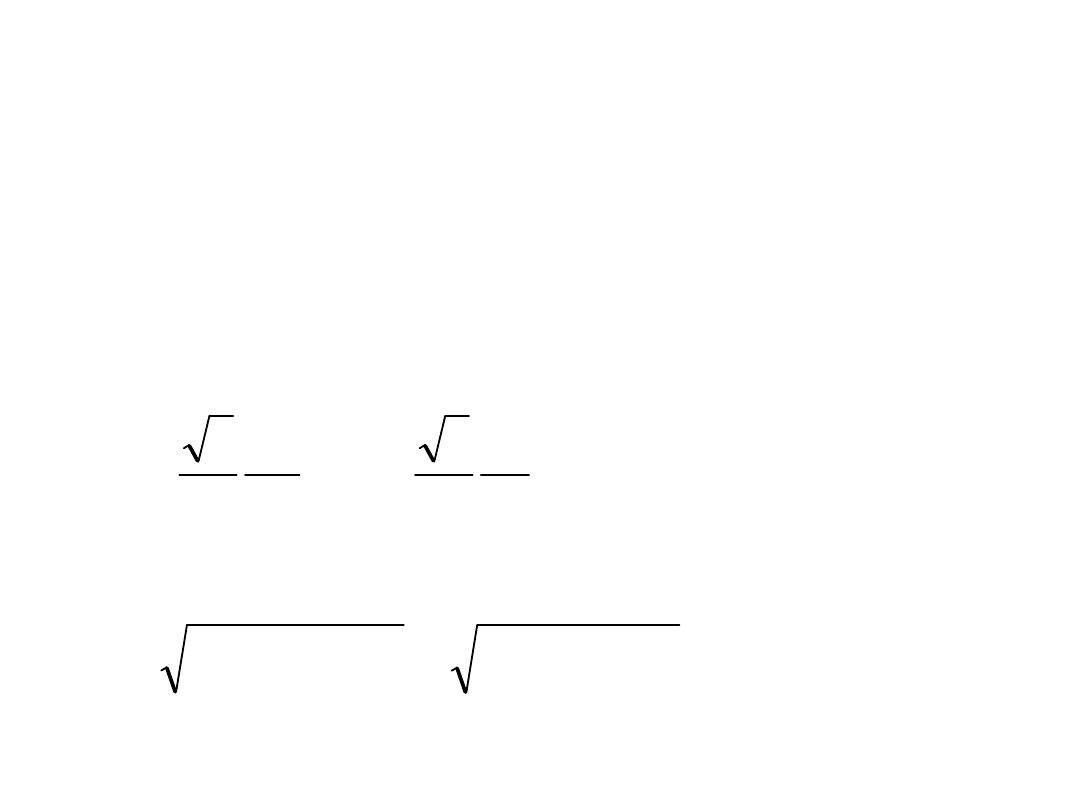
Autor: dr inż. Aleksander Karolczuk

14

Przykłady

• Zadanie 1

W pewnym przekroju wał jest obciążony momentem
zginającym
M

g

= 20Nm oraz momentem skręcającym M

s

= 10Nm.

Wyznaczyć moment zastępczy M

z

, minimalną średnicę

przekroju d.
Przyjąć k

so

= 45MPa, k

sj

= 85MPa , k

go

= 80MPa

Nm

M

k

k

M

s

sj

so

s

58

,

4

10

85

45

2

3

2

3

'







Nm

M

M

M

s

g

z

52

,

20

58

,

4

20

)

(

2

2

2

'

2











Zredukowany moment skręcający:

Moment zastępczy:

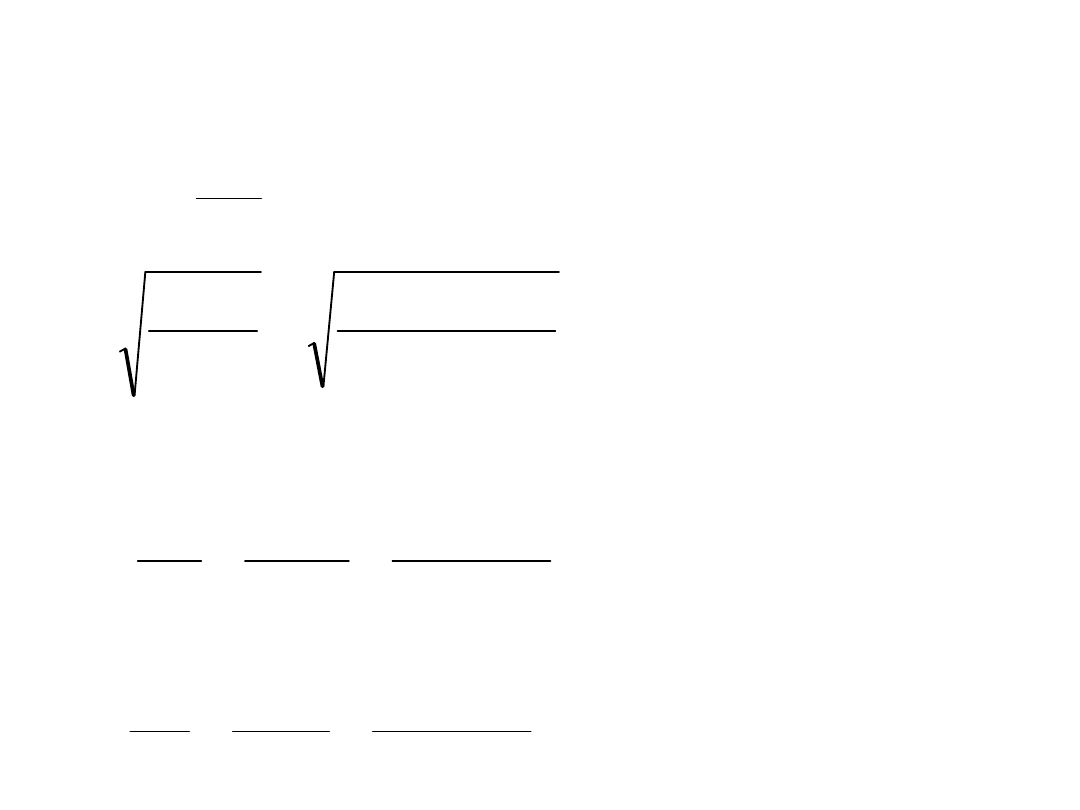
Autor: dr inż. Aleksander Karolczuk

15

Przykłady

Naprężenia zastępcze

Przyjmujemy d = 14mm
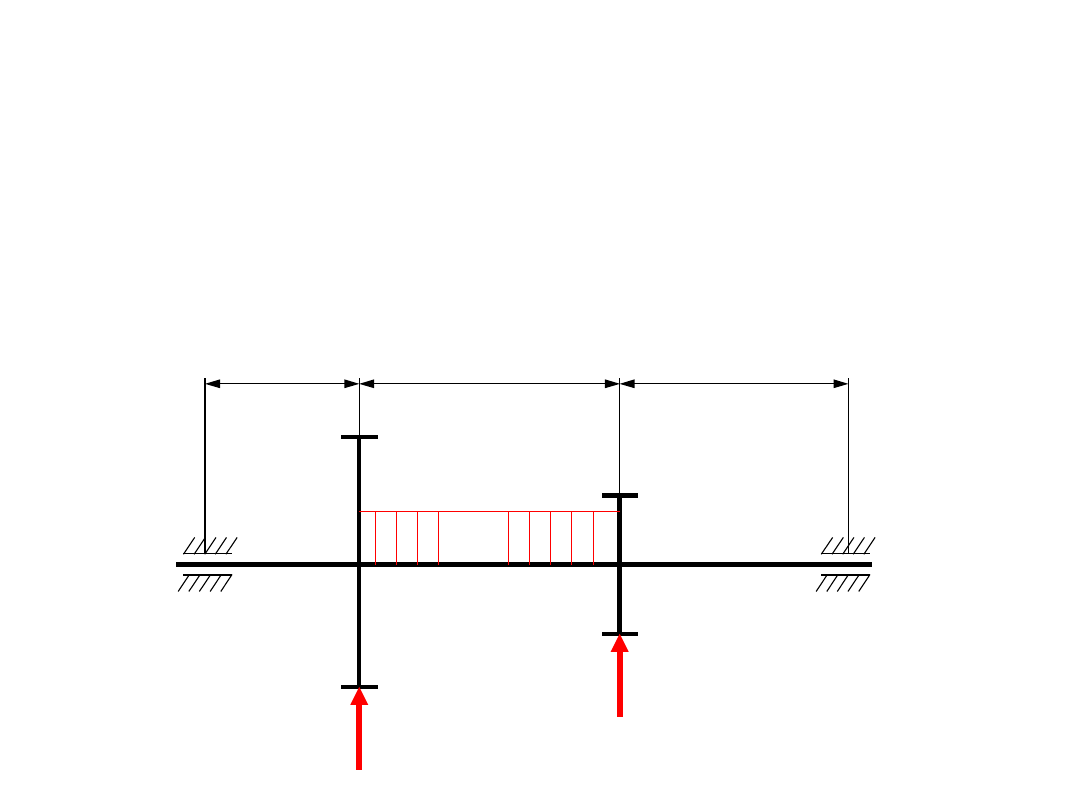
Naprężenia od zginania

Naprężenia od skręcania

go

x

z

z

k

W

M







mm

m

k

M

d

go

z

77

,

13

01377

,

0

10

80

14

,

3

52

,

20

32

32

3

6

3

















MPa

k

MPa

d

M

W

M

go

g

x

g

g

80

2

,

74

014

,

0

20

32

32

3

3

























MPa

k

MPa

d

M

W

M

sj

s

o

s

s

85

56

,

18

014

,

0

10

16

16

3

3

























Autor: dr inż. Aleksander Karolczuk

16

Przykłady

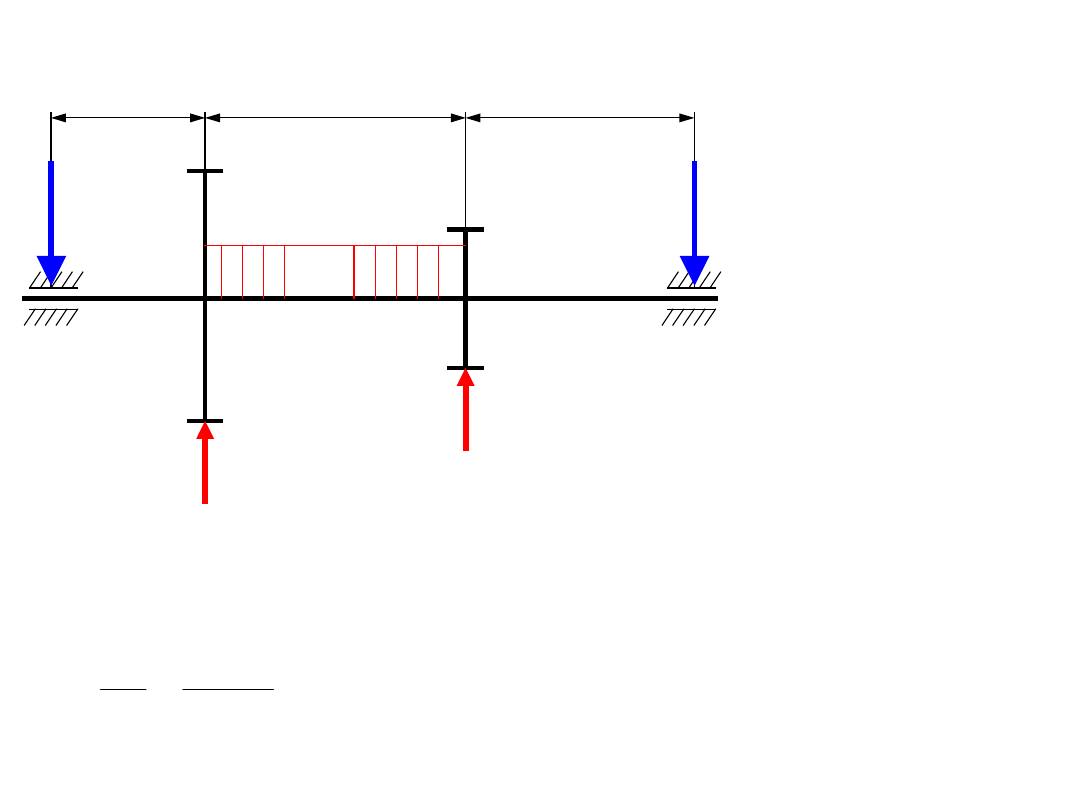
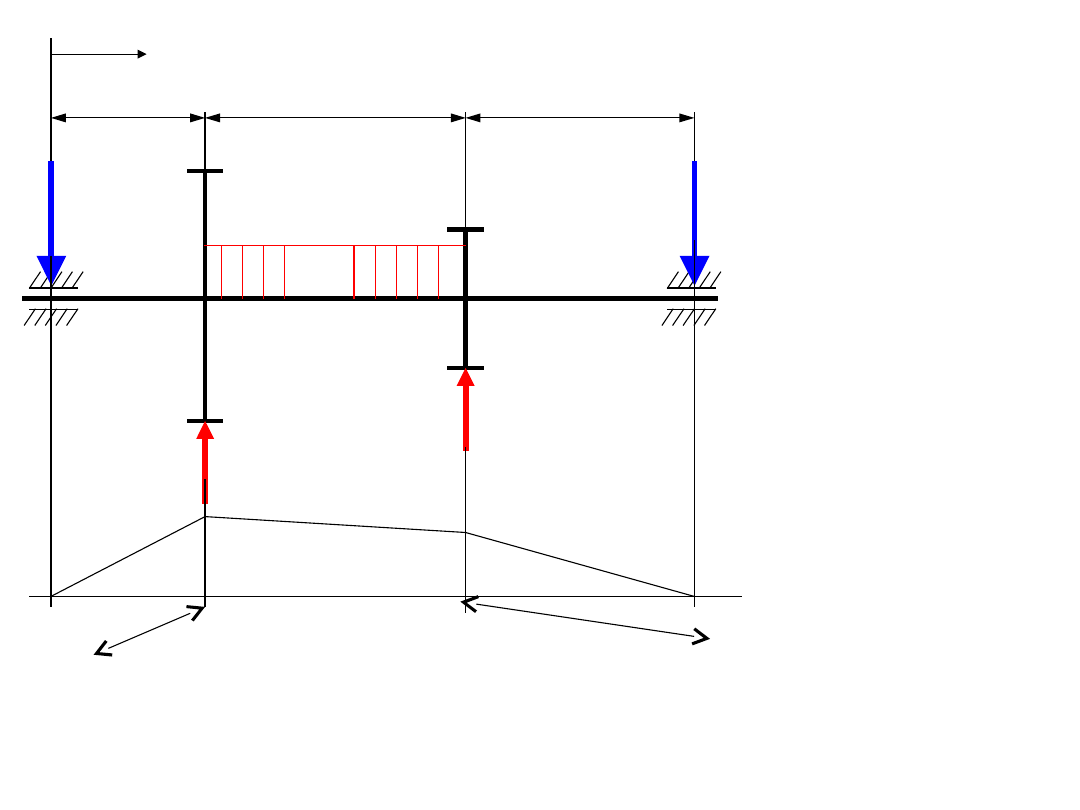
• Zadanie 2

Dla wału obciążonego jak na rysunku wyznaczyć wartości sił w
podporach (reakcję), narysować wykres momentów gnących
oraz zastępczych. Obliczyć średnicę wału w przekroju
najbardziej obciążonym. Materiał na wał: stal 45, k

sj

=80 MPa,

k

so

= 40 MPa,

k

go

= 75 MPa. Dane P = 200N, Ms = 20Nm, L = 0,2 m

L

L

L

2P

P

Ms

Autor: dr inż. Aleksander Karolczuk

17

Przykłady

N

P

R

L

R

L

P

L

P

M

b

b

Ai

7

,

266

3

200

4

3

4

0

3

2

2

0























L

L

L

2P

P

Ms

R

a

R

b

A

B

N

R

P

R

R

R

P

P

P

b

a

a

b

xi

3

,

333

7

,

266

200

3

3

0

2

0

























Autor: dr inż. Aleksander Karolczuk

18

Przykłady

Nm

L

R

L

x

M

a

g

7

,

66

2

,

0

3

,

333

)

(













L

L

L

2P

P

Ms

R

a

R

b

A

B

x

M

g

Nm

L

R

L

x

M

b

g

34

,

53

2

,

0

7

,

266

)

3

(















Autor: dr inż. Aleksander Karolczuk

19

Przykłady

Nm

M

k

k

M

s

sj

so

s

66

,

8

20

80

40

2

3

2

3

'







Nm

L

x

M

g

7

,

66

)

(





Maksymalny moment zastępczy

Zastępczy moment skręcający

Maksymalny moment zginający

Nm

M

M

M

s

g

z

3

,

67

66

,

8

7

,

66

)

(

2

2

2

'

2











mm

m

k

M

d

go

z

9

,

20

02091

,

0

10

75

14

,

3

3

,

67

32

32

3

6

3

















Przyjmujemy d = 24mm