NEWTONS METHOD
Roots of a Nonlinear Equation
is perhaps the best known method for finding successively
better approximations to the zeros (or
) of a
-valued
NEWTONS METHOD
Roots of a Nonlinear Equation
is perhaps the best known method for finding successively
better approximations to the zeros (or
) of a
-valued
INTRO
a teeny weeny bit of numerical analysis
“Never in the history of mankind
has it been possible to produce so
many wrong answers so quickly!”
Carl-Erik Fröberg*
The generation and propagation of errors
The study of errors forms an important part of numerical
analysis. There are several ways in which error can be
introduced in the solution of the problem.
One of them: the round-off errors, arise because it is
impossible to represent all real numbers exactly on a finite-state
machine (which is what all practical digital computers are).
‘Small’ numbers
On a pocket calculator, if one enters ‘
0.0000000000001
’ (or the
maximum number of zeros possible), then a ‘
+
’, and then
‘
100000000000000
’ (again, the maximum number of zeros
possible), one will obtain the number 100000000000000 again,
and not 100000000000000.0000000000001. The calculator's
answer is incorrect because of roundof in the calculation.
‘Large’ numbers
What about adding
9999999
999999999999
+
888888888888
88888888888888888
?
You can’t write the exact result, it’s too large (no computer
exists).
Example of quadratic equation
ax
2
+ bx + c = 0
Some occurrences can vastly increase the round-off errors.
Generally they can be traced to the the subtraction of two very
nearly equal numbers, giving a result whose only significant bits
are those (few) low order ones in which the operands differed.
For example in the formula for the solution of a quadratic
equation. The addition becomes "round-off-prone" whenever ac
<< b
2
('a times c' is much smaller than 'b square').
ac
b
4
2
(2)
(2 )
(2)
(2)
(1)
(2)
Newton’s Method
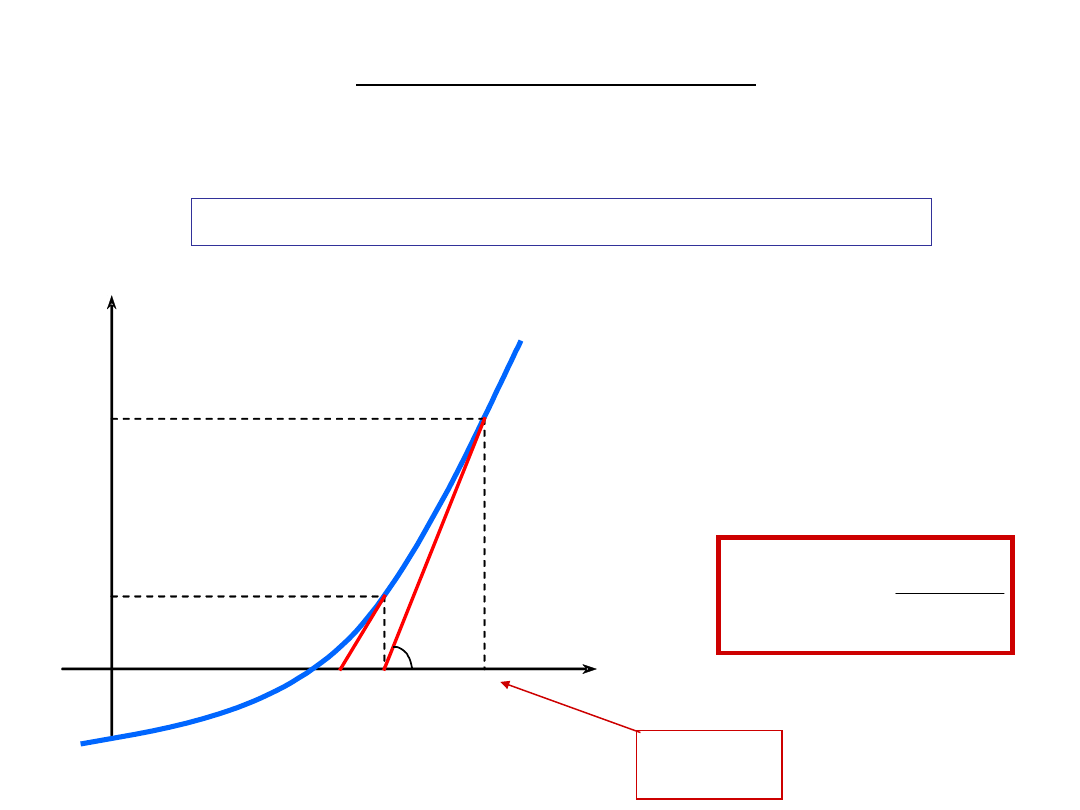
Newtons Method
)
x
f
x
f
-
= x
x
i
i
i
i
(
'
)
(
1
initial
guess
f (x)
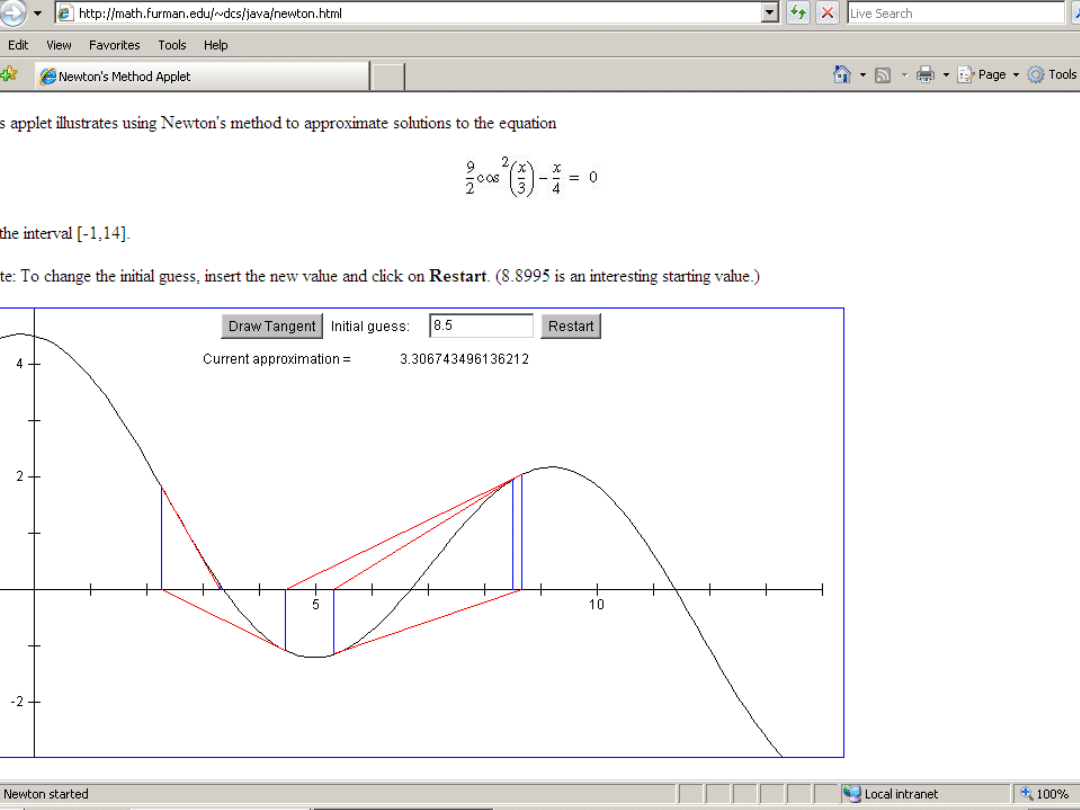
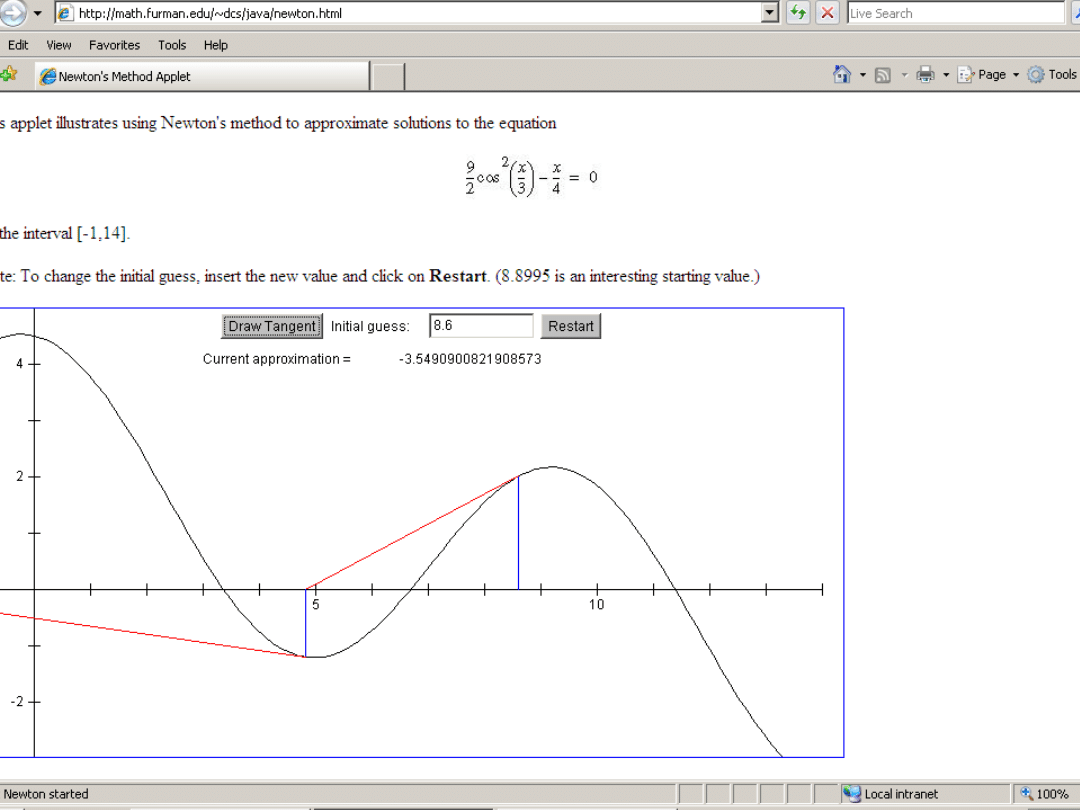
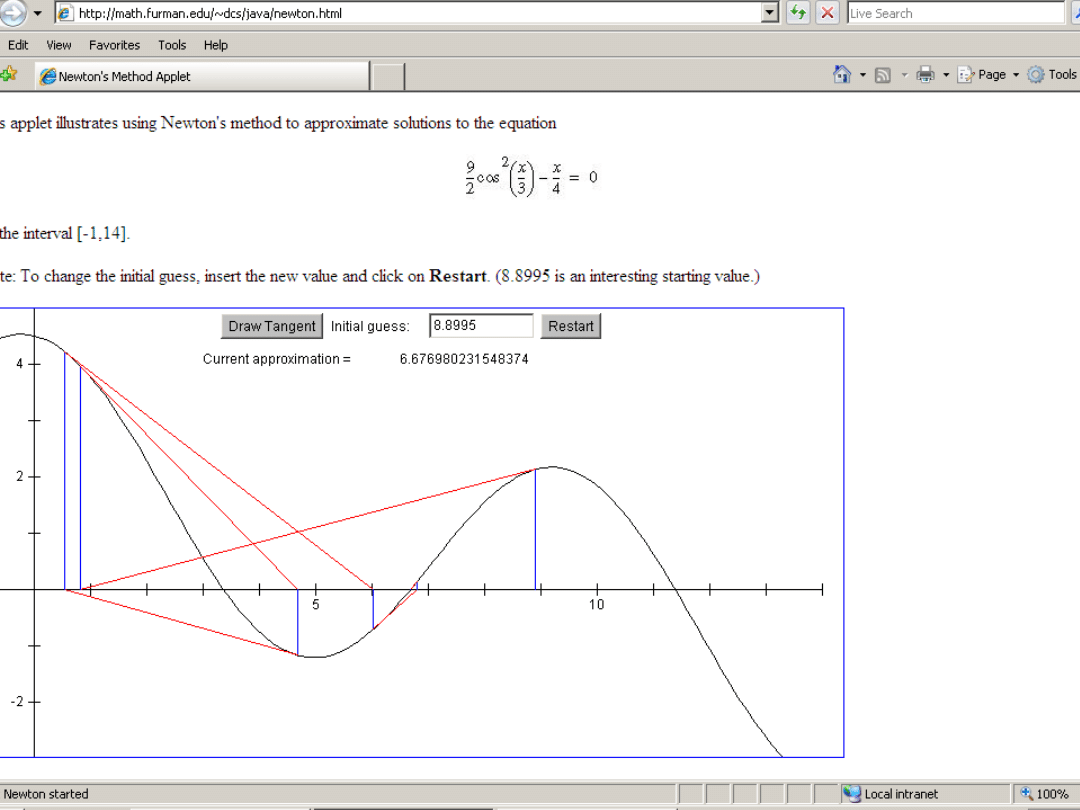
http://math.furman.edu/~dcs/java/newton.html
f (x)
f (x
i
)
f (x
i+1
)
x
i+2
x
i+1
x
i
x
is a simple iterative numerical method to
approximate roots of equations.
The sequence of
approximate roots x
0
,
x
1
, x
2
, x
3
, ... is created
by the rule:
Theorem (
Newton's method
)
Let f be a function twice differentiable in an interval [a,
b]. If the following conditions are satisfied
(1) f (a) · f (b) < 0,
(2) the function f ' does not change sign on [a, b],
(3) the function f '' does not change sign on [a, b],
then an equation f (x) = 0 has in the interval [a, b]
exactly one solution c, and for every point x
0
a < x
0
< b such that f (x
0
) · f '' (x
0
) > 0, all elements of a
sequence (x
n
) defined by a recursive formula
are in the interval [a, b] and this sequence converges to the number c.
Additionally:
if there exist real constants m, M such that
| f ' (x)| > m > 0 for every x, a < x < b and
| f '' (x)| ≤ M for every x, a < x < b then
2
1
c
x
2m
M
c
x
n
n
)
x
(
'
f
)
(x
f
x
x
n
n
n
n
1
m
)
(x
f
c
x
and
x
x
2m
M
c
x
n
n
n
n
n
2
1
and
FAMOUS BABYLONIAN METHOD
2
3
,
2
2
0
1
1
x
x
x
x
n
n
n
Let us find an approximation to to ten
decimal places.
5
Let us start this process by
taking x
1
= 2.
the results stabilise for more than ten decimal places after only 5 iterations!
In this example,
we stop when
the digits start
to repeat.
Example
5
)
(
2
x
x
f
20 correct digits
Consider the problem of finding the positive number x with
cos(x) = x
3
. We can rephrase that as finding the zero of f (x)
= cos(x) − x
3
. We have
f '(x) = −sin(x) − 3x
2
.
Since cos(x) ≤ 1 for all x and x
3
> 1 for x>1, we know that
our zero lies between 0 and 1. We try a starting value of x
0
=
0.5.
The correct digits are underlined in the above example,
illustrating the quadratic convergence.
Example
Example :
x
3
- 4x - 9 = 0 on [2, 3], 3 steps of the Newton's method.
We have:
f (x) = x
3
- 4x - 9,
f ' (x) = 3x
2
- 4 ³ 3· 4 - 4 > 0,
f '' (x) = 6x ³ 6 · 2 > 0,
f (2) · f (3) = (-9) · 6 < 0,
f (3) · f '' (3) = 6 · 18 > 0,
which means that the assumptions of the last theorem are
satisfied, and thus for x
0
= 3 the sequence
converges to the unique root of the equation in question,
which lies in the interval [2, 3]. We compute:
x
1
= 3 - (6/23) ≈ 2,7391, x
2
≈ 2,7070, x
3
≈ 2,7065.
)
(
'
)
(
1
n
n
n
n
x
f
x
f
x
x
4
3
9
4
2
3
1
n
n
n
n
n
x
x
x
x
x
Algorithm for Newton-Method
Step 1
Evaluate f
(x)
symbolically
)
(
'
)
(
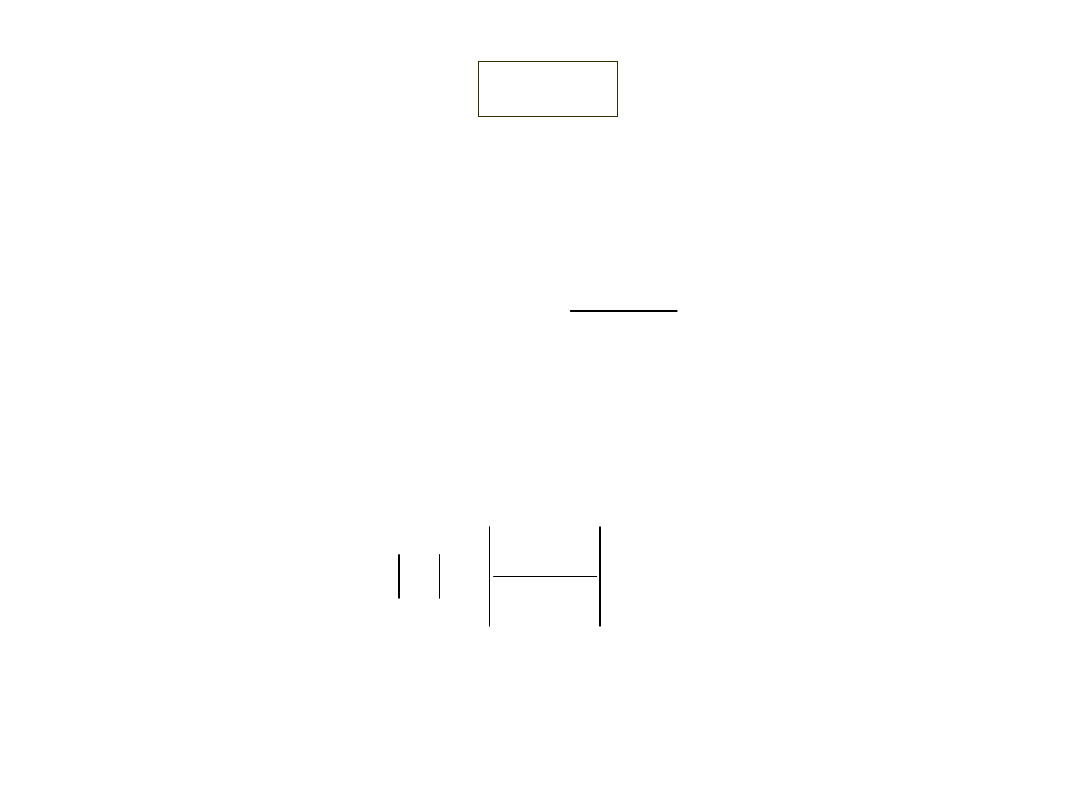
1
i
i
i
i
x
f
x
f
-
= x
x
100
1
1
x
- x
x
=
i
i
i
a
Calculate the next estimate of the root
Find the absolute relative approximate error
Step 2
Step 3
• Find if the absolute relative approximate
error is greater than the pre-specified
relative error tolerance.
• If so, go back to step 2, else stop the
algorithm.
• Also check if the number of iterations has
exceeded the maximum number of iterations
Advantages
• Converges fast (if it
converges)
• Requires only one guess
• Is simple
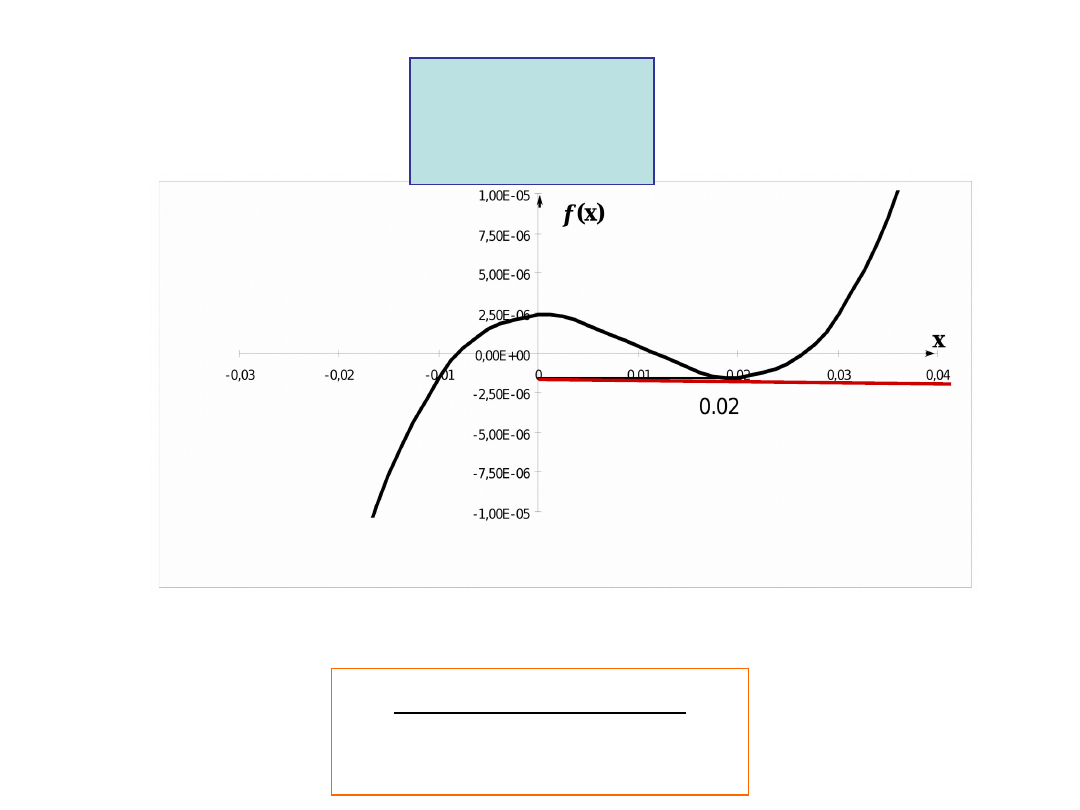
Division by zero
f(x) has a horizontal
tangent line
0
10
4
.
2
03
.
0
6
2
3
x
x
x
f
Drawbac
ks
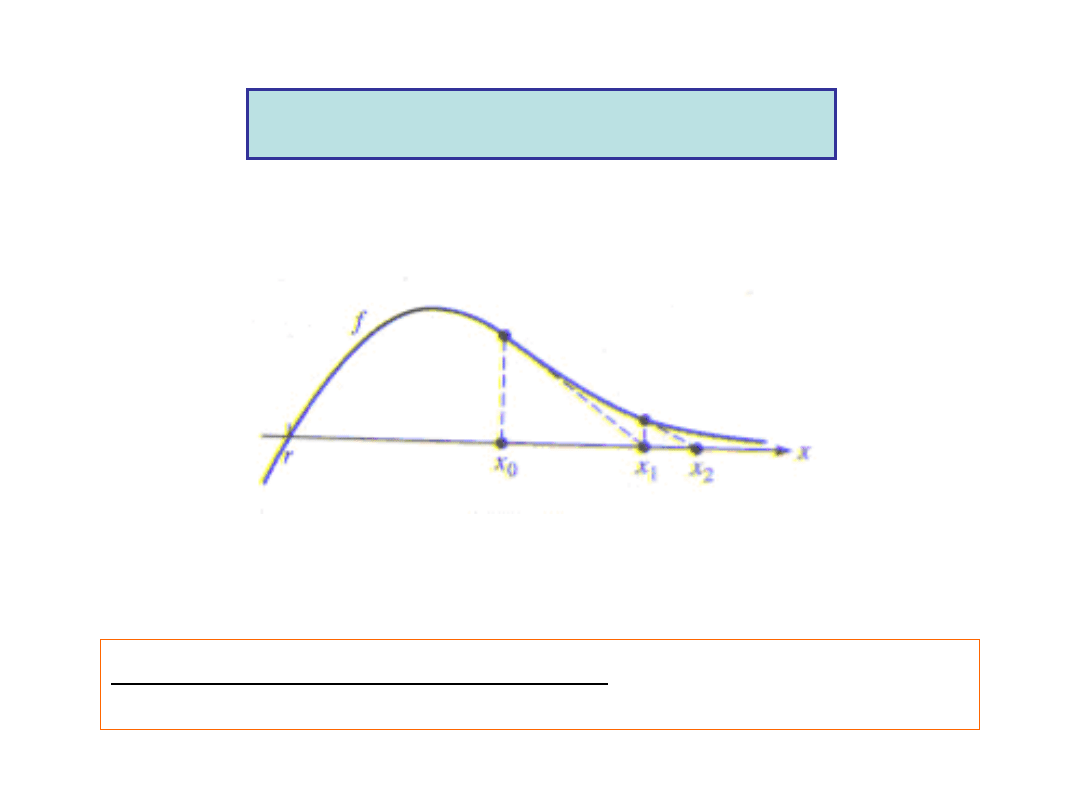
The x-values may run away.
This might occur
when the x-axis is an asymptote.
Drawbacks (continued)
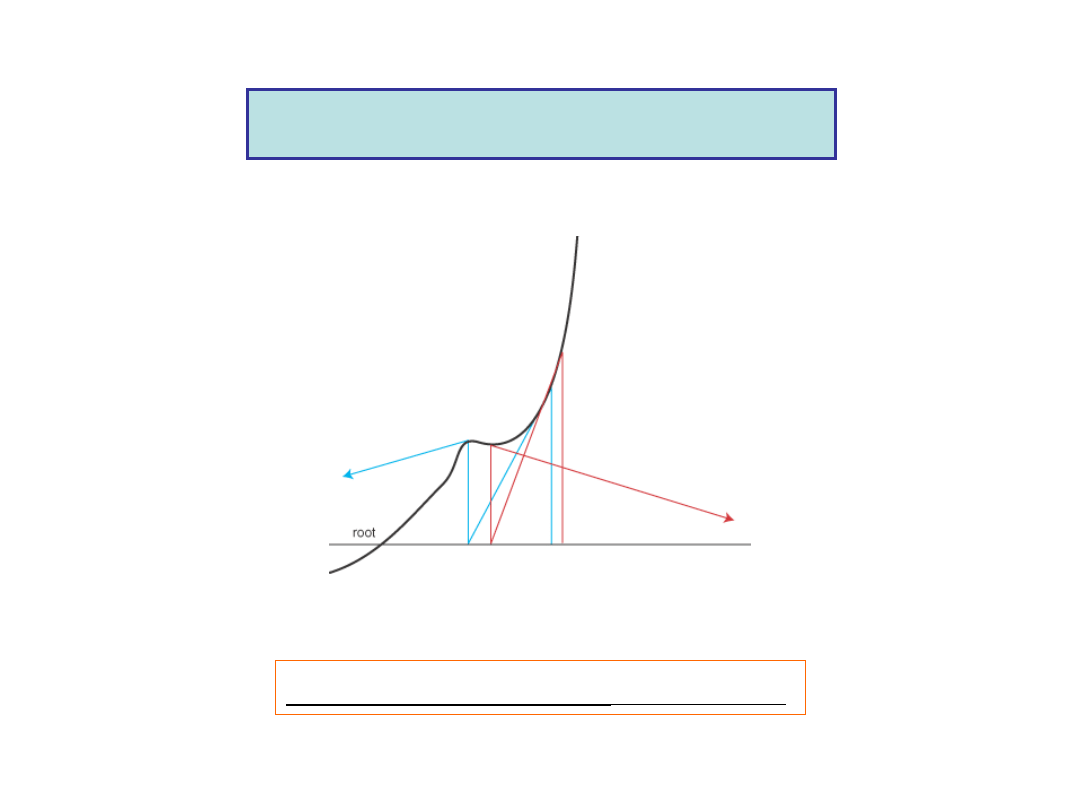
Inflection Point -
Divergence
Drawbacks (continued)
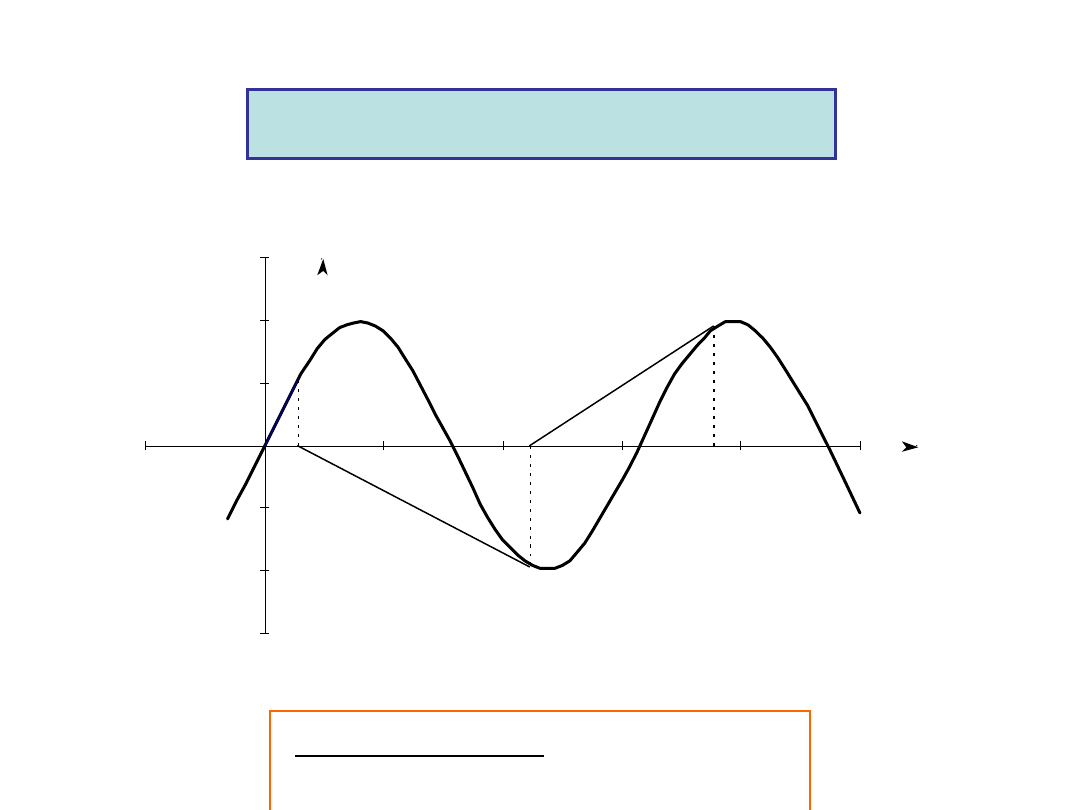
-1.5
-1
-0.5
0
0.5
1
1.5
-2
0
2
4
6
8
10
x
f(x)
-0.0630690.54990
4.462
7.53982
Root Jumping
– local extrema
in [a,b], you don’t get the root
you expect
0
sin
x
x
f
Drawbacks (continued)
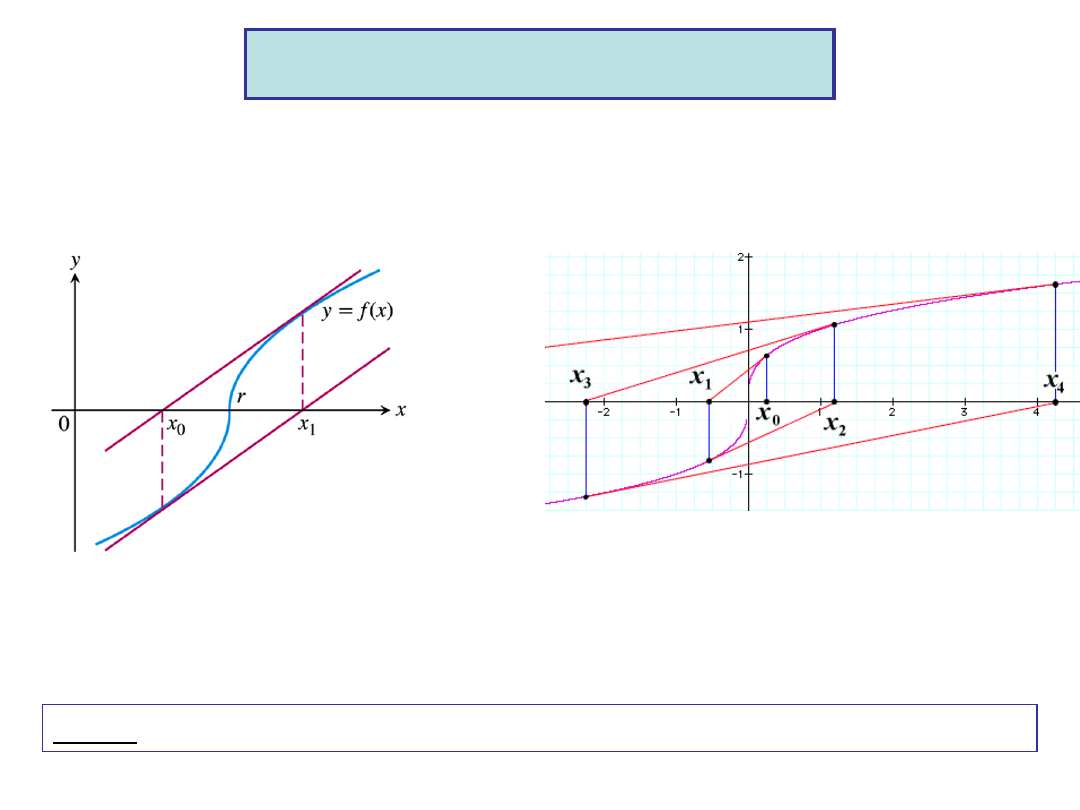
Cycle - the iteration jumps from one point to the same, forever.
Drawbacks (continued)
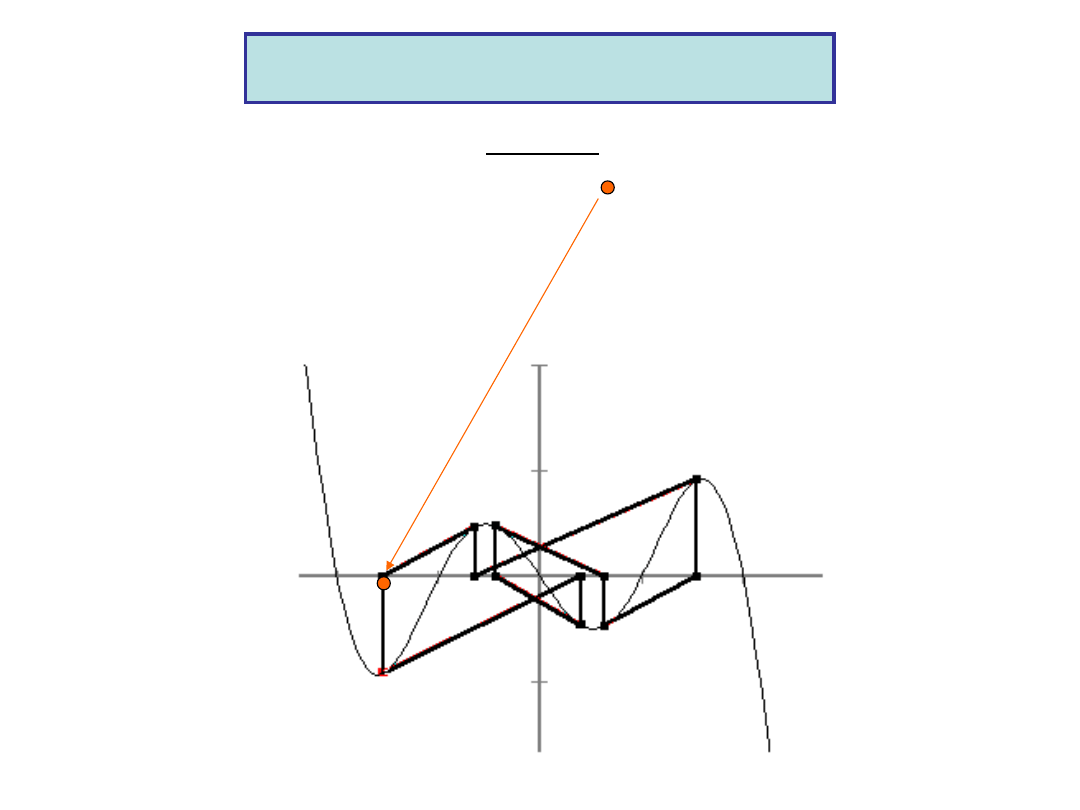
Finally, an example in which the starting value gives a point of period 6 ( below).
Drawbacks (continued)
CYCLE
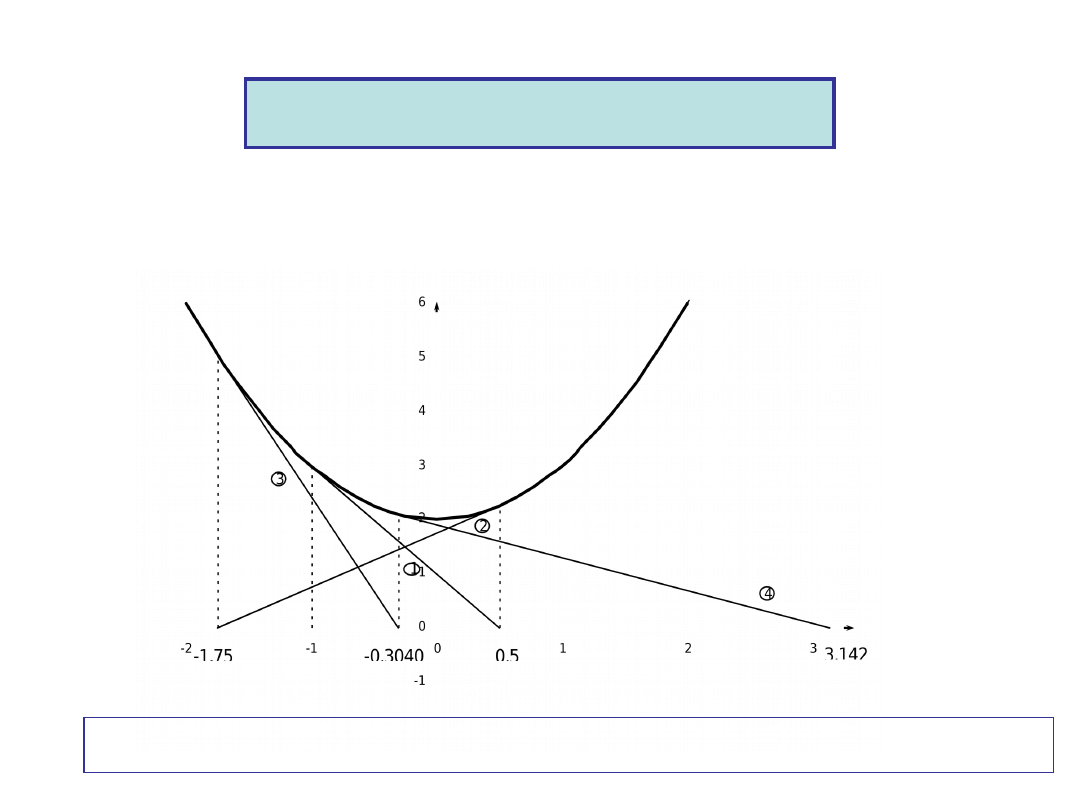
Oscillations near Local Maxima or Minima – no root
0
2
2
x
x
f
x
f(x)
Drawbacks (continued)
-20
-15
-10
-5
0
5
10
-2
-1
0
1
2
1
2
3
f(x)
x
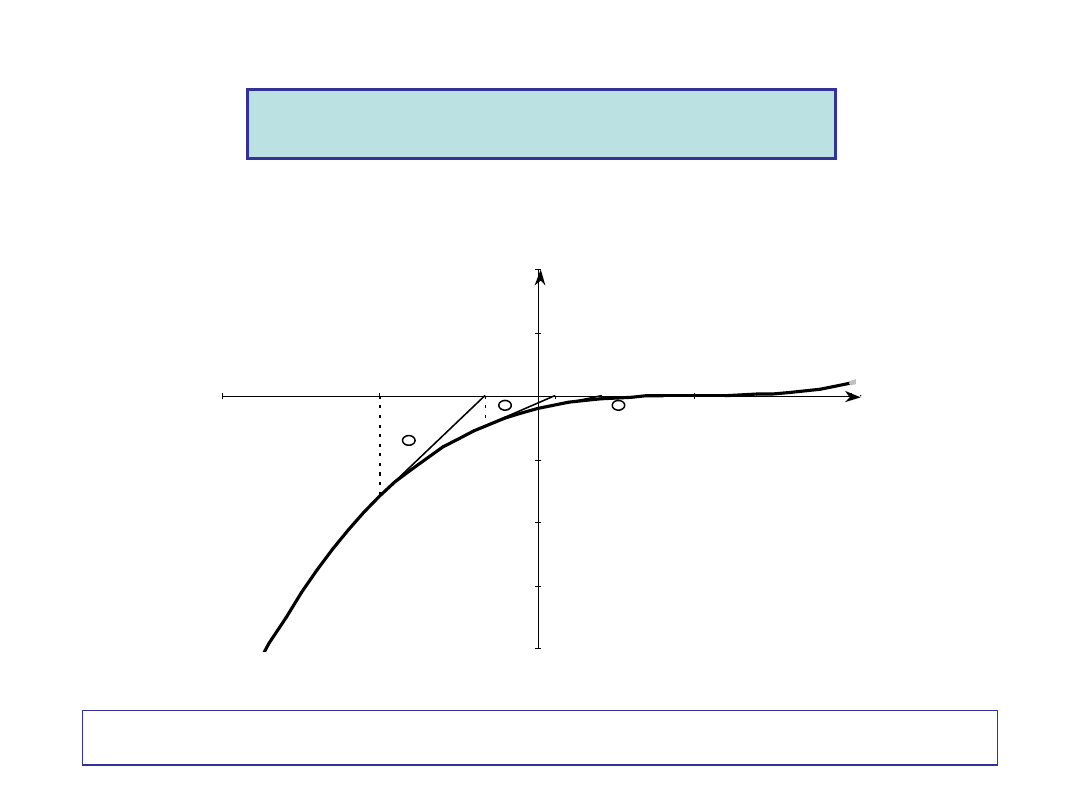
Inflection Point -
Slow convergence at inflection point
0
1
3
x
x
f
e.g.
Drawbacks (continued)
Good Newton;
http://www.math.umn.edu/~garrett/qy/Newton.html
Pathological Newton Method:
http://www.math.umn.edu/~garrett/qy/BadNewton.ht
ml
Newton Animations
http://math.fullerton.edu/mathews/a2001/Anima
tions/RootFinding/NewtonMethod/NewtonMetho
d.html
The Newton applet:
http://www.math.ucla.edu/~ronmiech/crew/euge
ne/java/Newton/Newton.html
http://www.win.tue.nl/~stephanh/toolbench/dicta
at1.html
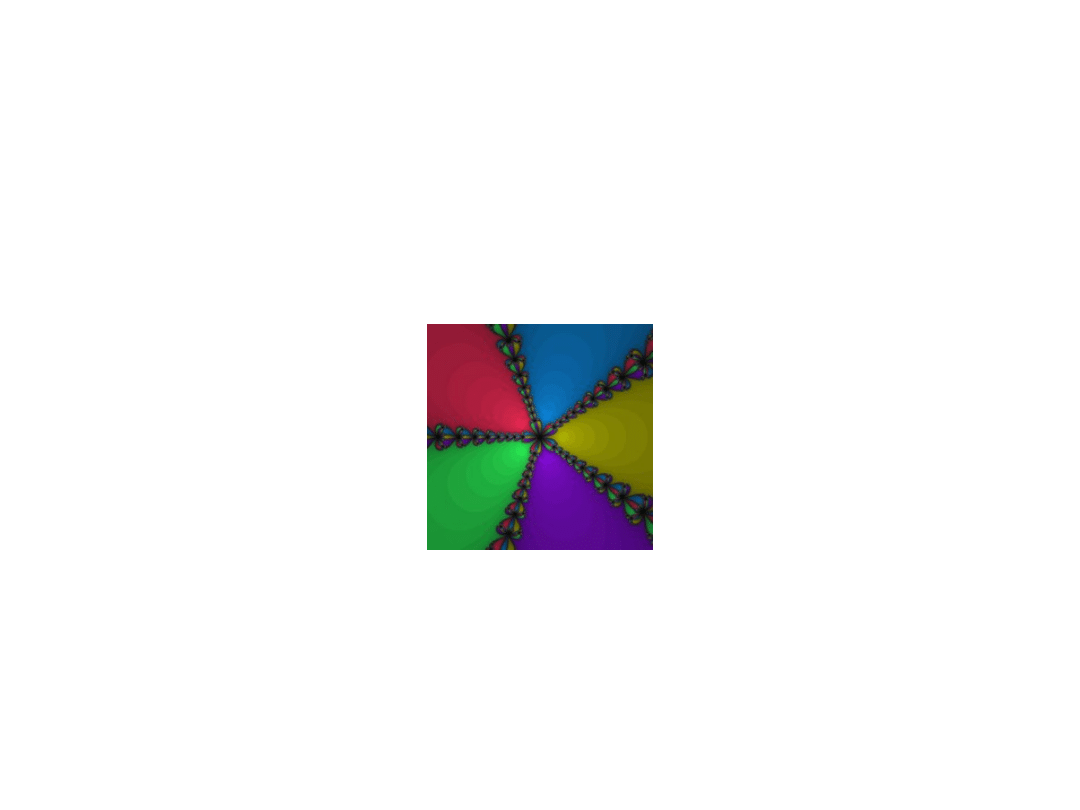
Generalisations
Newton Method for Complex Numbers
When dealing with complex functions, however, Newton's
method can be directly applied to find their zeros. For many
complex functions, the boundary of the set (also known as the
basin of attraction) of
all starting values
that cause the method
to converge to the true zero is a
fractal
Basins of attraction for x
5
− 1 = 0; darker means more iterations to converge.
Newton fractal for three degree-3 roots (p(z) = z
3
− 1),
coloured by number of iterations required
Newton fractal for x
8
+ 15x
4
− 16
“Never in the history of mankind
has it been possible to produce so
many wrong answers so quickly!”
Carl-Erik Fröberg*
J. Stewart pp 328
1. Explain why Newtons method doesn’t work for finding the root of the
equation
x
3
- 3x + 6 = 0, i the initial approximation is chosen to be x
0
= 1.
2. a) Use Newton’s method with x
0
= 1 to find the root of the equation x
3
– x = 1 correct to six decimal places.
b) Solve the equation in part a) using x
0
= 0.6 as the initial
approximation,
c) Solve the equation in part a) using x
0
= 0.57. (you definitely need a
programmable calculator for this part),
d) Graph f(x) = x
3
– x
–
1 and its tangent lines at x
0
= 1, 0.6, and 0.57 to
explain why Newton’s method is so sensitive to the value of the initial
approximation.
3. Expain why Newton’s method fails when applied to the
equation
with any initial approximation . Illustrate your explanation
with a sketch.
0
x
3
0
x
0
When Newton’s method fails – i.e. works slowly or does not work at all.
