Laboratorium z fizyki

Politechnika Łódzka

Instrukcja do ćwiczenia nr. 5

Temat: Badanie dyfrakcji światła laserowego

Przed wykonaniem ćwiczenia należy opanować następujący materiał teoretyczny:

1. Spójność światła

2. Dyfrakcja Fresnela i Fraunhofera

3. Budowa i działanie siatek dyfrakcyjnych różnego rodzaju

4. Budowa i działanie lasera

CEL ĆWICZENIA Celem ćwiczenia jest:

- zapoznanie się ze zjawiskiem dyfrakcji światła lasera

- wyznaczanie stałej siatki dyfrakcyjnej

SPÓJNOŚĆ ŚWIATŁA

Zdolność światła do interferencji da się określić przez współdziałanie dwóch wiązek promieniowania. A więc rozważmy dwie wiązki, których wektory pola elektrycznego są

które w dowolny sposób nakładają się na siebie. Wektor wypadkowego pola elektrycznego wyrazi się wzorem

(1)

Z elektrodynamiki wiemy, że w przypadku fal płaskich i monochromatycznych natężenie strumienia energii świetlnej jest proporcjonalne do

(2)

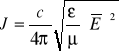
gdzie ostre nawiasy oznaczają uśrednienie rozciągnięte na przedział czasu od -T do T, długi w stosunku do okresu drgań świetlnych:

(3)

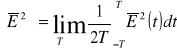
W dalszym ciągu rozważań ograniczymy się do jednego tylko ośrodka; zatem współczynnik we wzorze (2), zawierający prędkość światła c oraz przenikalność elektryczną ε i magnetooptyczną μ. ośrodka, możemy opuścić. Wówczas natężenie światła

(4)


Ze wzoru (l) otrzymujemy

(5)

czyli

6. J = J₁ + J₂ + J₁₂ ,

gdzie

(7)

oznacza wyraz mieszany, wyrażający natężenie światła wynikające z wzajemnego oddziaływania wiązek, czyli tzw. wyraz interferencyjny.

Niech rozważane fale, płaskie i monochromatyczne, rozchodzą się w kierunku osi z z wektorami
i
stale skierowanymi wzdłuż jednej z osi, np. osi x. Wówczas

(8)

(9)

gdzie: k - stała propagacji

ω - częstotliwość kołowa

(ϕ i ψ- stałe fazowe obu fal, przy czym różnica faz

(10) ϕ−ψ=δ

związana jest z różnicą dróg optycznych Δl związkiem

(11)

Prosty rachunek daje

(12)

gdyż średnia czasowa wyrazu periodycznego znika. A ponieważ

(13)

przeto

(14)

i wzór (6) przybierze postać

(15)

Jak widać z powyższego, w przypadku równości natężeń obu wiązek (I1=I2) oraz przy zgodności faz (δ = 0, 2π, 4π,...), otrzymujemy maksymalne natężenie, wynoszące J=4I, podczas gdy przy fazach przeciwnych ((δ = 0, π, 3π, ...) J=0. W tym przypadku mówimy, że obie wiązki interferują ze sobą i że są spójne.

Jeśli jednak między fazami (ϕ i ψ obu wiązek nie występuje żadna określona relacja, lecz zmieniają się one w sposób zupełnie przypadkowy i szybki w przedziale czasu potrzebnym do obserwacji czy detekcji światła, wówczas średnia czasowa będzie równa zeru, ponieważ z tym samym prawdopodobieństwem cosδ przyjmować będzie wartości dodatnie, jak i ujemne. Wtedy

(16) J=J₁+J₂

Widzimy, że wiązki nie interferują ze sobą; mówimy, że są niespójne.

Najczęściej mamy do czynienia z przypadkiem pośrednim, w którym natężenie światła w procesie interferencji zmienia się od 0 do 4J (przy równym natężeniu obu wiązek), lecz w

granicach węższych. Wówczas możemy napisać ,——

(17)

gdzie γ ≤ 1 jest miarą stopnia spójności. Jeżeli wyznaczymy największe i najmniejsze natężenie światła w zjawisku interferencji, tzn. natężenie prążków interferencyjnych, to przy jednakowych natężeniach wiązek pierwotnych mamy

(18) J_max=2J₁(1+γ)

J_min=2J₁(1−γ)

Stąd możemy obliczyć tzw. widzialność prążków interferencyjnych

(19)

która w tym przypadku (J₁ = J₂) równa się stopniowi spójności.

DYFRAKCJĄ CZYLI UGIĘCIEM ŚWIATŁA nazywamy zjawisko przejścia fali świetlnej przez szczelinę, w wyniku czego ta szczelina staje się źródłem światła. W przypadku, gdy rozmiary szczeliny są bardzo duże w porównaniu do długości fali zjawisko ugięcia jest zaniedbywane i przyjmuje się, że światło rozchodzi się po liniach prostych (optyka geometryczna), w przypadku kiedy rozmiary szczeliny są mniejsze od długości fali świetlnej uwzględnia się falową naturę światła, zjawiska opisuje się z punktu widzenia optyki falowej. Wyróżniamy dyfrakcję:

=> dyfrakcja Fresnela: wiązka rozbieżna przechodzi przez otwór uginający a wynik

jest obserwowany na ekranie ustawionym w skończonej odległości od ciała uginającego

światło

=> dyfrakcja Fraunhofera: na ciało uginające pada wiązka promieni równoległych, a

więc pochodzących ze źródła nieskończenie odległego, a efekt obserwowany jest na

nieskończenie odległym ekranie

Rys. l Uproszczony bieg promieni w przypadku dyfrakcji Fraunhofera na pojedynczej szczelinie.

Minimum pierwszego rzędu powstaje więc tam, gdzie, Γ₁₂ = ½, lub Γ₁₃ = λ. Lecz sinθ=Γ₁₃/a, a więc a sinθ=λ. Ogólny warunek dla minimów dyfrakcyjnych rzędu „m" jest:

a sinθ = ± m λ , m =1,2,3...

Metodą graficzną można otrzymać natężenie I_θ w punkcie ekranu odległym o kąt θ od osi optycznej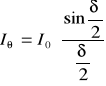
,

gdzie:

Zakładając, że maksima leżą w połowie odległości między minimami, otrzymuje się dla maksimów:

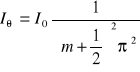
W przypadku dyfrakcji Fraunhofera na otworze kołowym otrzymujemy następujący wzór na natężenie I w funkcji odległości „x" od środka:

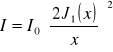
SIATKA DYFRAKCYJNA jest to zbiór równoległych do siebie szczelin przepuszczających światło, rozmieszczonych w jednakowych odstępach. W siatce dyfrakcyjnej w punkcie odpowiadającym centralnemu prążkowi jasnemu na ekranie natężenie promieniowania jest n² razy większe niż w przypadku jednej szczeliny.

ZASADA DZIAŁANIA LASERA

Chcąc rozpatrzyć zasadę pracy lasera musimy zacząć od omówienia podstawowych zjawisk, jakie mogą zajść między dwoma stanami energetycznymi Ej i Ek dowolnego atomu. Zakładamy, że Ej < Ek. Częstotliwość drgań odpowiadająca temu przejściu wynosi

(20)

Przejście atomu
odpowiada pochłonięciu energii i może nastąpić jedynie pod działaniem promieniowania zewnętrznego -jest to tzw. absorpcja promieniowania Natomiast przejście z k→i może odbywać się dwojako: samorzutnie (tzw. emisja spontaniczna) lub pod działaniem zewnętrznego promieniowania o częstotliwości ν_ki jako tzw. emisja wymuszona. Ilość każdego z tych przejść jest proporcjonalna do współczynników Einsteina: A_ki, B_ik, które nazwane są prawdopodobieństwami przejść i mają wymiar s^-1. Współczynniki te są stałe dla danego atomu i danego przejścia.

Jeżeli np. liczba wzbudzonych atomów do poziomu k - oznaczona nr maleje w czasie jedynie na skutek przejść spontanicznych, to po czasie τ

(21)

gdzie

(22)

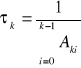
τ_k nazywa się całkowitym promienistym czasem życia k-tego poziomu. Jednocześnie Einstein ustalił pewne związki między współczynnikami A_ki, B_ik, B_ki, które pozwalają przy znajomości jednego z nich obliczyć pozostałe.

Widzimy więc stąd, że jeżeli w pewnym ośrodku rozchodzi się promieniowanie, którego rozkład widmowy pokrywa się z krzywą absorpcji danego przejścia, to uzyskamy pochłonięcie energii z jednoczesnym przejściem atomu na wyższy poziom energetyczny k. Jednocześnie, poza emisją spontaniczną, rozchodzące się promieniowanie oddziałuje na atomy znajdujące się w wyższych stanach energetycznych k, powodując emisję wymuszoną. Działają więc dwa przeciwne zjawiska. Rozważania teoretyczne tego zagadnienia doprowadziły do wzoru podanego przez Fuchtbaure-Ladenburga, wg którego współczynnik absorpcji równa się

(23)

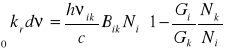
gdzie: k_r - wartość współczynnika absorpcji przy danej częstotliwości

c - prędkość światła

G_i, G_k - wagi statystyczne poziomu i i k N_k, N_i - obsadzenie poziomów: k i i

Z równania powyższego widać, że dla

(24)

wiązka promieniowania przy przejściu przez ośrodek ulegnie osłabieniu (wartość dodatnia współczynnika absorpcji). Natomiast dla przypadku

(25)

inaczej

(26)

uzyskujemy ujemne osłabienie, tzn. że wiązka przy przejściu przez ośrodek ulegnie wzmocnieniu.

Porównując te dwa przypadki ze wzorem Boltzmanna, opisującym obsadzenie poziomów energetycznych w stanie równowagi cieplnej

(27)

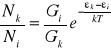
gdzie k -stała Boltzmanna, widzimy, że pierwszy z nich odpowiada normalnemu rozkładowi obsadzeń. Drugi przypadek natomiast opisuje prawo Boltzmanna jedynie w założeniu T < 0.

Stan taki nazywamy odwróceniem obsadzeń i w rzeczywistości można go otrzymać sztucznie - na drodze dostarczania do układu energii w pewien określony sposób przez tzw. pompowanie. Im większy poziom energetyczny, tym mniejsza liczba atomów wzbudzonych.

Rys.2 Schemat układu pomiarowego.

L - laser; P - wymienna przesłona (np. włos); E - ekran z fotoopornikiem.

Elementy P i E umocowane są na ławie optycznej. Do fotoopornika dołączony jest

mikroamperomierz z baterią.

gdzie Ji(x) jest funkcją Bessela pierwszego rodzaju i pierwszego rzędu.

Pierwsze minimum, odgraniczający jasny centralny krążek Airy'ego (na który pada 81% całej energii) leży w odległości kątowej 9 nieco większej niż w przypadku pojedynczej szczeliny, a mianowicie:

gdzie D - średnica otworu.

METODA POMIARU

Laser ustawiamy na ławie. Zapalamy źródło światła i tuż przed źródłem umieszczamy odpowiednią siatkę. Położenie siatki dobieramy w taki sposób, by uzyskać ostry obraz na ekranie. Należy zadbać o to, aby siatka i ekran były ustawione równolegle względem siebie. (Laser jest na stałe zamocowany tak, aby światło padało na siatkę prostopadle. Ważne!) Laser daje bardzo silnie zogniskowaną wiązkę spójnego światła i trzeba uważać aby nie wpadła ona wprost do oka. Duże natężenie światła pozwala obserwować wyraźny obraz na ekranie, umieszczony w znacznej odległości od siatki. Światło padające na siatkę doznaje ugięcia na szczelinach. Zauważamy, oprócz promienia biegnącego na wprost, pojawienie się dodatkowych wiązek skierowanych symetrycznie po obu stronach, a leżące w płaszczyźnie prostopadłej do szczelin siatki. Są to maksima promieni ugiętych. Na ekranie uzyskujemy duże rozsunięcie prążków, a ich odległość można zmierzyć śrubą mikrometryczną (mierzymy położenie prążka zerowego względem prążka pierwszego rzędu). Pomiary przeprowadzamy zarówno dla prążków leżących z lewej jak i z prawej strony prążka centralnego. Wykonujemy trzy pomiary, a wyniki doświadczenia zapisujemy w tabeli.

KOLEJNOŚĆ CZYNNOŚCI

1. Należy zmontować układ pomiarowy tak jak na rys.2.

2. Wykonać pomiary dla:

- szczeliny pojedynczej

- szczeliny kołowej

- szczeliny kwadratowej

- szczeliny Fresnela

- siatki dyfrakcyjnej

- włosa

3. Przy użyciu fotoopomika przesuwanego śrubą mikrometryczną, np. co l mm należy wykonać pomiar natężenia fotoprądu w funkcji odległości od osi optycznej w przypadku trzech pierwszych i dwu ostatnich eksperymentów. Odległość szczeliny i siatki dyfrakcyjnej od ekranu - około l m. Odległość przezroczy od ekranu - około 60 cm. Soczewka powinna być umieszczona blisko przesłony - sprawdzić wpływ usunięcia soczewki z układu.

4. Wyniki umieścić w tabelce.

Rodzaj szczeliny	Odległość (x) [mm]	Natężenie fotoprądu ruAi
Pojedyncza
Kołowa
Kwadratowa
Fresnela
Siatka dyfrakcyjna
Włos

5. Narysować wykresy do otrzymanych wyników.

6. Obliczyć stałą siatki dyfrakcyjnej wiedząc, że X, = 632,8 * l0⁻⁹ m.

7. Obliczyć błędy pomiarów.

8. Podać uwagi i wnioski

OPRACOWANIE SPRA WOZDANIA

Sprawozdanie powinno zawierać:

1. Krótki opis zastosowanej metody badania dyfrakcji światłą lasera.

2. Tabele zawierającą wartości wyników pomiarów.

3. Wykresy zależności natężeń prądu od odległości plamki od osi optycznej dla wszystkich badanych szczelin i dla włosa.

4. Obliczenie stałej siatki dyfrakcyjnej

5. Obliczenie błędu pomiaru metodą logarytmiczną

6. Wynik końcowy zapisać w postaci

D=D_obl ±ΔD

7. Dyskusję przebiegu ćwiczenia i błędów popełnionych przy pomiarach.

Literatura

1. J.R. Meyer - Arendt - Wstęp do optyki, PWN, warszawa 1977

2. A.H. Piekara - Nowe oblicze optyki (wyd II), PWN, warszawa 1976

3. F. Kaczmarek - Wstęp do fizyki laserów, PWN,Warszawa 1978

4. D. Halliday, R. Resnick - Fizyka, t. 2 (wyd.II), PWN, Warszawa 1972

5. Sz. Szczeniowski- Fizyka doświadczalna, cz. IV - Optyka (wyd. IV), PWN, Warszawa 1971

Ćwiczenie przygotował

dr Sylwester Kania

---