INTERFERENCJA ŚWIATŁA
Interferencja fal nazywamy zjawisko nakładania się fal, w których zachodzi stabilne w czasie ich wzajemne wzmocnienie w jednych punktach przestrzeni, oraz osłabienie w innych, w zależności od stosunków fazowych fal. Interferować mogą tylko fale spójne, dla których odpowiadające im drgania zachodzą wzdłuż tego samego lub podobnych kierunków.
Jeżeli założymy, że dwa punktowe źródła emitują dwie fale sinusoidalne o amplitudach A1 i A2, częstościach kołowych 1 i 2 i fazach 1(t) i ( to wypadkowa fala będzie opisana równaniem
![]()
W powyższym równaniu zaniedbano część zawierające współrzędne przestrzenne. (Dlaczego można tak zrobić?)
Jeżeli fale są niespójne to
i natężenie fali wypadkowej jest równe sumie natężeń fal składowych. Podczas nakładania się fal spójnych amplituda fali wypadkowej zmienia się od
do
w zależności od wartości trzeciego członu w równaniu (1). W najprostszym przypadku, aby zaszła interferencja muszą być spełnione następujące warunki
1=2 oraz 1(t)-2(t)=const
Podczas nakładania się światła pochodzącego z dwóch źródeł nie będących laserami lub nawet pochodzących z różnych miejsc tego samego źródła nie obserwujemy interferencji. Jest to spowodowane przez emisję światła przez wzbudzone atomy w postaci skończonych ciągów falowych, których fazy początkowe zmieniają się niezależnie. Dwie fale nazywamy falami spójnymi jeżeli różnica ich faz nie zależy od czasu. Spójne fale świetlne ze zwykłych (nie laserowych) źródeł otrzymujemy metodą dzielenia światła pochodzącego z jednego źródła na dwie lub więcej wiązek. Promieniowanie w każdej z nich pochodzi od tych samych atomów źródła i ze względu na wspólne pochodzenie, wiązki te są spójne. Do podziału światła na wiązki spójne można wykorzystać zjawiska odbicia lub załamania światła.
Okazuje się jednak, że powyższe warunki są zbyt silne i interferencję możemy obserwować nawet wtedy, gdy częstości nakładających się fal nie są dokładnie równe. Również nie musimy używać źródeł o punktowych rozmiarach. W ogólności, interferujące ze sobą fale muszą mieć spełnione tzw. warunki spójności czasowej i przestrzennej.
SPÓJNOŚĆ ŚWIATŁA
Zdolność światła do interferencji da się określić przez współdziałanie dwóch wiązek promieniowania. A więc rozważmy dwie wiązki, których wektory pola elektrycznego są ![]()
![]()
które w dowolny sposób nakładają się na siebie. Wektor wypadkowego pola elektrycznego wyrazi się wzorem
(1) ![]()
Z elektrodynamiki wiemy, że w przypadku fal płaskich i monochromatycznych natężenie strumienia energii świetlnej jest proporcjonalne do ![]()
(2) 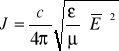
gdzie ostre nawiasy oznaczają uśrednienie rozciągnięte na przedział czasu od -T do T, długi w stosunku do okresu drgań świetlnych:
(3) 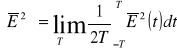
W dalszym ciągu rozważań ograniczymy się do jednego tylko ośrodka; zatem współczynnik we wzorze (2), zawierający prędkość światła c oraz przenikalność elektryczną ε i magnetooptyczną μ. ośrodka, możemy opuścić. Wówczas natężenie światła
(4) ![]()
![]()
![]()
Ze wzoru (l) otrzymujemy
(5) ![]()
czyli
J = J1 + J2 + J12 ,
gdzie
(7) ![]()
oznacza wyraz mieszany, wyrażający natężenie światła wynikające z wzajemnego oddziaływania wiązek, czyli tzw. wyraz interferencyjny.
Niech rozważane fale, płaskie i monochromatyczne, rozchodzą się w kierunku osi z z wektorami ![]()
i ![]()
stale skierowanymi wzdłuż jednej z osi, np. osi x. Wówczas
(8) ![]()
(9) ![]()
gdzie: k - stała propagacji
ω - częstotliwość kołowa
(ϕ i ψ- stałe fazowe obu fal, przy czym różnica faz
(10) ϕ−ψ=δ
związana jest z różnicą dróg optycznych Δl związkiem
(11) ![]()
Prosty rachunek daje
![]()
(12) ![]()
gdyż średnia czasowa wyrazu periodycznego znika. A ponieważ
![]()
(13) ![]()
przeto
(14) ![]()
i wzór (6) przybierze postać
(15) ![]()
Jak widać z powyższego, w przypadku równości natężeń obu wiązek (I1=I2) oraz przy zgodności faz (δ = 0, 2π, 4π,...), otrzymujemy maksymalne natężenie, wynoszące J=4I, podczas gdy przy fazach przeciwnych ((δ = 0, π, 3π, ...) J=0. W tym przypadku mówimy, że obie wiązki interferują ze sobą i że są spójne.
Jeśli jednak między fazami (ϕ i ψ obu wiązek nie występuje żadna określona relacja, lecz zmieniają się one w sposób zupełnie przypadkowy i szybki w przedziale czasu potrzebnym do obserwacji czy detekcji światła, wówczas średnia czasowa będzie równa zeru, ponieważ z tym samym prawdopodobieństwem cosδ przyjmować będzie wartości dodatnie, jak i ujemne. Wtedy
(16) J=J1+J2
Widzimy, że wiązki nie interferują ze sobą; mówimy, że są niespójne.
Najczęściej mamy do czynienia z przypadkiem pośrednim, w którym natężenie światła w procesie interferencji zmienia się od 0 do 4J (przy równym natężeniu obu wiązek), lecz w
granicach węższych. Wówczas możemy napisać ,——
(17) ![]()
gdzie γ ≤ 1 jest miarą stopnia spójności. Jeżeli wyznaczymy największe i najmniejsze natężenie światła w zjawisku interferencji, tzn. natężenie prążków interferencyjnych, to przy jednakowych natężeniach wiązek pierwotnych mamy
(18) Jmax=2J1(1+γ)
Jmin=2J1(1−γ)
Stąd możemy obliczyć tzw. widzialność prążków interferencyjnych
(19) ![]()
która w tym przypadku (J1 = J2) równa się stopniowi spójności.
DYFRAKCJĄ CZYLI UGIĘCIEM ŚWIATŁA
nazywamy zjawisko przejścia fali świetlnej przez szczelinę, w wyniku czego ta szczelina staje się źródłem światła. W przypadku, gdy rozmiary szczeliny są bardzo duże w porównaniu do długości fali zjawisko ugięcia jest zaniedbywane i przyjmuje się, że światło rozchodzi się po liniach prostych (optyka geometryczna), w przypadku kiedy rozmiary szczeliny są mniejsze od długości fali świetlnej uwzględnia się falową naturę światła, zjawiska opisuje się z punktu widzenia optyki falowej. Wyróżniamy dyfrakcję:
=> dyfrakcja Fresnela: wiązka rozbieżna przechodzi przez otwór uginający a wynik
jest obserwowany na ekranie ustawionym w skończonej odległości od ciała uginającego
światło
=> dyfrakcja Fraunhofera: na ciało uginające pada wiązka promieni równoległych, a
więc pochodzących ze źródła nieskończenie odległego, a efekt obserwowany jest na
nieskończenie odległym ekranie
Rys. l Uproszczony bieg promieni w przypadku dyfrakcji Fraunhofera na pojedynczej szczelinie.
Minimum pierwszego rzędu powstaje więc tam, gdzie, Γ12 = ½, lub Γ13 = λ. Lecz sinθ=Γ13/a, a więc a sinθ=λ. Ogólny warunek dla minimów dyfrakcyjnych rzędu „m" jest:
a sinθ = ± m λ , m =1,2,3...
Metodą graficzną można otrzymać natężenie Iθ w punkcie ekranu odległym o kąt θ od osi optycznej 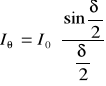
,
gdzie: ![]()
Zakładając, że maksima leżą w połowie odległości między minimami, otrzymuje się dla maksimów:
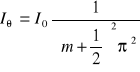
W przypadku dyfrakcji Fraunhofera na otworze kołowym otrzymujemy następujący wzór na natężenie I w funkcji odległości „x" od środka:
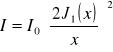
Wyszukiwarka
Podobne podstrony:
31, MIBM WIP PW, fizyka 2, laborki fiza(2), 25-Interferencja światła, pierścienie Newtona i interfer
cwicz-5, MIBM WIP PW, fizyka 2, laborki fiza(2), 25-Interferencja światła, pierścienie Newtona i int
LABORATORIUM FIZYKI I - sprawko nr25, MIBM WIP PW, fizyka 2, laborki fiza(2), 25-Interferencja świat
Doświadczenie 412, MIBM WIP PW, fizyka 2, laborki fiza(2), 25-Interferencja światła, pierścienie New
Ćw 523, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na sieci krystalic
Lab 24, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatk
CW 79, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatki
fizy2 sprawozdanie15 wersja2, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali ś
30, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na sieci krystalicznej
523 zabol, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła na sieci krysta
POPRAWA, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siat
kopiafiz28, MIBM WIP PW, fizyka 2, laborki fiza(2), 28-Zjawisko skręcenia płaszczyzny polaryzacji św
Odpowiedzi do laborki 523, MIBM WIP PW, fizyka 2, laborki fiza(2), 37-Dyfrakcja elektronów i światła
więcej podobnych podstron