Przewodniki z prądem 

w polu magnetycznym 

Marian Cholewa

Katedra Fizyki 

Politechniki Rzeszowskiej

Działanie pola magnetycznego na 

 przewodnik z prądem (HRW § 29.7)

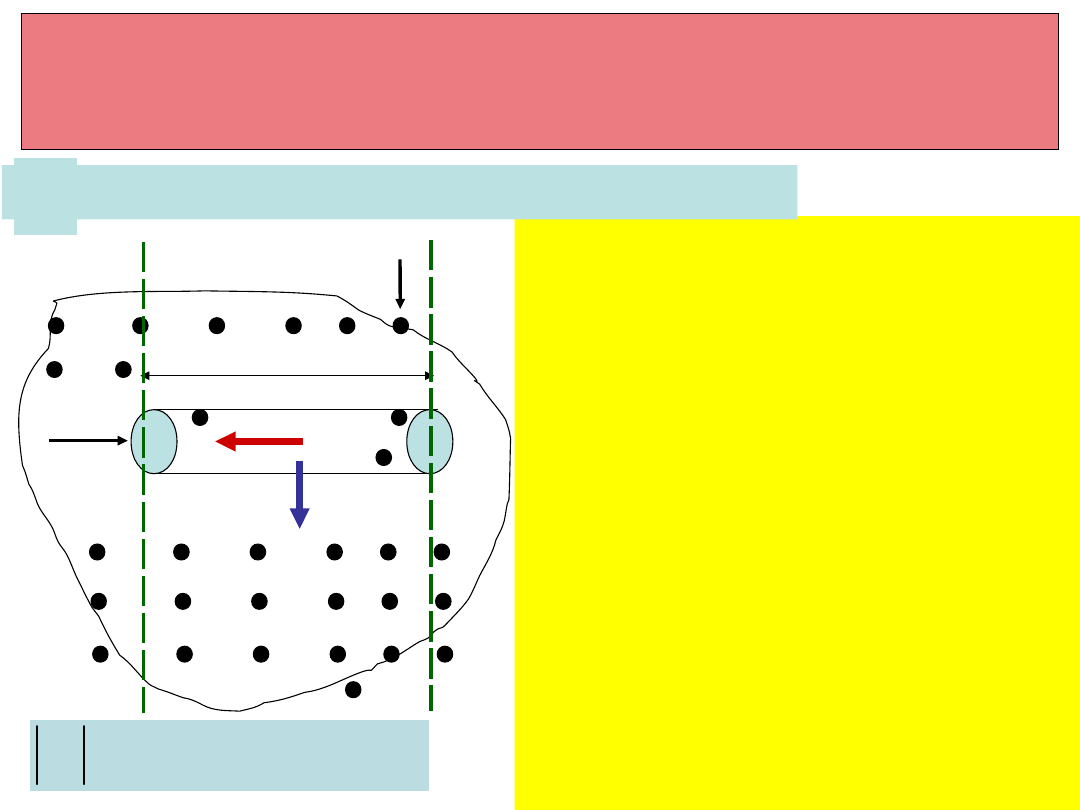
Niech przez prostoliniowy 
odcinek przewodnika płynie 
prąd o natężeniu I. 
Wybierzemy płaszczyznę   

w której leży ten odcinek. 
Przyjmijmy, że przewodnik 
znajduje się w jednorodnym 
polu magnetycznym, którego 
wektor indukcji      
skierowany jest prostopadle 
do płaszczyzny , przed 

płaszczyznę. Wtedy siła 
Lorentza       działająca na 
każdy elektron leży w 
płaszczyźnie . Ponieważ 

elektrony nie mogą opuścić 
przewodnika, siła działa nań.  

B

r

B

F

r

o

B

d

d

qv Bsin90

qv B

=

=

F

r

d

v

r

- prędkość unoszenia w polu elektrycznym

B

r

L

d

v

r



I

B

=q

d

F

v ×B

r

r

r

x

x

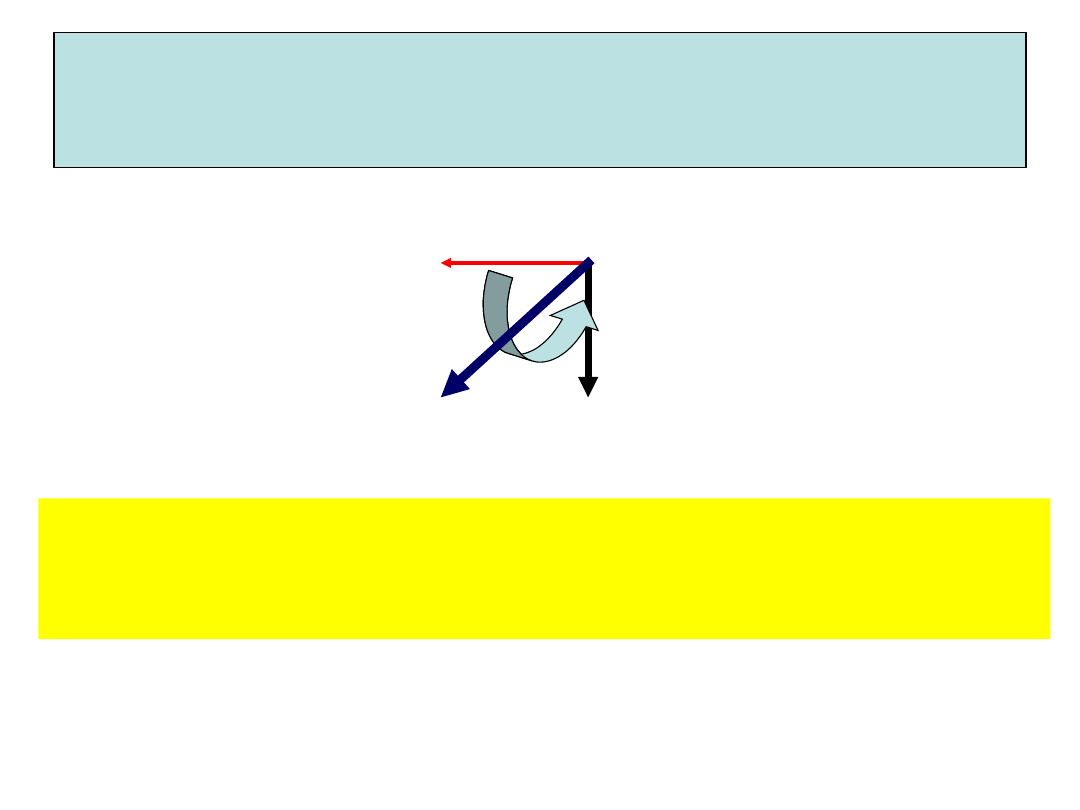
Kierunek siły Lorentza

d

v

r

B

r

B

=q

d

F

v ×B

r

r

r

Wtedy siła Lorentza       działająca na każdy elektron 
leży w płaszczyźnie . Ponieważ elektrony nie mogą 

opuścić przewodnika, siła działa nań.

B

F

r

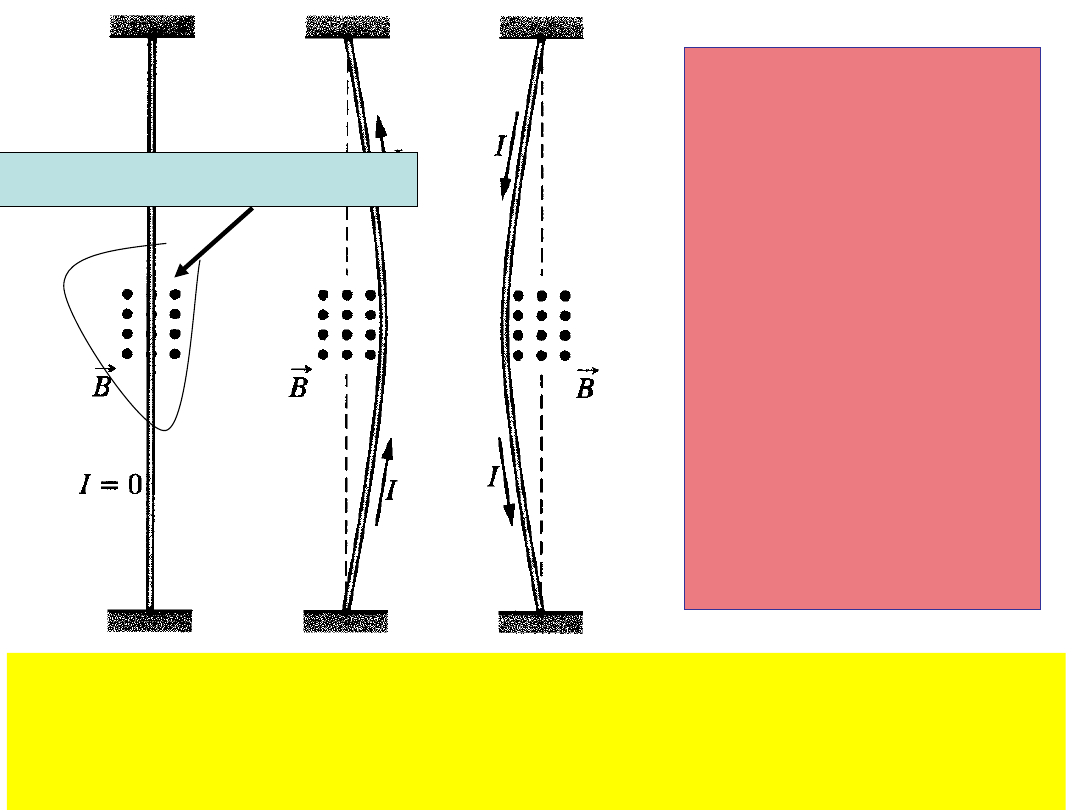
Pod 

wpływem 

siły 

Lorentza 

przewodni

k liniowy 

wygina się 

Wektor indukcji magnetycznej jest prostopadły do 
płaszczyzny rysunku przed nią.  Wektor gęstości prądu 
(zwrot I) jest skierowany przeciwnie do kierunku ruchu 
elektronów. 

Dolny biegun magnesu

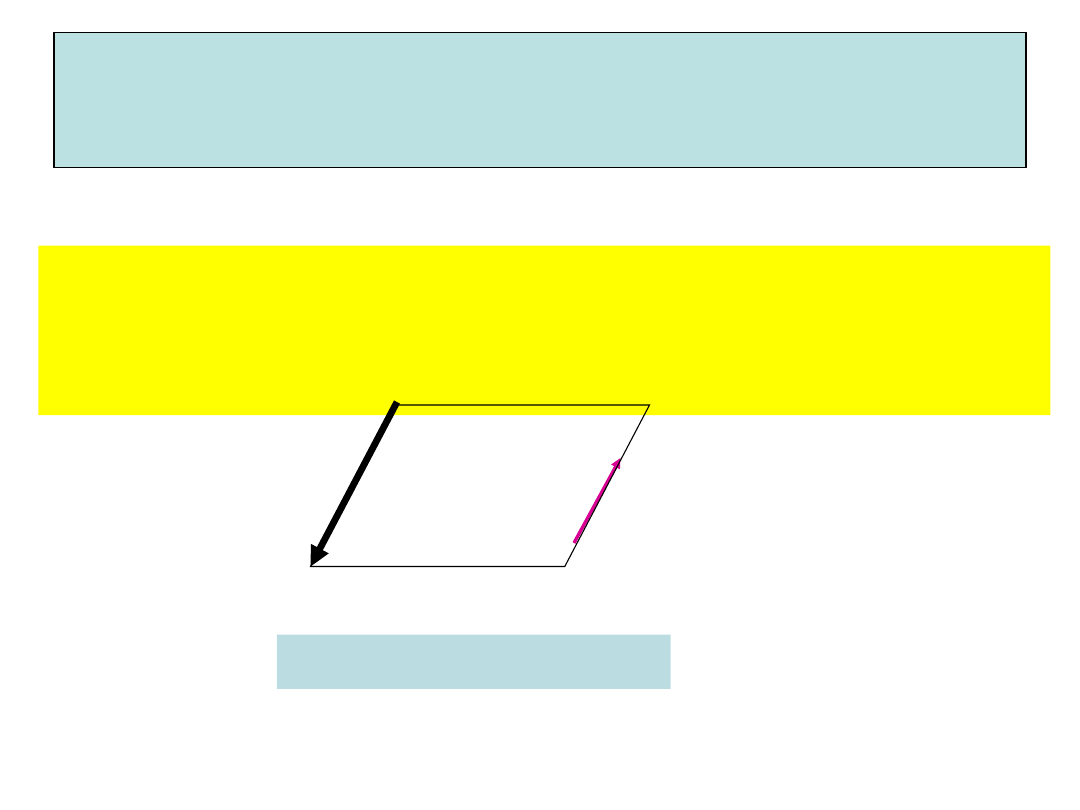
Wektor długości

Wprowadzimy wektor długości       o długości 

L

, skierowany zgodnie z umownym 

kierunkiem prądu I. 

L

r

L

r

I

L

r

L

C

Kontur C z prądem I

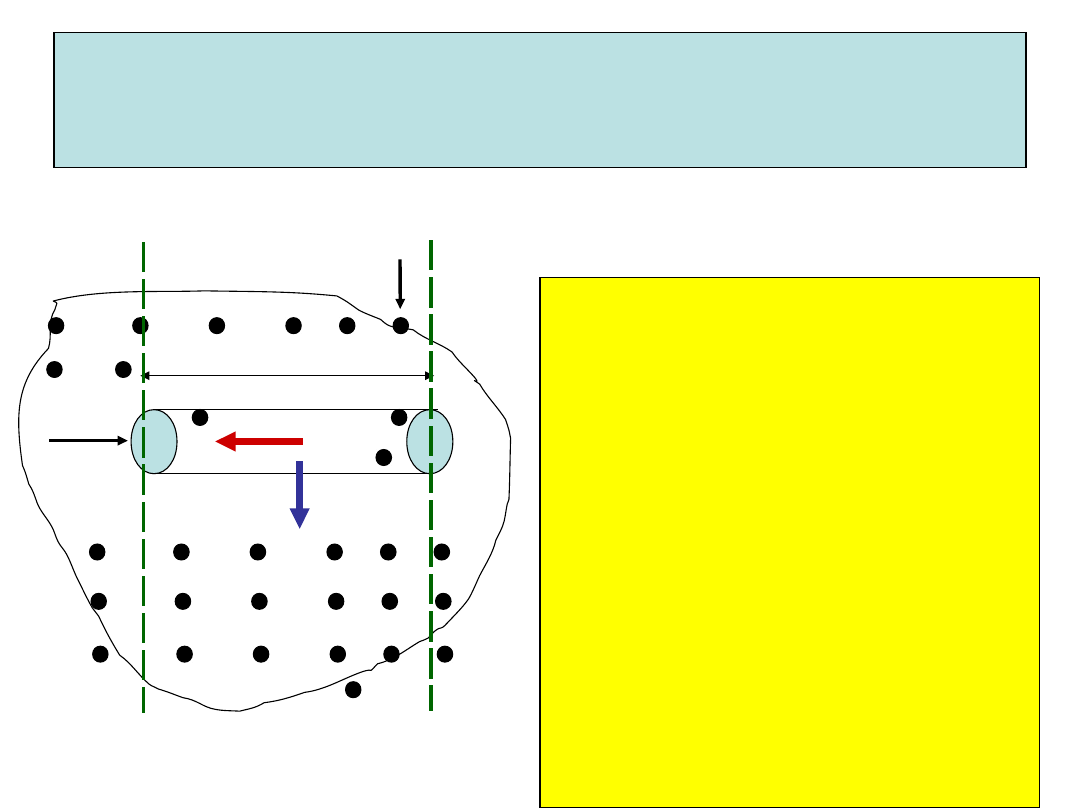
Ładunek przepływający 

przez przekrój przewodu z 

prądem

B

r

L

d

v

r



I

B

=q

d

F

v ×B

r

r

r

x

x

Rozpatrzymy fragment 
przewodnika 
prostoliniowego 
o długości L. W interwale 
czasu 
t = L/vd  wszystkie 
elektrony 
znajdujące się w tym 
odcinku przejdą przez 
płaszczyznę xx. Przez nią 
przepływa ładunek 
q= It = I L/vd.

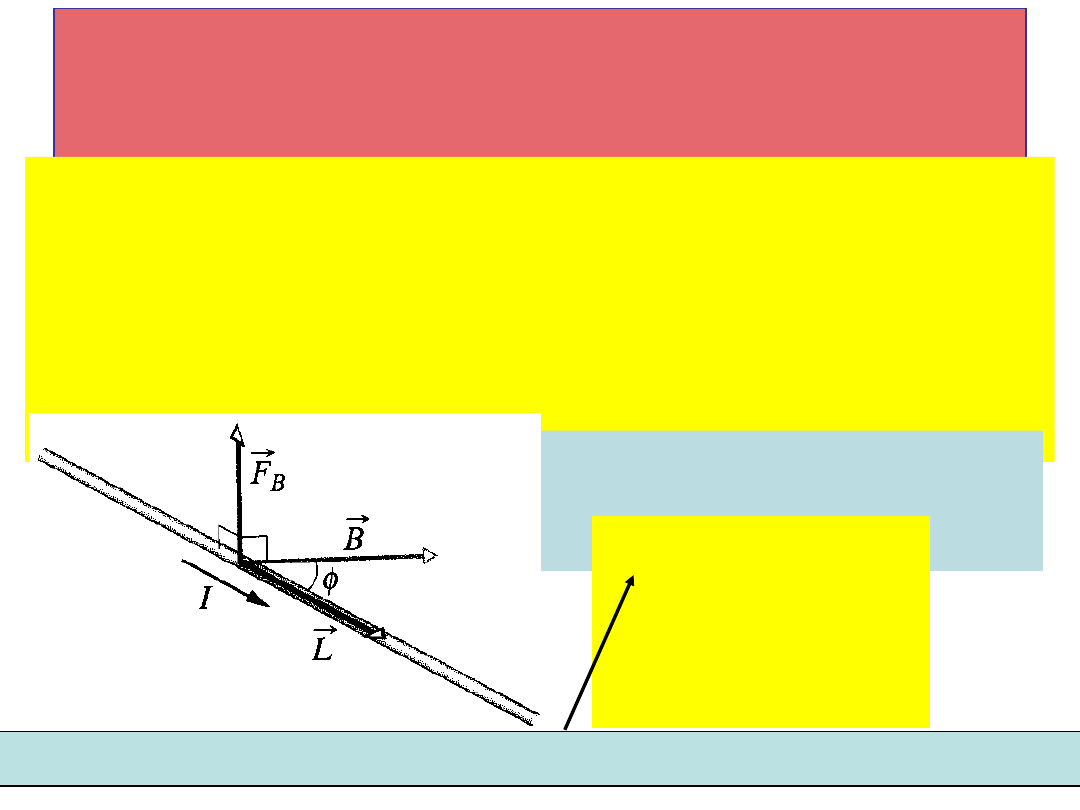
Wielkość siły działającej 

na odcinek przewodnika 

B

B

d

d

d

I L

F

qv B =

v B =ILB .

v

�

� =

F

r

Rozpatrzymy fragment przewodnika prostoliniowego o 
długości L. W interwale czasu t = L/v

d

  wszystkie 

elektrony znajdujące się w tym odcinku przejdą przez 
płaszczyznę xx. Przez nią przepływa ładunek q= It = I 
L/v

d

. Zatem wielkość siły magnetycznej działającej na 

odcinek przewodnika wynosi  

Jeżeli pole magnetyczne 
nie jest prostopadła do 
przewodnika, to  

B

B

=I

F =I L B sin .

f

�

�
���

F

L×B

r

r r

Równanie może służyć dla określenia wektora indukcji magnetycznej

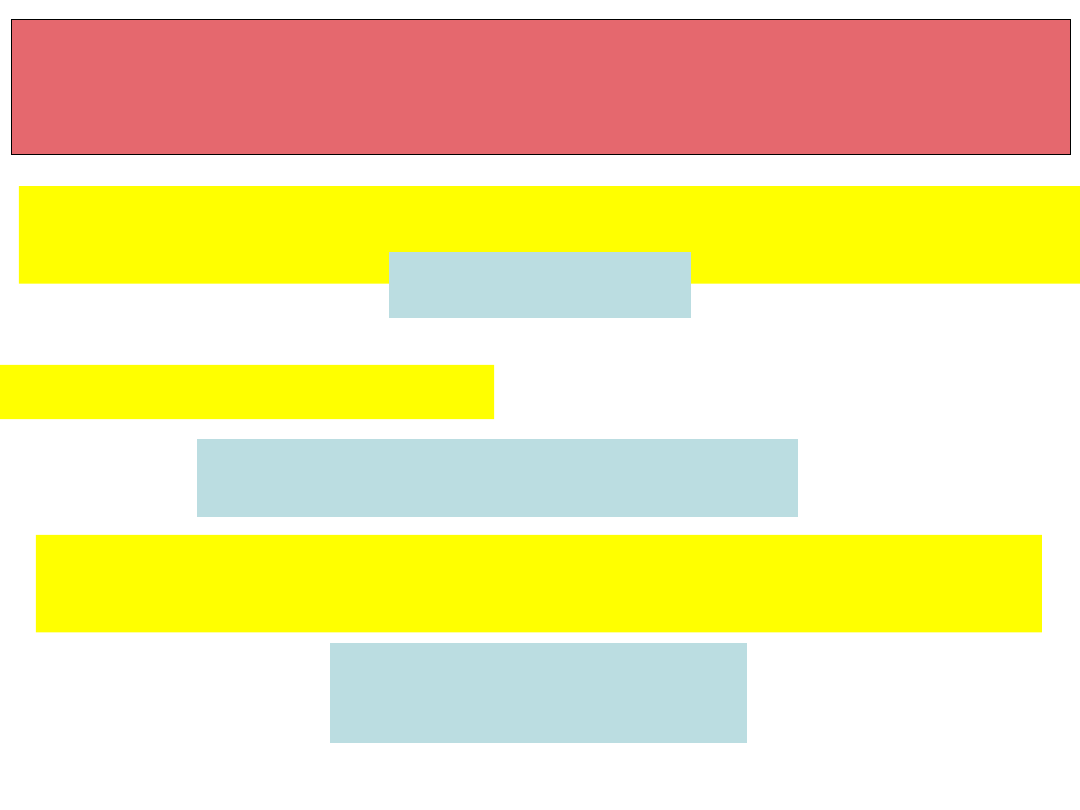
Gdy przewodnik nie jest 

prostoliniowy 

Dzielimy przewodnik liniowy na n małych 
prostoliniowych elementów 

d

(i =1,2,…,n)

i

L

r

Na i-ty element działa siła 

(i)

B

d

=I d

(i =1,2,…,n) .

i

F

L ×B

r

r

Następnie należy znaleźć wypadkową wszystkich 
tych sił , czyli obliczyć całkę

2

2

(i)

B

1

1

d

=I  d

.

�

�

i

F

L ×B

r

r

r

Moment siły działający 

na ramkę z prądem 

W prostokątnej ramce płynie prąd elektryczny o 
natężeniu I. Ramka może się  swobodnie obracać 
wokół stałej osi. Ramka znajduje się w stałym polu 
magnetycznym o wektorze indukcji     . 

B

r

Na długie odcinki ramki 
działa siła
       , a więc na ramkę 
działa para sił. Powstaje 
moment siły, który 
powoduje obrót ramki. 
Komutator (nie pokazany na 
rysunku) odwraca kierunek 
prądu co pół obrotu. 
Zapewnia to istnienie 
momentu sił, który zawsze 
działa w tę samą stronę.   

�F

r

2

L

r

4

L

r

1

L

r

3

L

r

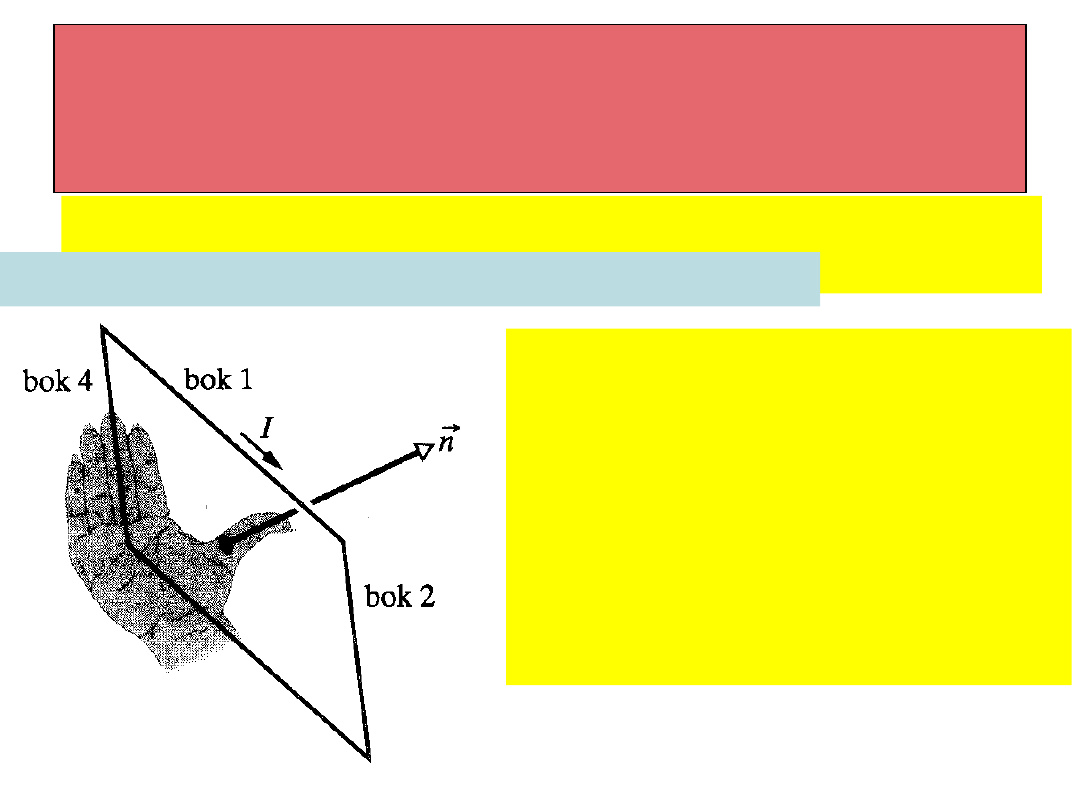
Określenie orientacji 

przestrzennej ramki 

Orientację przestrzenną ramki określa jednostkowy 
wektor 

n.

r

Jego orientację określa reguła prawej dłoni:  

Należy ułożyć lub zgiąć palce 
prawej ręki tak, aby 
wskazywały kierunek 
płynięcia prądu w dowolnym 
punkcie ramki. Kciuk 
wskazuje zwrot wektora    , 
który jest prostopadły do 
powierzchni ramki.  

n

r

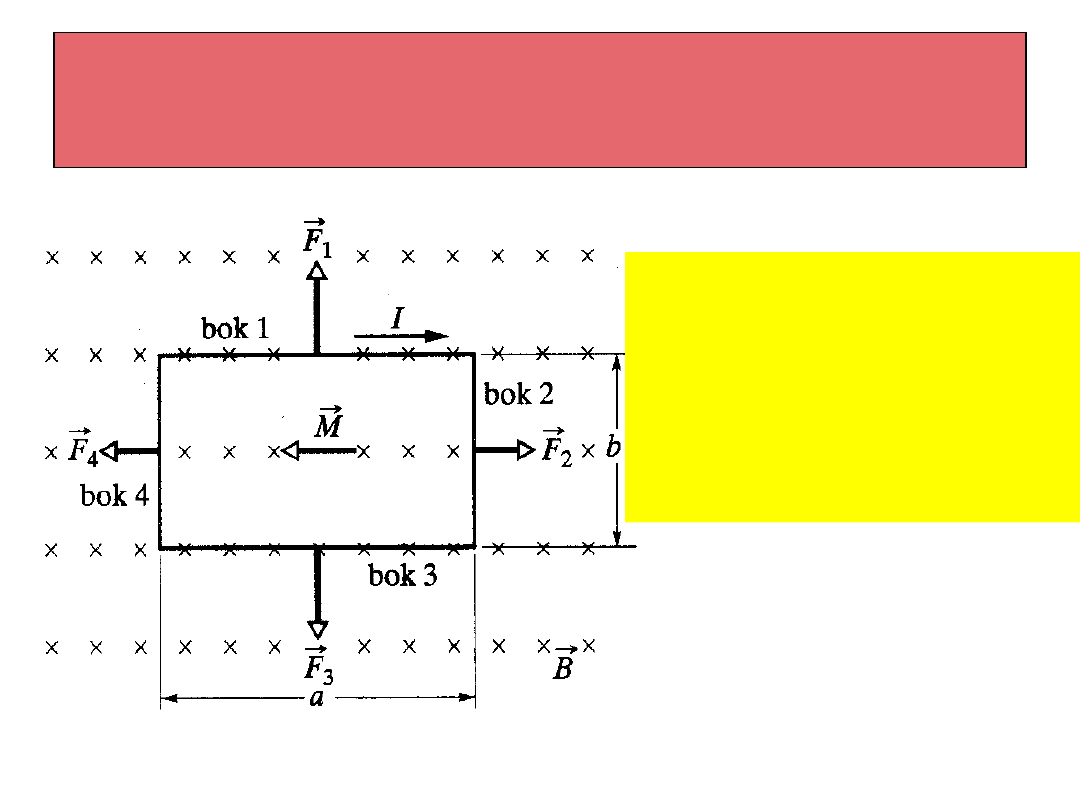
Opis prostokątnej ramki z 

prądem

Rozważymy położenie 
ramki, dla którego 
wektor      jest 
prostopadły do 
płaszczyzny rysunku, 
kierowany za nią. 

B

r

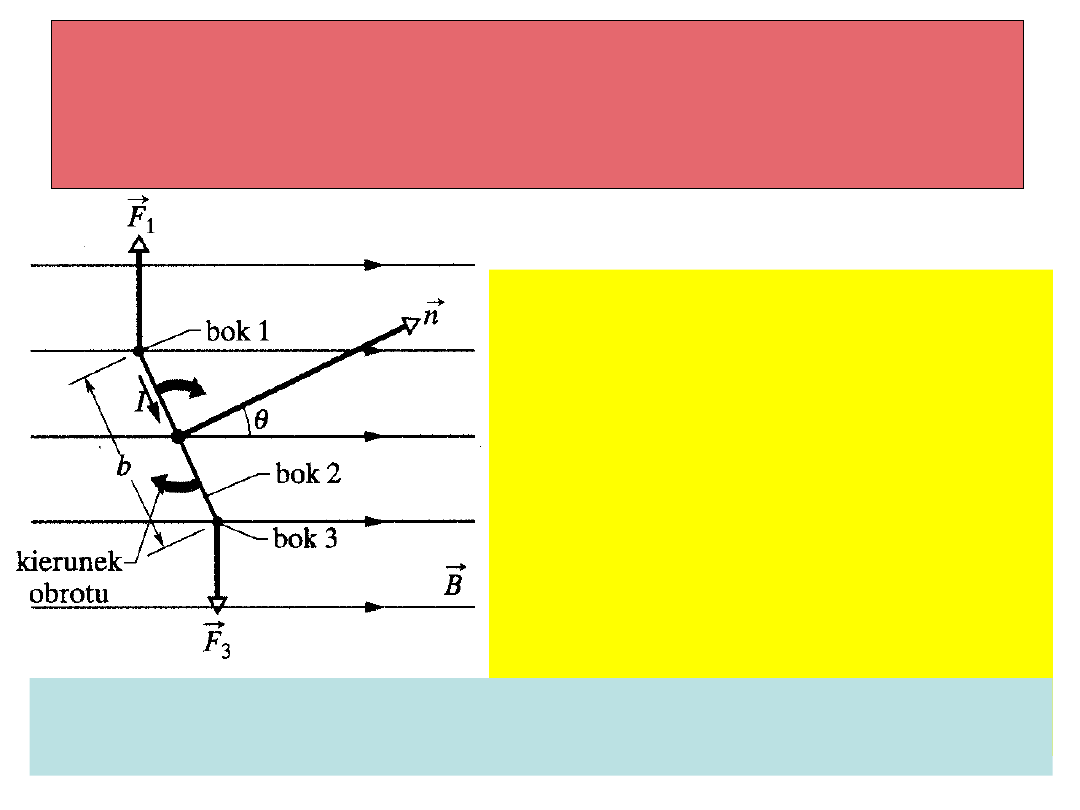
Wektor orientacji ramki tworzy 

z wektorem indukcji kąt   

Patrzymy na ramkę od strony 
jednego z krótszych boków 
(boku nr 2). Wektor indukcji 
leży w płaszczyźnie rysunku. 
Długie boki ramki są 
prostopadłe do płaszczyzny 
rysunku, a więc i do         , 
=/2. Krótkie boki leżą w 

płaszczyźnie rysunku. Na 
długi bok znajdujący się w 
górnej części rysunku (nr 1) 

B

r

działa siła     , na bok nr 2 -     , na bok 3 -     , na bok 
nr 4 siła      . 

1

F

r

2

F

r

3

F

r

4

F

r

Obliczenie sił działających na 

ramkę, której wektor orientacji 

tworzy 

z wektorem indukcji kąt  

o

1

1

=I

F =IL Bsin90

I a B,

�

�

= ��

1

1

F

L ×B

r

r

r

3

1

=I

I

F =- I L B =-I a B .

�

�

�

�

��

3

3

1

F

L ×B=- L ×B 

r

r

r

r

r

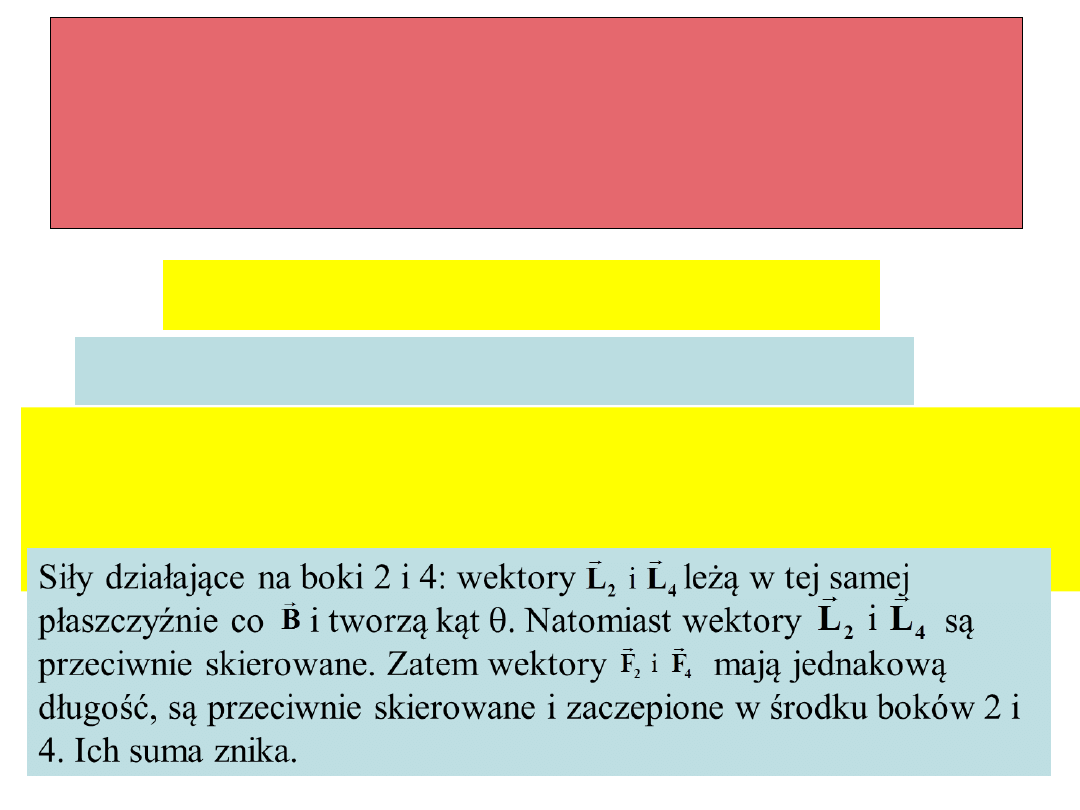
Siły     i      zaczepione są w środkach odpowiednich 
odcinków, są równoległe, skierowane przeciwnie i nie 
leżą na tej samej prostej, zatem nie kompensują się, lecz 
tworzą parę sił starających się obrócić ramkę.     

1

F

r

3

F

r

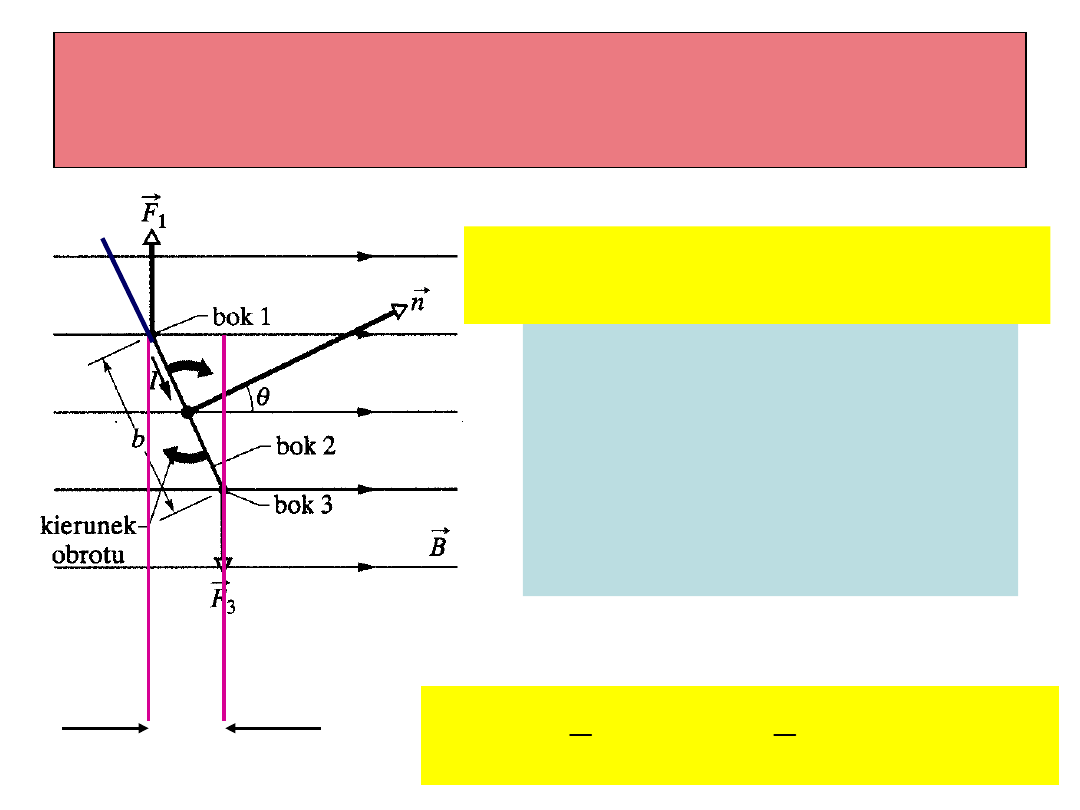
Para sił działająca na ramkę z 

prądem w polu magnetycznym 

Ramię siły: b/2, wielkość 
siły Iab, kąt jaki tworzą 
wektory siły z ramieniem 
siły: . Długość ramienia 

siły:  bsin/2. Wielkość 

siły F

B

=IaB. 

b

b

M'= IaB sinθ + IaB sinθ =IabBsinθ. 

2

2

�

� �

�

�

� �

�

�

� �

�

Moment siły  M’ działający na 
ramkę:

bsin

