Układy regulacji ciągłej

Wprowadzenie

Projektowanie ad hoc

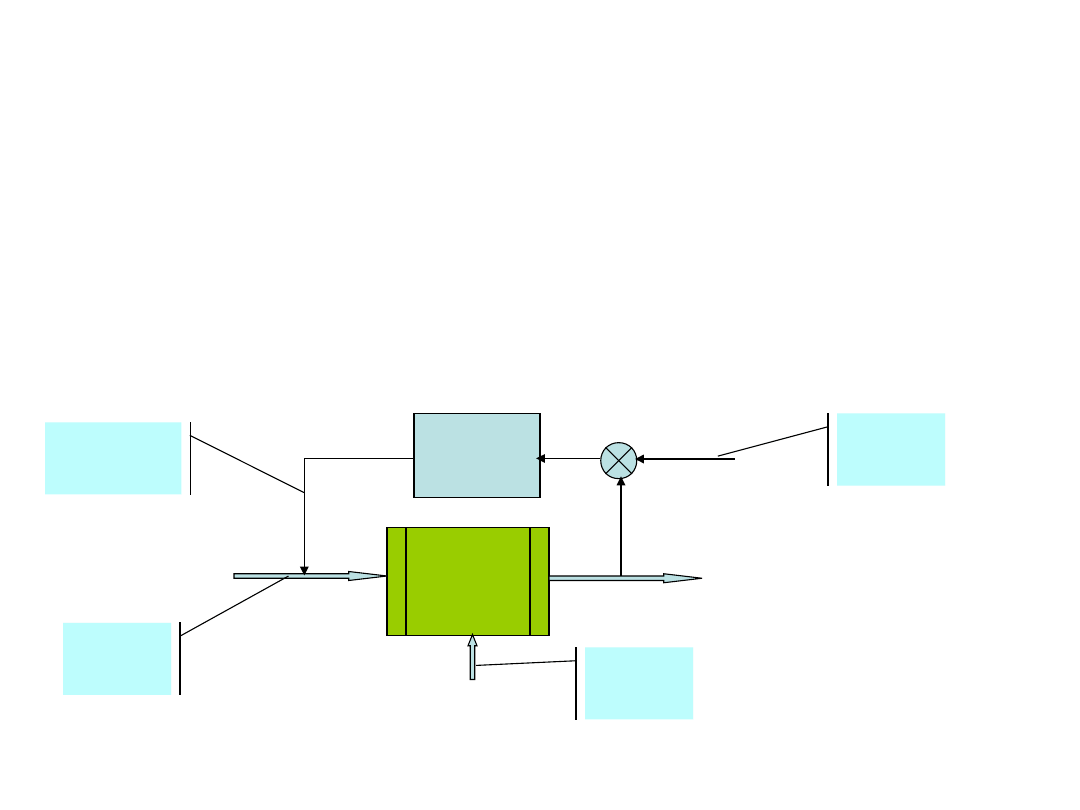
Układy regulacji; decyzje dotyczą wejść sterowanych w
postaci wielkości ciągłych, takich jak przepływy, napięcia,
prądy itp.; cel stanowi nadążanie odpowiednich wyjść obiektu
(wielkości wyjściowych procesu sterowanego) za zadanymi
przebiegami, w szczególnym przypadku stabilizacja tych wyjść na
zadanych wartościach; przykłady: stabilizacja temperatury w
pomieszczeniu, stabilizacja temperatury przepływającej wody w
podgrzewaczu, stabilizacja prędkości obrotowej turbiny,
naprowadzanie lufy działa na cel o zmieniającym się położeniu
(regulacja nadążna).

Regulator

+

-

Wartość

zadana

Wejścia

sterowan

e

Wejścia

swobodne

Obiek
t

Sterowani

e

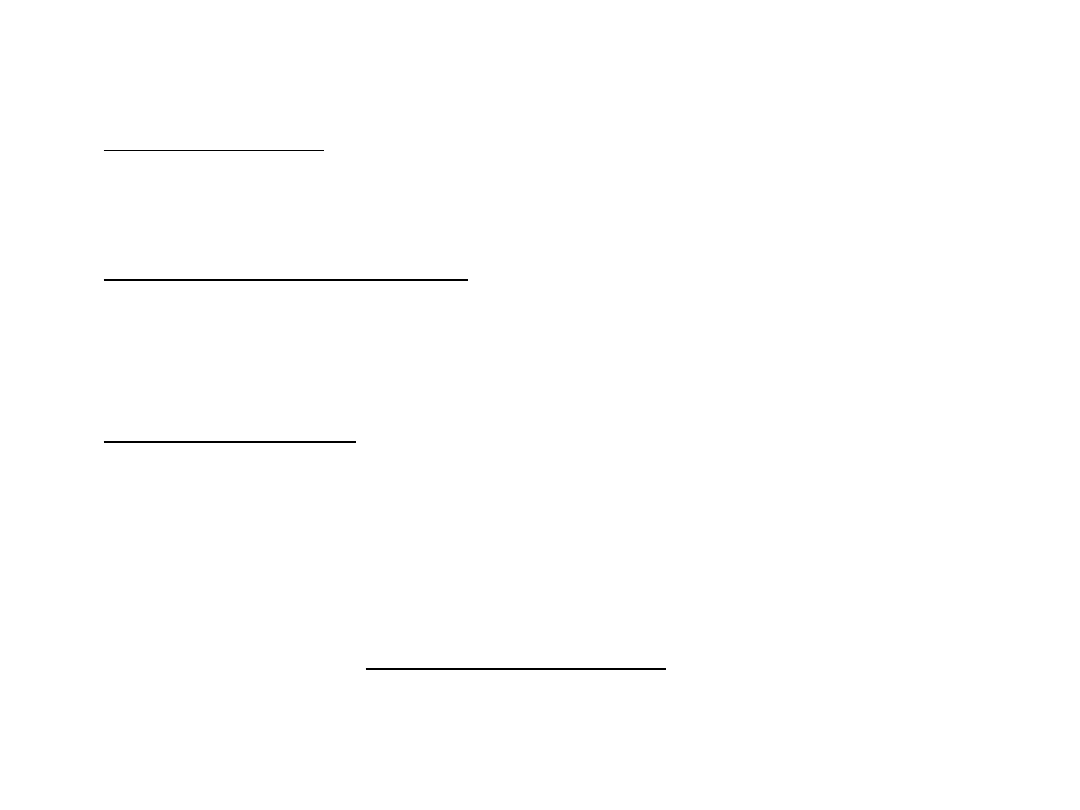
Regulacja obiektów ciągłych może być realizowana jako:

Regulacja ciągła – zmienna wyjściowa regulatora jest ciagła,
tzn. może przyjmować dowolną wartość z odpowiedniego
zakresu,

Regulacja dwupołożeniowa – zmienna wyjściowa regulatora
może przyjmować jedną z dwóch możliwych wartości, lub
trójpołożeniowa -- zmienna wyjściowa regulatora może
przyjmować jedną z trzech możliwych wartości,

Regulacja krokowa – tzn. trójpołożeniowa z korekcją, jest to
sposób (przybliżony) realizacji regulacji ciągłej z elementem
wykonawczym trójpołożeniowym (tani element
wykonawczy).

Do regulacji można także, w szerszym sensie, nawiązywać
wprowadzając tzw. regulację ekstremalną, będącą w istocie
eksperymentalnym poszukiwaniem najlepszego punktu
pracy dla obiektu w stanie ustalonym.

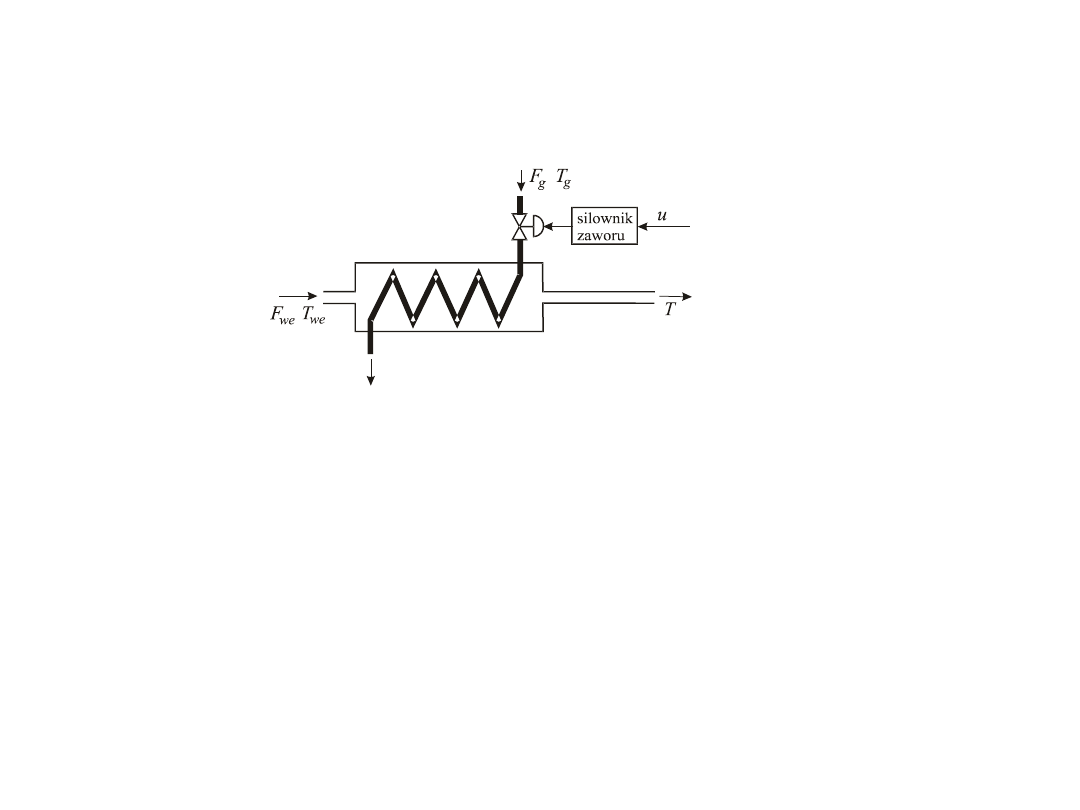
Temperatura T jest zmienną regulowaną,
Sygnał u sterujący siłownikiem zmieniającym położenie
zaworu jest zmienną sterującą,
Natężenie przepływu F

we

oraz temperatury T

we

i T

g

są

wielkościami swobodnymi, niesterowanymi („zakłóceniami”).

Zależność (model):

Przykład – wymiennik ciepła

 

 

 

 

))

(

,

,

,

),

(

(

)

(

0

,

,

,

,

0

0

0

0

t

T

T

T

F

u

F

f

t

T

t

t

we

t

t

g

t

t

we

t

t

g



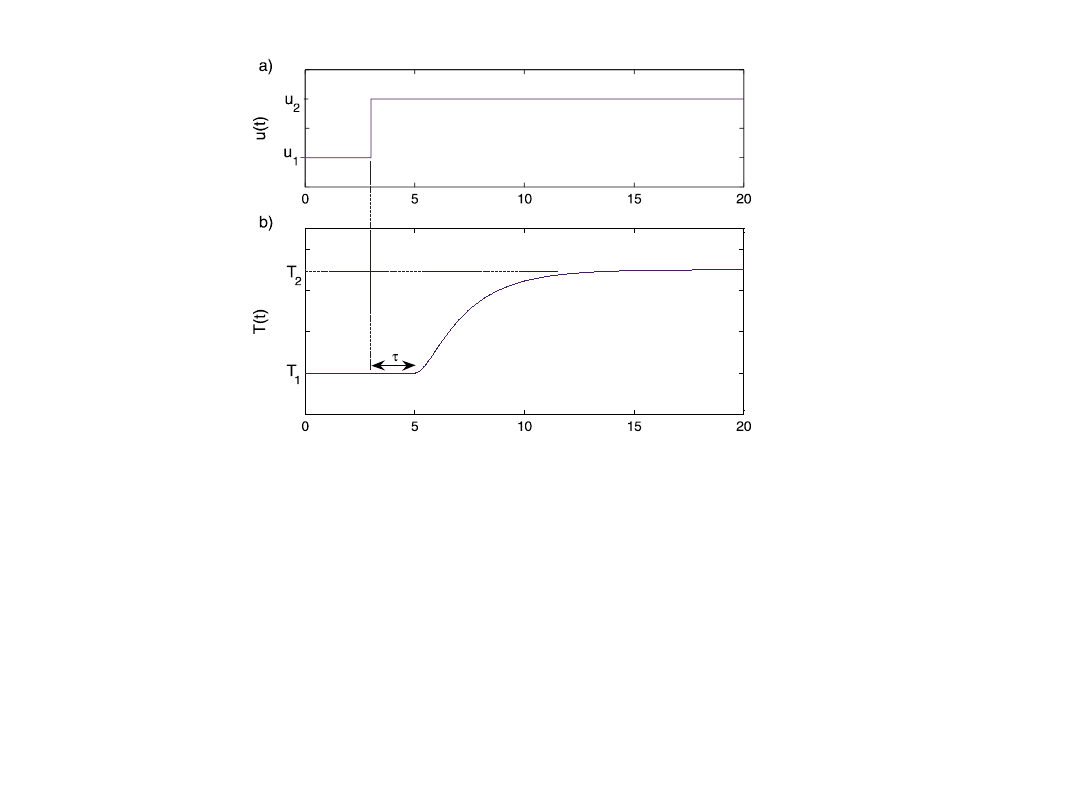
Skokowy przebieg sterowania u(t) (górna
krzywa) i odpowiadający mu przebieg
temperatury wyjściowej T(t) obiektu - tzw.
odpowiedź skokowa

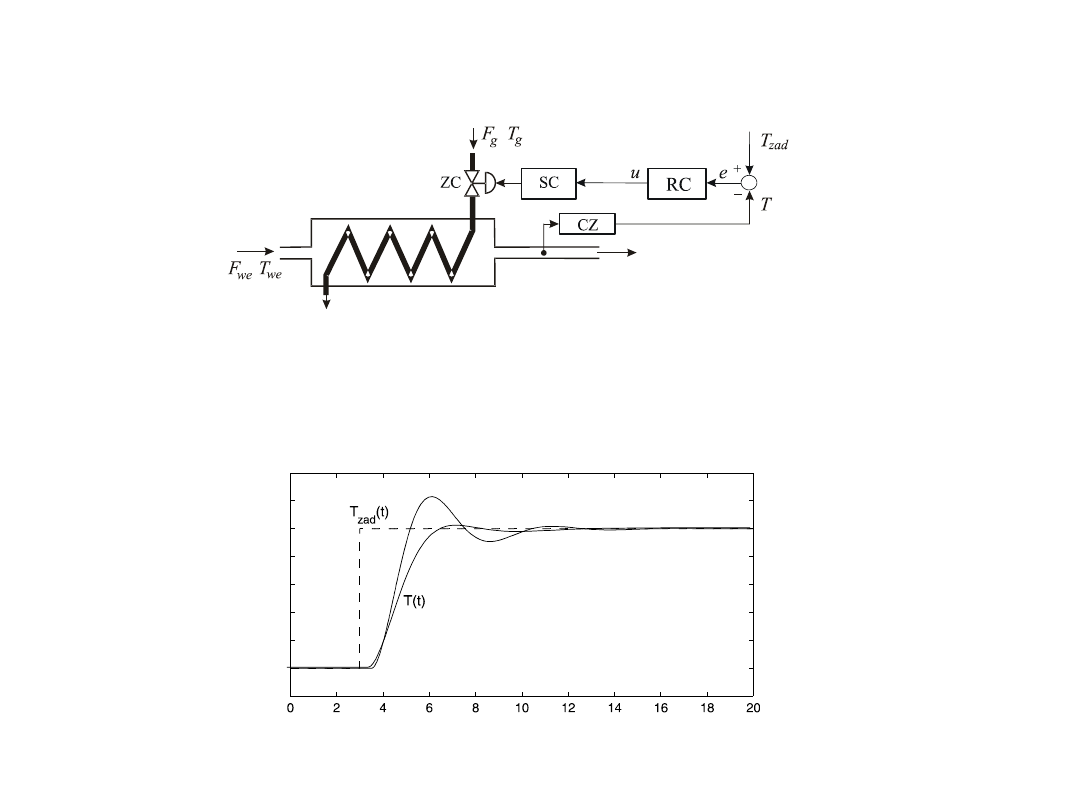
RC – regulator ciągły, np. PI lub PID

Regulacja
ciągła

Reg. PI

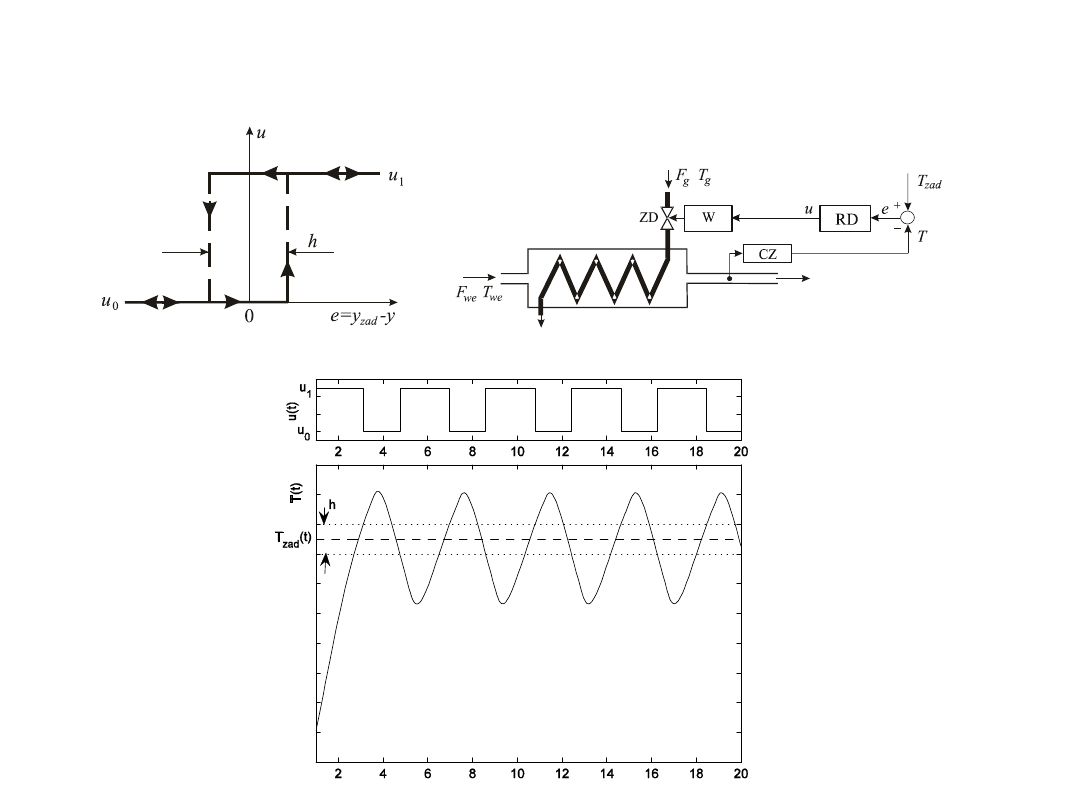
Regulacja dwupołożeniowa

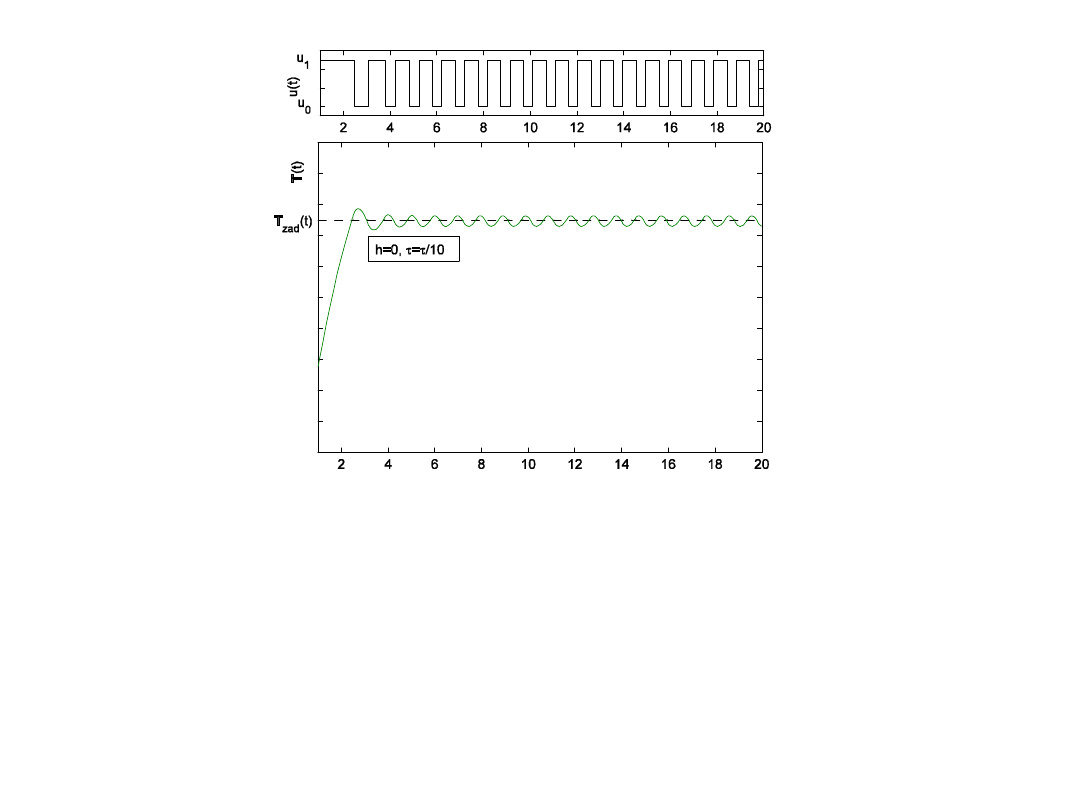
Przebiegi w układzie regulacji dwupołożeniowej z
zerową strefą histerezy, z obiektem o charakterystyce
skokowej z dziesięciokrotnie mniejszym, od
poprzedniego, opóźnieniem τ.

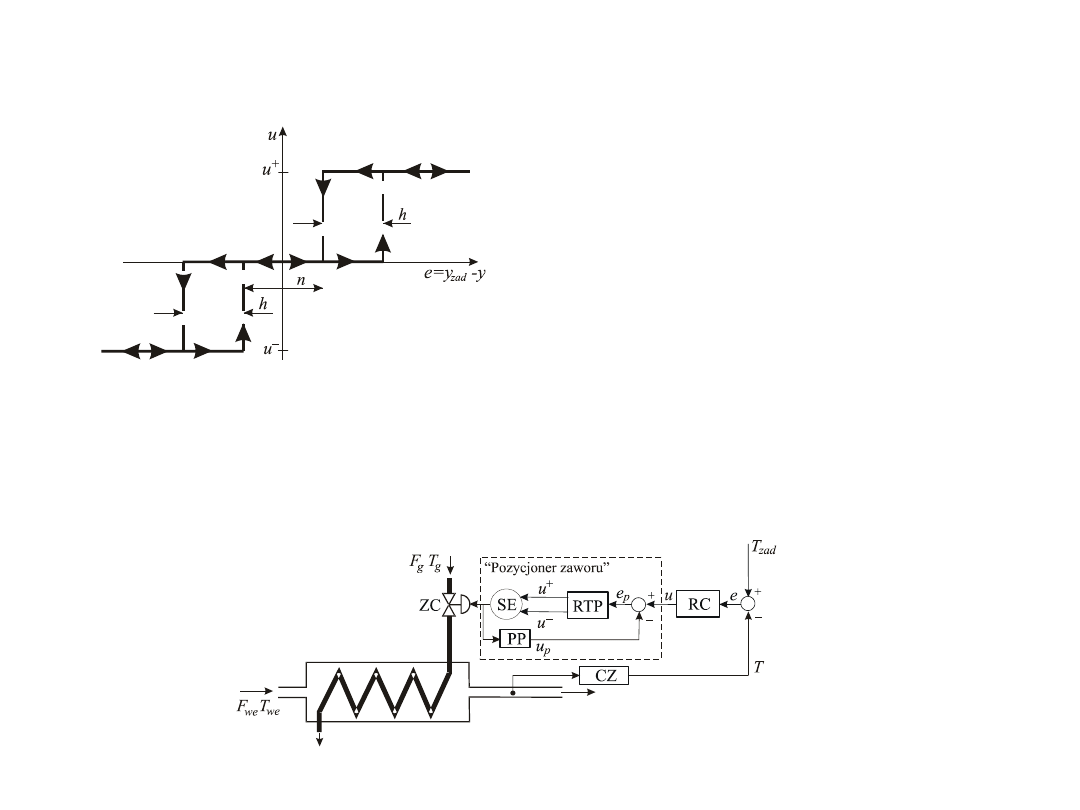
Regulacja trójpołożeniowa, trójpołożeniowa z korekcją

Charakterystyka elementu
trójpołożeniowego (RTP)
(h – szerokość stref
histerezy, n – szerokość
strefy nieczułości).

Wykorzystanie RTP w układzie regulacji ciągłej do pozycjonowania
zaworu, jeśli siłownik powinien być pobudzany sygnałem o dużej
wartości (np. wobec tarcia statycznego pomiędzy elementami
zaworu).

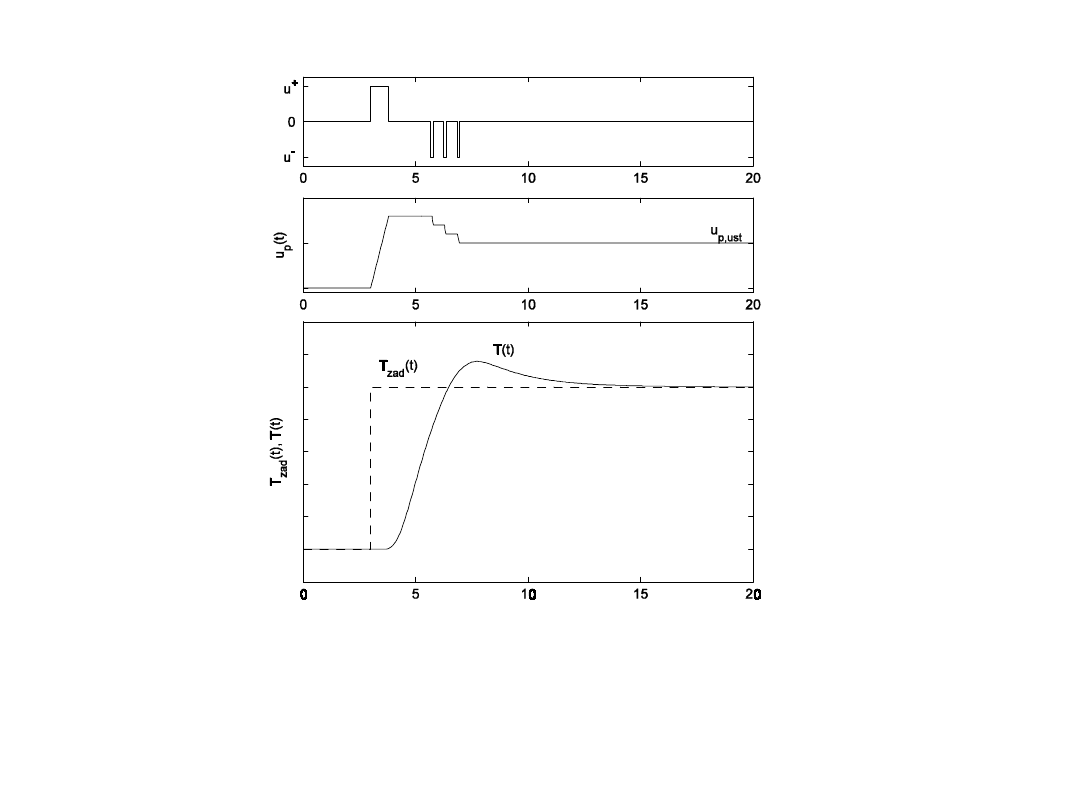
Działanie regulatora krokowego

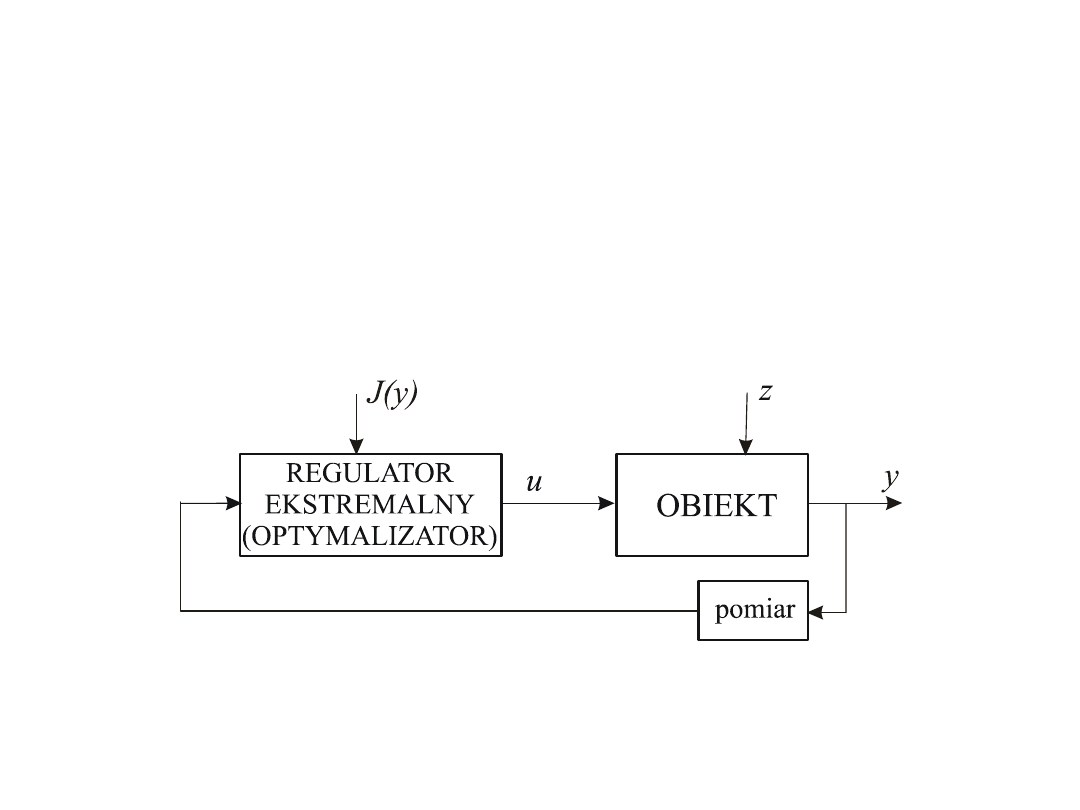
Regulacja ekstremalna

Regulacja ekstremalna stanowi szczególny przypadek układu
sterowania ze sprzężeniem zwrotnym, w którym celem
działania regulatora jest wyznaczanie sygnałów sterujących
obiektem w taki sposób, aby maksymalizować (lub
minimalizować, co jest równoważne, bo minJ(y) = -max(-J(y) )
pewną funkcję, zwaną funkcją jakości działania układu.

Czy projektowanie układu regulacji jest łatwe?

Tak…, jeśli potrafimy odpowiednio opisać i zrozumieć
działanie obiektu i regulatora oraz będziemy wiedzieli w jaki
sposób spełnić określone wymagania (stabilność, dokładność,
mała wrażliwość na niedokładną znajomość parametrów
obiektu oraz na wpływ zakłóceń zewnętrznych).

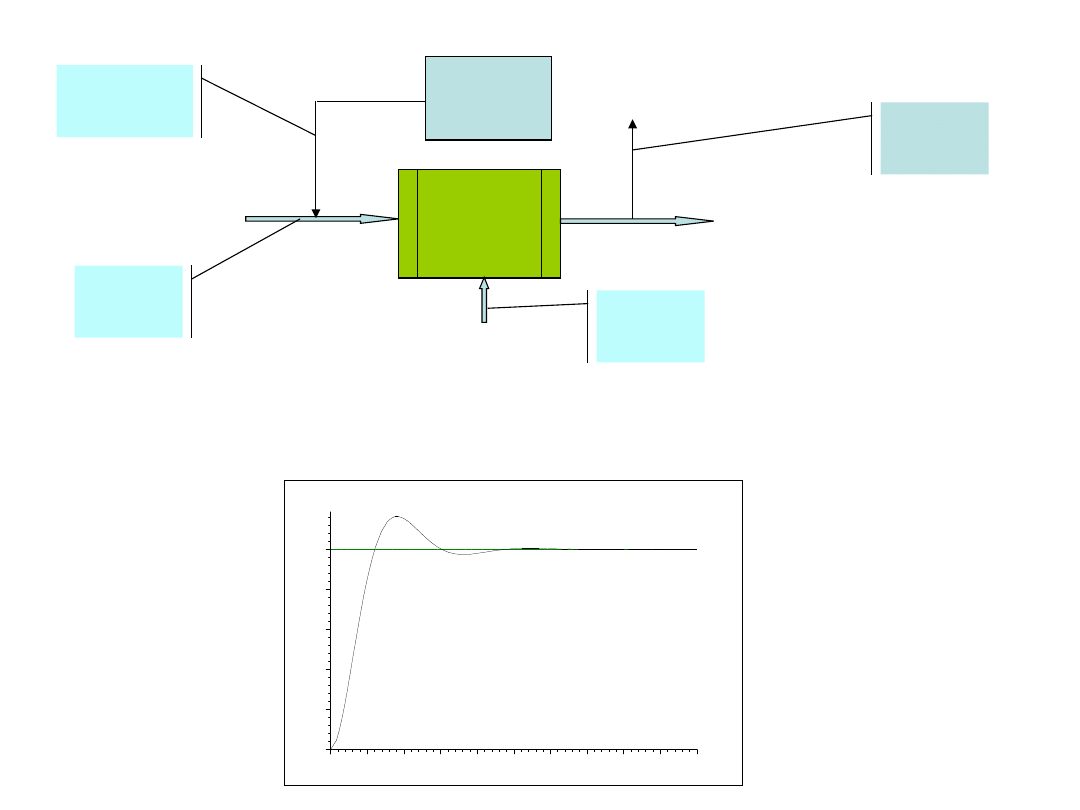
u

Wejścia

sterowan

e

Wejścia

swobodne

z

Obiek
t

Sterowanie

u

Obiekt: równanie ruchu y’’+y’+y=u

(prosty typowy obiekt

drugiego rzędu

Sterowanie w układzie otwartym, u= 10, wartość zadana r = 10

r=10

y(0)=0,
y’(0)=0

Uwagi:

1. Brak uchybu

ustalonego

2. Niewielkie

przeregulowanie

Ale…

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

t

wyjście
mierz. y

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

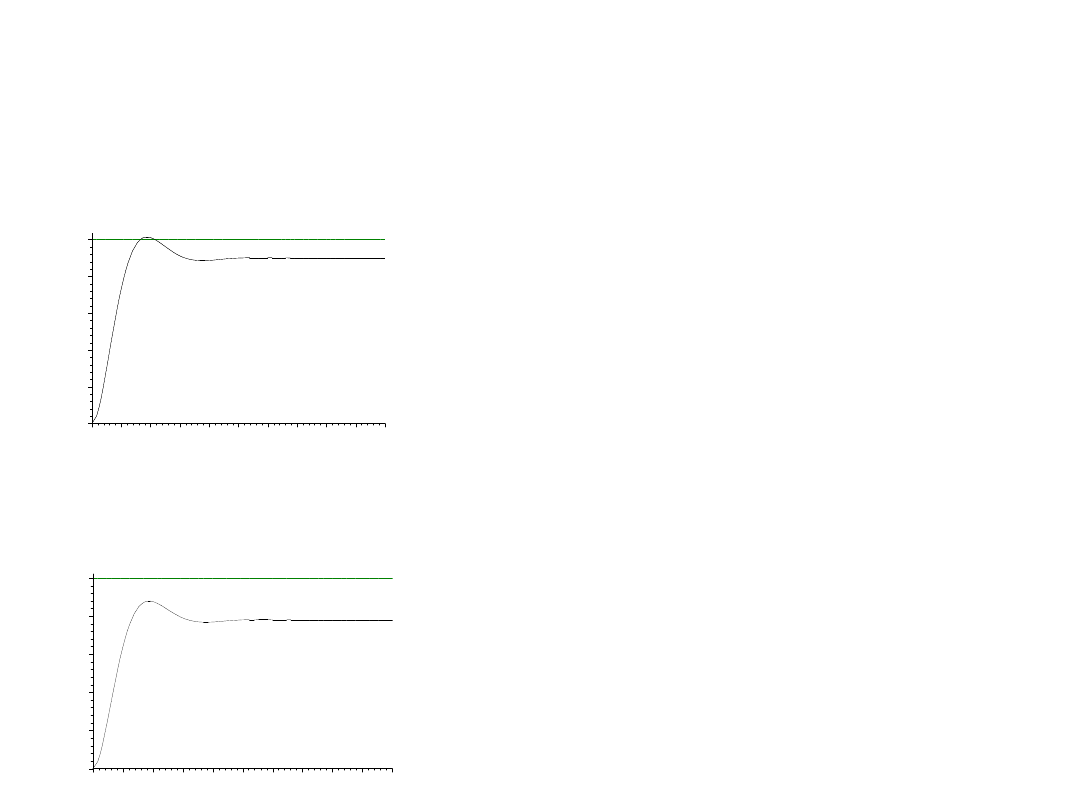
Przypuśćmy, że w rzeczywistości obiekt
zachowuje się zgodnie z nieco innym opisem,
np.:

y’’+1.1y’+y = 0.9u + 0.3z

a) u =10, z =0

b) u=10, z=-4

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

Uwagi:

1. Układ otwarty jest wrażliwy na

zmianę, nawet niewielką, parametrów
obiektu; źle działa w przypadku błędu
w identyfikacji (lub zmiany)
parametrów – duży uchyb w stanie
ustalonym.

2. Duża wrażliwość na zmiany wejścia

swobodnego (zakłócenia) z.

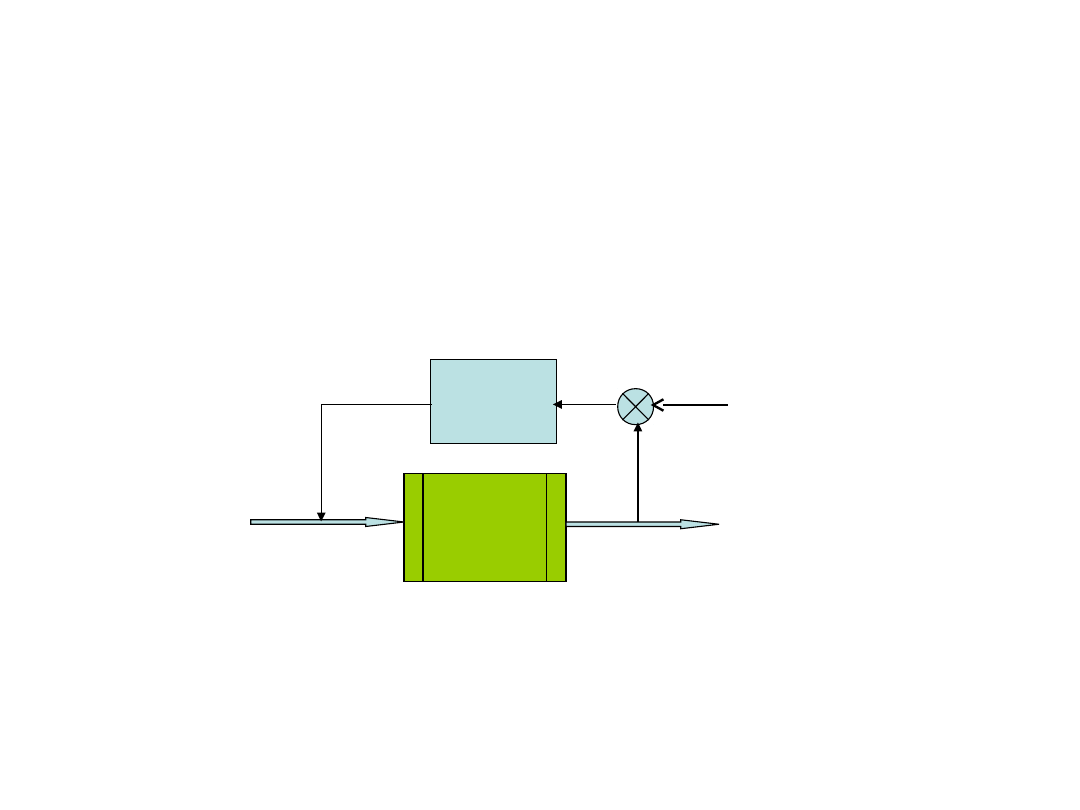
Spróbujmy, bez wnikania w materię

rzeczy, projektować regulator

stosując podejście ad hoc.

Regulat
or

+

-

Obiek
t

Regulat
or

wzm. K

+

-

Wartość

zadana r

Wejścia

sterowan

e

Obiek
t

Sterowanie

u

wyjście

mierz. y

Obiekt: y’’+y’+y=u Regulator: u=K(r-y)
(Typ P)

r=10

K=5

y(0)=0,
y’(0)=0

Uwagi:

1. Uchyb ustalony

ponad 15%,
y(12)= 8. 3535

2. Wyraźne

oscylacje

0

2

4

6

8

10

12

2

4

6

8

10 12 14 16 18 20

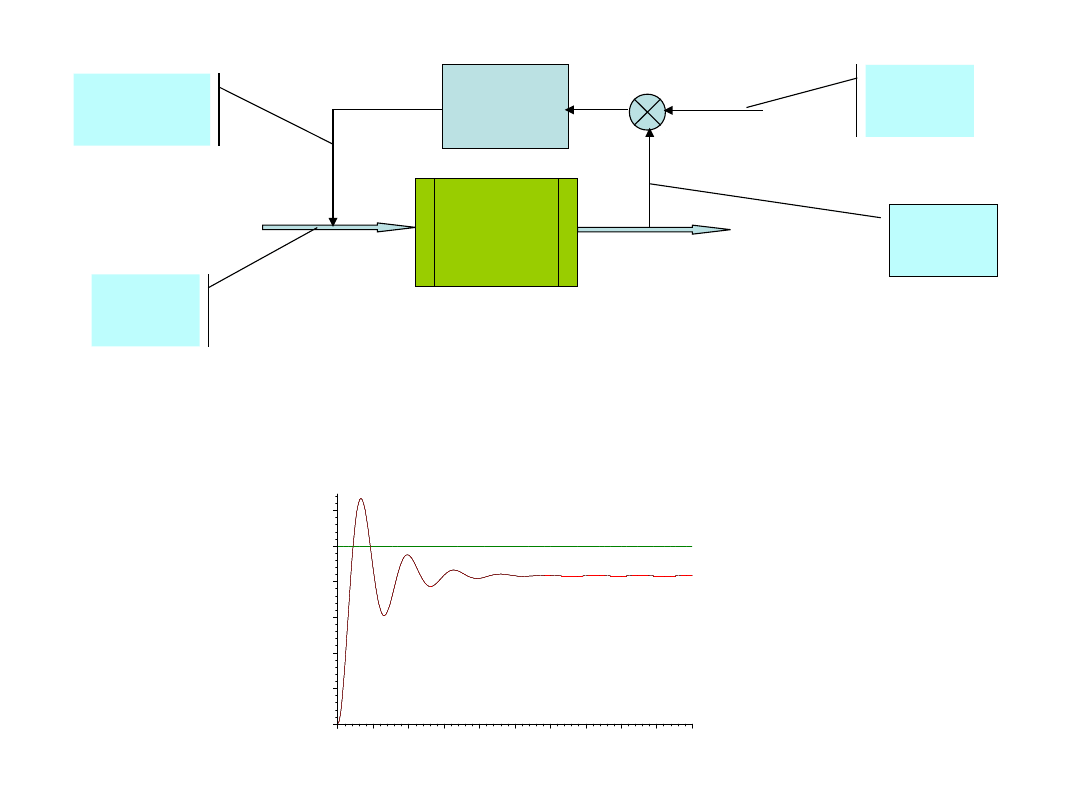
Regulat
or

wzm. K

+

-

Wartość

zadana r

Wejścia

sterowan

e

Obiek
t

Sterowanie

u

e=r-y

wyjście

mierz. y

Obiekt: y’’+y’+y=u Regulator:
u=K(r-y)

r=10

K=10

y(0)=0,
y’(0)=0

0

2

4

6

8

10

12

14

2

4

6

8

10 12 14 16 18 20

Uwagi:

1. Uchyb ustalony

mniejszy, ok.
10%

2. Znaczne

oscylacje
(przeregulowani
e ponad 50%)

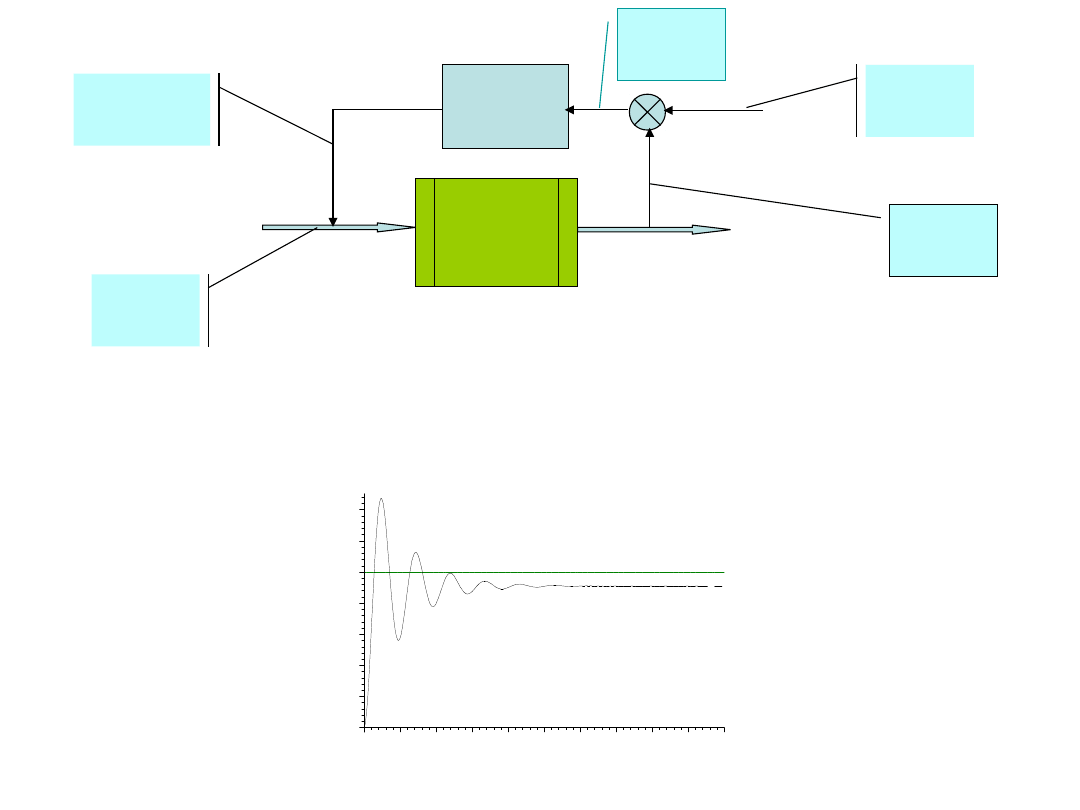
Regulat
or

wzm. K

+

-

Wartość

zadana r

Wejścia

sterowan

e

Obiek
t

Sterowanie

u

wyjście

mierz. y

Obiekt: y’’+y’+y=u Regulator:
u=K(r-y)

r=10

K=40

y(0)=0,
y’(0)=0

Uwagi:

1. Uchyb ustalony

mały, ok. 2.5%,
y(12)= 9.
7457

2. Duże oscylacje

(przereg. ok.
80%)!

0

2

4

6

8

10

12

14

16

2

4

6

8

10 12 14 16 18 20

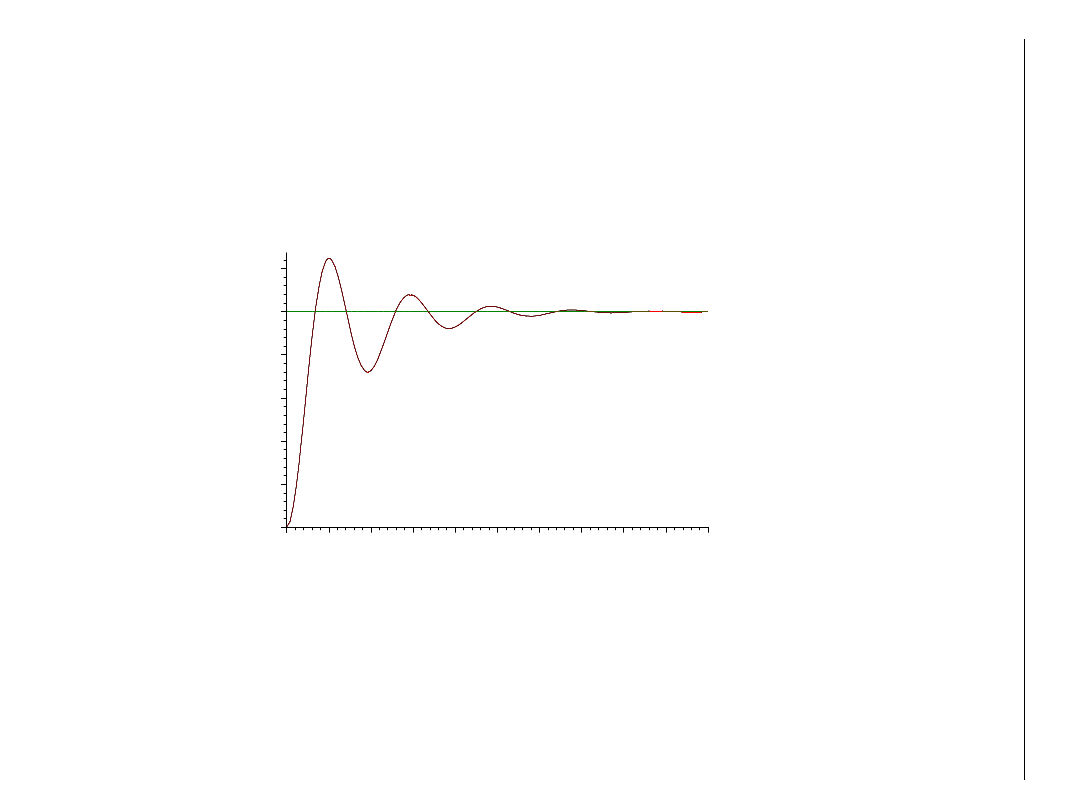
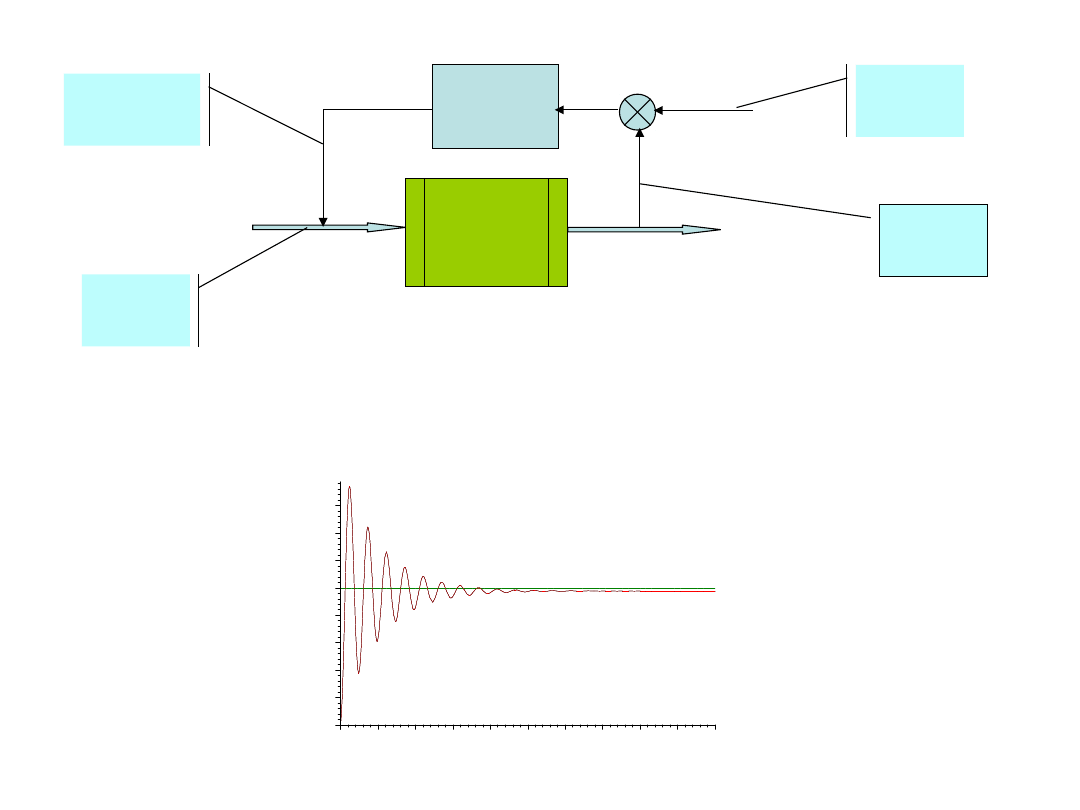
Obiekt: y’’+y’+y=u Regulator:

PI: u(t) =

K(e+(1/T

I

)∫edτ)

r =10; K = 2, T

I

=2

0

2

4

6

8

10

12

2

4

6

8

10 12 14 16 18 20

Uchyb ustalony zerowy, ale regulacja niezbyt szybka i znaczne
oscylacje.

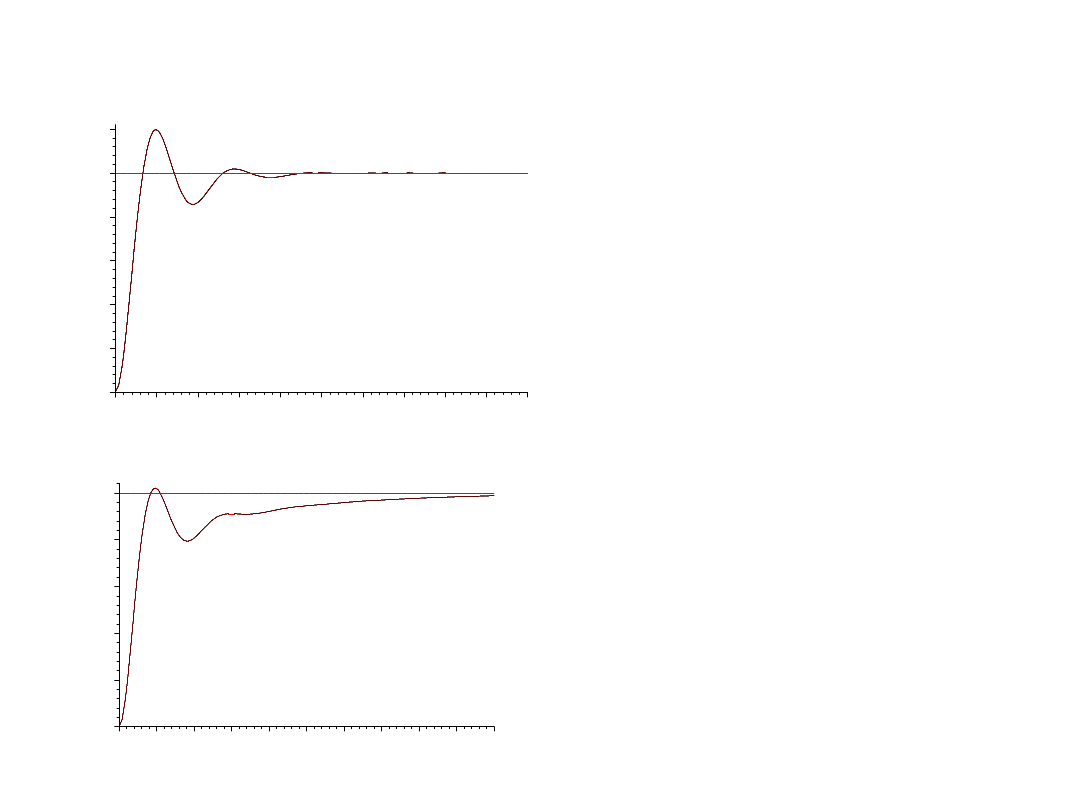
Niech
r =10; K = 2.5, T

I

=2, T

D

= 0.2

Powiedzmy, że może tak być.

Spróbujmy j.w., tylko T

I

=

5

Powolna regulacja,
„brzydki” przebieg
przejściowy.

0

2

4

6

8

10

12

2

4

6

8

10 12 14 16 18 20

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

Spróbujmy zastosować
regulator

PID:

u(t) = K(e+(1/T

I

)∫edτ +

T

D

de/dt

)

(Obiekt: y’’+y’+y=u )

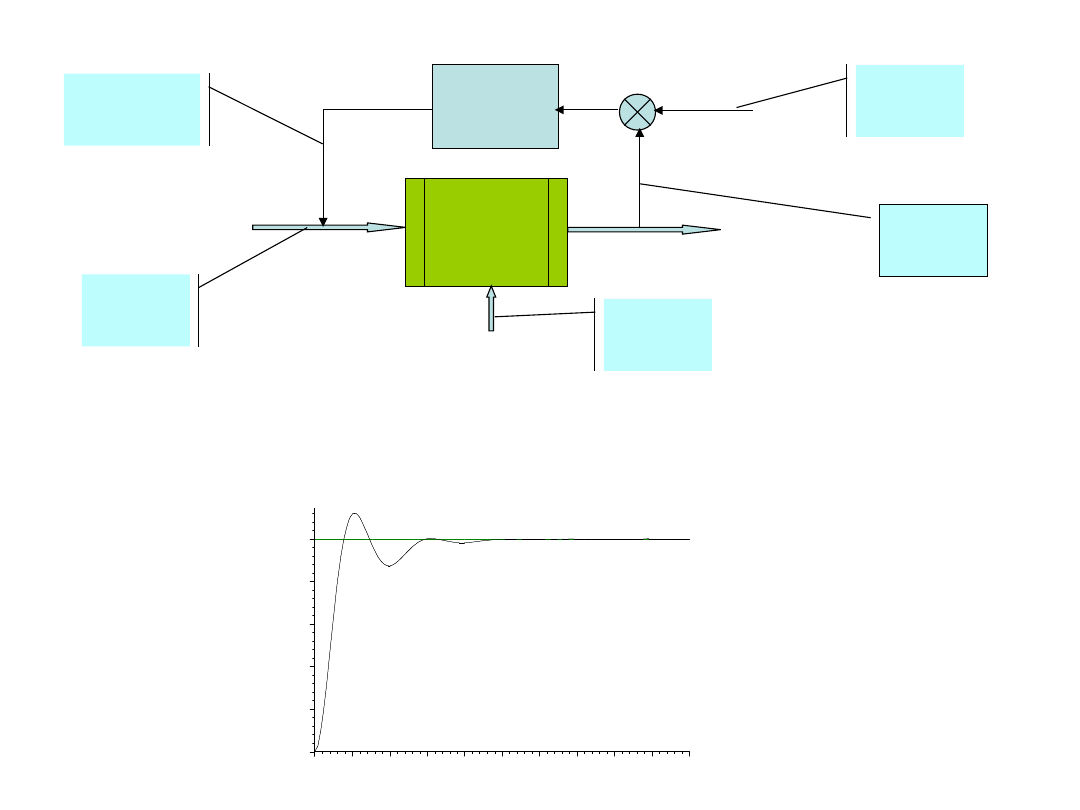
Regulat
or

PID

+

-

Wartość

zadana r

Wejścia

sterowan

e

Wejścia

swobodne

z

Obiek
t

Sterowanie

u

wyjście

mierz. y

Obiekt: y’’+1.1y’+y=0.9u+0.3z ; Regulator: u=K[(r-y)+(1/T

I

)

∫(r-y)dτ-T

D

y’ ]

(Regulator PID)

r=10

z=-4

K=2.5

T

I

=2

T

D

=0.2

y(0)=0,
y’(0)=0

Uwagi:

1. Brak uchybu

ustalonego

2. Małe oscylacje

3. Niewrażliwy na

nawet dość
znaczne zmiany
parametrów
obiektu i
zakłócenia!

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

Metodą prób i błędów udało się dobrać

niezły regulator typu PID; tym
niemniej, nie rozumiemy dobrze,
dlaczego takie, a nie inne nastawy są
właściwe.

Roważmy teraz inny prosty obiekt

T(dy/dt)+y(t) = Ku(t-T₀)

Jest to obiekt typowy (inercja z
opóźnieniem); występuje w wielu
prostych zastosowaniach.

Przykład: regulacja temperatury w
danym pomieszczeniu.

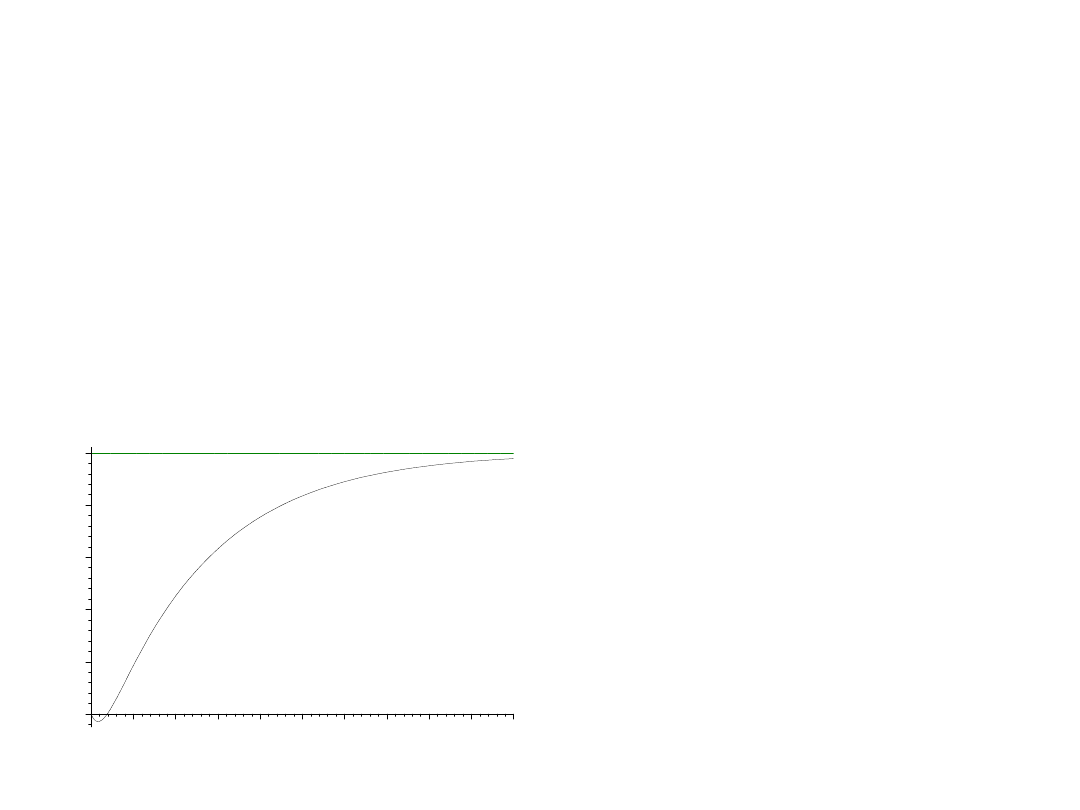
wartość zadana r =10,
obiekt typu (1/T)y’(t)+y(t) = u(t-T₀)

(transmitancja (e

sT₀

)/(Ts+1)),

aproksymowany transmitancją ((1-(T₀/2)s)/((1+(T₀/2)s)(Ts+1))).

Opis obiektu aproksymowanego przy pomocy równań różniczkowych:
Tw′+w=((2T+T

0

)/(2T-T

0

))u,

T

0

x′+x= -(2T

0

/(2T-T

0

))u

T=5, T

0

=1

oraz y=x+w (y - wyjście);

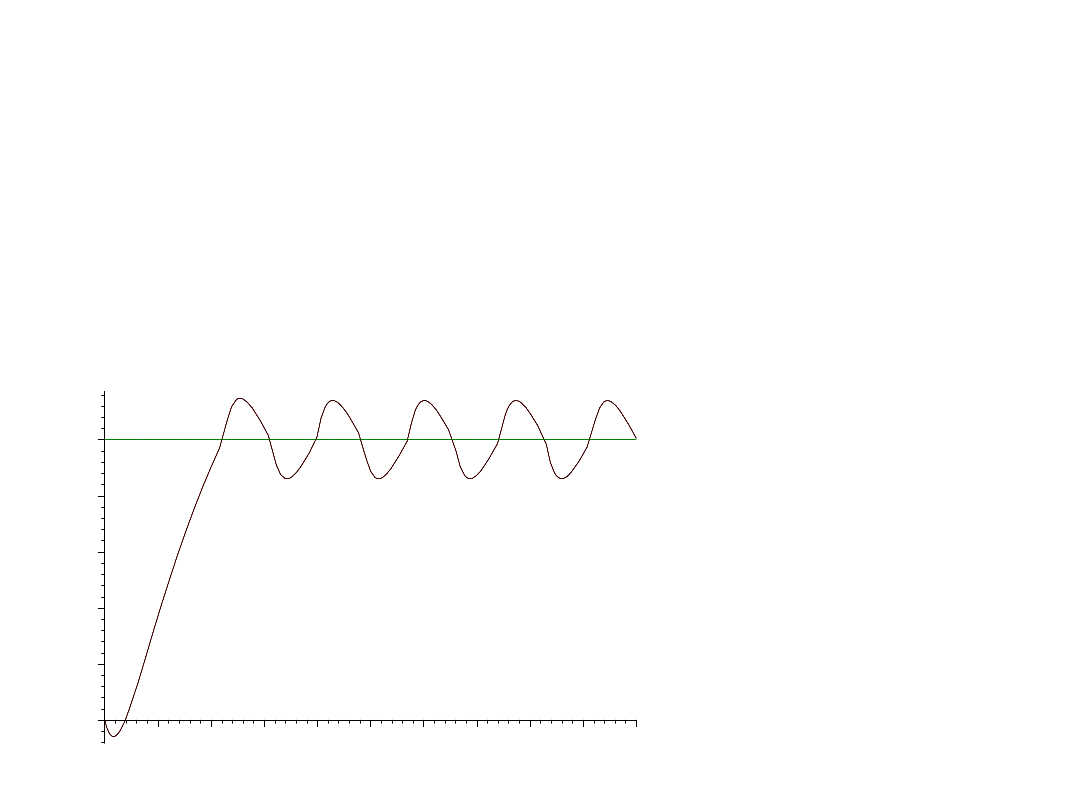
Układ otwarty; u=10

Uwagi:

1. Powolne działanie

obiektu.

2. Układ wrażliwy na

zmiany parametrów
obiektu.

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

Regulacja dwupołożeniowa

; wartość zadana r =

10,obiekt typu

1/T)y’(t)+y(t)=u(t-T₀)

);

T=5, T

0

=1

(trans.

(e(-sT₀))/(Ts+1)),

(aproksymowany transmitancją ((1-(T₀/2)s)/((1+(T₀/2)s)(Ts+1))).
Opis obiektu aproksymowanego przy pomocy równań
różniczkowych: Tw′+w=((2T+T₀)/(2T-T₀))u, T

0

x′+x=-(2T₀/(2T-

T₀))u oraz y=x+w, y - wyjście);
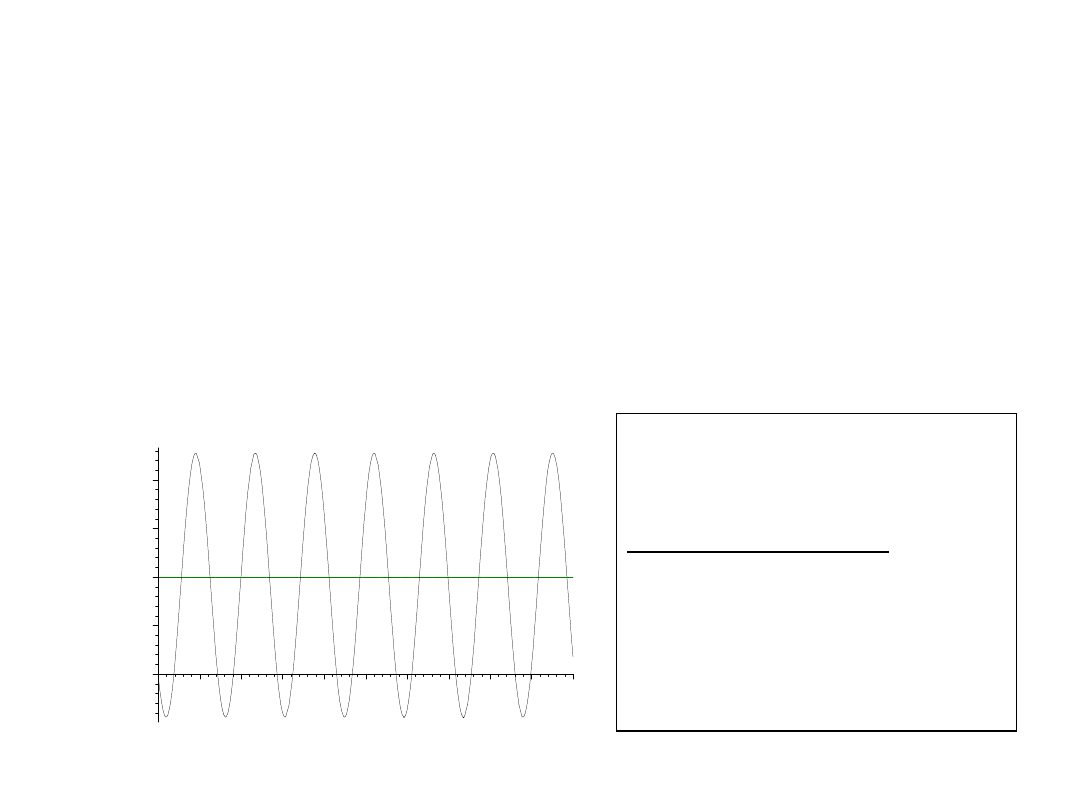
Spróbujmy
Reg. dwupołożeniowy:

u = 20

jeśli

y≤10

oraz

u = 0

jeśli

y >10

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

Uwaga: Wyraźny
brak stanu
ustalonego!
Znaczne oscylacje.

Regulacja ciągła P, PI i PID

; wartość zadana r = 10,obiekt

typu ((e

{sT₀}

)/(Ts+1)) ( tj.

(1/T)((dy)/(dt))+y=u(t-T₀)

),

aproksymowany transmitancją ((1-(T₀/2)s)/((1+(T₀/2)s)(Ts+1))).
Opis obiektu aproksymowanego przy pomocy równań
różniczkowych: Tw′+w=((2T+T

0

)/(2T-T

0

))u, T

0

x′+x= -(2T

0

/(2T-T

0

))u

oraz y=x+w (y - wyjście); T=5, T

0

=1

Eksperyment Zieglera-Nicholsa: K

osc

=11, T

osc

=

2.5;

0

5

10

15

20

2

4

6

8

10 12 14 16 18 20

u = K(r-w);

regulator P

Eksperyment Z-N:
zwiększamy wartość K,
do wartości K

osc

, przy

której pojawiają się
drgania niegasnące (z
okresem T

osc

)

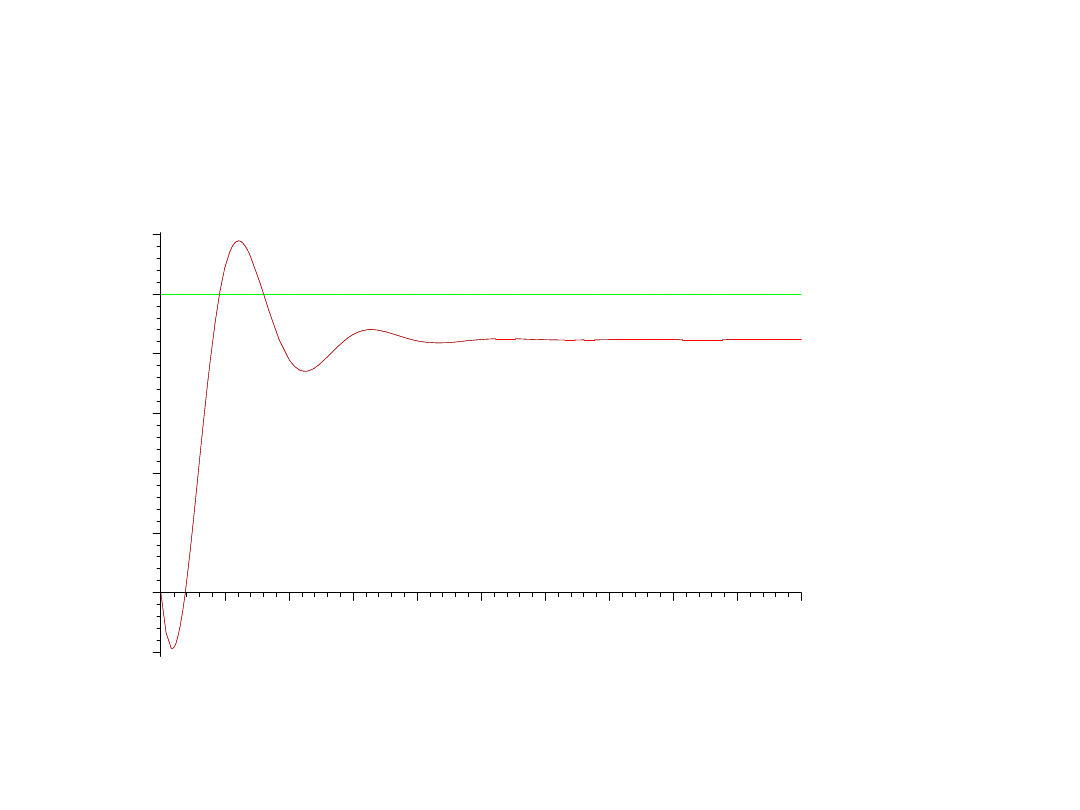
Regulator P; nastawa Z-N: Reguła:

K=0.5K

osc

Zatem

K=5.5

-2

0

2

4

6

8

10

12

2

4

6

8

10 12 14 16 18 20

Duży uchyb w stanie ustalonym.

Oscylacyjny przebieg
przejściowy.

-2

0

2

4

6

8

10

12

14

16

2

4

6

8

10

12

14

16

18

20

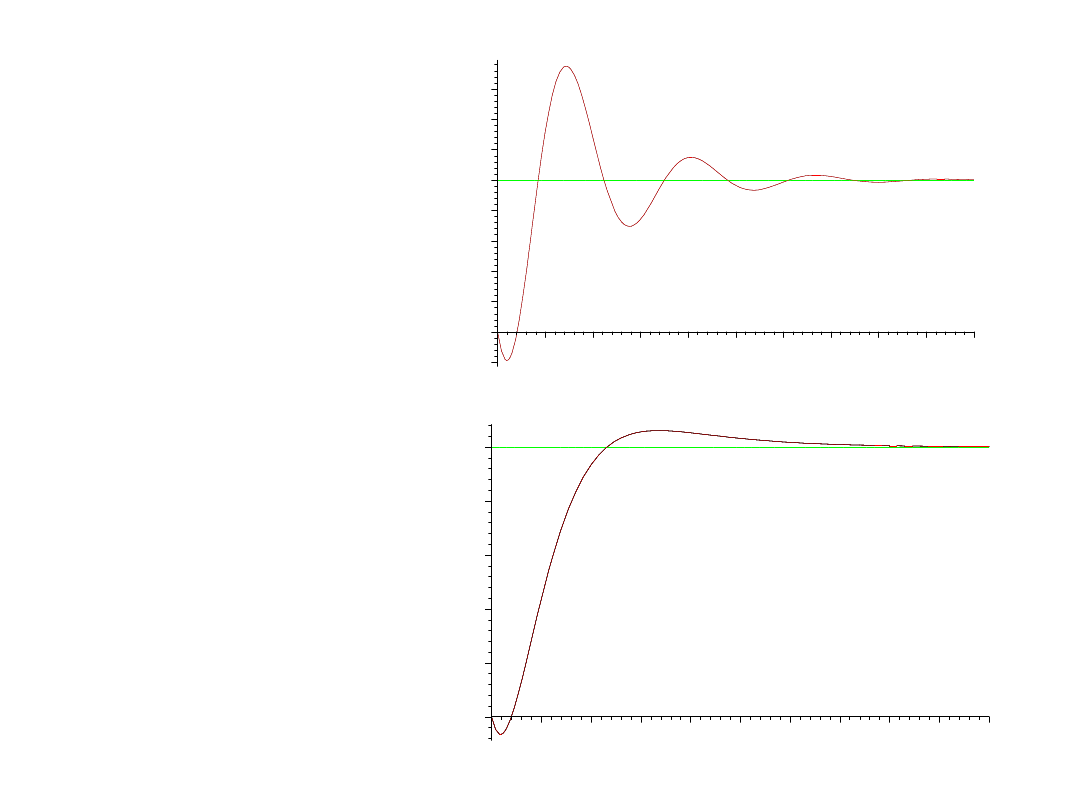
Reg. PI; nastawy Z-

N

:

Reguła:

K=0.45K

osc

,

T

I

= T

osc

/1.2

Zatem

K= 4. 95, T

I

= 2.

0833

Niestety, za duże
oscylacje!

Próbujemy ręcznej
korekty nastaw.
Korekta nastaw PI:

K=2, T

I

=4

Powolna (nieco)
regulacja.

0

2

4

6

8

10

2

4

6

8

10

12

14

16

18

20

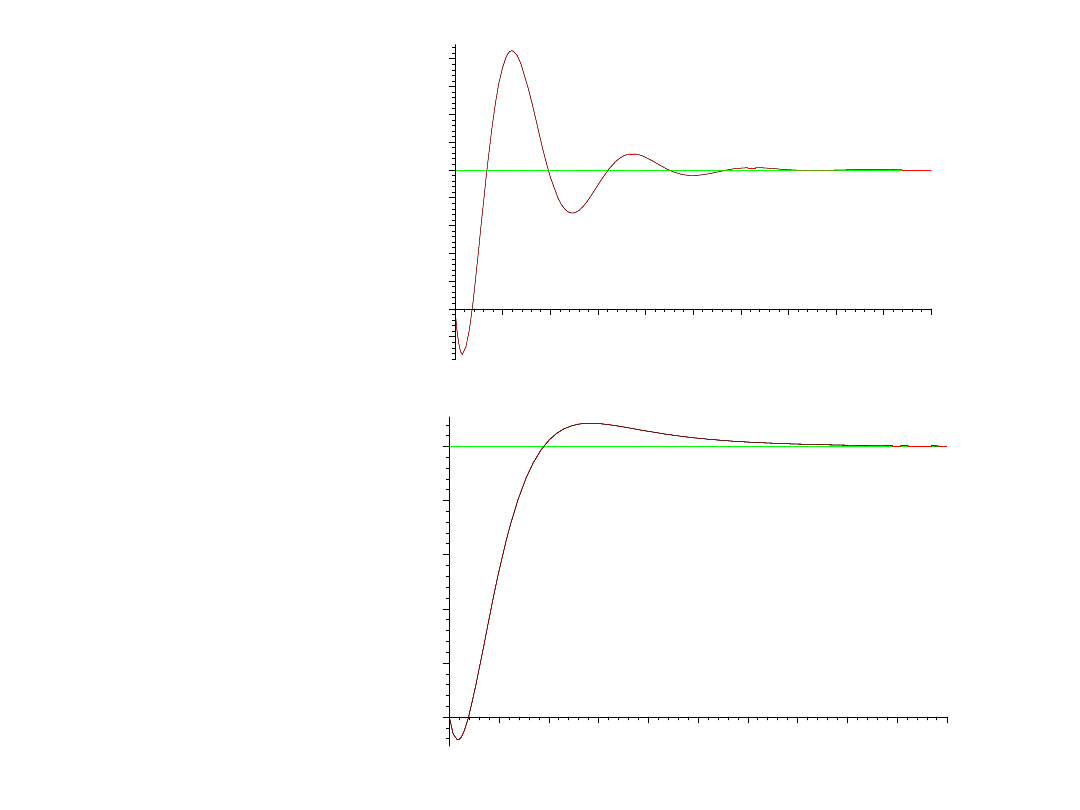
Reg. PID;

nastawy Z-N:

Reguła:

K = 0.6K

osc

,

T

I

= T

osc

/2,

T

D

= T

osc

/8

Zatem

K=6.6, T

I

= 1.25,

T

D

=0.3152

Za duże oscylacje.

-2

0

2

4

6

8

10

12

14

16

18

2

4

6

8

10 12 14 16 18 20

0

2

4

6

8

10

2

4

6

8

10 12 14 16 18 20

Próbujemy ręcznej
korekty nastaw PID
(metoda „prób i błędów) ,
przykł. nastawy
skorygowane:
K=2.5, T

I

= 4, T

D

=

0.15625

Uzyskaliśmy stosunkowo niezły

regulator, aczkolwiek regulacja nadal
jest niezbyt szybka, ale… czy
możemy otrzymać lepszy? Dlaczego
takie a nie inne nastawy są właściwe?
Dlaczego taki a nie inny regulator?

Bez pogłębienia znajomości teorii nie

odpowiemy na te pytania.

Satelita; problem stabilizacji

kąta ustawienia w określonej

osi

Równanie ruchu:

y′′′+2y′′=1.8u

(transmitancja obiektu G(s)=((0.9)/(s²))(2/
(s+2)))

Próbujemy układ zamknięty z

regulatorem P

u=K(r-y)

; niech

r =5

,

równanie ruchu (układ zamknięty):

y′′′+2y′

′=1.8K(5-y); K=1

(trans. u. z. G

z

(s)=((1.8K)/(s³+2s²+1.8K)))

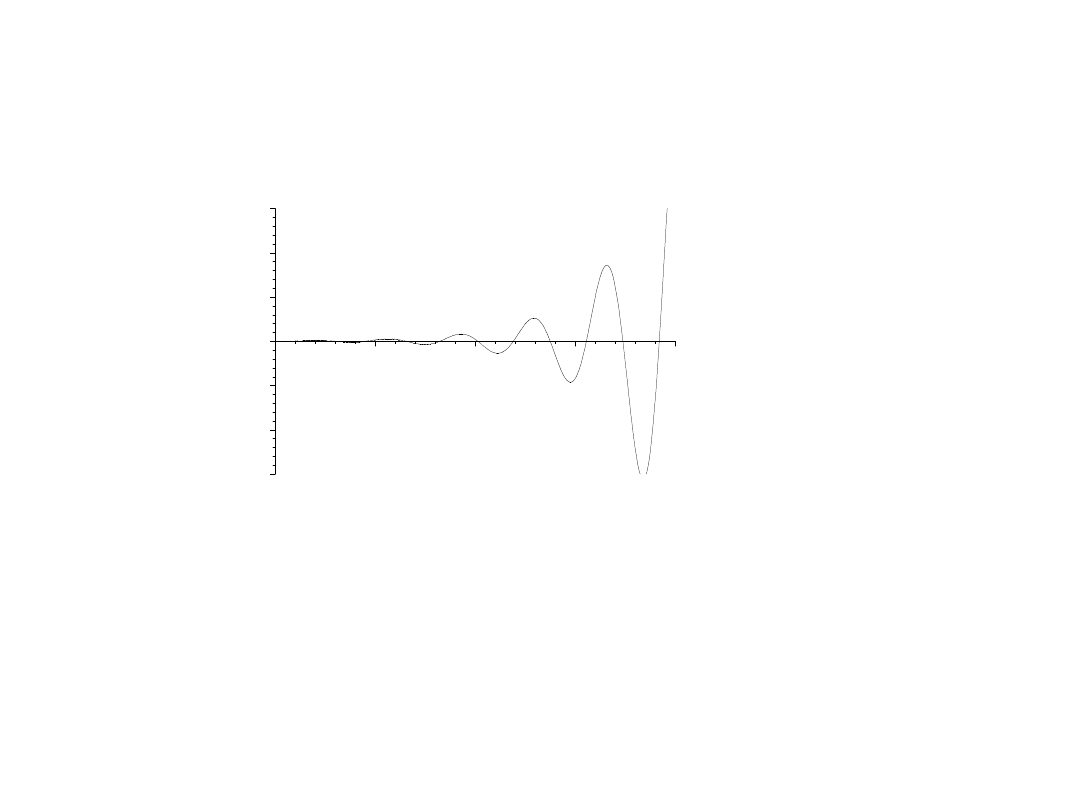
-1500

-1000

-500

0

500

1000

1500

10

20

30

40

Symulacja rozwiązania

y′′′

+2y′′=1.8K(5-y); K=1

Układ niestabilny!

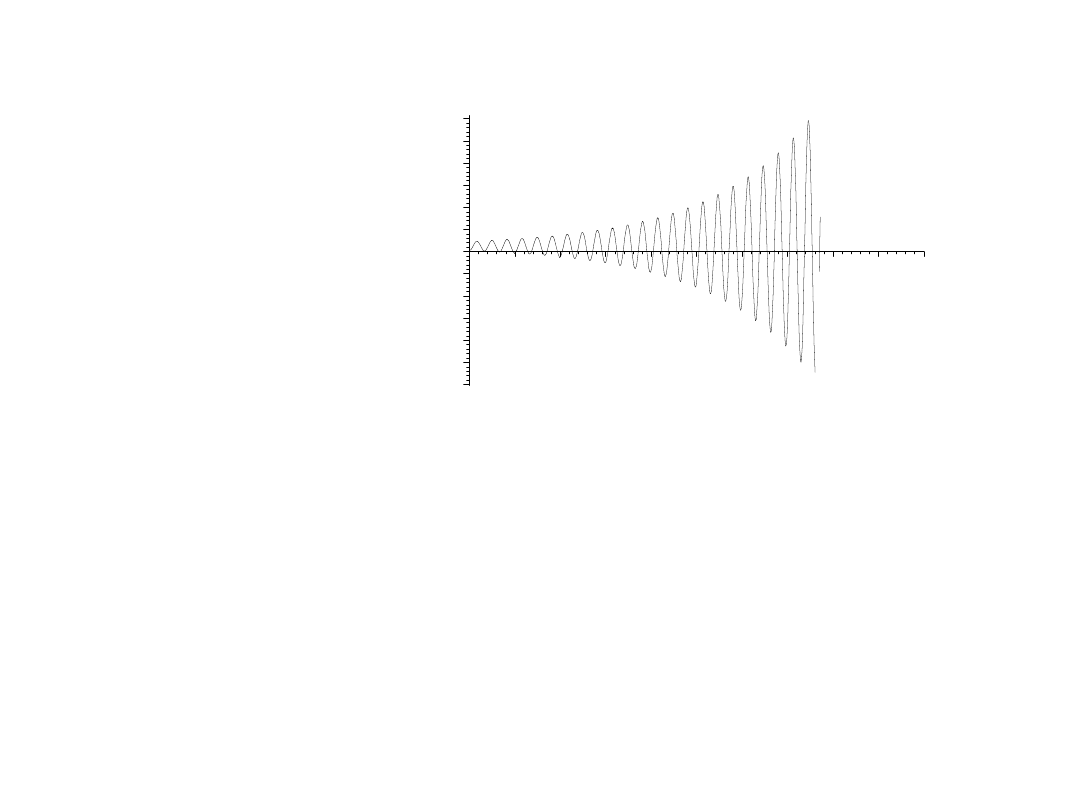
Spróbujmy K=0.01

-120

-100

-80

-60

-40

-20

0

20

40

60

80

100

120

200 400 600 800 100012001400160018002000

Także układ niestabilny. Jest on niestabilny dla dowolnego
K>0!

Nie możemy zastosować nastaw Zieglera-Nicholsa, bo, po
pierwsze, nie jest wykonalny eksperyment z regulatorem P.
Ponadto, nie wiemy, czy regulator PID może być
zastosowany.

W jaki sposób zaprojektować dobry regulator?

Widać, że nie jest to takie proste. Trzeba
zrezygnować z metody ad-hoc i głębiej wniknąć w
teorię, zrozumieć działanie układów dynamicznych i
ich własności, poznać metody projektowania.

Symulacja rozwiązania

y′′′+2y′′=1.8K(5-y);
K=0.01

Sterowniki przemysłowe,

sterownik PLC

Uwagi

•

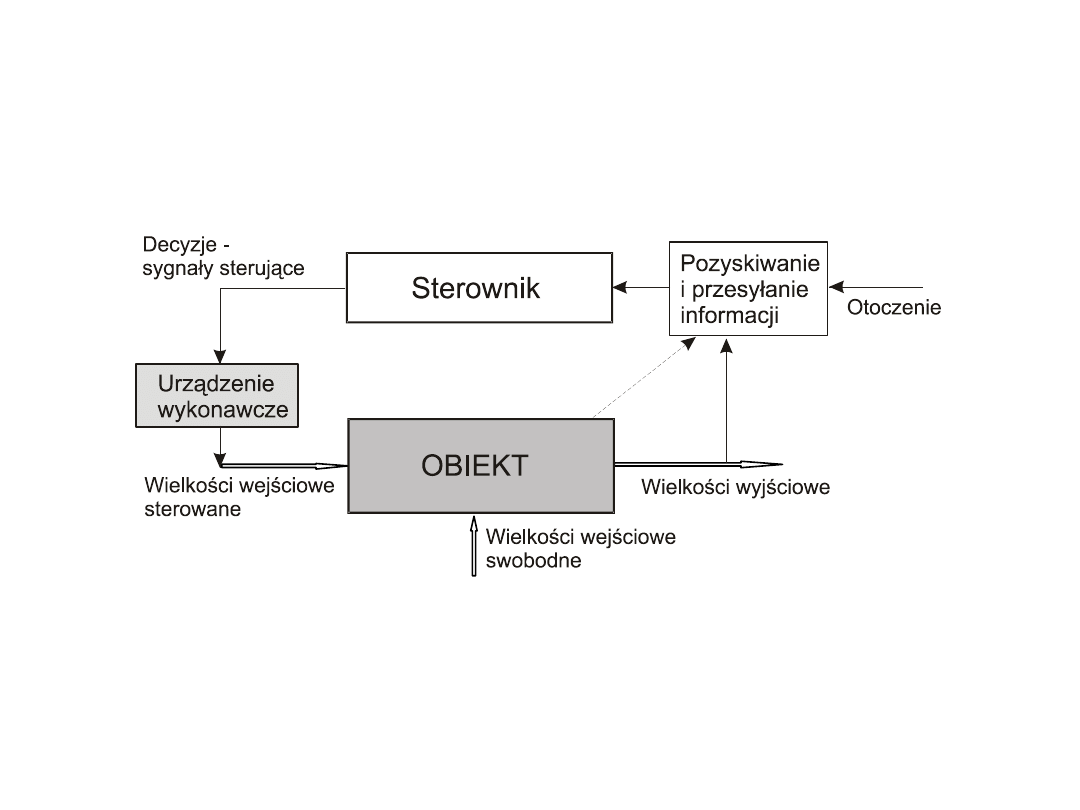
W zależności od natury obiektu i stopnia złożoności zadania sterowania logicznego lub

zadania regulacji automatycznej może ono być realizowane przez:

•

Stosunkowo proste specjalizowane układy elektromechaniczne lub elektroniczne (w tym

mikroprocesorowe) zintegrowane z obiektem sterowania (np. sterowanie bramą garażową,

kuchenką mikrofalową, pralką automatyczną, wtryskiem paliwa do silnika spalinowego w

samochodzie, itd.). Układy tego typu określa się jako układy wbudowane (embedded

systems).

•

Programowalne sterowniki logiczne (PLC – Programmable Logic Controllers),

wyodrębnione, specjalizowane urządzenia do realizacji zadań sterowania logicznego. Są one

produkowane z reguły jako całe rodziny urządzeń, od prostszych obsługujących jedynie

niewiele sygnałów binarnych (dla realizacji zadań sterowania logicznego – jak np. sterowanie

linią butelkowania) do bardziej złożonych obsługujących zarówno wiele sygnałów binarnych

jak i sygnały ciągłe (dla realizacji zadań sterowania binarnego i zadań regulacji).

•

Zadania programowalnych sterowników logicznych realizowane są również obecnie przez

typowe komputery PC (najczęściej w wykonaniu przemysłowym) wyposażone w

odpowiednie karty wejścia/wyjścia umożliwiające obsługę sygnałów pomiarowych (binarnych

i ciągłych) i wyprowadzanie sygnałów sterujących.

•

Regulatory i sterowniki przemysłowe – samodzielne urządzenia sterujące konstruowane

dla realizacji jednej pętli regulacji bądź kilku pętli regulacyjnych. Te ostatnie to z reguły

urządzenia wielofunkcyjne (multifunction controllers), umożliwiające równoczesną realizację

kilku pętli regulacyjnych i zadań sterowania binarnego (mają wejścia/wyjścia zarówno ciągłe

jak i binarne). Stąd regulatory wielofunkcyjne (sterowniki przemysłowe - PAC) upodabniają

się do sterowników PLC – z tą różnicą, że są konstruowane z reguły przede wszystkim dla

realizacji zadań regulacji, a PLC z reguły przede wszystkim do zadań sterowania binarnego.

•

Podobnie jak w przypadku PLC, zadania regulatorów realizowane są również obecnie przez

typowe komputery PC (w wykonaniu przemysłowym) wyposażone w odpowiednie karty

wejścia/wyjścia umożliwiające obsługę sygnałów pomiarowych i wyprowadzanie sygnałów

sterujących.

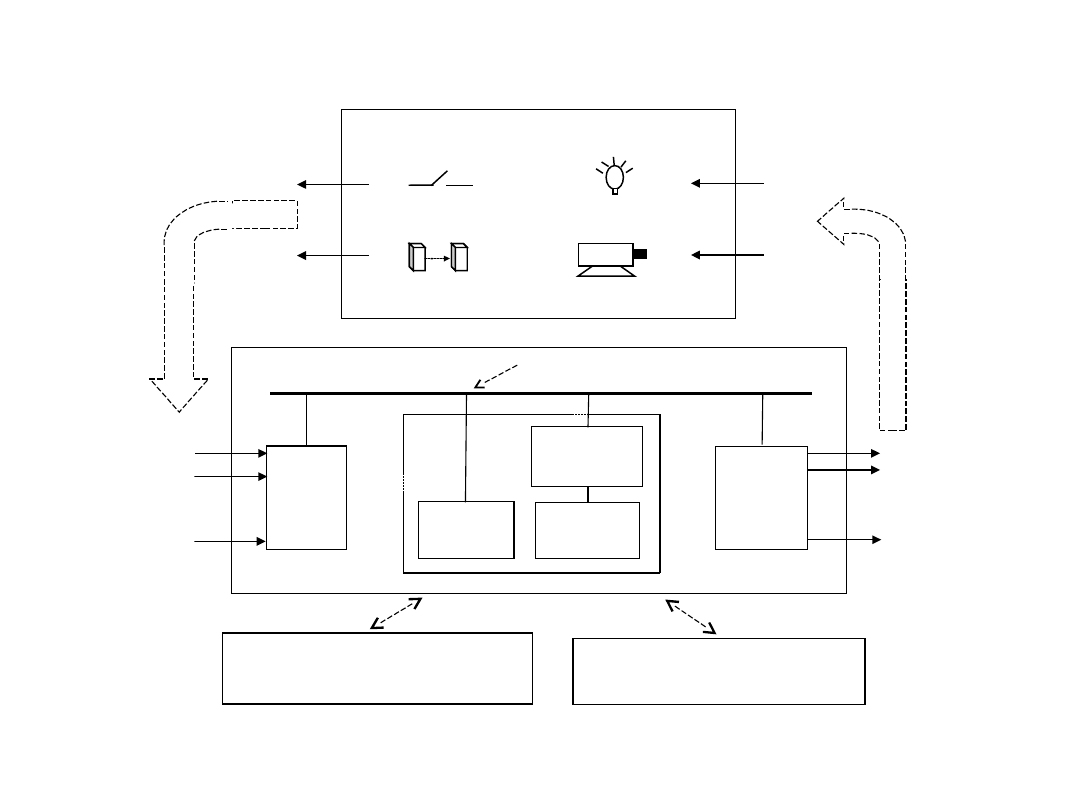
PLC

Procesor

główny

Pamięć

danych

Pamięć

programu

CPU

Moduł

wejść

Moduł

wyjść

I0.0
I0.1

I1.5

Q0.0
Q0.1

Q1.1

Obiekt sterowany

Przyciski

Czujniki optyczne

Oświetlenie

Napędy

silników

Programator

PC + STEP7, MicroWin

Stacja Operatora Procesu

PC+ProTool/Pro, WinCC

Magistrala

PLC

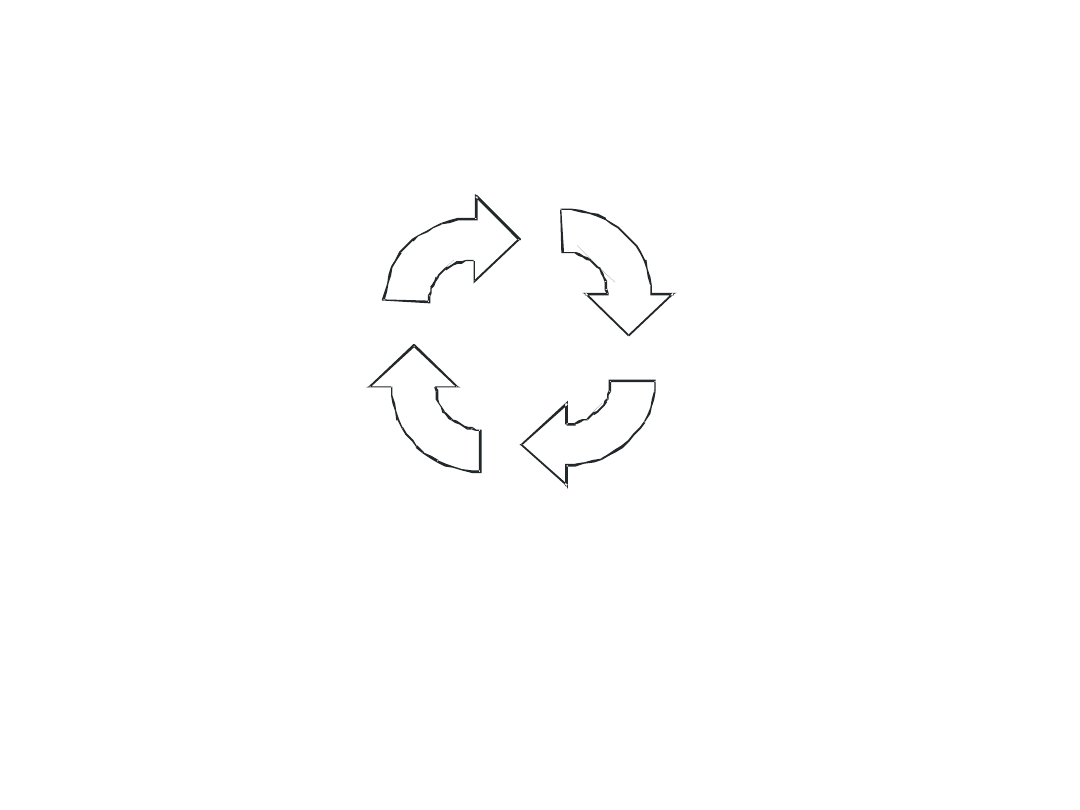
Cykl

PL C

2. W y konani e

programu

3. Uaktualnienie

wy jsc

1. O dczyt

wejsc

4. D iagno styka

i ko munikacja

Pętla programowa PLC

Ad. 2. – Program użytkownika
Sterownik obsługuje przerwania w dowolnej części cyklu
programu

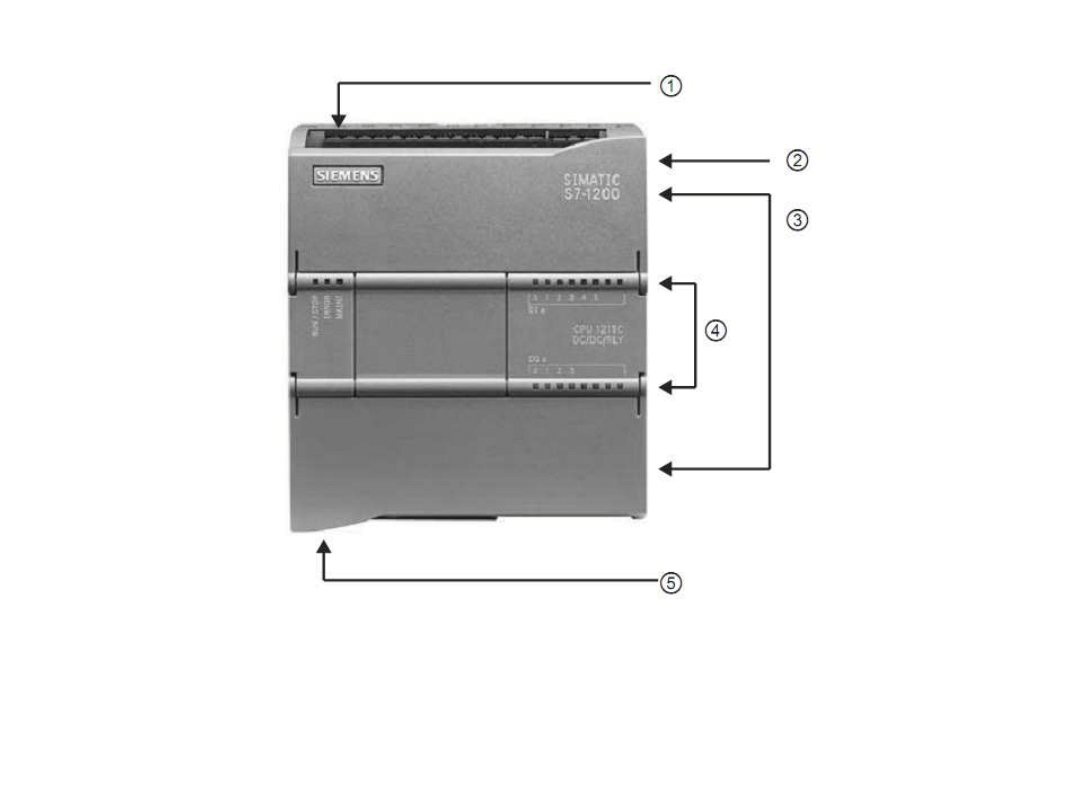
1-złącze zasilające, 2-gniazdo karty pamięci, 3-rozpinane złącza
na przewody pod
klapkami, 4-sygnalizacyjne diody LED dla zintegrowanych
We/Wy, 5-złącze PROFINET