Weryfikacja i testy

statystyczne

Weryfikacja H

0

• H

0

: hipoteza zerowa (

1

=



2

)

•

H

1

: hipoteza alternatywna (

1





2,

)

• W oparciu o wynik obliczonego testu z danych z próby

możemy H

0

: odrzucić lub nie.

• Nie wiemy czy H

0

: zachodzi

w populacji.

• Zatem można popełnić:
• błąd I rodzaju jeśli odrzucimy H

0

jeśli jest prawdziwa w

populacji

• błąd II rodzaju jeśli nie odrzucimy H

0

wtedy kiedy jest

ona fałszywa w populacji

• W naukach medycznych przyjmujemy poziom istotności

 =

0,05

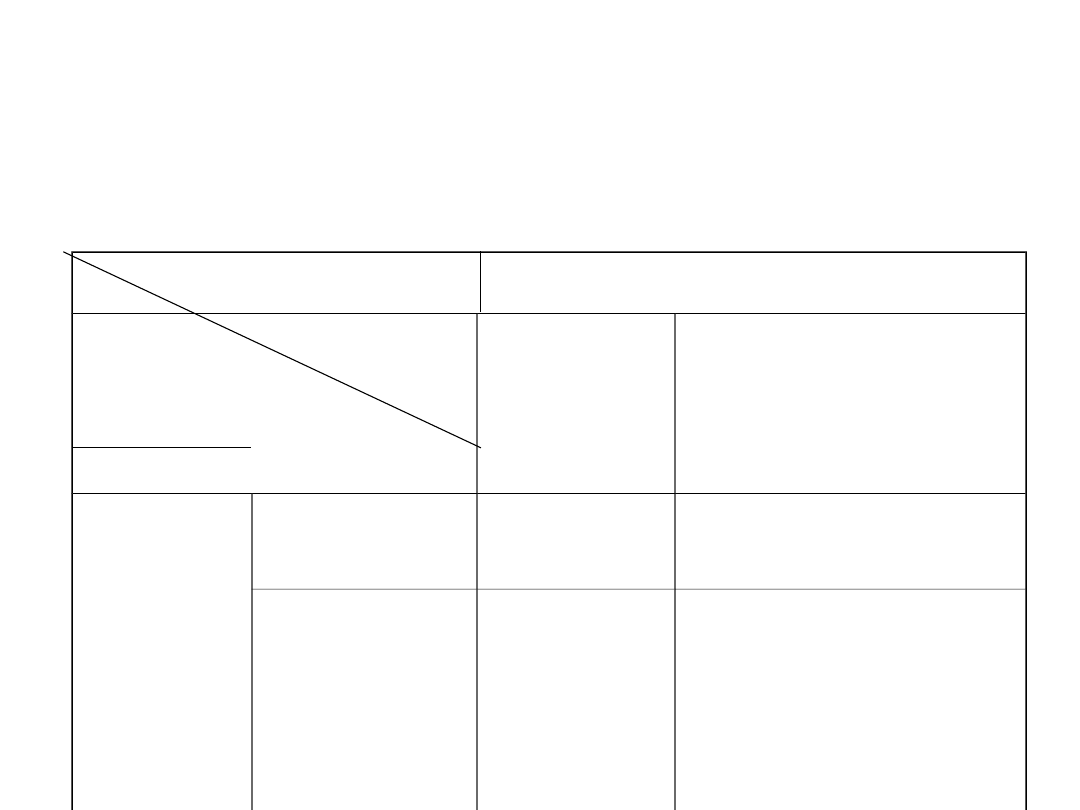
Błędy przy wnioskowaniu

 = prawdopodobieństwo popełnienia błędu

I rodzaju

= prawdopodobieństwo popełnienia błędu

II rodzaju

Populacja

H

0

jest

prawdziw

a

H

0

jest fałszywa

Czyli prawdziwa

jest

H

1

Decyzja
z
wynikó
w
oblicze
ń

z

próby

Przyjęcie

H

0

1- 

Błąd II rodzaju



Odrzucenie

H

0

Błąd I

rodzaju



1- 

Schemat weryfikacji hipotez

Sformułować hipotezę zerową H

o

i alternatywną H

1

oraz dobrać odpowiedni test do weryfikacji

Wykonać obliczenia i wybrać potrzebne wyniki,

przede

wszystkim

wartość

p

określającą

prawdopodobieństwo popełnienia błędu odrzucenia

H

o

, gdy jest prawdziwa w populacji (błąd I rodzaju).

Przyjąć poziom istotności , ale mniejszy niż lub

równy 0,05.

Podjąć decyzję o hipotezie zerowej H

o

:

jeżeli obliczona wartość p ≤ , odrzucamy H

o

i

przyjmujemy H

1

jeżeli obliczona wartość p > , to brak podstaw do

odrzucenia H

o

.

• Wniosek w populacji z obliczeń w grupie

.

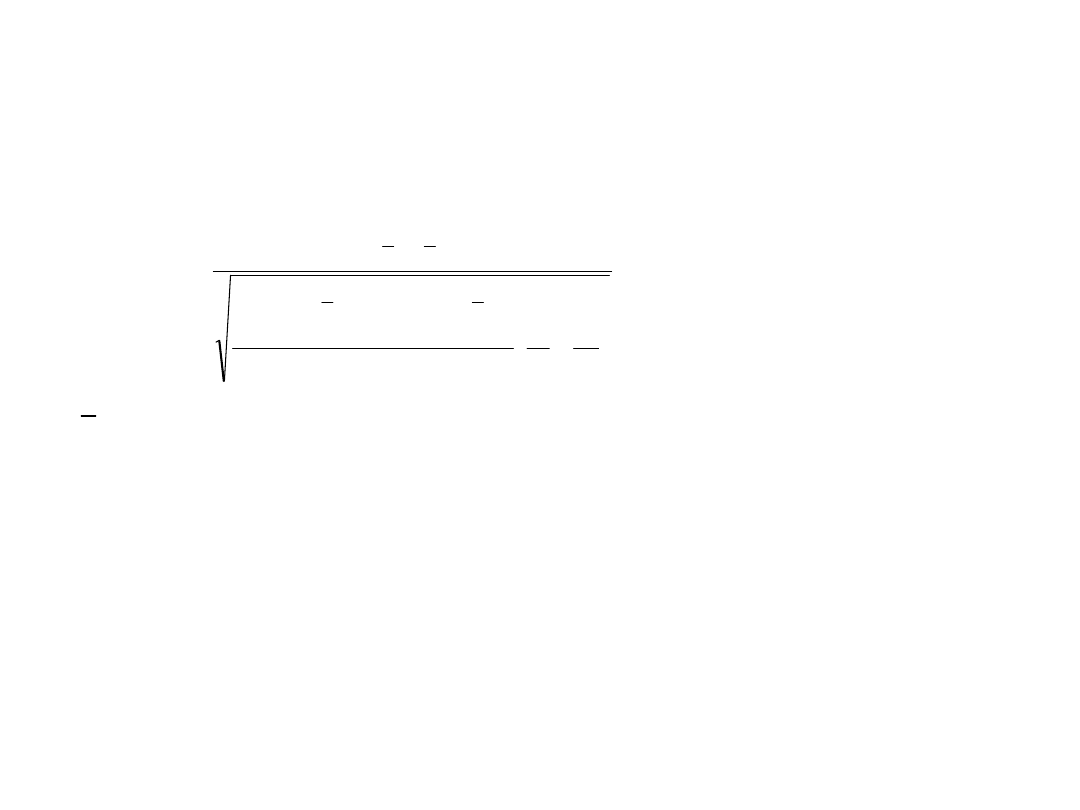
Test t-Studenta

Założenie:

Cecha X ma rozkład normalny w obu

populacjach o jednorodnych wariancjach, czyli N(



1

,

)

i

N(



2

,

)

• H

0

: 

1

=



2

hipoteza zerowa

•

H

1

: 

1





2,

hipoteza alternatywna

• Gdzie
dane, średnie i liczebności w próbach

• W pakiecie statystycznym wyliczamy t i wartość p równą

prawdopodobieństwu popełnienia błędu I rodzaju (odrzucenie prawdziwej

H

0

)

• Wartość p porównujemy z przyjętym poziomem istotności



• Jeżeli p<



odrzucamy H

0

i stwierdzamy istotną różnicę między średnimi

• Przykłady w STATISTICA

)

1

1

(

2

)

(

)

(

2

1

2

1

2

2

2

2

1

1

2

1

n

n

n

n

x

x

x

x

x

x

t

i

i





















j

j

ij

n

x

x

,

,

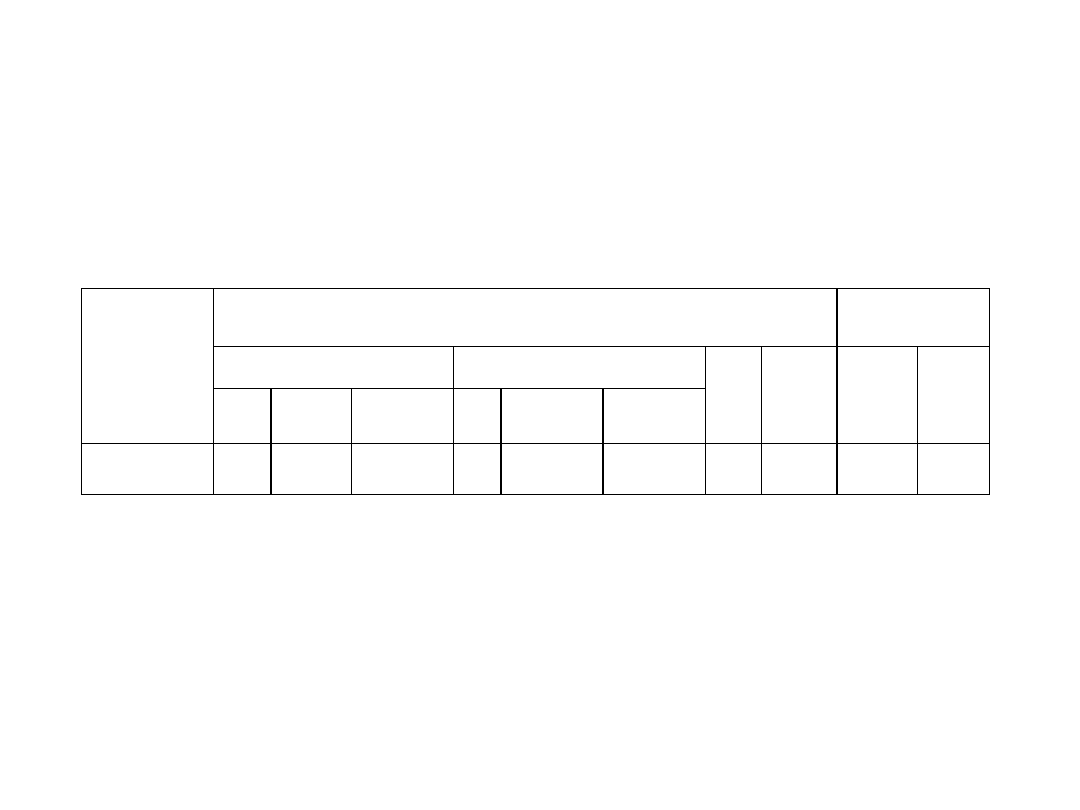
Przykład

n Średnia Odch.std. n

Średnia Odch.std.

WZROST (m) 65

1,72

0,05

81

1,67

0,05

6,25 0,000

1,22

0,40

Cecha

Równość średnich

jednorodność

wariancji

Mężczyźni

Kobiety

t

p

iloraz F

p

H

0

: średni wzrost mężczyzn= średni wzrost kobiet w populacji

H

0

: średni wzrost mężczyzn średni wzrost kobiet w populacji

Analiza wariancji

-

kilka populacji

• Dodatkowym założeniem które powinno być

spełnione to jednorodność wariancji. Należy

więc zweryfikować hipotezę zerową

H

o

: 

2

1

=. . .

=

2

k

kontra alternatywnej

H

1

: wariancje są

niejednorodne (test Levene’a)

• ANOVA
Hipoteza zerowa H

o

: 

1

=. . . =

k

H

1

: średnie są różne pomiędzy sobą.

• Jeżeli stwierdza się istotność różnic pomiędzy

średnimi, to należy znaleźć pomiędzy

którymi

średnimi te różnice są istotne (test Scheffego)

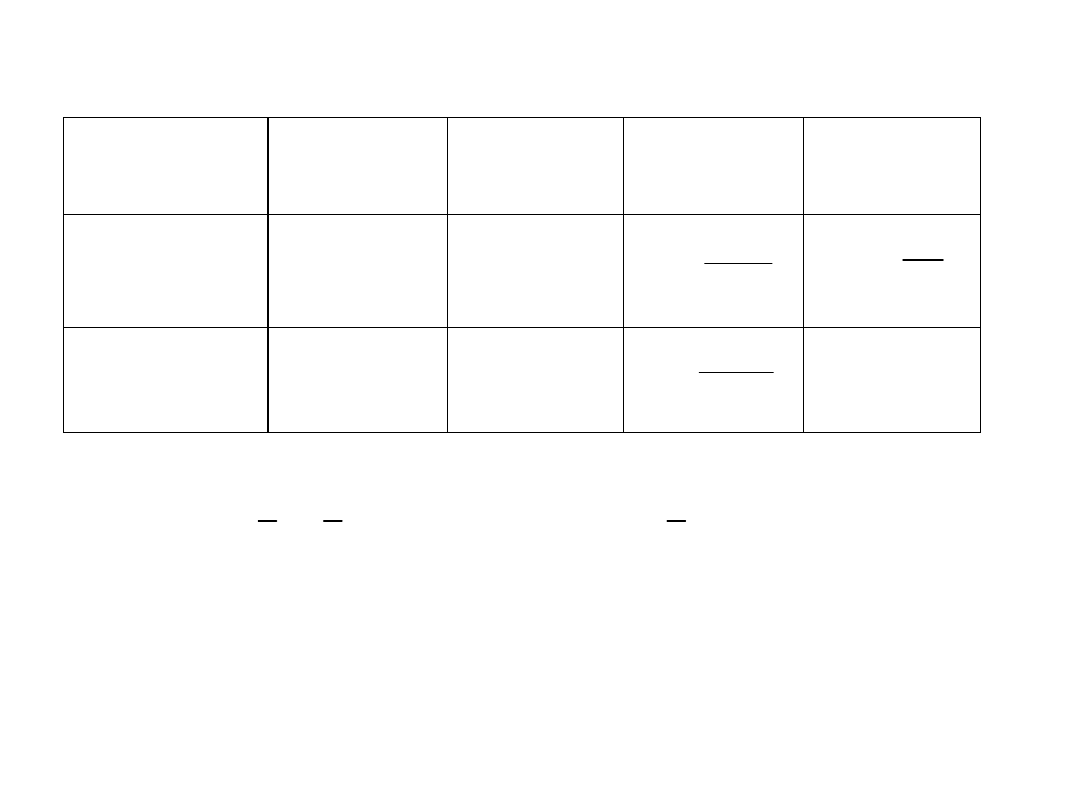
Tablica z wynikami analizy wariancji

Ź

r

ó

d

ł

o

S

u

m

a

k

w

a

d

r

a

t

ó

w

S

t

o

p

n

i

e

s

w

o

b

o

d

y

Ś

r

e

d

n

i

a

k

w

a

d

r

a

t

ó

w

W

a

r

t

o

ś

ć

F

(

W

a

r

t

o

ś

ć

p

)

Z

m

i

e

n

n

o

ś

ć

m

i

ę

d

z

y

g

r

u

p

o

w

a

S

S

m

k

-

1

V

m

=

1

m

S

S

k



m

b

V

F

V



B

ł

ą

d

S

S

b

n

-

k

V

b

=

b

S

S

nk



G d z ie: k – licz b a g r u p ; n – licz b a w sz y stk ich o só b z e w sz y stk ich g r u p

2

2

1

1

1

(

) ;

(

)

j

n

k

k

m

j

j

b

ij

j

j

j

i

S S

n x

x

S S

x

x

















 

x

ij

w y n ik cech y u i-tej o so b y w j-tej g r u p ie, n

j

– licz b a o só b w j-tej g r u p ie

 x

j

– śr ed n ia w j -tej g r u p ie,  x – śr ed n ia z w sz y stk ich p o m ia r ó w

Jeżeli wartość p <0,05 to są różnice między średnimi, należy

znaleźć między którymi (test Scheffe’go)

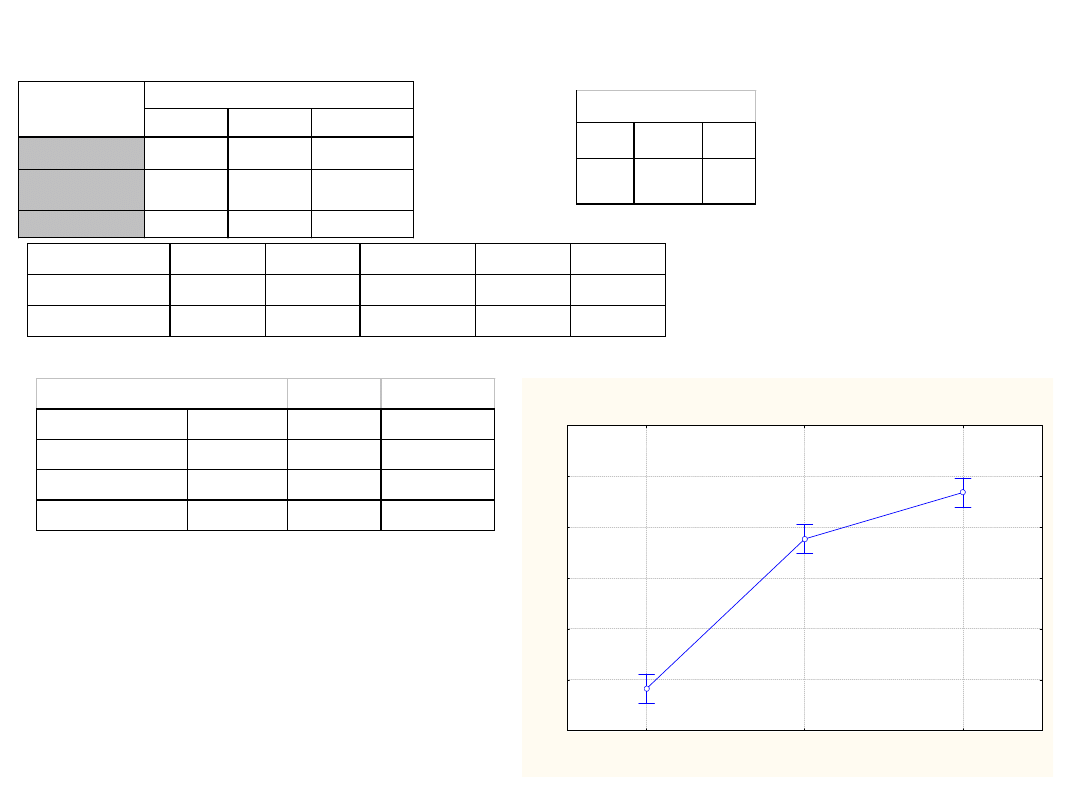
Przykład ANOVA

n

x

s

chirurgia

21

39,1

2,8

interna

21

53,9

3,4

ginekologia

21

58,4

3,6

oddział

wiek

Źródło

SS

Stopnie

V

F

p

oddział

4265,4

2

2132,7 198,00

0,00

Błąd

646,3

60

10,8

Test Scheffego

oddział

chirurgia interna

ginekologia

chirurgia

0,000

0,000

interna 0,000

0,000

ginekologia 0,000

0,000

Bieżący efekt: F(2, 60)=198,00, p=0,0000

Pionowe słupki oznaczają 0,95 przedziały ufności

chirurgia

interna

ginekologia

oddział

35

40

45

50

55

60

65

w

ie

k

Test Levene'a

F

p

wiek

1,61 0,21

Test Manna-Whitneya

Stosowany do oceny różnic jednej cechy pomiędzy

dwoma populacjami, gdy nie spełnione założenia przy

teście t_Studenta

Dane: x

11

, . . . x

n1

z 1-szej populacji; x

12

, . . . x

m2

z 2-giej populacji.

Porządkujemy obie próby razem i nadajemy im rangi oddzielnie.

Wartość tego testu wyliczana jest z wzoru:

1

(

1)

2

n n

U nm

R









gdzie: n, m liczebności grup, R

1

jest sumą rang w 1-szej grupie.

Jeżeli p<



stwierdzamy istotną różnicę analizowanej cechy między populacjami

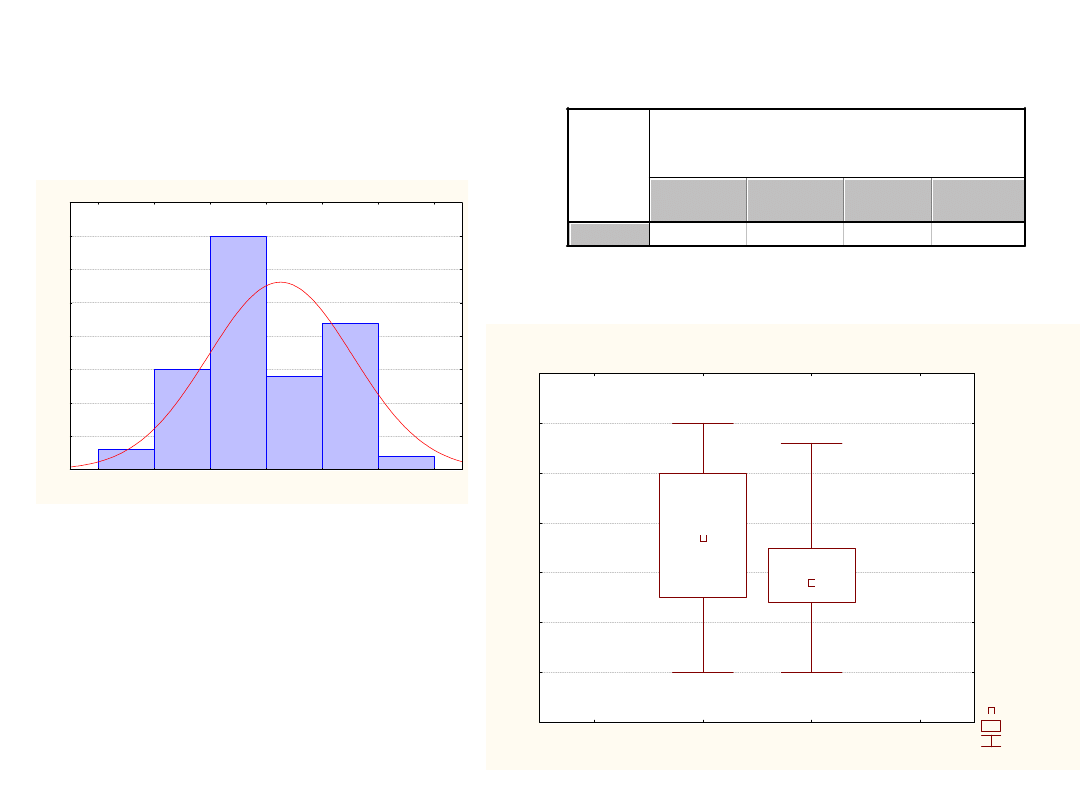
Przykład

U kobiet tętno w cukrzycy

Test U Manna-Whitneya (bazaStomat)
Wzg.zmienn. Cukrzyca

zmienna

Sum.rang

NIE

Sum.rang

TAK

U poziom p

Tętno

2470

1717

771

0,038

Wykres ramka-wąsy dla grup

Zmienna: Tętno

Mediana
25%-75%
Min.-Maks.

NIE

TAK

Cukrzyca

50

60

70

80

90

100

110

120

Tę

tn

o

Shapiro-Wilk W=,93951,
p=,00037

Histogram: Tętno

50

60

70

80

90

100

110

X <= Granica klasy

0

5

10

15

20

25

30

35

40

Li

cz

b

a

o

b

s.

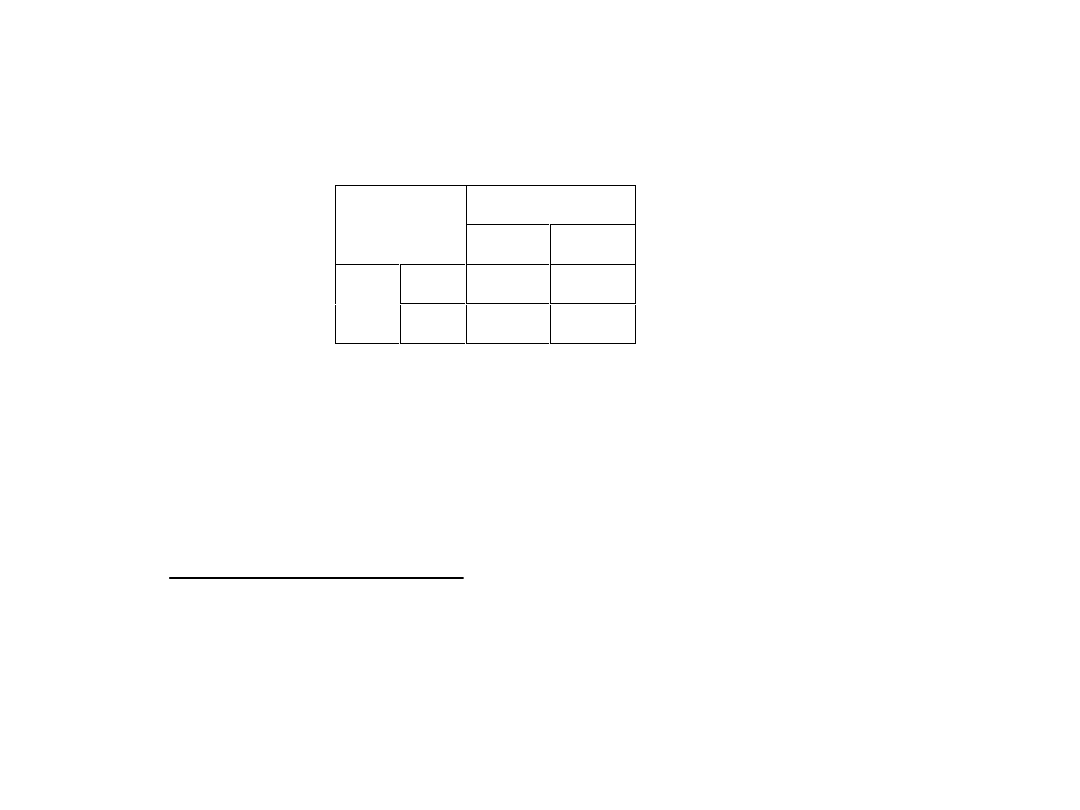
Test Chi

2

Dane w tabeli czteropolowej:

X

Cechy

1

0

1

a

b

Y

0

c

d

H

0

: cechy X, Y są niezależne

H

1

: cechy X, Y są zależne

C

h

i

2

=

2

(

)(

)

(

)

(

)

(

)

(

)

a

db

cabcd

acbdabcd





   

Jeżeli wartość p <0,05 to cechy X, Y są zależne

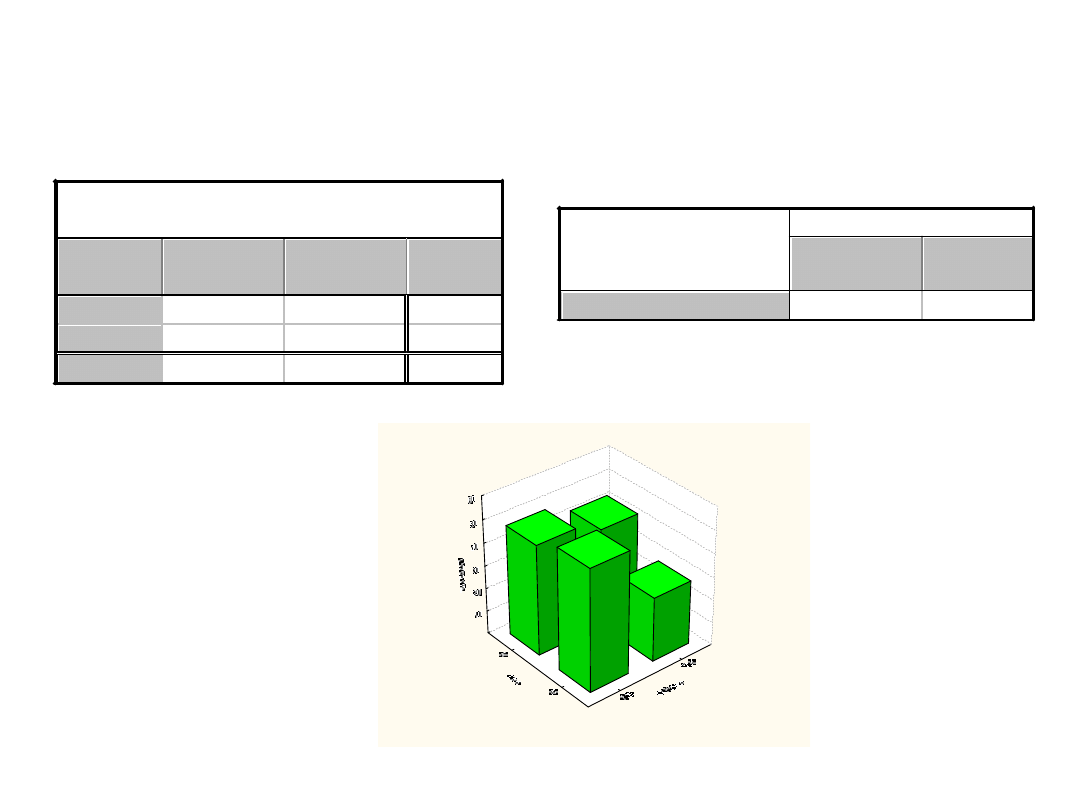
Przykład

Cukrzyca i płeć

Tabela liczności (bazaStomat)
Tabela:Płeć(2) x Cukrzyca(2)

Płeć

Cukrzyca

NIE

Cukrzyca

TAK

Wiersz

Razem

M

53

28 81

K

48

43 91

Ogół grp

101

71 172

Płeć x Cukrzyca

Statystyki:

Chi-kwadr.

p

Chi kwadrat Pearso

2,844759

p=,09168

Rozkład dwuwymiarowy: Płeć x Cukrzyca

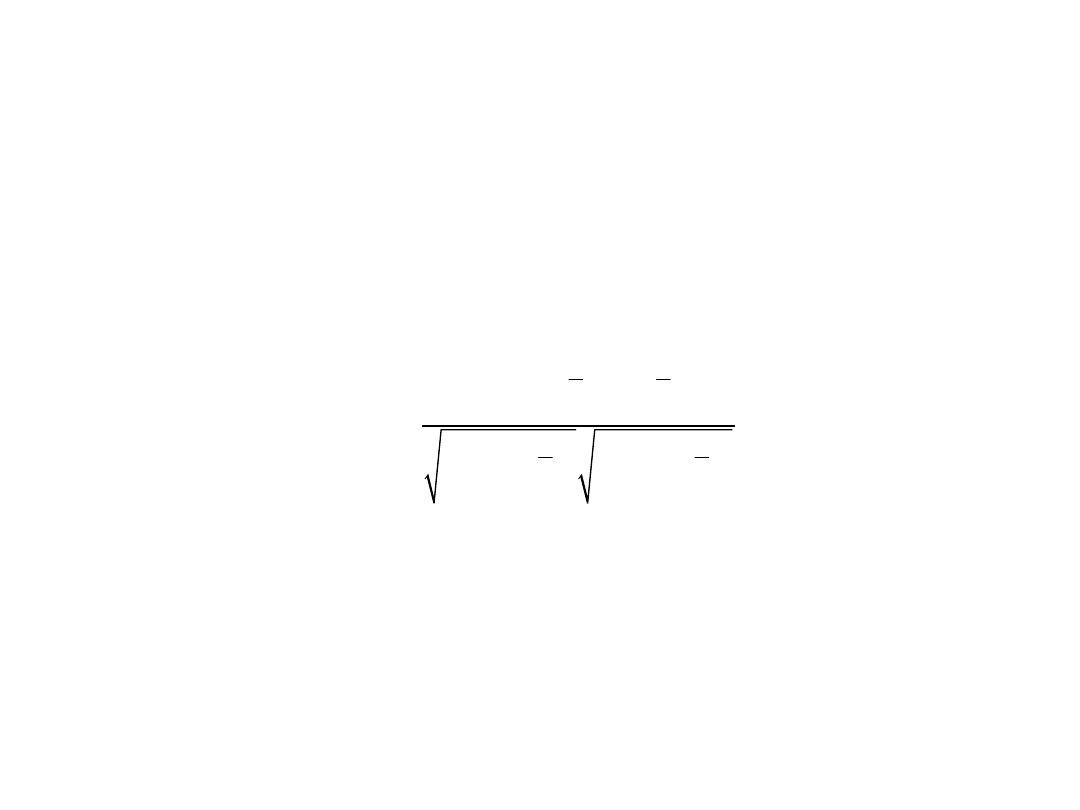
Korelacja prostoliniowa Pearsona

Jeżeli r>0 to zależność między cechami jest wprost proporcjonalna
Jeżeli r<0 to zależność między cechami jest odwrotnie

proporcjonalna

H

0

: cechy X, Y są niezależne

H

1

: cechy X, Y są zależne

Dane: x

1

, . . . x

n

wyniki 1-szej cechy; y

1

, . . . y

n

2-giej cechy

w n-elementowej próbie.

W

a

r

t

o

ś

ć

w

s

p

ó

ł

c

z

y

n

n

i

k

a

1

2

2

1

1

(

)

(

)

(

)

(

)

n

i

i

i

n

n

j

j

i

i

x xy y

r

x x

y y























Jeżeli wartość p <0,05 to cechy X, Y są zależne

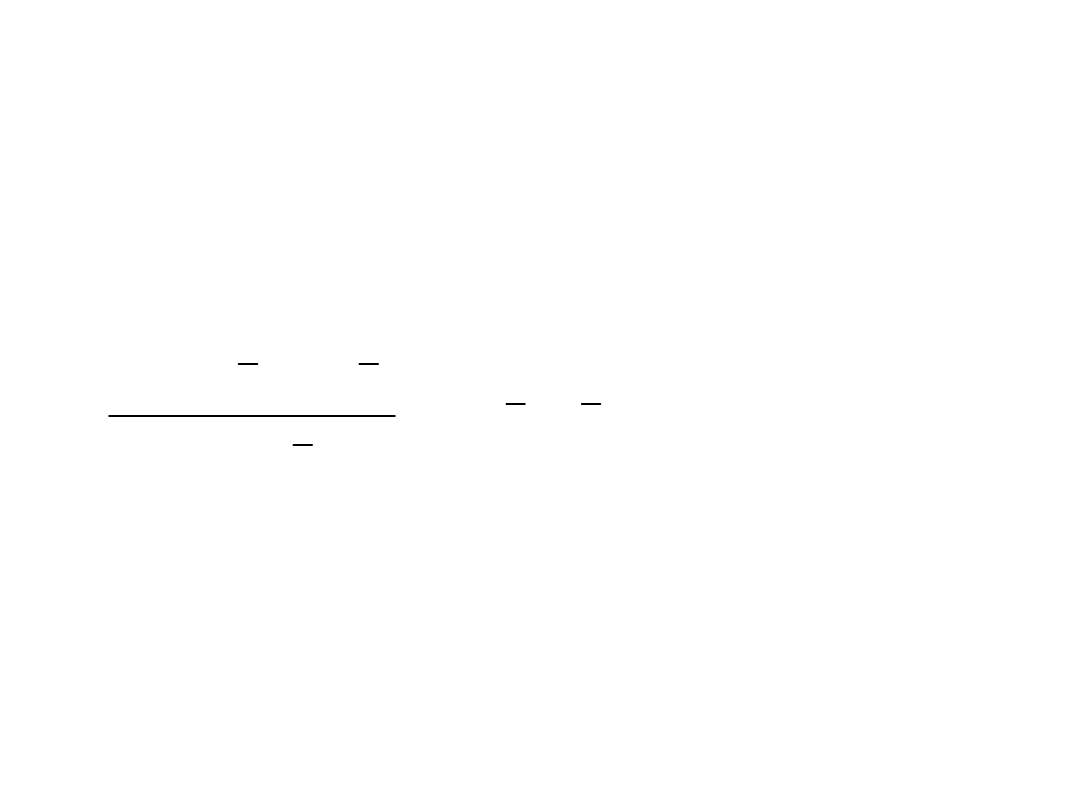
Regresja prostoliniowa

y=ax+b

• Współczynniki regresji a i b liczymy wtedy

jeżeli x i y są skorelowane

Dane: x

1

, . . . x

n

wyniki 1-szej cechy; y

1

, . . . y

n

2-giej cechy

w n-elementowej próbie.

1

2

1

;

(

)(

)

(

)

n

i

i

i

n

j

i

x

x y

y

a

b y ax

x

x











 







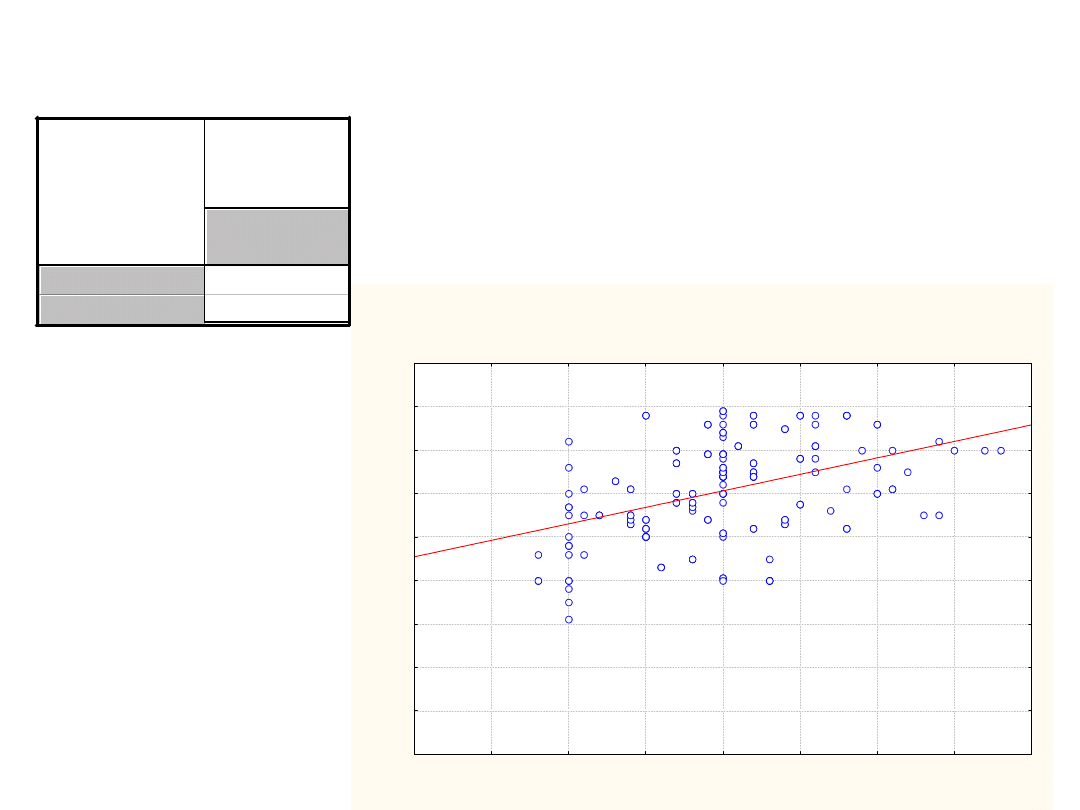
Przykład: waga i wzrost

Korelacje

Zmienna

WAGA (kg)

WZROST (m)

r=0,4340

p=,000

WZROST (m) vs. WAGA (kg)

WAGA (kg) = -48,32 + 75,884 * WZROST (m)

Korelacja: r = ,43400

1,50

1,55

1,60

1,65

1,70

1,75

1,80

1,85

1,90

WZROST (m)

20

30

40

50

60

70

80

90

100

110

W

A

G

A

(

k

g

)

Propozycja doboru testu statystycznego w zależności

od rodzaju cechy i typu analizy

Rodzaj cechy

Ilościowa

Spełnione założenia stosowania testu

parametrycznego

Typ analizy

Tak

Testy parametryczne

Nie

Testy

nieparametryczne

Jakościowa

1 cecha

2

grupy

Test t-Studenta

dla prób

niezależnych

Test Manna-

Whitney’a

Wilcoxona

Test



2

1 cecha

Więcej

niż 2

grupy

Analiza

wariancji

ANOVA

Test

Kruskala-

Wallisa

Test



2

1 cecha

mierzona

2 razy

1

grupa

Test t-Studenta

dla prób

zależnych

Test rang

Wilcoxona

dla prób

zależnych

Test 

2

lub test McNemary

2 cechy

1

grupa

Współczynnik

korelacji

prostoliniowej

Pearsona

Współczynnik

korelacji rang

Spearmana

Test



2

i współczynniki

siły związku