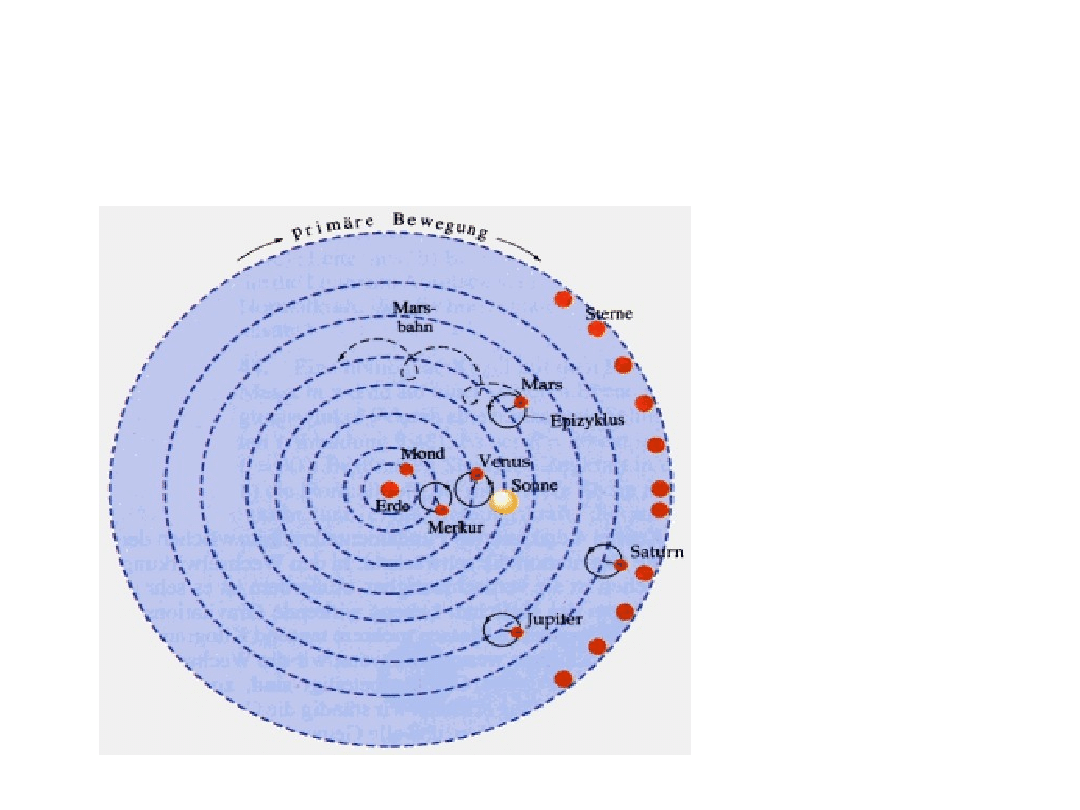
Prawa Keplera
W roku 140 n.e. Claudius Ptolemeus
zaproponował swój geocentryczny model
Świata.
Gwiazdy stałe
zostały ustalone, a
wszystkie inne
planety razem ze
Słońcem i
Księżycem krążyły
wokół Ziemi, przy
czym planety po
skomplikowanych
torach. System
ptolomeuszowski
był w stanie
wytłumaczyć
obserwowane
pętle kreślone
przez Mars.
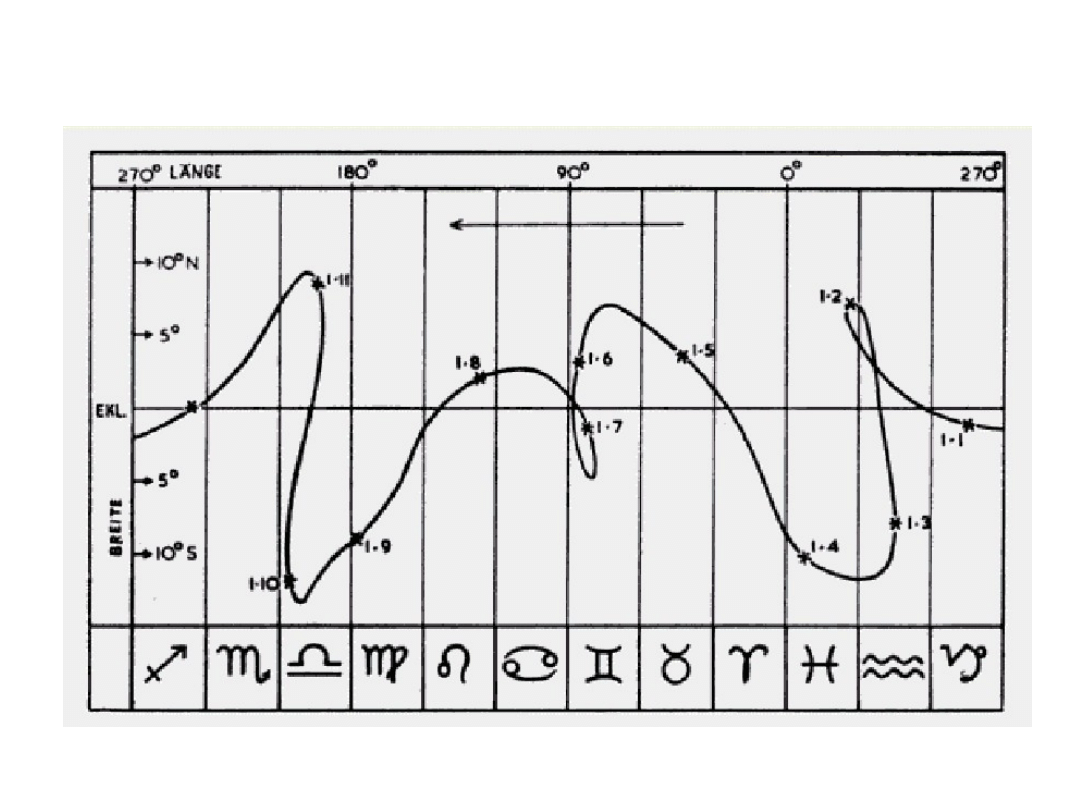
Zobaczmy, jak wyglądała linia zakreślana przez
Merkurego w 1955 r.
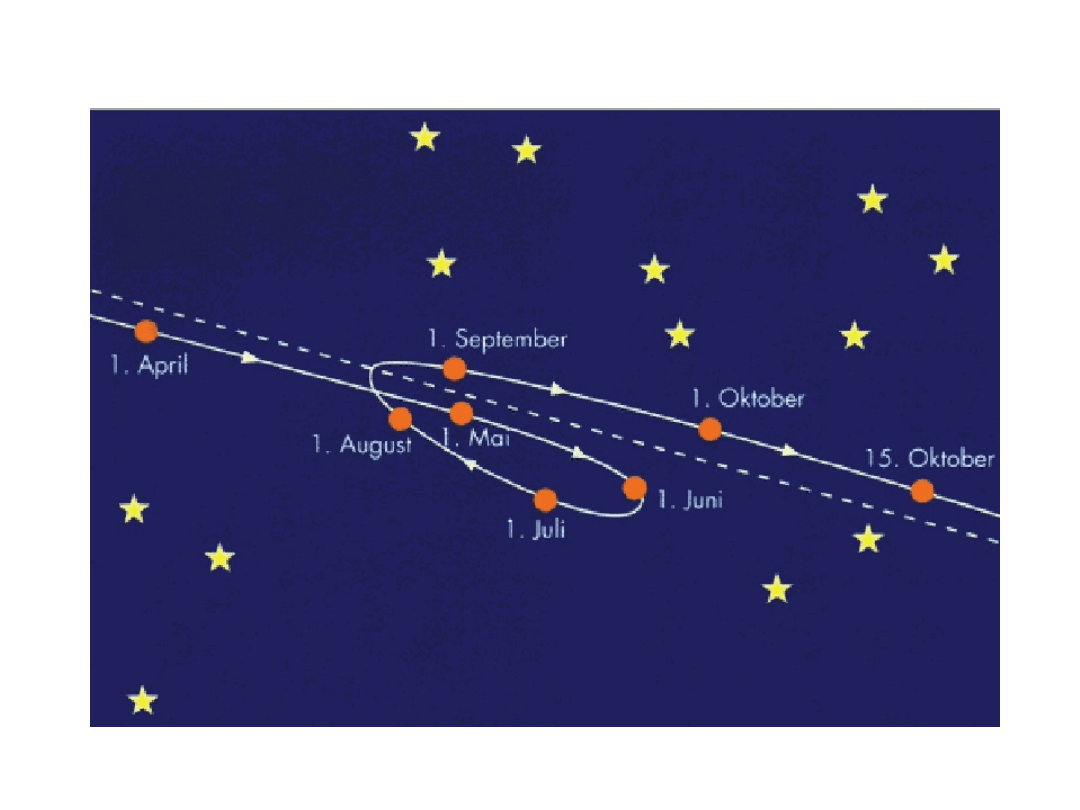
Poniżej widzimy pętle kreślone przez Marsa.
U.J. Schrewe
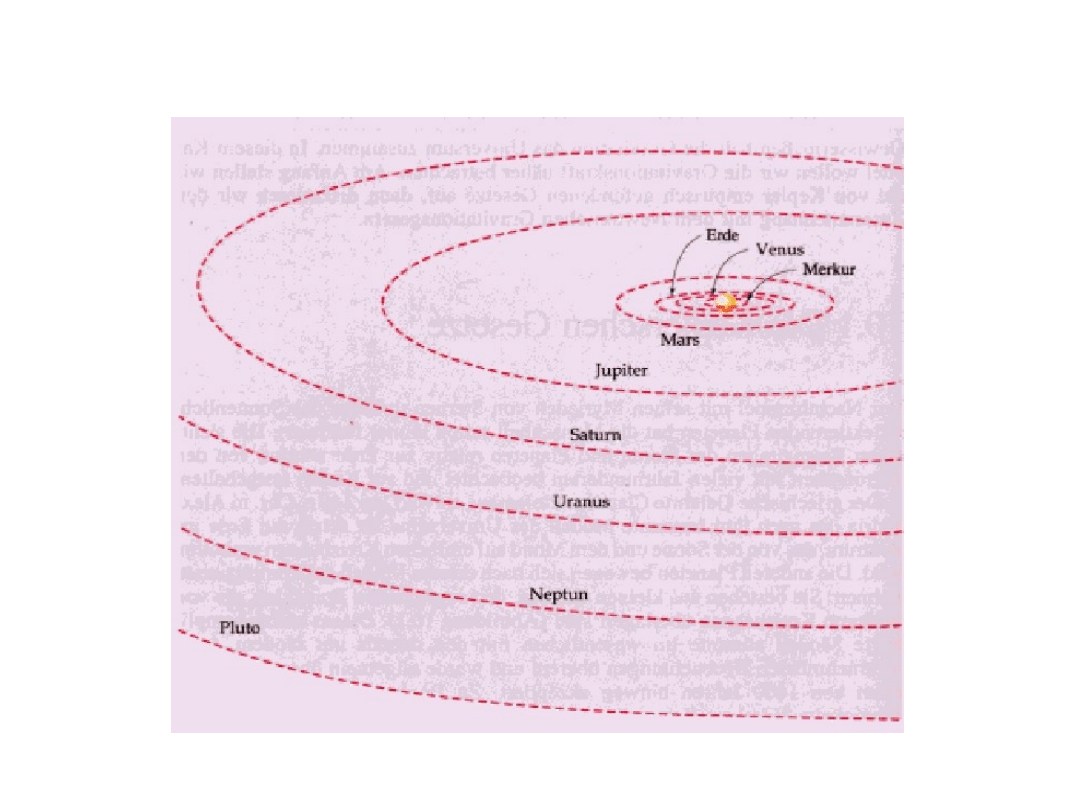
Układ heliocentryczny został zaproponowany przez
Kopernika w 1543 r.
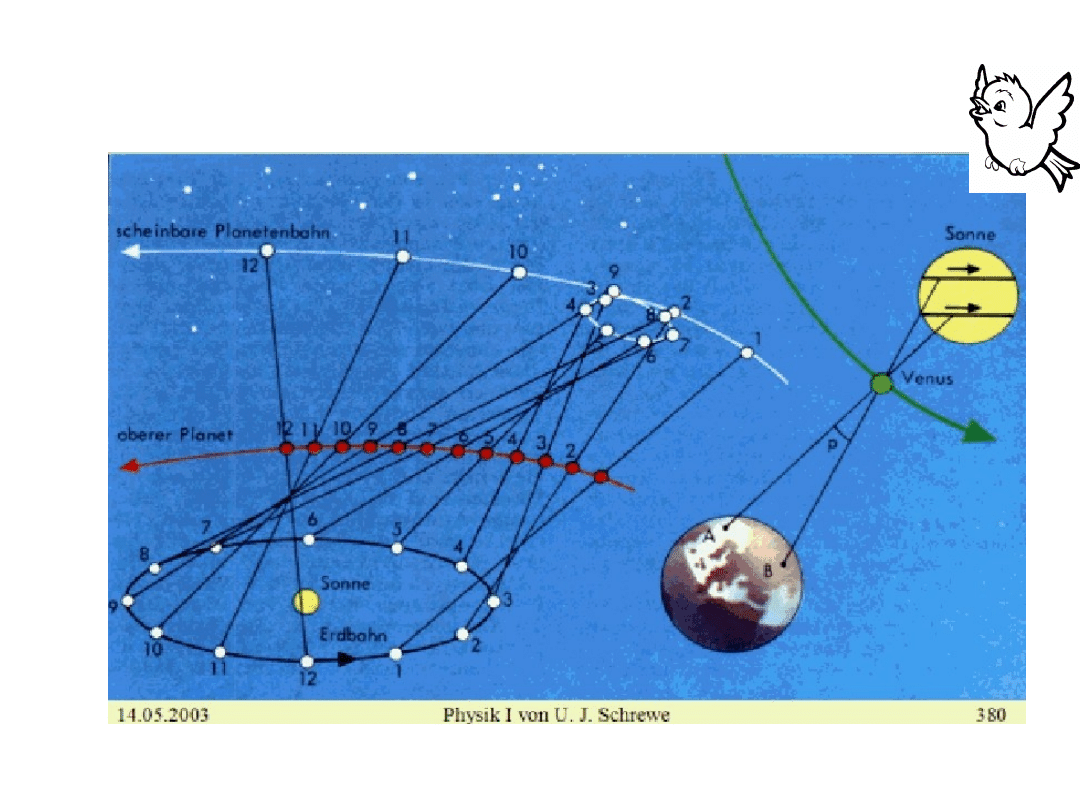
Wytłumaczenie pętli zataczanych przez
Marsa w oparciu o
układ heliocentryczny.
W końcu wieku 16 Tycho de Brache doszedł
do wniosku, że aby odpowiedzieć na pytanie,
czy planety naprawdę obracają się dookoła
Słońca, należy raczej przeprowadzić dokładne
pomiary, a nie debatować nad tym. Przez
wiele lat wykonywał pomiarów w swoim
obserwatorium na wyspie Hven koło
Kopenhagi. Wyniki pomiarów Tycho de
Brache opracowywał jego asystent Kepler,
który odkrył prawa ruchu planet nazwane
później jego imieniem.
Oto do czego doszedł Kepler.
1. Planety poruszają się dookoła Słońca po
elipsach, a Słońce
znajduje się w jednym z ognisk elipsy
b
a
r
P
r
’
F
F’
a
a
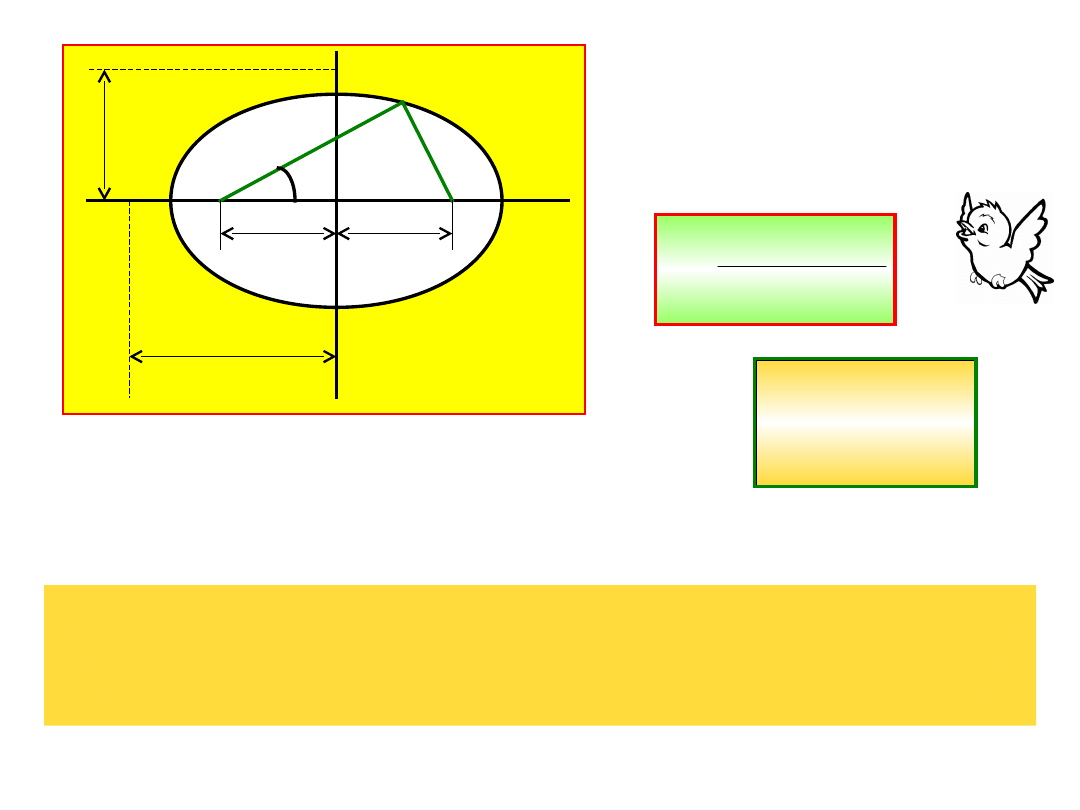
Elipsa posiada dwie
półosie, dużą i małą,
oraz dwa ogniska.
W układzie biegunowym
równanie elipsy ma
postać:
cos
a
k
r
przy czym,
2
2
2
2
)
1
(
b
a
a
k
.
stanowi mimośród
elipsy.
2. Promień wodzący od Słońca do Planety
zatacza w tych samych odcinkach czasy te
same pola powierzchni.
Tylko dla Merkurego i „Plutona” > 0.02.
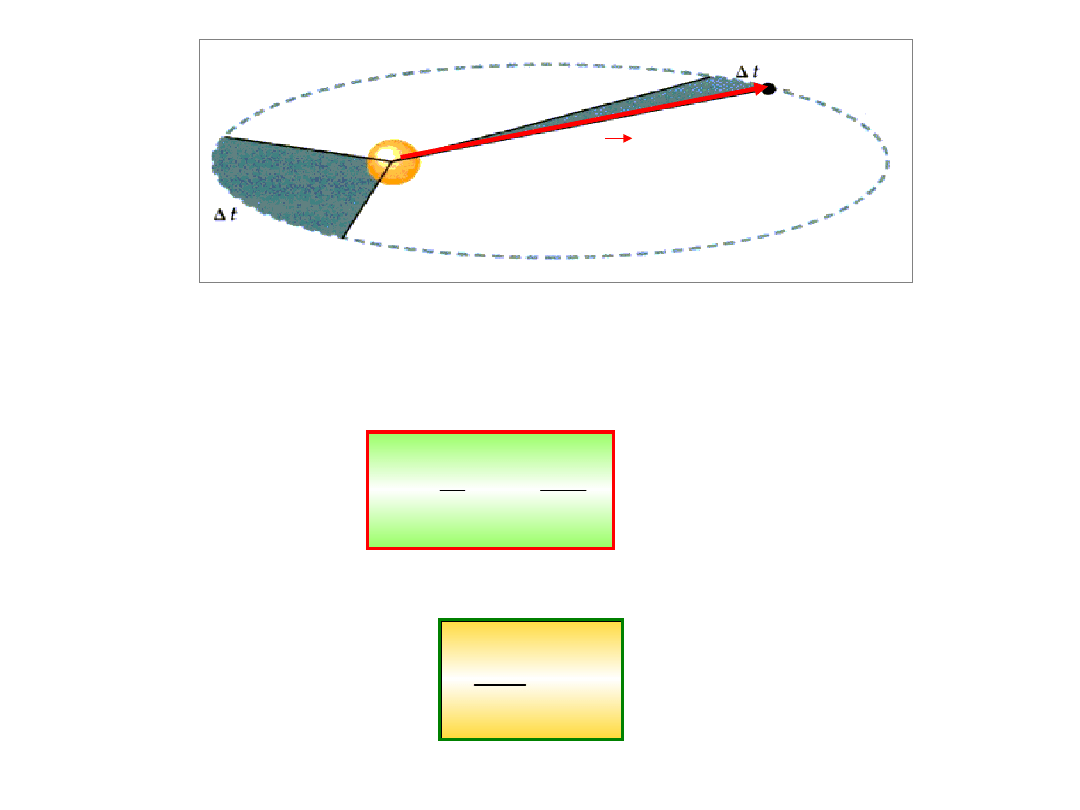
Słońce
Plane
ta
r
Pamiętamy, że pole trójkąta jest dane przez równanie:
S = ½ a · b · sin, możemy wprowadzić
wektor pola zakreślanego przez wektor r jako:
dt
r
d
r
S
2
1
Zgodnie z drugim prawem Keplera:
2
0
dS
dt
r
,
2
2
0
dr dr
d r
r
dt dt
dt
r
r
r
r
czyli,
.
Pierwszy człon w równaniu jest równy zero.
Zostaje więc,
2
2
0
d r
r
dt
r
r
.
Widzimy więc, że przyśpieszenie, a tym
samym też siła są równoległe do promienia
r, czyli linii łączącej Planetę i Słońce.
Taką siłę nazywamy siłą centralną.
Zdefiniujmy sobie jeszcze trzecie prawo Keplera.
3.
Stosunek kwadratu okresu obiegu Planety
dookoła Słońca do trzeciej potęgi dłuższej
półosi elipsy jest równy dla wszystkich orbit
planetarnych .
Prawo to porównuje okresy ruchu różnych
planet i stwierdza;
3
3
18
2
2
3.354 10
a
m
C
T
s
Załóżmy, że orbity po których krążą Planety są kołowe.
Możemy wtedy znaleźć zależność siły grawitacji od
odległości. Przyśpieszenie radialne w ruchu po okręgu
jest równe
2
2
2
4
r
a
r
r
T
.
Wstawmy 1/T
2
=C/r
3
w oparciu o trzecie prawo
Keplera.
Zestawienie Praw
Keplera
1.
Planety poruszają się dookoła
Słońca po elipsach, a Słońce
znajduje się w jednym z ognisk
elipsy
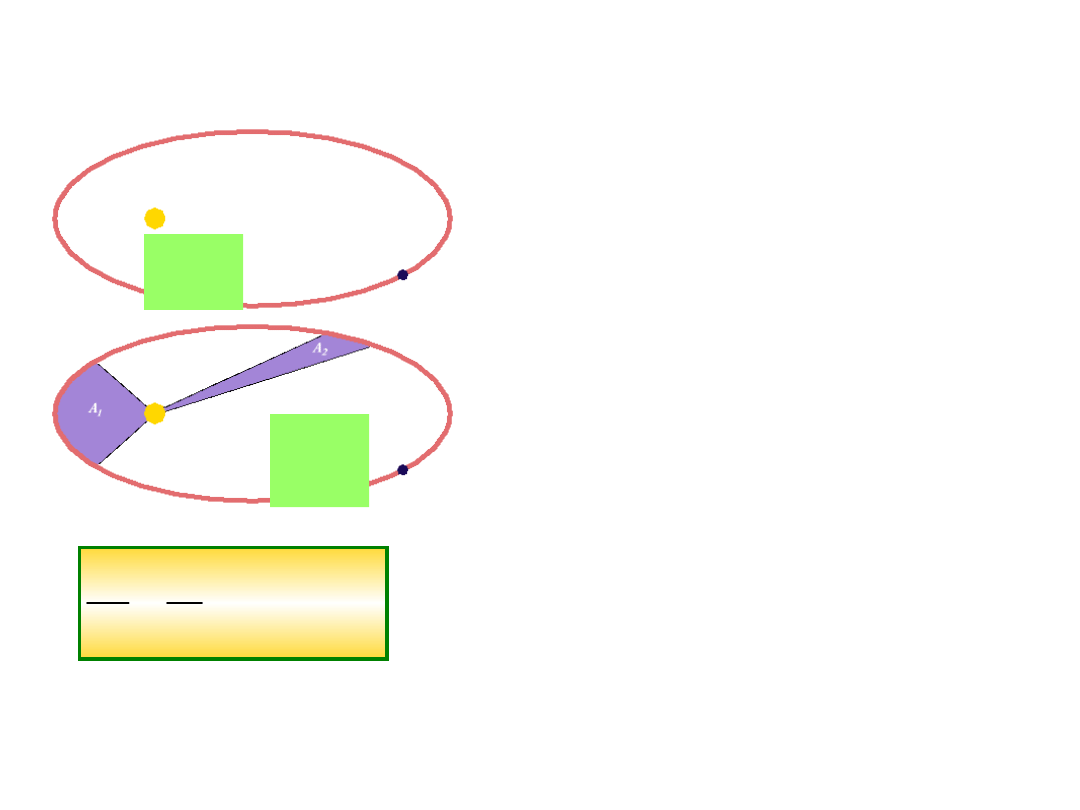
2.
Promień wodzący od Słońca
do Planety zatacza w tych
samych odcinkach czasy te same
pola powierzchni
3.
Stosunek kwadratu okresu
obiegu Planety dookoła Słońca
do trzeciej potęgi
dłuższej półosi elipsy jest równy
dla
wszystkich orbit planetarnych
2
3
1
1
2
3
2
2
T
r
C const
T
r
Słoń
ce
S
1
=
S
2
Wyznaczenie stałej grawitacji
Stała grawitacji może zostać wyznaczona
tylko w oparciu o Prawo Powszechnego
Ciążenia Newtona.
2
1
2
F r
G
m m
Musimy więc wyznaczyć siłę F działającą
pomiędzy dwoma masami m
1
i m
2
znajdującymi się w odległości r.
Dane astronomiczne nie wystarczą, gdyż nie
znamy dokładnie mas.
Pomiarów dokonał Cavendish w oparciu o dwie znane masy
wykorzystując wagę skręceń w 1798 r.
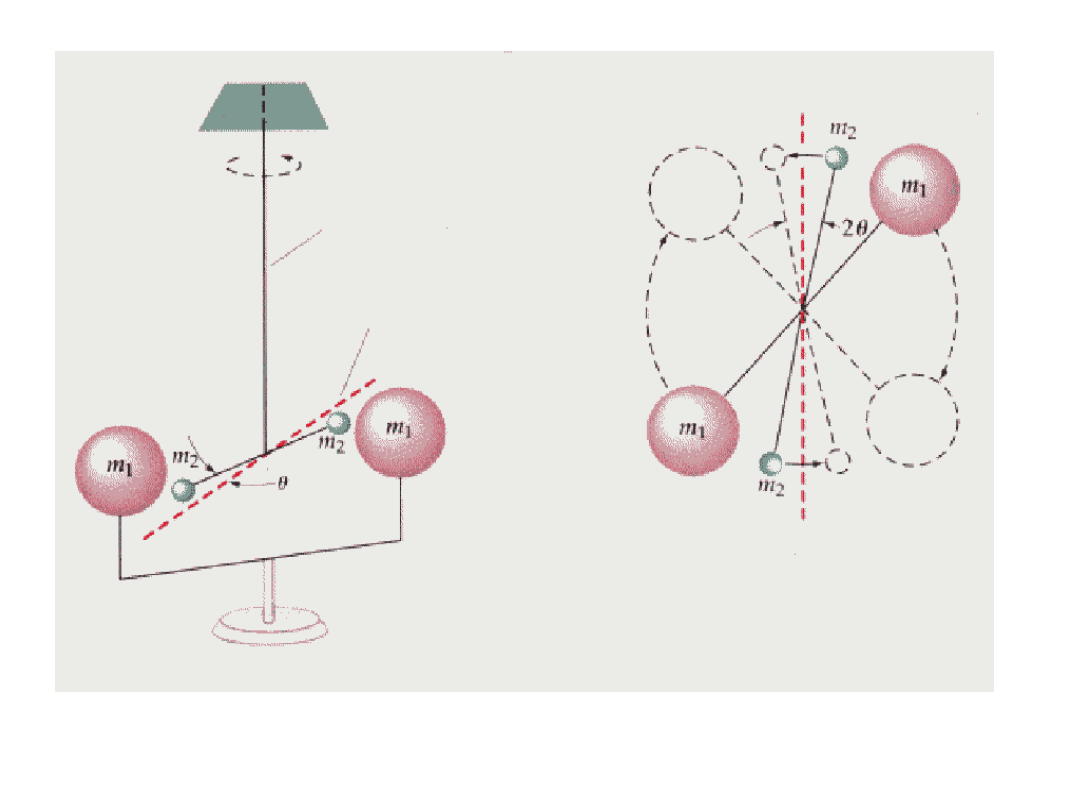
Widok z boku
Widok z góry
nitka sprężysta
Pozycja równowagi
równowaga
Pozycja 1
Pozycja 2
Równania opisujące ruch
planet
Jeśli chcemy opisać ruch planety o masie
m
dookoła Słońca, które ma masę
M
, musimy
napisać następujące równanie ruchu.
2
dv
mM r
m
F
F
G
dt
r r
r
r
r
r
Ponieważ ruch odbywa się na płaszczyźnie,
możemy napisać,
3
3
x
x
y
y
dv
x
m
GMm
k
dt
r
dv
y
m
GMm
k
dt
r
,