1

ZAGADNIENIA:

• Jak atomy rozmieszczone są w ciałach stałych?
(w metalach)

• Jak gęstość zależy od struktury krystalicznej?

• Kiedy własności zależą od orientacji próbki?

Struktura krystaliczna ciał

stałych

2

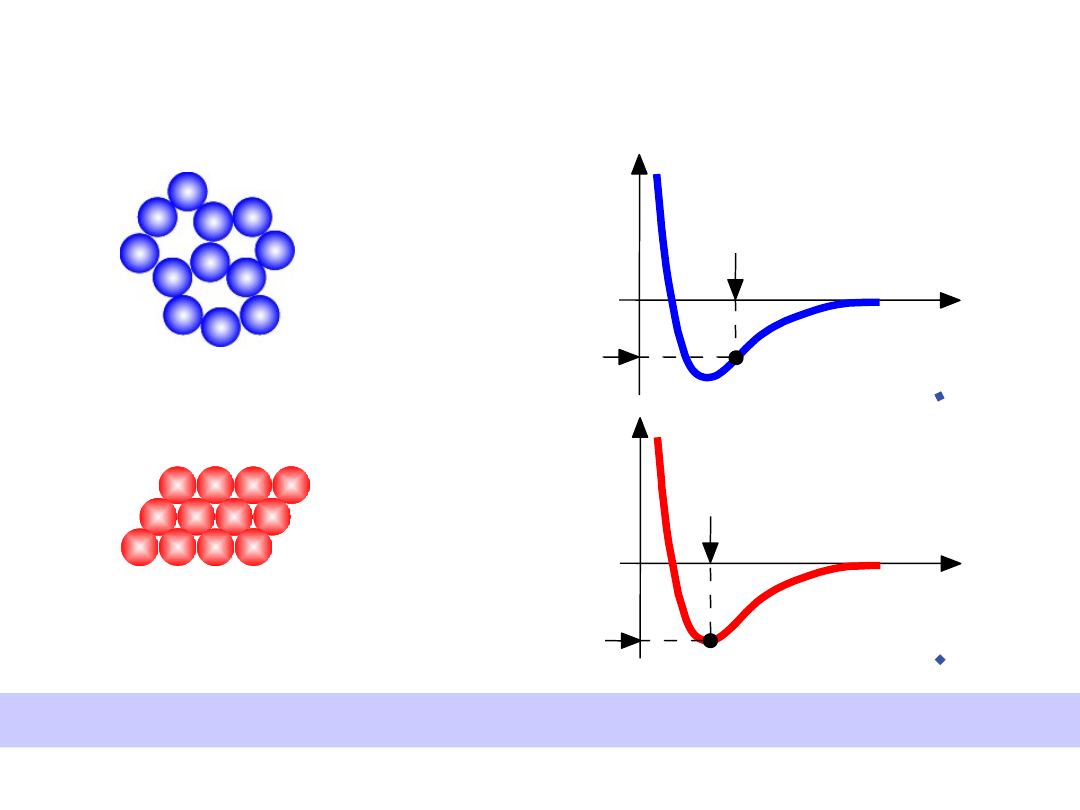
• Mała gęstość,

przypadkowe

• Gęste,

uporządkowane

Struktury o gęstym wypełnieniu przestrzeni mają mniejsze energie

Energia i Upakowanie

Energy

r

typowa długość

wiązania

typowa energia

wiązania

Energy

r

typowa długość

wiązania

typowa energia

wiązania

3

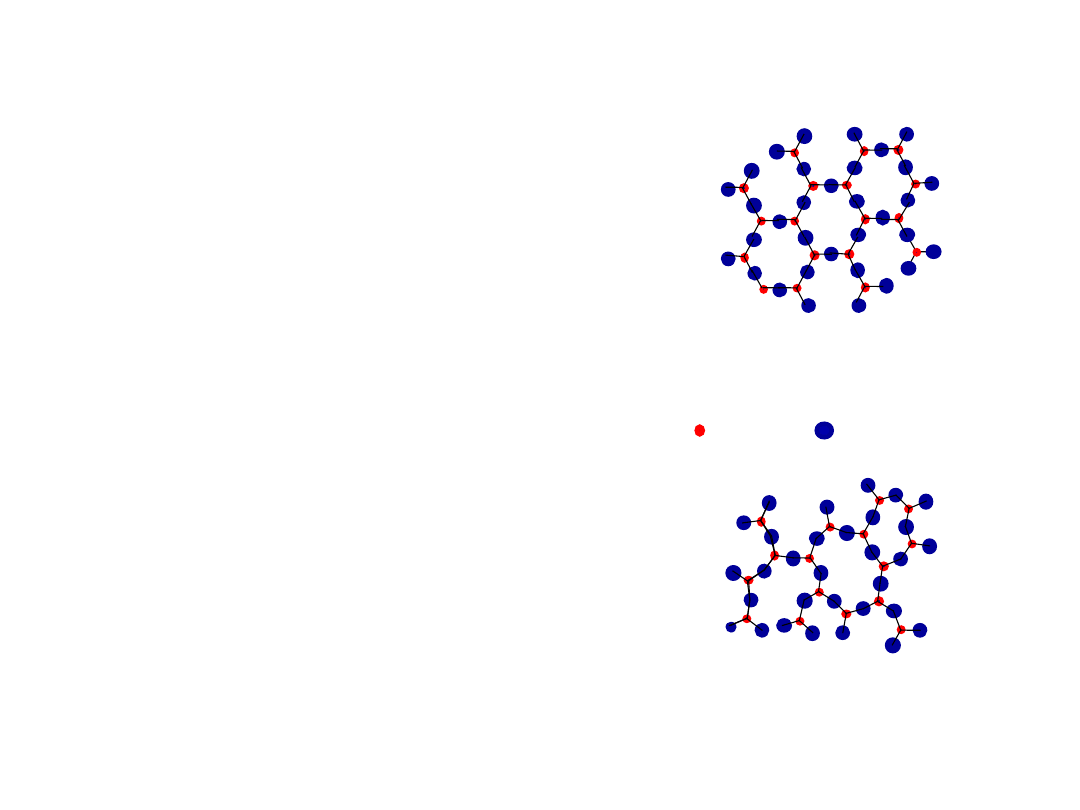
• atomy ułożone periodycznie

Materiały krytaliczne

-metali
-wielu ceramik
-niektórych polimerów

• brak periodycznego ułożenia

Niekrystaliczne

materiały

-złozonych strukturach
-po gwałtownym chłodzeniu

crystaliczny SiO

2

niecrystaliczny SiO

2

"

Amorficzny

" = Niekrystaliczny

Energia i Upakowanie

Si

Oxygen

• typowe dla:

• wystepują w:

4

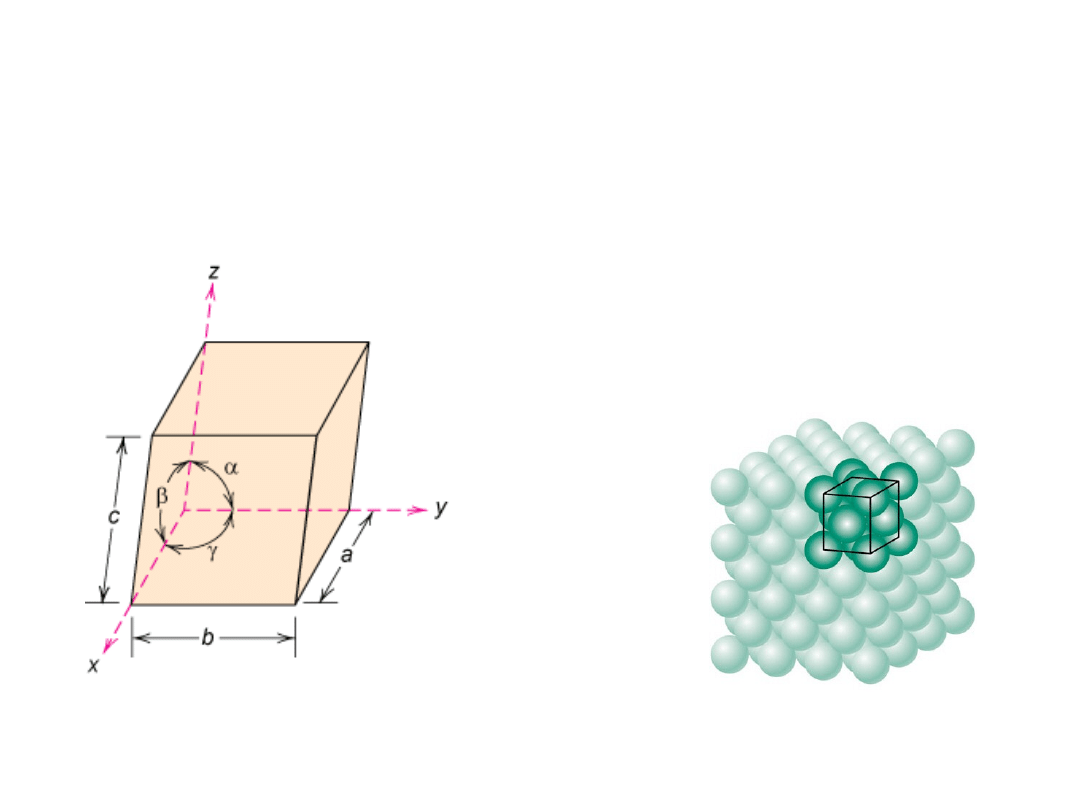
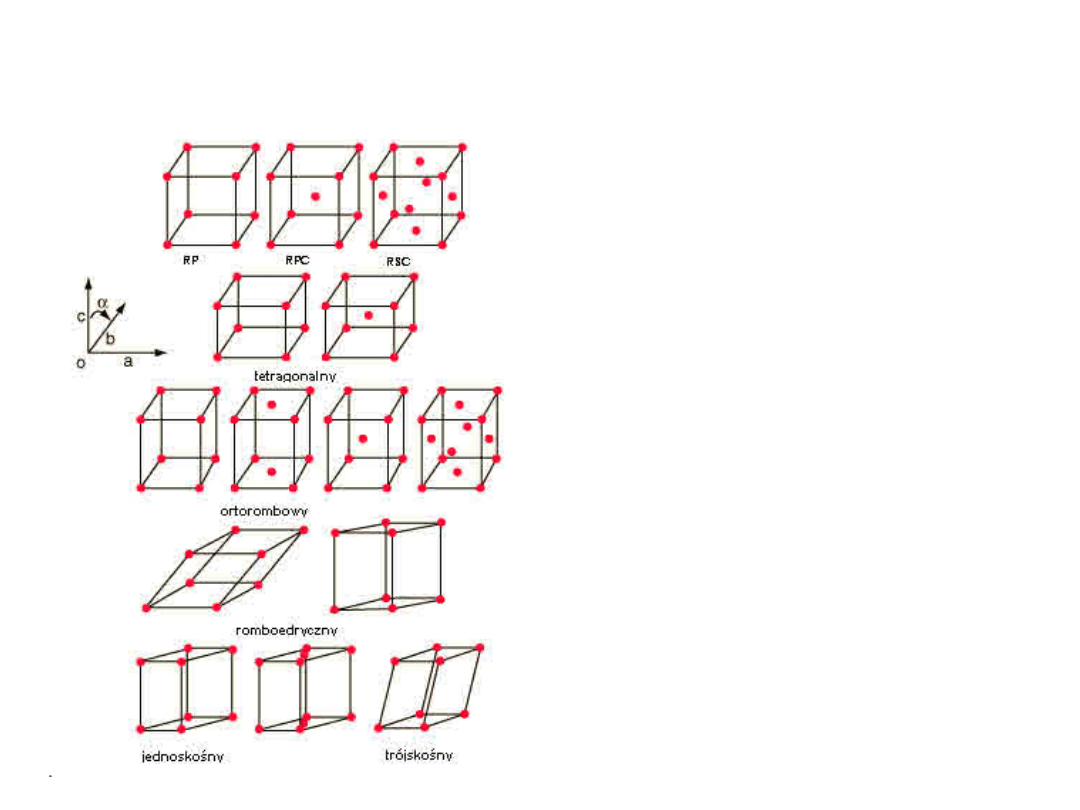
Elementy Krystalografii

7 układów

krystalograficznych

14 typów sieci

Komórka elementarna:

najmniejsza

powtarzalna objętość kryształu zawierająca pełną
informację o rozmieszczeniu atomów (wzorzec).

a, b,

i

c

są

stałymi
sieciowymi

a, b, c,

oraz

, , 

są

parametra
mi
sieciowymi

Komórki elementarne są
równoległościanami

5

Charakteristyka kryształów

• Liczba atomów w komórce

elementarnej

• Liczba koordynacyjna

Liczba najbliższych sąsiadów

• Współczynnik wypełnienia

Atomy (lub jony) w strukturze krystalicznej
można traktować jako sztywne kule o określonej
średnicy. Jest to tzw.

model sztywnych

kul

Ważne parametry:

6

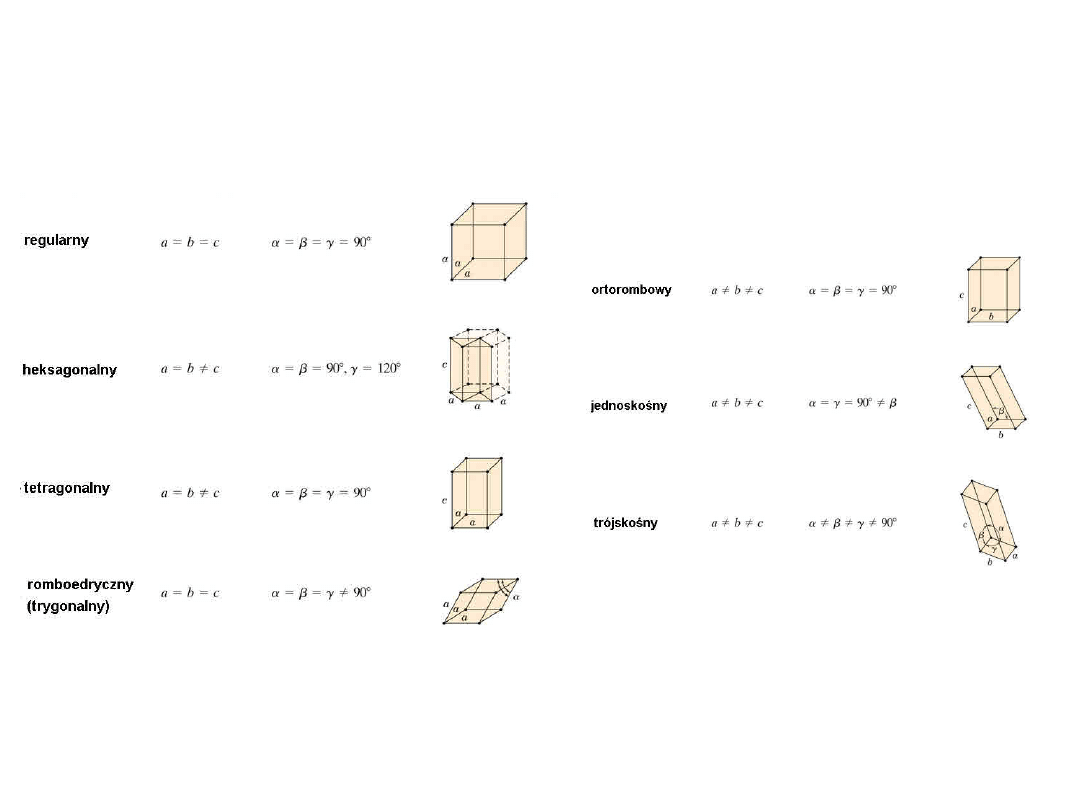
Siedem Systemów

Krystalograficznych

7

Czternaście typów sieci

• P – Prymitywna (prosta)

• F – Ściennie centrowana:

dodatkowy

punkt na

środku każdej ściany

• I - Przestrzennie centrowana:

dodatkowy punkt w środku

komórki

• C - Centerowana: dodatkowy punkt

na przeciwległych ścianach

• R - Romboedryczna

8

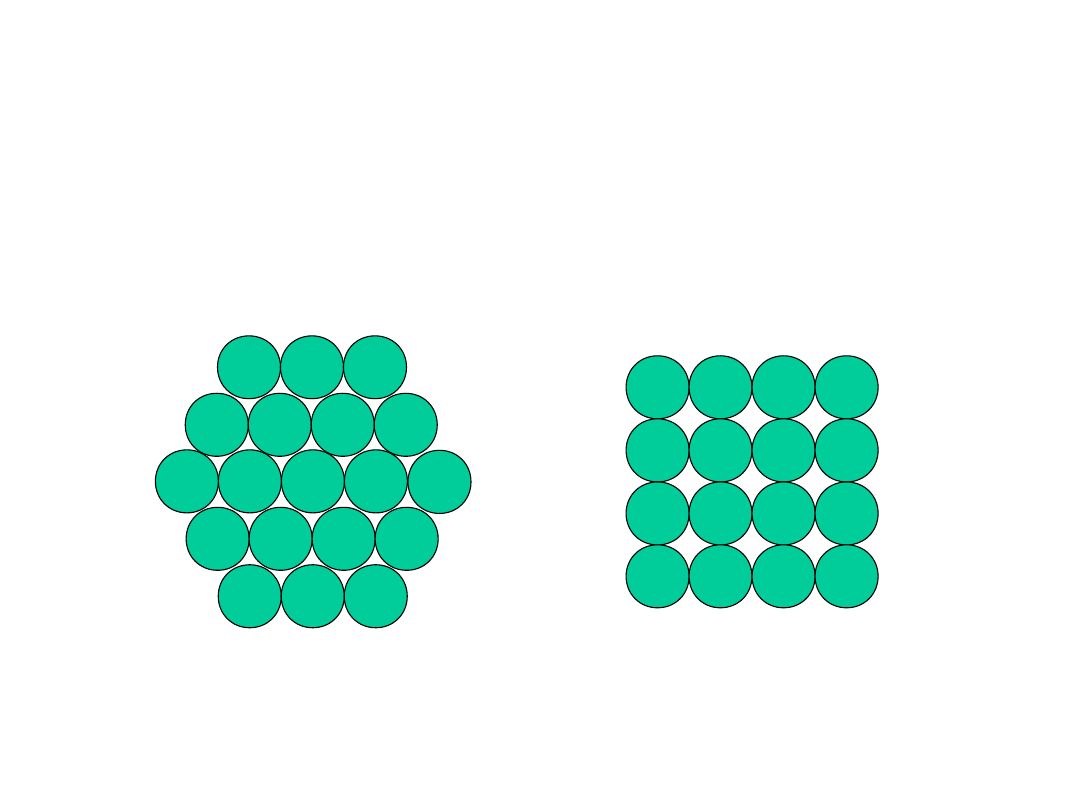
 Struktura krystaliczna metali

• J

ak rozmieścić atomy, aby zminimalizować

zajmowaną przestrzeń?

2-wymiary

vs.

Nałóżmy teraz drugą warstwę aby uzyskać

strukturę trójwymiarową

9

• Tendencja do gęstego upakowania

• Przyczyny:

- Zazwyczaj, tylko jeden pierwiastek, promienie

wszystkich atomów są jednakowe

- Wiązanie metaliczne jest bezkierunkowe
- Odległości pomiędzy sąsiednimi atomami są małe,

gdyż to minimalizuje energię wiązań

- Chmura elektronowa jest wspólna dla wszystkich

jonów

• Mają najprostsze struktury krystaliczne

Rozpatrzymy trzy takie struktury...

Struktura krystaliczna metali

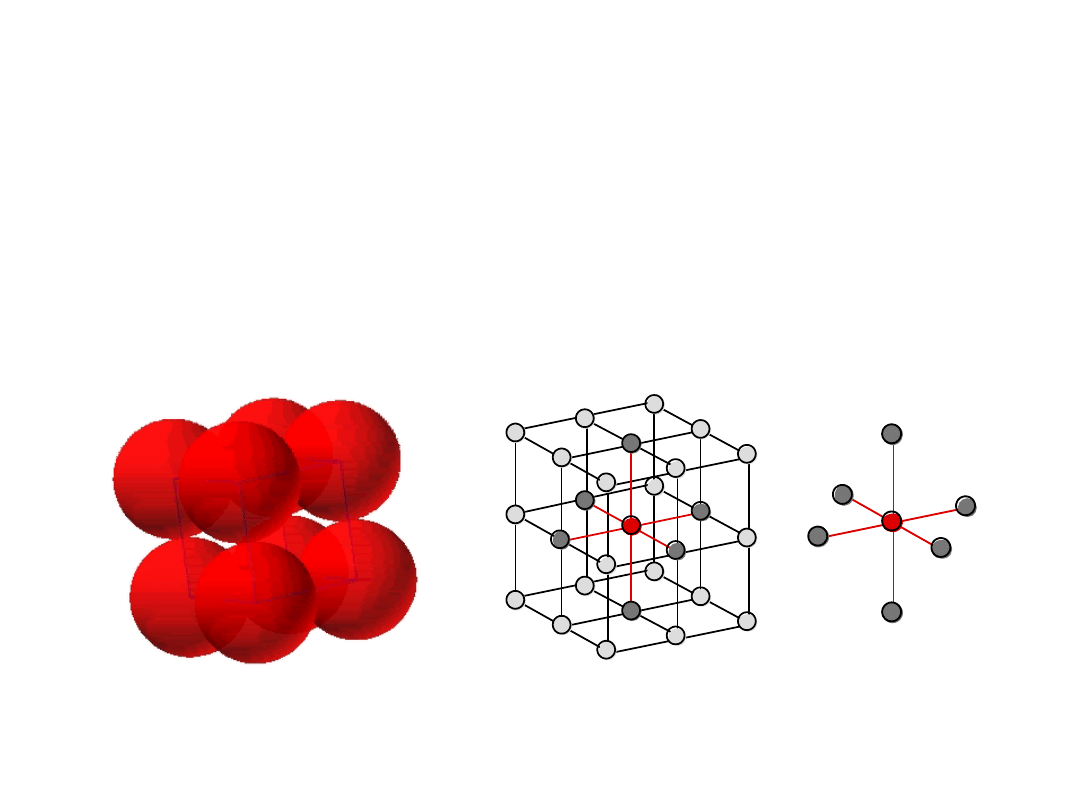
10

• B. rzadka, bo mała gęstość upakowania atomów

(tylko Po

•

Kierunki o najgęstszym ułożeniu;

krawędzie sześcianu

•

# koordynacyjna

= 6

(# najbliższych sąsiadów)

Struktura Regularna

Prymitywna (RP)

11

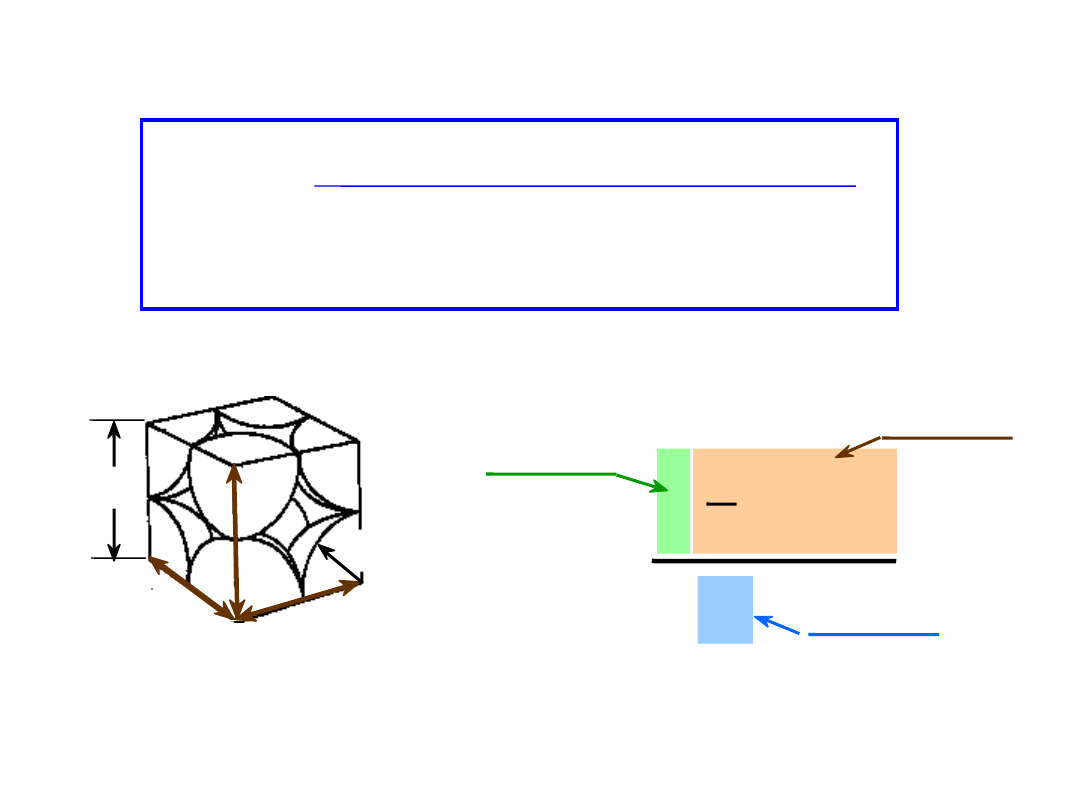
• WWP dla struktury regularnej prymitywnwej = 0.52

APF =

a3

4

3

(0.5a)3

1

atomy

kom. el.

atom

objętość

kom. el.

objętość

Współczynnik Wypełnienia

Przestrzeni

WWP =

Objętość atomów w komórce el.*

Objętość komórki el.

* w modelu sztywnych kul

kierunki o najgęstszym ułożeniu

a

R=0.5a

zawiera 8 x 1/8 =

1

atom/kom. el.

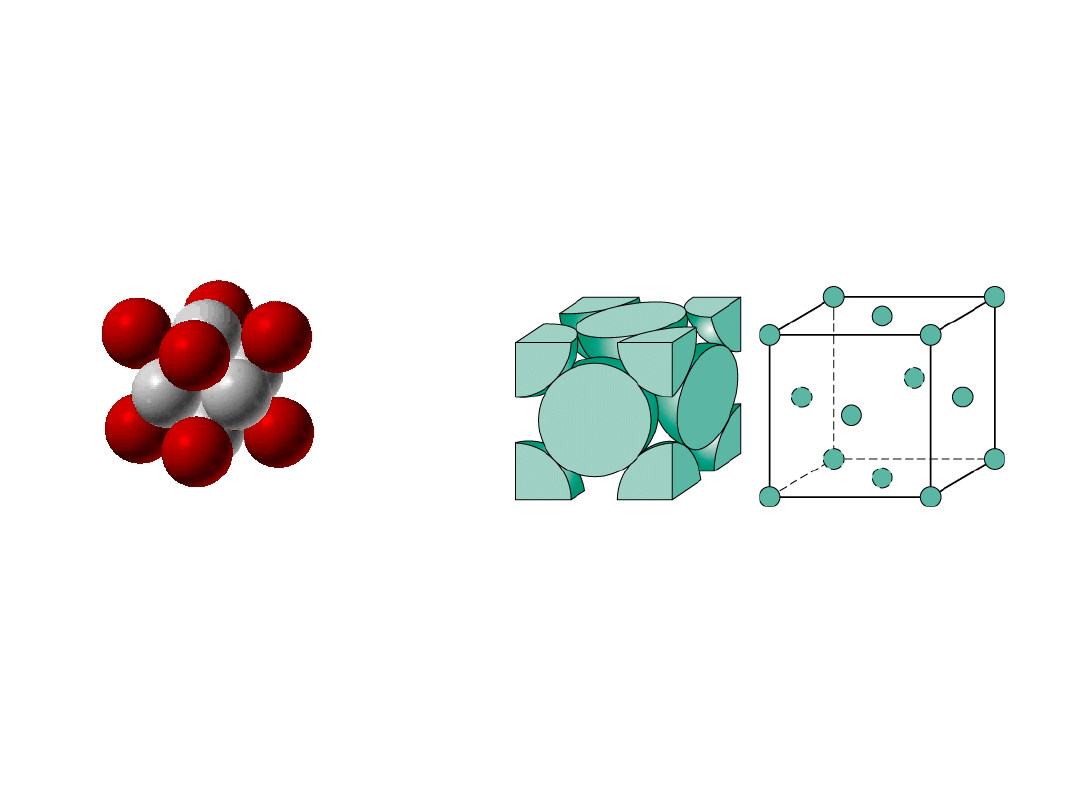
12

• # K

oordynacyjna = 12

• Atomy stykają się wzdłuż przekątnych ścian

Struktura regularna ściennie

centrowana

np.: Al, Cu, Au, Pb, Ni, Pt, Ag

4 atomy/kom. el.: 6 ścian x 1/2 + 8 naroży x 1/8

Uwaga: Wszystkie
atomy są jednakowe;

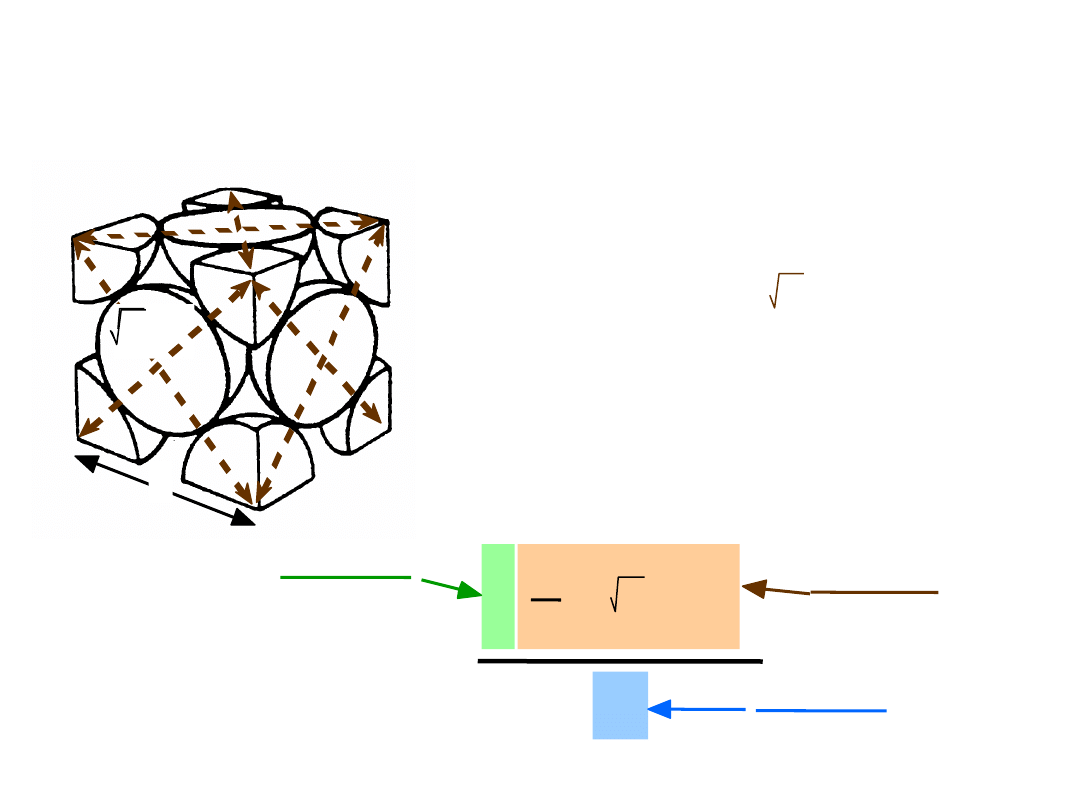
13

• Wsp. wypełnienia przestrzeni = 0.74

Współczynnik Wypełnienia Przestrzeni:

RSC

maksymalny

WW =

4

3

( 2a/4)3

4

atomy

kom. el.

atom

obj.

a3

kom. el.

obj.

Kierunki najgęstszego ulożenia:

długość = 4R =

2 a

Kom. el. zawiera:

6 x

1/2 + 8 x

1/8

=

4 atomy/kom. el.

a

2 a

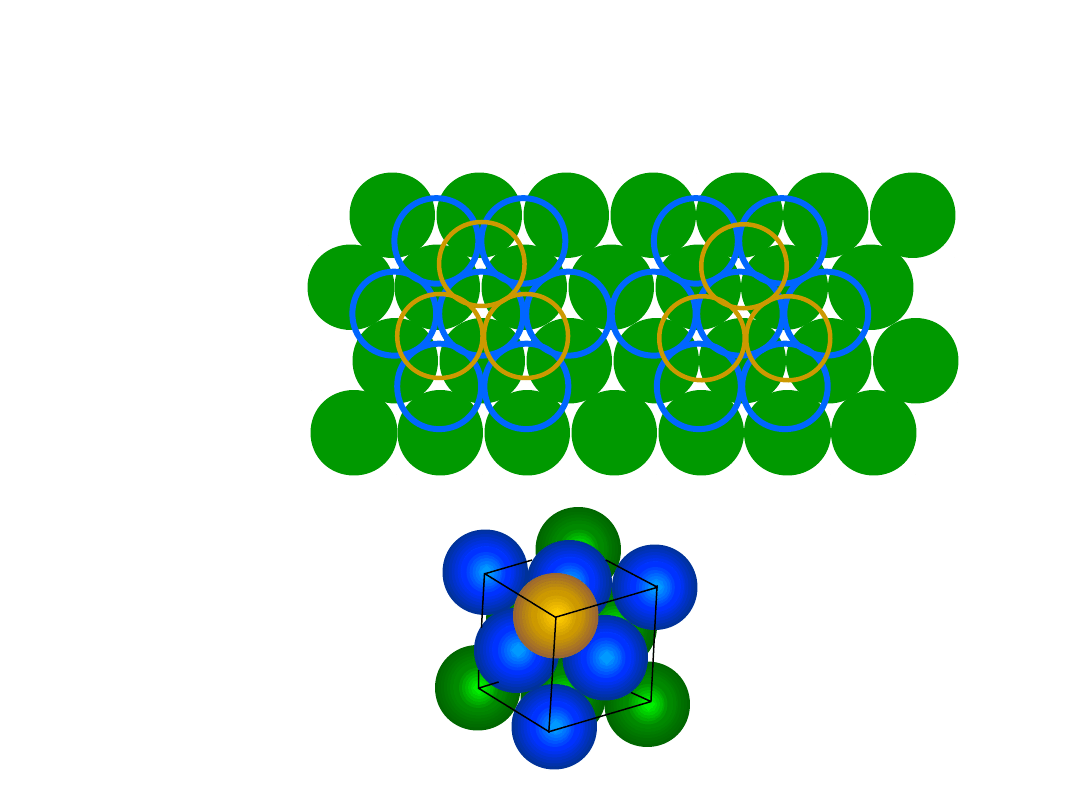
14

A

B

B

B

B

B

B

B

C

C

C

C

A

B

B

• ABCABC... Sekwencja ułożenia

Komórka
elementarna
RSC

Ułożenie atomów w strukturze RSC

B

B

B

B

B

B

B

C

C

C

A

C

C

C

A

A

B

C

15

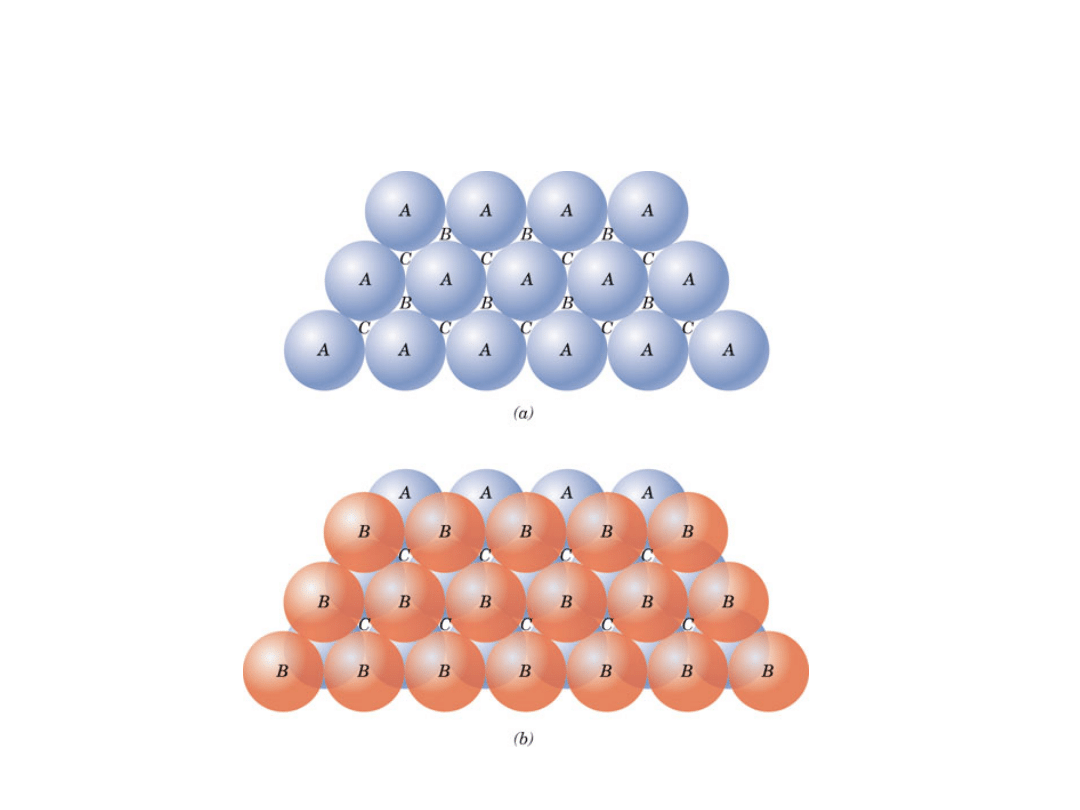
Struktury o najgęstszym ułożeniu

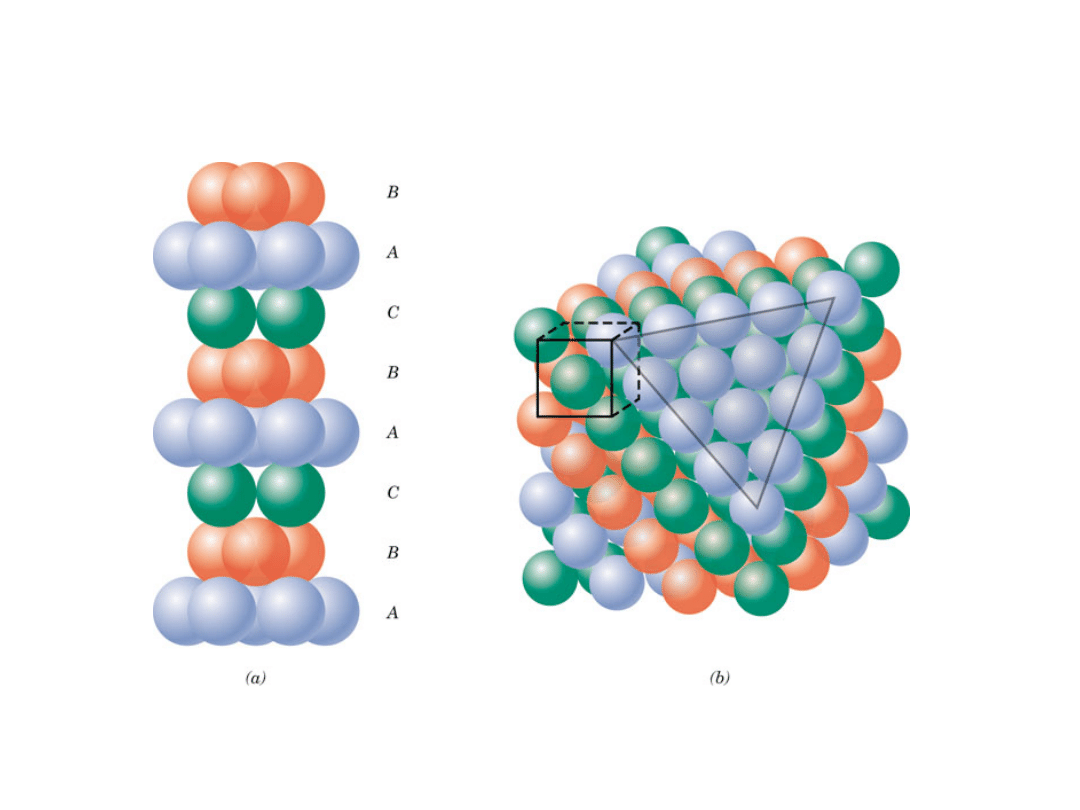
16

Regularna Ściennie

Centrowana

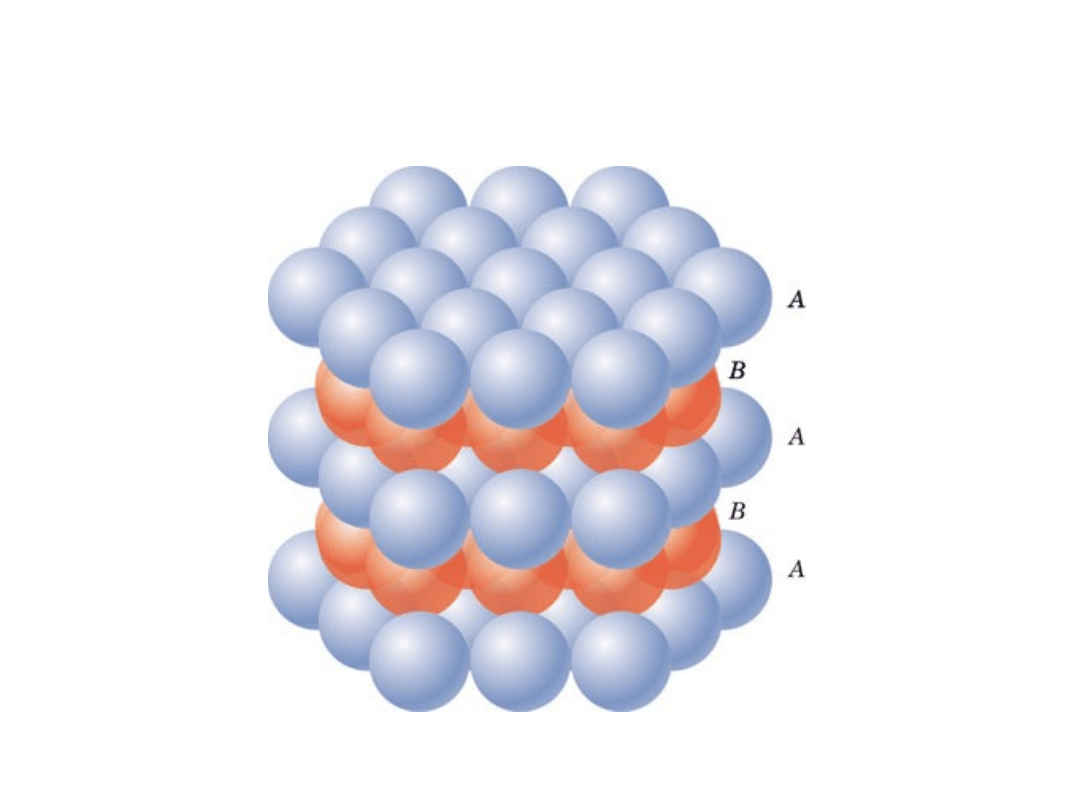
17

Heksagonalna Zwarta

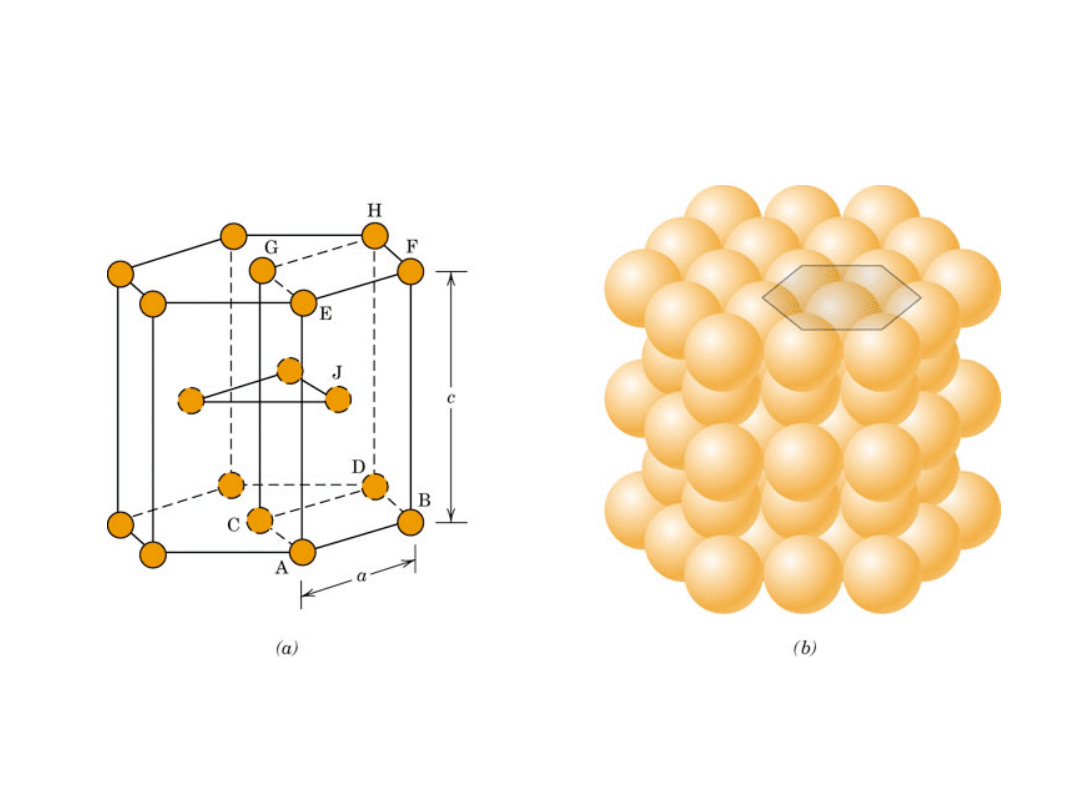
18

Heksagonalna Zwarta

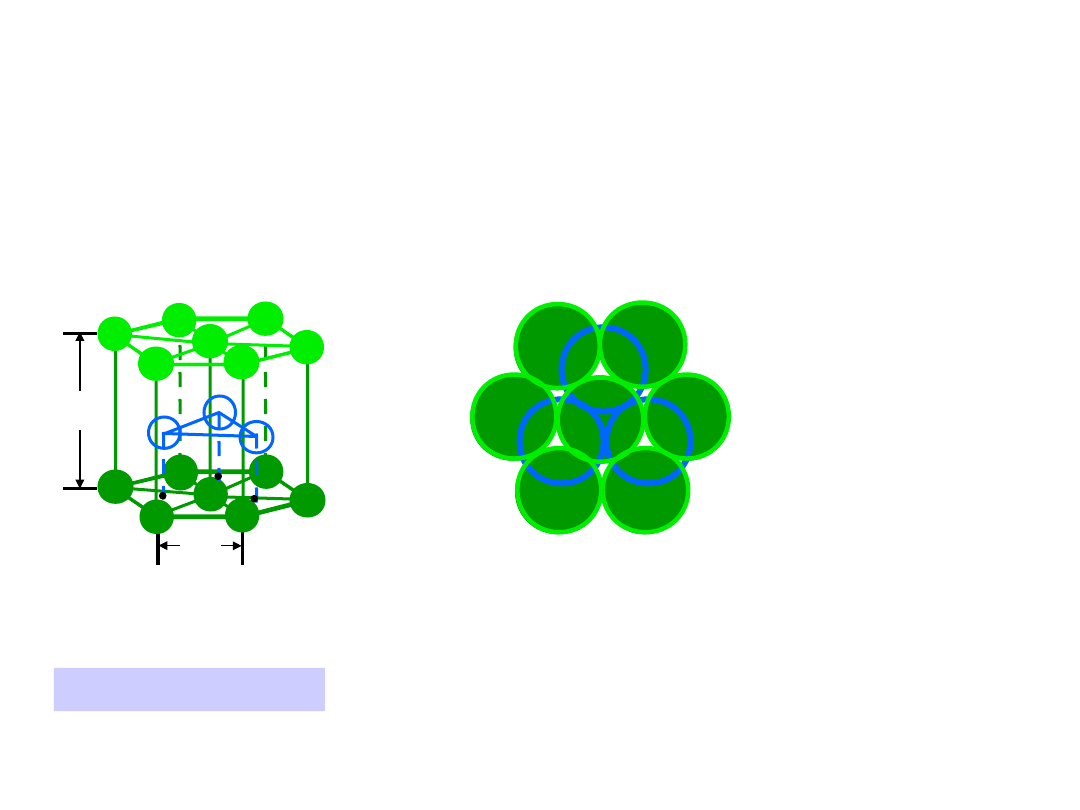
19

• # Koordynacyjna = 12

• ABAB... Sekwencja ułożenia

• WWP = 0.74

• 3D

• 2D

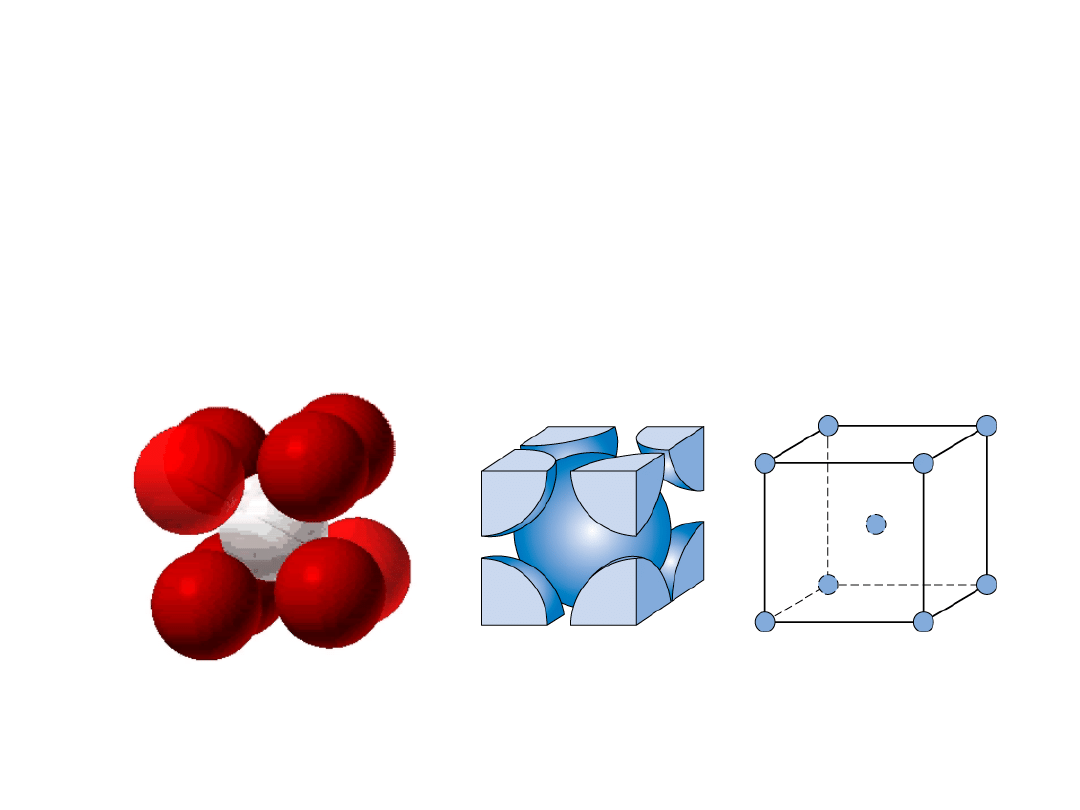
Heksagonalna Zwarta (HZ)

6 atomów/kom. el.

np.: Cd, Mg, Ti,

Zn

• c/a = 1.633

c

a

A

B

A

Dolna warstwar

Środkowa warstwa

Górna warstwa

r

20

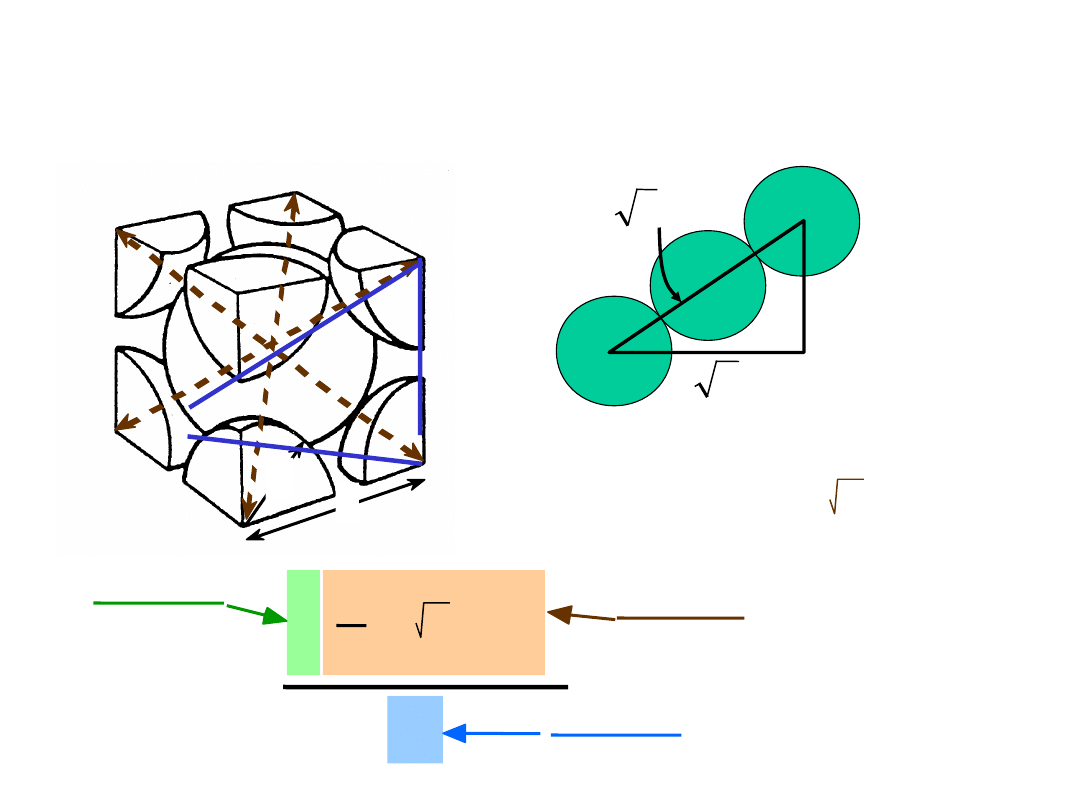
• # Koordynacyjna = 8

• Atomy stykają się wzdłuż przekątnej sześcianu

Struktura regularna przestrzennie

centrowana

np.: Cr, W, Fe (), Ta, Mo

2 atomy/kom. el.: 1 środek + 8 naroży x 1/8

21

Współczynnik Wypełnienia

Przestrzeni

a

WWP =

4

3

 ( 3a/4)3

2

atomy

kom. el.

atom

objętość

a3

kom. el.

objętość

długość = 4R =

Kierunek najgęstszego ułożenia:

3 a

• WWP dla struktury RPC = 0.68

a

R

a

2

a

3

22

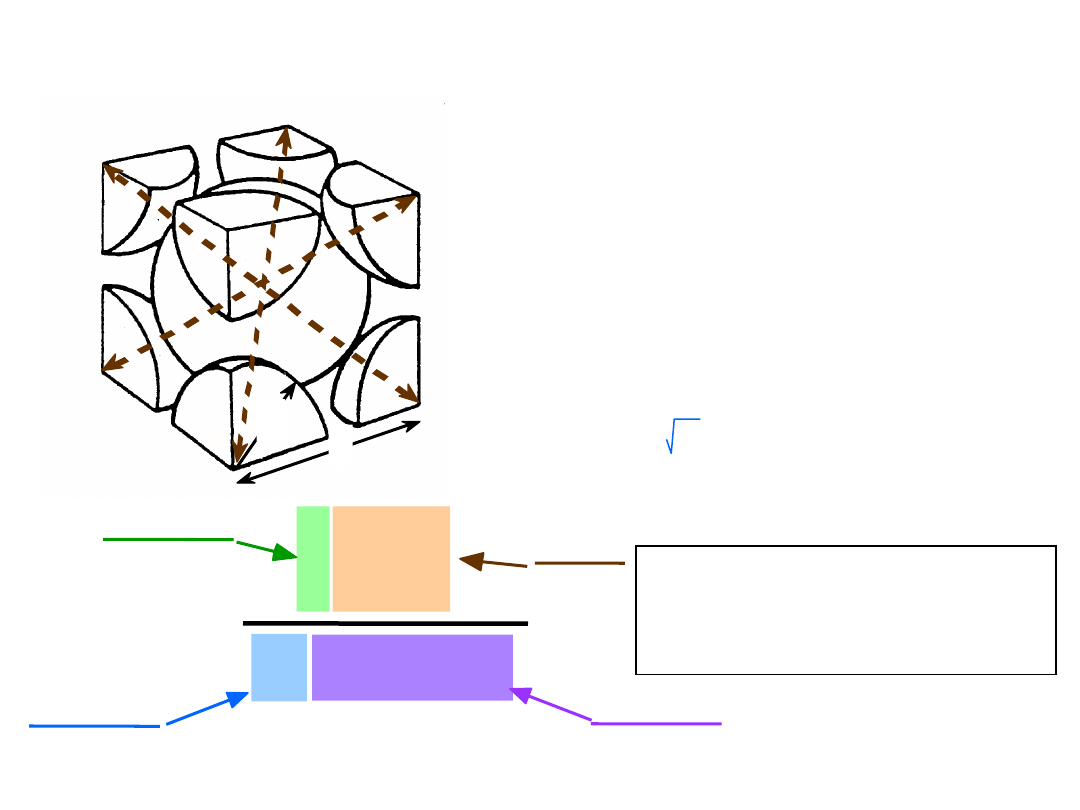
Gęstość Teoretyczna, 

gdzie

n = liczba atomów/kom. el.

A =

masa

atomowa

V

C

= Objętość kom. el. = a

3

for cubic

N

A

= Liczba Avogadra

= 6.023 x 10

23

atomów/mol

Gęstość =  =

V

C

N

A

n

A

 =

Całkowita obj. kom. el.

el.

kom.

w

Atomów

Masa

23

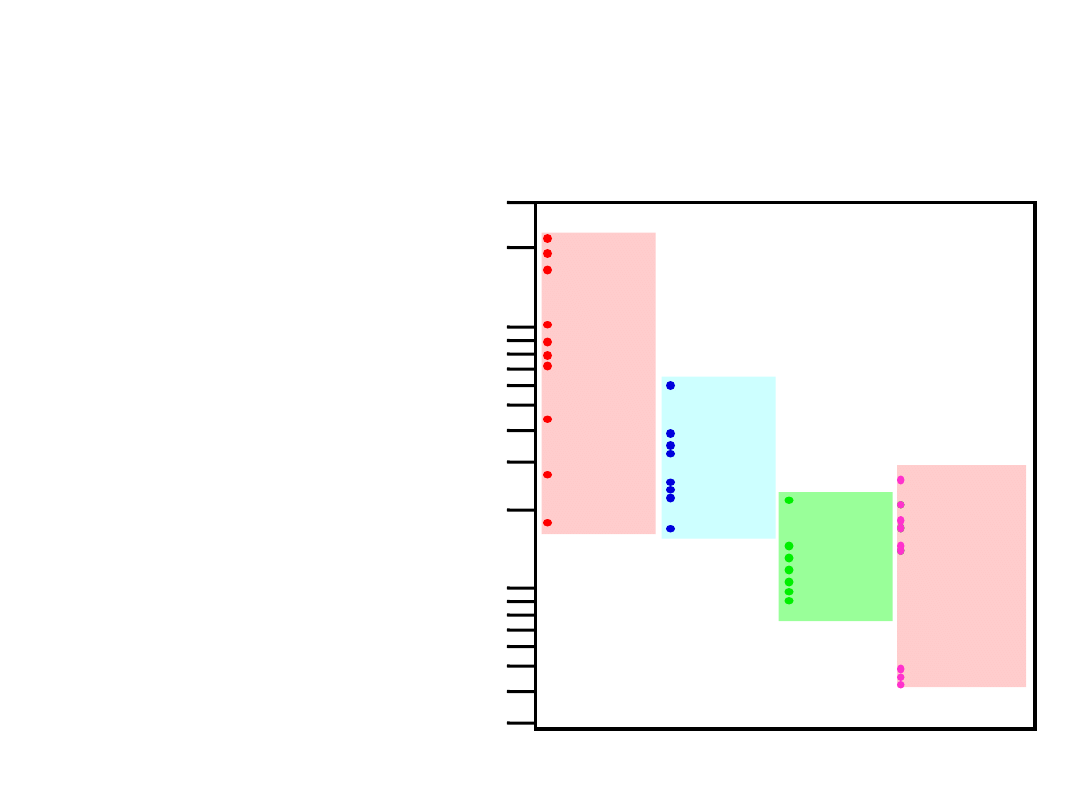
• Np.: Cr (RPC)

A =

52.00 g/mol

R = 0.125 nm

n = 2



teoret

a = 4R/ 3 = 0.2887
nm



rzecz.

a

R



=

a3

52.00

2

atomy

kom. el.

mol

g

kom. el.

objętość

atomy

mol

6.023

x

10

23

Gęstość Teoretyczna, 

= 7.18 g/cm

3

= 7.19 g/cm

3

24

Gęstości różnych materiałów



metali

>



ceramik

>



polimerów



(g

/c

m

)

3

Grafite/

Ceramiki/

Półprzewod.

Metale/

Stopy

Kompozyty/

Włókna

Polimery

1

2

20

30

B

ased on data in Table B1, Callister

*GFRE, CFRE, & AFRE are Glass,

Carbon, & Aramid Fiber-Reinforced

Epoxy composites (values based on

60% volume fraction of aligned fibers

in an epoxy matrix).

10

3

4

5

0.3

0.4

0.5

Magnesium

Aluminum

Steels

Titanium

Cu,Ni

Tin, Zinc

Silver, Mo

Tantalum

Gold, W

Platinum

Graphite

Silicon

Glass-soda

Concrete

Si nitride

Diamond

Al oxide

Zirconia

HDPE, PS

PP, LDPE

PC

PTFE

PET

PVC

Silicone

Wood

AFRE*

CFRE*

GFRE*

Glass fibers

Carbon fibers

Aramid fibers

Metale

mają:

• gęste upakowanie
(wiązanie metaliczne)
• często duże masy atomowe

Ceramiki

mają:

• mniej gęste upakowanie
• często lekkie pierwiastki

Polimery

mają:

• małą gęstość upakowaia
(często niekrystaliczne)
• lekkie pierwiastki (C,H,O)

Compozyty

mają:

• wartości pośrednie

Ogólnie:

25

• Niektóre zastosowania wymagają monokryształóws:

• Własności zależą od
struktury krystalicznej

-diament, do
cięcia,
szlifowania

- łopatki turbin

Zastosowanie Kryształów

Kwarc

26

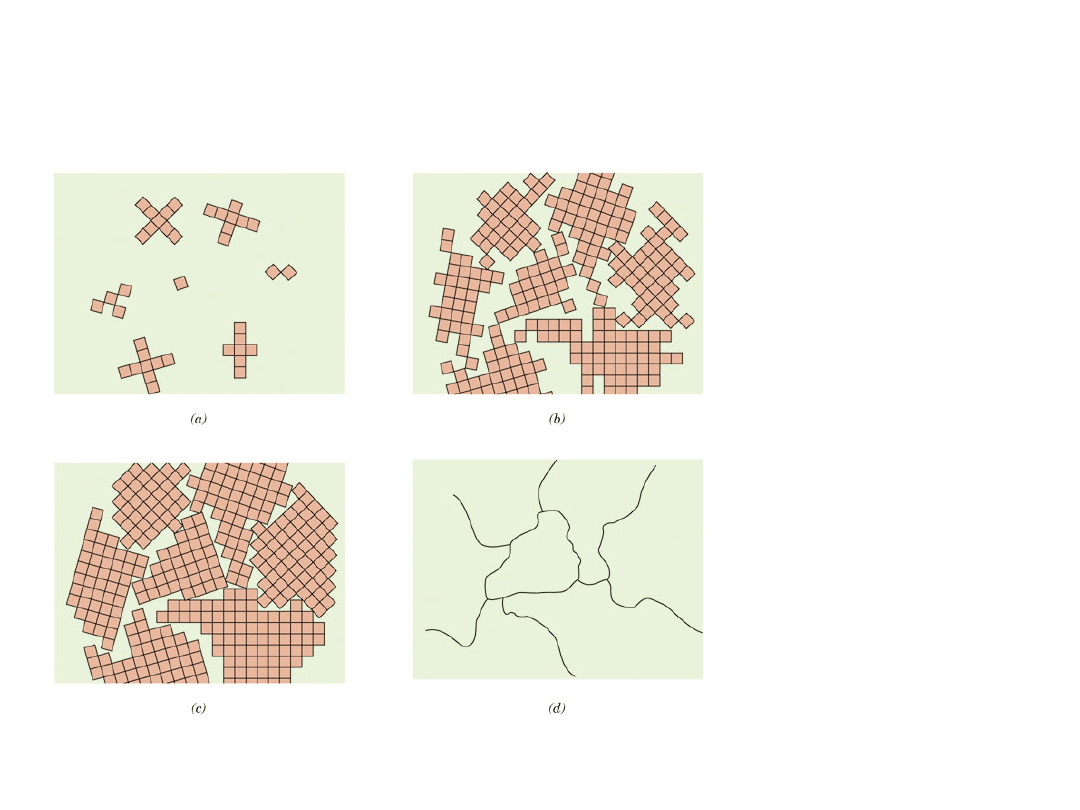
Polikryształy

Stadia
krzepnięcia
polikrystaliczne
go materiału

27

• Większość materiałów inżynierskich to

polikryształy

•

Każde „ziarno" jest monokryształem

• Gdy ziarna są zorientowane przypadkowo, to
własności nie zależą od kierunku
• Wielkości ziarn: od 1 nm do 2 cm

1 mm

Polikryształy

Izotropowy

Anizotropowy

Spoina stopu Nb-Hf-W

28

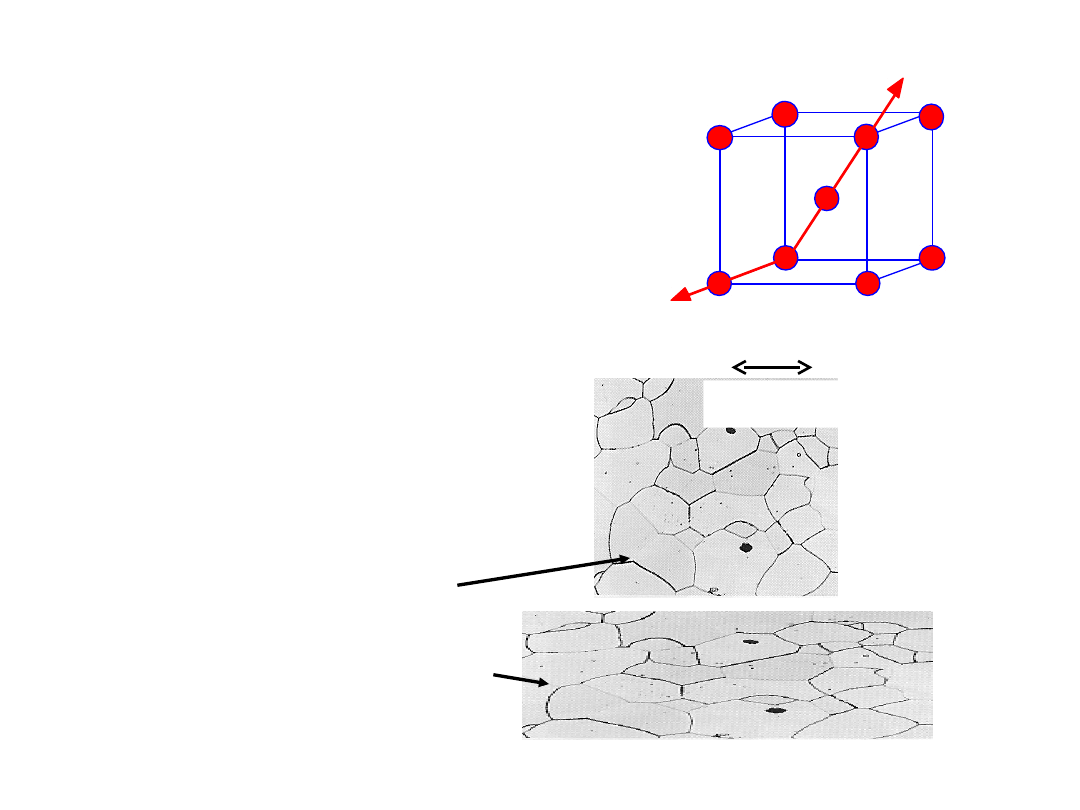
• Monokryształy

-Własności zależą od
kierunku:

anizotropia

-Przykład: moduł
Younga (E) w Fe-

• Polikryształy

-Własności mogą lub nie

zależeć od kierunku

-Gdy ziarna są

zorientowane
przypadkowo:

isotropowe

.

(E

poli iron

= 210 GPa)

-Gdy ziarna mają

uprzywilejowaną
orientację (

texturę

),:

anizotropowe

200 m

Mono- vs.

Polikryształy

E (przekątna) = 273 GPa

E (krawędź) = 125 GPa

29

Polimorfizm

• Dwie lub więcej struktur krystalicznych dla

tego samego pierwiastka (alotropia)

•  

  tytan
  , -Ti

carbon

diamond, graphite

BCC

FCC

BCC

1538ºC

1394ºC

912ºC

-Fe

-Fe

-Fe

ciecz

Żelazo

30

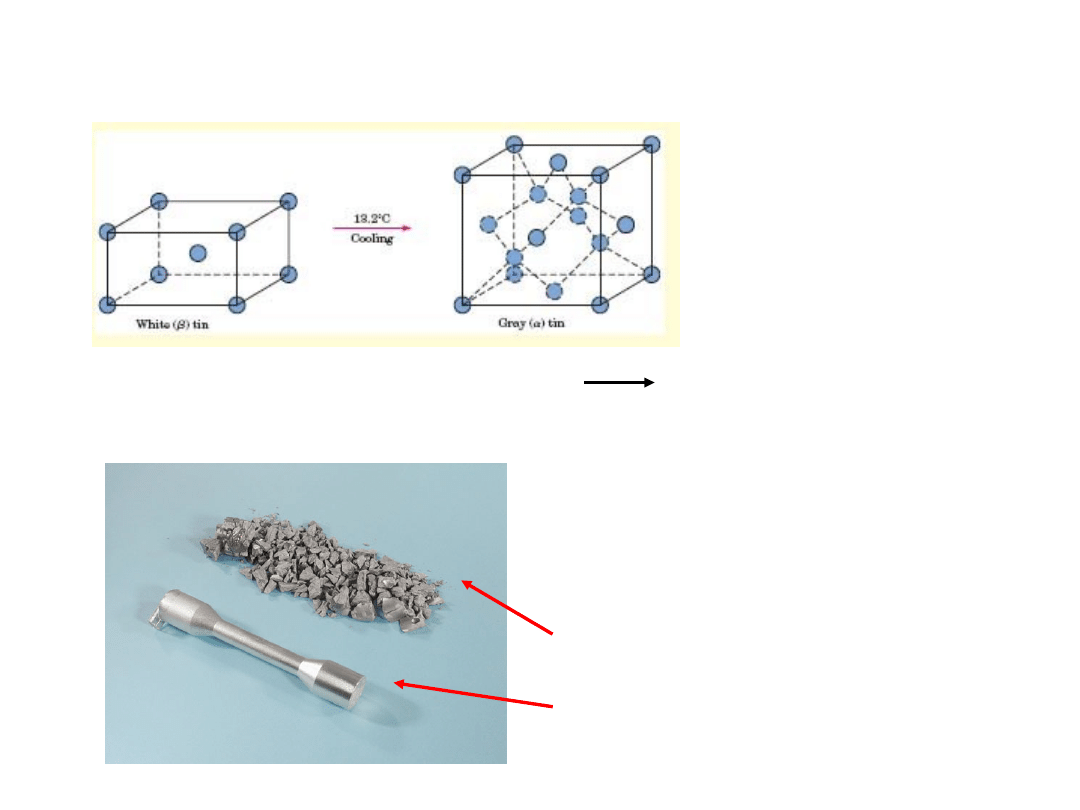
Przemiana Alotropowa w cynie

Tetragonalna Przestrzennie centrowana diamond
cubic

Szara
cyna

Biała
cyna

Wzrost objętości (27%) i
spadek gęstości z 7.30
g/cm

3

do 5.77 g/cm

3

31

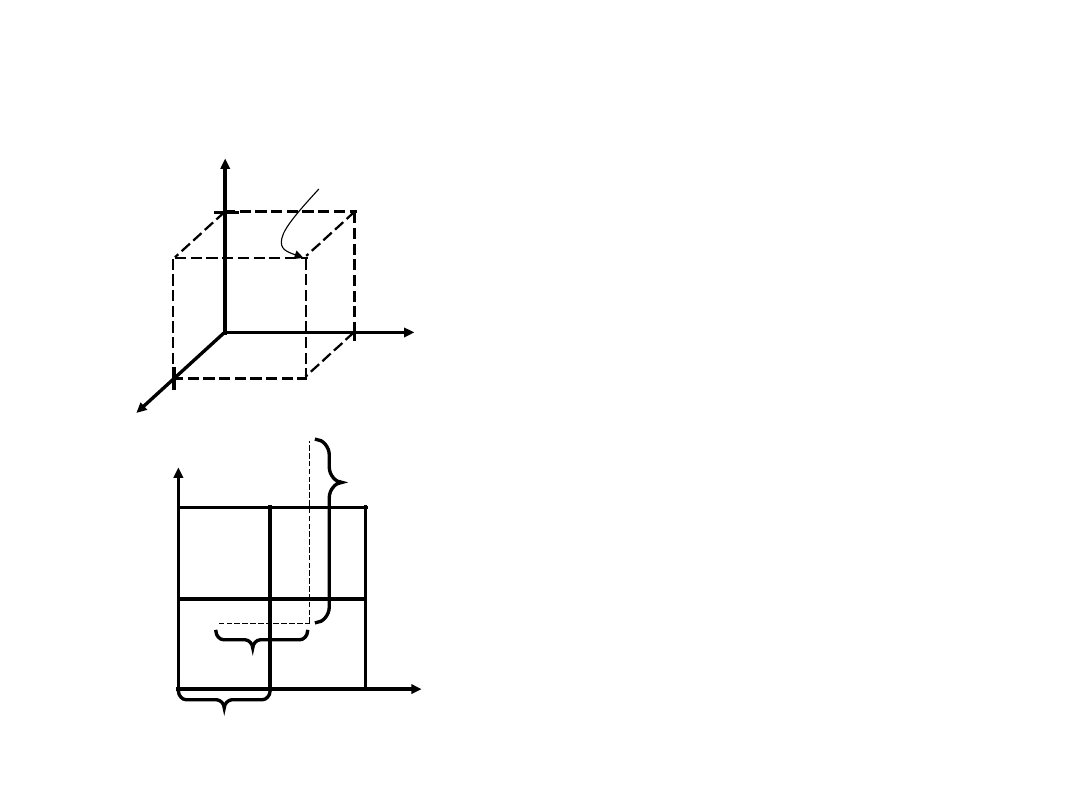
Współrzędne Punktu

Współrzędne punktu dla

komórki elementarnej

a/2, b/2, c/2 ½

½

½

Współrzędne punktu dla

naroża 111

Translacja: integer multiple

of lattice constants 

identical position in

another unit cell

z

x

y

a

b

c

000

111

y

z



2c







b

b

32

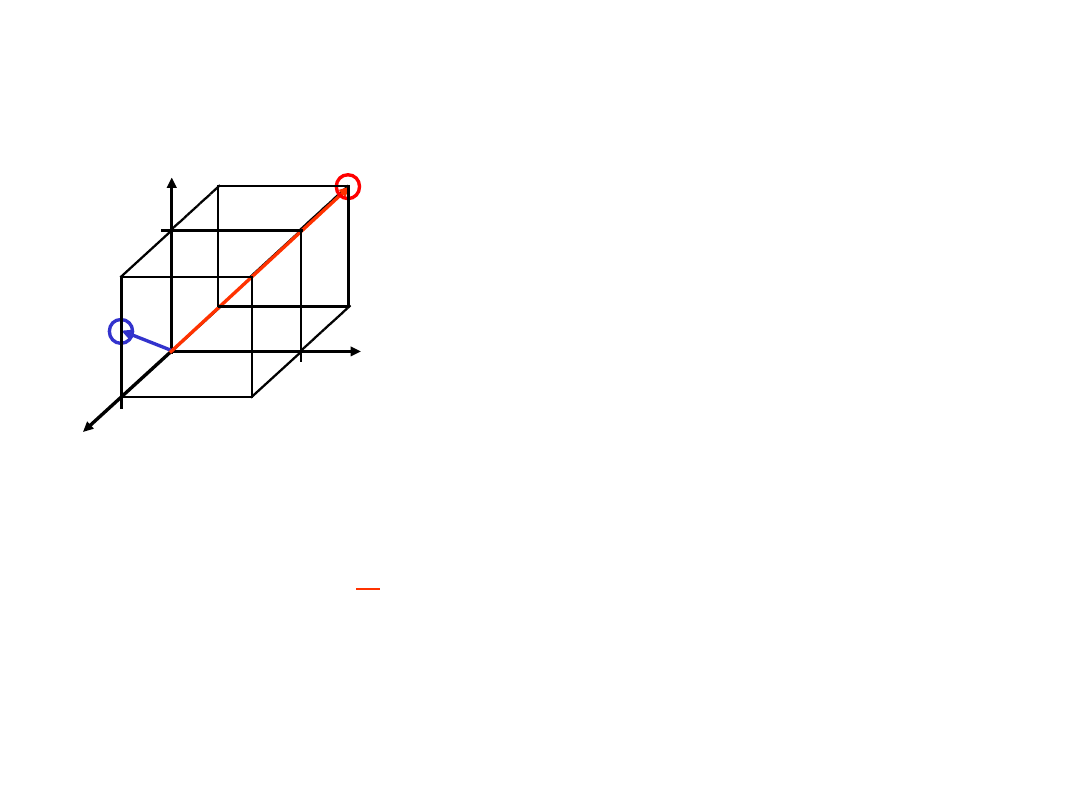
Kierunki Krystalograficzne

1. Przesunąć wektor (gdy to konieczne)
tak aby przechodził przez początek
układu wsp.
2. Odczytać położenia w jednostkach
komórki elementarnej a, b, i c
3. Sprowadzić do najminiejszych liczb
całkowitych
4. Umieścić w nawiasach kwadratowych,
bez przecinków

[uvw]

np.:

1, 0,

½

=> 2, 0,
1

=> [

201

]

-1, 1,
1

rodzina kierunków <uvw>

z

x

Algorytm

gdzie „minus” nad cyfrą
oznacza wskaźnik ujemny

[

111

]

=>

y

33

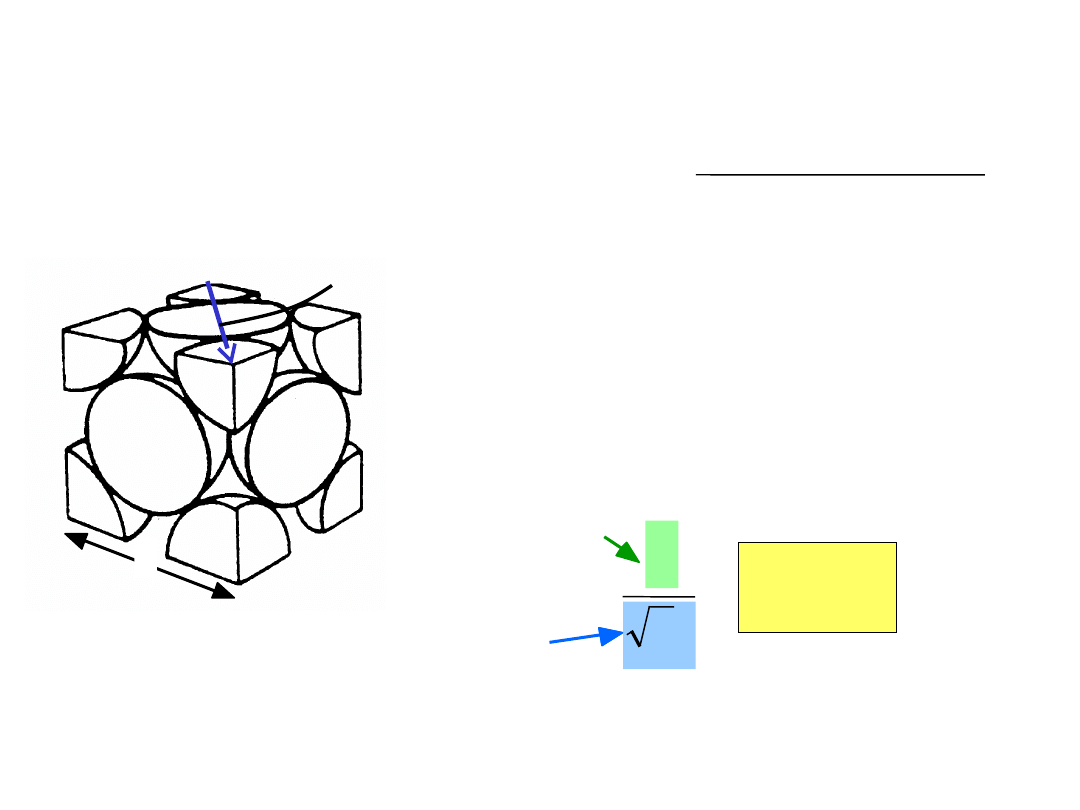
np.: gęstość liniowa Al w
kierunku [110] 

a = 0.405 nm

Gęstość Liniowa

• Gęstość Liniowa Atomóws  GL = 

a

[110]

Długość wektora jedn.

Liczba atomów

# atomów

długość

1

3.5 nm

a

2

2

LD







34

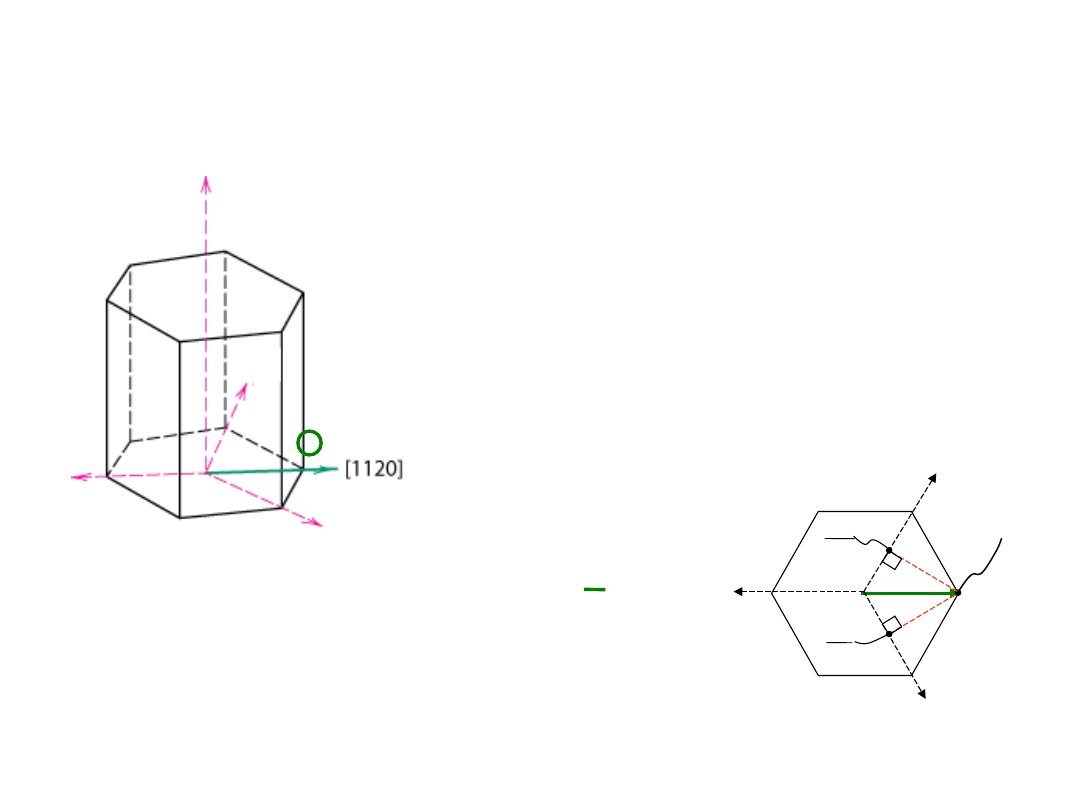
Kierunki w strukturze HZ

1. Przesunąć wektor (gdy to
konieczne) tak aby przechodził przez
początek układu wsp.
2.  Odczytać położenia w jednostkach
komórki elementarnej a

1

, a

2

, a

3

, lub c

3.  Sprowadzić do najminiejszych liczb
całkowitych
4.  Umieścić w nawiasach
kwadratowych, bez przecinków

[uvtw]

[

1120

]

np.:

½, ½, -1, 0

=>

linie przerywane
pokazują rzuty na osie a

1

i a

2

a

1

a

2

a

3

-a

3

2

a

2

2

a

1

-

a

3

a

1

a

2

z

Algorytm

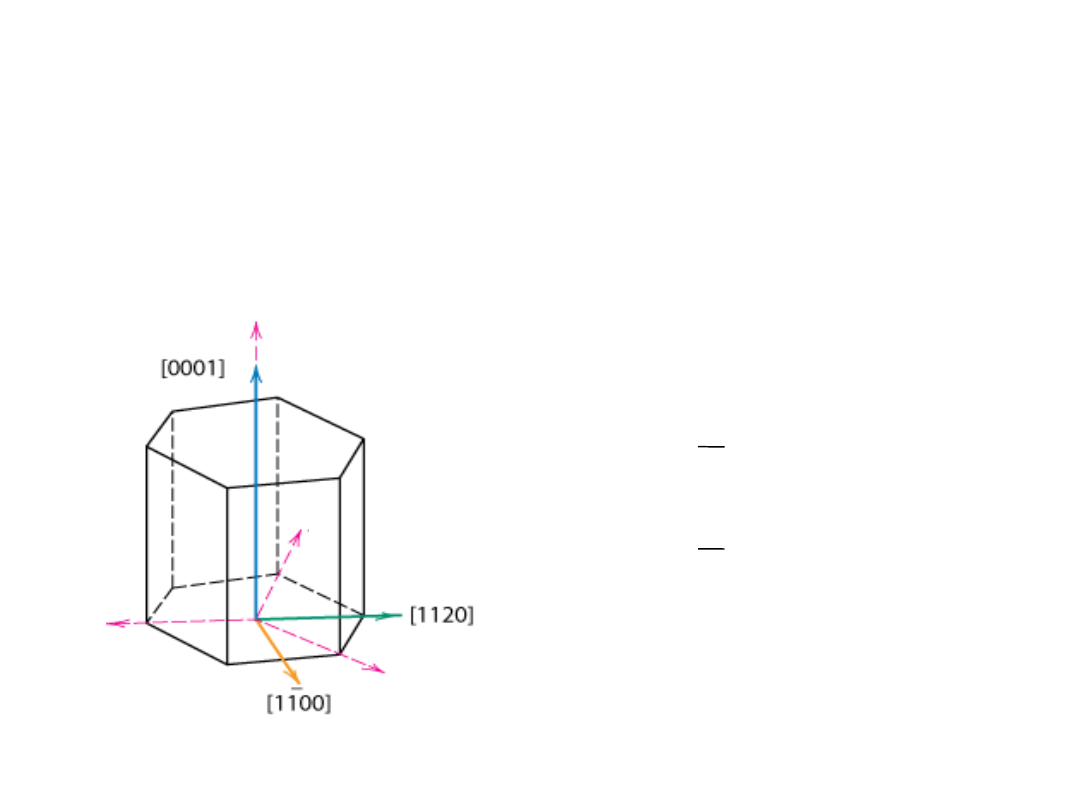
35

Kierunki w strukturze HZ

Cztery wskaźniki mają odpowiednik w trzech
wskaźnikiach sieci Bravais’go (u'v'w'):







'

w

w

t

v

u

)

v

u

( +

-

)

'

u

'

v

2

(

3

1

-

)

'

v

'

u

2

(

3

1

-



]

uvtw

[

]

'

w

'

v

'

u

[



-

a

3

a

1

a

2

z

36

Płaszczyzny

Krystalograficzne

37

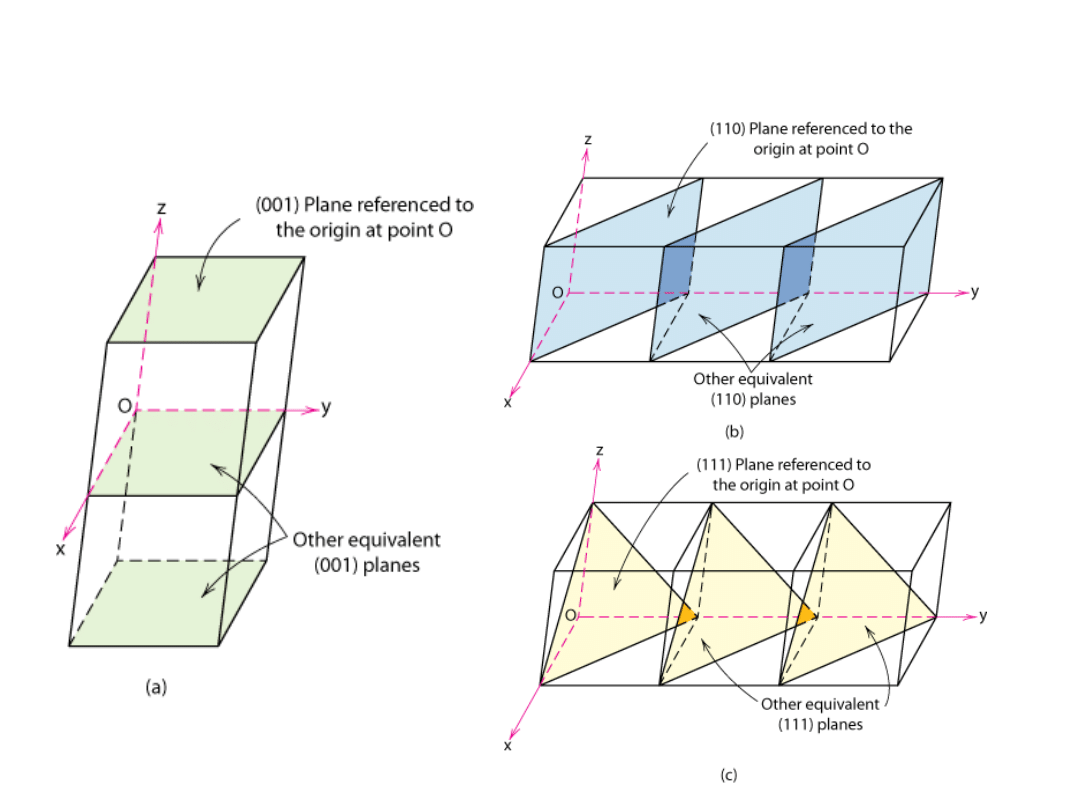
Płaszczyzny Krystalograficzne

• Wskaźniki Millera:

odwrotności

długości odcinków odciętych na osiach

układu przez rozpatrywaną płaszczyznę,

sprowadzone do najmniejszych liczb

całkowitych. Wszystkie płaszczyzny

równoległe mają te same wskaźniki

• Algorytm

 

1. Odczytać współrzędne przecięć płaszczyzny

z osiami w jednostkach a, b, c

2. Obliczyć odwrotności

3.  Sprowadzić do liczb całkowitych

4. Umieścić w nawiasach okrągłych, bez

przecinków

(hkl)

38

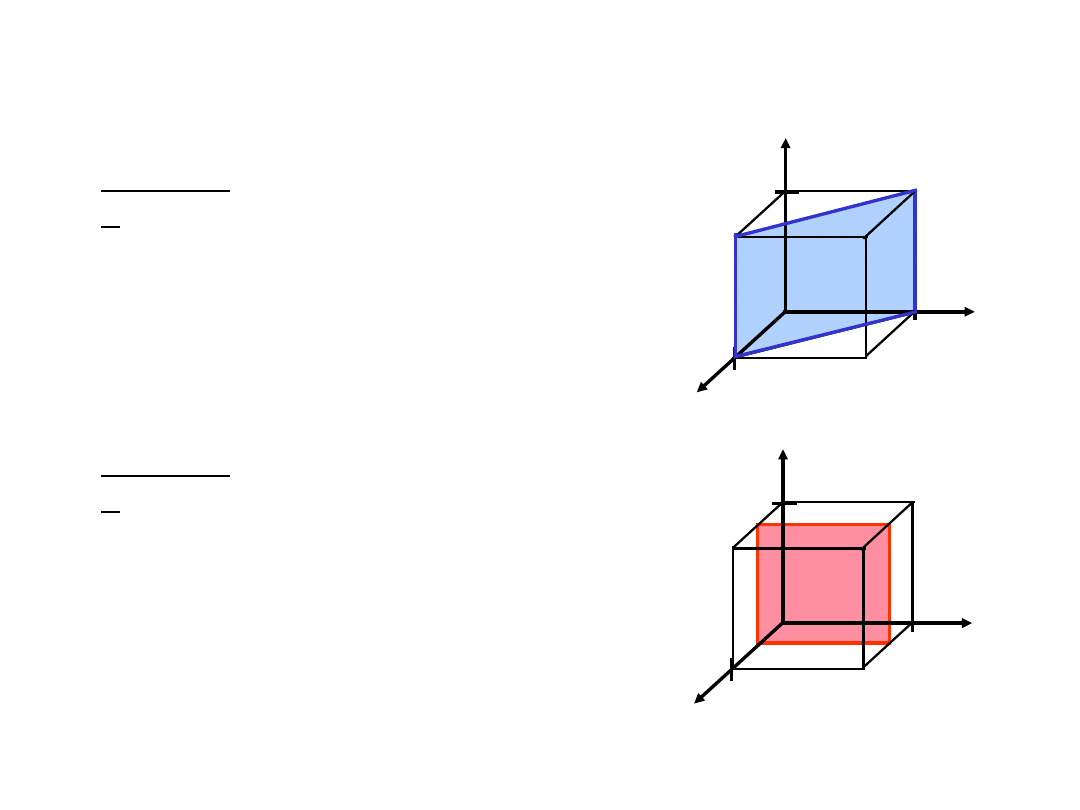
Płaszczyzny Krystalograficzne

z

x

y

a

b

c

4. Wskaźniki Millera
(110)
przykład
2

a b c

z

x

y

a

b

c

4. Wskaźniki Miller (100)

1. Przecięcia

1 1 

2.
Odwrotności

1/1 1/1 1/

1 1 0

3. Redukcja

1 1 0

1.
Przecięcias

1/2  

2.
Odwrotności

1/½ 1/ 1/

2 0

0

3. Redukcja 2 0

0

przykład
1

a b c

39

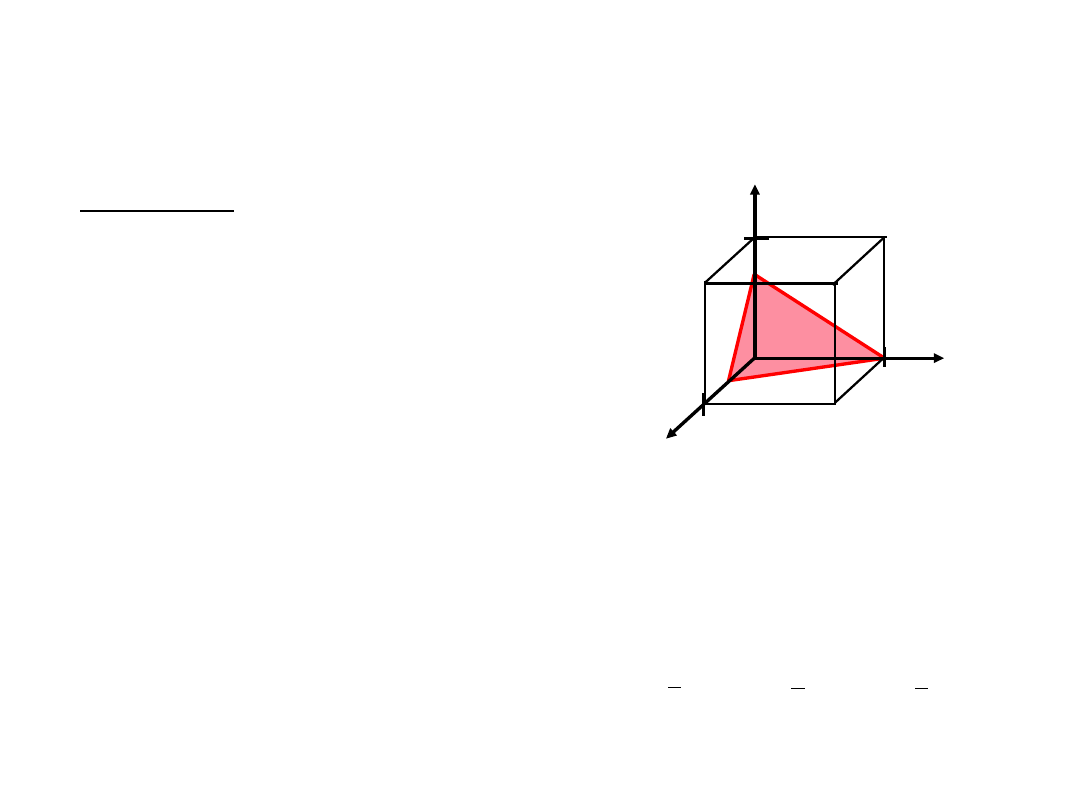
Płaszczyzny Krystalograficzne

z

x

y

a

b

c







4. Wskaźniki Millera
(634)

przykład

1. Przecięcia

1/2

1

3/4

a b c

2.
Odwrotności

1/½ 1/1 1/¾

2

1

4/3

3. Redukcja

6

3 4

(001)

(010),

Rodzina płaszczyzn
{hkl}

(100),(010),

(001),

Np.: {100} = (100),

40

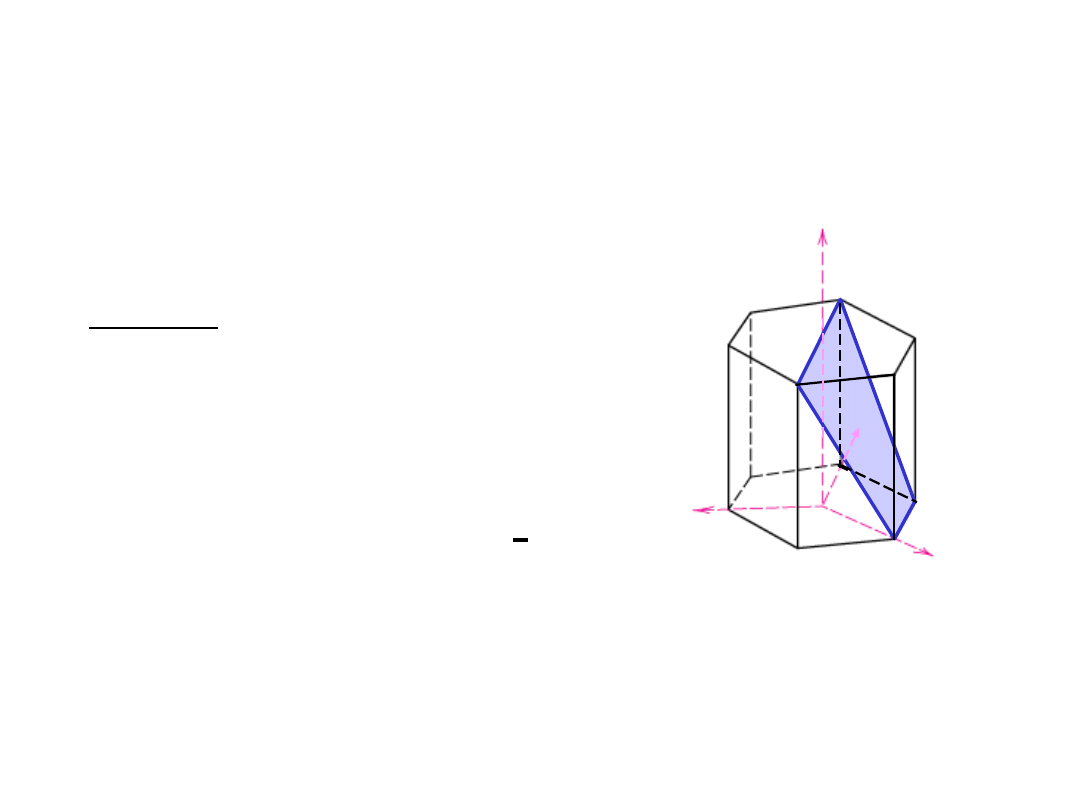
Płaszczyzny Krystalograficzne (HZ)

• W strukturze heksagonalnej ta sama

procedura

przykład

a

1

a

2

a

3

c

4. Wskaźniki Millera

(1011)

1. Przecięcia

1 

-1

1

2. Odwrotności

1 1/
1 0

-1
-1

1
1

3. Redukcja

1 0

-1

1

a

2

a

3

a

1

z

41

Ułożenia atomów

Ułozenie atomów na płaszczyźnie
krystalograficznej zależy od struktury
krystalicznej

Przykład:

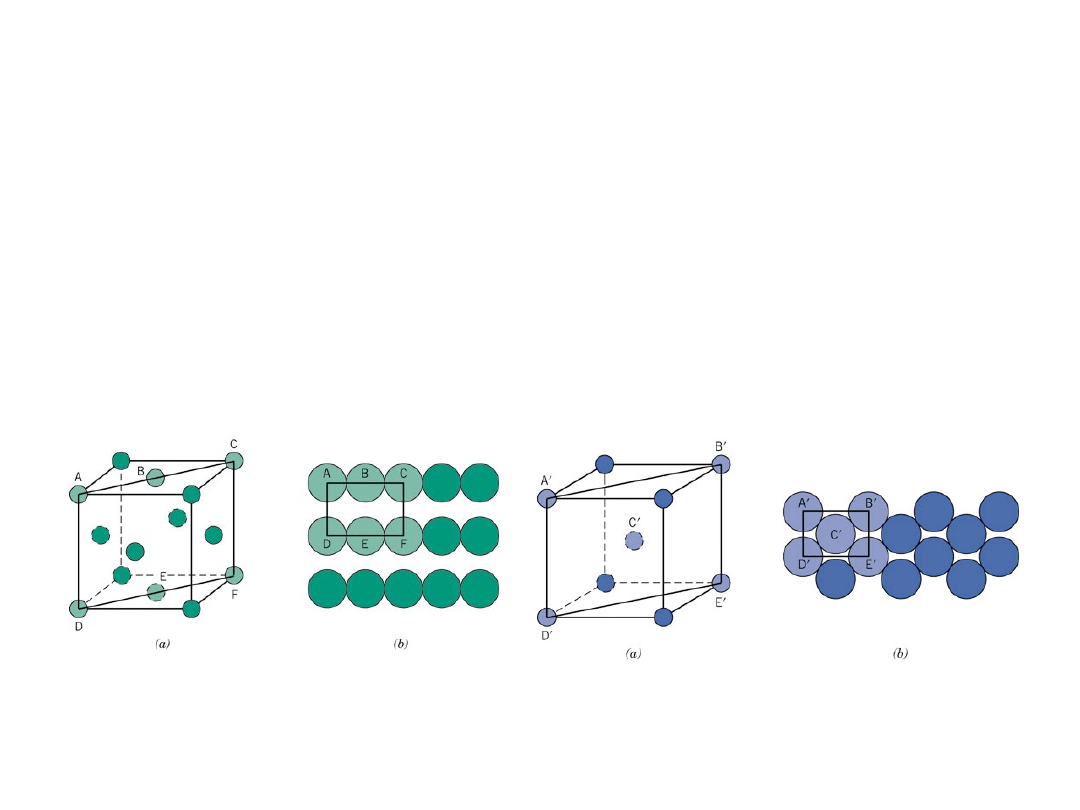
płaszcyzna (110) w kryształach RSC i RPC

RSC

RPC

42

Gęstość płaszczyznowa

• We want to examine the atomic

packing of crystallographic planes

• Iron foil can be used as a catalyst. The

atomic packing of the exposed planes
is important.

a) Draw (100) and (111) crystallographic

planes
for Fe.

b) Calculate the planar density for each of

these planes.

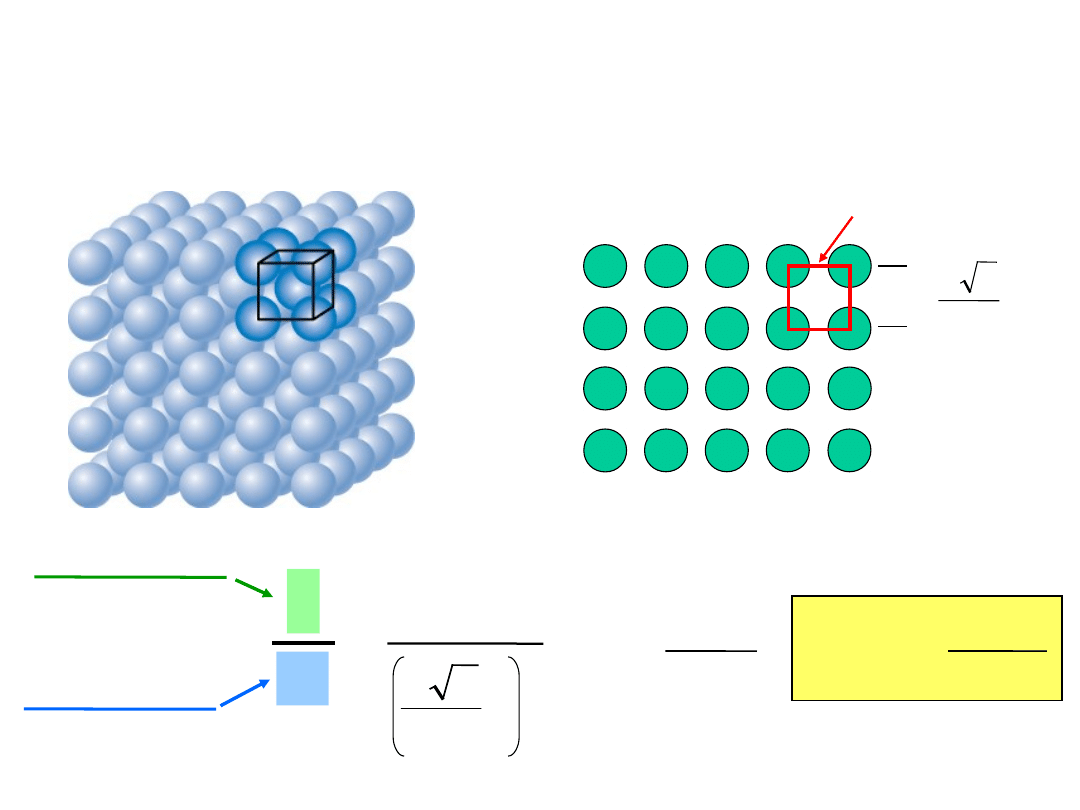
43

Gęstość płaszczyznowa (100) Fe

Rozwiązanie:  W T < 912C Fe ma strukturę RPC

(100

)

Promień at. Fe R = 0.1241
nm

R

3

3

4

a



2D komórka

=

Gęstość pow. =

a

2

1

atomy

2D komórka

=

nm

2

atomów

12.1

m

2

atomów

= 1.2 x 10

19

1

2

R

3

3

4

pow.

2D komórka

44

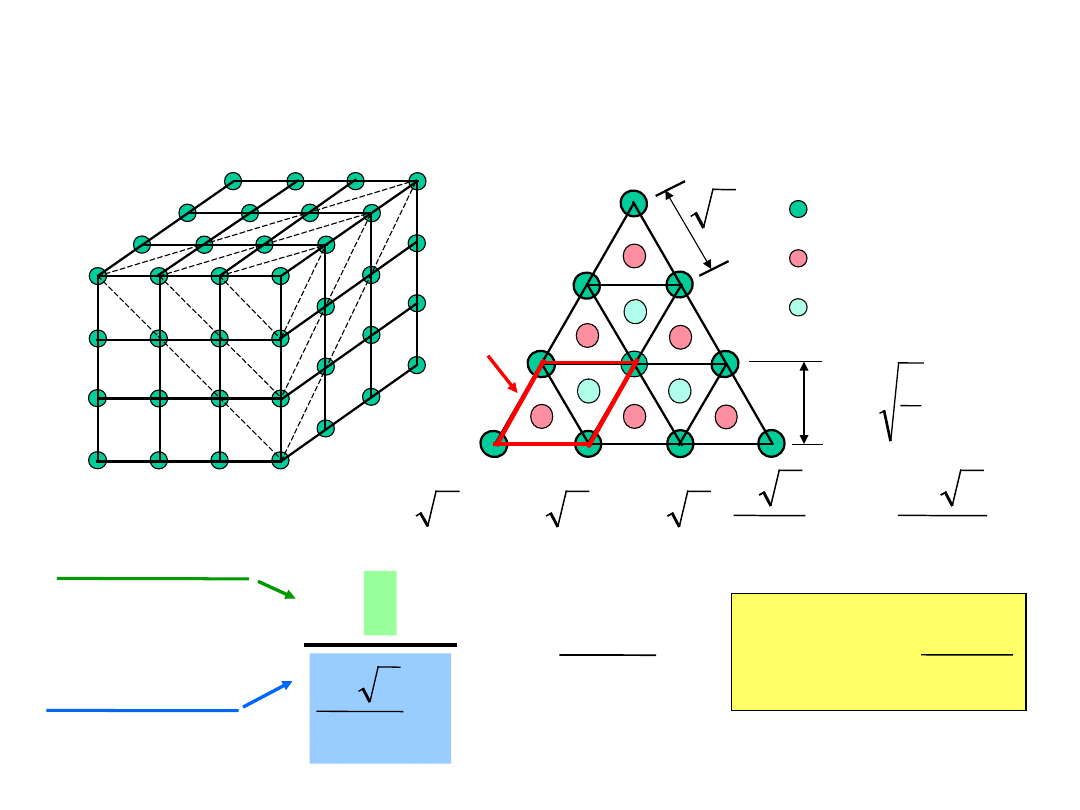
Gęstość Płaszczyznowa (111) Fe

  (111) plane

1 atom w pł./ jedn. pow.
kom.

3

3

3

2

2

R

3

16

R

3

4

2

a

3

ah

2

pow.





















atomy w pł.

atomy powyżej
pł.

atomy poniżej
pł.

a

h

2

3



a

2

2D

k

om

ór

ka

1

=

=

nm

2

atom

7.0

m

2

atom

0.70 x 10

19

3

2

R

3

16

Gęstość pow. =

atoms

2D komórka

pow.

2D komórka

45

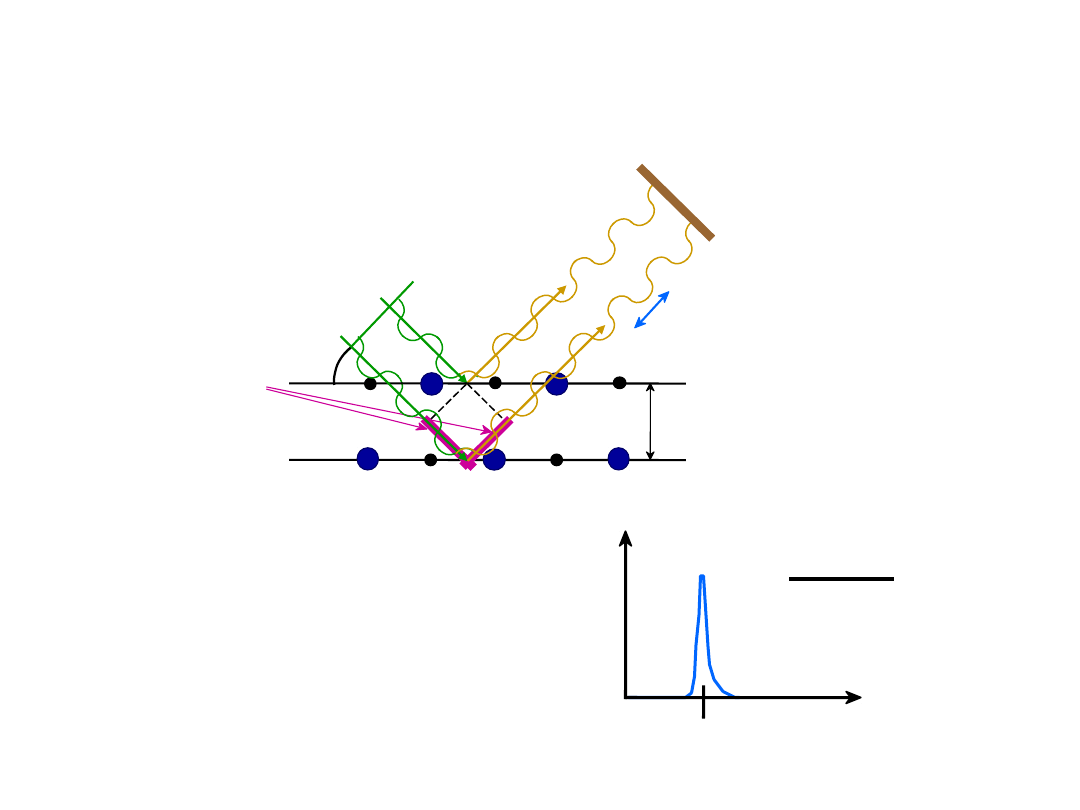
Wyznaczanie Struktury Kryształu

intensywność



c

d



n



2

sinc

Pomiar kąta 

c

, pozwala

na obliczenie odległości
międzypłaszczyznowych
, d.

Padające promieniowanie X ulega

dyfrakcji

na pł. kryształu

odbite promienie

muszą być w fazie

odległość

pomiędzy

płaszczyznami

d

Pa

da

jąc

e

pr.

X

pr

om

ie

ni

e

X

de

tek

tor







extra

odległość

pokonana

przez “2”

“1

”

“2

”

“1

”

“2

”

46

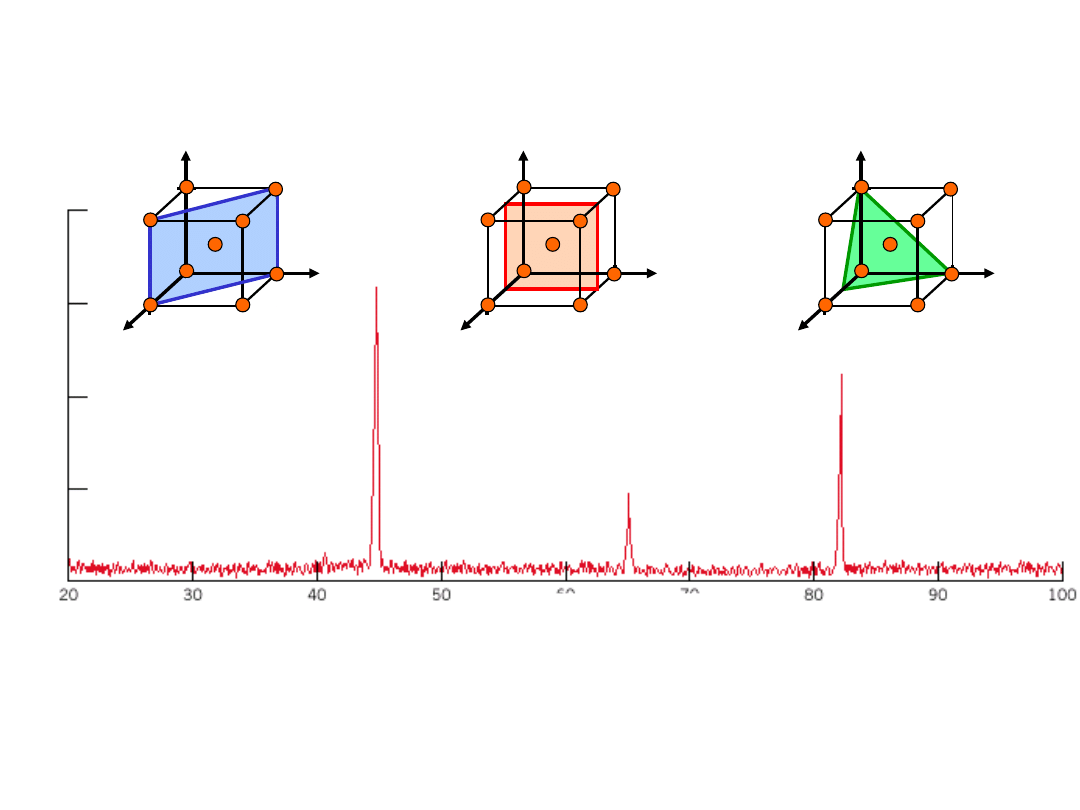
Dyfraktogram rentgenowski

(110)

(200)

(211)

z

x

y

a

b

c

Kąt Odbicia 2

Dyfraktogram polikrystalicznego Fe- (RPC)

In

te

n

sy

w

n

o

ść

(

w

zg

lę

d

n

a

)

z

x

y

a

b

c

z

x

y

a

b

c