PRZEKRÓJ TEOWY
POJEDYŃCZO ZBROJONY
W konstrukcjach monolitycznych płyta opierając się
na żebrach współpracuje z nimi. Oba elementy
tworzą łącznie przekrój w kształcie litery T – zwany
teowym.
Współpraca płyty z żebrem może być uwzględniana
w obliczeniach tylko wtedy gdy płyta znajduje się w
strefie ściskanej.
W obszarze momentów ujemnych – rozciągających
płytę może ona ulec zarysowaniu i tam nie
uwzględnia się współpracy z żebrem.
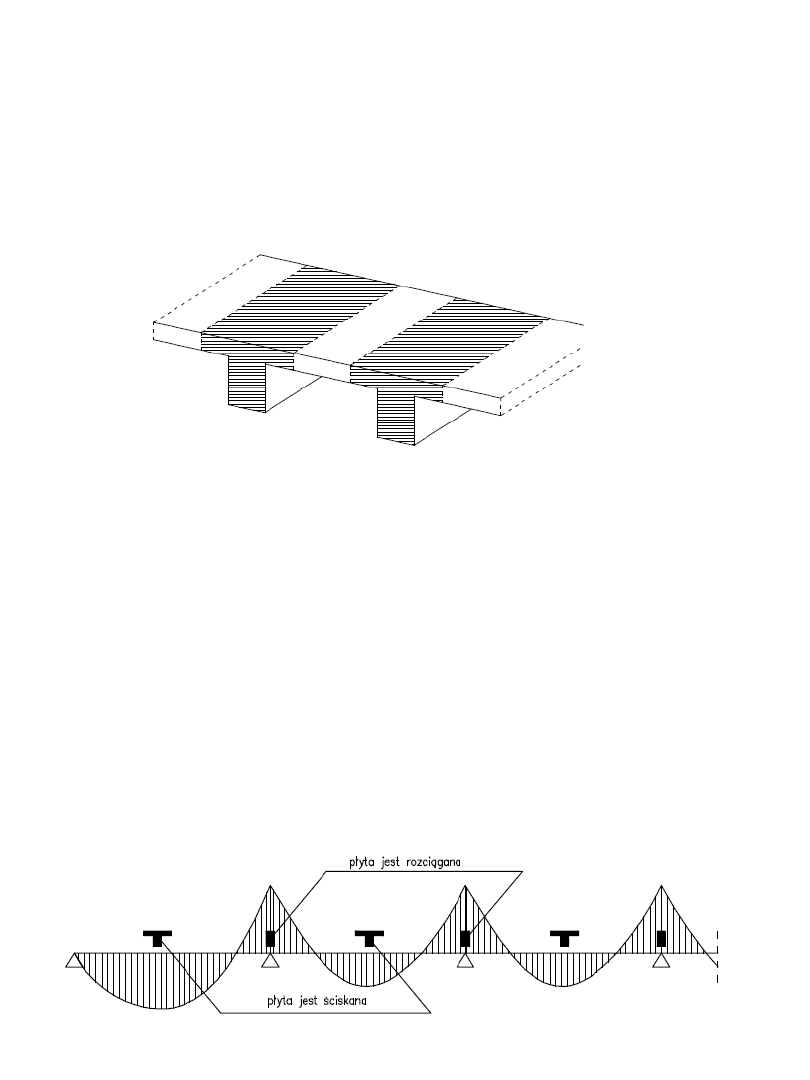
Np. belka ciągła o kształcie teowym:
- w przekrojach przęsłowych płyta jest ściskana
więc belka w obliczeniach ma przekrój teowy,
- w przekrojach podporowych płyta jest rozciągana,
belka ma przekrój prostokąta ( nie uwzględnia się
współpracy z płytą).
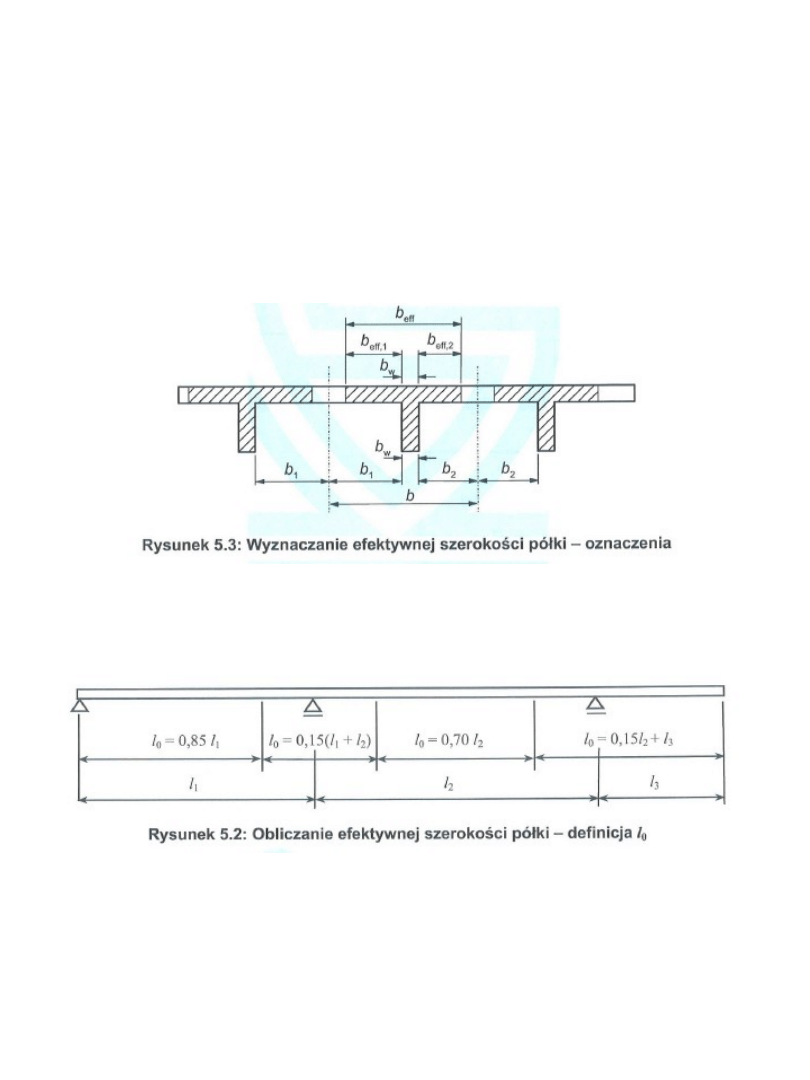
Efektywną szerokość półki b
ef
belek teowych i
półteowych (z półką z jednej strony) można określać ze
wzoru:
b
ef
= b
ef ,i
+ b
w
, lecz nie więcej niż b
w którym:
b
ef ,i
= 0,2b
i
+ 0,1
0
, lecz nie więcej niż 0,2l
0
i nie więcej
niż b
i
Efektywną szerokość półki ustala się na podstawie
odległości l
0
między punktami zerowymi momentu
zginającego, którą określa się na podstawie rys.5.2
Jeżeli nie wymaga się dużej dokładności to, w
obliczeniach można przyjąć, że szerokość belki jest
stała wzdłuż całej rozpiętości.
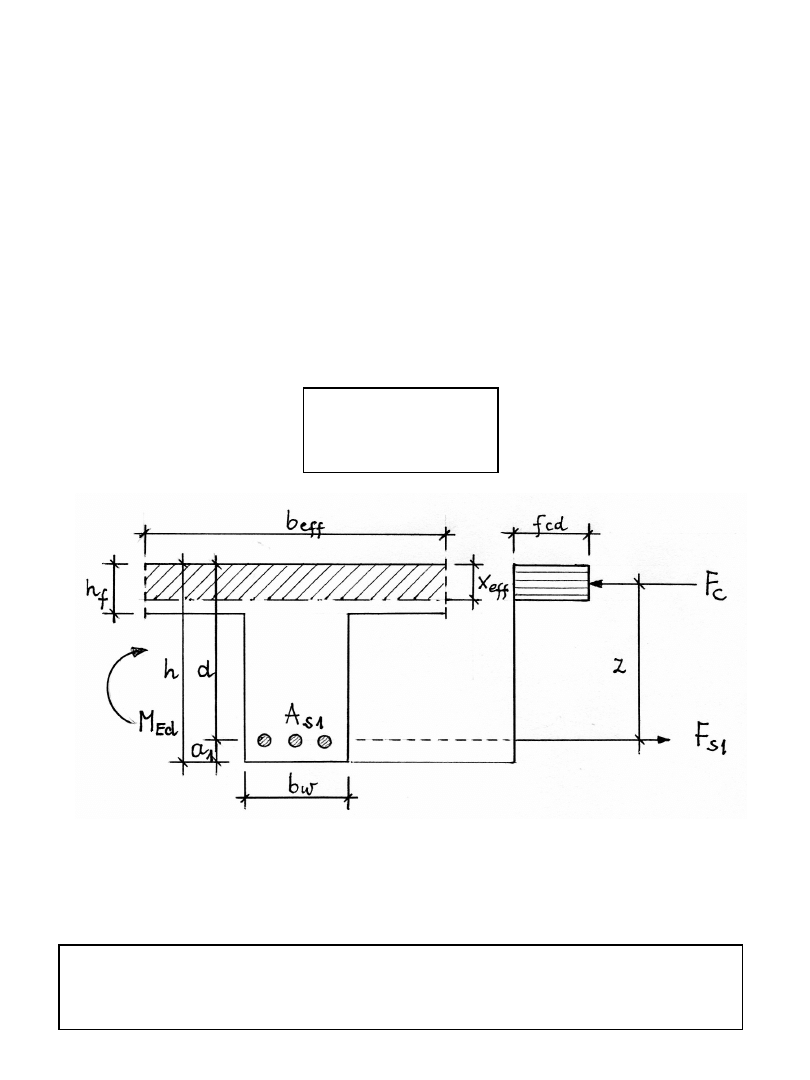
WYMIAROWANIE PRZEKROJU TEOWEGO
O sposobie wymiarowania belki teowej decyduje kształt
strefy ściskanej przekroju.
Wyróżnia się dwa przypadki obliczeniowe w zależności od
położenia osi obojętnej.
PRZEKRÓJ POZORNIE TEOWY
Oś obojętna znajduje się w półce, strefa ściskana ma
kształt prostokąta, ponieważ
x
ef
≤ h
f
Beton w strefie rozciąganej nie pracuje, przekrój można
więc traktować jako prostokąt o wymiarach b
ef
• h
Przekrój nazywa się pozornie teowy, bo jest liczony jak
prostokąt
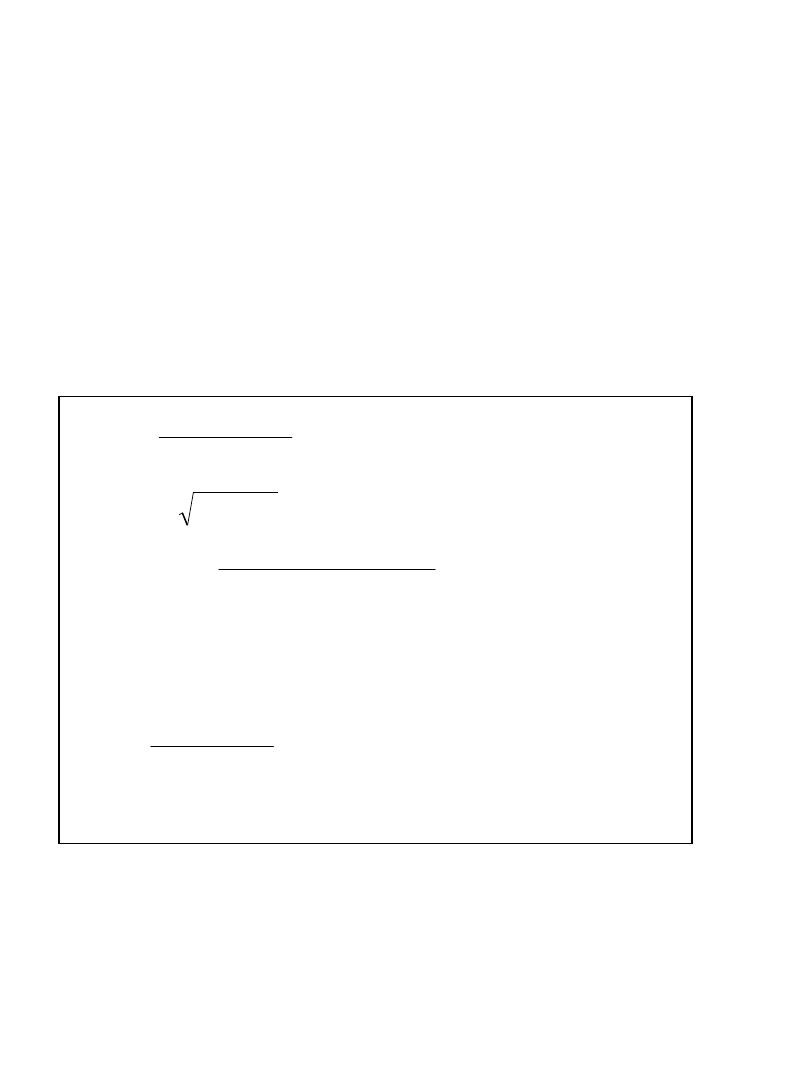
Nośność przekroju określa się jak dla przekroju
prostokątnego z warunków równowagi
M
Ed
= F
c
z = f
cd
b
ef
x
ef
(d - 0,5x
ef
)
lub
M
Ed
= F
s1
z = f
yd
A
s1
(d - 0,5x
ef
)
Algorytm wymiarowania przekroju o kształcie
teowym jest taki sam jak przekroju prostokątnego.
jeżeli ξ
ef
ξ
ef,lim
– przekrój pojedynczo
zbrojony
2
d
b
f
M
ef
cd
Ed
ef
ef
ef
2
1
1
200000
/
0035
,
0
0035
,
0
8
,
0
lim
,
yd
ef
f
ef
ef
,
5
0
1
d
f
M
A
yd
ef
Ed
s
1
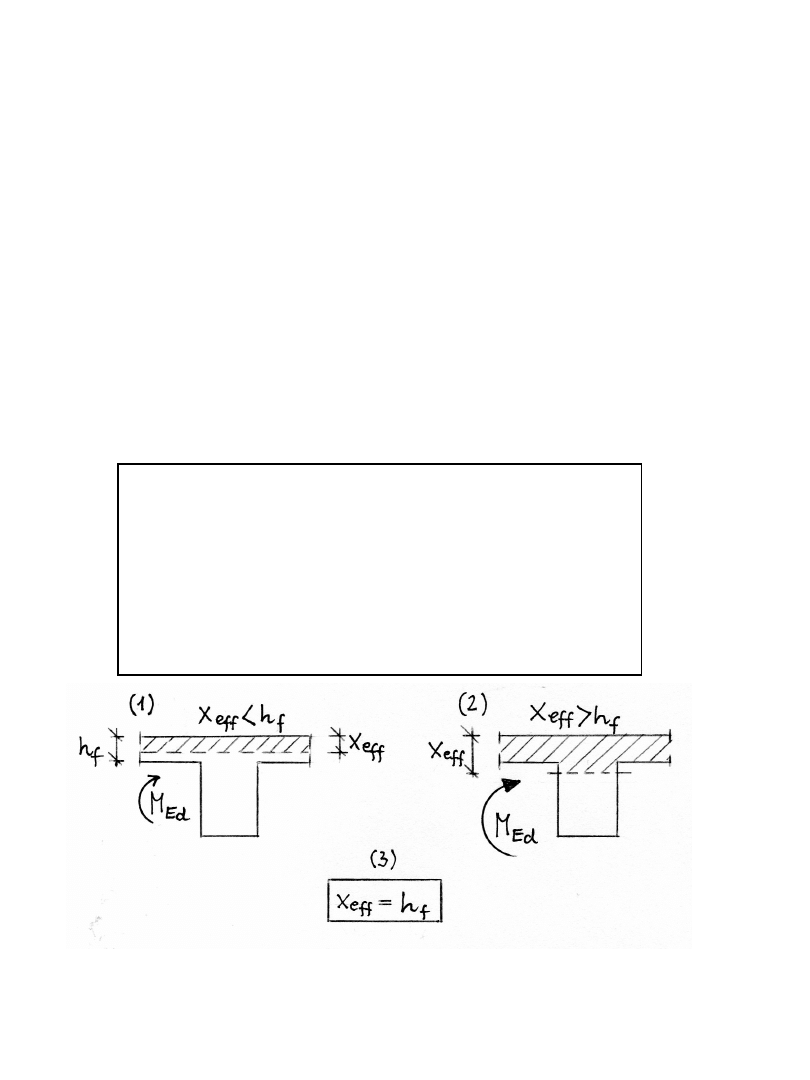
W obliczeniach praktycznych nie możemy z góry określić
z jakim przypadkiem przekroju teowego mamy do
czynienia.
Ponieważ nie znamy wysokości strefy ściskanej
przyjmujemy
x
ef
= h
f
Przy tym założeniu obliczamy nośność przekroju
M
Rd
= f
cd
b
ef
h
f
(d – 0,5h
f
)
Moment jaki może przenieść przekrój przy założeniu
x
ef
= h
f
porównujemy z momentem M
Ed
od obciążeń
obliczeniowych
Jeżeli : M
Ed
M
Rd
to przekrój pozornie teowy (1)
Jeżeli : M
Ed
M
Rd
to przekrój rzeczywiście teowy (2)
(3) x
ef
= h
f
wtedy nośność M
Rd
= f
cd
b
ef
h
f
(d – 0,5h
f
)
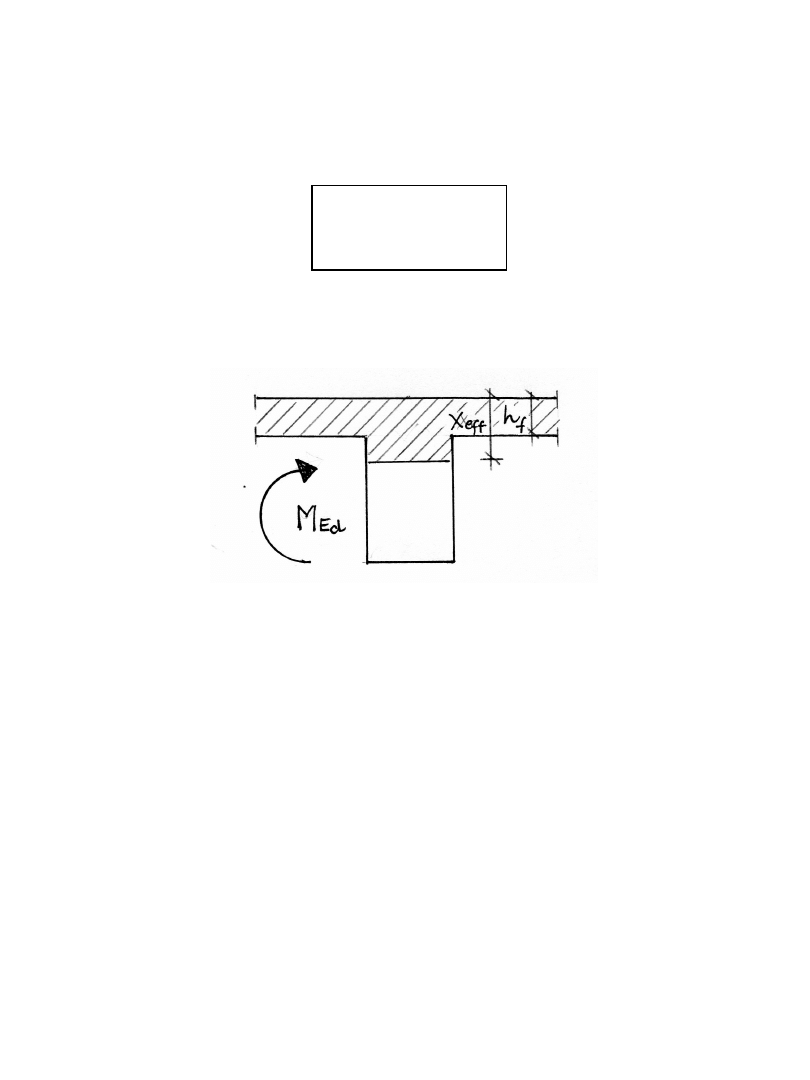
PRZEKRÓJ RZECZYWIŚCIE TEOWY
Oś obojętna znajduje się w środniku, strefa
ściskana ma kształt teowy, ponieważ
x
ef
> h
f
Strefa ściskana ma kształt teowy tylko wtedy, gdy
na przekrój działają bardzo duże obciążenia
Omawiany przypadek, występuje w praktyce
stosunkowo rzadko.
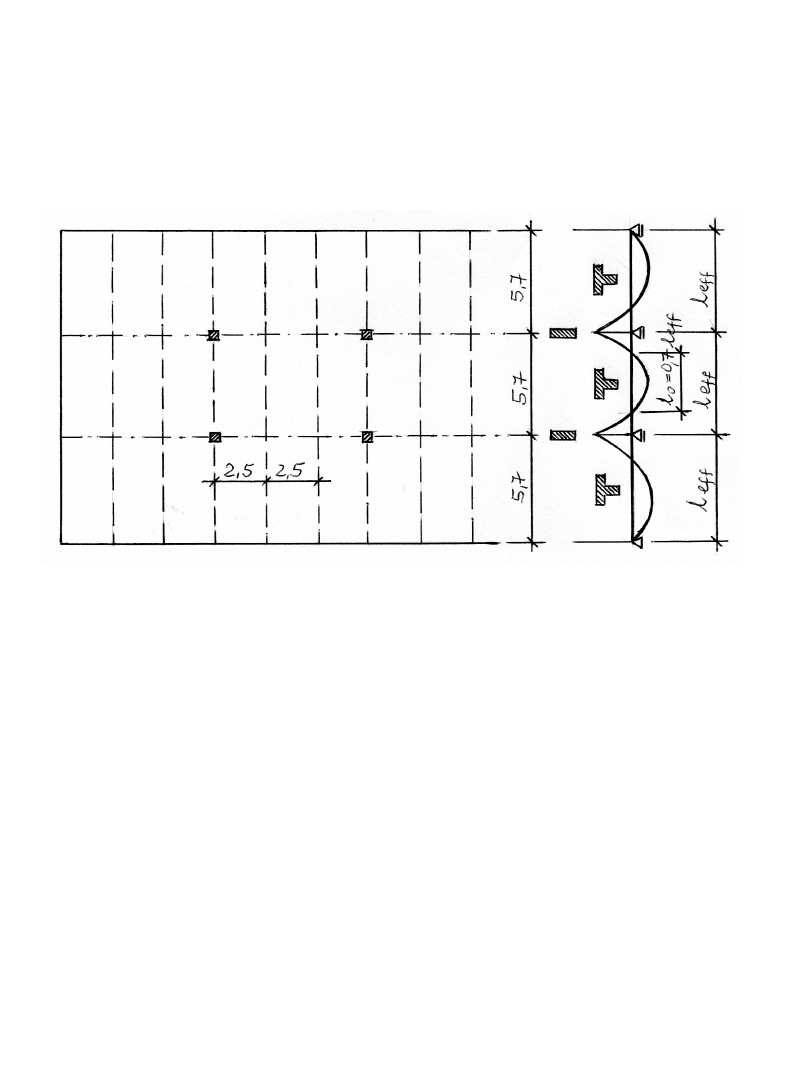
PRZYKŁAD 5
Zaprojektować zbrojenie w przęśle środkowym i na
podporze trójprzęsłowego żebra stropu płytowo-
żebrowego.
Dane:
M
2-2
= 240,0 kNm (w przęśle środkowym)
M
2
= 300,0 kNm (na podporze)
l
ef
=5,7 m,
odległość miedzy belkami b = 2,5 m
wymiary żebra:
h = 0,55 m
b
w
= 0,25 m
h
f
= 0,12 m
beton C30/37), f
cd
= 30/1,4 = 21,4 MPa
stal B500SP klasy C, f
yd
= 500/1,15 = 435 MPa,
ef,lim
=
0,50
klasa konstrukcji S4, klasa ekspozycji XC3
przyjęto:
max
= 20 mm
- Określenie nominalnej grubości otuliny
c
min
= maxc
min,b
= ; c
min,dur
; 10mm =
= max20mm; 25mm; 10mm = 25 mm
c
dev
= 10 mm
c
nom
= c
min
+ c
dev
= 25 + 10 = 35 mm
- Obliczenie a
1
oraz d
dla przyjętego
strzem
= 8 mm
a
1
= 35 + 8 + 0,5 20 = 53 mm
przyjęto a
1
= 55 mm
d = h – a
1
= 0,55 – 0,055 = 0,495 m
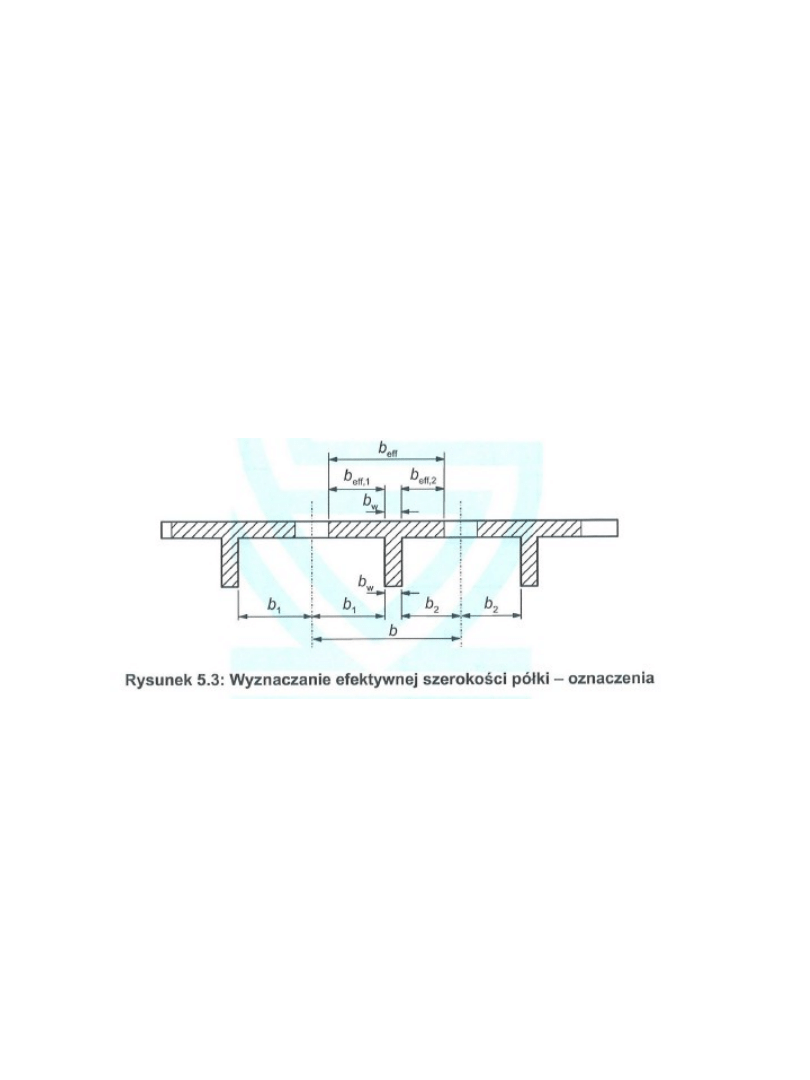
- Określenie efektywnej szerokości półki b
ef
(rys.5.3)
b
ef
= b
ef ,i
+ b
w
, lecz nie więcej niż b
b
ef ,i
= 0,2b
i
+ 0,1l
0
, lecz nie więcej niż 0,2l
0
i nie więcej
niż b
i
Wartość l
0
między punktami zerowych momentów w
przęśle środkowym przyjęto zgodnie z EC2, rys. 5.2
l
0
= 0,7 l
ef
= 0,7 5,7 = 3,99 m = 4,0 m
b
i
= b
1
= b
2
= 0,5(2,5 – 0,25) = 1,125 m
b
ef ,i
= b
ef,1
= b
ef,2
= 0,2b
i
+ 0,l
0
= 0,2 ∙ 1,125 + 0,1 ∙
4,0=0,625 m
b
ef
= b
ef ,i
+ b
w
= 2 ∙ 0,625 + 0,25 = 1,50 m
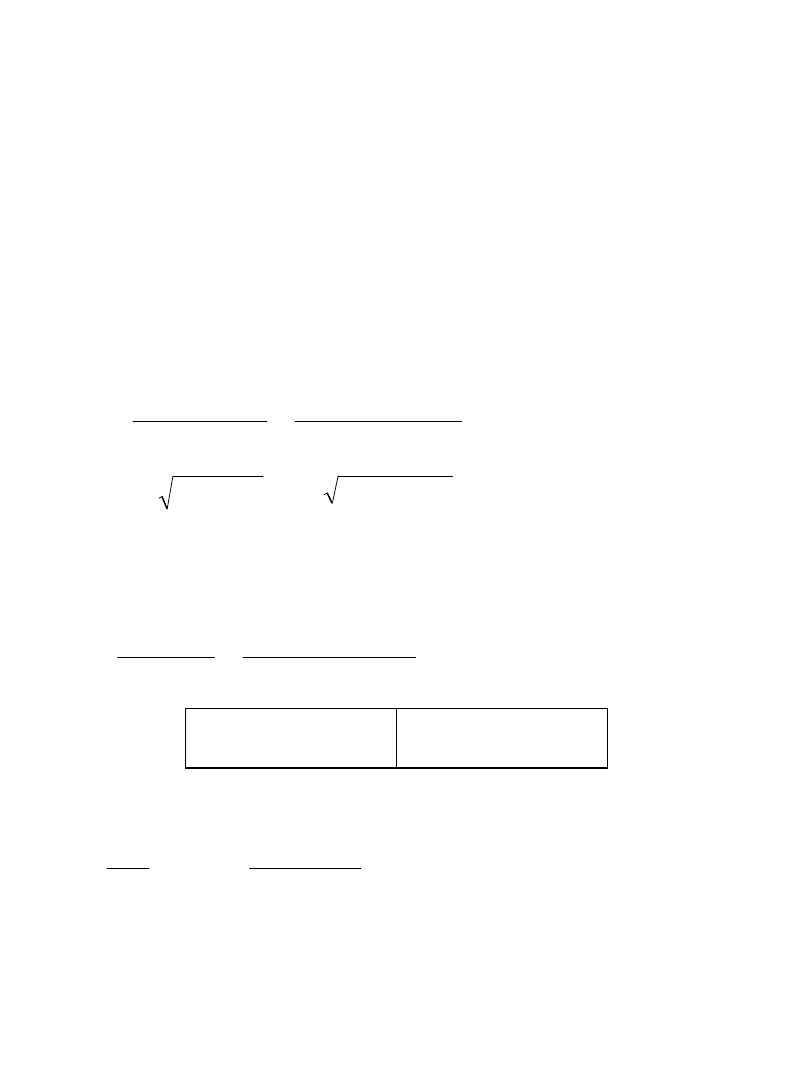
- Rozstrzygnięcie, z którym przypadkiem przekroju
teowego mamy do czynienia:
zakładamy x
ef
= h
f
obliczamy nośność przekroju przy tym założeniu
oznacza to, że x
ef
< h
ef
czyli przekrój jest pozornie
teowy.
- Obliczenie przekroju zbrojenia w przęśle żebra
przekrój jest pojedynczo zbrojony
m
2
=11,34 cm
2
przyjęto 4 20 A
s1
= 12,56 cm
2
MNm
MNm
h
d
h
b
f
M
f
f
ef
cd
Rd
240
,
0
676
,
1
12
,
0
5
,
0
495
,
0
12
,
0
5
,
1
4
,
21
5
,
0
030
,
0
495
,
0
5
,
1
4
,
21
240
,
0
2
2
2
2
d
b
f
M
ef
cd
ef
50
,
0
033
,
0
030
,
0
2
1
1
2
1
1
lim
,
ef
ef
ef
983
,
0
033
,
0
5
,
0
1
5
,
0
1
ef
ef
001134
,
0
495
,
0
435
983
,
0
240
,
0
2
2
1
d
f
M
A
yd
s
%
0
,
1
010
,
0
495
,
0
25
,
0
001256
,
0
%
100
1
d
b
A
s
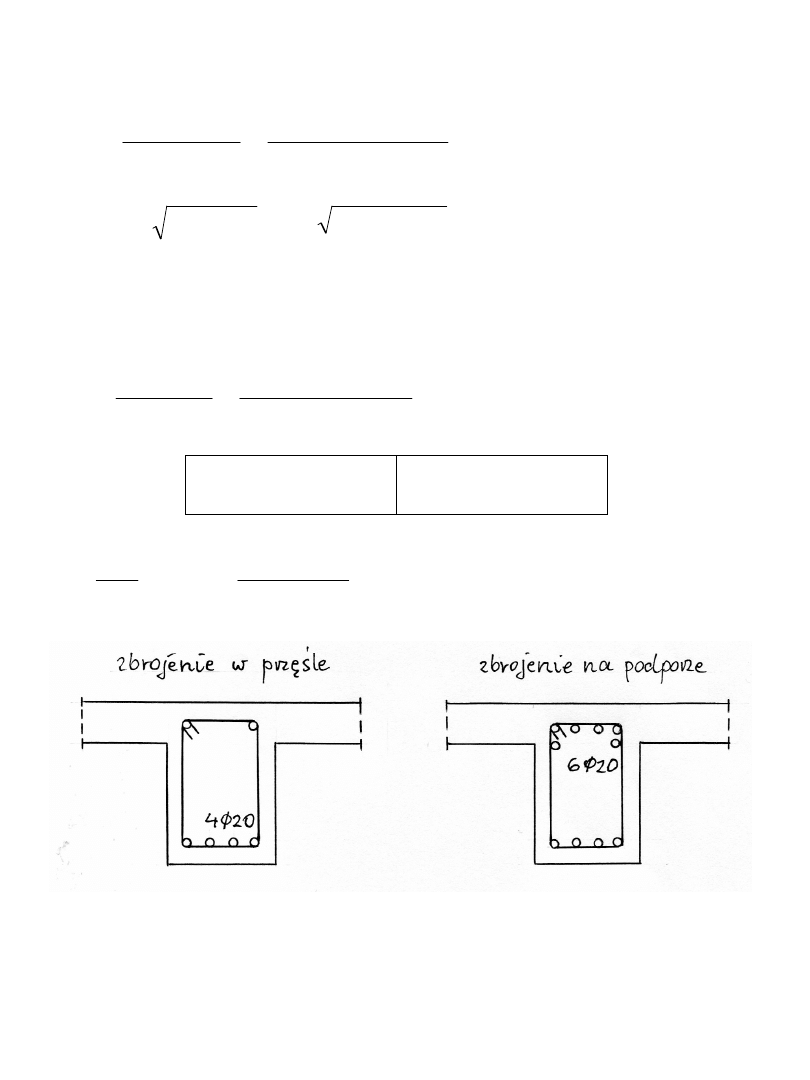
- Obliczenie przekroju zbrojenia na podporze żebra
przekrój jest pojedynczo zbrojony
m
2
=16,05 cm
2
przyjęto 6 20 A
s1
= 18,84 cm
2
230
,
0
495
,
0
25
,
0
4
,
21
300
,
0
2
2
2
d
b
f
M
cd
ef
50
,
0
265
,
0
230
,
0
2
1
1
2
1
1
lim
,
ef
ef
ef
868
,
0
265
,
0
5
,
0
1
5
,
0
1
ef
ef
001605
,
0
495
,
0
435
868
,
0
300
,
0
2
1
d
f
M
A
yd
s
%
5
,
1
015
,
0
495
,
0
25
,
0
001884
,
0
%
100
1
d
b
A
s
Document Outline