FUNKCJA

KWADRATOWA

Z PARAMETREM

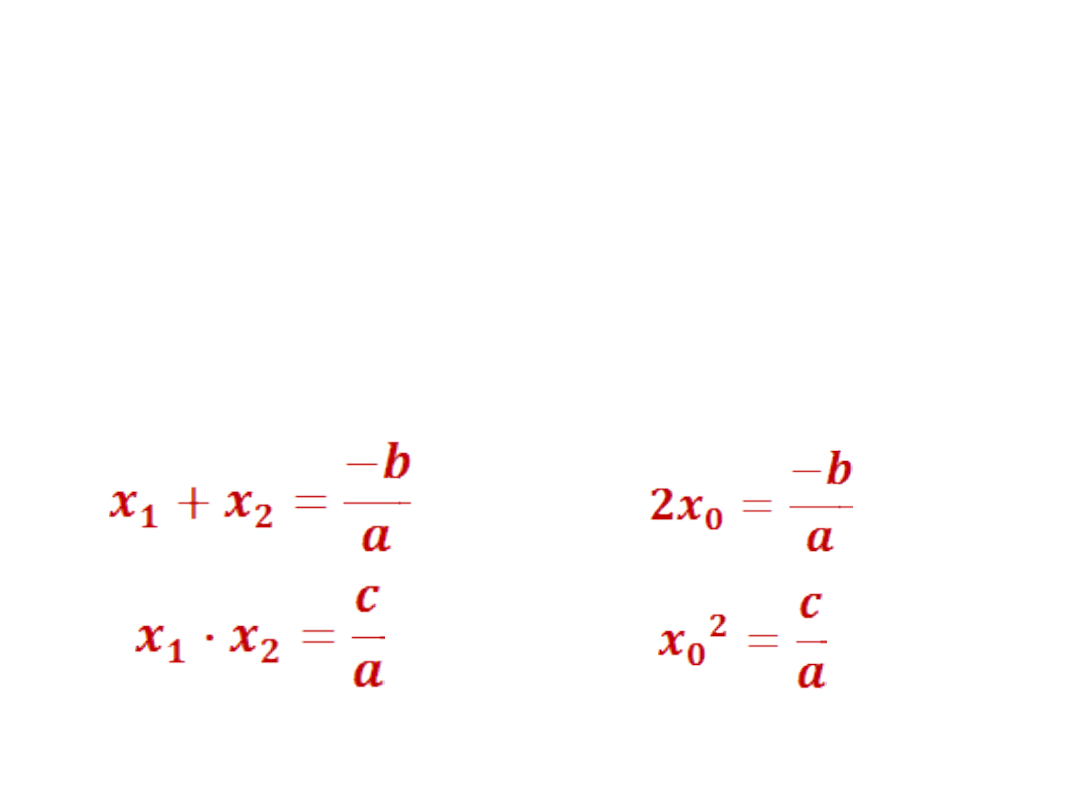
Funkcja kwadratowa w swoim wzorze może mieć
oprócz argumentu x parametr – dowolną liczbę
rzeczywistą na przykład m, która w zadaniu
będzie spełniać określone warunki.
Do rozwiązywania zadań z funkcji kwadratowej
z parametrem będą potrzebne wzory Viète’a,
stosowane dla funkcji mającej dwa lub jedno
miejsce zerowe.

f(x)=ax

2

+bx+c

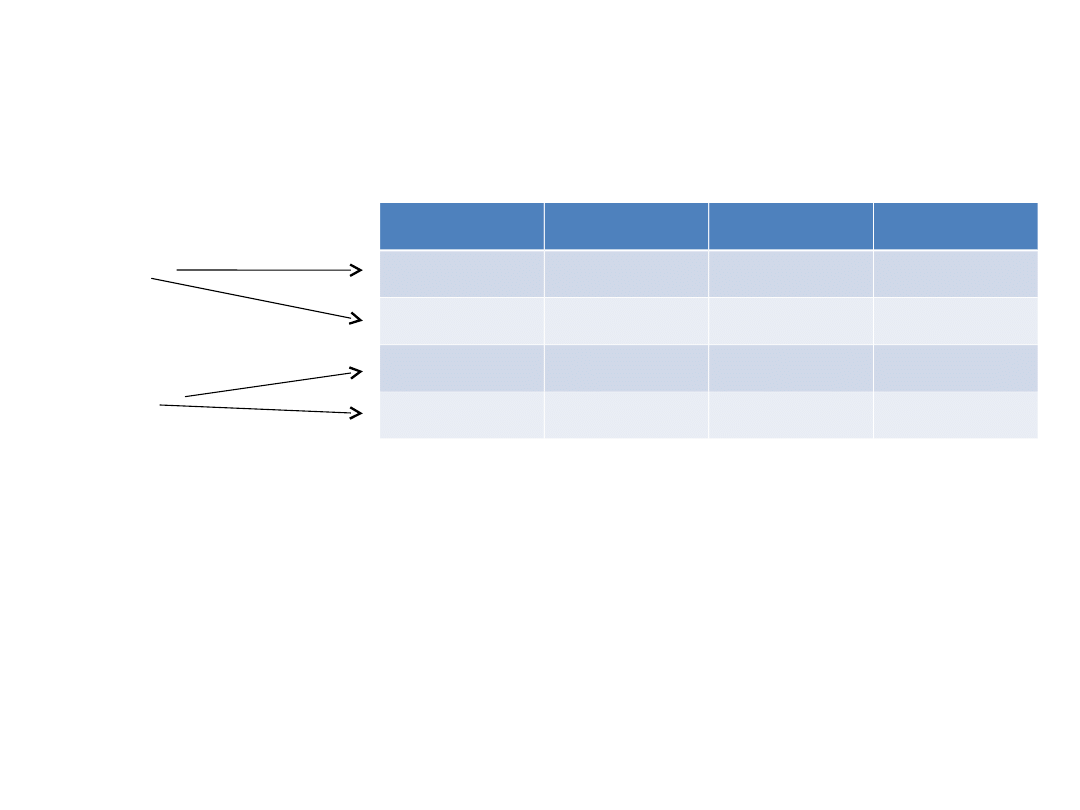
TABELA ZNAKÓW: PIERWIASTKÓW, ICH SUMY I ILOCZYNU

pierwiastki są jednakowych
znaków

pierwiastki są różnych
znaków

Z tabelki wnioskujemy, że jeżeli:
- iloczyn jest dodatni to pierwiastki są jednakowych
znaków
(obydwa dodatnie albo obydwa ujemne)
- iloczyn jest ujemny to pierwiastki są różnych znaków
(jeden
dodatni drugi ujemny)
- iloczyn dodatni i suma dodatnia to pierwiastki są
dodatnie
- iloczyn dodatni i suma ujemna to pierwiastki są ujemne

x

1

x

2

x

1

x

2

x

1

+x

2

+

+

+

+

-

-

+

-

+

-

-

+ -

-

+

-

+ -

Ćw.1: Zbadaj liczbę pierwiastków funkcji kwadratowej f
w zależności od parametru m.

a) f(x)=x

2

+4x+m

a=1 b=4 c=m

Aby zbadać liczbę miejsc zerowych funkcji najpierw
obliczymy deltę (wyróżnik) funkcji kwadratowej.

=b

2

-4ac

=16-4m

Funkcja kwadratowa ma dwa miejsca zerowe jeżeli >0.

>0 ⇔ 16-4m>0

-4m>-16
m<4
mϵ(-∞ ,4)

Funkcja kwadratowa ma jedno miejsce zerowe jeżeli =0.

=0 ⇔ 16-4m=0 ⇔ m=4

Funkcja kwadratowa nie ma miejsc zerowych jeżeli <0.

<0 ⇔ 16-4m<0

-4m<-16
m>4
mϵ(4,+∞)

Odp.: Funkcja kwadratowa f(x)=x

2

+4x+m posiada dwa

różne miejsca zerowe, gdy mϵ(-∞,4); jedno miejsce

zerowe, gdy m=4; nie posiada miejsc zerowych, gdy

mϵ(4,+∞).

b) f(x)=(6+m)x

2

-4

a=6+m b=0 c=-4

Najpierw musimy rozważyć przypadki:
1.Jeżeli 6+m=0 ⇒ m=-6 to nasza funkcja przyjmie postać
f(x)=-4 – wykresem jest prosta równoległa do osi x,
funkcja nie ma miejsc zerowych.
2. Jeżeli 6+m≠0 to funkcja jest kwadratowa i najpierw
obliczymy deltę – jej wyróżnik.

=b

2

-4ac

=0-4(6+m)(-4)=96+16m

Funkcja kwadratowa ma dwa miejsca zerowe jeżeli >0.

>0 ⇔ 96+16m>0

16m>-96
m>-6
mϵ(-6,+∞)

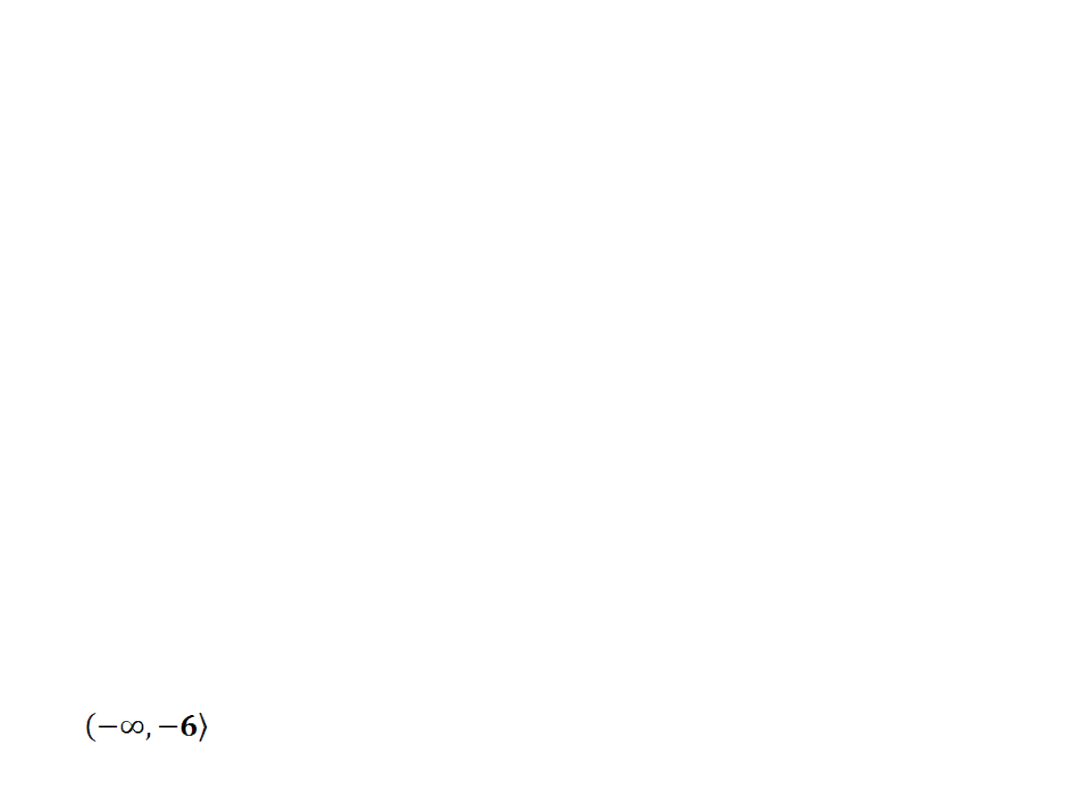
Funkcja kwadratowa ma jedno miejsce zerowe jeżeli =0.

=0 ⇔ 96+16m =0 ⇔ 16m=-96

m=-6
Już wiemy, że dla m=-6 funkcja nie jest kwadratowa tylko
liniowa i nie ma miejsc zerowych bo wykres jest
równoległy do osi x.

Sprawdzamy kiedy <0.

<0 ⇔ 96+16m<0

16m<-96
m<-6
mϵ(-∞,-6)

Odp.: Funkcja kwadratowa f(x)=(6+m)x

2

-4 posiada dwa

różne miejsca zerowe, gdy mϵ(-6,+∞); nie posiada miejsc

zerowych, gdy mϵ .

c) f(x)=x

2

+(m+3)x+1

a=1 b=m+3 c=1

Aby zbadać liczbę miejsc zerowych funkcji najpierw
obliczymy deltę (wyróżnik) funkcji kwadratowej.

=b

2

-4ac

=(m+3)

2

-4=m

2

+6m+9-4=m

2

+6m+5

Funkcja kwadratowa ma dwa miejsca zerowe jeżeli >0.

>0 ⇔ m

2

+6m+5>0 -

musimy rozwiązać nierówność z

niewiadomą m

a

1

=1 b

1

=6 c

1

=5



1

=6

2

-4·1·5=36-20=16

m

1

=-5 m

2

=-1

>0 ⇔ mϵ(-∞,-5)∪(-1,+∞)

-1

-5

-

+

+

Funkcja kwadratowa ma jedno miejsce zerowe jeżeli =0.

=0 ⇔ m

2

+6m+5=0



1

=6

2

-4·1·5=36-20=16

m

1

=-5 m

2

=-1

=0 ⇔ m ϵ {-5,-1}

Funkcja kwadratowa nie ma miejsc zerowych jeżeli <0.

<0 ⇔ m

2

+6m+5<0



1

=6

2

-4·1·5=36-20=16

m

1

=-5 m

2

=-1

<0 ⇔ mϵ(-5,-1)

Odp.: Funkcja kwadratowa f(x)=x

2

+(m+3)x+1 posiada

dwa różne miejsca zerowe, gdy mϵ(-∞,-5)∪(-1,+∞); jedno

miejsce zerowe, gdy mϵ{-5,-1}; nie posiada miejsc

zerowych, gdy mϵ(-5,-1).

Ćw.2: Dla jakiej wartości parametru m funkcja
kwadratowa
f(x)=x

2

+6x+(2m+1)

ma dwa miejsca zerowe różnych znaków?

f(x)=x

2

+6x+(2m+1)

a=1 b=6 c=2m+1
=b

2

-4ac

=36-4·1·(2m+1)=36-4(2m+1)=36-8m-4=32-8m

Aby funkcja kwadratowa miała dwa miejsca zerowe
różnych znaków
muszą być spełnione warunki: (które trzeba rozwiązać)
1) >0

2) x

1

·x

2

<0

Ad 1) >0 ⇔ 32-8m>0

-8m>-32
m<4
mϵ(-∞ ,4)

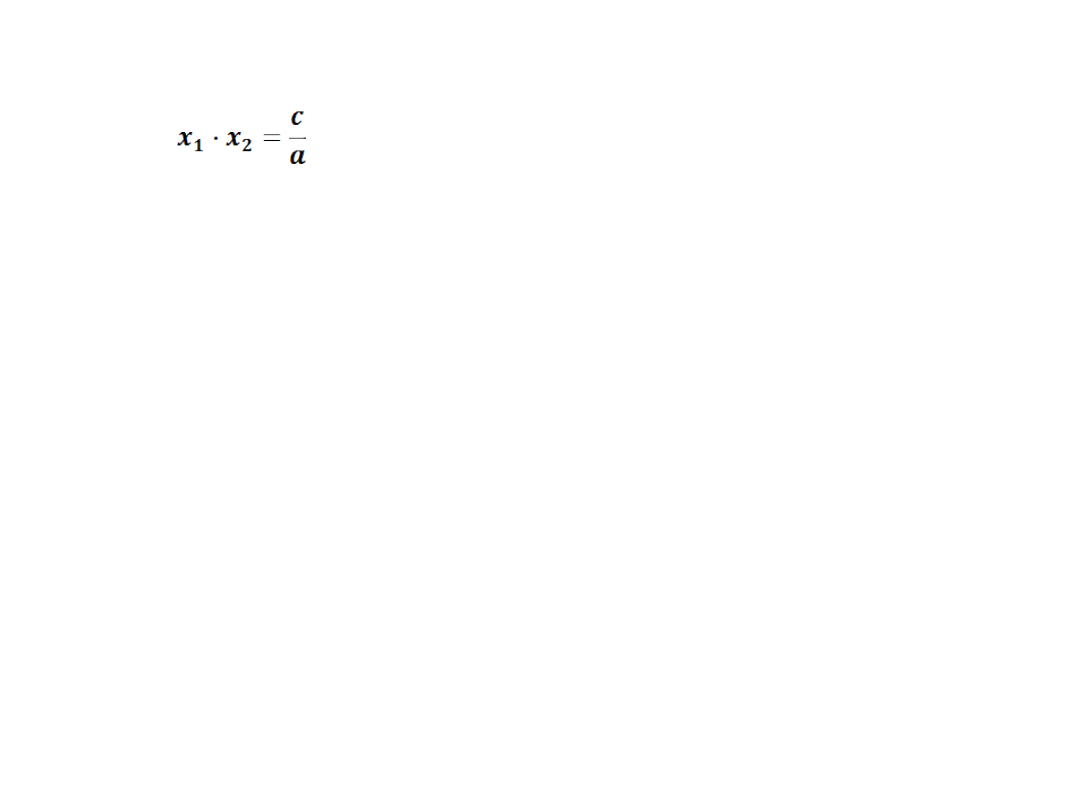
Ad 2) x

1

·x

2

<0

2m+1<0
2m<-1
m<-½
mϵ(-∞; -½)

Biorąc pod uwagę jeden i drugi warunek wyznaczamy

część wspólną:

Odp.: Dla mϵ(-∞ , -½) funkcja kwadratowa

f(x)=x

2

+6x+(2m+1) ma

dwa miejsca zerowe różnych znaków.

m ϵ (-∞, -½) ∧ m ϵ (-∞,4) ⇒ m ϵ (-∞ , -½)

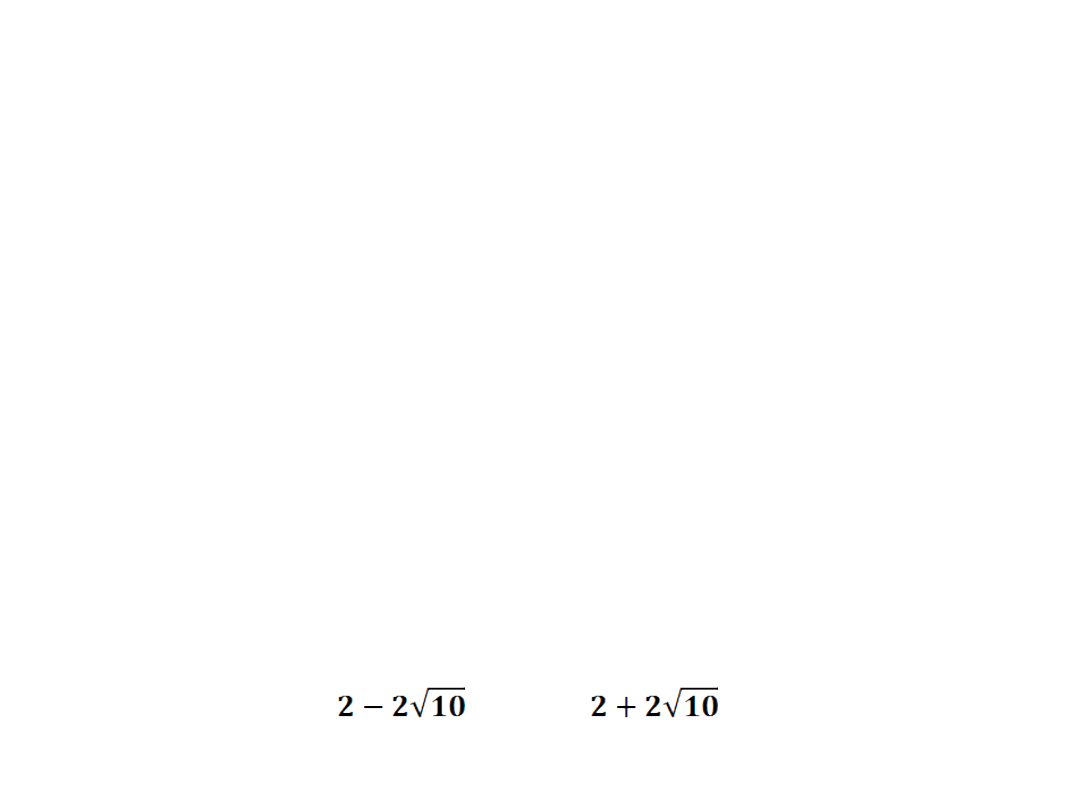
Ćw.3: Dla jakiej wartości parametru m funkcja
kwadratowa
f(x)=x

2

+(2-m)x+10 ma dwa różne ujemne miejsca

zerowe?

a=1 b=2-m c=10
=b

2

-4ac

=(2-m)

2

-4·1·10=4-4m+m

2

-40=m

2

-4m-36

Aby funkcja kwadratowa miała dwa różne ujemne miejsca
zerowe
muszą być spełnione warunki:
1) >0

2) x

1

·x

2

>0

3) x

1

+x

2

<0

Ad 1) >0 ⇔ m

2

-4m-36>0 -

musimy rozwiązać nierówność

a

1

=1 b

1

=-4 c

1

=-36



1

=(-4)

2

-4·1·(-36)=16+144=160

m

1

= m

2

=

>0 ⇔ mϵ(-∞ , m

1

)∪(m

2

,+∞)

Ad 2) x

1

·x

2

>0

10>0 ⇒ mϵR

Ad 3) x

1

+x

2

<0

-(2-m)<0
-2+m<0
m<2
mϵ(-∞,2)

Biorąc pod uwagę jeden i drugi warunek wyznaczamy
część wspólną.

Odp.: Dla mϵ(-∞ , ) funkcja kwadratowa
f(x)=x

2

+(2-m)x+10 ma dwa różne ujemne miejsca

zerowe.

m

2

m

1

-

+

+

Ćw.4: Dla jakiej wartości parametru m funkcja
kwadratowa
f(x)=x

2

-2x+2m-7 ma dwa różne dodatnie miejsca

zerowe?

a=1 b=-2 c=2m-7
=b

2

-4ac

=(-2)

2

-4·1·(2m-7)=4-8m+28=32-8m

Aby funkcja kwadratowa miała dwa różne dodatnie
miejsca zerowe
muszą być spełnione warunki:
1) >0

2) x

1

·x

2

>0

3) x

1

+x

2

>0

Ad 1) >0 ⇔ 32-8m>0

-8m>-32
m<4

mϵ(-∞,4)

Ad 2) x

1

·x

2

>0

2m-7>0
2m>7
m>3½
mϵ(3½,+∞)

Ad 3) x

1

+x

2

>0

2>0
mϵR

Wymienione wyżej przedziały
zaznaczamy na osi liczbowej
i odczytujemy część wspólną
tych warunków.

Odp.: Dla mϵ(3½,4) funkcja kwadratowa
f(x)=x

2

-2x+2m-7 ma dwa różne dodatnie miejsca

zerowe.

3½ 4