
Osie i wały

Pojęcie osi i wału
Osią lub wałem nazywa się element maszyny podparty w łożyskach
i podtrzymujący osadzone na nim części maszyn. Na wale mogą być
osadzone różne elementy wykonujące ruchy obrotowe (np. koła zębate,
piasty, tarcze hamulcowe itp.) lub ruchy wahadłowe (np. koło zębate
współpracujące z zębatką).
Różnica pomiędzy osią a wałem:
Oś
– element obciążony jedynie momentem gnącym
Wał
– element, którego głównym zadaniem jest
przenoszenie momentu obrotowego

Typy osi i wałów
Gładkie
Stopniowane
Korbowe
Rozrządu

Osie
Stałe
– kierunek działania obciążenia jest stały względem
osi
Ruchome
– obciążenie zmienia kierunek działania
Schematy: a, b) wału, c) osi nieruchomej, d) osi ruchomej

Przykłady wałów
Głównym zadaniem wału jest przenoszenie momentu obrotowego, zatem
wał wykonuje zawsze ruch obrotowy. W związku z tym wał jest narażony
jednocześnie na skręcanie oraz - pod wpływem sił poprzecznych - na
zginanie. W niektórych przypadkach wał może być narażony tylko na
skręcanie (np. samochodowy wał napędowy w sprzęgle Cardana).
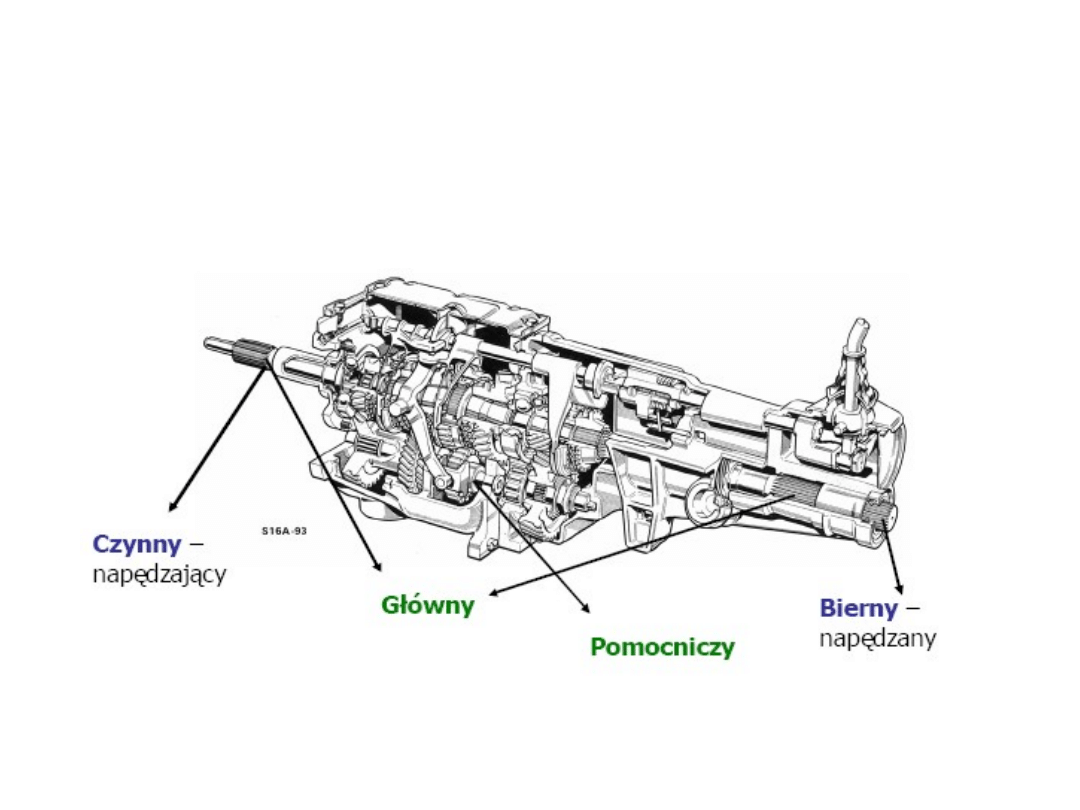
Przykłady wałów c.d.

Przykłady wałów c.d.
Wał wykonany z kompozytów
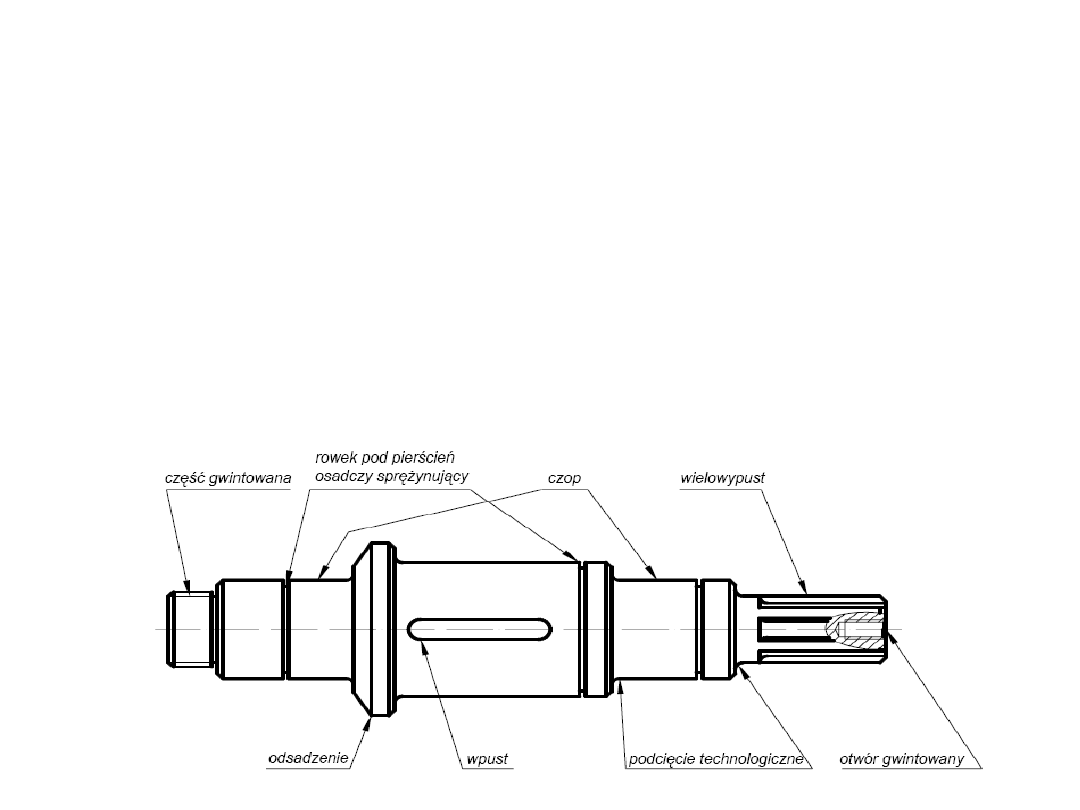
Charakterystyczne
powierzchnie wału
Czopami nazywa się odcinki osi lub wału, których powierzchnie stykają się ze
współpracującymi elementami: łożyskami, kołami zębatymi itd. Rozróżnia się
czopy ruchowe i czopy spoczynkowe. Czopy ruchowe współpracują z panewkami
łożysk ślizgowych, z kołami przesuwnymi lub obracającymi się względem
nieruchomej osi itp., natomiast czopy spoczynkowe współpracują z elementami
osadzonymi na stałe względem wału i obracającymi się wraz z nim.

Czopy - wymiary

Materiały stosowane na osie i
wały
Osie i wały wykonuje się najczęściej ze stali:
•
konstrukcyjnej węglowej
konstrukcyjnej węglowej
zwykłej jakości
zwykłej jakości (najczęściej E295, E360), gdy
elementy są mało obciążone w maszynach mniej ważnych, stosowane bez
obróbki cieplnej i gdy bardziej wymagana jest sztywność elementu niż jego
wytrzymałość;
•
konstrukcyjnej węglowej wyższej jakości
konstrukcyjnej węglowej wyższej jakości (najczęściej C25, C35 i C45).
Stale C25 i C35 stosuje się w stanie normalizowanym i ulepszonym lub
hartowanym powierzchniowo (45), stosowane gdy wyższe obciążenia i
temperatura;
•
konstrukcyjnej
stopowej
do
ulepszania
cieplnego
konstrukcyjnej
stopowej
do
ulepszania
cieplnego,
najczęściej
chromoniklowej, gdy wymagana jest mała średnica wału (w tym przypadku
zalecane jest ulepszanie cieplne) oraz gdy na wale są odkute elementy
pracujące jak koła zębate lub połówki sprzęgła, wymagające powierzchni
odpornych na ścieranie – duże obciążenia zmienne i udarowe;
•
konstrukcyjnej stopowej do nawęglania lub azotowania
konstrukcyjnej stopowej do nawęglania lub azotowania - jak w
powyższym punkcie, ale gdy bardziej zależy nam na twardości powierzchni niż
na wytrzymałości rdzenia elementu (zawsze nawęglone lub azotowane oraz
zawsze hartowane przynajmniej na niektórych powierzchniach) – bardzo duże
obciążenia zmienne, udarowe oraz wysokie obroty np wałki wirówek, wałki
rozrządu;
•
konstrukcyjnej stopowej o szczególnych własnościach
konstrukcyjnej stopowej o szczególnych własnościach, gdy wymagane
są szczególne cechy, jak żaroodporność, nierdzewność, kwasoodporność itp.
W wyjątkowych przypadkach wykonuje się wały odlewane, staliwne lub żeliwne
(głównie do wykonania wałów wykorbionych). Najczęściej stosuje się żeliwo
modyfikowane lub sferoidalne.

Projektowanie osi i wałów -
dane
• Schematy dotyczące wymiarów wałka,
wymiary elementów osadzonych na
wale oraz ich rozmieszczenie
• Dane dotyczące obciążenia wału
ilościowe (siły, momenty, prędkości
obrotowe, zmienność wartości) jak i
jakościowe (kierunki działania sił, ich
zwroty)
• Dane dotyczące oceny sztywności wałka
(dopuszczalne ugięcie, typy łożysk, itp.)

Etapy projektowania
• Etap I – Projektowanie wstępne
– Obliczenia reakcji i momentów
– Wyznaczenie średnic (zarys teoretyczny)
• Etap II – Obliczenia sprawdzające
– Obliczenia sztywności (strzałka ugięcia, kąt ugięcia, kąt skręcenia)
– Obliczenia dynamiczne (prędkość krytyczna)
– Obliczenia zmęczeniowe
• Etap III – Ostateczne ukształtowanie
wału
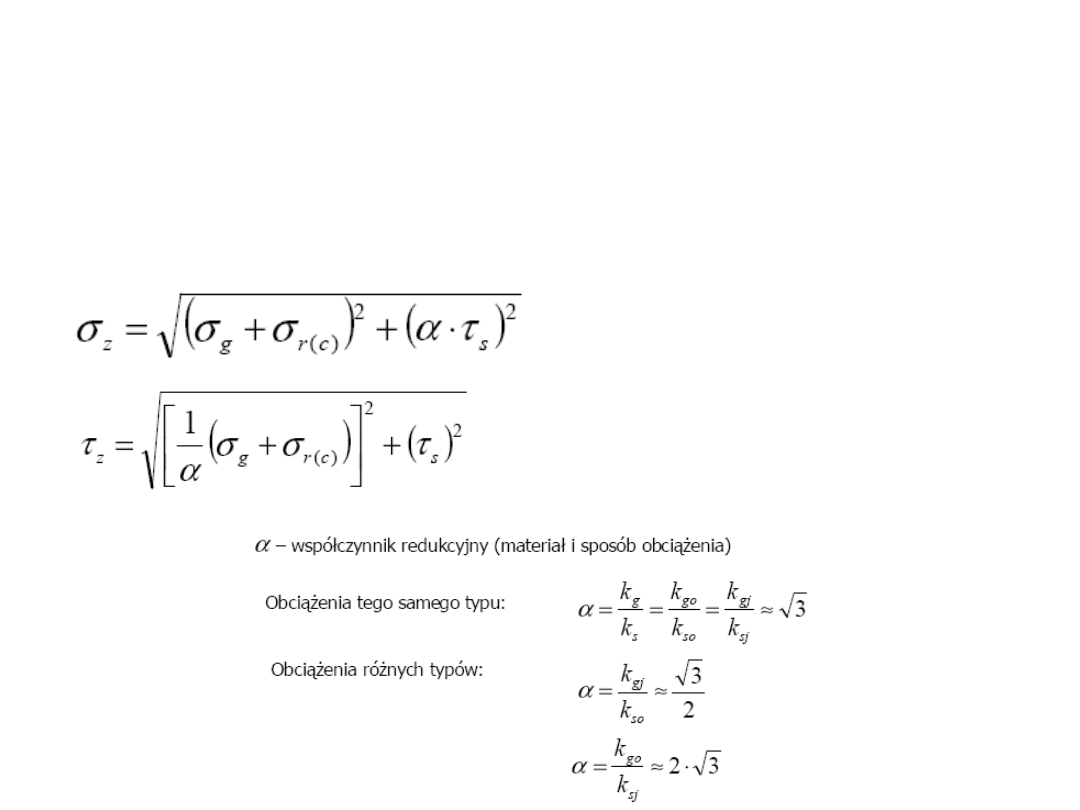
Etap I
Wały mogą być zginane, skręcane oraz rozciągane (ściskane),
zatem niezbędne jest zastosowanie odpowiedniej teorii
wytężeniowej - Hubera
Gdy naprężenia
normalne są
dominujące
Gdy naprężenia
styczne są
dominujące
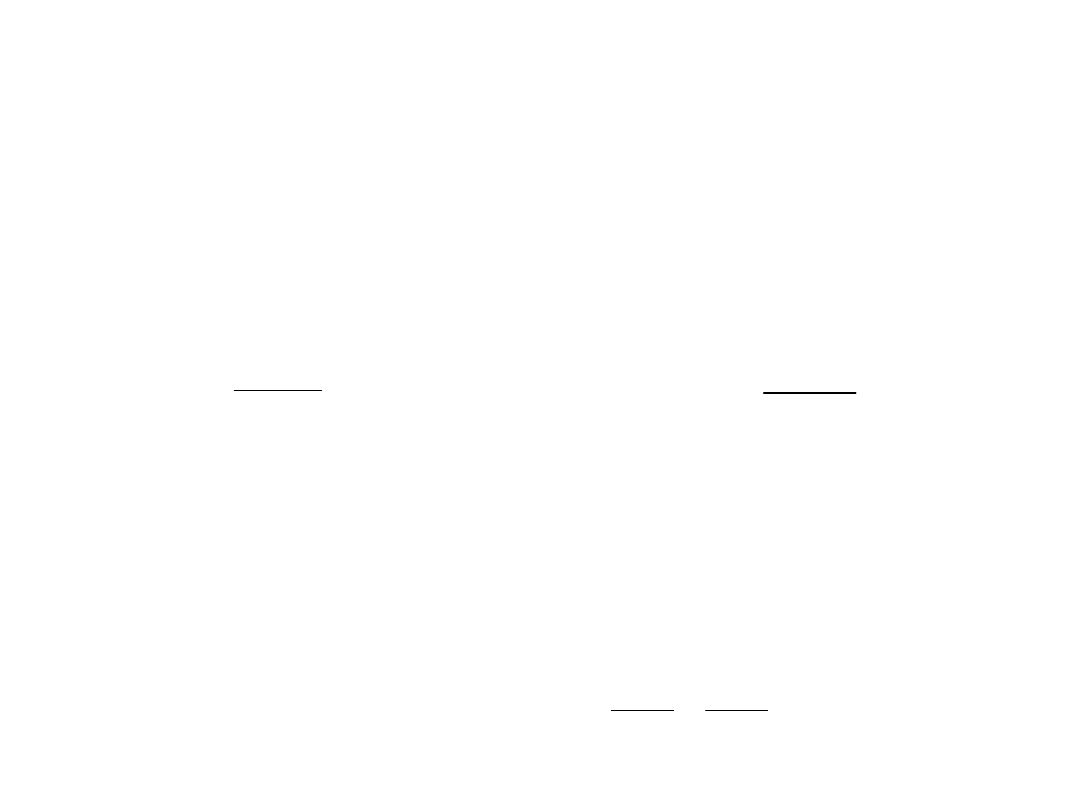
Etap I c.d.
k
W
M
jo
g
x
g
g
)
(
k
W
M
jo
s
o
s
s
)
(
Rozpoczynając obliczenia nie znamy naprężeń, natomiast
obciążenia są znane.
16
32
2
2
3
3
d
d
W
W
x
o
Dla przekroju kołowego, typowego dla osi i wałów, wskaźniki przekrojów
można policzyć:
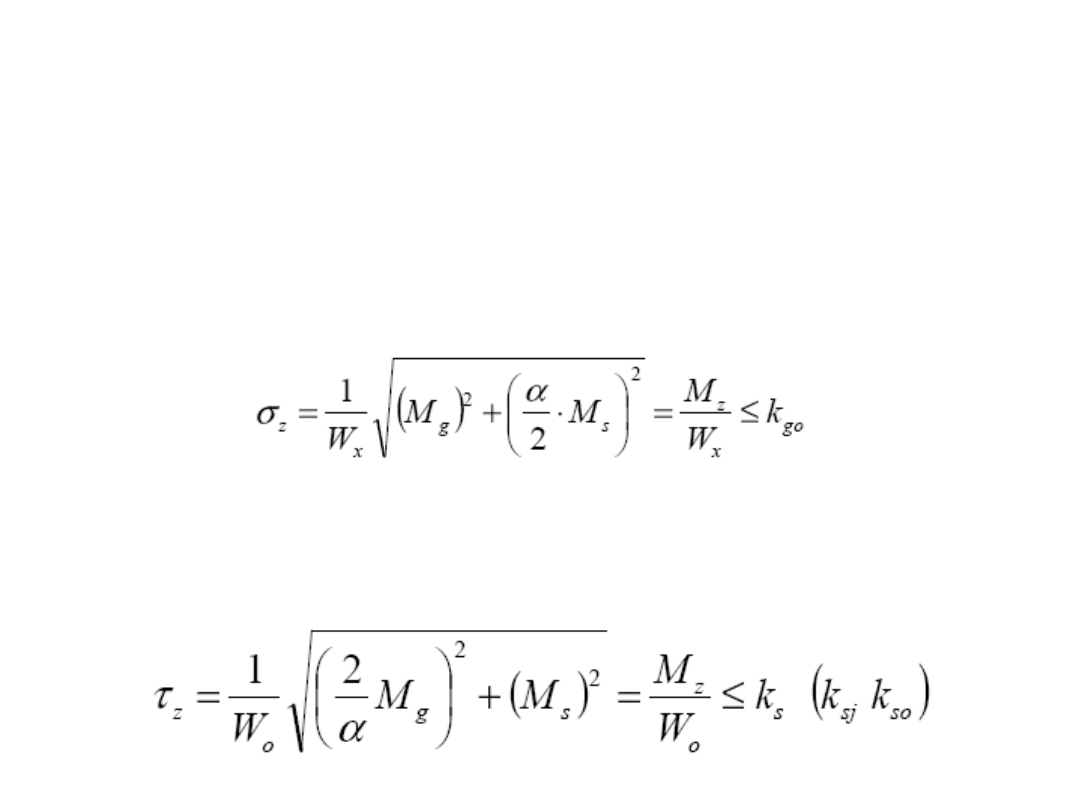
Etap I c.d.
ZATEM
W przypadku przewagi naprężeń normalnych (M
s
< 2M
g
)
W przypadku przewagi naprężeń stycznych (M
s
> 2M
g
)
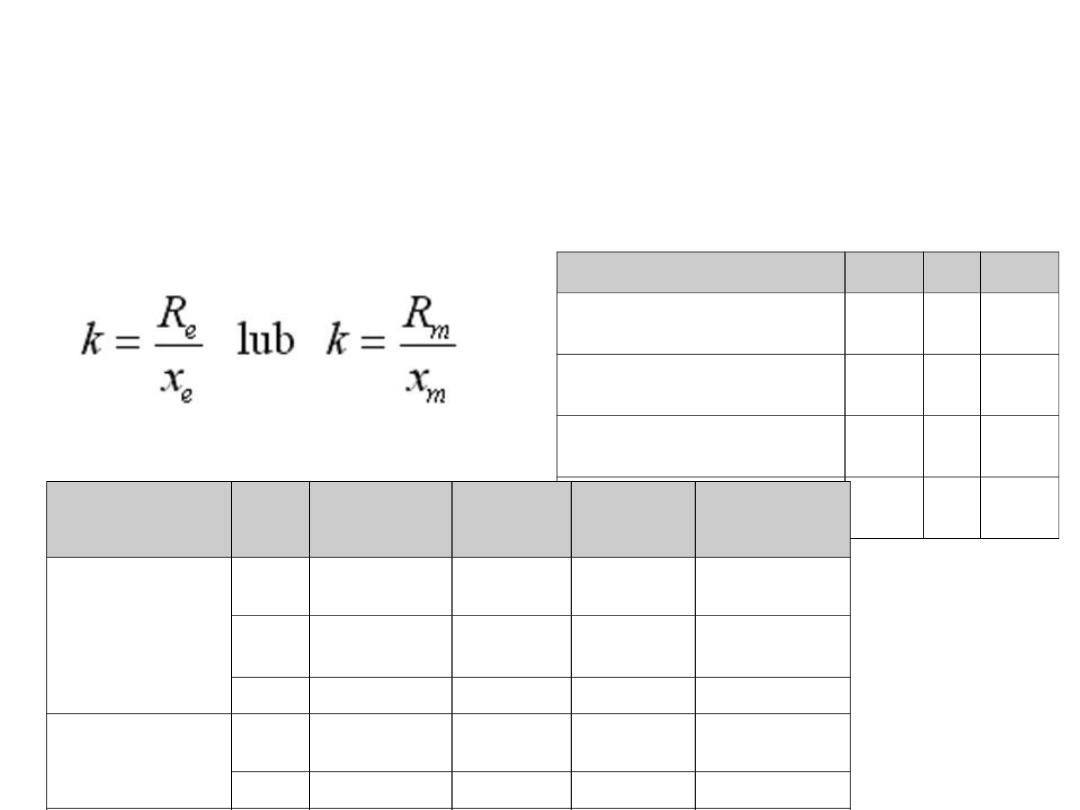
Etap I c.d.
Materiał
x
e
x
m
x
z
Stale, staliwa, żeliwa
ciągliwe
2÷2,
3
-
3,5÷
4
Żeliwa szare
-
3,
5
3
Stopy miedzi
3÷4
-
4,5÷
6
Stopy aluminium
3,5÷
4
-
5÷7
Naprężenia dopuszczalne
Rodzaj
obciążenia
Symb
o
l
Stale,
staliwa
Żeliwa
szare
Stopy
miedzi
Stopy
aluminiu
m
Rozciąganie i
ściskanie
Z
rj
(0,55÷0,63)
R
m
~1,5 Z
rc
śr. 0,50 R
m
śr. 0,48 R
m
Z
rc
(0,28÷0,4)
R
m
śr. 0,7 Z
go
śr. 0,28 R
m
0,7 Z
go
≈0,25
R
m
Z
cj
Z
rj
(3,4÷4) Z
rj
Z
rj
Z
rj
Zginanie
Z
gj
(0,66÷0,75)
R
m
~1,5 Z
go
~1,8 Z
go
~1,8 Z
go
Z
go
śr. 0,45 R
m
śr. 0,4 R
m
śr. 0,35 R
m
śr. 0,34 R
m
Skręcanie i
ścinanie
Z
sj
(0,46÷0,5)
R
m
~1,5 Z
so
~1,7 Z
so
~1,7 Z
so
Z
so
(0,22÷0,25)
R
m
~0,8 Z
go
~0,58 Z
go
~0,56 Z
go
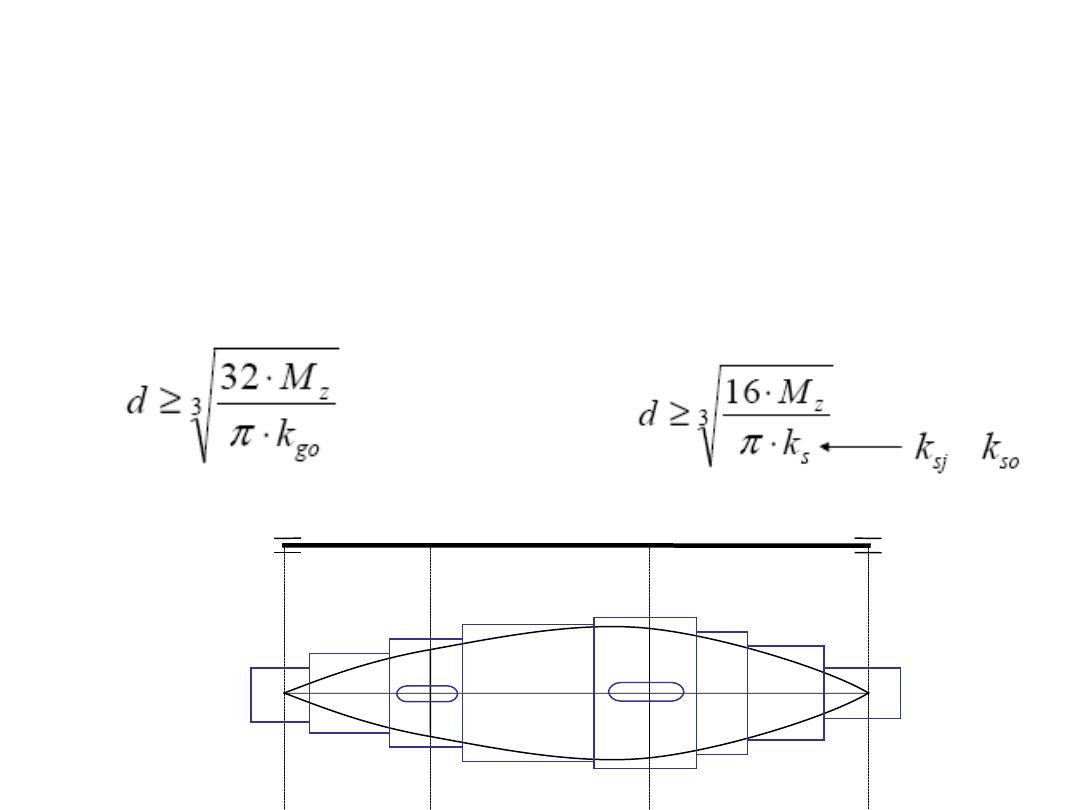
Etap I c.d.
Wyznaczenie średnic wału
W przypadku przewagi
naprężeń normalnych
W przypadku przewagi
naprężeń stycznych
1
2
A
B
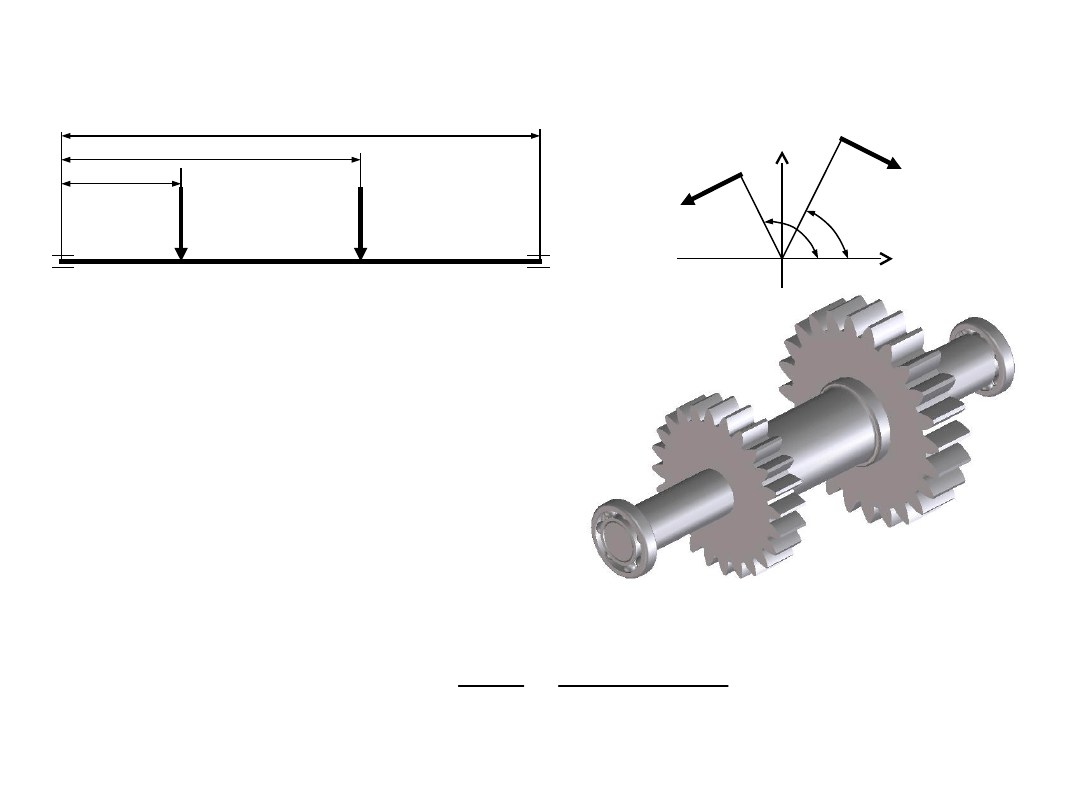
l
1
l
2
l
P
1
P
2
A
B
P
2
P
1
α
1
α
2
r
1
r
2
x
y
Dane:
P
1
=10000N r
1
=0,08m
l=0,4m
r
2
=0,05m
l
1
=0,1m
α
1
=60
0
l
2
=025m
α
2
=120
0
stal 45 ulepszana cieplnie
Z
go
=250MPa Z
sj
=300MPa
Obliczamy wartości siły P
2
z warunku równowagi momentów:
kN
m
m
kN
r
r
P
P
r
P
r
P
16
05
,
0
08
,
0
10
2
1
1
2
2
2
1
1
Obliczenia wstępne -
przykład
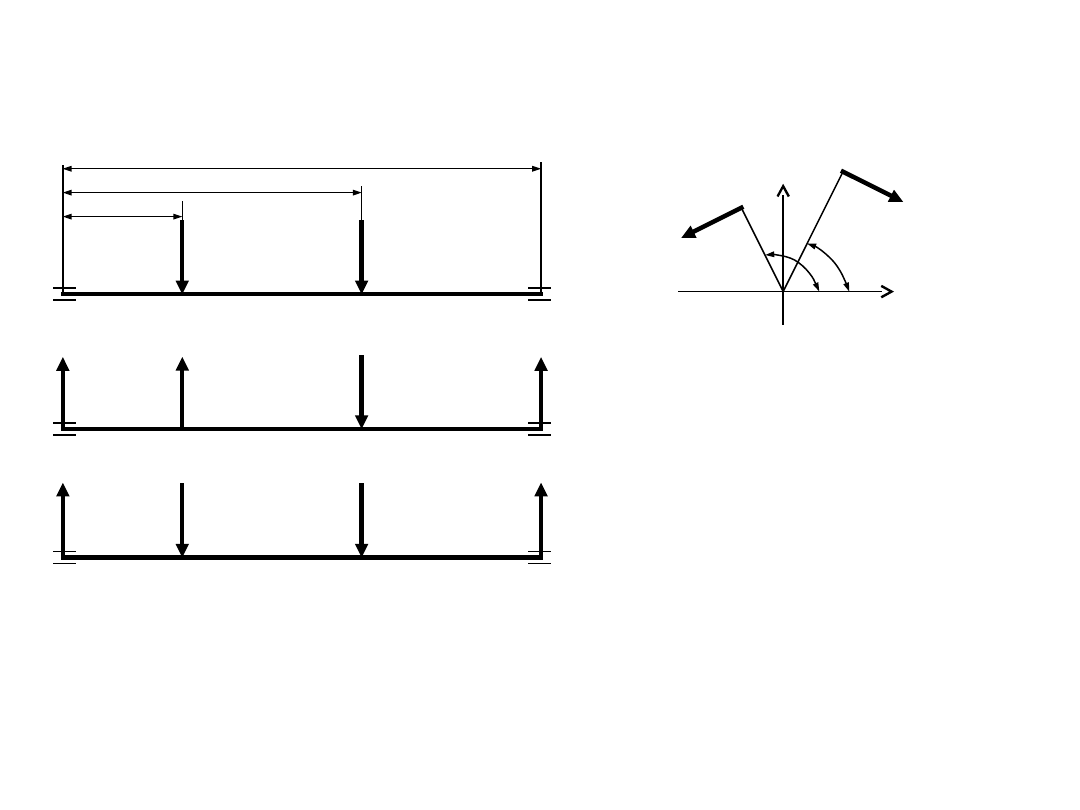
Obliczenia wstępne -
przykład
l
1
l
2
l
P
1
P
2
P
1x
P
2x
P
1y
P
2y
A
B
R
Bx
R
By
R
Ax
R
Ay
płaszczyzna xz
płaszczyzna yz
Dane:
P
1
=10000N r
1
=0,08m
l=0,4m
r
2
=0,05m
l
1
=0,1m
α
1
=60
0
l
2
=025m
α
2
=120
0
stal 45 ulepszana cieplnie
Z
go
=250MPa Z
sj
=300MPa
Obliczamy wartości składowych sił w płaszczyznach xz i yz:
kN
kN
P
P
kN
kN
P
P
kN
kN
P
P
kN
kN
P
P
y
y
x
x
8
5
,
0
16
60
cos
5
5
,
0
10
60
cos
856
,
13
8660
,
0
16
60
sin
66
,
8
8660
,
0
10
60
sin
0
2
2
0
1
1
0
2
2
0
1
1
P
2
P
1
α
1
α
2
r
1
r
2
x
y
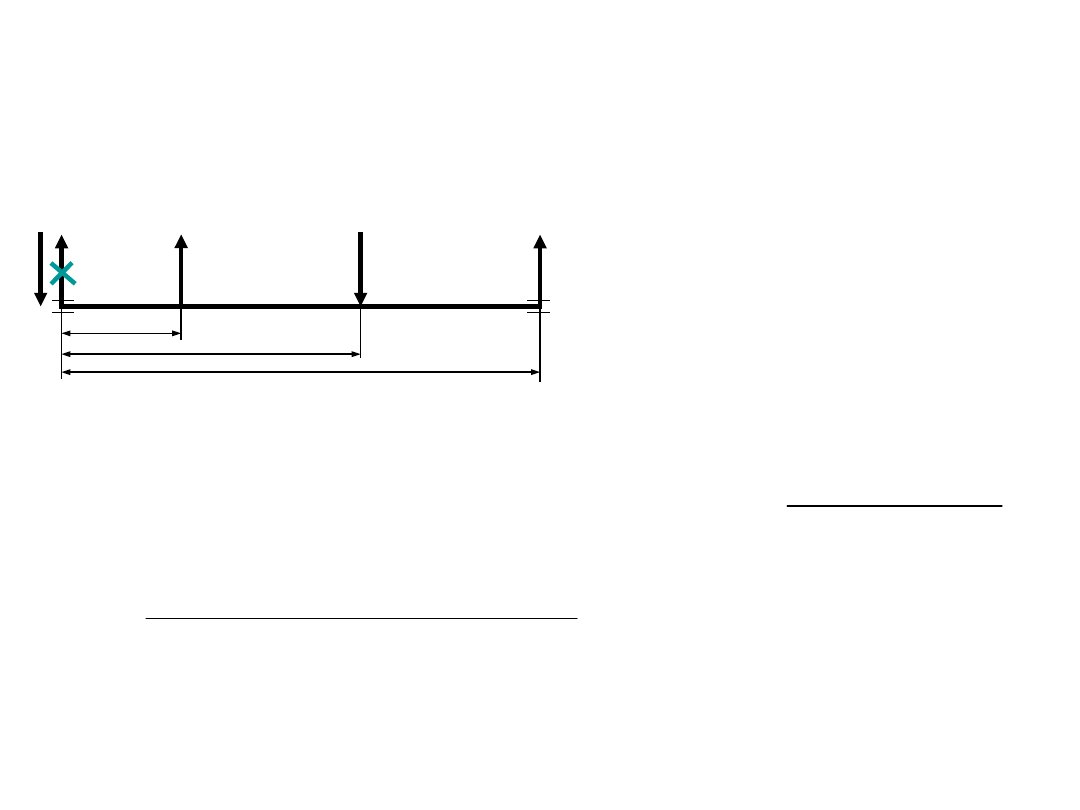
Obliczenia wstępne -
przykład
0
0
2
1
Bx
x
x
Ax
ix
R
P
P
R
P
0
0
2
2
1
1
l
R
l
P
l
P
M
Bx
x
x
ixA
Bx
x
x
Ax
R
P
P
R
2
1
Obliczamy wartości reakcji z warunków równowagi sił w kierunku x i y, oraz z warunków
równowagi momentów względem łożysk:
P
1x
P
2x
R
Bx
R
Ax
płaszczyzna xz
l
l
P
l
P
R
x
x
Bx
2
2
1
1
kN
m
m
kN
m
kN
R
Bx
495
,
6
4
,
0
25
,
0
856
,
13
1
,
0
66
,
8
kN
kN
kN
kN
R
Ax
299
,
1
495
,
6
856
,
13
66
,
8
Ujemna wartość reakcji R
Ax
oznacza błędnie założony zwrot. Należy więc go
skorygować.
l
1
l
2
l
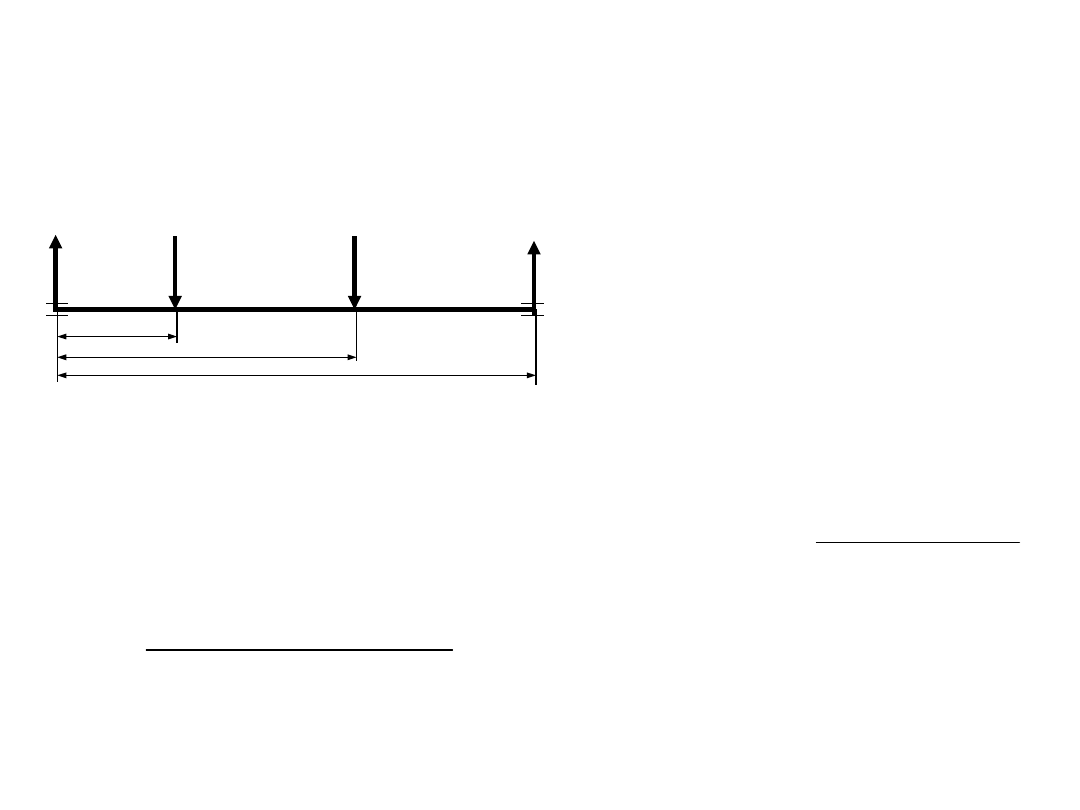
Obliczenia wstępne -
przykład
płaszczyzna yz
0
0
2
1
By
y
y
Ay
iy
R
P
P
R
P
0
0
2
2
1
1
l
R
l
P
l
P
M
By
y
y
iyA
By
y
y
Ay
R
P
P
R
2
1
l
l
P
l
P
R
x
x
Bx
2
2
1
1
kN
m
m
kN
m
kN
R
By
25
,
6
4
,
0
25
,
0
8
1
,
0
5
kN
kN
kN
kN
R
Ay
75
,
6
25
,
6
8
5
P
1y
P
2y
R
By
R
Ay
l
2
l
l
1
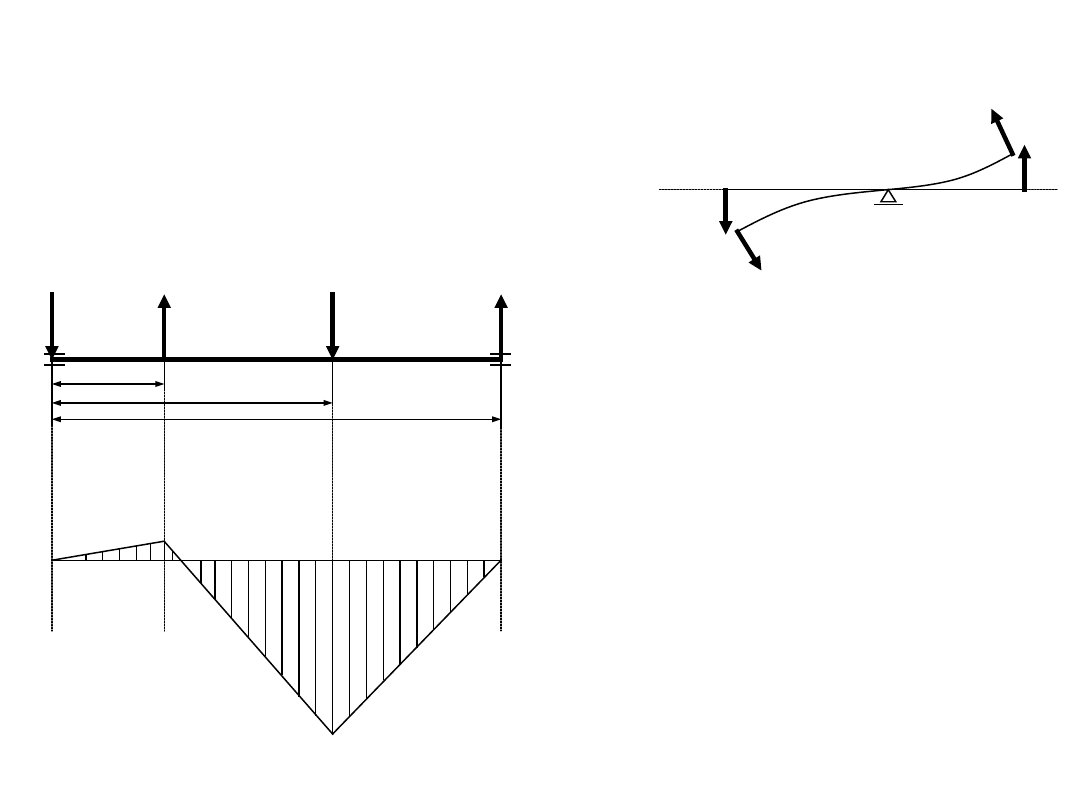
Obliczenia wstępne -
przykład
0
gxA
M
Nm
m
kN
l
R
M
Ax
gx
9
,
129
1
,
0
299
.
1
1
1
Nm
m
m
kN
m
kN
l
l
P
l
R
M
x
Ax
gx
25
,
974
)
1
,
0
25
,
0
(
66
,
8
25
,
0
299
,
1
1
2
1
2
2
Obliczamy wartości momentów gnących w płaszczyznach xz i yz.
płaszczyzna xz
Nm
m
m
kN
l
l
R
M
Bx
gx
25
,
974
)
25
,
0
4
,
0
(
495
,
6
2
2
lub
0
gxB
M
P
1x
P
2x
R
Bx
R
Ax
M
gx
A
M
gx
1
M
gx
2
M
gx
B
l
2
l
l
1
P
P
M
M
g
g
(+)
(+)
M
M
g
g
(-)
(-)
Za dodatni moment
gnący przyjmujemy
ten, który powoduje
ugięcie
wału
ku
dołowi.
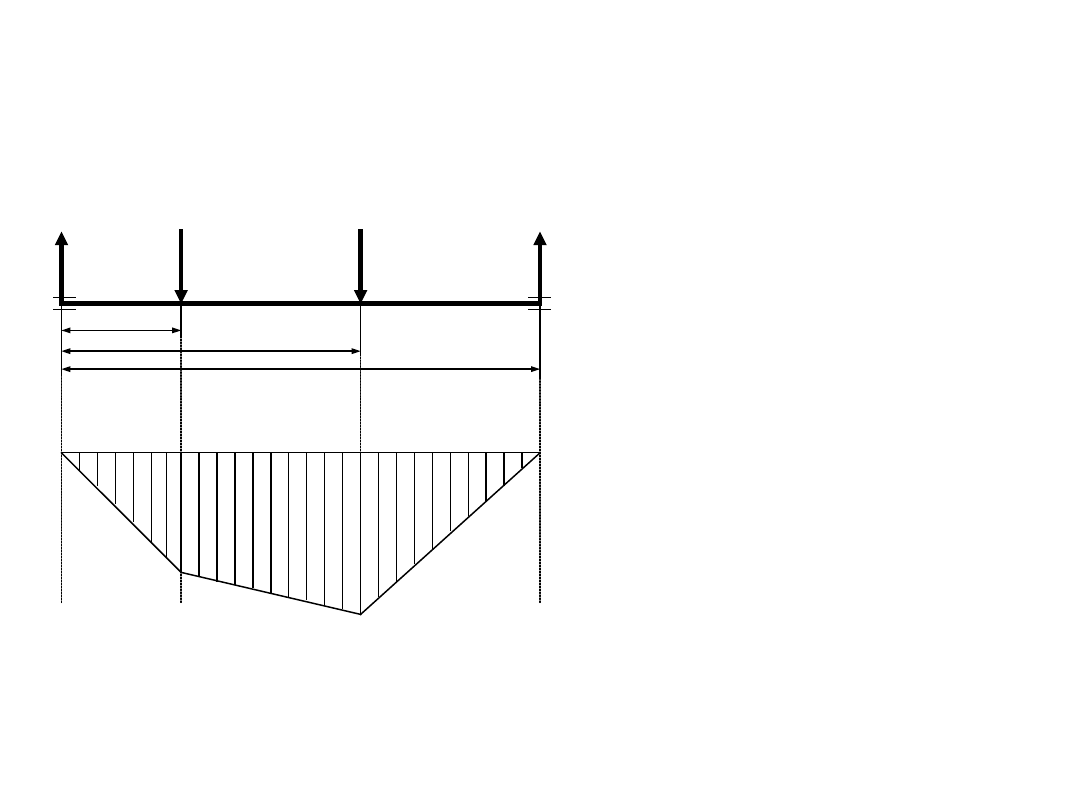
Obliczenia wstępne - przykład
0
gyA
M
Nm
m
kN
l
R
M
Ay
gy
675
1
,
0
75
,
6
1
1
Nm
m
m
kN
m
kN
l
l
P
l
R
M
y
Ay
gy
5
,
937
)
1
,
0
25
,
0
(
5
25
,
0
75
,
6
1
2
1
2
2
Nm
m
m
kN
l
l
R
M
By
gy
5
,
937
)
25
,
0
4
,
0
(
25
,
6
2
2
lub
0
gyB
M
M
gyB
P
1y
P
2y
R
By
R
Ay
płaszczyzna yz
M
gyA
M
gy1
M
gy2
l
2
l
l
1
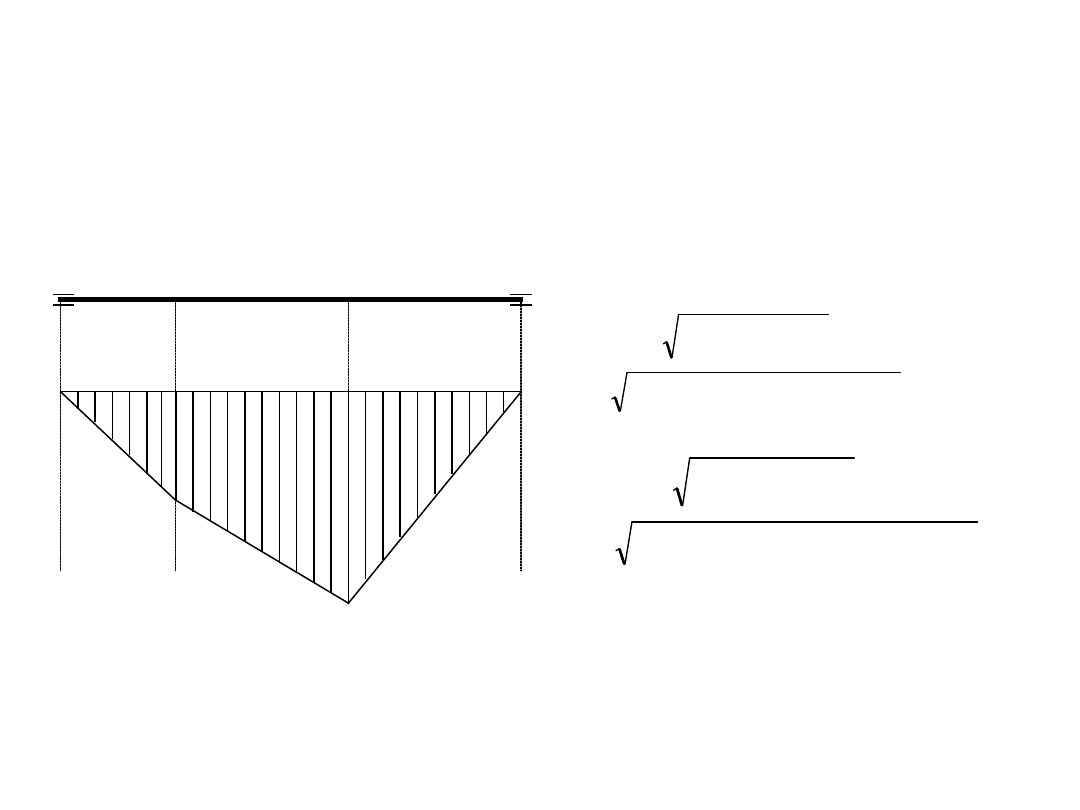
Obliczenia wstępne - przykład
0
gA
M
Nm
Nm
Nm
M
M
M
gy
gx
g
385
,
687
675
9
,
129
2
2
2
1
2
1
1
Nm
Nm
Nm
M
M
M
gy
gx
g
061
,
1352
5
,
937
25
,
974
2
2
2
2
2
2
2
Obliczamy wartości momentów gnących wypadkowych
0
gB
M
M
gB
1
2
A
M
gA
M
g1
M
g2
B
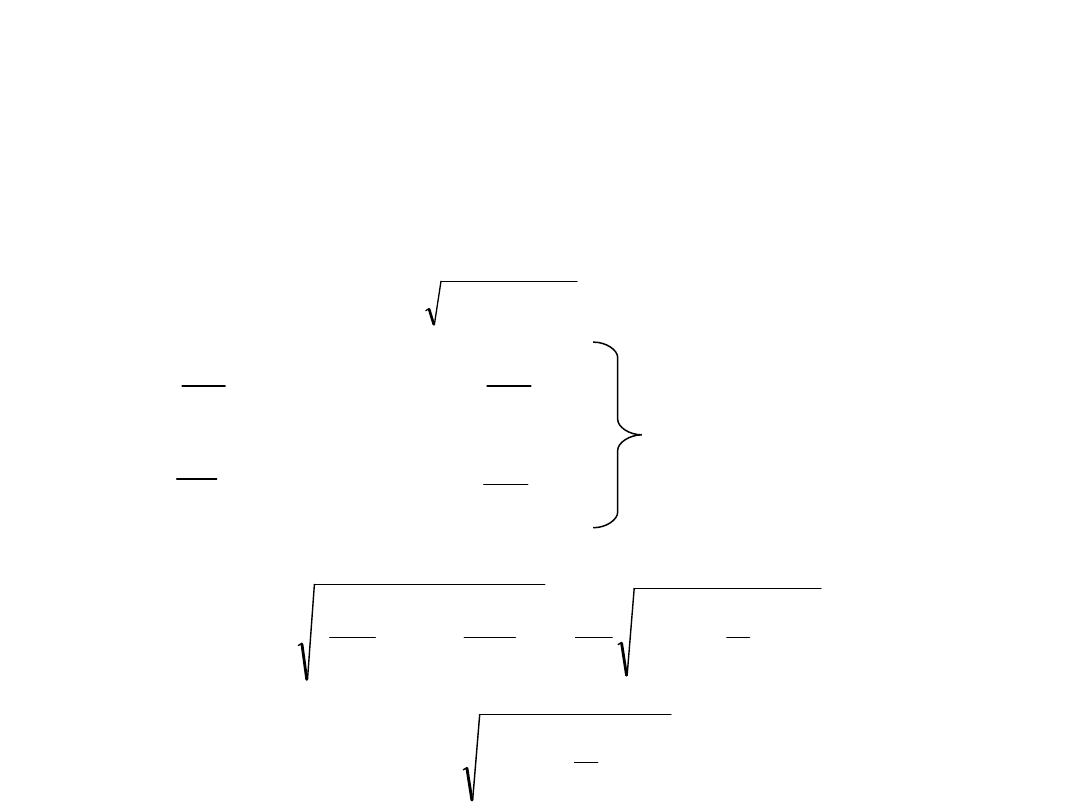
Obliczenia wstępne - przykład
Nm
m
kN
r
P
r
P
M
s
800
08
,
0
10
2
2
1
1
2
2
2
2
2
1
2
s
g
x
x
s
x
g
red
M
M
W
W
M
W
M
Obliczamy moment skręcający, który działa pomiędzy przekrojem 1 i 2
Wyznaczamy moment zastępczy zakładając obustronne zginanie wału i
jednostronne zmienne skręcanie.
2
2
s
g
red
x
g
g
W
M
o
s
s
W
M
32
3
d
W
x
16
3
d
W
o
o
x
W
W
2
gdzi
e
gdzi
e
zate
m
i
2
2
2
s
g
z
M
M
M
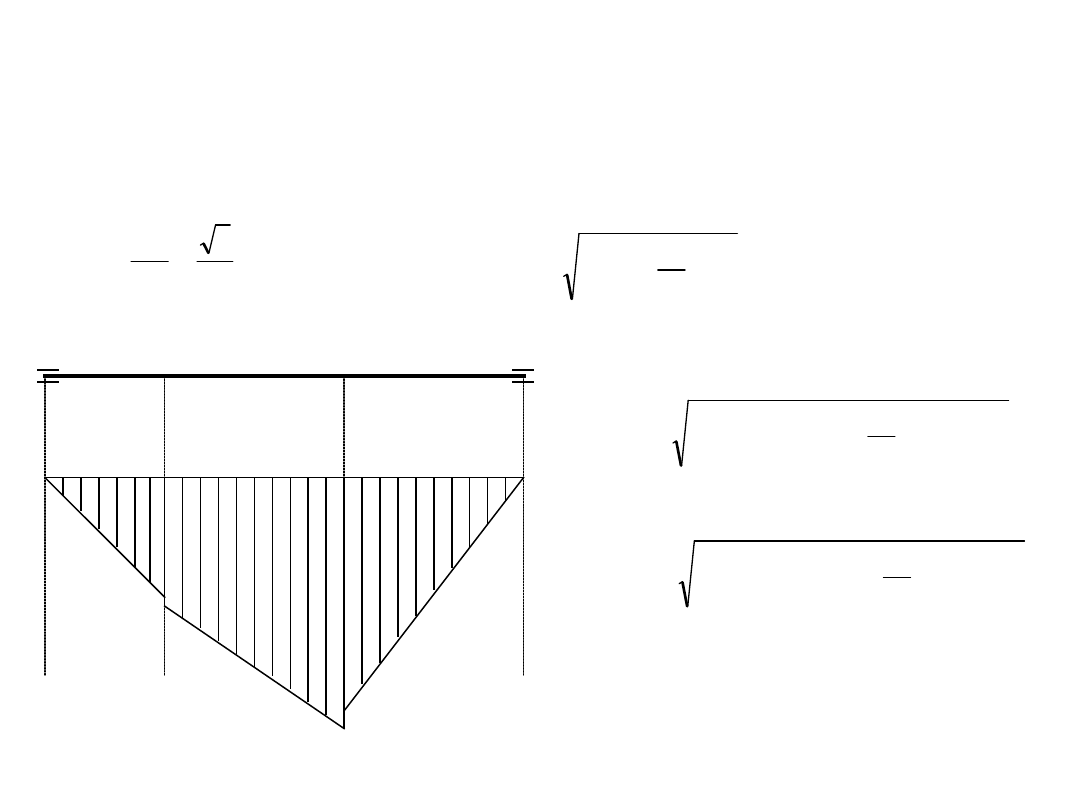
Obliczenia wstępne - przykład
0
zA
M
Nm
Nm
Nm
M
z
75
,
769
)
800
(
16
3
)
385
,
687
(
2
2
1
Nm
Nm
Nm
M
z
73
,
1395
)
800
(
16
3
)
061
,
1352
(
2
2
2
2
3
sj
go
k
k
Dla tego typu zmienności obciążenia wartość współczynnika redukcyjnego α wynosi:
zatem:
2
2
16
3
s
gi
zi
M
M
M
1
2
A
M
zA
M
z1
M
z2
B
0
zB
M
M
zB
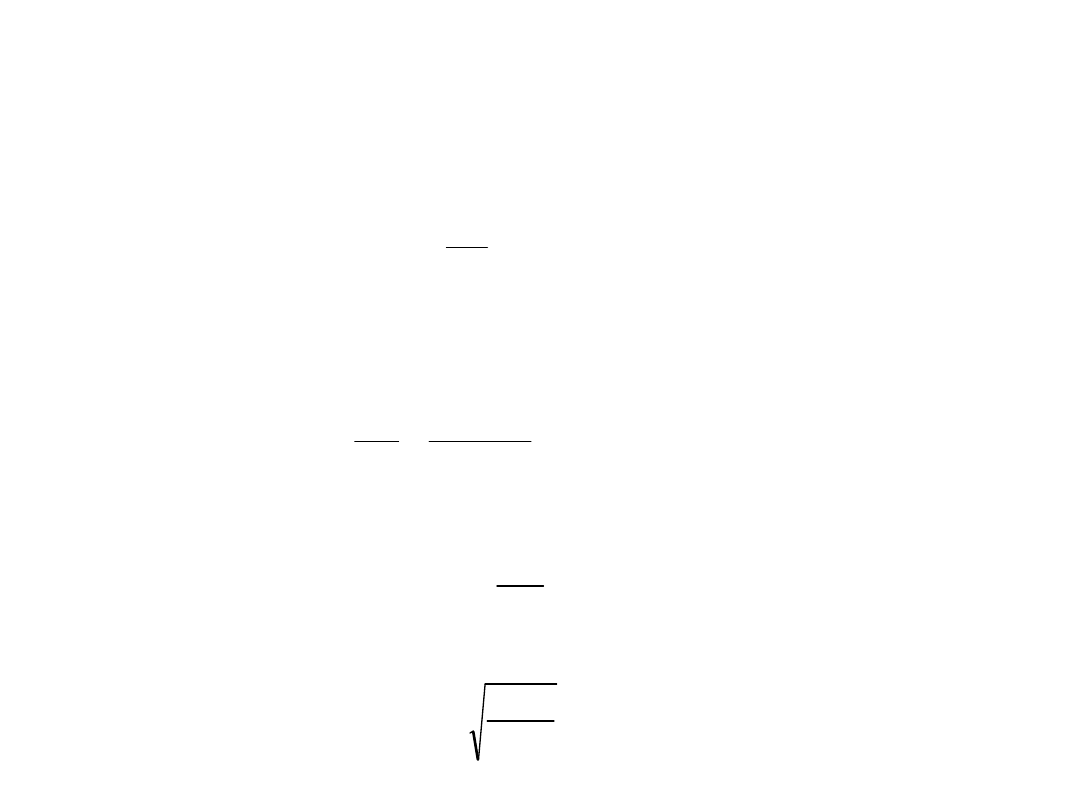
Obliczenia wstępne - przykład
go
x
z
red
k
W
M
MPa
MPa
x
Z
k
go
go
5
,
62
4
250
W przypadku, gdy dominuje zginanie mamy warunek:
Dopuszczalne naprężenia przy obustronnie zmiennym zginaniu przyjmujemy
przy założonym współczynniku bezpieczeństwa x=4 wynoszą:
Dla przekroju okrągłego wału mamy:
32
3
d
W
x
Stąd po przekształceniach otrzymujemy wzór na średnicę wału:
3
32
go
z
k
M
d
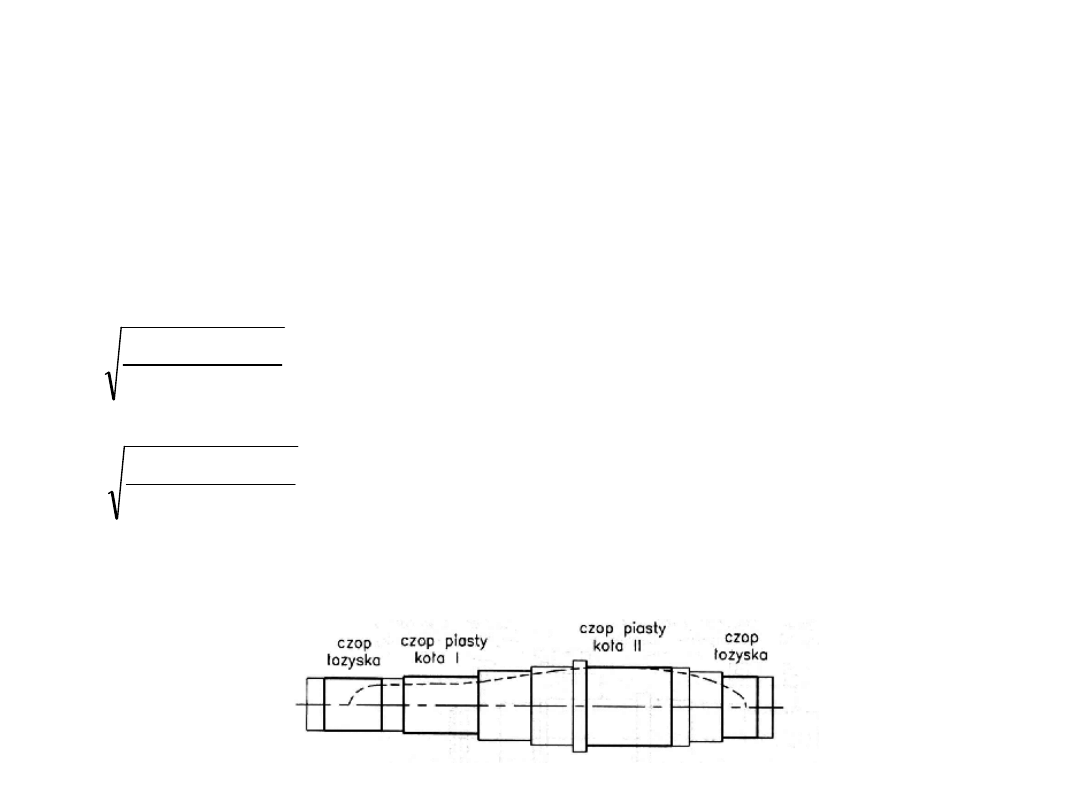
Obliczenia wstępne - przykład
mm
m
MPa
Nm
d
6
,
50
05060
,
0
5
,
62
75
,
769
32
3
1
mm
m
MPa
Nm
d
96
,
84
08496
,
0
5
,
62
73
,
1395
32
3
2
0
A
d
Obliczenia średnic teoretycznych wału
0
B
d

Etap II – Sztywność wału
EJ
x
M
y
g
)
(
''
C
dx
x
EJ
M
y
g
)
(
1
'
Strzałka ugięcia i kąt skręcenia
Równanie linii ugięcia belki
D
dx
C
dx
x
EJ
M
y
g
)
(
1
Kąt ugięcia
Strzałka ugięcia

Etap II – Sztywność wału
•
Podpora przegubowa lub przesuwna – w miejscu
podpory zakłada się zerowe przemieszczenie (y=0)
•
Wspornik – zerowe przemieszczenie oraz zerowy kąt
obrotu (y=0 oraz y’=0)
•
W miejscu maksymalnego ugięcia, kąt ugięcia jest
równy zero (y’=0)
•
Koniec swobodny – zerowy moment gnący (y’’ = 0)
Wyznaczenie stałych całkowania
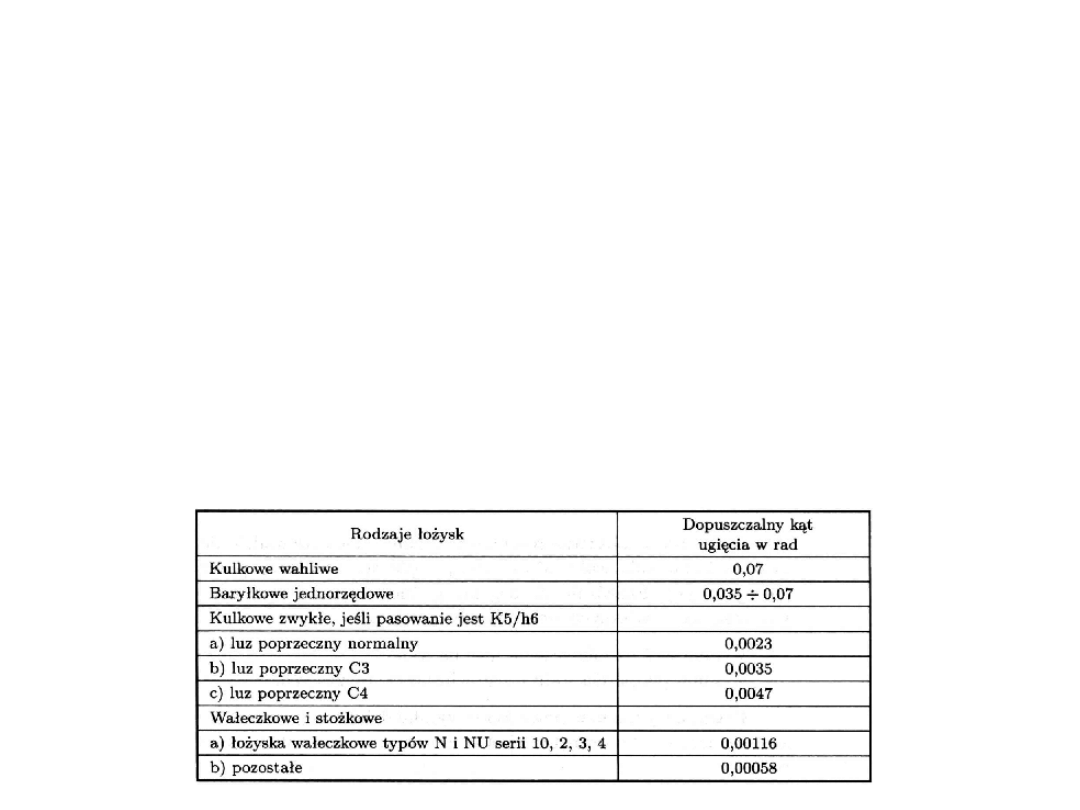
Etap II – Sztywność wału
Dopuszczalne wartości strzałek ugięcia:
f
dop
= (0.0002÷0.0003)l
f
dop
= (0.005÷0.01)m
Dopuszczalny kąt ugięcia
przyjmuje się w granicach od
0,0003 rad dla łożysk ślizgowych do 0,05 rad dla łożysk
wahliwych (ślizgowych lub tocznych).
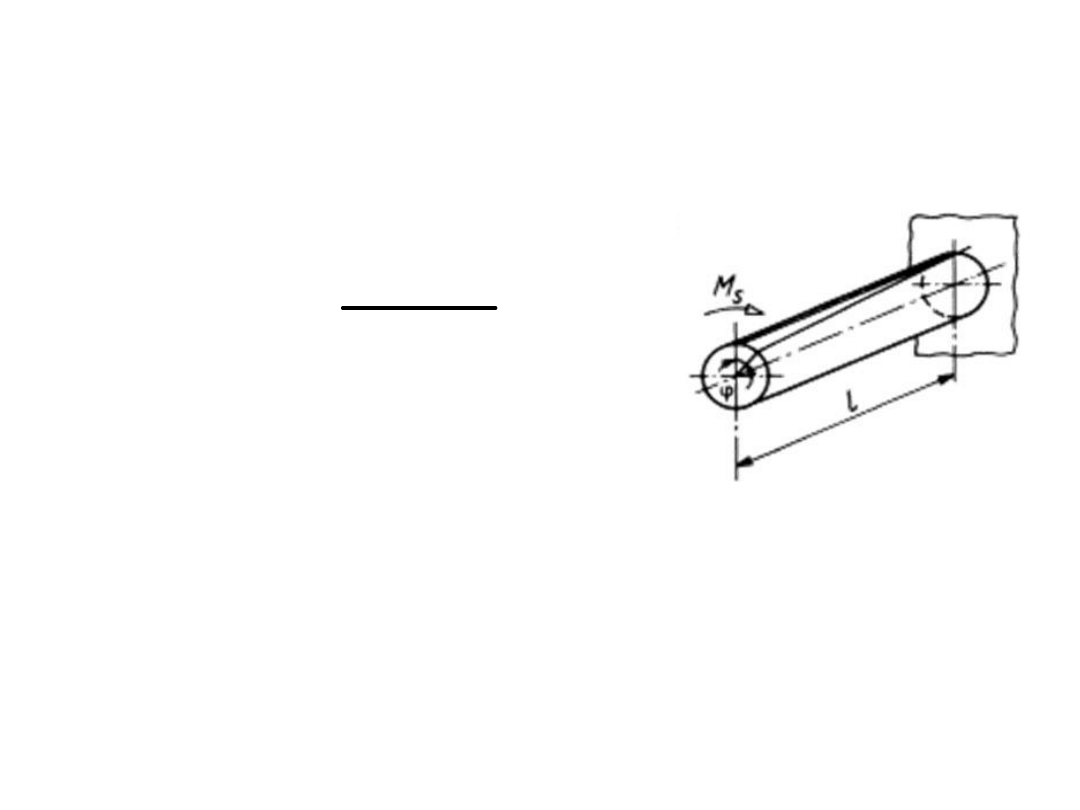
Etap II – Sztywność wału
J
G
l
M
o
s
gdzie:
M
s
– moment skręcający,
G – moduł sprężystości poprzecznej (dla stali G=80 000 – 85 000 MPa),
J
o
– biegunowy moment bezwładności przekroju,
l – długość wału
Wartość dopuszczalnego kąta skręcenia φdop zależy od funkcji wału w
maszynie. Dla wałów maszynowych najczęściej przyjmuje się φ ≤ 0,25°,
tj.
φ ≤ 0,0044 rad na 1 m długości wału. W przypadku wałków skrętnych,
służących m.in. do łagodzenia nierównomierności momentu
obrotowego, dopuszcza się
φ ≤ 11° i więcej (np. dla wałka w sprzęgle Cardana, półosi
samochodowych itp.).
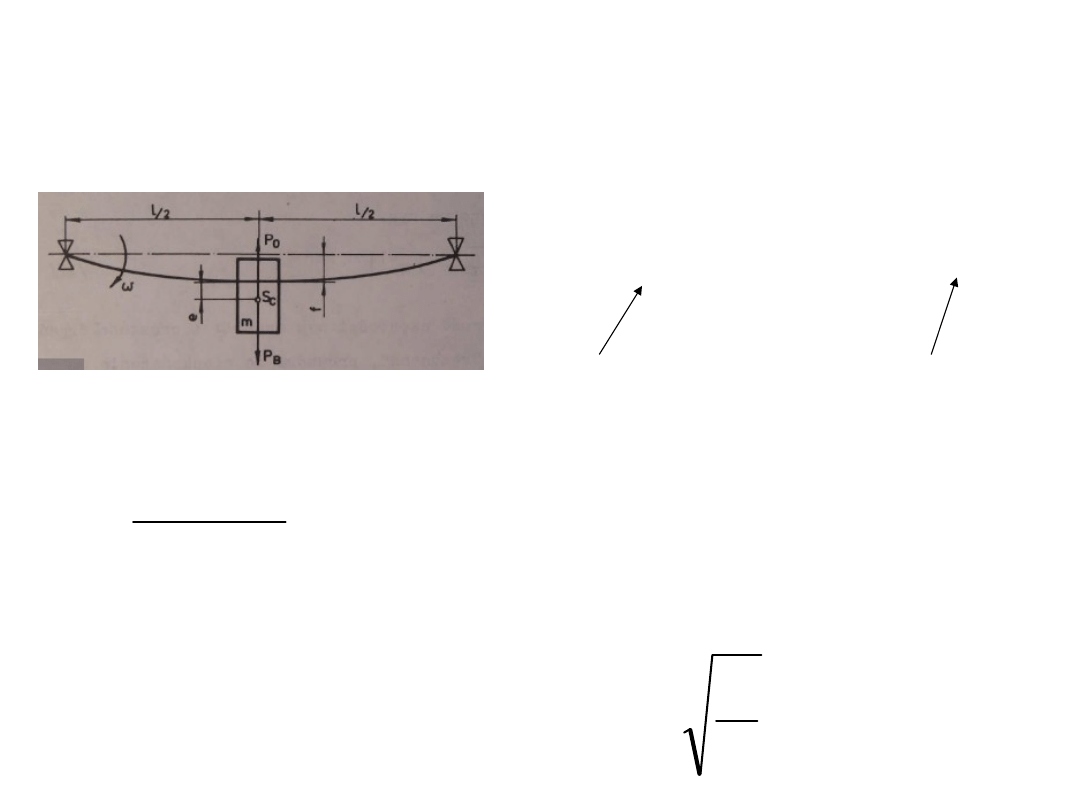
Etap II - drgania
f
c
e
f
m
)
(
2
2
2
m
c
e
m
f
Dla f=∞ =
kr
f=∞ gdy c-m
2
= 0
r
m
c
kr
Siła
odśrodkowa
Siła
sprężystości
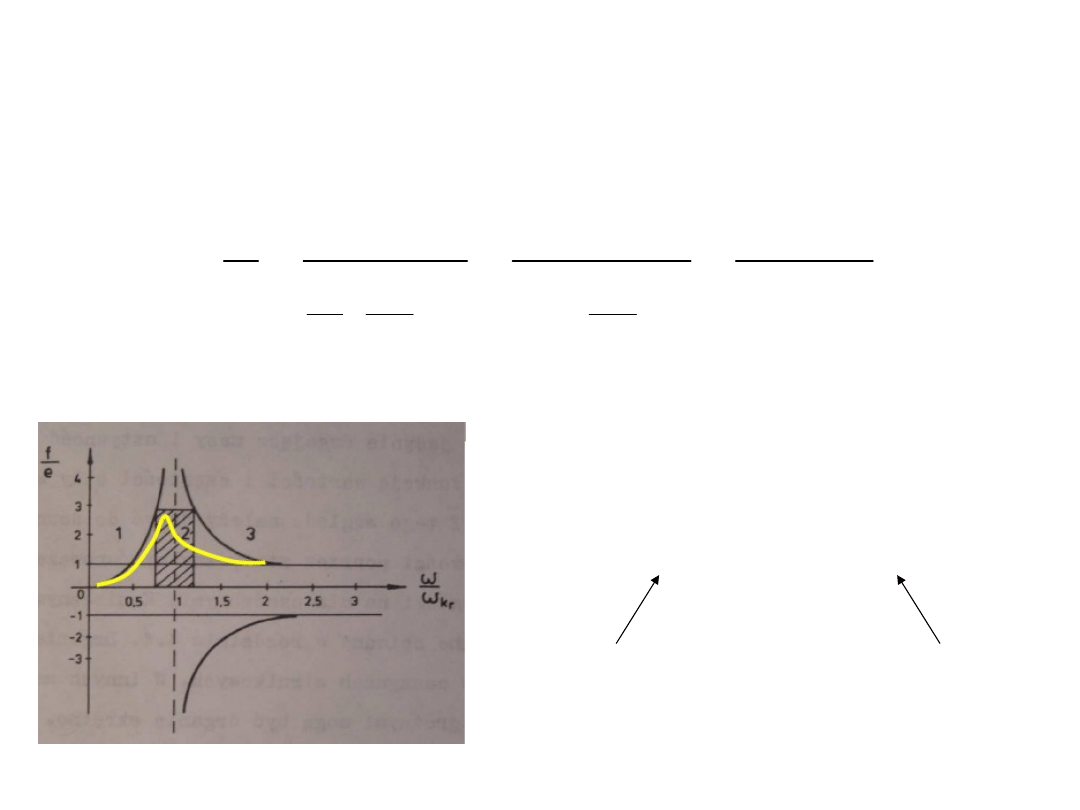
Etap II - drgania
2
2
2
2
2
2
1
1
1
1
1
1
kr
kr
m
k
e
f
Zakres pracy
0.85
kr
≤ ≤ 1.25
kr
Wały
podkrytyczn
e
Wały
nadkrytyczn
e
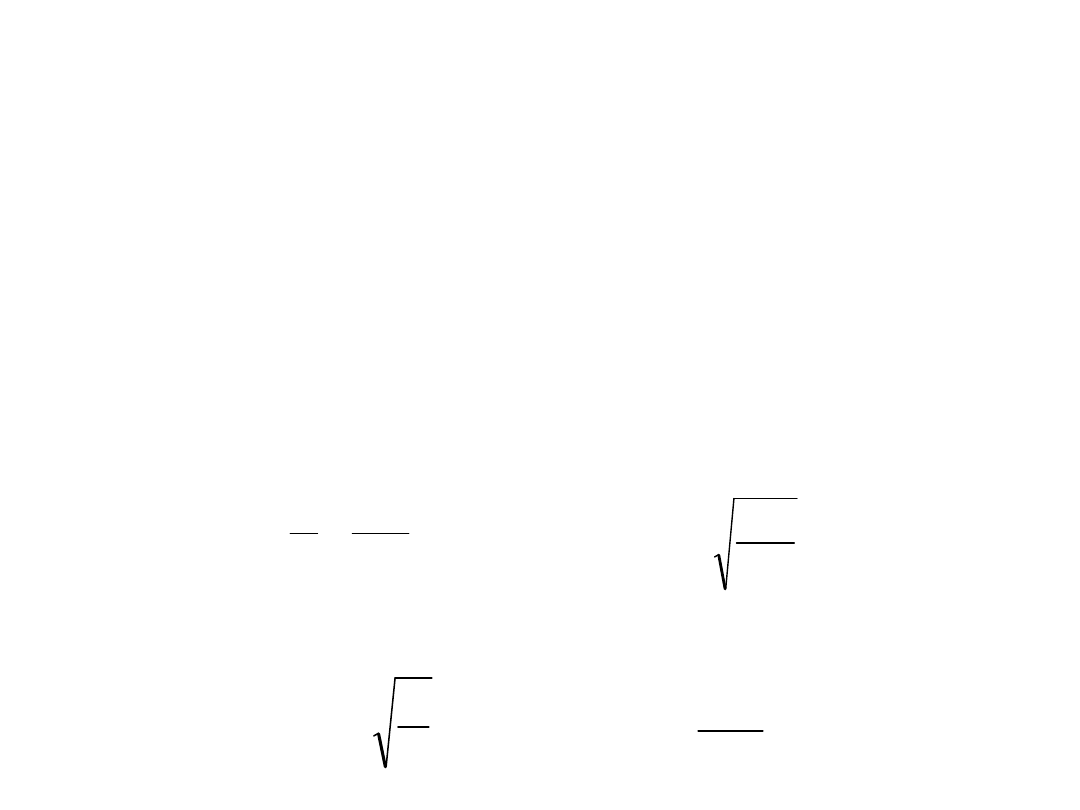
Etap II - drgania
2
kr
stat
f
g
m
c
f
g
stat
kr
2
c
s
kr
2
Metody inżynierskie szacowania prędkości
krytycznej
Q = mg
P
s
= cf
stat
Ciężar wału i elementów na nim
osadzonych
Ugięcie wału pod wpływem siły Q
mg=cf
stat
L
G
J
c
o
s
W przypadku skręcania
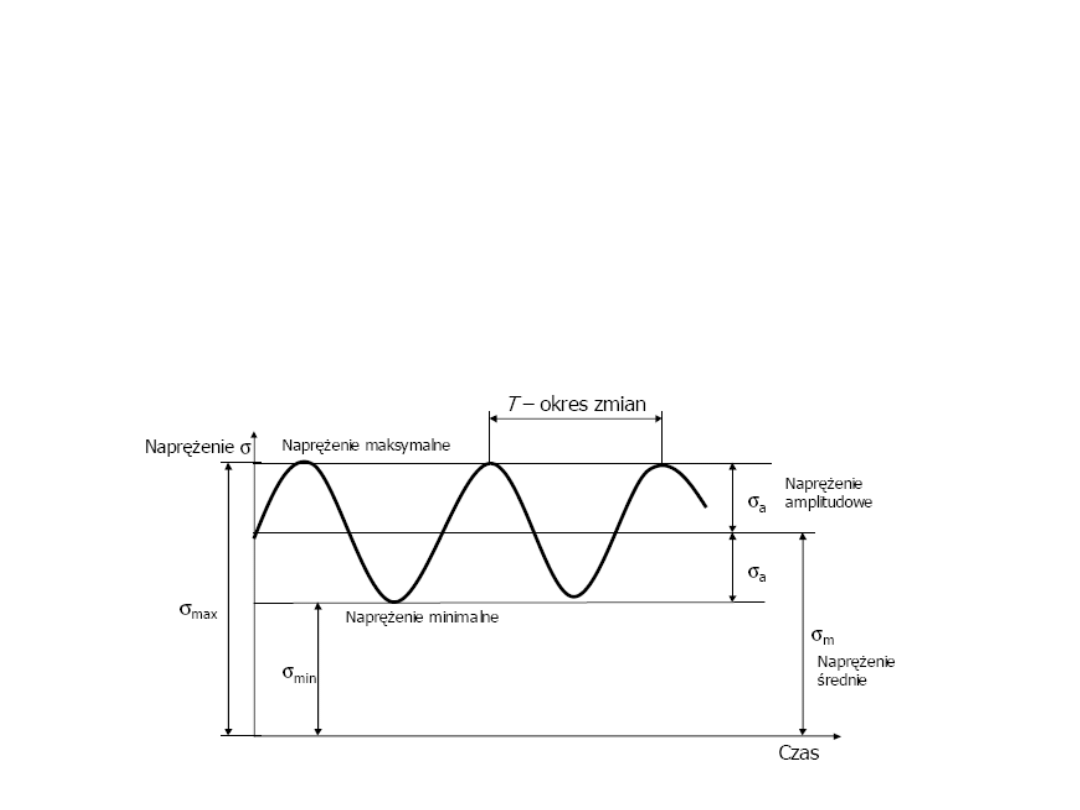
ETAP II – obliczenia
zmęczeniowe
Jeśli wartość, kierunek lub zwrot obciążenia ulega
zmianie w czasie to mamy do czynienia
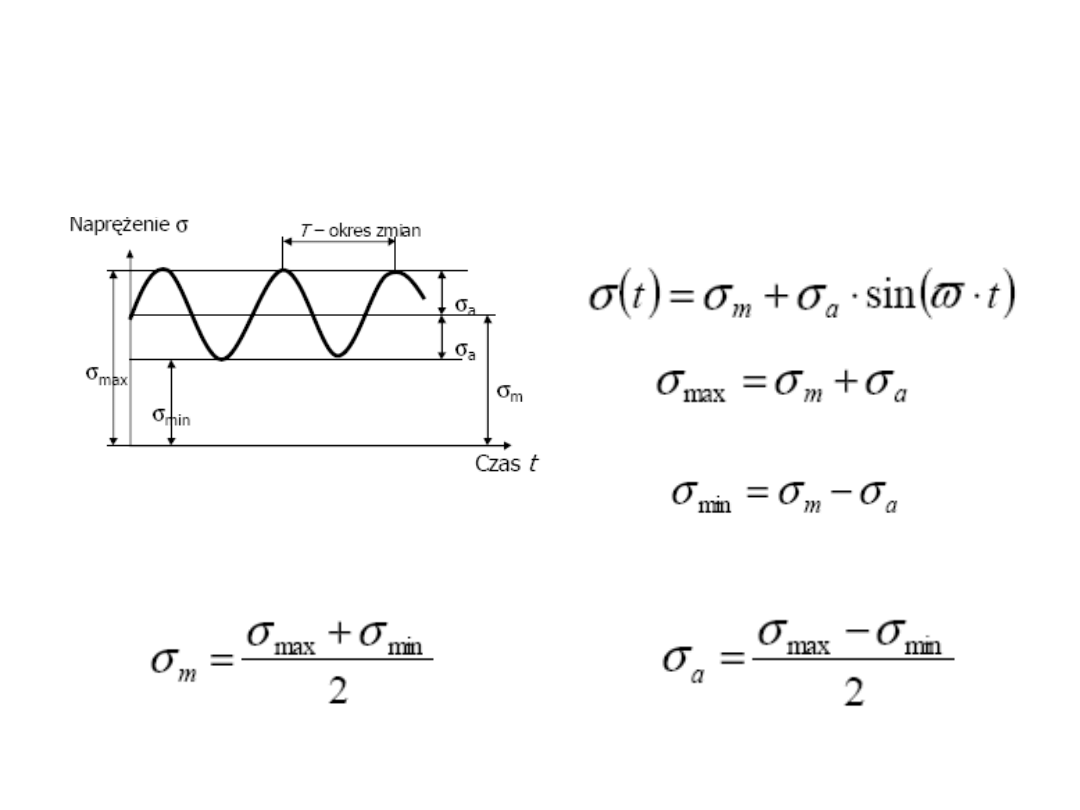
ETAP II – obliczenia
zmęczeniowe
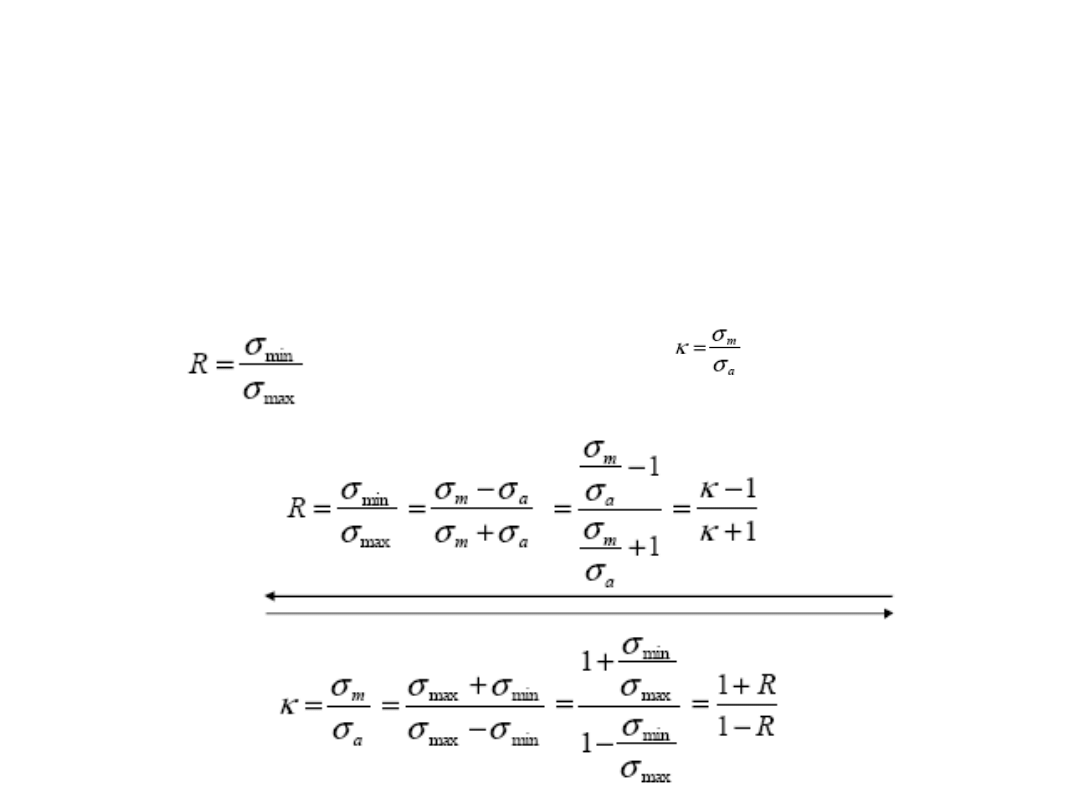
ETAP II – obliczenia
zmęczeniowe
Współczynnik
amplitudy cyklu
Współczynnik stałości
obciążenia
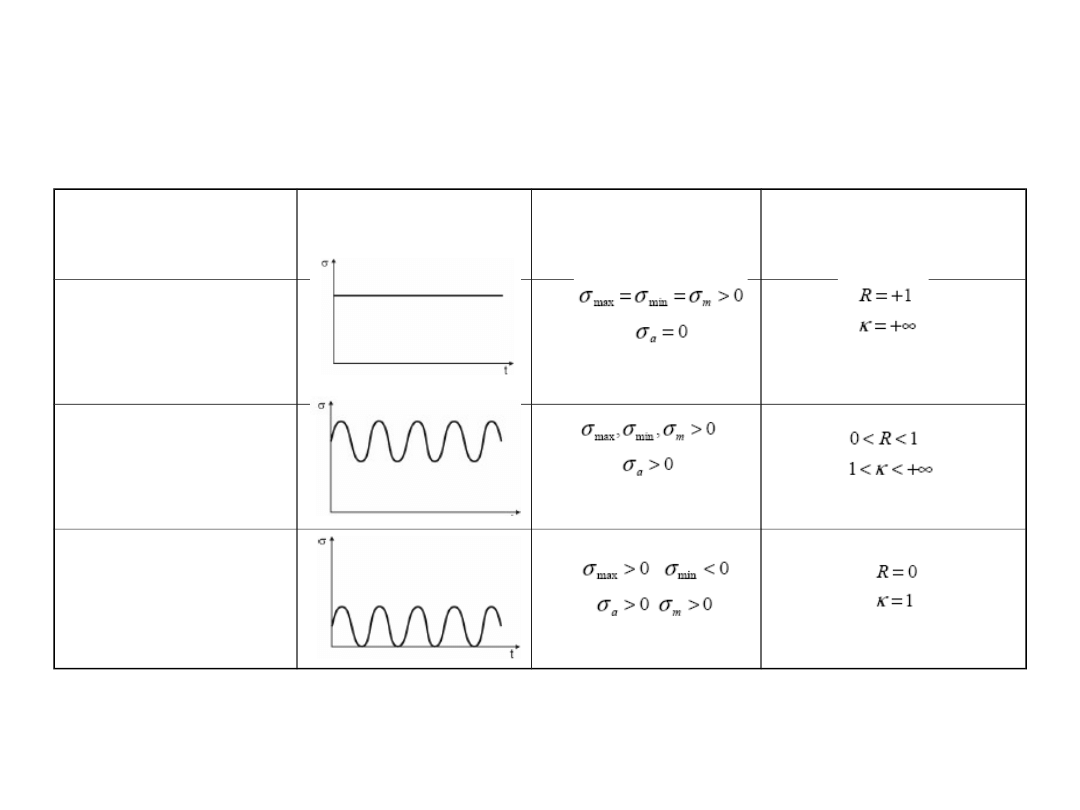
ETAP II – obliczenia
zmęczeniowe
Rodzaj
cyklu
Schemat
Naprężeni
a
Współczynni
ki
Stałe
Jednostronne
Odzerowo-
tęniace
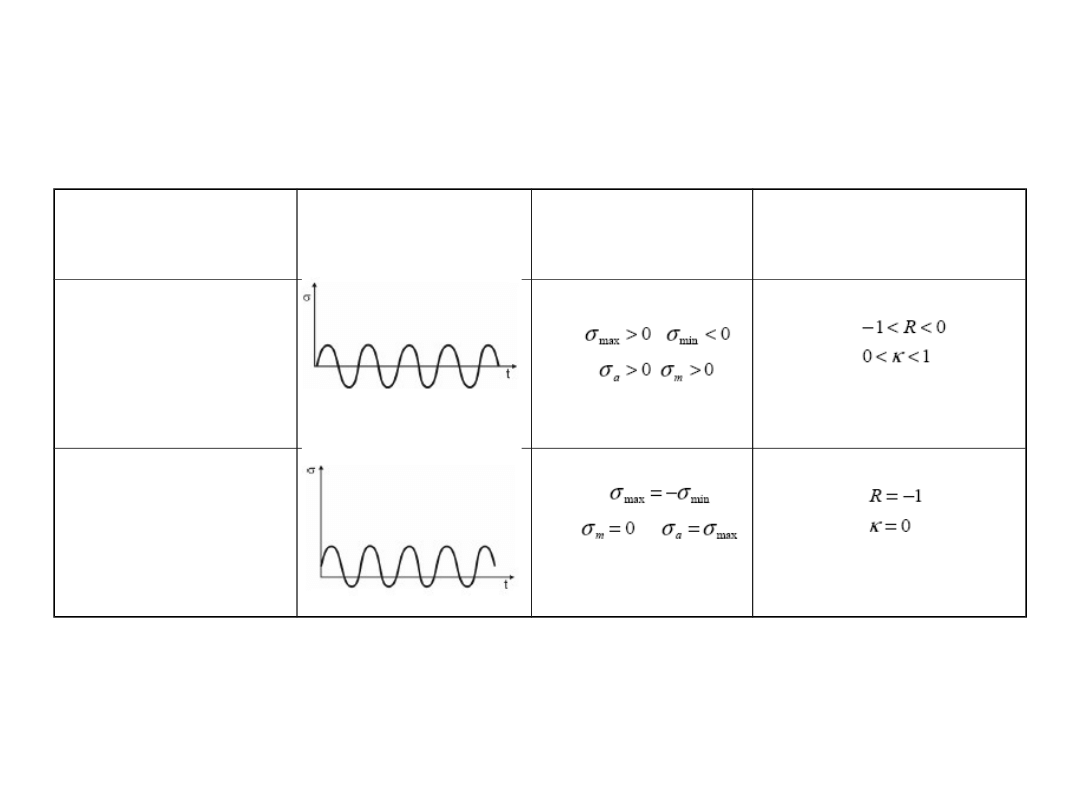
ETAP II – obliczenia
zmęczeniowe
Rodzaj
cyklu
Schemat
Naprężeni
a
Współczynni
ki
Dwustronne
Wahadłowe
ETAP II – obliczenia
zmęczeniowe
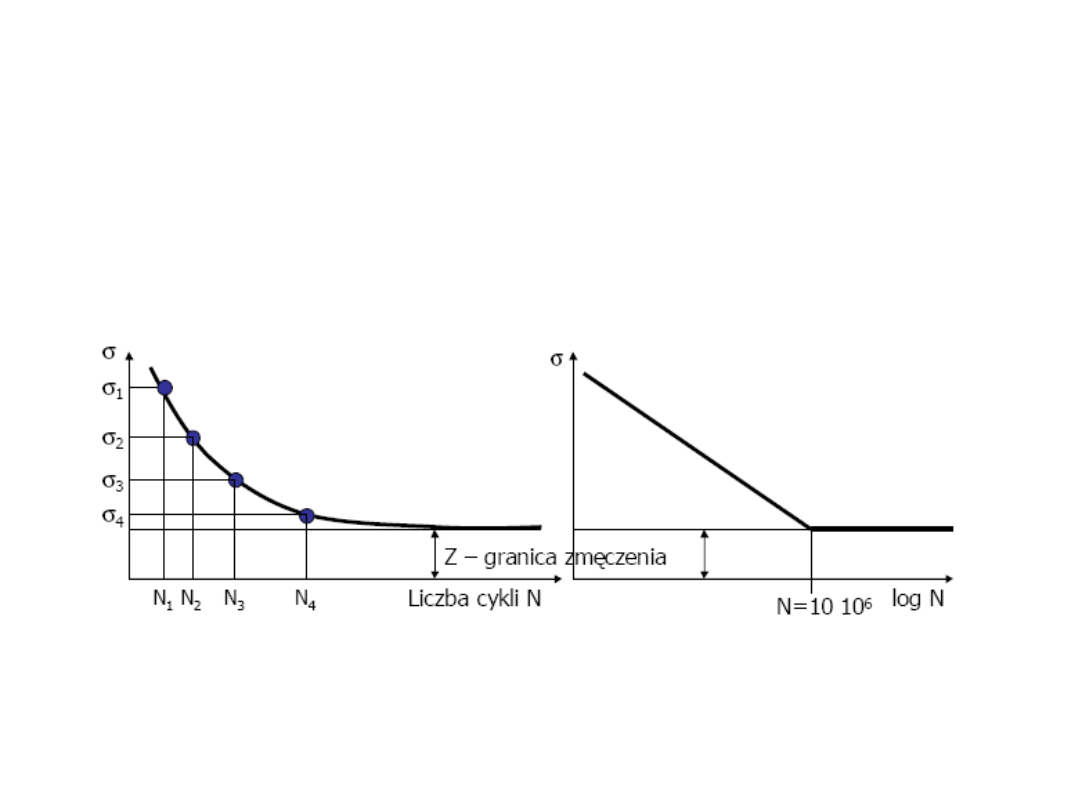
Wykres Wöhlera
Wytrzymałość zmęczeniowa Z – to takie naprężenie Smax dla danego
cyklu naprężeń, określonego przez R, że element nie ulega zniszczeniu po
osiągnięciu umownej granicznej liczby cykli N, nazywanej podstawą próby
zmęczeniowej
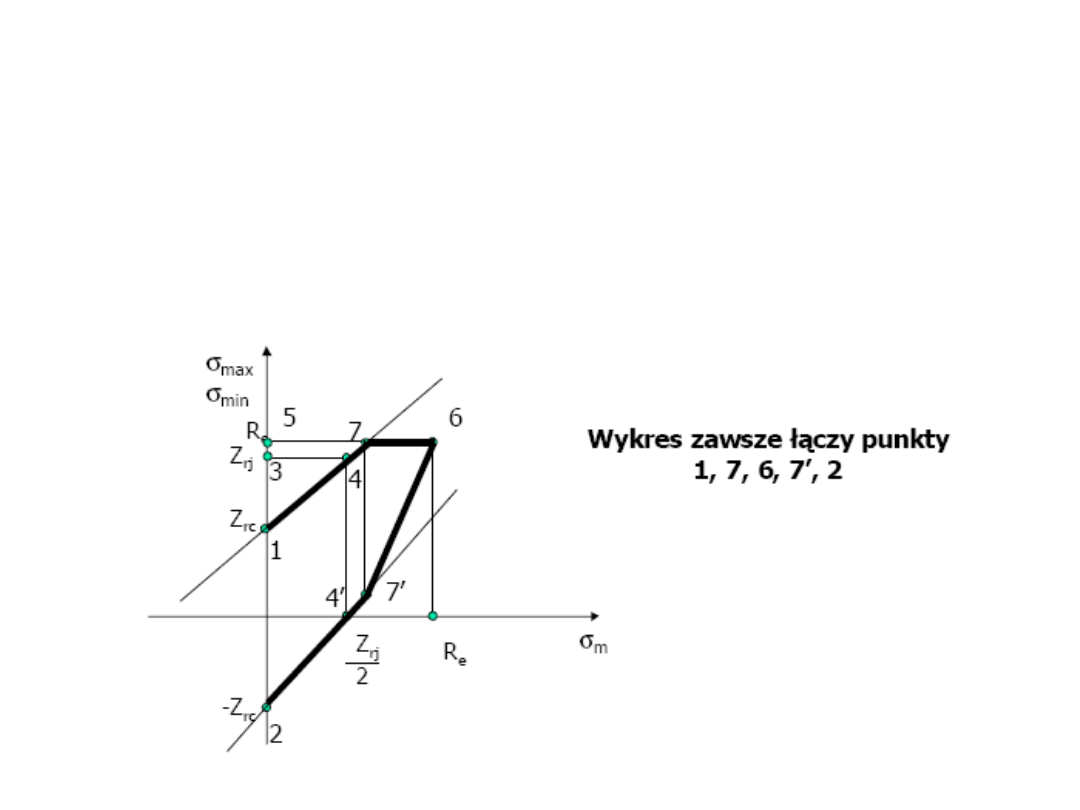
ETAP II – obliczenia
zmęczeniowe
Uproszczony wykres Smitha
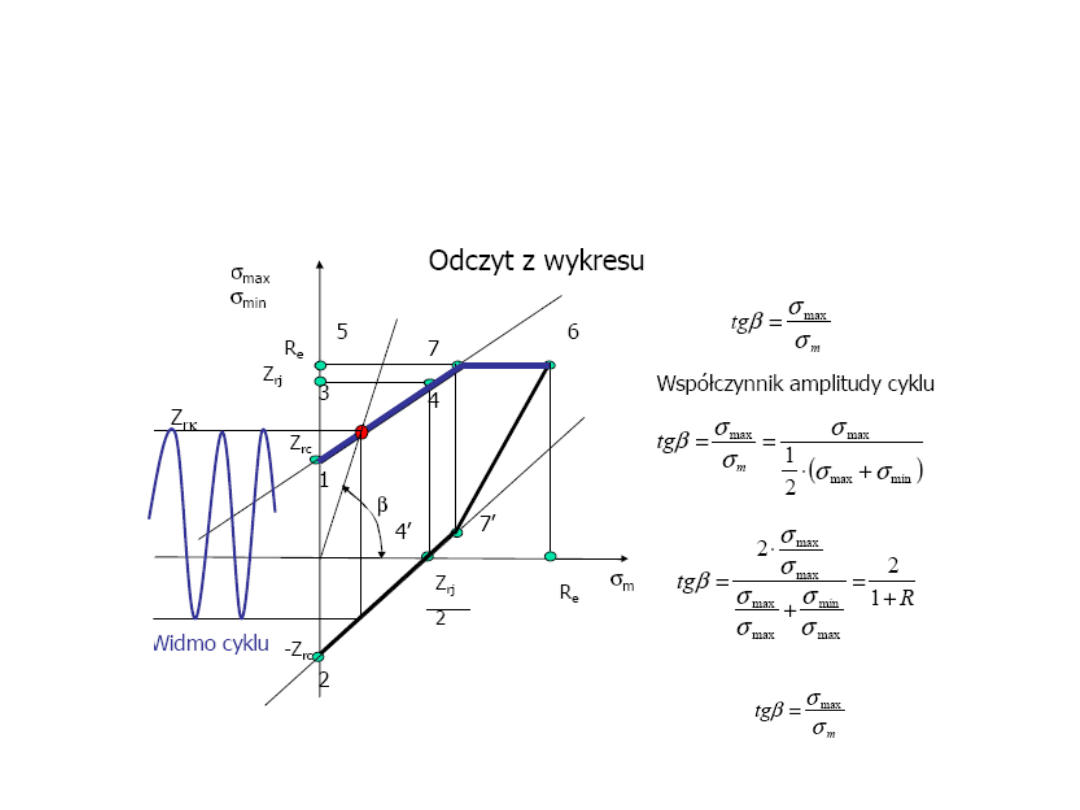
ETAP II – obliczenia
zmęczeniowe
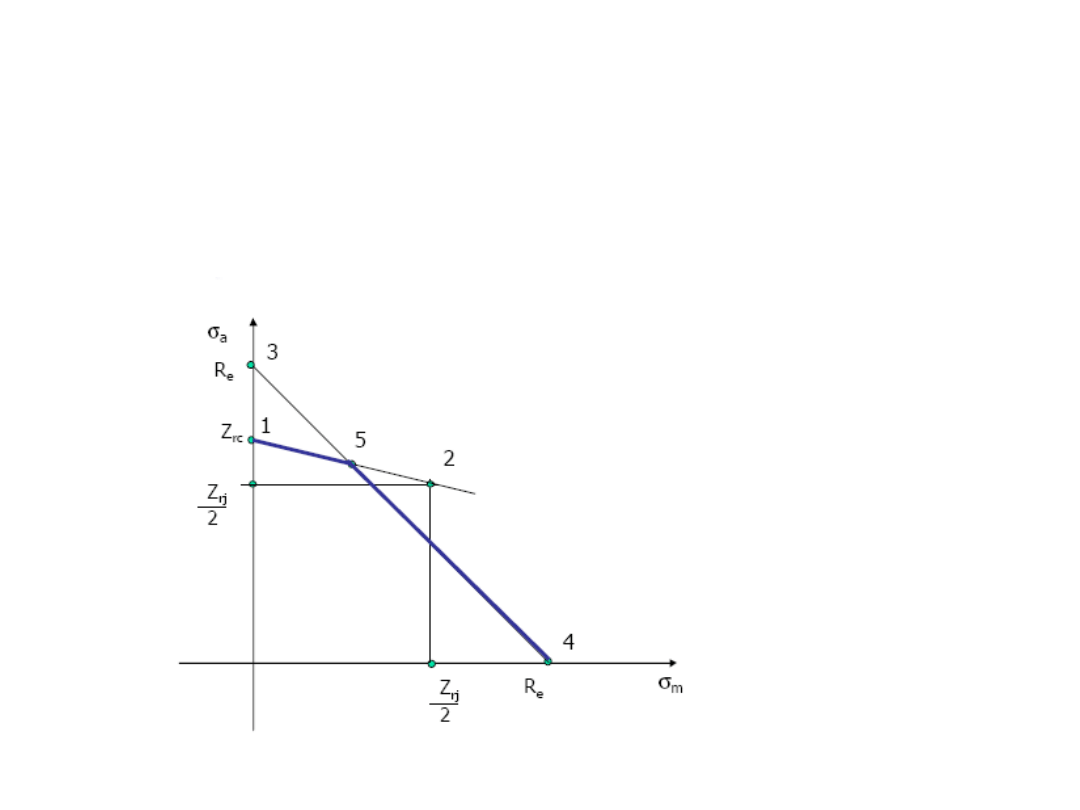
ETAP II – obliczenia
zmęczeniowe
Wykres Haigha - uproszczony
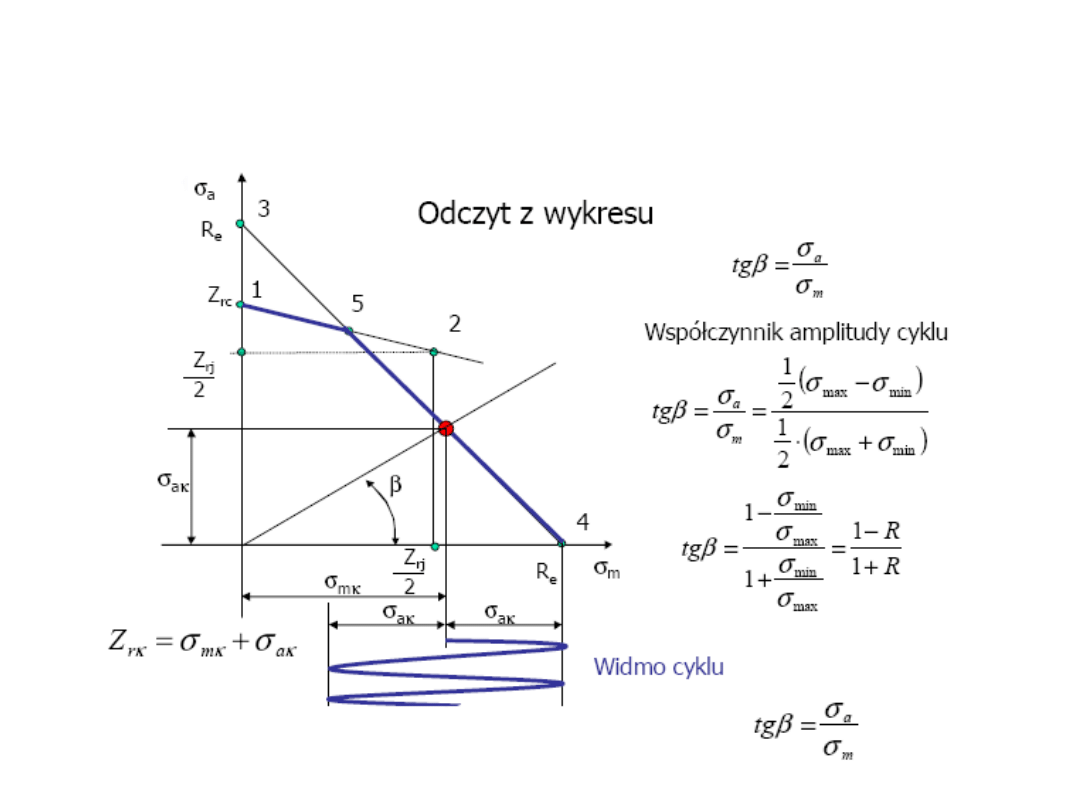
ETAP II – obliczenia
zmęczeniowe

ETAP II – obliczenia
zmęczeniowe
Czynniki wpływające na wytrzymałość
zmęczeniową:
• Materiał elementu
• Charakter zmian obciążenia
• Kształt przedmiotu
• Stan powierzchni
• Wielkość przedmiotu
• Środowisko pracy
• Temperatura pracy
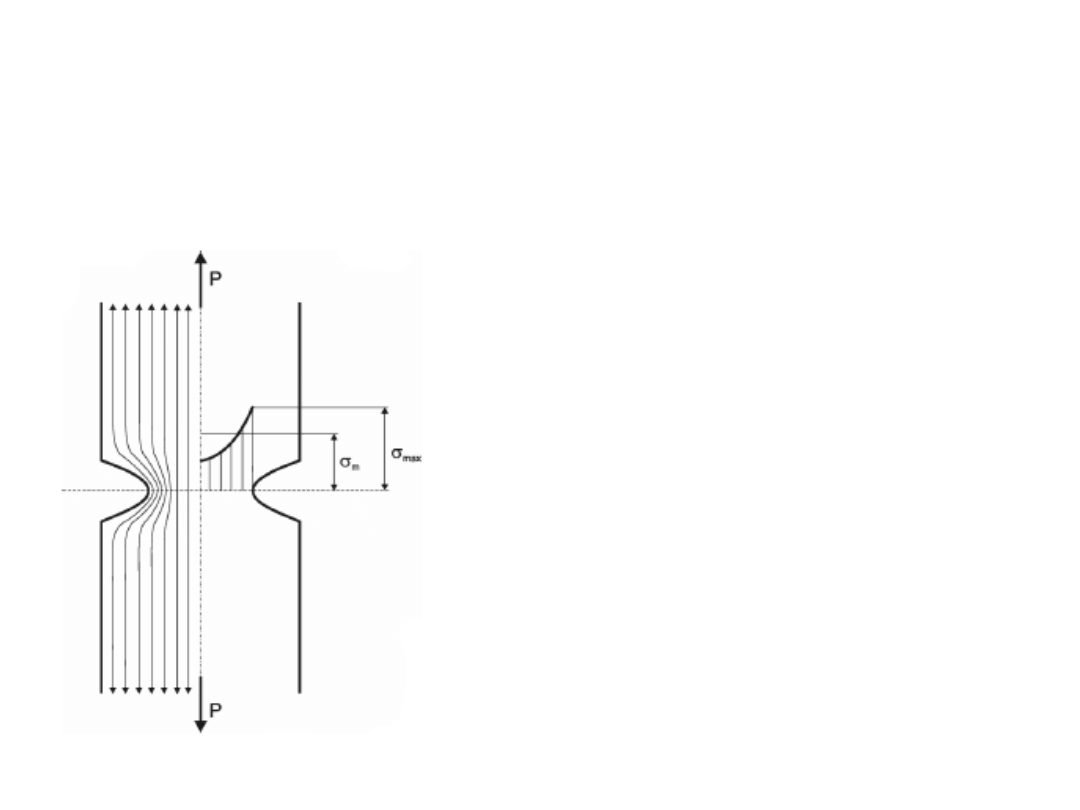
ETAP II – obliczenia
zmęczeniowe
Kształt przedmiotu - KARB
Karb – miejsce zmian
poprzecznych przekrojów
elementów lub zmian krzywizny
powierzchni ograniczających
przedmiot:
- odsadzenia,
- rowki,
- wycięcia,
- gwinty,
- otwory,
- itp.
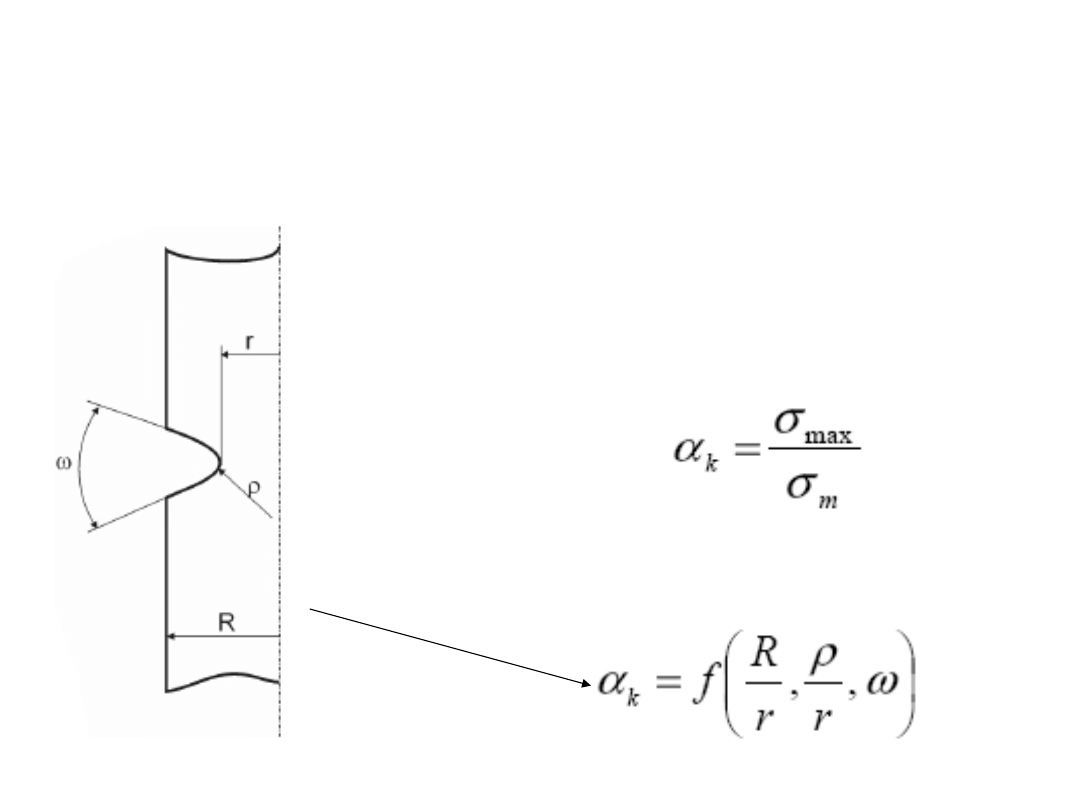
ETAP II – obliczenia
zmęczeniowe
Kształt przedmiotu - KARB
Współczynnik
kształtu karbu
Dla konkretnej geometrii karbu
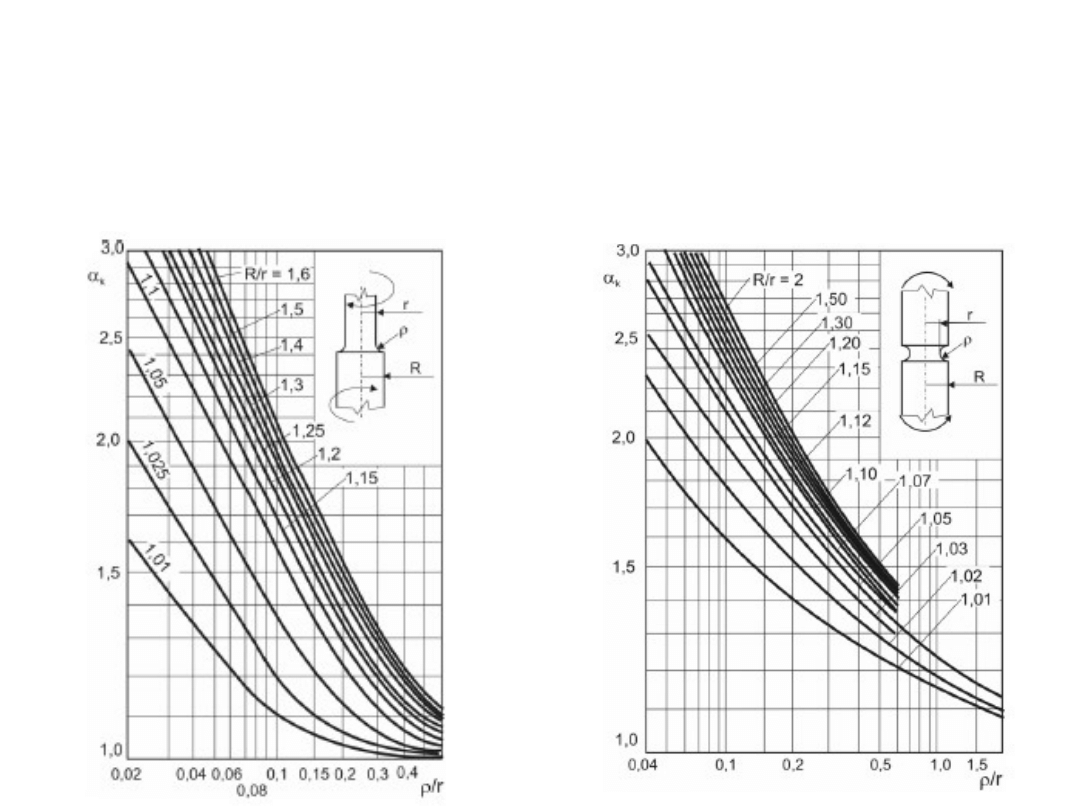
ETAP II – obliczenia
zmęczeniowe
Kształt przedmiotu - KARB
ETAP II – obliczenia
zmęczeniowe
1
p
k
Z
Z
obr
pol
p
Sumaryczny współczynnik
spiętrzenia naprężeń
Współczynnik
działania karbu
Współczynnik
wpływu
chropowatości
Z
pol
– granica zmęczenia próbki
polerowanej
Z
obr
– granica zmęczenia przy
zadanej chropowatości
Z
Z
K
gł
k
Z
gł
– granica zmęczenia próbki
gładkiej
Z
K
– granica zmęczenia próbki z
karbem
ETAP II – obliczenia
zmęczeniowe
pz
k
Z
Z
pz
pz
Sumaryczny współczynnik
spiętrzenia naprężeń
Współczynnik
działania karbu
Współczynnik
wpływu obróbki
powierzchni
Z – granica zmęczenia próbki bez
obróbki powierzchniowej
Z
pz
– granica zmęczenia próbki po
obróbce powierzchniowej
Z
Z
K
gł
k
Z
gł
– granica zmęczenia próbki
gładkiej
Z
K
– granica zmęczenia próbki z
karbem
ETAP II – obliczenia
zmęczeniowe
Współczynnik działania karbu
1
1
k
k
k
Współczynnik kształtu
karbu
Współczynnik wrażliwości materiału na działanie karbu
(im wyższe Rm tym większa wrażliwość)
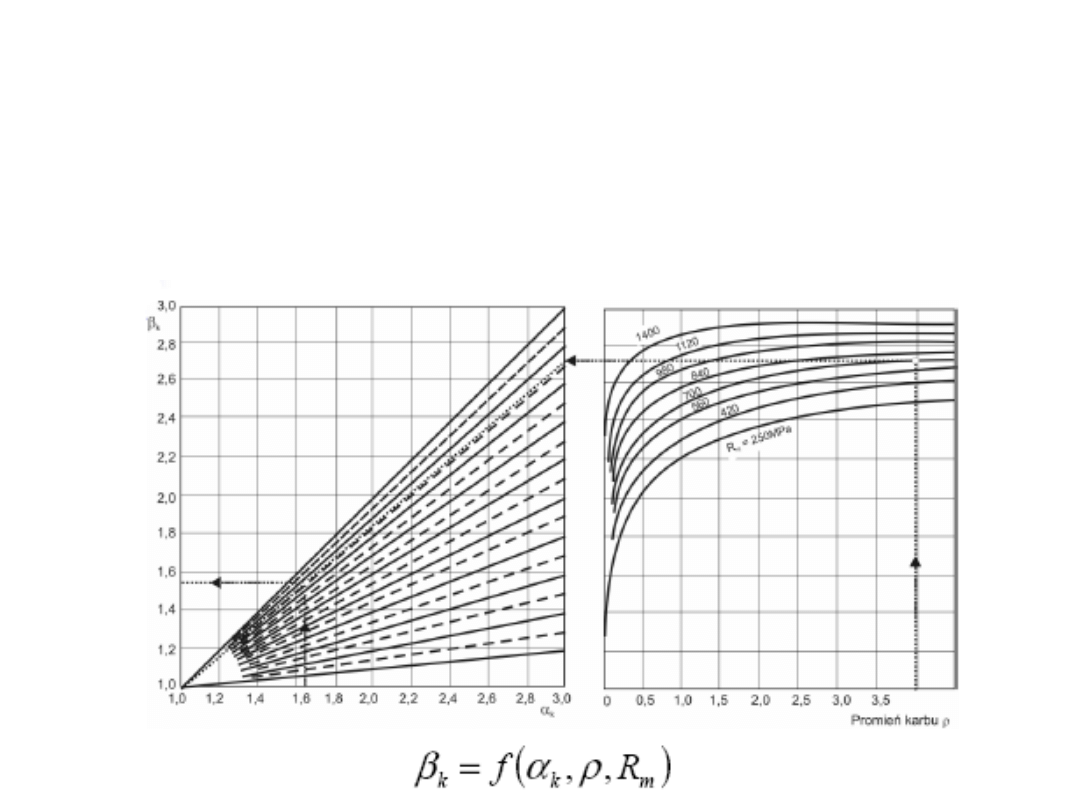
ETAP II – obliczenia
zmęczeniowe
Współczynnik działania karbu
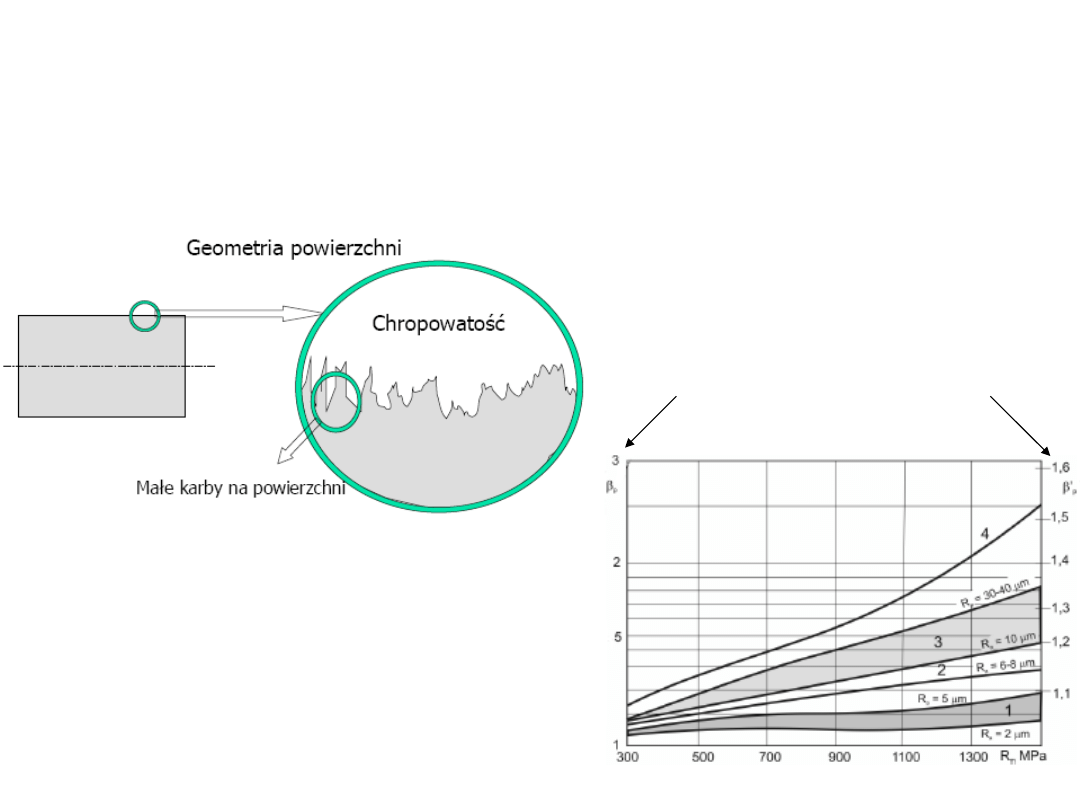
ETAP II – obliczenia
zmęczeniowe
Współczynnik wpływu chropowatości
Rozciągani
e i zginanie
Skręcanie i
ścinanie
1 – szlifowanie
2 – toczenie, frezowanie dokładne
3 – toczenie, frezowanie zgrubne,
4 – odlewanie, kucie, ….

ETAP II – obliczenia
zmęczeniowe
Wielkość elementu – współczynnik
wielkości przekroju
Większe elementy to większe prawdopodobieństwo
wad, pęknięć i uszkodzeń.
Z
Z
d
granica zmęczenia dla próbki o
dowolnym przekroju
granica zmęczenia dla próbki o
przekroju wzorcowym (koło o średnicy
7mm)
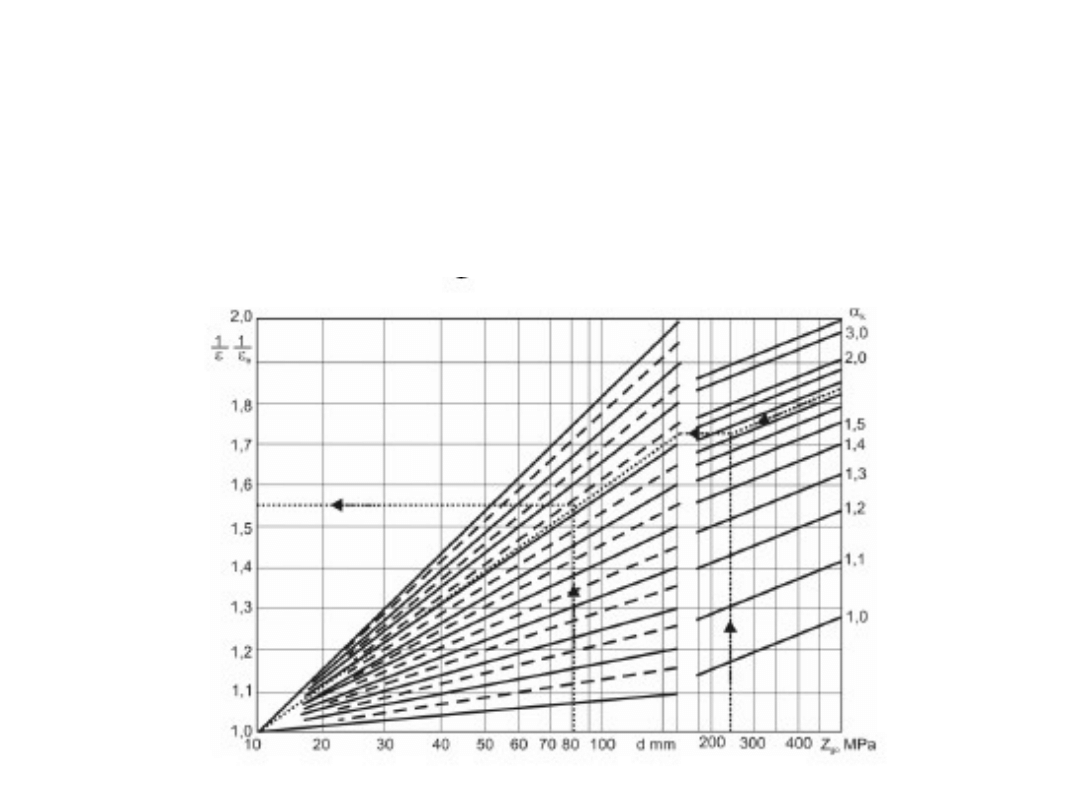
ETAP II – obliczenia
zmęczeniowe
Wielkość elementu – współczynnik
wielkości przekroju

ETAP II – obliczenia
zmęczeniowe
Współczynnik bezpieczeństwa – wartość
graniczna
g
Wartości
g
:
1,3 – 1,5
: znany rozkład naprężeń, wysoka technologia
wykonania i przy
stosowaniu dobrych metod defektoskopowych
1,5 – 1,7
: zwykła dokładność obliczeń, dobra technologia
wykonania i
czynności kontrolne
1,7 – 2,0
: elementy o większych wymiarach, średnia
dokładność
obliczeń i wykonania
2,0 – 2,5
: przy orientacyjnym określeniu obciążeń i naprężeń,
dla
nieznanych dokładnie warunków pracy

ETAP II – obliczenia
zmęczeniowe
Współczynnik bezpieczeństwa –
określenie wartości rzeczywistej
1 Cykle symetryczne
g
Z
max
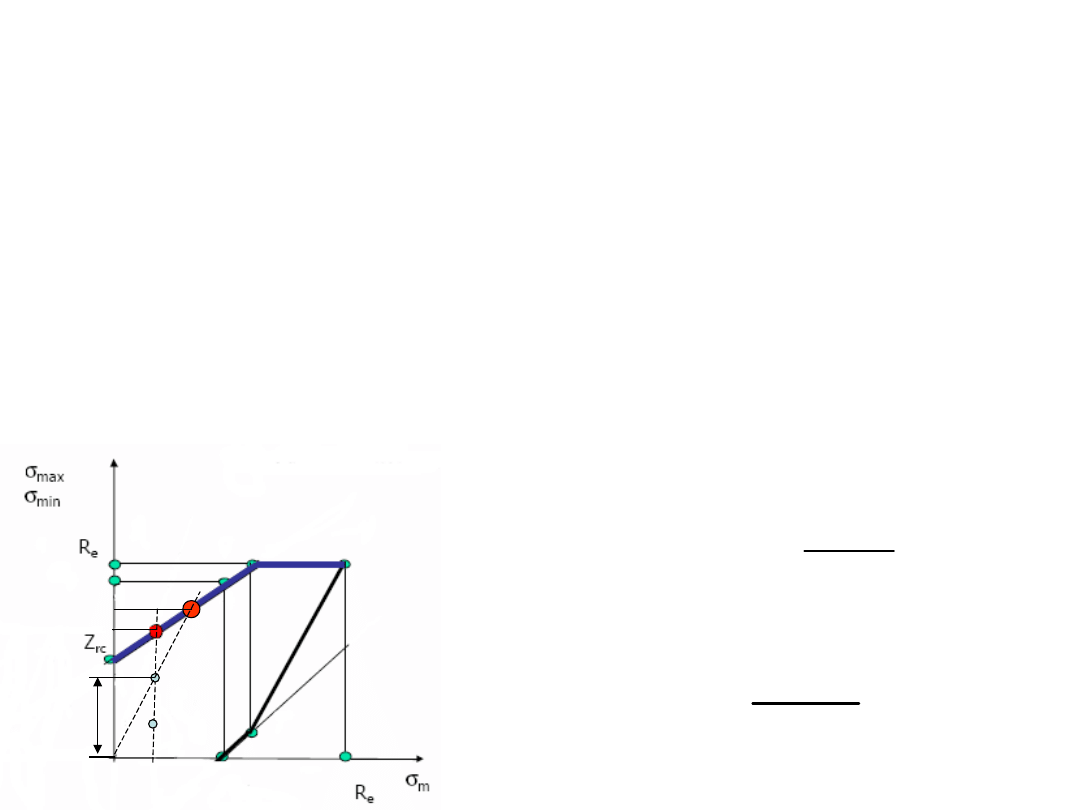
ETAP II – obliczenia
zmęczeniowe
g
C
Z
max
az
m
Współczynnik bezpieczeństwa –
określenie wartości rzeczywistej
2 Cykle niesymetryczne dla R=const
az
m
max
a
az
m
max
Z
B
Z
C
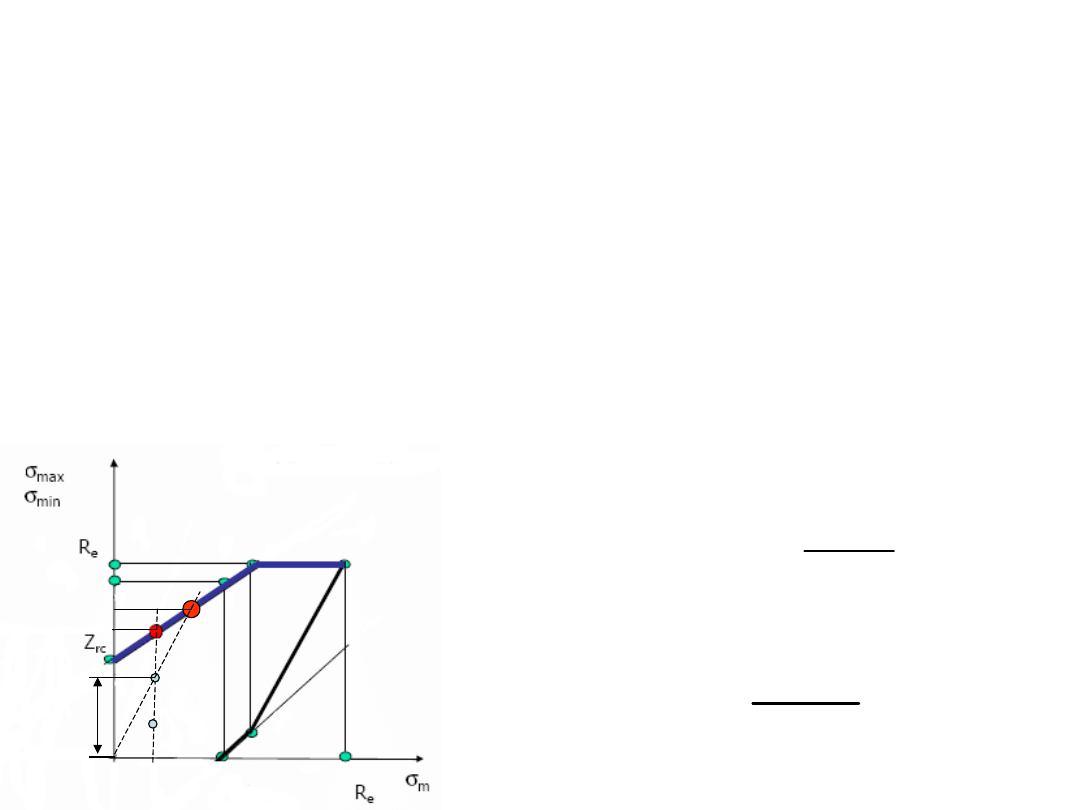
ETAP II – obliczenia
zmęczeniowe
g
B
Z
max
az
m
Współczynnik bezpieczeństwa –
określenie wartości rzeczywistej
3 Cykle niesymetryczne – przyrost obciążenia ze stałym
m
az
m
max
a
az
m
max
Z
B
Z
C
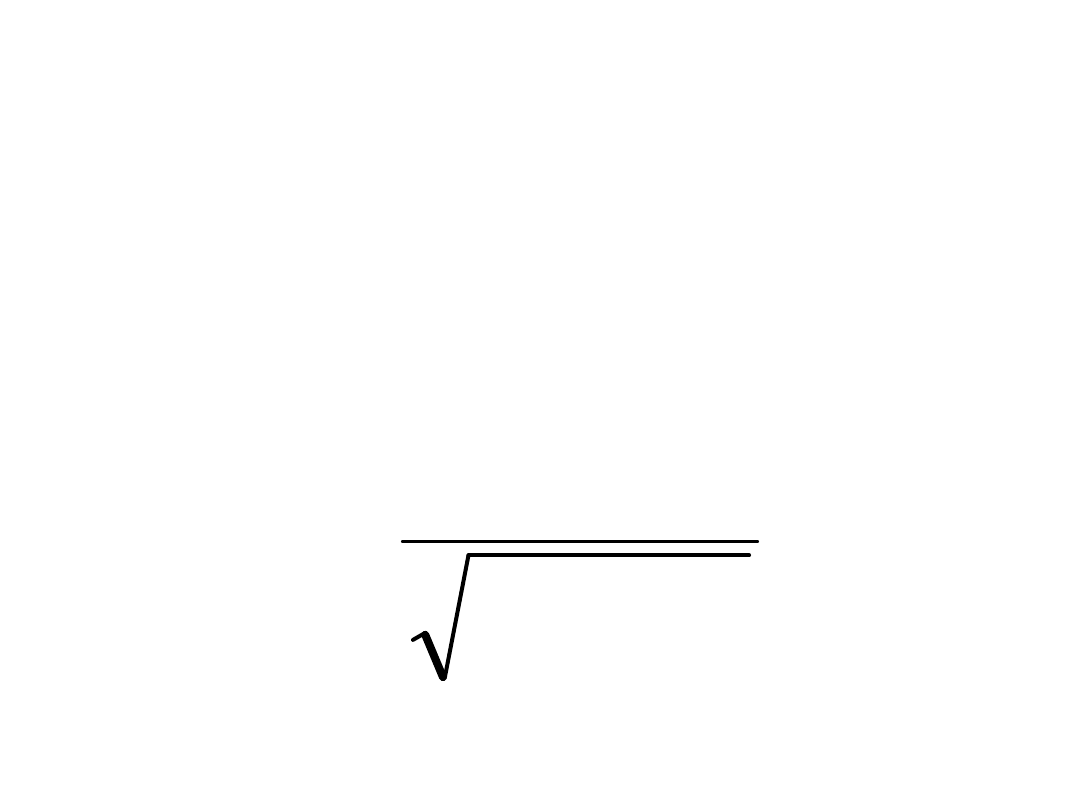
ETAP II – obliczenia
zmęczeniowe
Współczynnik bezpieczeństwa –
określenie wartości rzeczywistej
4 Naprężenia złożone
2
2
k
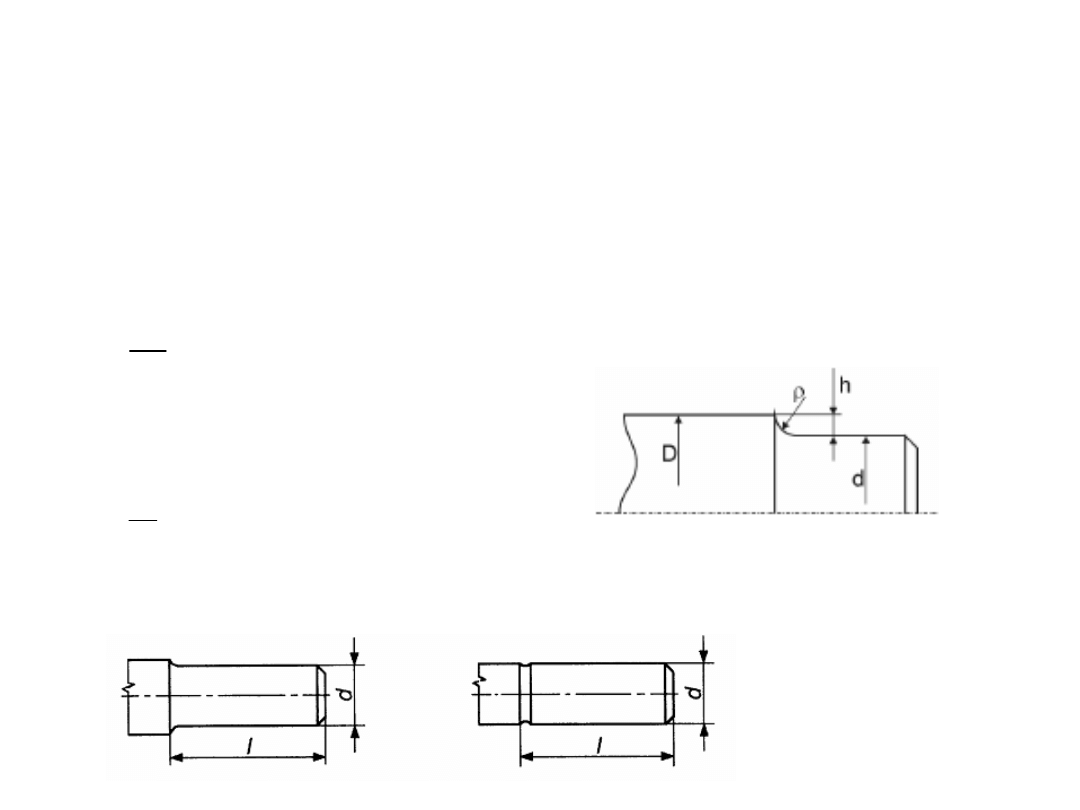
ETAP III – kształtowanie
wałów
1. Wszystkie średnice muszą być większe od zarysu
teoretycznego
2. Stopniowanie średnic
3. Promienie zaokrągleń
02
.
0
d
2
.
1
d
D
4. Średnice i długości czopów
PN-78/M-85000
PN-78/M-85000
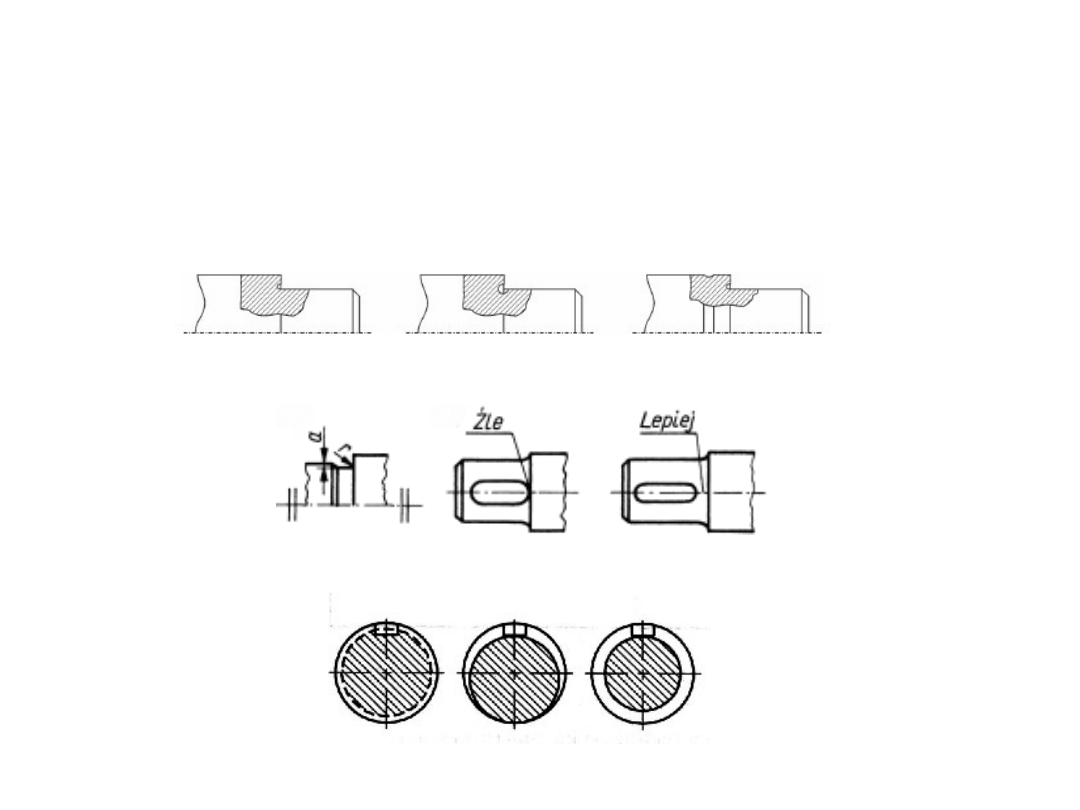
ETAP III – kształtowanie
wałów
4. Poprawa wytrzymałości zmęczeniowej
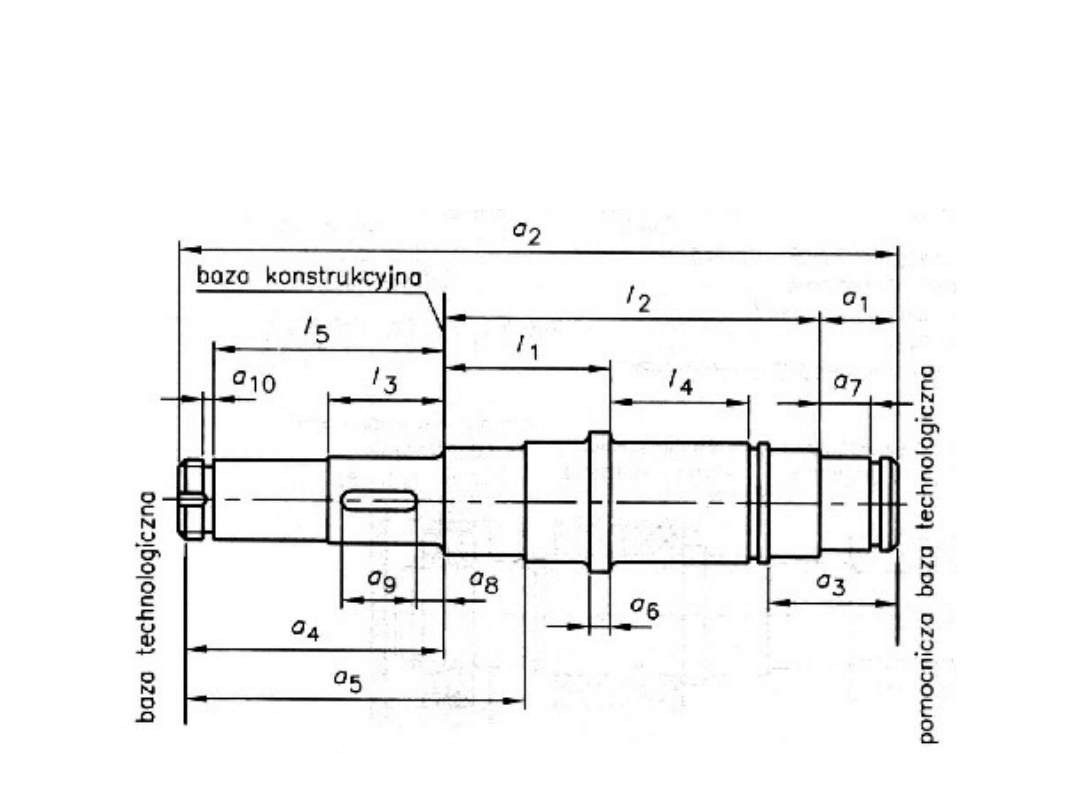
ETAP III – kształtowanie
wałów
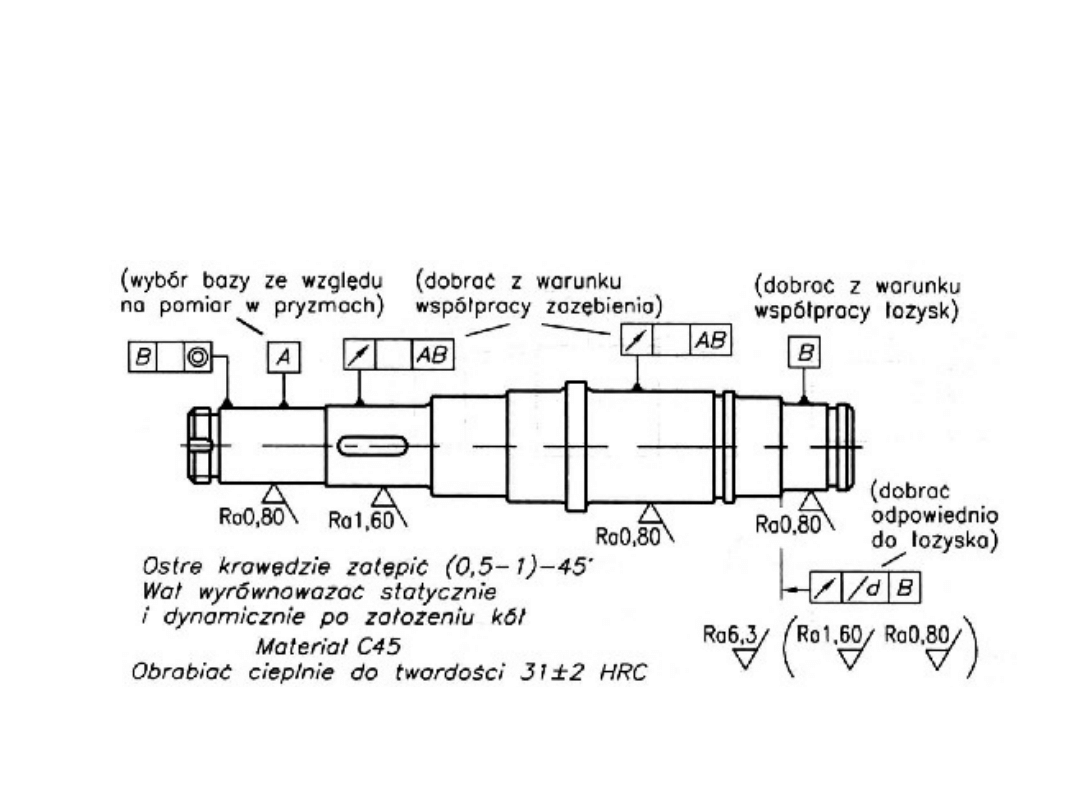
ETAP III – kształtowanie
wałów
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
Wyszukiwarka
Podobne podstrony:
Pokaz 1 dusznica niestabilna
nowy INFLACJA DEFINICJA stacjon niestacj
MiTR Projekt 1 A B GiG III gr 1 niestacjonarne
bazodanowe aspekty systemow nauczania niestacjonarnego VO3J75COSVPPOOUN5TKHLCXK6ZMWUTQXKUXZF4I
PKM w9 osie waly III id 360040 Nieznany
PROCESY NIESTACJONARNEJ WYMIANA CIEPŁA, Uczelnia, Metalurgia
Niestandardowe usługi, Windows porady
Wały i łożyska ślimak
Elektronika Przemysłowa Laboratorium niestacjonarni Grupa IV
badop Zarz niestac IIst 12 13 zima zadania
niestacjonarne KDR II v1[1]
Peugeot 406 niestabilna temp we wnetrzu
DZIENNICZEK PRAKTYK DLA STUDIOW NIESTACJONARNYCH ISTOPNIA
El siatki 2007 inz niestac
niestabilnosc barku 1, Fizjoterapia, Ortopedia
Wały Napędowe, Różne
więcej podobnych podstron