ACT/ACT

ACT/ACT

bieżący/bieżący

bieżący/bieżący

Pomiędzy rozpoczęciem, a wygaśnięciem

Pomiędzy rozpoczęciem, a wygaśnięciem

inwestycji naliczana jest rzeczywista liczba

inwestycji naliczana jest rzeczywista liczba

dni, która dzielona jest przez 365 (366 w

dni, która dzielona jest przez 365 (366 w

przypadku roku przestępnego); formuła

przypadku roku przestępnego); formuła

stosowana dla instrumentów rynku

stosowana dla instrumentów rynku

kapitałowego.

kapitałowego.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

Występuje np. przy amerykańskich

Występuje np. przy amerykańskich

obligacjach rządowych oraz niektórych

obligacjach rządowych oraz niektórych

obligacjach polskich nominowanych

obligacjach polskich nominowanych

w złotych - obligacjach dziesięcioletnich

w złotych - obligacjach dziesięcioletnich

i obligacjach o stałym oprocentowaniu

i obligacjach o stałym oprocentowaniu

.

.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

ACT/360

ACT/360

bieżący/360

bieżący/360

Pomiędzy rozpoczęciem, a wygaśnięciem

Pomiędzy rozpoczęciem, a wygaśnięciem

inwestycji naliczana jest rzeczywista ilość

inwestycji naliczana jest rzeczywista ilość

dni,

dni,

która dzielona jest przez 360; formuła

która dzielona jest przez 360; formuła

stosowana przy instrumentach rynku

stosowana przy instrumentach rynku

pieniężnego.

pieniężnego.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

Występuje np. przy krótkoterminowych

Występuje np. przy krótkoterminowych

pożyczkach rządowych (bony skarbowe),

pożyczkach rządowych (bony skarbowe),

przy

przy

depozytach międzybankowych i bonach

depozytach międzybankowych i bonach

pieniężnych; nie dotyczy długu

pieniężnych; nie dotyczy długu

denominowanego w takich walutach jak:

denominowanego w takich walutach jak:

GBP, AUD, NZD, JPY

GBP, AUD, NZD, JPY

.

.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

ACT/365

ACT/365

bieżący/365

bieżący/365

Pomiędzy rozpoczęciem, a wygaśnięciem

Pomiędzy rozpoczęciem, a wygaśnięciem

inwestycji naliczana jest rzeczywista ilość

inwestycji naliczana jest rzeczywista ilość

dni,

dni,

która dzielona jest przez 365

która dzielona jest przez 365

. Formuła

. Formuła

stosowana przy instrumentach rynku

stosowana przy instrumentach rynku

pieniężnego dla takich walut jak: GBP,

pieniężnego dla takich walut jak: GBP,

AUD,

AUD,

NZD, JPY

NZD, JPY

.

.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

30/360 US

30/360 US

Pomiędzy rozpoczęciem, a wygaśnięciem

Pomiędzy rozpoczęciem, a wygaśnięciem

inwestycji naliczana jest rzeczywista liczba dni

inwestycji naliczana jest rzeczywista liczba dni

przy założeniu, że każdy miesiąc ma 30 dni; w

przy założeniu, że każdy miesiąc ma 30 dni; w

przypadku 31 dnia miesiąca następuje przejście

przypadku 31 dnia miesiąca następuje przejście

o 1 dzień do przodu, następuje zatem 1 dzień

o 1 dzień do przodu, następuje zatem 1 dzień

następnego miesiąca; wyznaczona liczba dni

następnego miesiąca; wyznaczona liczba dni

jest dzielona przez 360.

jest dzielona przez 360.

Stosowana przy

Stosowana przy

wycenie weksli w systemie anglosaskim.

wycenie weksli w systemie anglosaskim.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

30/360 EUR

30/360 EUR

Pomiędzy rozpoczęciem, a wygaśnięciem

Pomiędzy rozpoczęciem, a wygaśnięciem

inwestycji naliczana jest rzeczywista liczba

inwestycji naliczana jest rzeczywista liczba

dni przy założeniu, że każdy miesiąc ma

dni przy założeniu, że każdy miesiąc ma

30

30

dni; w przypadku 31 dnia miesiąca

dni; w przypadku 31 dnia miesiąca

następuje przejście o 1 dzień do tyłu,

następuje przejście o 1 dzień do tyłu,

następuje zatem 30 dzień tego samego

następuje zatem 30 dzień tego samego

miesiąca; wyznaczona liczba dni jest

miesiąca; wyznaczona liczba dni jest

dzielona przez 360.

dzielona przez 360.

Stosowana przy

Stosowana przy

wycenie weksli w systemie konwencyjnym.

wycenie weksli w systemie konwencyjnym.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

Przykład

Przykład

W dniu 27.02 2012 roku przedsiębiorstwo X

W dniu 27.02 2012 roku przedsiębiorstwo X

udzieliło przedsiębiorstwu Y pożyczki w

udzieliło przedsiębiorstwu Y pożyczki w

kwocie 1.000 PLN (K). Termin spłaty pożyczki

kwocie 1.000 PLN (K). Termin spłaty pożyczki

wraz z odsetkami upłynął 31.03.2012 roku. Ile

wraz z odsetkami upłynął 31.03.2012 roku. Ile

wynoszą odsetki (O) od udzielonej pożyczki,

wynoszą odsetki (O) od udzielonej pożyczki,

jeżeli oprocentowanie (r) wynosi 17% p.a.?

jeżeli oprocentowanie (r) wynosi 17% p.a.?

Obliczenie wykonać dla wszystkich formuł

Obliczenie wykonać dla wszystkich formuł

naliczania czasu trwania pożyczki.

naliczania czasu trwania pożyczki.

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

Rozwiązanie

Rozwiązanie

30/360 US

30/360 US

30/360 EUR

30/360 EUR

ACT/ACT

ACT/ACT

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

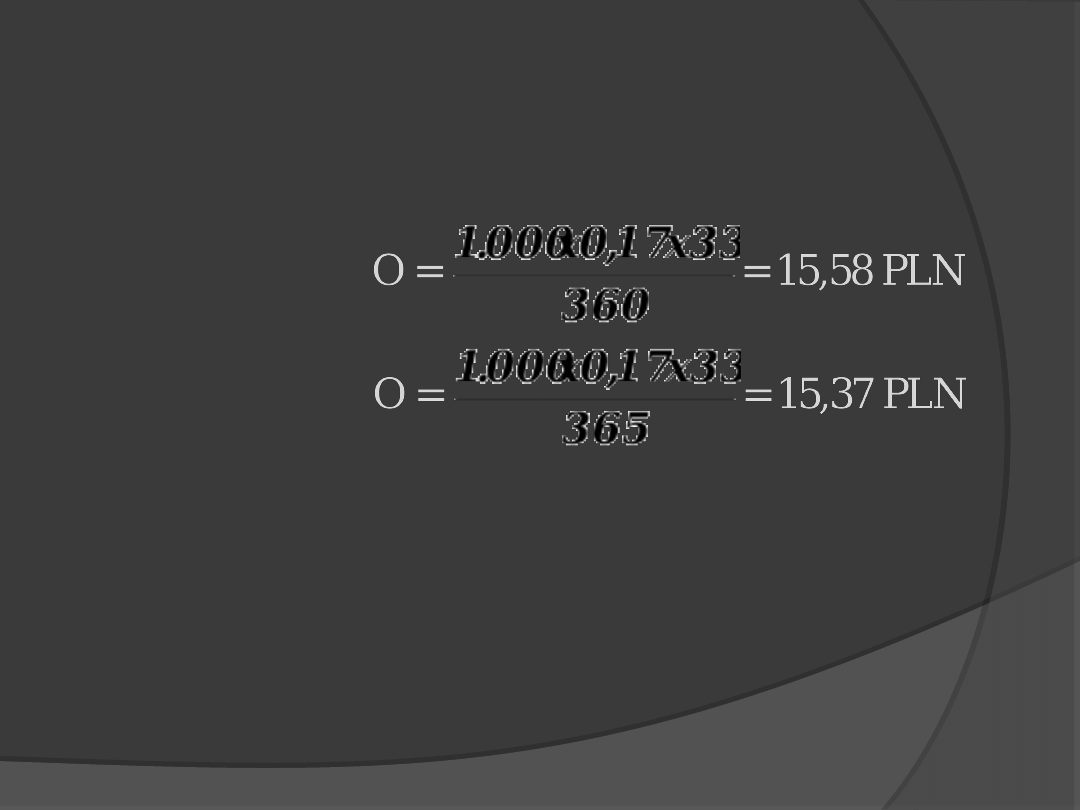
ACT/360

ACT/360

ACT/365

ACT/365

Baza głównych walut rezerwowych:

ACT/365 – dla PLN i GBP
ACT/360 – dla EUR, USD, CHF

1. TYPY FORMUŁ

1. TYPY FORMUŁ

ODSETKOWYCH

ODSETKOWYCH

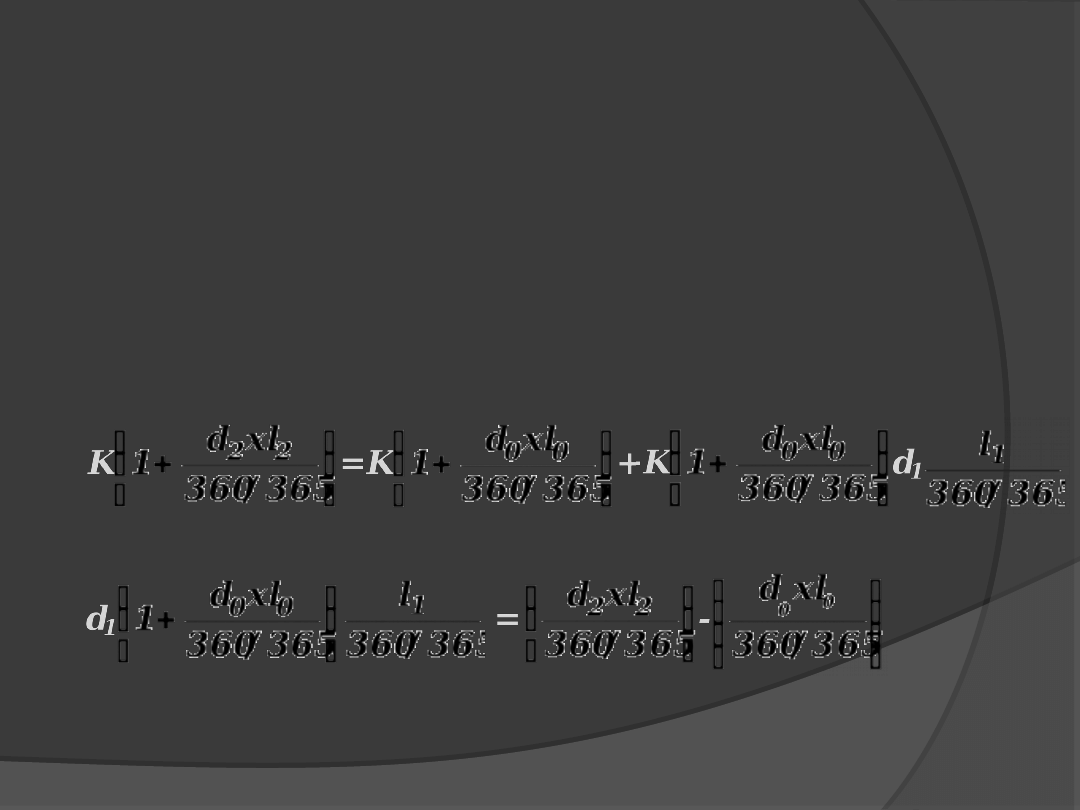
Sposób wyznaczenia stopy terminowej

Sposób wyznaczenia stopy terminowej

dla

dla

"punktu obojętności" inwestora:

"punktu obojętności" inwestora:

2. STOPA TERMINOWA RYNKU

2. STOPA TERMINOWA RYNKU

PIENIĘŻNEGO

PIENIĘŻNEGO

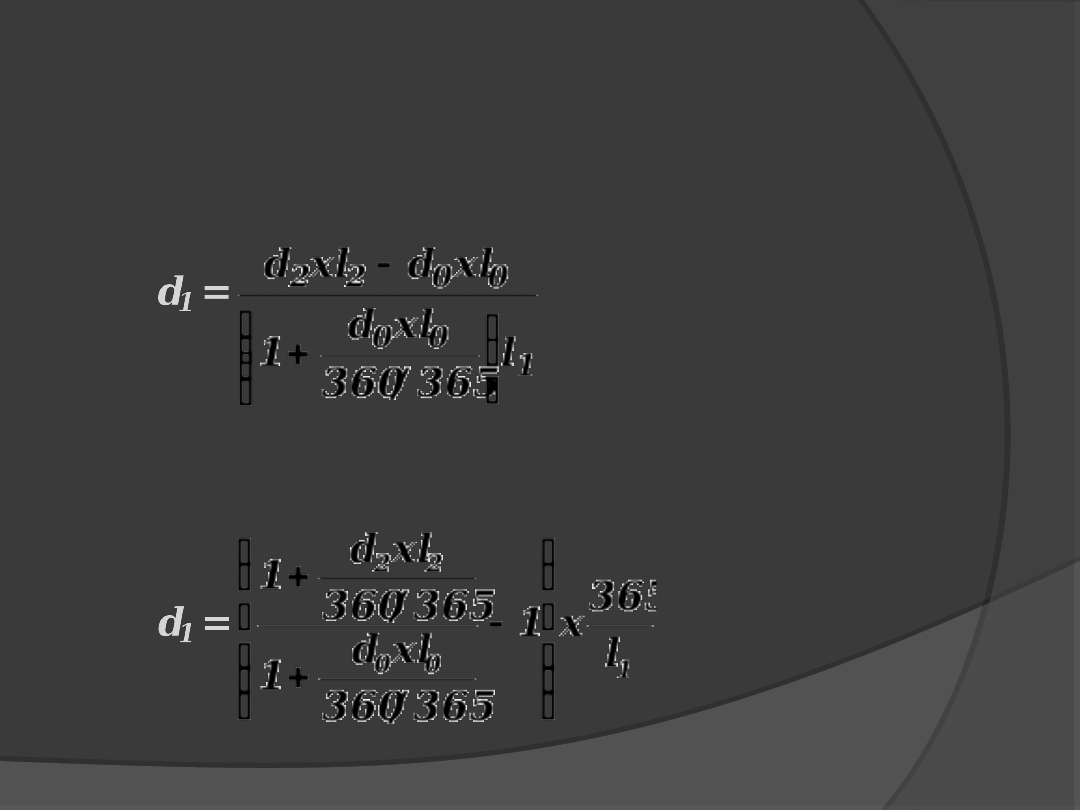
lub zapis równoważny:

2. STOPA TERMINOWA RYNKU

2. STOPA TERMINOWA RYNKU

PIENIĘŻNEGO

PIENIĘŻNEGO

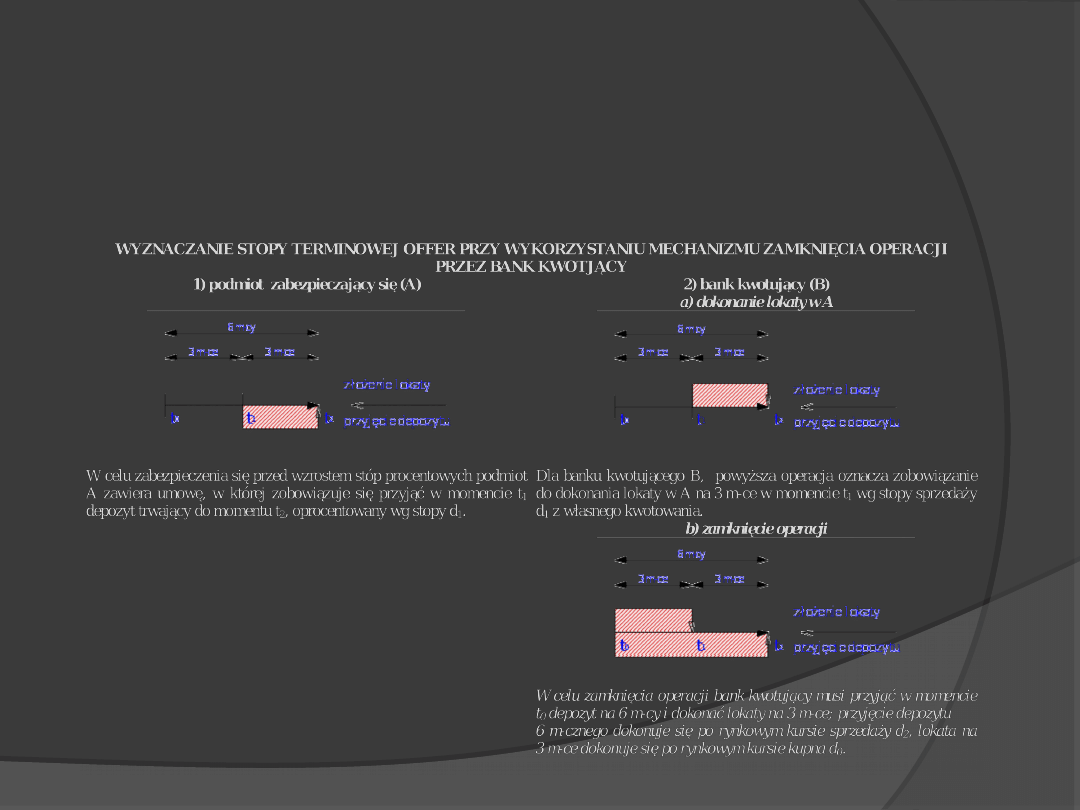
2. STOPA TERMINOWA RYNKU

2. STOPA TERMINOWA RYNKU

PIENIĘŻNEGO

PIENIĘŻNEGO

2. STOPA TERMINOWA RYNKU

2. STOPA TERMINOWA RYNKU

PIENIĘŻNEGO

PIENIĘŻNEGO

metoda 1

metoda 1

– zastosowanie wyłącznie stóp

– zastosowanie wyłącznie stóp

OFF/BID do wyznaczenia odpowiednich stóp

OFF/BID do wyznaczenia odpowiednich stóp

terminowych:

terminowych:

2.1.

2.1.

FAIR VALUE

FAIR VALUE

STOPY

STOPY

TERMINOWEJ – METODY

TERMINOWEJ – METODY

WYZNACZANIA

WYZNACZANIA

fair value OFF =

1

0

OFF

0

2

OFF

2

l

365

x

1

365

xl

d

1

365

xl

d

1































fair value BID =

1

0

BID

0

2

BID

2

l

365

x

1

365

xl

d

1

365

xl

d

1



























metoda 2

metoda 2

– średnich stóp OFF i BID, do

– średnich stóp OFF i BID, do

których/od których dodaje się/odejmuje

których/od których dodaje się/odejmuje

się

się

połowę marży rynku

połowę marży rynku

spot

spot

:

:

2.1.

2.1.

FAIR VALUE

FAIR VALUE

STOPY

STOPY

TERMINOWEJ – METODY

TERMINOWEJ – METODY

WYZNACZANIA

WYZNACZANIA

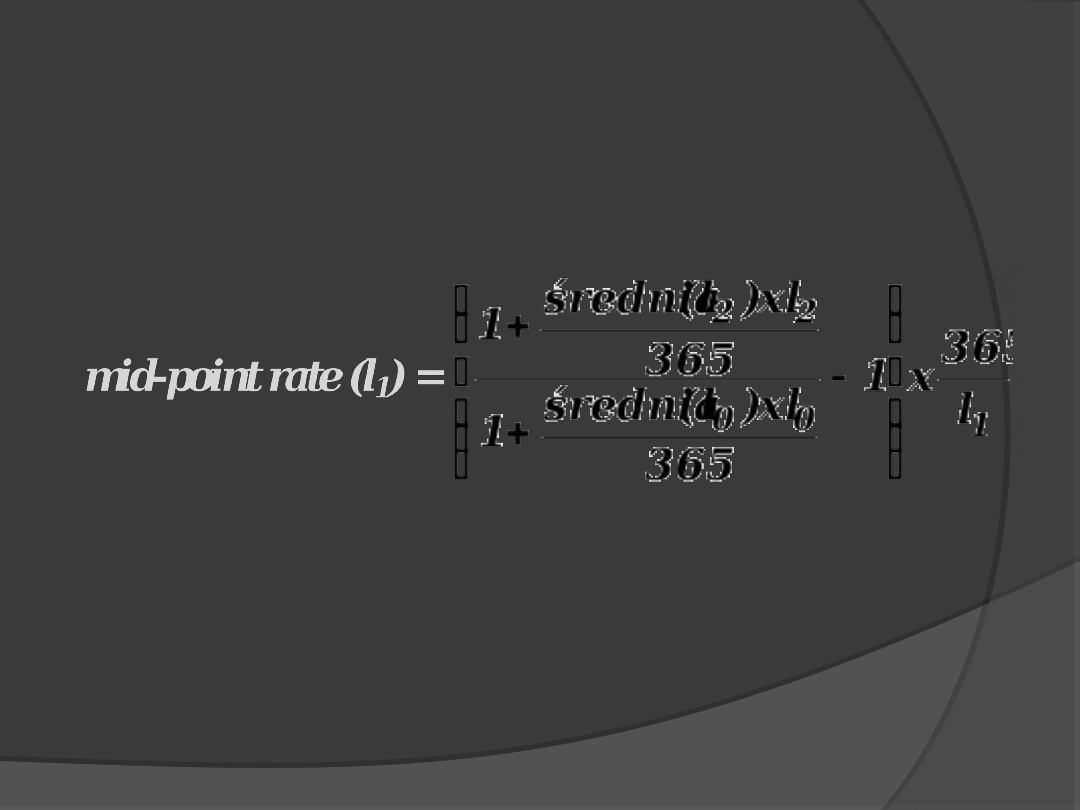
fair value OFF/BID = mid-point rate ±

fair value OFF/BID = mid-point rate ±

½ marży rynku

½ marży rynku

spot

spot

2.1.

2.1.

FAIR VALUE

FAIR VALUE

STOPY

STOPY

TERMINOWEJ – METODY

TERMINOWEJ – METODY

WYZNACZANIA

WYZNACZANIA

metoda 3

metoda 3

– średniej stóp BID/OFFER dla

– średniej stóp BID/OFFER dla

kontraktów terminowych (

kontraktów terminowych (

mid-point rate

mid-point rate

),

),

do

do

której/od której dodaje się/odejmuje się

której/od której dodaje się/odejmuje się

połowę marży rynku

połowę marży rynku

spot

spot

:

:

2.1.

2.1.

FAIR VALUE

FAIR VALUE

STOPY

STOPY

TERMINOWEJ – METODY

TERMINOWEJ – METODY

WYZNACZANIA

WYZNACZANIA

Dochodowość do wykupu a stopa

Dochodowość do wykupu a stopa

spot

spot

i terminowa

i terminowa

3. STOPA TERMINOWA RYNKU

3. STOPA TERMINOWA RYNKU

KAPITAŁOWEGO

KAPITAŁOWEGO

Stopa procentowa

Stopa procentowa

spot

spot

(S –

(S –

spot rate

spot rate

,

,

natychmiastowa stopa procentowa, kasowa

natychmiastowa stopa procentowa, kasowa

stopa procentowa) jest to stopa zwrotu w

stopa procentowa) jest to stopa zwrotu w

terminie do wykupu z obligacji, która przynosi

terminie do wykupu z obligacji, która przynosi

inwestorowi dochód tylko w postaci jednego

inwestorowi dochód tylko w postaci jednego

strumienia gotówkowego, czyli z obligacji

strumienia gotówkowego, czyli z obligacji

zerokuponowej lub dyskontowej. Zbiór

zerokuponowej lub dyskontowej. Zbiór

natychmiastowych stóp procentowych S jest

natychmiastowych stóp procentowych S jest

to czasowa struktura stóp procentowych,

to czasowa struktura stóp procentowych,

inaczej nazywana w literaturze zerokuponową

inaczej nazywana w literaturze zerokuponową

krzywą dochodowości.

krzywą dochodowości.

3.1. STOPA

3.1. STOPA

SPOT

SPOT

RYNKU

RYNKU

KAPITAŁOWEGO

KAPITAŁOWEGO

Korzystając ze wzoru na wartość obligacji

Korzystając ze wzoru na wartość obligacji

traktowaną jako zbiór obligacji

traktowaną jako zbiór obligacji

zerokuponowych, można wyznaczyć stopę

zerokuponowych, można wyznaczyć stopę

spot dla obligacji o dowolnym czasie

spot dla obligacji o dowolnym czasie

trwania. Jeśli odsetki wypłacane są

trwania. Jeśli odsetki wypłacane są

raz w

raz w

roku

roku

:

:

3.1. STOPA

3.1. STOPA

SPOT

SPOT

RYNKU

RYNKU

KAPITAŁOWEGO

KAPITAŁOWEGO

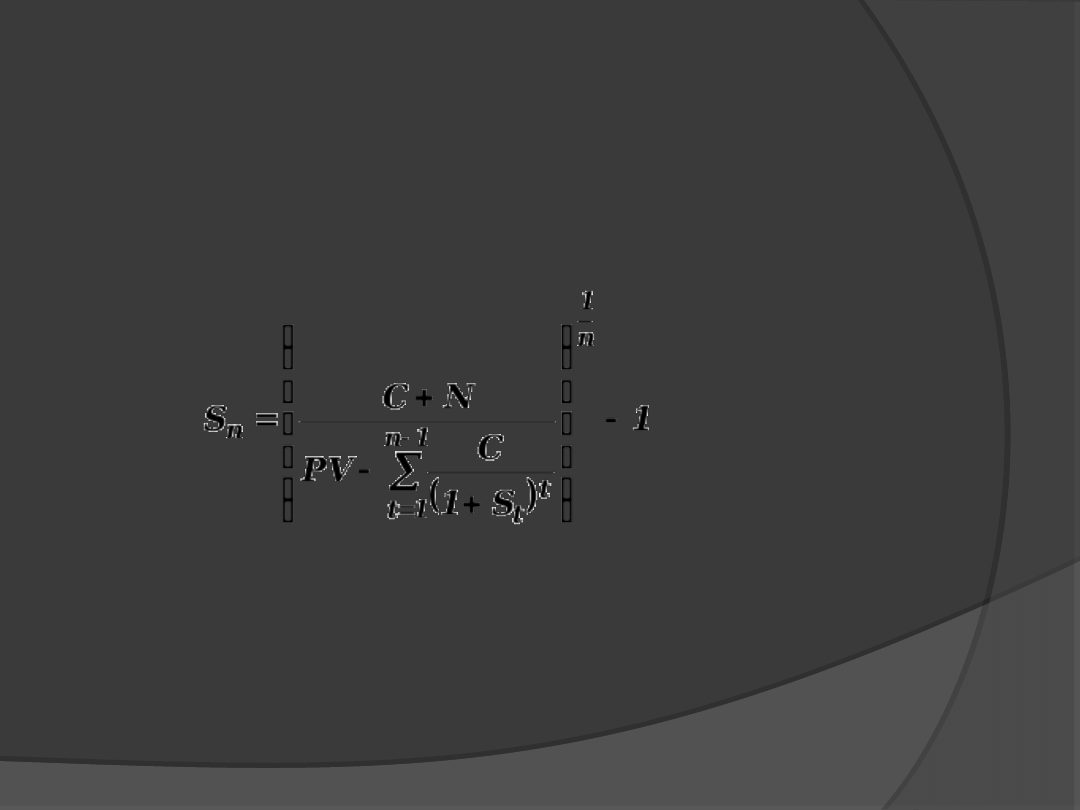
stąd:

stąd:

gdzie:
S

n

– stopa spot zerokuponowej obligacji n-
letniej

3.1. STOPA

3.1. STOPA

SPOT

SPOT

RYNKU

RYNKU

KAPITAŁOWEGO

KAPITAŁOWEGO

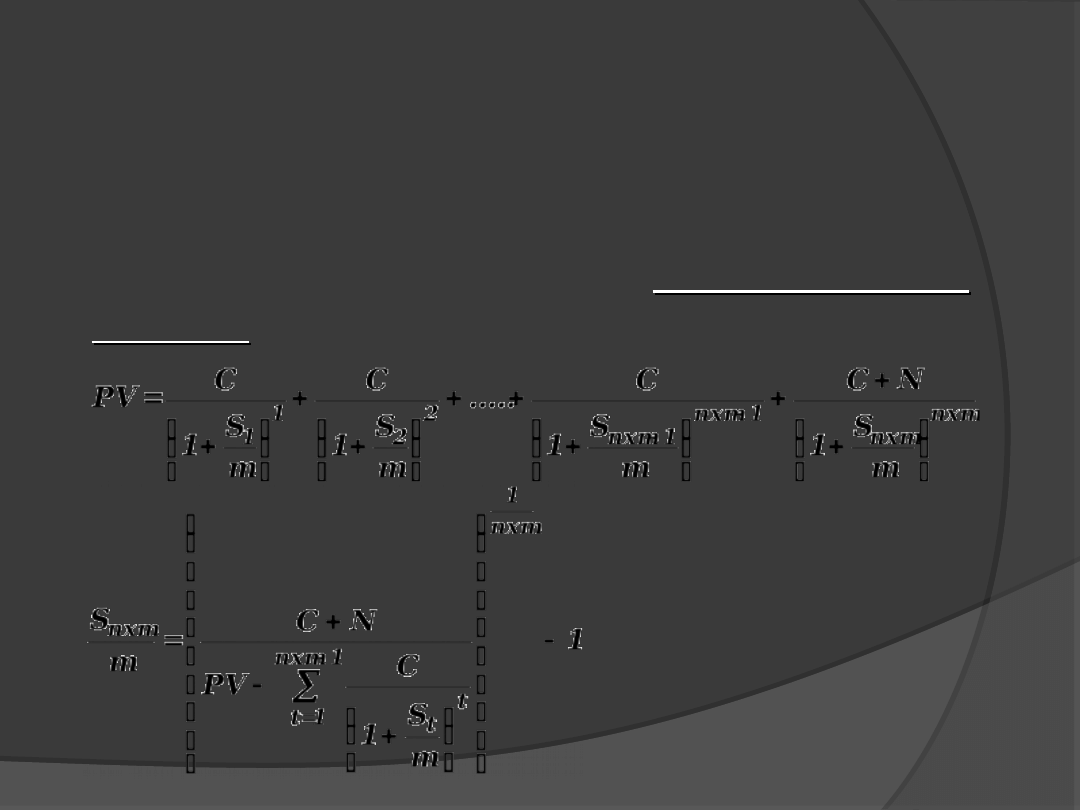
Jeśli odsetki wypłacane są

Jeśli odsetki wypłacane są

częściej niż raz

częściej niż raz

do roku

do roku

:

:

3.1. STOPA

3.1. STOPA

SPOT

SPOT

RYNKU

RYNKU

KAPITAŁOWEGO

KAPITAŁOWEGO

gdzie:
n

– liczba lat

m

– częstotliwość wypłat odsetek w ciągu roku
dla obligacji kuponowych

3.1. STOPA

3.1. STOPA

SPOT

SPOT

RYNKU

RYNKU

KAPITAŁOWEGO

KAPITAŁOWEGO

Stopa terminowa

Stopa terminowa

(F –

(F –

forward rate,

forward rate,

implied forward rate

implied forward rate

) to oczekiwana

) to oczekiwana

przyszła stopy zwrotu z obligacji.

przyszła stopy zwrotu z obligacji.

Określana pośrednio przy wykorzystaniu

Określana pośrednio przy wykorzystaniu

modelu teorii oczekiwań, bazującej na

modelu teorii oczekiwań, bazującej na

równaniach zachodzących dla tzw. punktu

równaniach zachodzących dla tzw. punktu

obojętności inwestora.

obojętności inwestora.

3.2. STOPA TERMINOWA

3.2. STOPA TERMINOWA

RYNKU KAPITAŁOWEGO

RYNKU KAPITAŁOWEGO

Związki bezpośrednie:

Związki bezpośrednie:

Stopy spot są średnią geometryczną stóp
terminowych (F).

3.3. ZWIĄZKI POMIĘDZY

3.3. ZWIĄZKI POMIĘDZY

STOPAMI

STOPAMI

SPOT

SPOT

I

I

TERMINOWYMI

TERMINOWYMI

RYNKU KAPITAŁOWEGO

RYNKU KAPITAŁOWEGO

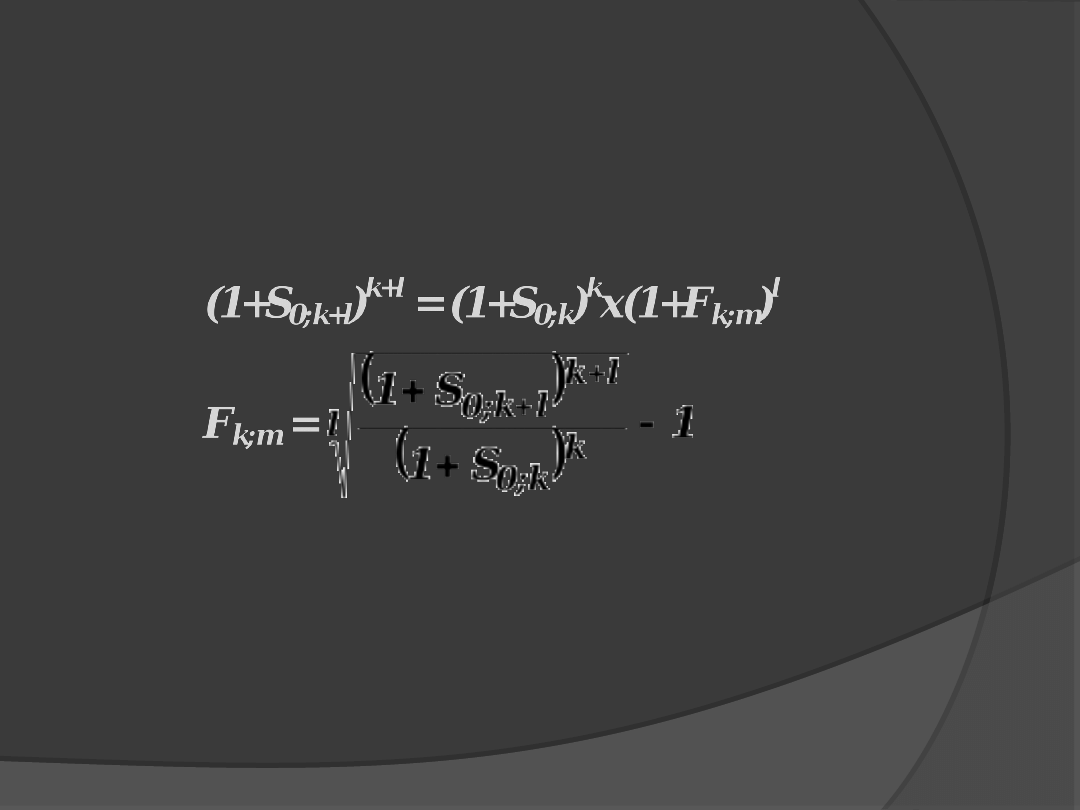
gdzie:
S

0,k+l

– stopa natychmiastowa zerokuponowej

obligacji o terminie wykupu k+l = m
S

0,k

– stopa natychmiastowa zerokuponowej

obligacji k-letniej
F

k,m

– stopa forward dla obligacji l letniej za k lat

3.3. ZWIĄZKI POMIĘDZY

3.3. ZWIĄZKI POMIĘDZY

STOPAMI

STOPAMI

SPOT

SPOT

I

I

TERMINOWYMI

TERMINOWYMI

RYNKU KAPITAŁOWEGO

RYNKU KAPITAŁOWEGO

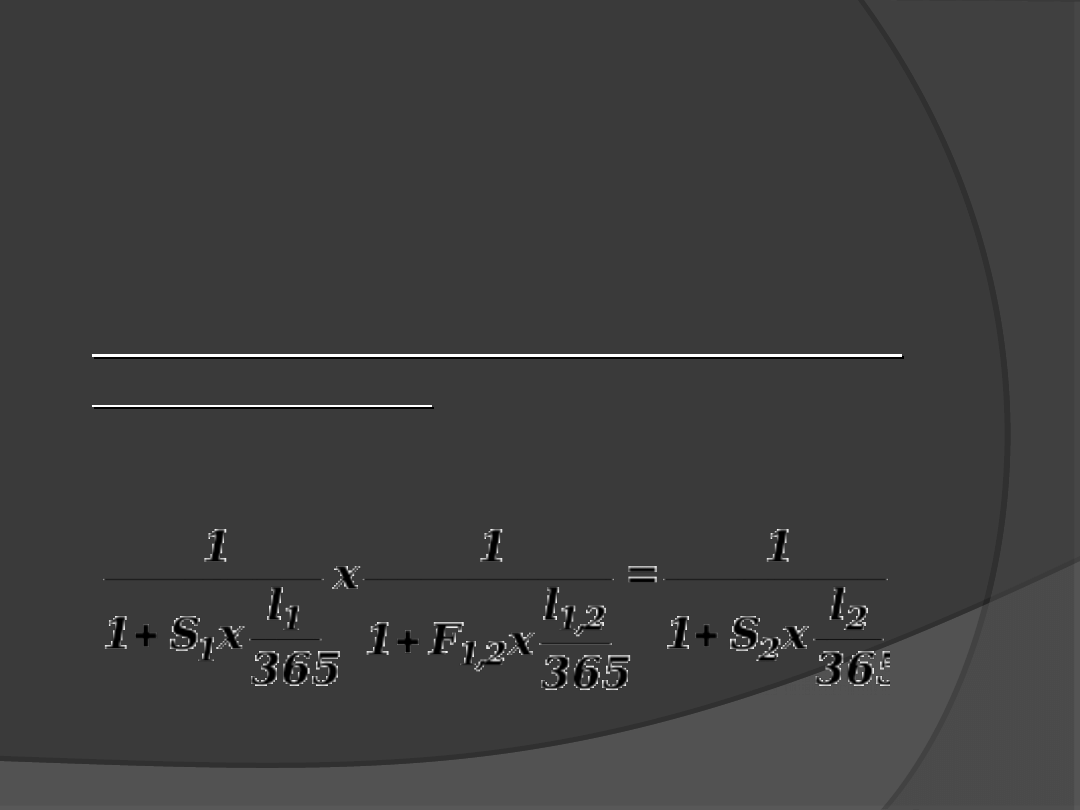
Związki opisane współczynnikami

Związki opisane współczynnikami

dyskontowymi

dyskontowymi

:

:

1. Instrumenty do roku (bez kapitalizacji):

1. Instrumenty do roku (bez kapitalizacji):

3.3. ZWIĄZKI POMIĘDZY

3.3. ZWIĄZKI POMIĘDZY

STOPAMI

STOPAMI

SPOT

SPOT

I

I

TERMINOWYMI

TERMINOWYMI

RYNKU KAPITAŁOWEGO

RYNKU KAPITAŁOWEGO

stąd:

stąd:

gdzie:
DF

t

– współczynnik dyskontowy dla strumienia w

okresie t

DF

t-1

– współczynnik dyskontowy dla strumienia w okresie t-1

F

t-1

,

t

– stopa terminowa dla okresu od t-1 do t

3.3. ZWIĄZKI POMIĘDZY

3.3. ZWIĄZKI POMIĘDZY

STOPAMI

STOPAMI

SPOT

SPOT

I

I

TERMINOWYMI

TERMINOWYMI

RYNKU KAPITAŁOWEGO

RYNKU KAPITAŁOWEGO

2. Instrumenty wieloletnie (z kapitalizacją

2. Instrumenty wieloletnie (z kapitalizacją

wewnątrzokresową)

wewnątrzokresową)

3.3. ZWIĄZKI POMIĘDZY

3.3. ZWIĄZKI POMIĘDZY

STOPAMI

STOPAMI

SPOT

SPOT

I

I

TERMINOWYMI

TERMINOWYMI

RYNKU KAPITAŁOWEGO

RYNKU KAPITAŁOWEGO

1. Przybliżona wartość YTM

1. Przybliżona wartość YTM

:

:



średnia ważona stóp terminowych (F

średnia ważona stóp terminowych (F

t

t

),

),

gdzie wagi to udziały wartości

gdzie wagi to udziały wartości

rynkowych

rynkowych

strumieni przepływów (DC

strumieni przepływów (DC

t

t

) w wartości

) w wartości

bieżącej obligacji (PV):

bieżącej obligacji (PV):

3.4. WARTOŚCI PRZYBLIŻONE

3.4. WARTOŚCI PRZYBLIŻONE

STÓP PROCENTOWYCH

STÓP PROCENTOWYCH



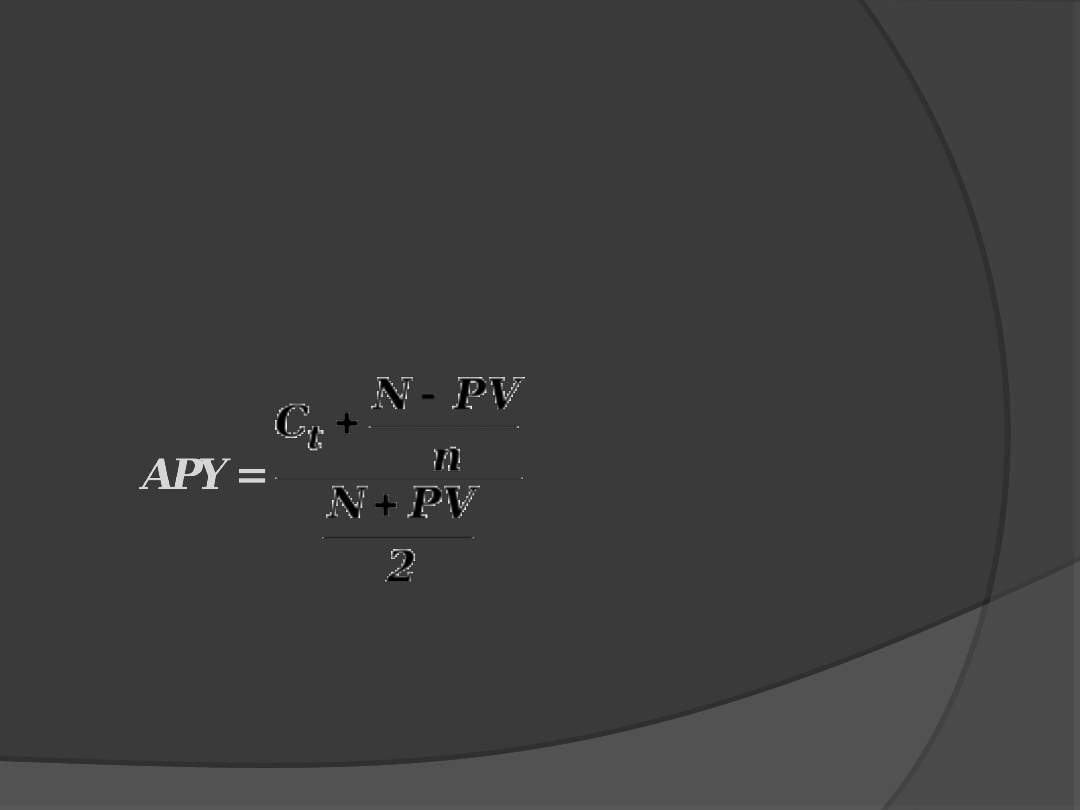
APY (

APY (

Approximate Promised Yield

Approximate Promised Yield

):

):

3.4. WARTOŚCI PRZYBLIŻONE

3.4. WARTOŚCI PRZYBLIŻONE

STÓP PROCENTOWYCH

STÓP PROCENTOWYCH

2. Przybliżona wartość stopy terminowej

2. Przybliżona wartość stopy terminowej

:

:

gdzie:
S

n

– natychmiastowa stopa procentowa dla okresu n
lat

S

k

– natychmiastowa stopę procentową dla okresu k
lat
gdzie n > k

F

k,n

– stopa terminowa dla okresu między n i k

3.4. WARTOŚCI PRZYBLIŻONE

3.4. WARTOŚCI PRZYBLIŻONE

STÓP PROCENTOWYCH

STÓP PROCENTOWYCH