Ćwiczenie VI. Podstawy algebry macierzy, cz. I

Strona internetowa ćwiczeń:

http://www.home.umk.pl/~henroz/matm1112

Dodatkowe materiały dydaktyczne:

1.

Ulrich W., 2009: Matrix algebra for students of biotechnology (for

students of the first year of master studies). Copyright © 2009 W.

Ulrich. http://www.home.umk.pl/~ulrichw/Matrix/Matrix1.pptx (11

października 2011).

2.

Ulrich W., 2007, 2008: Skrypt do matematyki, cz II (wektory i macierze) i

cz III (łańcuchy Markowa). Copyright © 2007-2008 W. Ulrich.

http://www.home.umk.pl/~ulrichw/MathStat/MathII.pdf

http://www.home.umk.pl/~ulrichw/MathStat/MathIII.pdf (11

października 2011).

3. Miszczyńska D., 2011a: Podstawy algebry liniowej (Matematyka –

materiały dydaktyczne). Copyright © 2011 D. Miszczyńska i Wyższa

Szkoła Ekonomiczno-Humanistyczna w Skierniewicach (Wydz.

Zarządzania).

http://wsehsk.home.pl/files/zarzadzanie/materialy/Podstawy_algebry_lini

owej.pdf (11 października 2011).

4. Miszczyńska D., 2011b: Wyznaczniki (Matematyka – materiały

dydaktyczne). Copyright © 2011 D. Miszczyńska i Wyższa Szkoła

Ekonomiczno-Humanistyczna w Skierniewicach (Wydz. Zarządzania).

http://wsehsk.home.pl/files/zarzadzanie/materialy/Wyznaczniki.pdf (11

października 2011).

5. Volpi L. & Foxes Team, 2007: Matrix Functions and Linear Algebra for Excel

(freeware). Copyright © 2007 L. Volpi.

http://digilander.libero.it/foxes/SoftwareDownload.htm (11 października

2011).

Biologiczne bazy danych

bardzo często mają charakter macierzy

. Np.

występowanie różnych organizmów żywych w różnych miejscach

(stanowiskach)

można zapisać w formie tabeli

, w której

gatunki będą

wierszami

, a

stanowiska – kolumnami

. Z matematycznego punktu

widzenia jest to

macierz prostokątna

, której zapis i definicja są

następujące:

Macierze, w których

m = n, nazywamy

kwadratowymi

,

gdzie

n – to stopień

macierzy

. Ponadto

mogą jeszcze być
macierze

diagonal-

ne

,

jednostkowe

(ang. „unity matrix”;
odpowiednik „1”
wśród liczb, ozn.

„I”),

zerowe

,

symetryczne

,

ortogonalne

,

górnotrójkątne

i

dolnotrójkątne

.

Źródło – poz. 3 z dodatkowych materiałów dydaktycznych

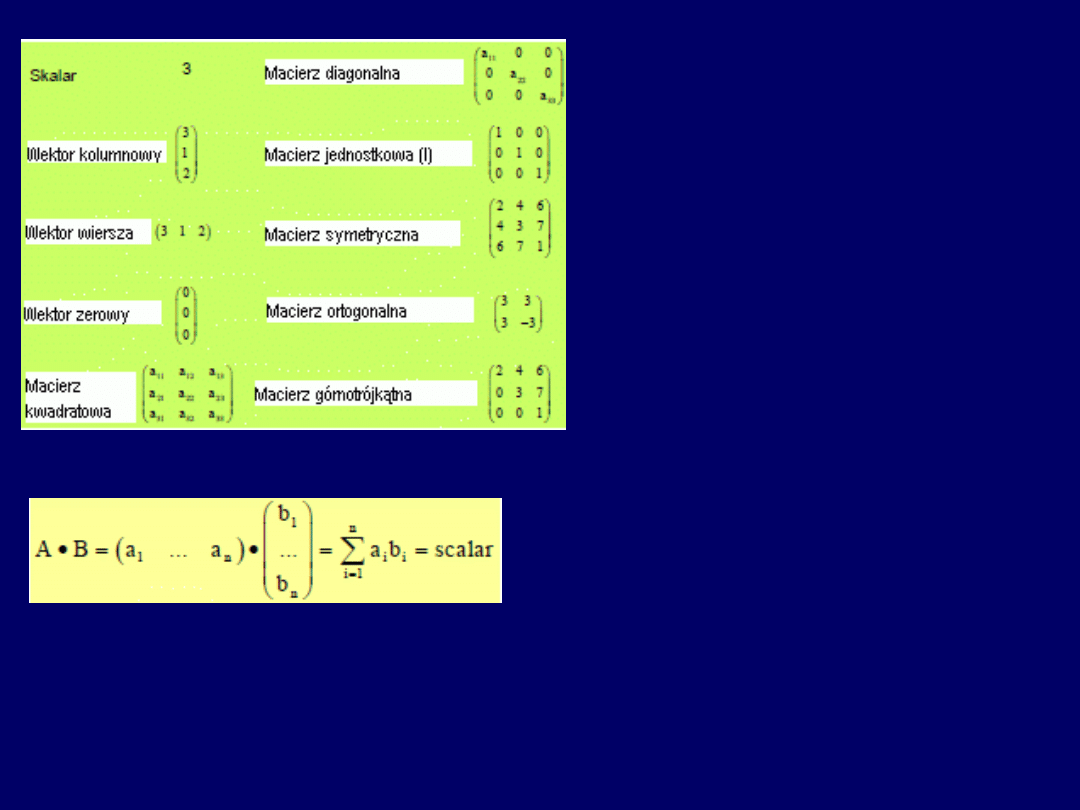
Przegląd podstawowych elementów macierzy i ich typów:

Liczby

, które np. mogą być

elementami macierzy, z mate-

matycznego punktu widzenia są

skalarami

,zaś

wiersze i kolumny

-

wektorami

. Znajomość alge-

bry macierzy, wymaga

podsta-

wowej znajomości algebry

wektorów

i praw/twierdzeń

związanych z nimi. Wektory
można

dodawać

,

odejmować

do/od siebie. Można je także

mnożyć

lub

dzielić

(mnożenie

przez odwrotność)

przez skalar

.

Możliwy jest także

iloczyn skalarny wektorów

, zgodnie z równaniem:

Tego typu iloczyn jest

zerowy

wtedy, gdy jeden z wektorów

jest zerowej długości lub wtedy,
gdy

mnożone wektory są prostopa-

dłe

, czyli ortogonalne. Istnieje

również inny typ iloczynu wektorów – tzw.

iloczyn wektorowy

, którego

wynikiem jest

inny wektor

– pod warunkiem, że wektory znajdują się nie

na płaszczyźnie, ale

w przestrzeni, co najmniej trójwymiarowej

. Mnożenie

wektorów jest

łączne

i

rozdzielne

.

Iloczyn

skalarny

jest

przemienny

, ale

wektorowy – nie

.

Dzielenie przez

wektor, nie jest możliwe

(brak jednoznacznego wyniku – nieskończenie

wiele rozwiązań).

W

biologii

(ekologia, genetyka, taksonomia) często spotykane są

kwadratowe macierze asocjacji

, które mogą być albo

macierzami

podobieństwa

(1 na przekątnej) lub

odległości

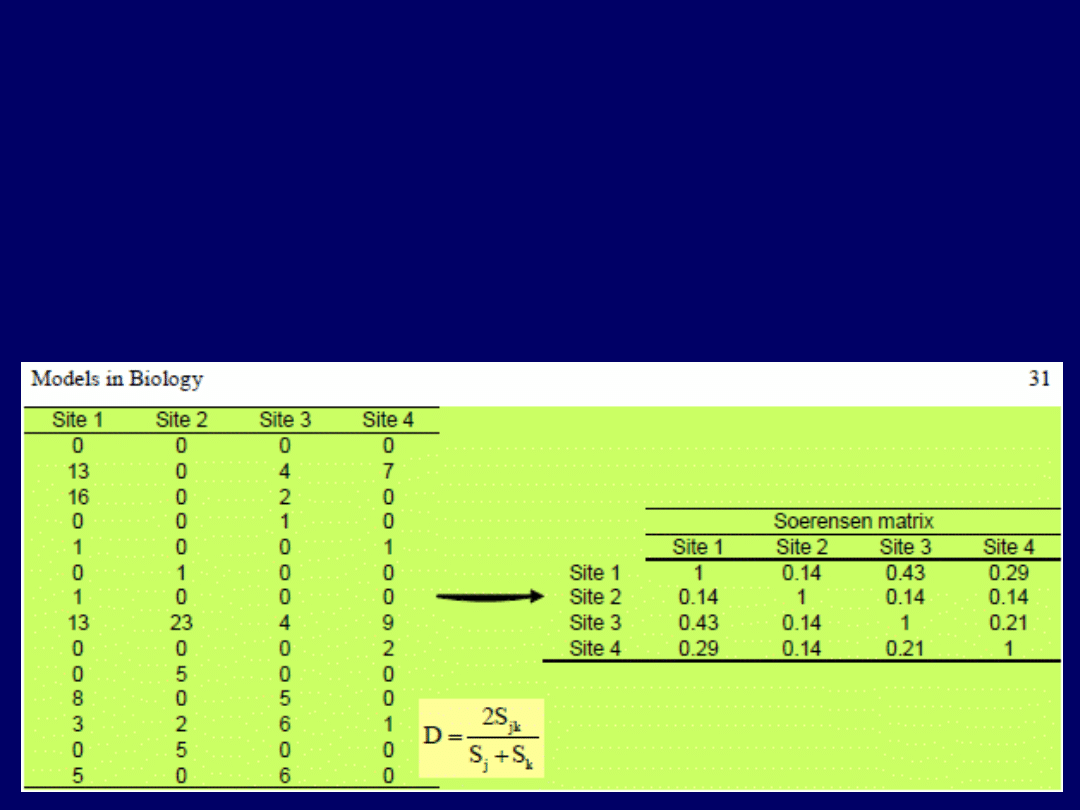
(0 na przekątnej). Miarami

podobieństwa mogą być współczynniki Soerensena lub Jackarda, a
odległości – odległość euklidesowa lub jej kwadrat (wykorzystanie w
praktyce: taksonomia numeryczna/analiza skupień). Przykład tworzenia
tego typu macierzy (ze skryptu):

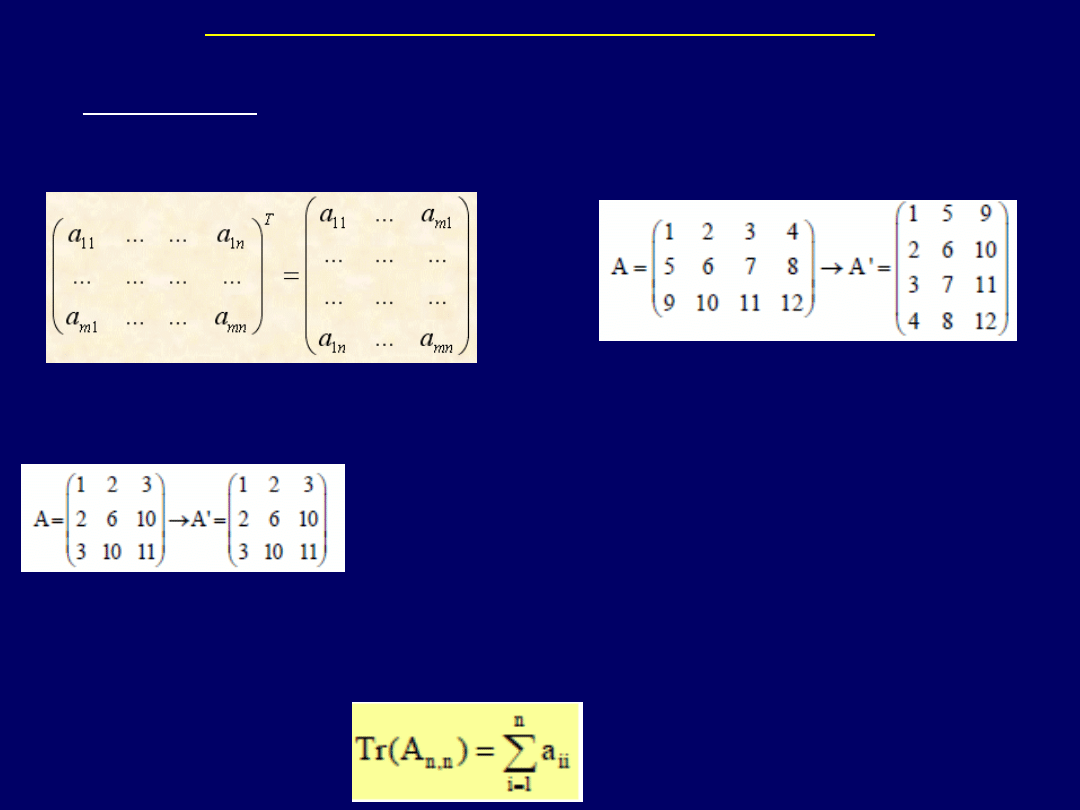
I. Podstawowe operacje i działania na macierzach

1.

Transpozycja (przestawienie) macierzy – polega na

zamianie jej wierszy

na kolumny, a kolumn – na wiersze

(transponowaną macierz A,

oznaczamy

A’

lub

A

T

).

Przykład:

W wyniku

transpozycji kwadratowej macierzy symetrycznej

, uzyskuje-my

macierz identyczną z wyjściową

:

Transpozycja macierzy ma własności:

(A

T

)

T

= A

(A + B)

T

= A

T

+ B

T

(A  B)

T

= B

T

 A

T

Suma wszystkich elementów na przekątnej

kwadratowej macierzy

symetrycznej, nazywana jest jej

śladem

(ang.: trace):

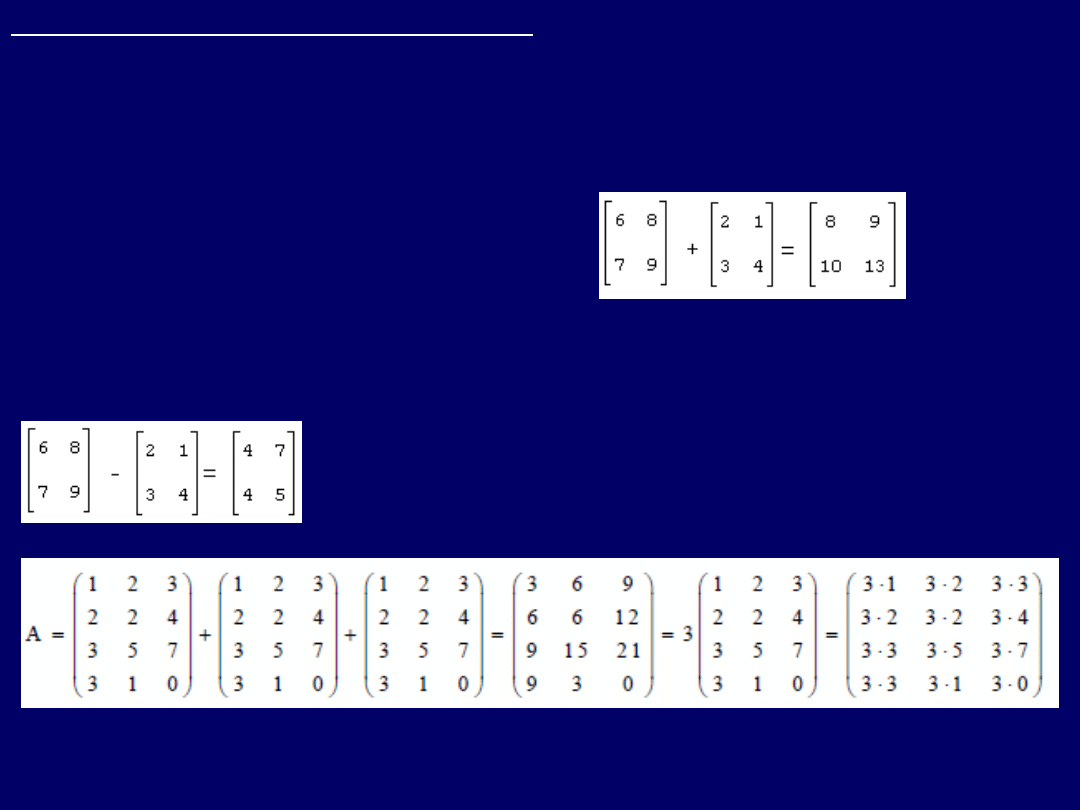
2. Dodawanie i odejmowanie macierzy

Sumą macierzy

A

mxn

i B

mxn

nazywamy taką macierz

C

mxn

(C = A + B),

że dla

każdej pary

wskaźników (i,j) zachodzi

równość

:

c

ij

= a

ij

+ b

ij

.

Stąd wniosek, że

można dodawać tylko macierze o takich samych wymiarach

(w przypadku macierzy kwadratowych – tego samego stopnia). Przykład
dodawania:
Dodawanie macierzy jest

przemien-

ne: A + B = B + A

i

łączne:

(A + B) + C = A + (B + C)

.

Odejmowanie macierzy

można potraktować, jako

dodawanie

elementów

macierzy

ze znakiem ujemnym/przeciwnym

. Przykład odejmowania

macierzy:

Powtarzane dodawanie

do siebie tej samej

macierzy, równoważne jest jej

przemnożeniu

przez skalar

, odpowiadający liczbie

powtarzanych operacji dodawania:

Mnożenie macierzy przez skalar jest przemienne, łączne i rozdzielne

względem dodawania

.

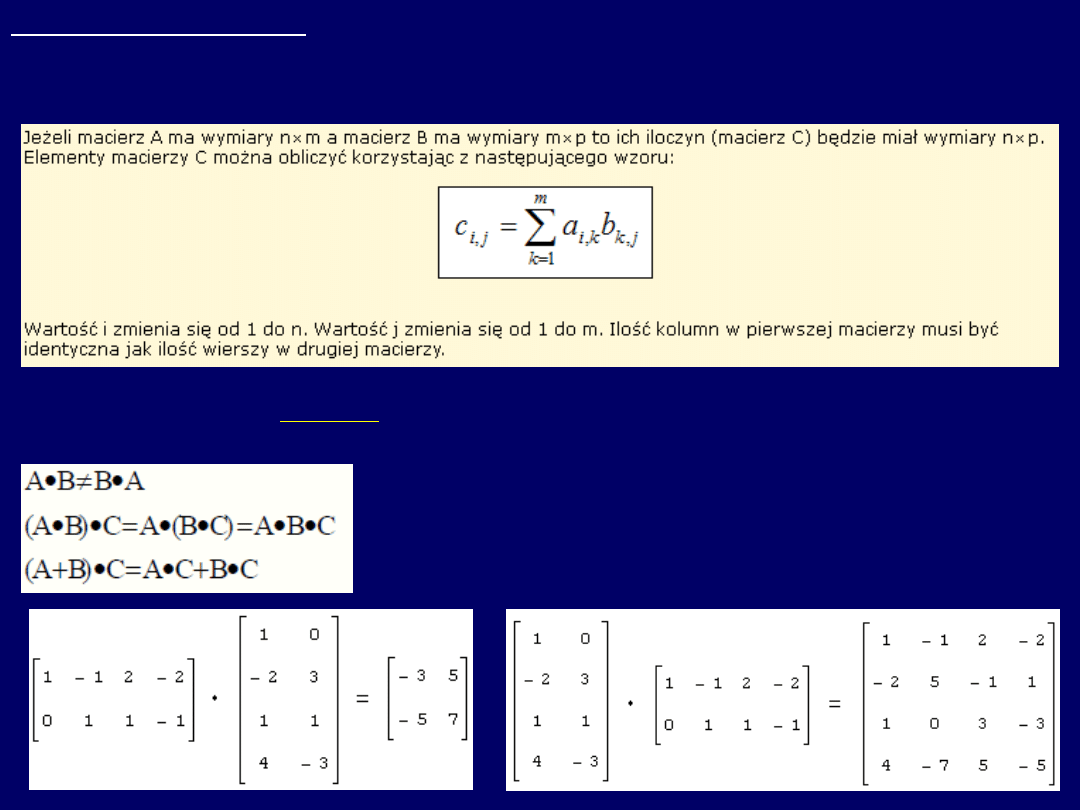
3. Mnożenie macierzy
Ogólny algorytm mnożenia przez siebie macierzy jest następujący (za

źródłem: http://www.bazywiedzy.com/mnozenie-macierzy.php ):

Mnożenie macierzy

nie jest przemienne

, jest

łączne

i

rozdzielne wzglę-dem

dodawania

:

Macierze można mnożyć  liczba kolu-

mn I-szej mac.=liczbie wierszy mac.II.

Przykład na

nieprzemienność

mnożenia

macierzy:

Nawet

mnożenie macierzy kwadratowych

najczęściej

nie jest przemienne

;

jeśli tak – to macierze nazywamy

przemiennymi

. Mnożenie macierzy

kwadratowej przez siebie, równoznaczne jest z podnoszeniem jej do
potęgi, np.:

A  A = A

2

i

A  A  A = A

3

.

Iloczyn macierzy diagonalnych jest

macierzą diagonalną

. Przykład na mnożenie macierzy – z rozpisaniem

wyników pośrednich:

4. Odwracanie macierzy
O ile macierze,

można dzielić przez skalar

(co jest traktowane jako mnożenie

– przez jego odwrotność), to

dzielenie macierzy przez macierz nie jest

możliwe

(podobnie, jak w przypadku wektorów: brak jednoznacznego

wyniku – nieskończenie wiele rozwiązań).

Macierze można odwracać

.

Odwracanie macierzy polega na

znajdowaniu macierzy odwrotnej

w

stosunku do danej. Jest ono możliwe tylko wtedy, gdy macierz jest

niesosobliwa

i gdy ma

nieze-rowy

wyznacznik

(patrz dalej). Macierz

kwadratową B = [b

ij

]

nxn

nazy-wamy

odwrotną

do macierzy kwadratowej A

= [a

ij

]

nxn

, jeśli spełniony jest warunek:

A  B = B  A = I

n

.

Macierz odwrotną

wobec A ozn. A

–1

.

Macierz osobliwa

, to taka macierz kwadratowa, która

nie daje się odwrócić

. W

macierzach osobliwych,

pewne wiersze lub kolumny można wyrazić jako

kombinacje liniowe innych kolumn/wierszy

. Takie kolumny wiersze

nie

zawierają unikalnej informacji

(są zbyteczne). Macierz 22, można

odwrócić zgodnie z równaniem:

Odwracanie większych macierzy jest kłopot-
liwe i w praktyce są tu pomocne programy
komputerowe. Przy analitycznym odwracaniu

macierzy, przydatna jest

znajomość jej wyznacznika

(patrz dalej). Jeżeli A

jest macierzą nieosobliwą, to:

(A

–1

)

T

=

(A

T

)

–1

oraz

(A

–1

)

–1

= A

. Jeżeli A i B są

nieosobliwymi macierzami tego samego stopnia, to:

(A  B)

–1

= B

–1

 A

–1

(kolejność jest tu istotna, gdyż zazwyczaj mnożenie macierzy jest
nieprzemienne). Macierz kwadratową A spełniającą warunek:

A

T

 A = A 

A

T

= I

, jest

macierzą ortogonalną

. Przykład odwracania macierzy:

Przykład macierzy osobliwej:

(inaczej: zdegenerowanej;
ang.: „singular”)

W podanym uprzednio przykładzie macierzy osobliwej, trzecia kolumna

powstała przez przemnożenie kolumny II-giej przez 4 – czyli

jest jej liniową

kombinacją

. Odwracanie macierzy można przeprowadzić zgodnie z

algorytmem Gaussa-Jordana (wykład, skrypt). Przy

odwra-caniu macierzy

diagonalnej

, uzyskujemy również

macierz diagonal-ną

, na przekątnej

której są odwrotności elementów macierzy wyjś-ciowej:

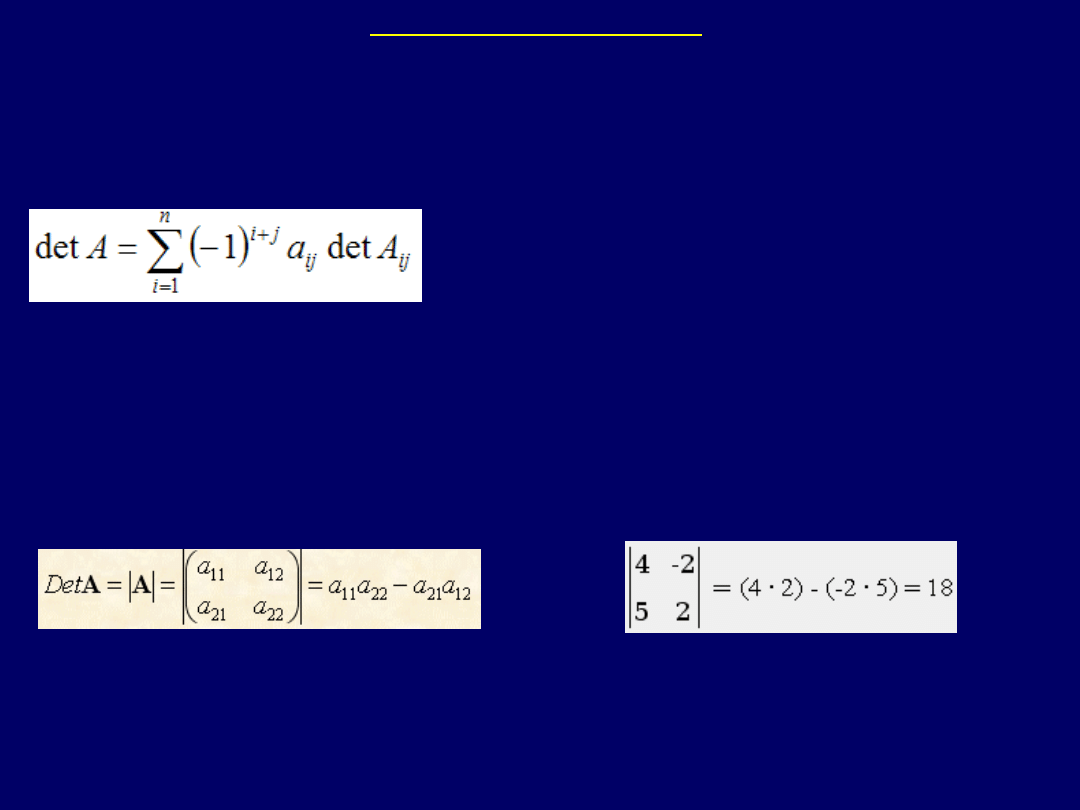
II. Wyznaczniki macierzy

Ważnym parametrem macierzy kwadratowych są ich

wyznaczniki

(dla

macierzy A

nxn

, wyznacznik zapisywany jest jako

det A

lub

|A|

). Dla

n = 1, wyznacznik jest równy jedynemu elementowi macierzy. Jeżeli
macierz A ma stopień n > 1, to jej wyznacznik można obliczyć
ze wzoru:

, gdzie

det A

ij

oznacza wyznacznik

powstały po skreśleniu i-tego wiersza
i j-tej kolumny wyjściowej macierzy
(czyli jej

minor

).

Dopełnieniem algebrai-

cznym

(D

ij

) elementu macierzy kwadratowej nazywamy

iloczyn jej minora

przez (–1)

i+j

. Wartość wyznacznika |A| stopnia n obliczamy ze wzoru:

|A| =

a

1j

D

1j

+ a

2j

D

2j

+…+ a

nj

D

nj

(j = 1, 2, 3,…n) lub

|A| = a

i1

D

i1

+ a

i2

D

i2

+…+ a

in

D

in

(i = 1, 2, 3,…n). Są to tzw.

wzory Laplace’a

na rozwinięcie wyznacznika

odpowiednio wg j-tej kolumny lub i-tego

wiersza. W praktyce, wyznacznik macierzy 22, można wyliczyć z

równania:

Przykład:

Dla

macierzy 33

, możemy zastosować tzw.

regułę Sarrusa

, gdzie po prawej

stronie macierzy dopisujemy jej I-sze 2 kolumny, a następnie tworzymy
iloczyny elementów macierzy ze znakami „+” wzdłuż strzałek czerwonych
i „–” – wzdłuż strzałek niebieskich:

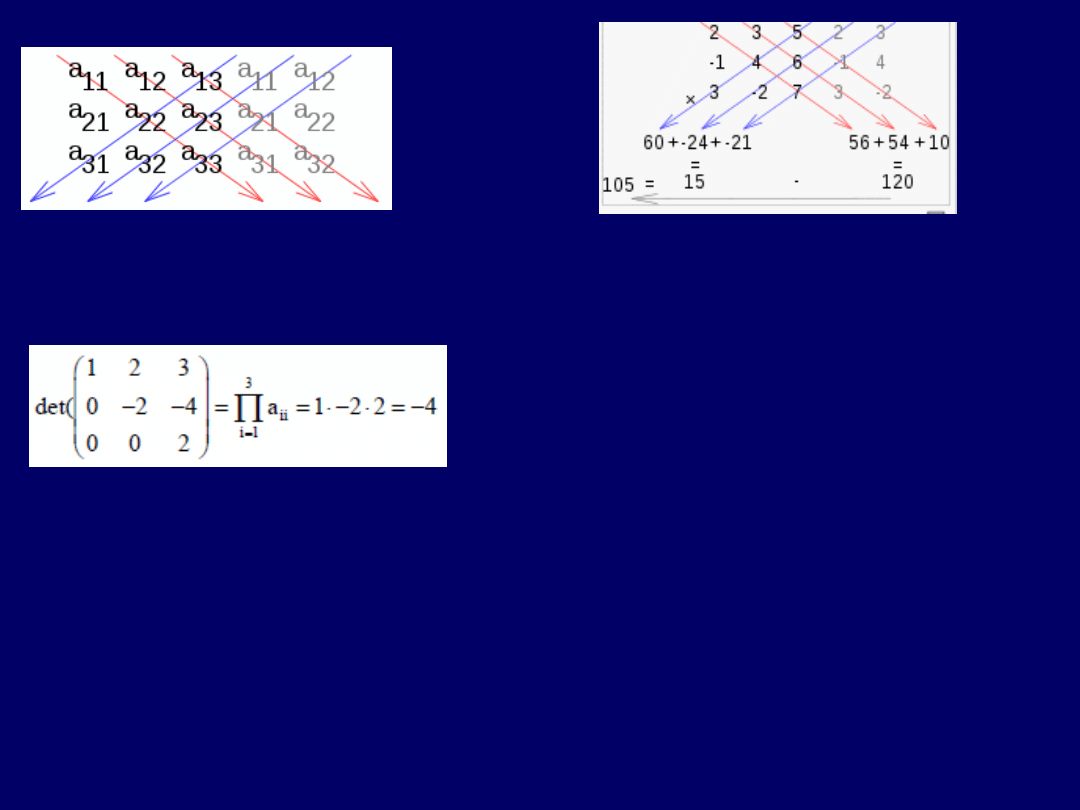
Ogólny schemat Sarrusa:

Przykład:

Współcześnie,

wyznaczniki macierzy większych niż 33, wyliczane są za

pomocą programów komputerowych

.

Wyznacznik macierzy trój-kątnej

(tak

górnej, jak i dolnej), jest

iloczynem elementów jej prze-kątnej głównej

:

Podstawowe własności wyznaczników:

1. Wyznacznik transpozycji macierzy,
równy jest wyz. macierzy wyjściowej:

det A

T

= det A

;

2. Jeżeli 1 z wierszy (lub kolumn) macierzy

A składa się

z samych zer

, to

det A = 0

;

3. Jeżeli zamienimy miejscami 2 wiersze (lub 2 kolumny), to

wyzna- cznik

zmieni znak na przeciwny

;

4. Jeżeli do elementów jednego wiersza (lub kolumny) dodamy odpo-wiednie

elementy innego wiersza (lub kolumny) pomnożone przez pewną stałą, to

wartość wyznacznika nie zmieni się

;

5.

det (AB) = det A  det B

;

6. Jeżeli w macierzy A 2 wiersze (lub 2 kolumny) są

identyczne

,to

|A|=0

.

Zależność pomiędzy wyznacznikiem a odwracaniem macierzy

:

Z definicji macierzy odwrotnej – dla odwracalnych macierzy:

AA

–1

= I

. Można

to rozpisać:

Wniosek:

macierz jest odwracal-

na  ma niezerowy wyznacznik

.

Tylko wtedy nie jest ona osobli-
wa. Dla każdej

macierzy osobli-

wej, |A| = 0

.

Wyznacznik można też wykorzystać przy analitycznym odwracaniu ma-cierzy:

Dopełnienie algebraiczne elemen-

tu a

ij

macierzy A liczymy:

d

ij

= (–1)

i+j

 M

ij

, gdzie

M

ij

jest mi-

norem macierzy A

, czyli wyznacz-

nikiem podmacierzy powstałej po
skreśleniu i-tego wiersza i j-tej
kolumny z wyjściowej macierzy A.

Transponowana macierz dopeł-nień

algebraicznych

, nazywana jest też

macierzą dodaną

(A

D

, ang: „adjoint

matrix”):

A

D

= [d

ij

]

T

.

Wyznaczniki, są ważne przy

rozwiązywaniu układów równań liniowych

oraz

przy

wyznaczaniu rzędu macierzy

.

III. Rząd macierzy

Rząd macierzy A (rzA) o wymiarach mn jest to

maksymalna liczba

niezależnych liniowo kolumn/wierszy

lub jest

stopniem najwiekszej

kwadratowej podmacierzy nieosobliwej

, zawartej w A. Dla macierzy

prostokątnej o wymiarach mn,

rzA  min (m, n)

.

Minorem

(podwyznacznikiem) stopnia k macierzy A

(o wymiarach mn),

nazywamy

wyznacznik macierzy kwadratowej stopnia k, która powstała

po skreśleniu m – k wierszy oraz n – k kolumn

w macierzy A

. Rzędem macierzy niezerowej nazywamy

największy

stopień jej niezerowego minora

. Rząd macierzy nie ulega zmianie, gdy:

a.

wykreślimy kolumnę (wiersz) zerową;

b. --------”------------ wszystkie kolumny (wiersze) proporcjonalne do danej

kolumny (wiersza);

c. Przestawimy kolumny (wiersze);
d.

Dodamy do kolumny (wiersza) inną kolumnę (wiersz) lub sumę in-nych

kolumn (wierszy) pomnożonych przez współczynniki rzeczy-wiste.

Podstawowe własności rzędu macierzy:
1.

rzA  min (m, n)

.

2.

rzA = 0  A = 0

(tj. A jest macierzą zerową).

3. Macierz kwadratowa jest

odwracalna  jej rząd = jej stopniowi

.

4. Jeżeli B jest macierzą prostokątną o wymiarach nk rzędu n, to

rz(AB) = rzA

. Podobnie jeśli C jest macierzą o wymiarach lm rzędu m,

to

rz(CA) = rzA

.

5. Dla macierzy kwadratowych A i B stopnia n, zachodzi nierówność:

rzA + rzB – n  rz(AB)

(nierówność Sylvestera).

6. Jeżeli B jest macierzą o wymiarach o wymiarach mn, to:

rz(A + B)  rzA + rzB

.

7.

rzA

T

= rzA

, czyli transpozycja nie zmienia rzędu.

Rząd macierzy można oszacować

wyliczając wyznaczniki pod-

macierzy kwadratowych, pozostających po wykreśleniu kolejnych wierszy i
kolumn

(jeśli wyznacznik jest niezerowy, to rząd macierzy wyjściowej jest

równy stopniowi podmacierzy, której wyznacznik wyliczono). Postępowanie
takie jest bardzo żmudne i obecnie rząd macierzy wylicza się

korzystając z

programów komputerowych

(patrz – ostatnie zadanie w praktycznej części

ćwiczenia). Znajo-mość rzędu macierzy jest niezbędna przy

rozwiązywaniu

układów równań liniowych z wykorzystaniem algebry macierzy

.

Wskazówki do wykonania zadań praktycznych ćw. VI.

• Wskazówki do zadania 1:

Licząc

iloczyn skalarny wektorów

: [1 2 3 4] i , mnożymy I-szy wyraz (liczbę)

z wektora poziomego z I-szym – z wektora pionowego. Analo-gicznie –
mnożymy: II z II, III z III i IV z IV.

Uzyskane iloczyny – sumu-jemy

:

[1 2 3 4]  = 1  5 + 2  6 + 3  7 + 4  8 = 5 + 12 + 21 + 32 =

70

Chcąc wyliczyć to samo, stosując program on-line – po otwarciu

wskazanej witryny internetowej, uzyskujemy następujący ekran
(następne przeźrocze):

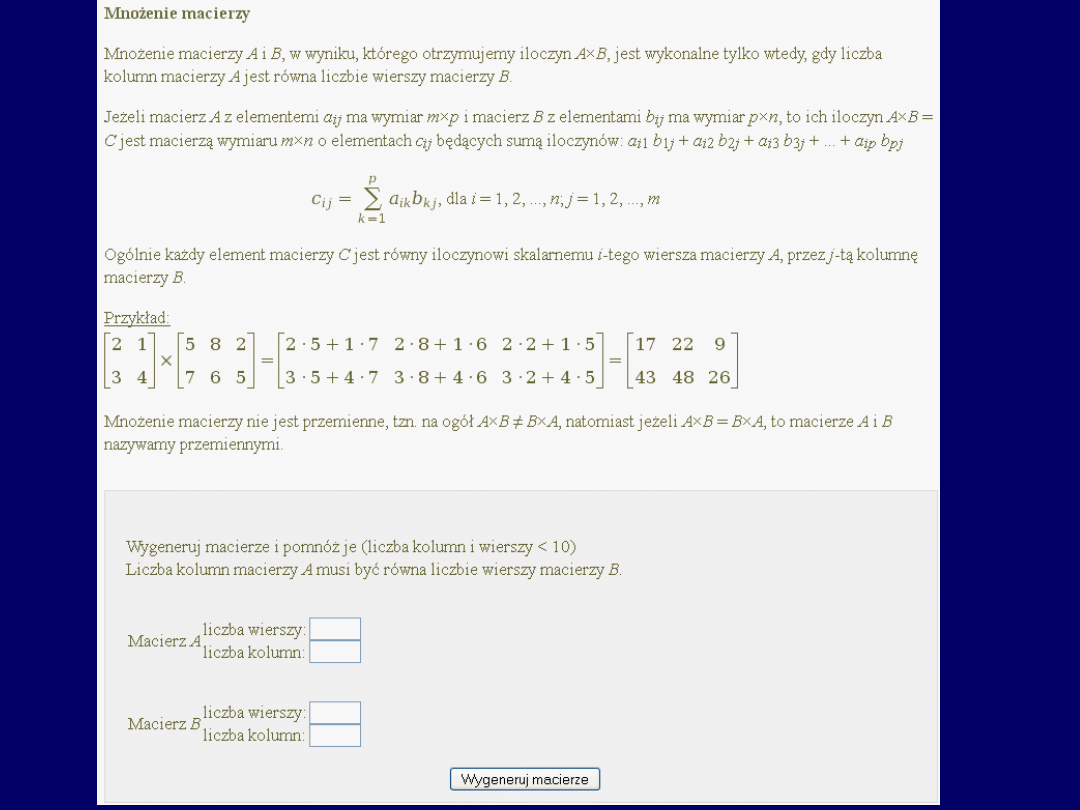
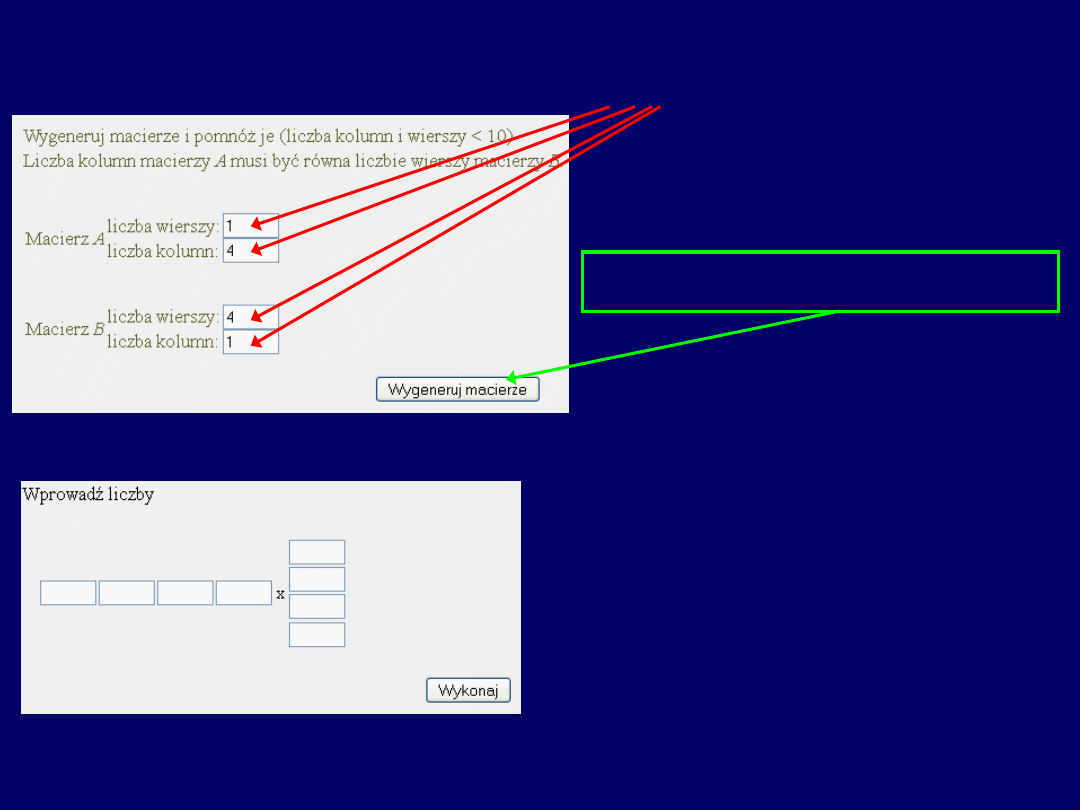
Traktując mnożone przez siebie wektory, jako szczególne przypadki macierzy

(

pierwsza: 1  4, druga: 4  1

), należy wskazać

liczbę kolumn i wierszy w

odpowiednich polach

:

Następnie klikamy w przycisk:

Uzyskujemy wektory/macierze:

z polami do wprowadzania liczb:

Po wprowadzeniu liczb,
otrzymujemy (następne
przeźrocze):

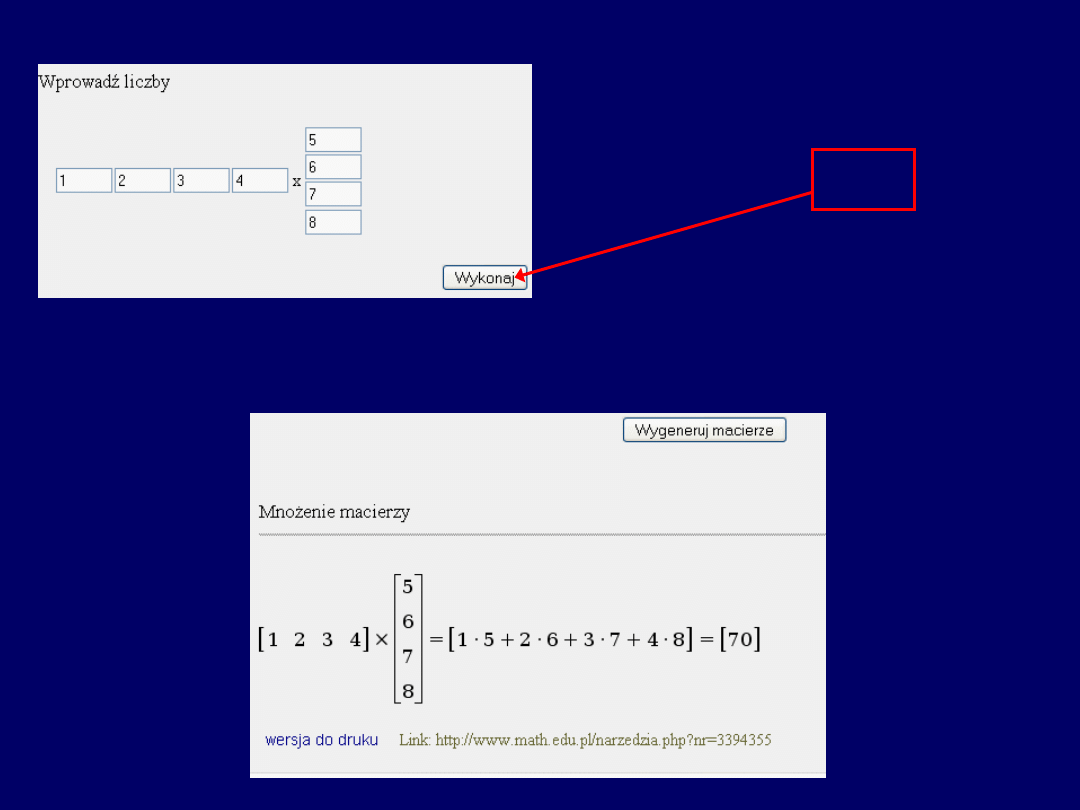
…gotowe do mnożenia (wypełnione liczbami) wektory/macierze:

Dalej – klikamy w przycisk:
„Wykonaj”

Klik

.....i uzyskujemy wynik:

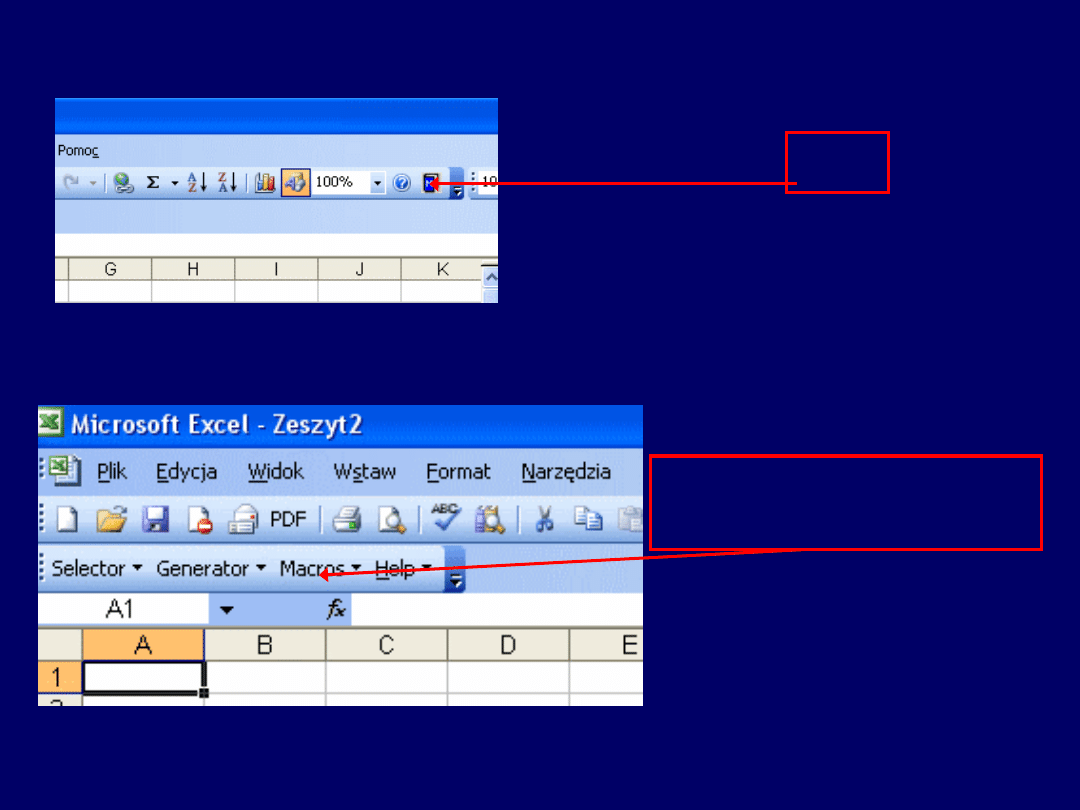
W celu uruchomienia rozszerzenia MS Excel 2003 („Matrix Functions and

Linear Algebra”), należy kliknąć w odpowiednią ikonę MS Excel:

Klik

Ukazuje się zestaw menu
rozszerzenia:

Klikamy w celu otwarcia
w menu „Macros”

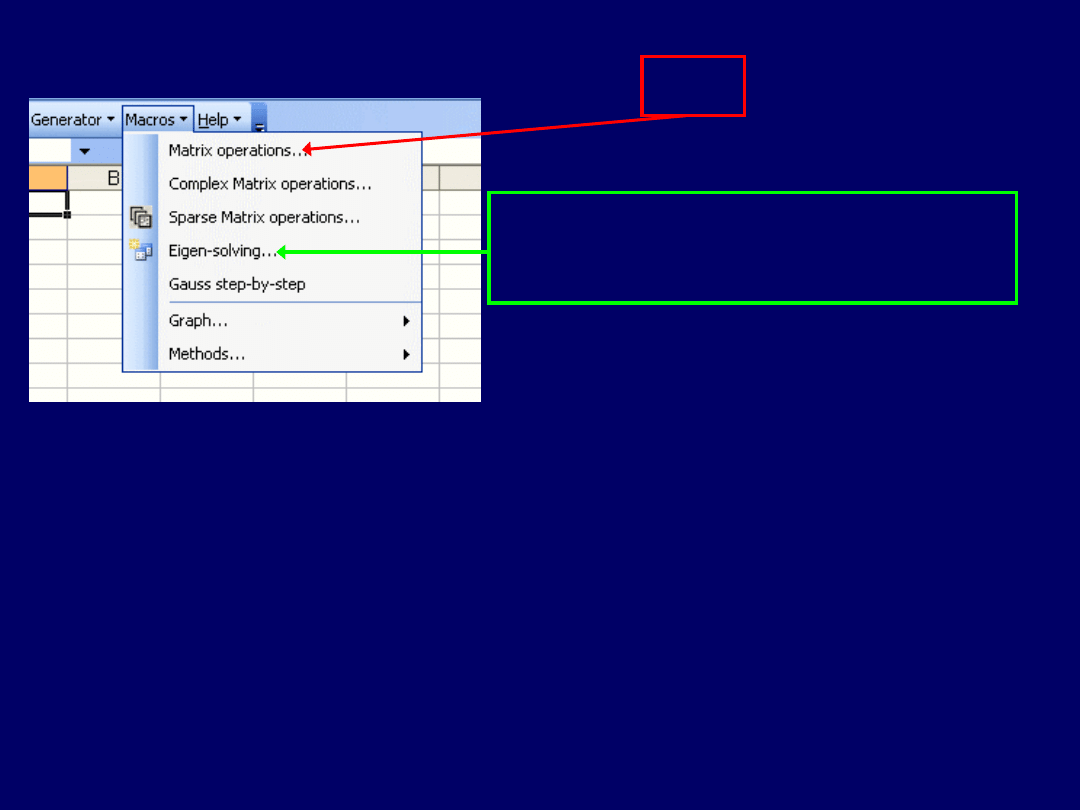
Spośród komend menu „Macros”, na niniejszym ćwiczeniu potrzebna będzie

komenda „Matrix operations…”

Klik

Na ćwiczeniu kolejnym, użyteczna
będzie też komenda:
„Eigen-solving…”:

Po wprowadzeniu do roboczego arkusza Excela odpowiednich
wektorów/macierzy, uruchamiamy: Matrix  Matrix operations. Dalej –

wybieramy „Multiplication” (następne przeźrocze):

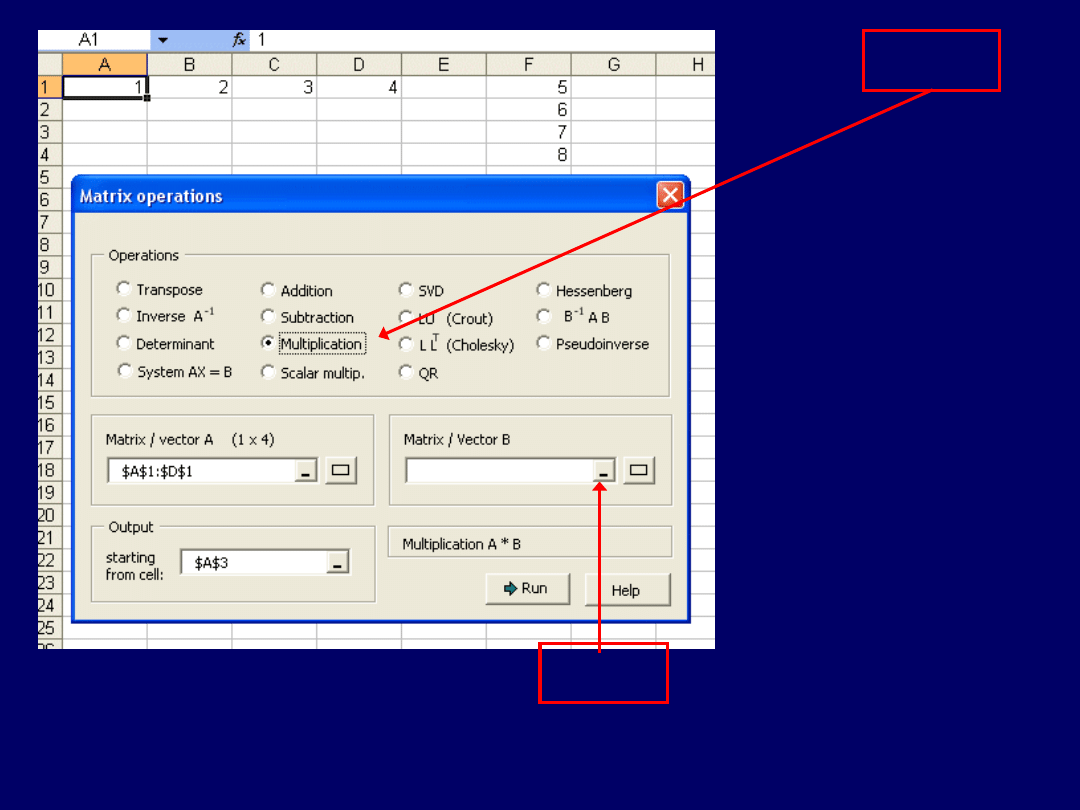
Klik (1)

Wreszcie klikamy w
suwak pola wyboru
drugiej macierzy /
wektora: „Matrix /
Vector B” (pierwsza
macierz/wektor –
„Matrix / Vector A”,
jak również zakres
pola wyników –

Klik (2)

„Output, są już

wybrane)

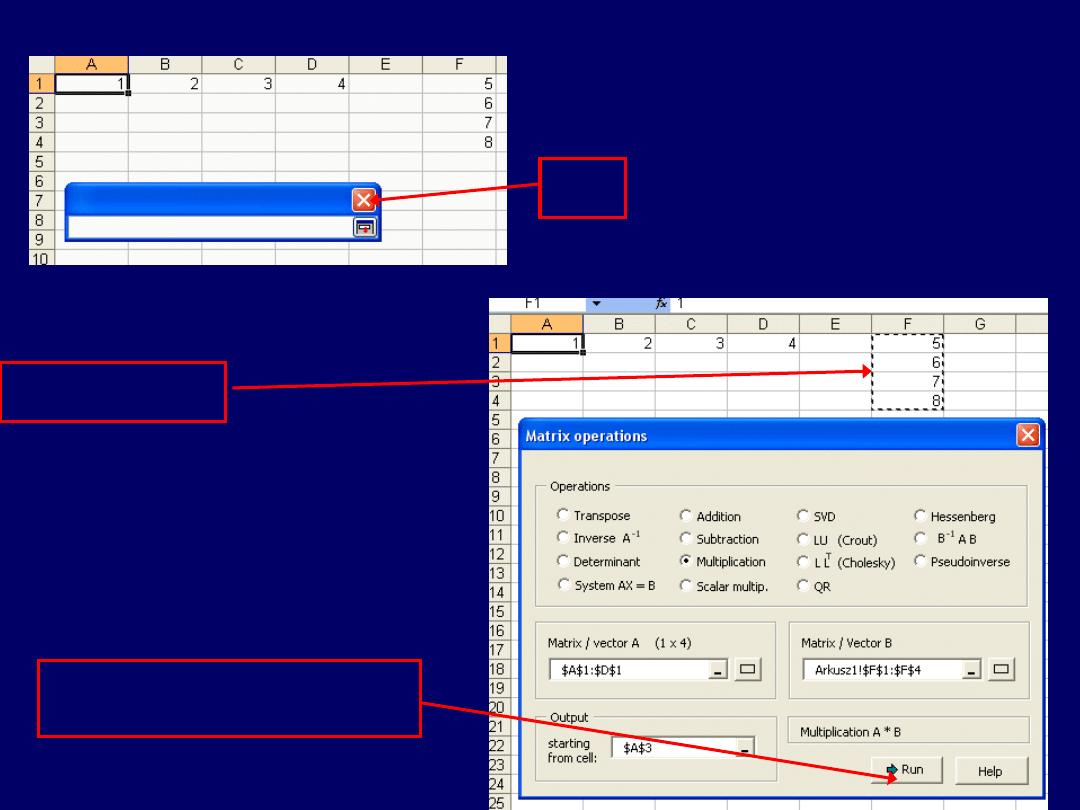
…pojawia się okienko:

…które zamykamy (o ile nie
zamknie się samo) i wybie-
ramy blok z II-gim
wektorem/macierzą.

Klik

Ekran po wyborze:

Wybrany blok:

Dalej klikamy w przycisk
„Run”

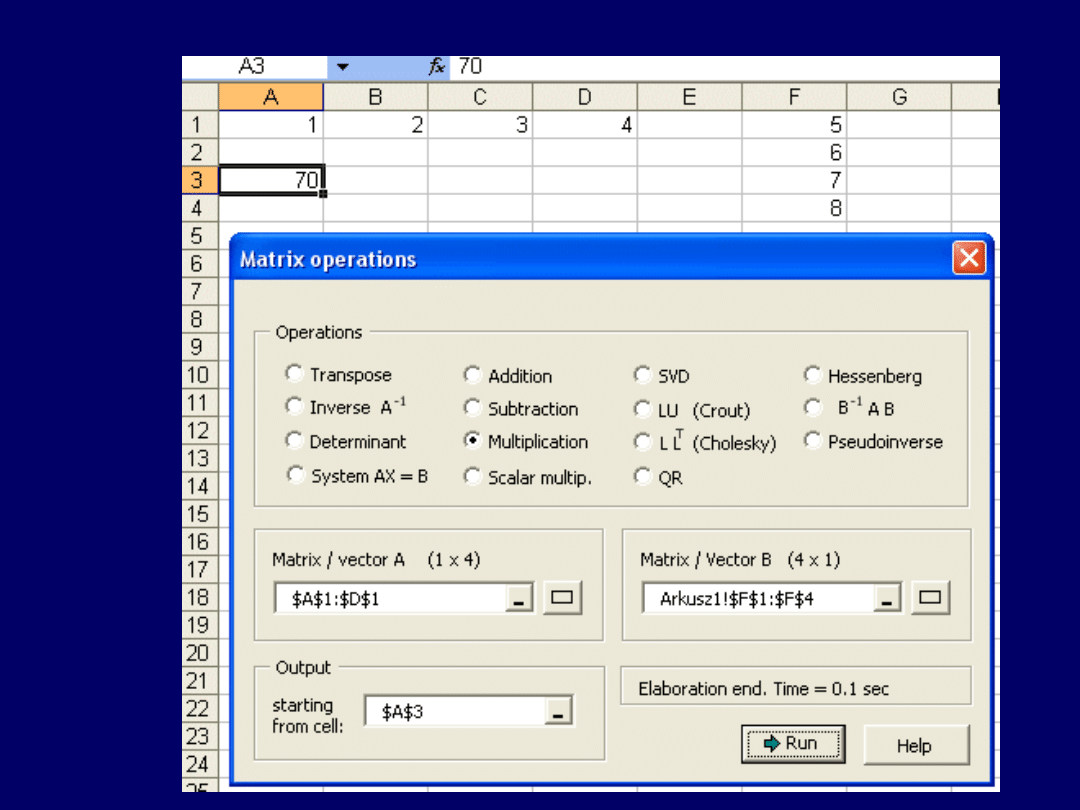
Uzyskujemy wynik:

Wskazówki do zadania 2:

Czynności mnożenia, zarówno za pomocą

programu on-line

, jak

i dodatku do MS Excel: „

Matrix Functions and Linear Algebra

” –

wykonujemy

analogicznie

, jak w zadaniu poprzednim. Końcowy wynik

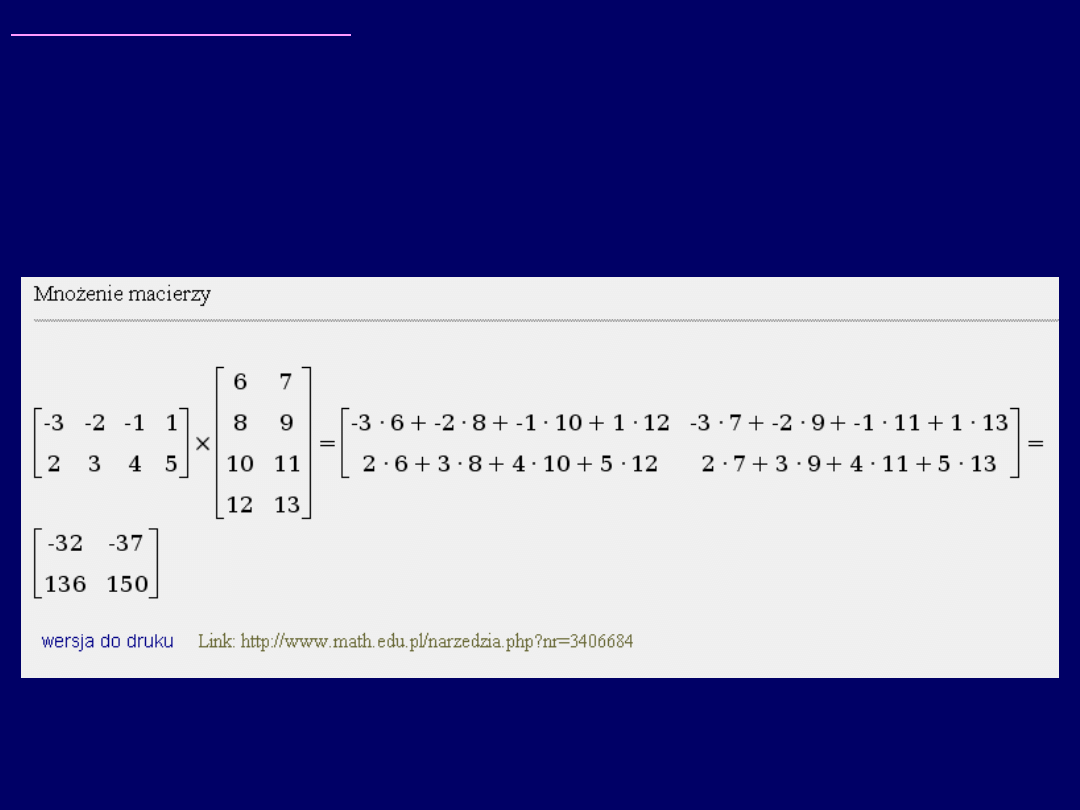
mnożenia wymienionych w zadaniu macierzy (AB),

w programie on-line – wygląda

następująco

:

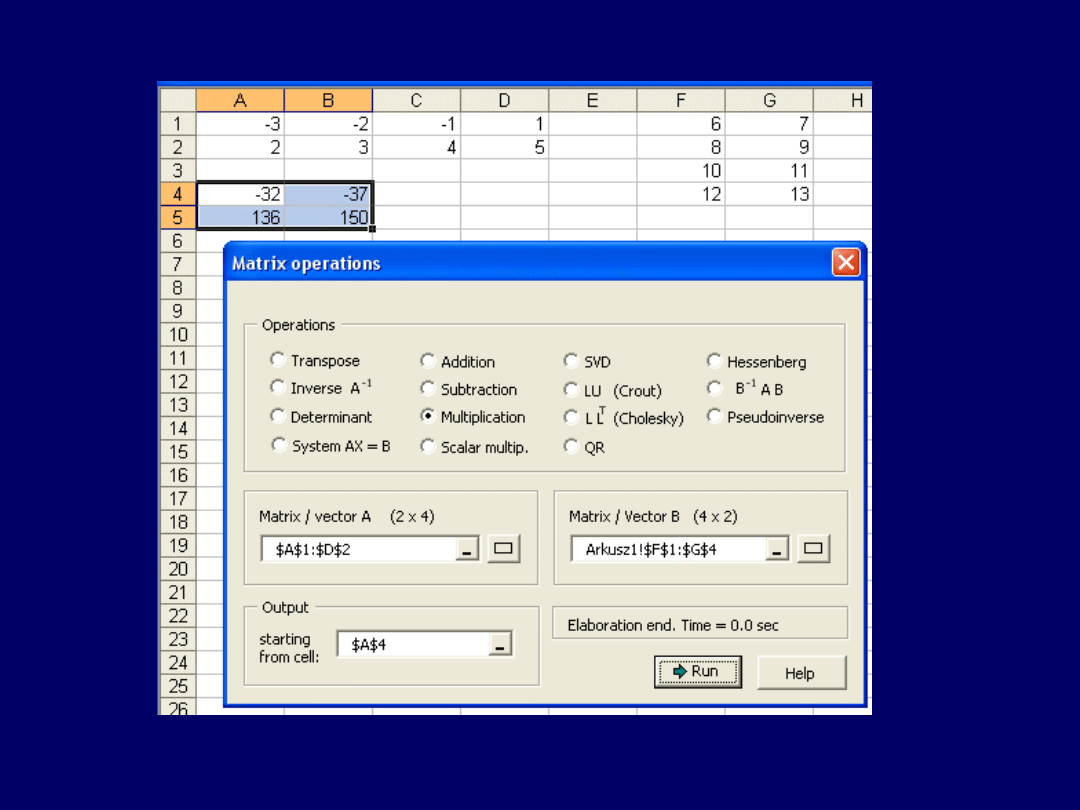
Ostateczny wynik mnożenia tych samych macierzy w MS Excel + „Matrix

Functions and Linear Algebra”:

Wyniki są identyczne – niezależnie od programu użytego do liczenia.

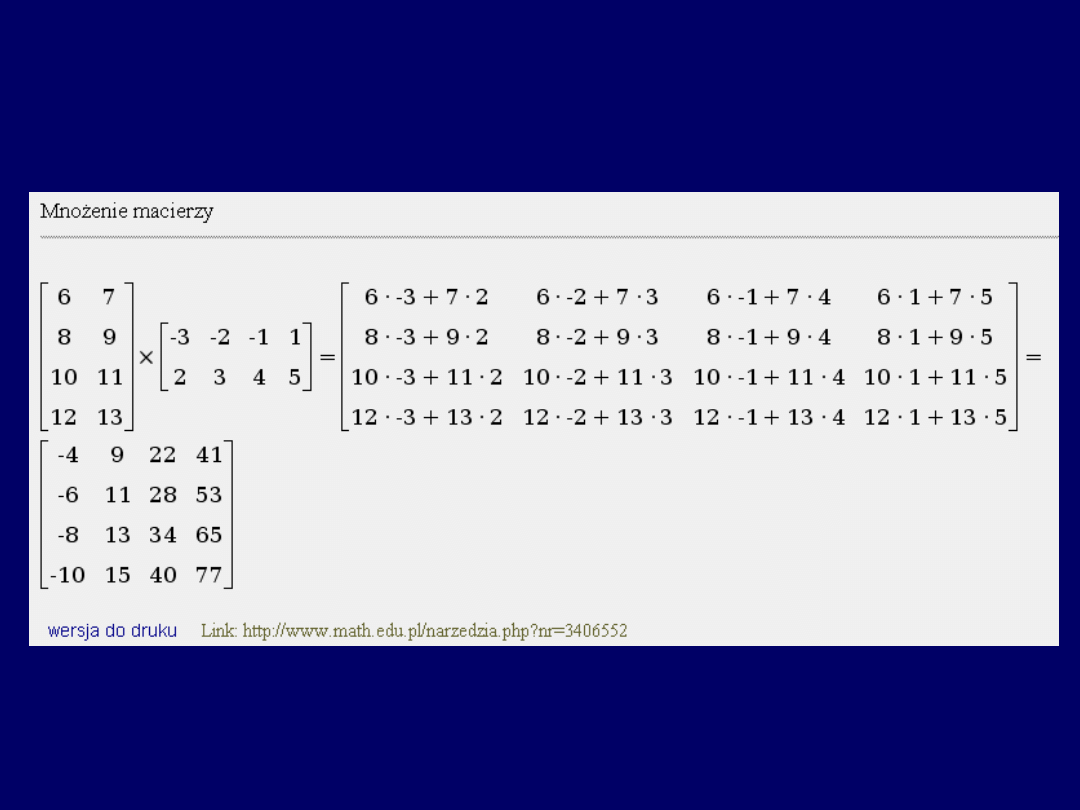
Wyniki mnożenia macierzy w odwróconej kolejności (BA), są odmienne.

Licząc w programie on-line, uzyskujemy:

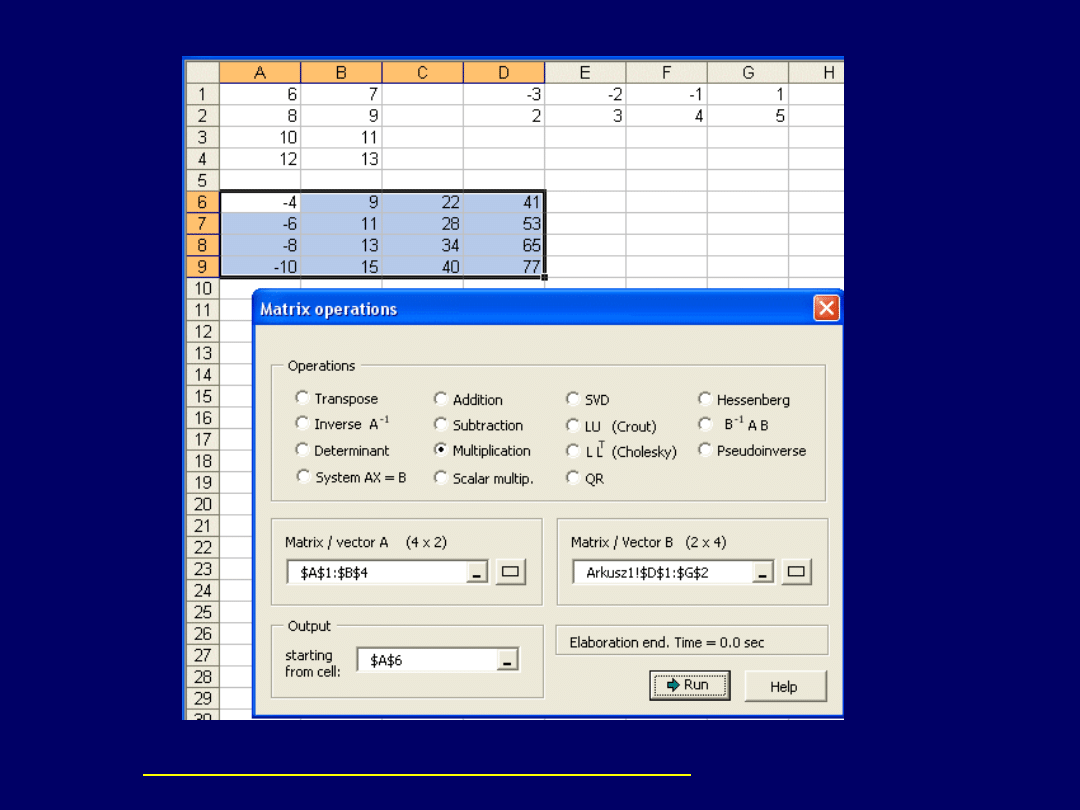
W MS Excel + „Matrix Functions and Linear Algebra”:

Wniosek:

mnożenie macierzy nie jest przemienne.

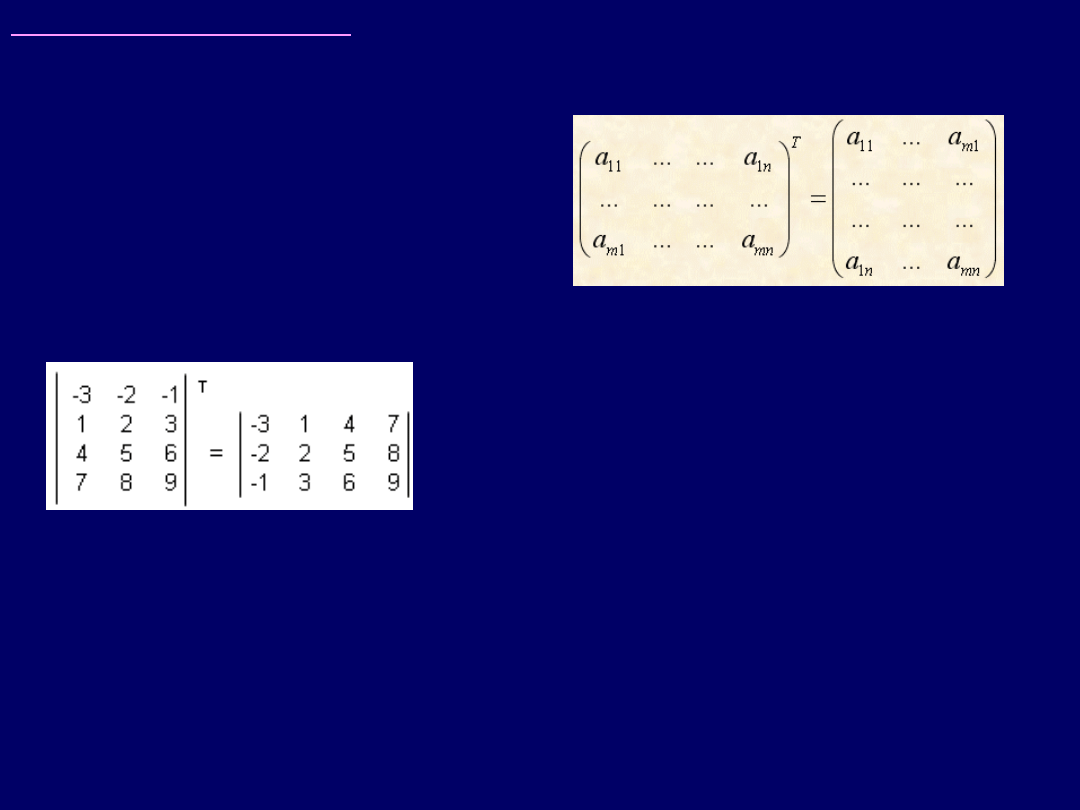
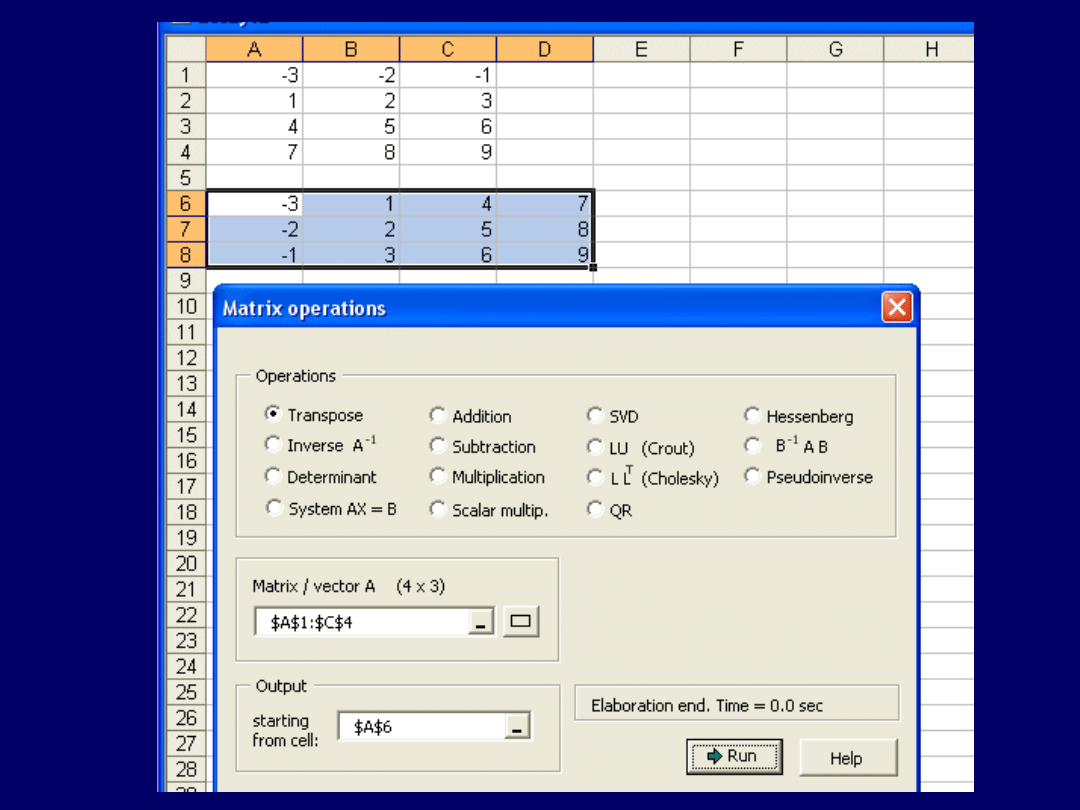
Wskazówki do zadania 3:

Operacja transpozycji macierzy polega na takim jej przekształceniu, aby

wiersze stały się kolumnami

:

W rozpatrywanej na ćwiczeniu
macierzy:

To samo zadanie, wykonane za pomocą MS Excel + „Matrix Functions and
Linear Algebra” – wyniki zgodne! (następne przeźrocze):

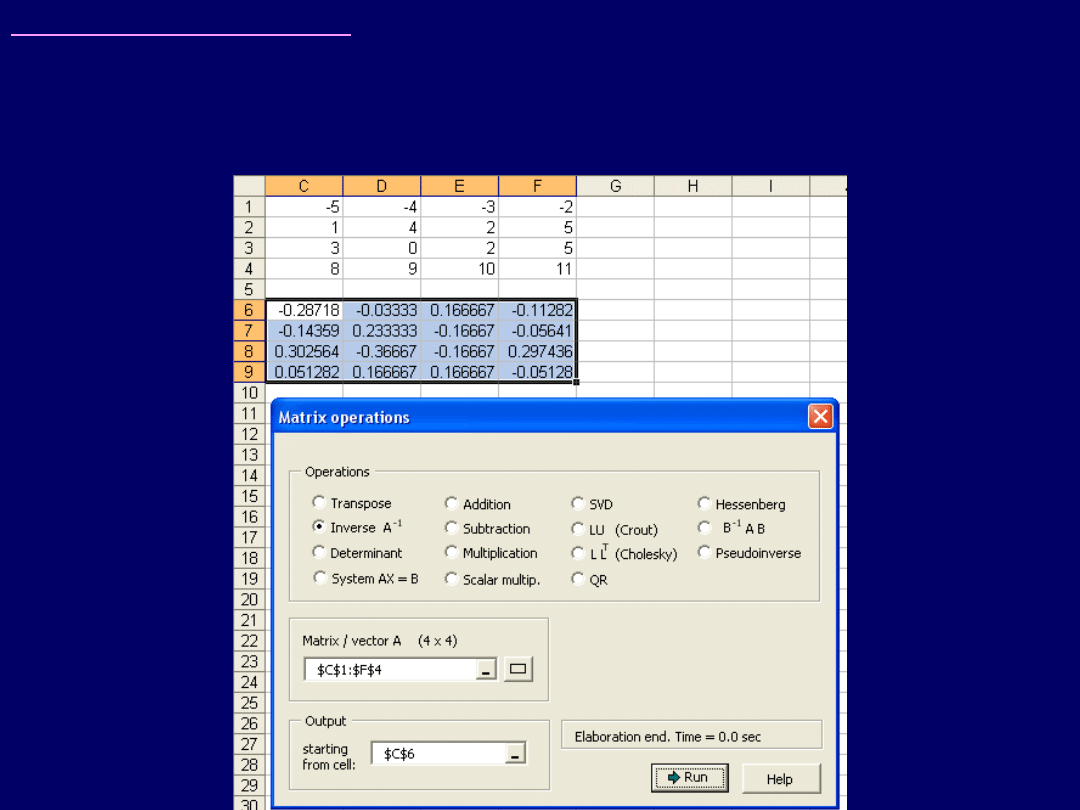
Wskazówki do zadania 4:

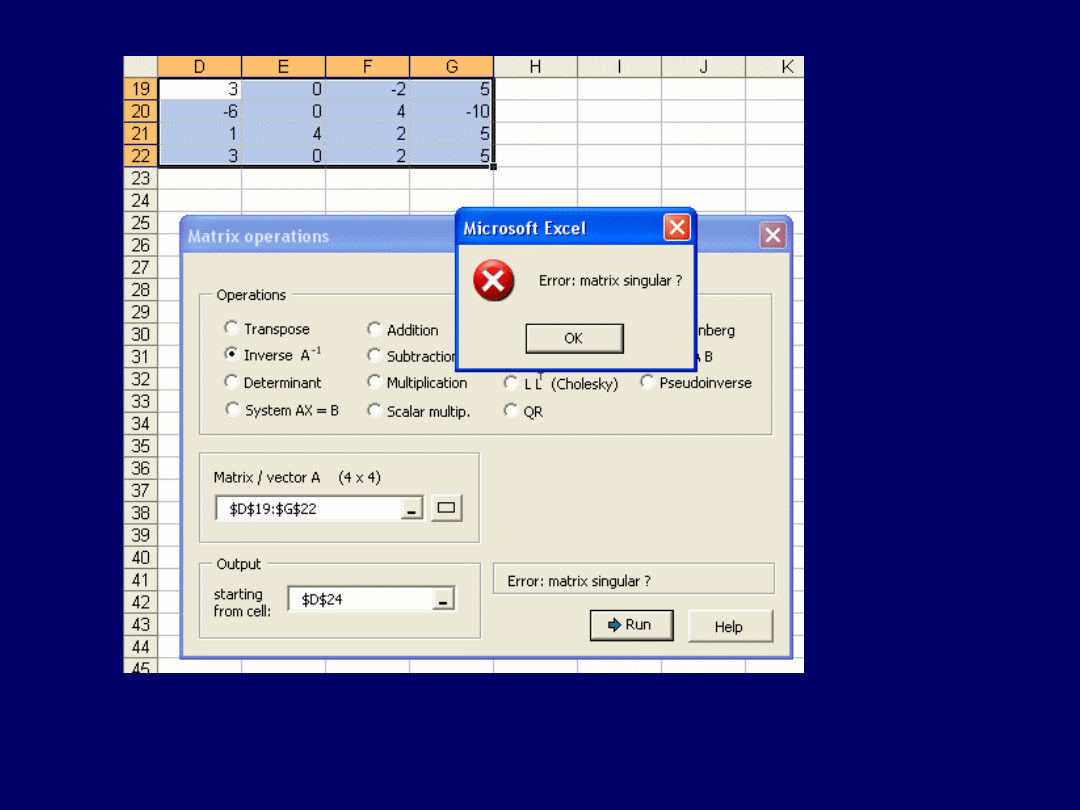
Odwracanie macierzy jest możliwe tylko wtedy,

gdy nie jest ona osobliwa

(ang.: „singular”), czyli – gdy żaden jej element (wiersz, kolumna) nie jest
liniową kombinacja innych elementów. Wynik odwrócenia I-szej macierzy:

Wynik odwracania II-giej macierzy

nie jest pomyślny

:

Poddawana odwracaniu macierz,

jest osobliwa

– gdyż jej drugi wiersz, jest

wynikiem przemnożenia wiersza pierwszego przez -2.

Wskazówki do zadania 5:

Wyznacznik macierzy 22, liczony jest

zgodnie z równaniem

:

W konkretnym przypadku naszego
zadania,

będzie to:

Wyliczenie wyznacznika pierwszej spośród dwu macierzy z poprzedniego

zadania (w „Matrix Functions…”), jest na następnym przeźroczu:

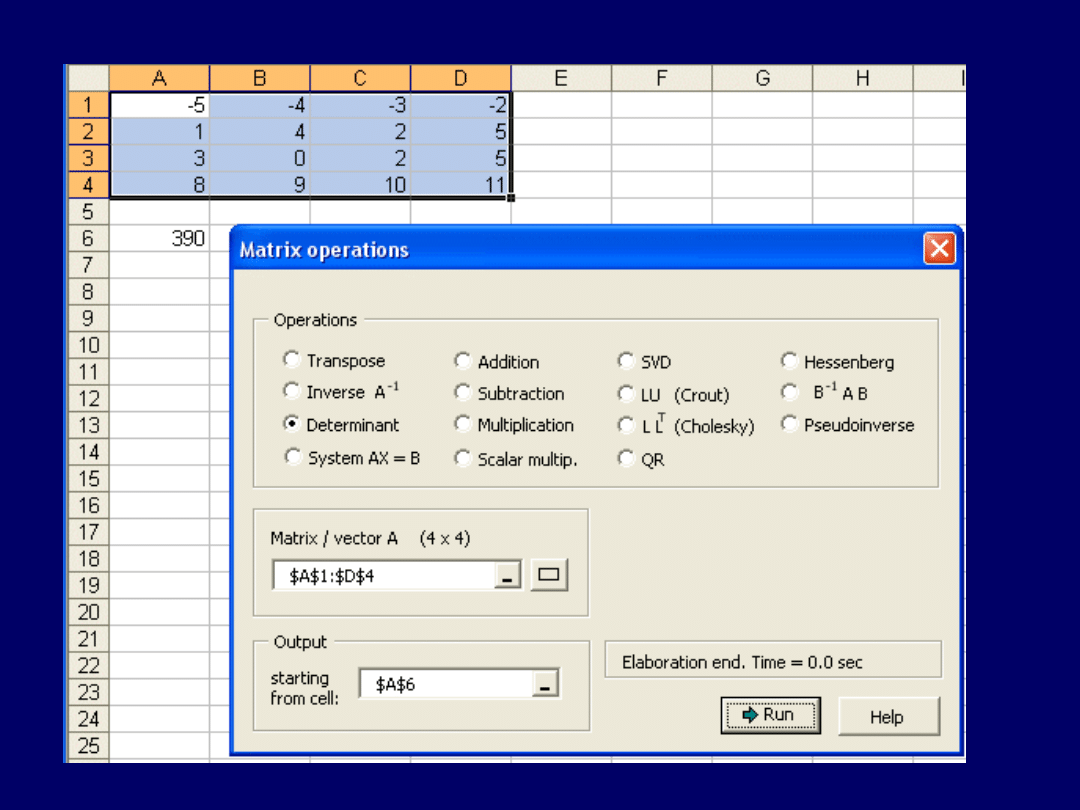
Wyznacznik niezerowy – stąd wniosek, że

macierz nie jest osobliwa

:

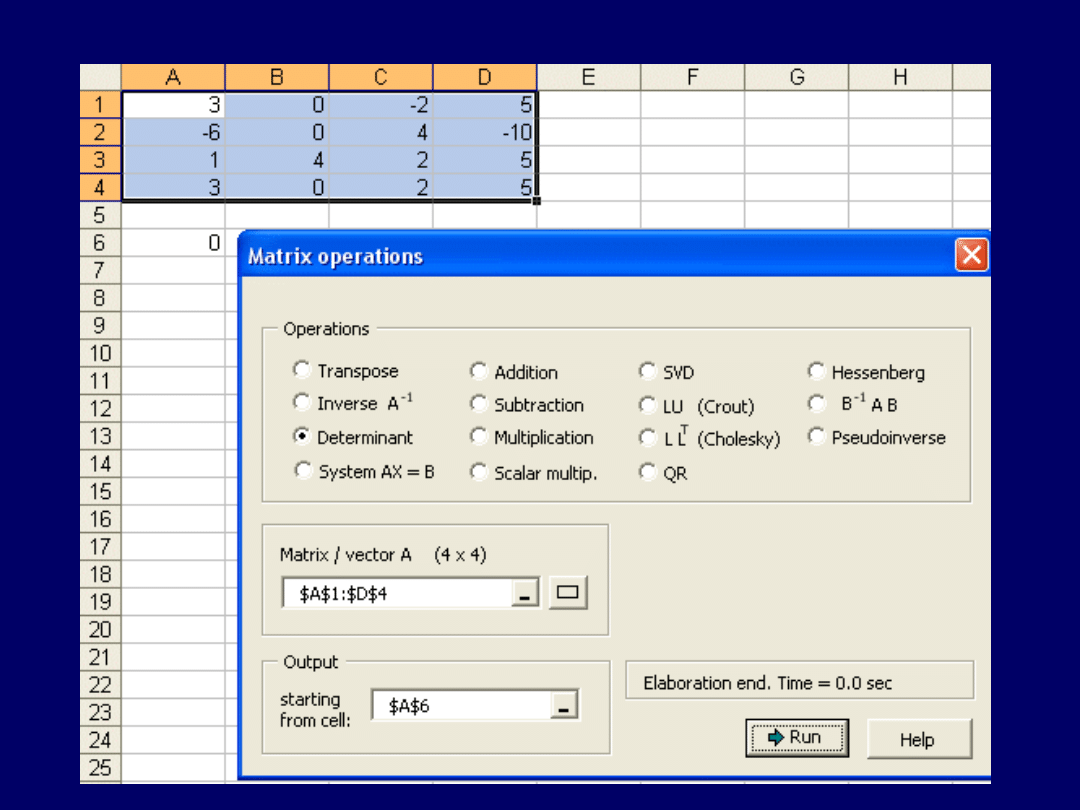
Wyznacznik = 0 

macierz osobliwa

!

Wskazówki do zadania 6:

Macierz A jest

ortogonalna

, gdy A

T

 A = I. W przypadku macierzy z na-szego

zadania:

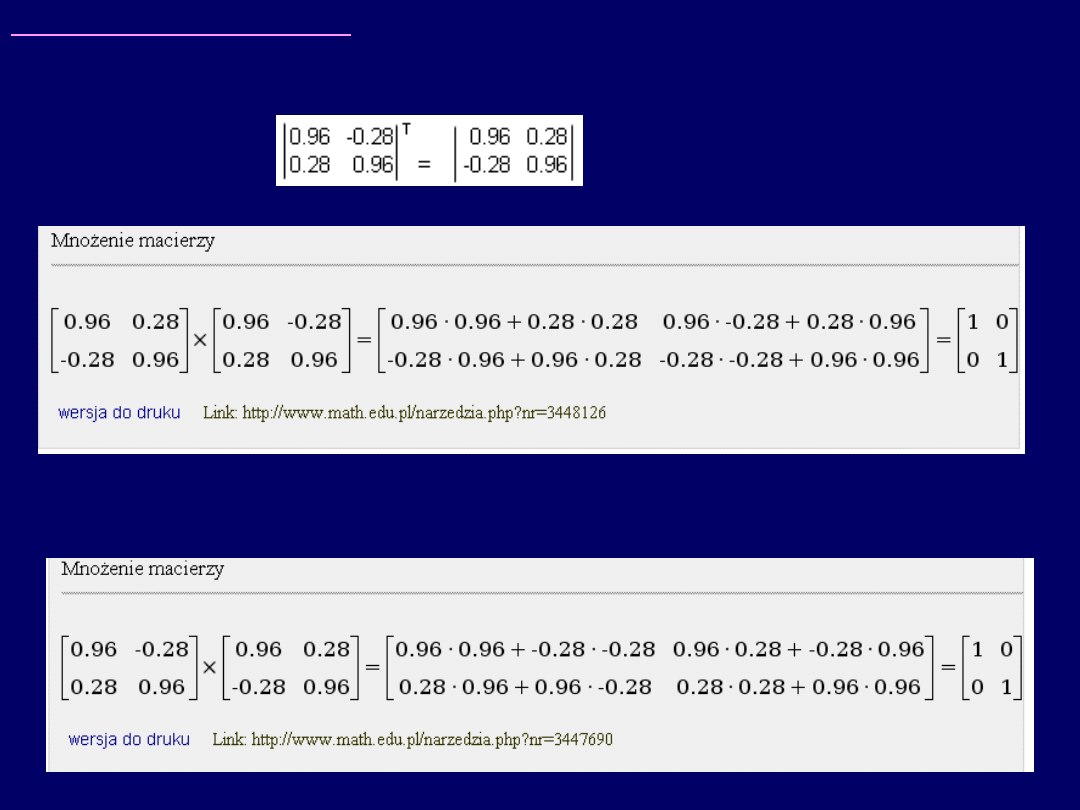
Po przemnożeniu macierzy transponowa

-nej przez wyjściową, uzyskujemy (zgodnie z

definicją) –

macierz jednostkową (I)

:

Identyczny wynik uzyskujemy, mnożąc macierze w

kolejności odwrotnej

,

czyli A  A

T

:

Macierz

odwrotna

rozpatrywanej macierzy ortogonalnej,

jest równa jej

transpozycji

, czyli:

A

T

= A

-1

:

Macierz ortogonalna, która spełnia powyższy warunek, nazywana jest

ortonormalną

.

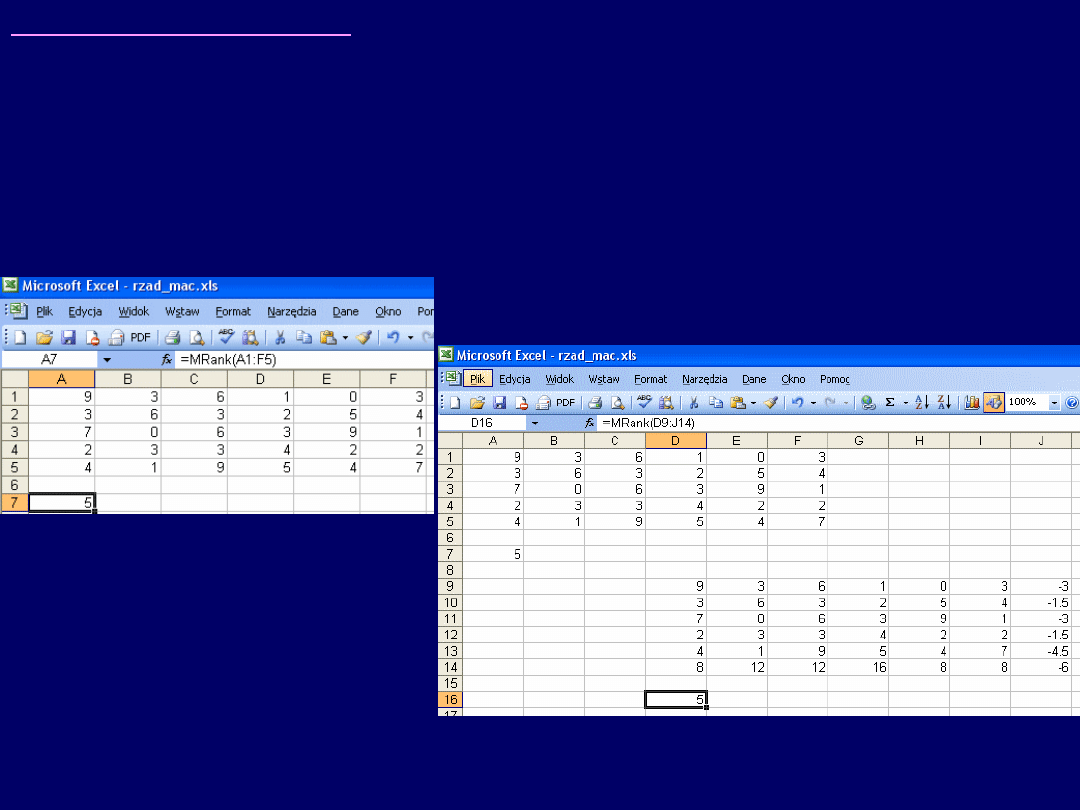
Wskazówki do zadania 7:

Poprzez rząd macierzy rozumiemy

maksymalny wymiar nieosobliwej

podmacierzy

, jaką możemy wyznaczyć w obrębie macierzy badanej. Mając

zainstalowany dodatek „Matrix Functions…”, rząd macierzy możemy łatwo
wyznaczyć w MS Excel za pomocą funkcji „MRank”, którą wprowadzamy
następująco:

„=mrank(k_pocz:k_końc)”

, gdzie:

k_pocz – adres komórki początkowej macierzy, k_końc – adres komórki

końcowej macierzy. Dla pierwszej macierzy z zadania:

Dla drugiej:

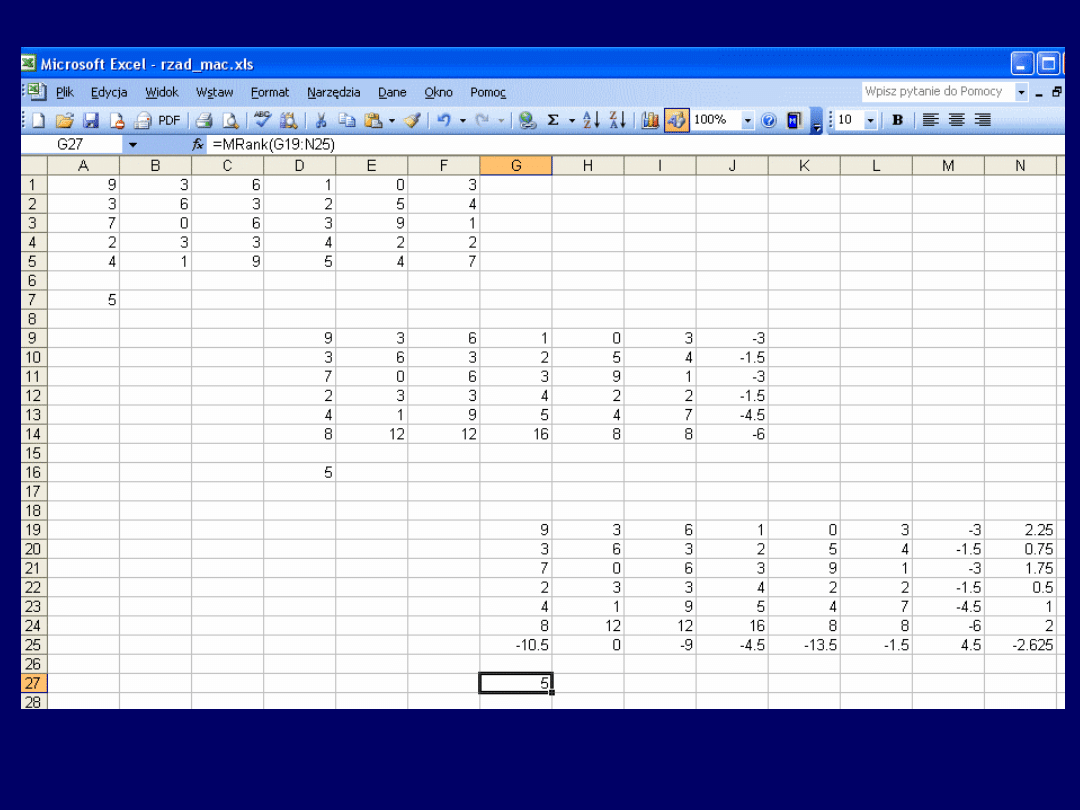
Zaś dla trzeciej:

W każdym przypadku rząd badanej macierzy

wynosił 5

.

Wskazuje to, że w pierwszym przypadku cała

macierz

(a ściślej mówiąc – jej

podmacierz kwadratowa: 55)

jest nieosobliwa

, a jej wszystkie wektory

(kolumny i wiersze) są

liniowo niezależne

.

W przypadku drugiej macierzy, ostatnia (VII-ma) kolumna zawie-ra

wyniki przemnożenia liczb występujących w kolumnie III-ciej – przez –0,5,
a ostatni (VI-ty) wiersz – wyniki przemnożenia liczb zawartych w wierszu
IV-tym przez 4. Tak więc wspomniane:

ostatni wiersz i kolumna są liniowo

zależne od innych wierszy/kolumn wewnątrz macierzy

.

Trzecia macierz: obok takiej samej zawartości, jak macierz 2-ga, jej

ostatnia (VIII-ma) kolumna zawiera wyniki przemnożenia kolumny I-szej
przez 0,25, a w ostatnim (VII-mym) wierszu – są wyni-ki przemnożenia
wiersza III-go przez –1,5. Tak więc

liniowo niezależ-na jest tutaj górna

podmacierz 55

– podobnie, jak w przypadku macierzy 1 i 2.

Z powyższych względów

rząd wszystkich trzech badanych macierzy

jest taki sam i wynosi 5

.

Znajomość rzędu macierzy może być przydatna przy

rozwiązywaniu

układów równań liniowych

(zapisanych w formie macierzowej) – a

konkretnie przy wstępnej ocenie, czy dany układ równań jest niesprzeczny
(rozwiązywalny) i czy ma jednoznaczne rozwiązanie.

Dziękuję

za uwagę ;-)