Ruch drgający

Ruch drgający



Ruch harmoniczny

Ruch harmoniczny



Ruch harmoniczny tłumiony

Ruch harmoniczny tłumiony



Drgania wymuszone

Drgania wymuszone



Rezonans

Rezonans



Analiza jakościowa drgań elektromagnetycznych

Analiza jakościowa drgań elektromagnetycznych



Analiza ilościowa drgań elektromagnetycznych

Analiza ilościowa drgań elektromagnetycznych



Drgania elektromagnetyczne wymuszone

Drgania elektromagnetyczne wymuszone



Rezonans

Rezonans



Elektryczne obwody drgające otwarte

Elektryczne obwody drgające otwarte

Wykład

Wykład

3

3

Drgania mechaniczne

Drgania mechaniczne



Ruch harmoniczny

Ruch harmoniczny

•

Ruch harmoniczny prosty

Ruch harmoniczny prosty

•

Wahadło matematyczne

Wahadło matematyczne

•

Wahadło torsyjne

Wahadło torsyjne

•

Wahadło fizyczne

Wahadło fizyczne

•

Ruch harmoniczny prosty a ruch jednostajny po okręgu

Ruch harmoniczny prosty a ruch jednostajny po okręgu

•

Składanie ruchów harmonicznych

Składanie ruchów harmonicznych



Ruch harmoniczny tłumiony

Ruch harmoniczny tłumiony



Drgania wymuszone

Drgania wymuszone



Rezonans

Rezonans

Wykład

Wykład

3

3

Ruch harmoniczny

Ruch harmoniczny

definicje

definicje

Wykład

Wykład

3

3

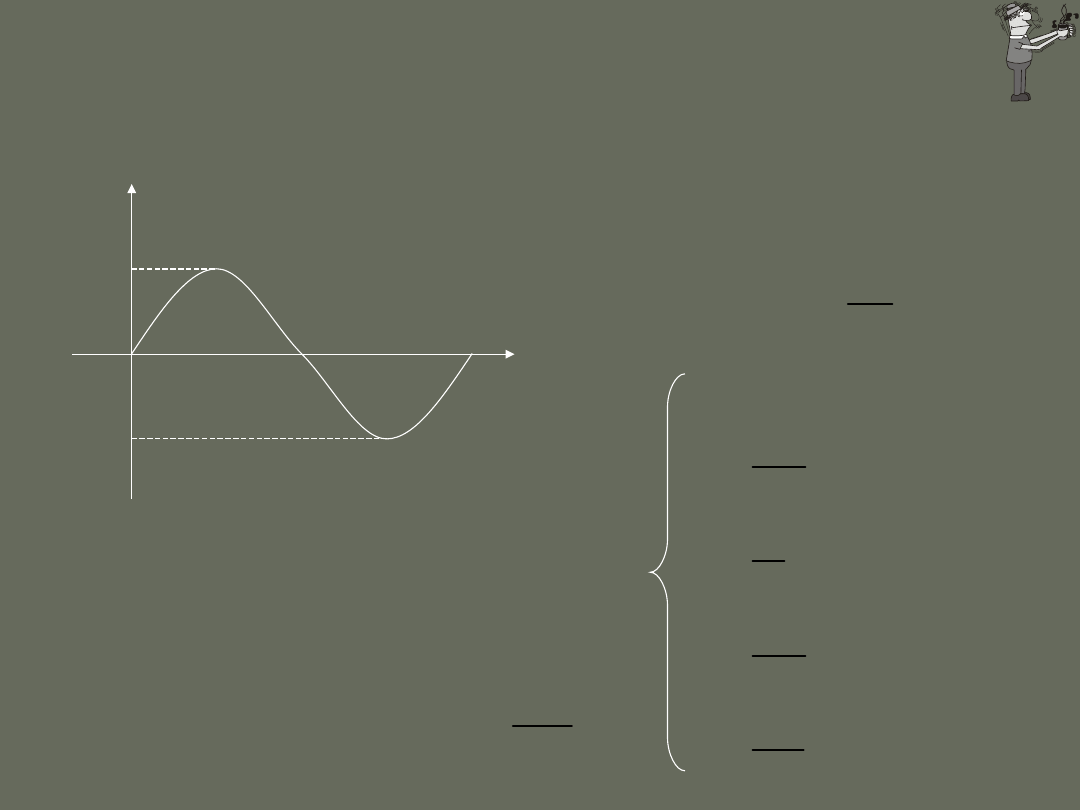
Jeżeli punk materialny porusza się ruchem okresowym tam i z powrotem

po tej samej drodze, to ruch taki nazywamy ruchem drgającym.

Tego rodzaju przemieszczenie punktu materialnego można zawsze

wyrazić przy pomocy funkcji sinus i cosinus. Funkcje te nazywane są

funkcjami harmonicznymi i dlatego ruch który one opisują nazywamy

ruchem harmonicznym.

sin

s A

t

w

=

wychylenie punktu z
położenia równowagi

wielkości stałe
w danym ruchu

czas

A s A

- � �

sin

1 sin

1

y

x

x

=

- �

�

y

x

1

-1

amplituda ruchu
harmonicznego

Ruch harmoniczny

Ruch harmoniczny

definicje

definicje

Wykład

Wykład

3

3

2

T

p

w

=

położenie równowagi

Zasadniczą cechą ruchu

harmonicznego jest

okresowość.

Czas trwania jednego

pełnego drgnienia

nazywany jest okresem:

maksymalne wychylenie
z położenia równowagi A

0

2

2

0

t

t

w

p

p

w

� �

� �

x

s

sin

0

2

s A

x

x

p

=

� �

A

-A

0

2

3

2
2

t

t

t

t

t

p

w

p

w

p
w
p

w

=

=

=

=

=

położenie równowagi

położenie równowagi

maksymalne wychylenie
z położenia równowagi -A

Poszczególne fazy
ruchu powtarzają
się w tym samym
rytmie.

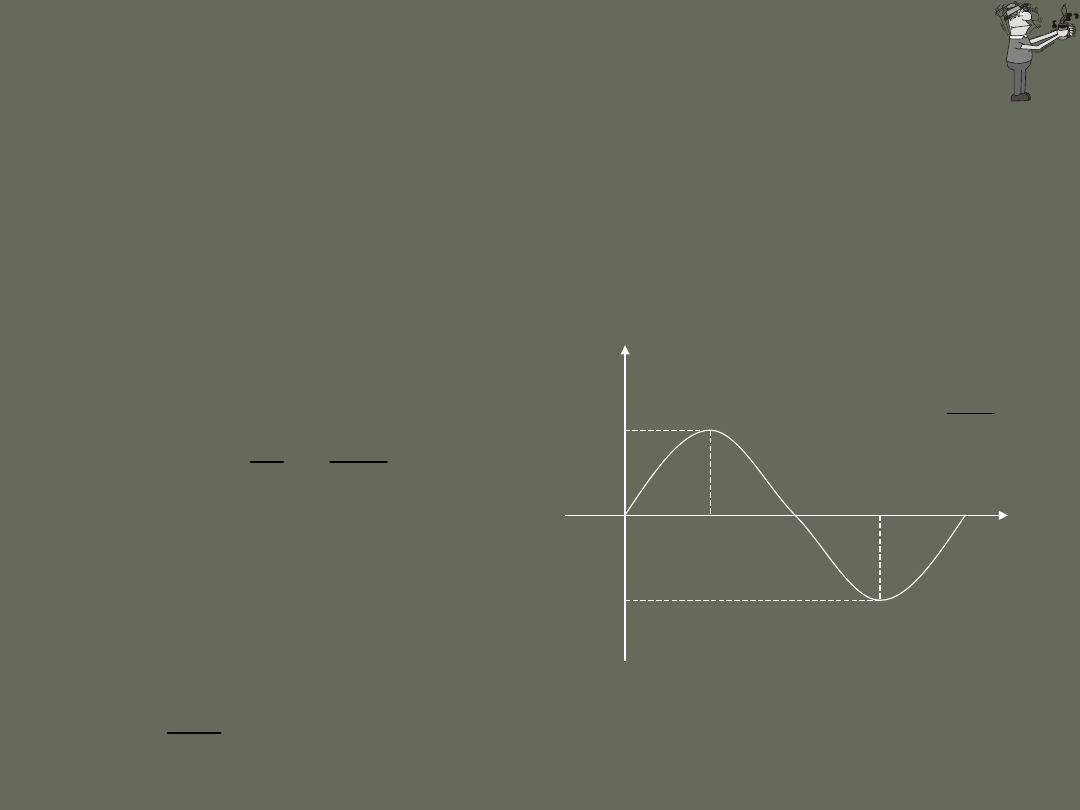
Ruch harmoniczny

Ruch harmoniczny

definicje

definicje

Wykład

Wykład

3

3

1

2

T

w

n

p

= =

Częstotliwość drgań, czyli liczba
pełnych drgnień dokoła położenia
równowagi wykonanych w jednostce
czasu definiujemy jako odwrotność
okresu:

2

2

T

p

w

w

pn

=

=

Stała  zwana jest pulsacją

czyli częstością kątową.

2

sin

s A

t

T

p

=

Równanie ruchu
harmonicznego
prostego:

t

s

A

-A

0

T/4

2T/4

3T/4

T

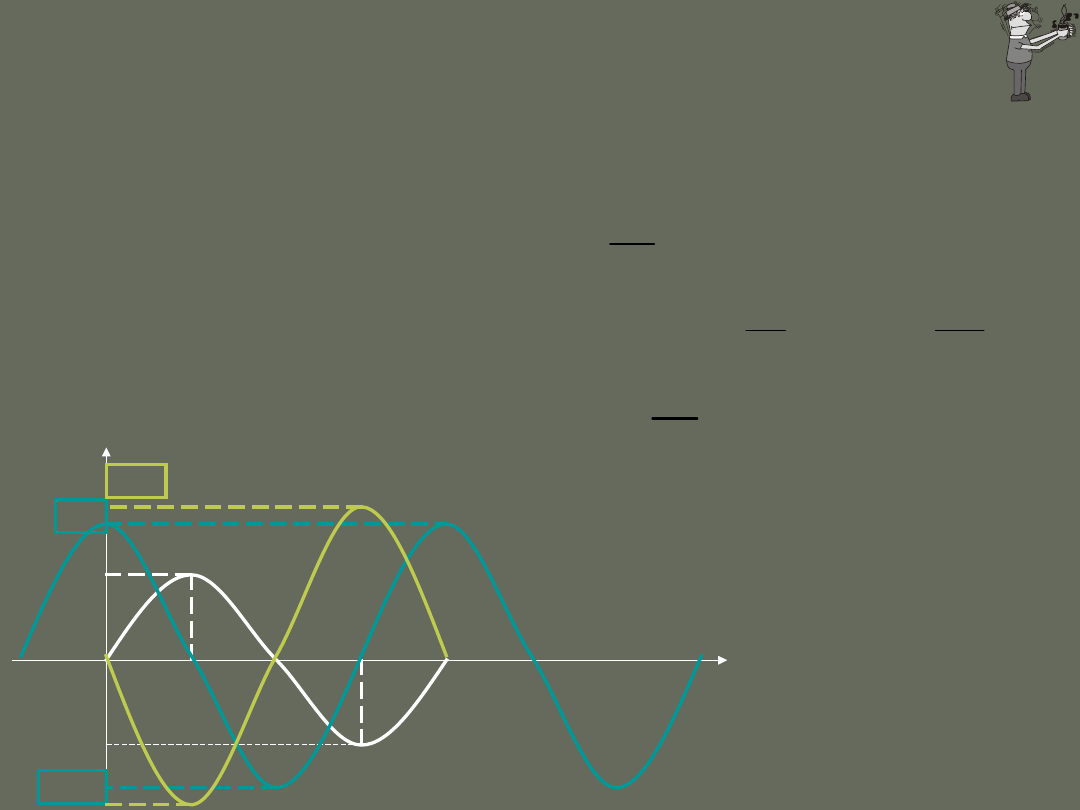
Ruch harmoniczny

Ruch harmoniczny

ruch harmoniczny prosty -

ruch harmoniczny prosty -

kinematyka

kinematyka

Wykład

Wykład

3

3

2

sin

s A

t

T

p

=

Prędkość w ruchu harmonicznym:

2

cos

ds

v

A

t

dt

T

p

w

=

=

2

2

sin

dv

a

A

t

s

dt

w

w

w

=

=-

=-

Przyspieszenie w ruchu harmonicznym:

A

-A

t

0

T/4

T/2

3T/4

T

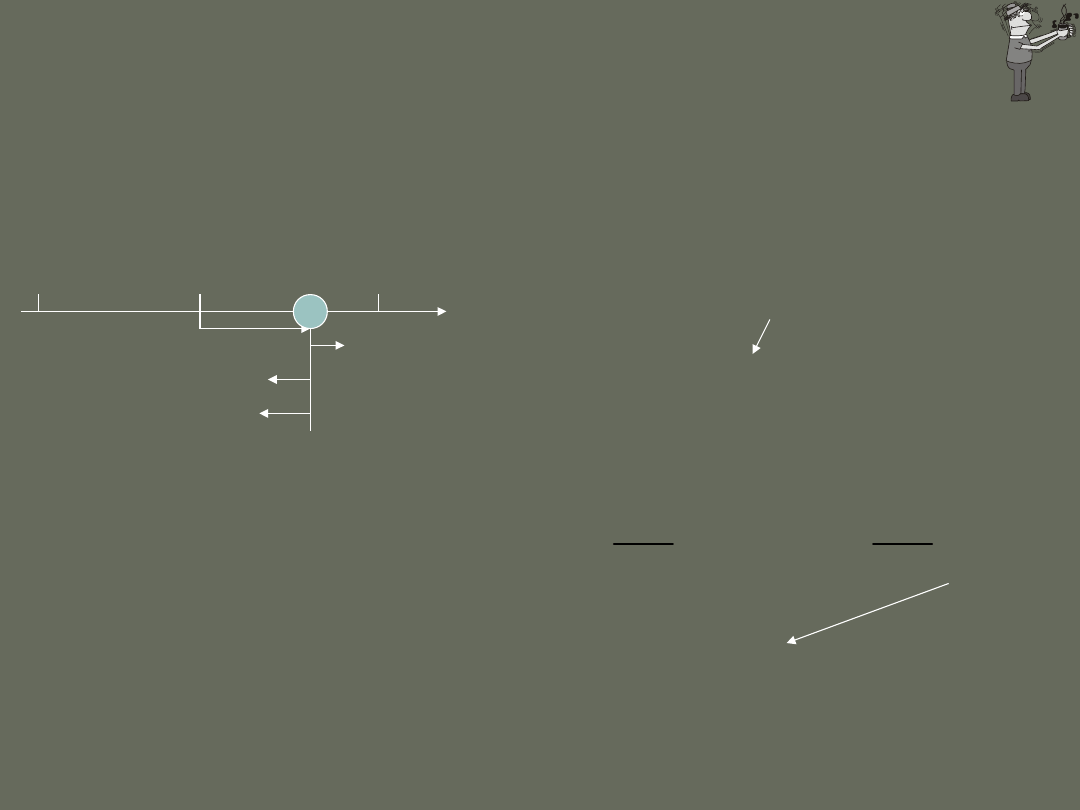
Droga w ruchu harmonicznym:

A

-A



2

A

Uwagi:

1. Przyspieszenie jest
proporcjonalne do
wychylenia z położenia
równowagi.

2. Zwrot przyspieszenia
jest zawsze przeciwny do
zwrotu wychylenia z
położenia równowagi.

Ruch harmoniczny

Ruch harmoniczny

ruch harmoniczny prosty -

ruch harmoniczny prosty -

dynamika

dynamika

Wykład

Wykład

3

3

2

F

m s

ks

w

=-

=-

2

2

2

2

0

d s

d s

m

ks

m

ks

dt

dt

=-

+ =

Z drugiej zasady dynamiki Newtona

-x

1

x

1

0

v

a

F (=ma)

siła sprężystości

współczynnik
sprężystości

Jest to równanie różniczkowe, nazywane
równaniem oscylatora harmonicznego,
którego rozwiązanie prowadzi do znalezienia
zależności s(t).

m

x

Ruch harmoniczny

Ruch harmoniczny

ruch harmoniczny prosty – rozwiązywanie równania

ruch harmoniczny prosty – rozwiązywanie równania

oscylatora

oscylatora

Wykład

Wykład

3

3

2

2

2

2

0

d x

d x

k

m

kx

x

dt

dt

m

+ =

=-

Aby znaleźć rozwiązanie równania różniczkowego musimy znaleźć pewną funkcję

x(t), której druga pochodna równa się jej samej ze znakiem przeciwnym i ze

stałym współczynnikiem k/m.

Taką własność ma funkcja sinus i cosinus.

2

2

cos

sin ,

cos

sin

cos

d

d

d

t

t

t

t

t

dt

dt

dt

=-

=-

=-

Własność ta zostaje zachowana jeżeli funkcję tę pomnożymy przez stały czynnik A.

Proponujemy rozwiązanie w postaci:

(

)

cos

x A

t

w j

=

+

Ruch harmoniczny

Ruch harmoniczny

ruch harmoniczny prosty – rozwiązywanie równania

ruch harmoniczny prosty – rozwiązywanie równania

oscylatora

oscylatora

Wykład

Wykład

3

3

(

)

sin

dx

A

t

dt

w

w j

=-

+

(

)

2

2

2

cos

d x

A

t

dt

w

w j

=-

+

(

)

cos

x A

t

w j

=

+

(

)

(

)

2

cos

cos

k

A

t

A

t

m

w

w j

w j

-

+ =-

+

2

k

m

w =

Jeżeli

to x w zadanej postaci
spełnia równanie oscylatora
harmonicznego.

Wracając do fizyki

2

2

/

T

m k

p

p

w

=

=

Okres drgań sprężyny zależy od masy
drgającej i od współczynnika
sprężystości materiału, z którego
wykonana jest sprężyna.

Ruch harmoniczny

Ruch harmoniczny

ruch harmoniczny prosty – rozwiązywanie równania

ruch harmoniczny prosty – rozwiązywanie równania

oscylatora

oscylatora

Wykład

Wykład

3

3

(

)

cos

x A

t

w j

=

+

cos

sin

2

2

x A

t

A

t

p

p

j

w

w

�

�

=-

=

-

=

�

�

�

�

czyli przemieszczenie jest
zerowe w chwili t równej zero

0

cos

x A

t

j

w

=

=

Amplituda i faza początkowa drgań zależą od początkowego położenia i prędkości
oscylującego ciała. Cząstka raz wprawiona w ruch będzie drgać ze stałą amplitudą,
częstością i stałą fazą tak długo, jak długo inne siły nie podziałają na układ.

faza ruchu

faza początkowa

czyli przemieszczenie jest
maksymalne w chwili t równej zero

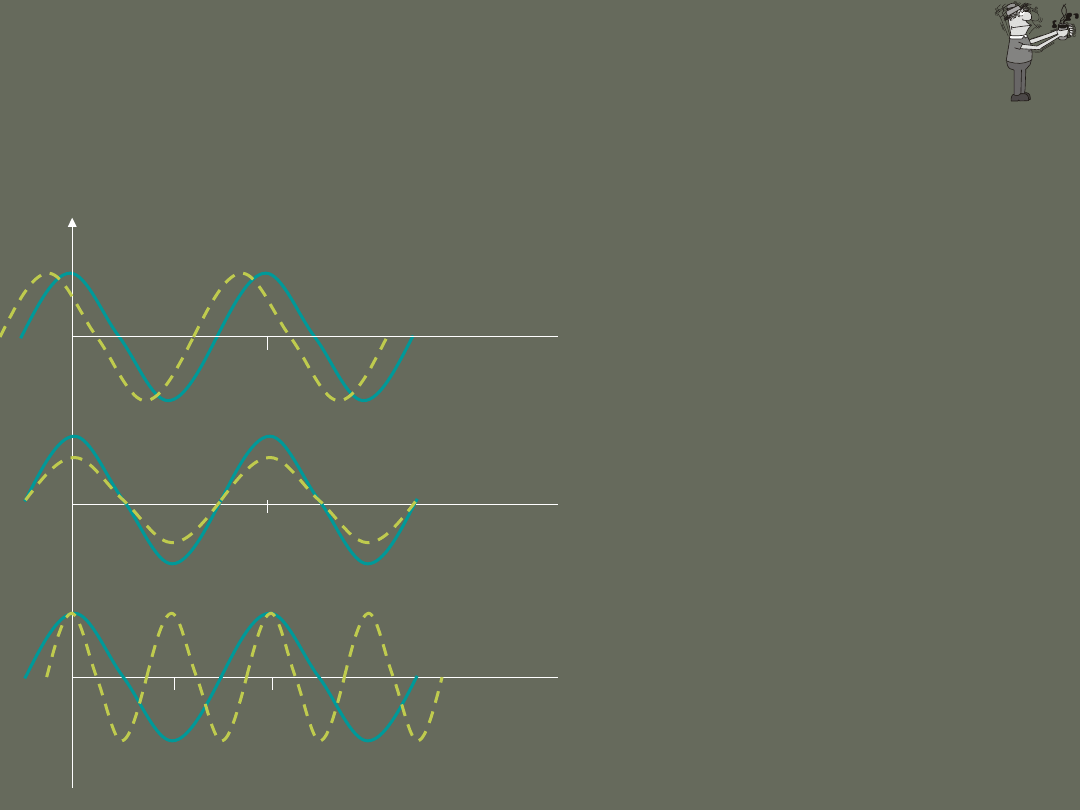
Ruch harmoniczny

Ruch harmoniczny

różne rozwiązania równania oscylatora

różne rozwiązania równania oscylatora

harmonicznego

harmonicznego

Wykład

Wykład

3

3

x

t

A

T

=45°

=0

T

t

A

=0

=0

A

t

T

T

=0

=0

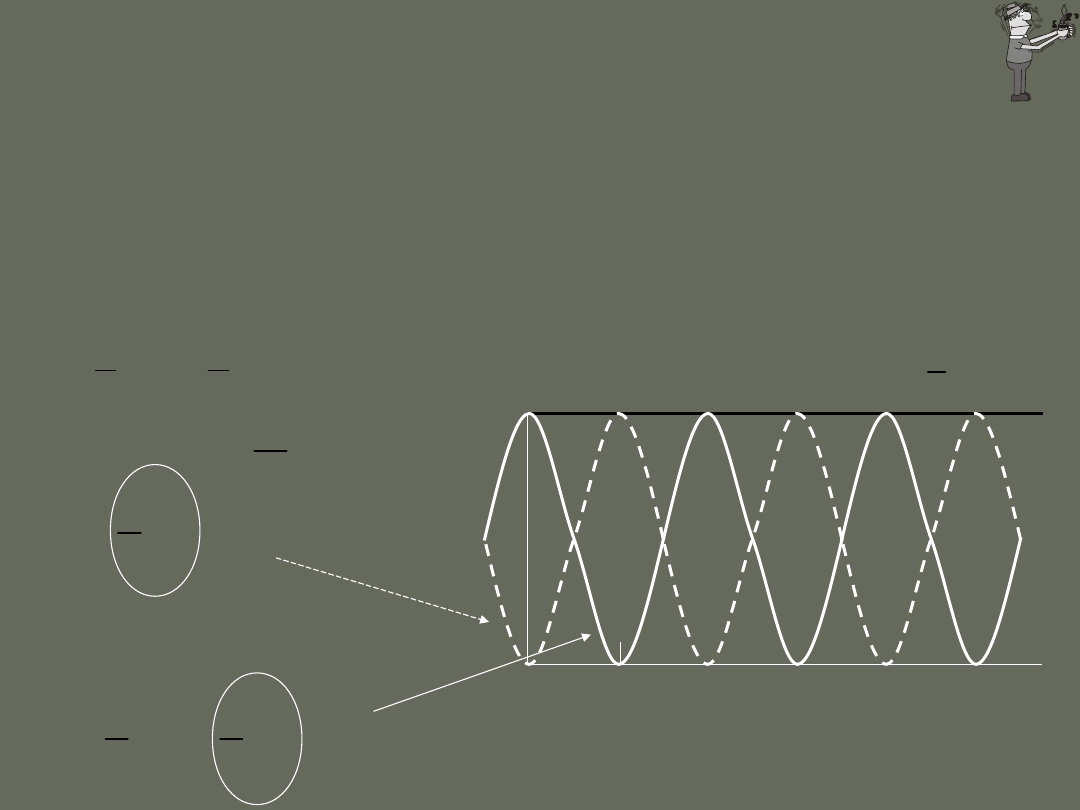
taka sama amplituda i okres; różne fazy

takie same okres i faza; różne amplitudy

taka sama amplituda i faza; różne okresy

Ruch harmoniczny

Ruch harmoniczny

ruch harmoniczny prosty

ruch harmoniczny prosty

Wykład

Wykład

3

3

x=A

x=-A

a=-A

2

a=A

2

v=-A

v=A

F=-kx

F=-kx

v=0

v=0

F=0

x=0

a=0

F=0

x=0

a=0

Ruch harmoniczny

Ruch harmoniczny

energia w ruchu harmonicznym

energia w ruchu harmonicznym

prostym

prostym

Wykład

Wykład

3

3

(

)

2

2 2

2

1

1

sin

2

2

K

mv

m A

t

w

w j

=

=

+

(

)

cos

x A

t

w j

=

+

2

k

m

w =

(

)

2

2

1

sin

2

K

kA

t

w j

=

+

Energia kinetyczna

Energia potencjalna

(

)

2

2

2

1

1

cos

2

2

U

kx

kA

t

w j

=

=

+

T

t

2

max

max

1

2

K U K

U

kA

+ =

=

=

Ruch harmoniczny

Ruch harmoniczny

energia w ruchu harmonicznym

energia w ruchu harmonicznym

prostym

prostym

Wykład

Wykład

3

3

2

max

max

1

2

E K

U

kA

=

=

=

( )

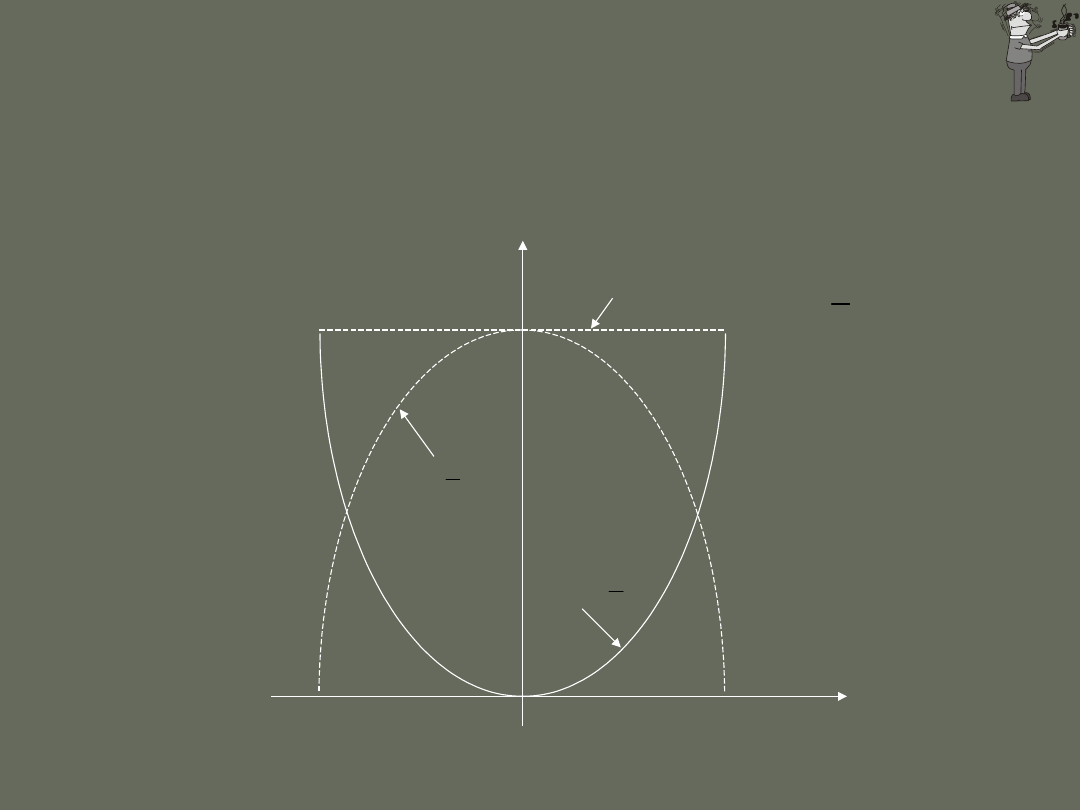
2

1

2

K x

mv

=

( )

2

1

2

U x

kx

=

x

E

0

A

-A



l

Ruch harmoniczny

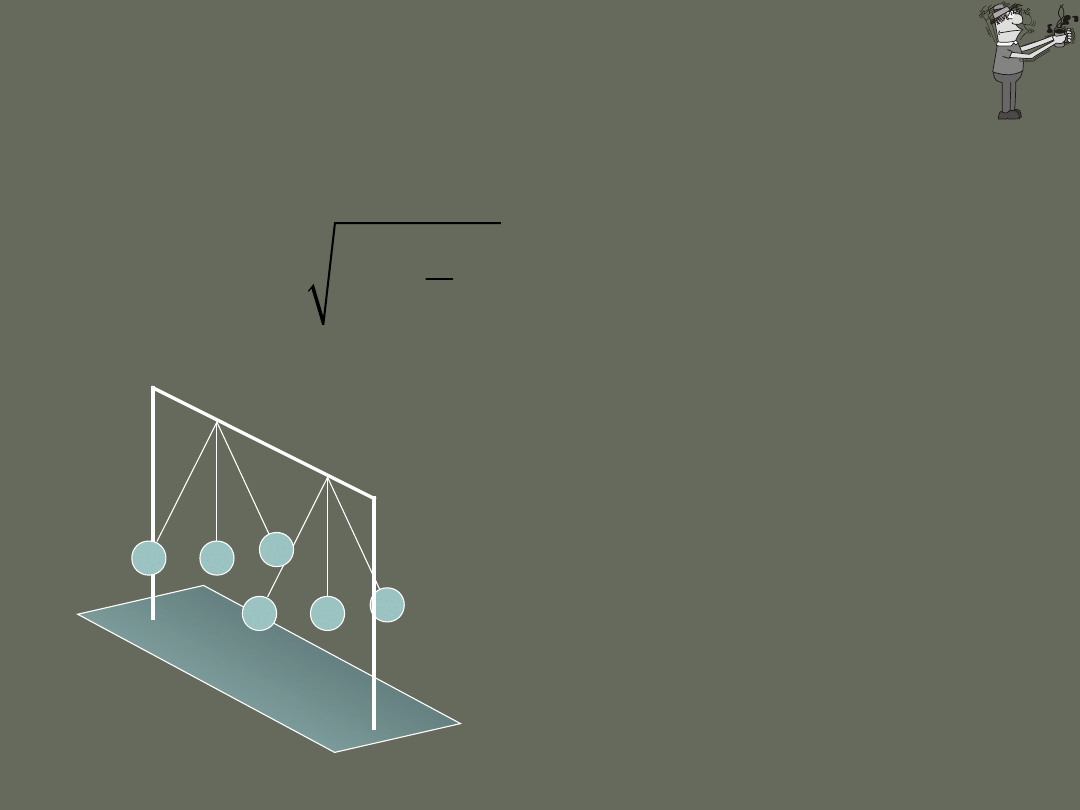
Ruch harmoniczny

wahadło matematyczne

wahadło matematyczne

Wykład

Wykład

3

3

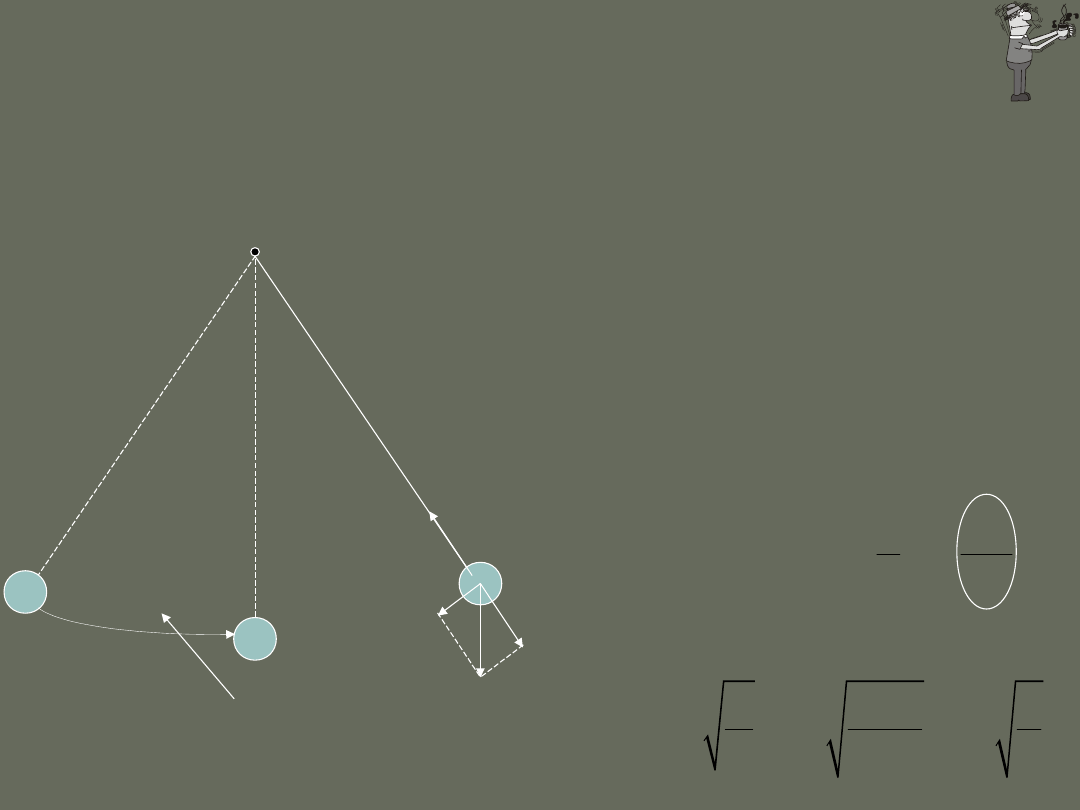
sin

F

mg

b

=-

x

mg

F

mg

mg

x

l

l

b

=-

=-

=-



mg cos

mg sin

mg

N

siła, będąca składową styczną jest siłą
przywracającą równowagę

Uwaga:

Siła ta nie jest proporcjonalna do przemieszczenia
kątowego , lecz do sin.
Ruch ten nie jest prostym ruchem harmonicznym

Założenie:

sinb b

@

x lb

=

m

k

2

2

2

/

m

m

l

T

k

mg l

g

p

p

p

=

=

=

Okres wahadła:

15°=0.2618 rad sin15°=0.25882 1.14%

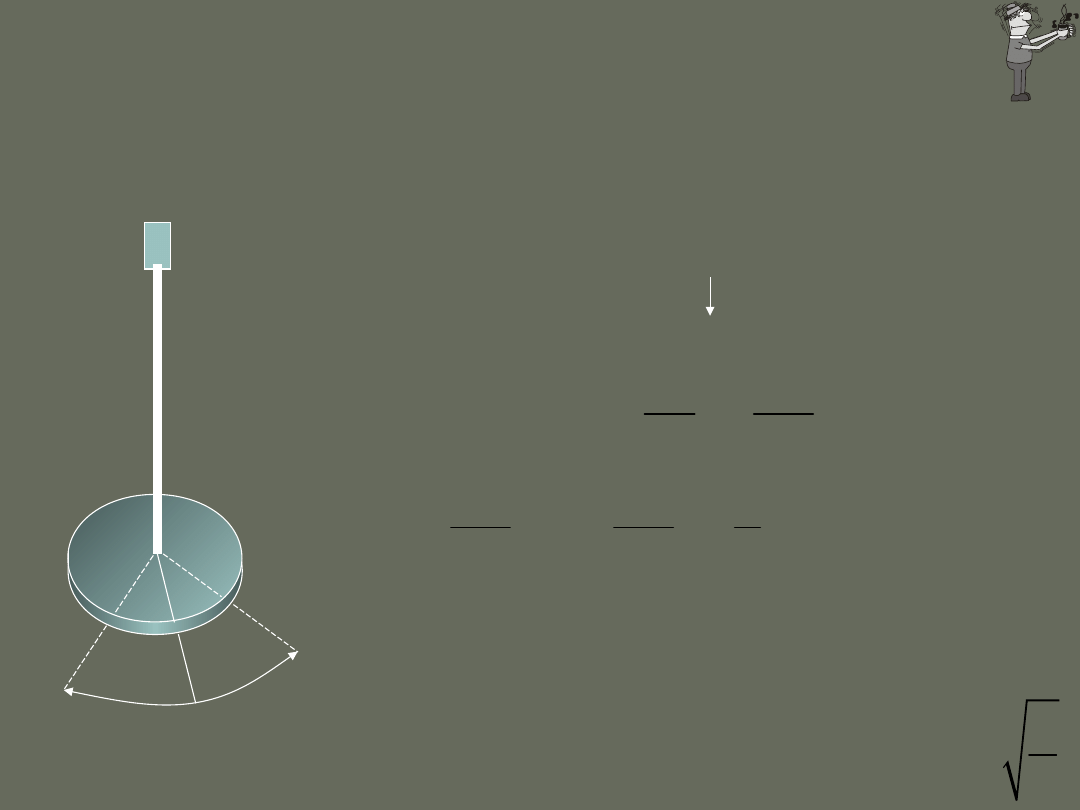
Ruch harmoniczny

Ruch harmoniczny

wahadło torsyjne

wahadło torsyjne

czyli kątowy ruch

czyli kątowy ruch

harmoniczny

harmoniczny

Wykład

Wykład

3

3

2

2

2

2

d

d

I

dt

dt

I

q

q

k

kq

q

-

=

=-

W układzie takim
działa moment
siły skręconego
pręta i jest on
momentem siły
przywracającej
równowagę.



moment kierujący

M

kq

=-

z prawa Hooke’a

2

2

d

d

M I

I

I

dt

dt

w

q

a

=

=

=

równanie ruchu

równanie oscylatora
harmonicznego dla
ruchu kątowego

 - przemieszczenie kątowe

Rozwiązaniem równania oscylatora harmonicznego dla ruchu

kątowego jest proste drganie harmoniczne we współrzędnej

kątowej 

(

)

max

cos t

q q

w j

=

+

2

I

T

p

k

=

Ruch harmoniczny

Ruch harmoniczny

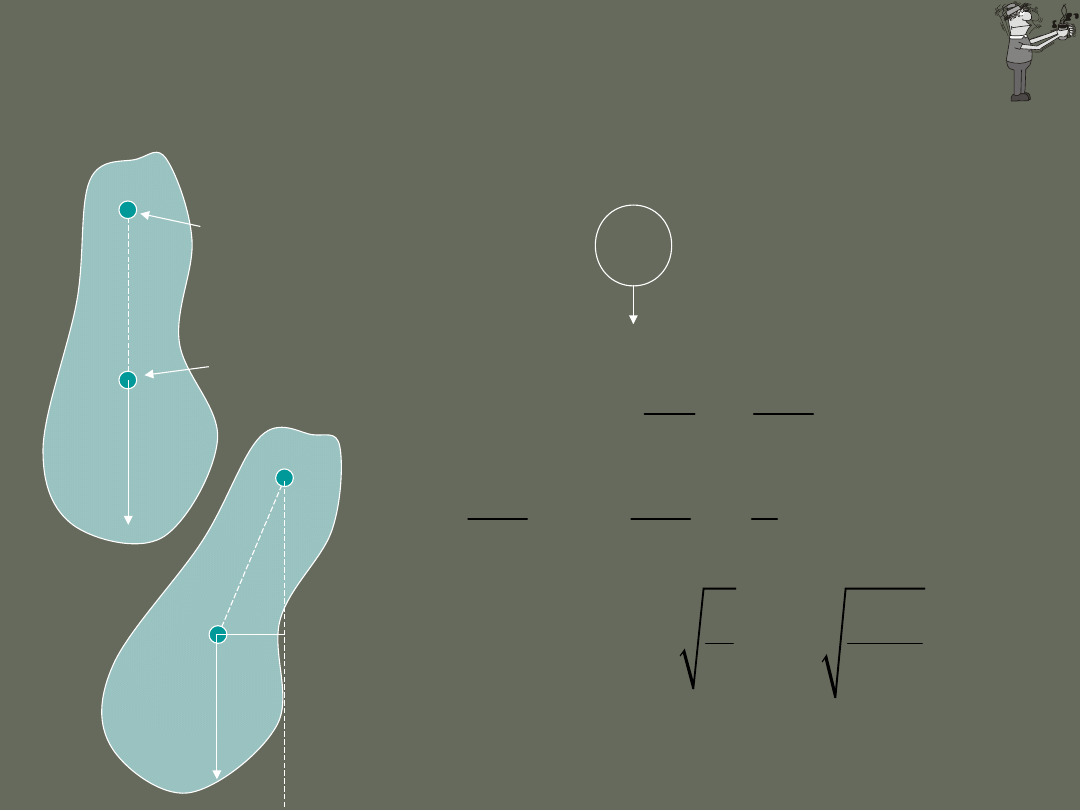
wahadło fizyczne

wahadło fizyczne

Wykład

Wykład

3

3

sin

M

mgd

q

kq

=-

@-

W układzie takim
ciężar wahadła
dostarcza
momentu siły
przywracającego
równowagę

moment kierujący

2

2

d

d

M I

I

I

dt

dt

w

q

a

=

=

=

równanie ruchu

2

2

2

2

d

d

I

dt

dt

I

q

q

k

kq

q

-

=

=-

równanie oscylatora
harmonicznego dla
ruchu kątowego

oś obrotu

2

2

I

I

T

mgd

p

p

k

=

=

mg

d



mg

d

d sin

środek masy

Dowolny kształt
zawieszony na
dowolnej osi

Wahadło fizyczne stosuje się przy
dokładnych pomiarach przyspieszenia g.

Ruch harmoniczny

Ruch harmoniczny

wahadło fizyczne a wahadło

wahadło fizyczne a wahadło

matematyczne

matematyczne

Wykład

Wykład

3

3

zred

l

I

g

k

=

2

I ml

mgl

k

=

=

zred

Ig

I

l

md

k

=

=

Pojęcie długości zredukowanej wiąże się ze związkami pomiędzy wahadłem
fizycznym i matematycznym. Przez długość zredukowaną wahadła fizycznego
rozumie się długość wahadła matematycznego mającego ten sam okres wahań.

wzór na okres
wahadła
matematyczneg
o

2

2

I

l

T

g

p

p

k

=

=

odległość od osi obrotu
do środka masy wahadła
fizycznego

Wahadło matematyczne można uważać za przypadek szczególny

wahadła fizycznego.

Ruch harmoniczny

Ruch harmoniczny

związek z ruchem jednostajnym po

związek z ruchem jednostajnym po

okręgu

okręgu

Wykład

Wykład

3

3

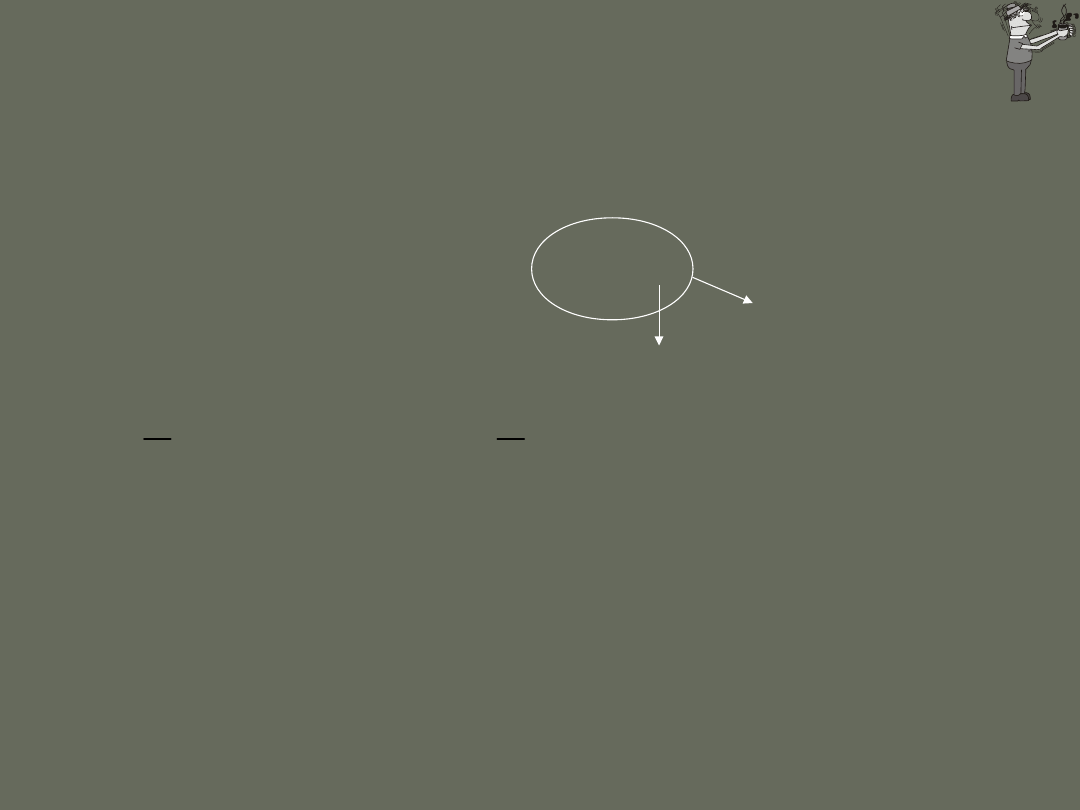
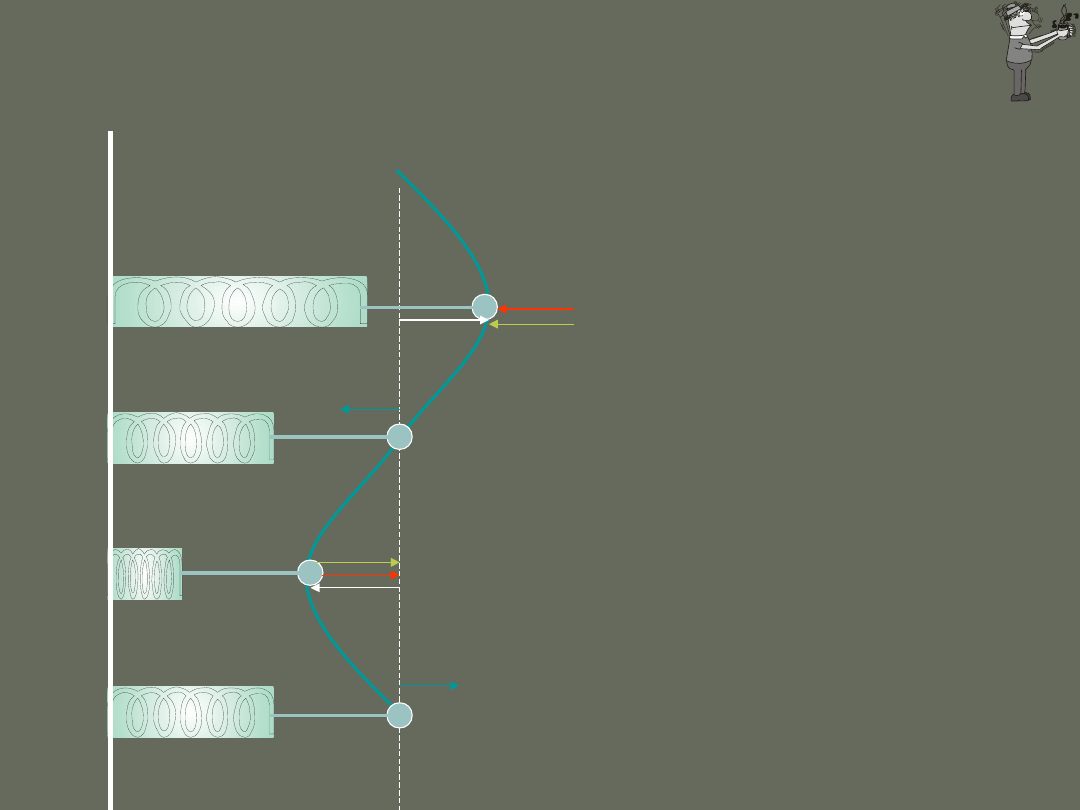
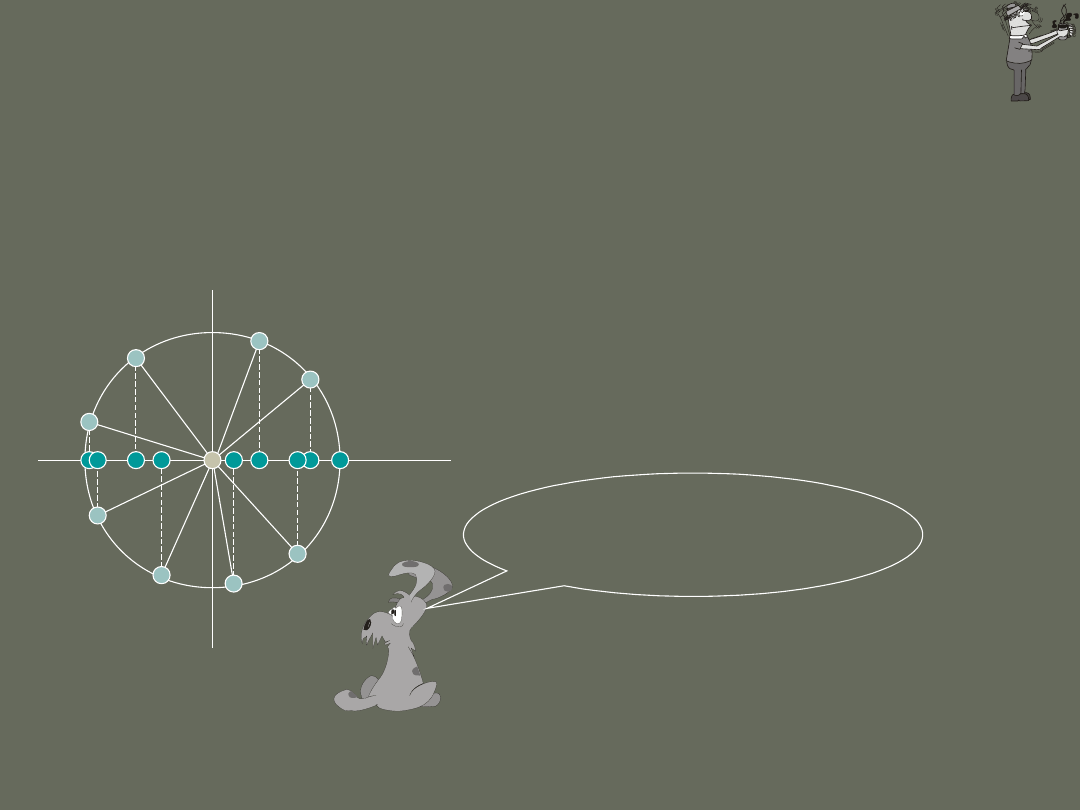
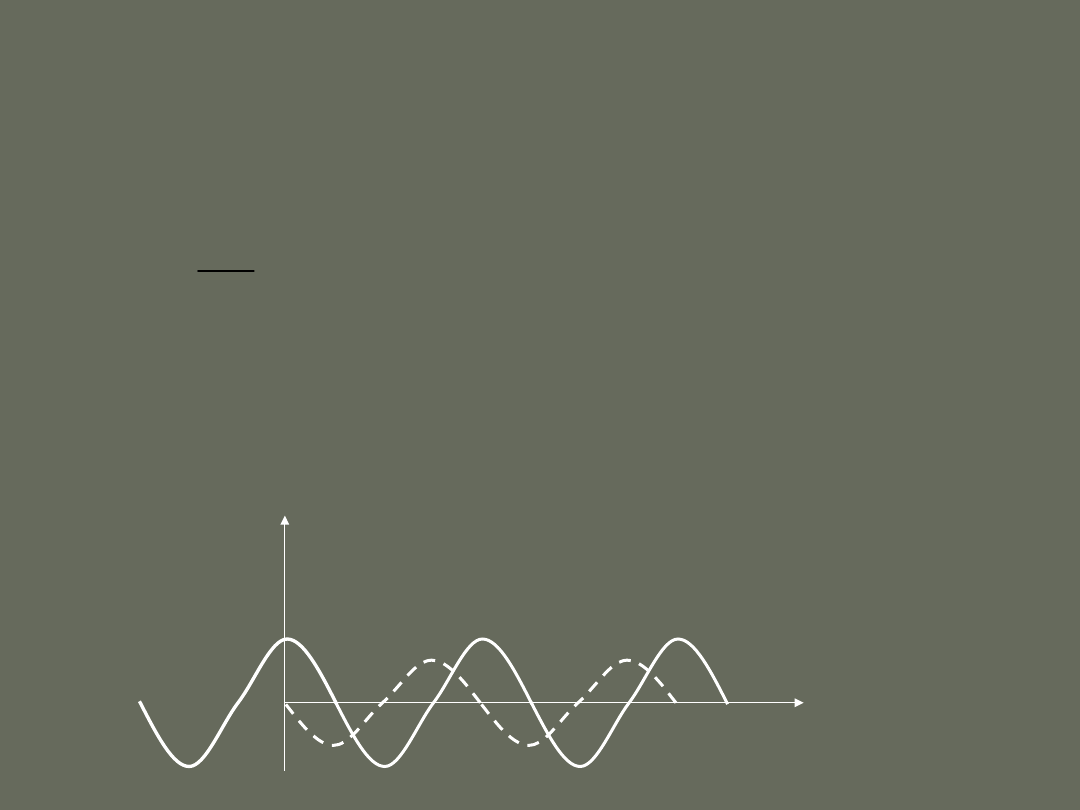
Ruch harmoniczny można zatem opisać jako rzut
jednostajnego ruchu po okręgu na jego średnicę.

x

y

Jasne kuleczki poruszają się po
okręgu, a ciemne kuleczki poruszają
się ruchem oscylacyjnym

P

Ruch harmoniczny

Ruch harmoniczny

związek z ruchem jednostajnym po

związek z ruchem jednostajnym po

okręgu

okręgu

Wykład

Wykład

3

3

(

)

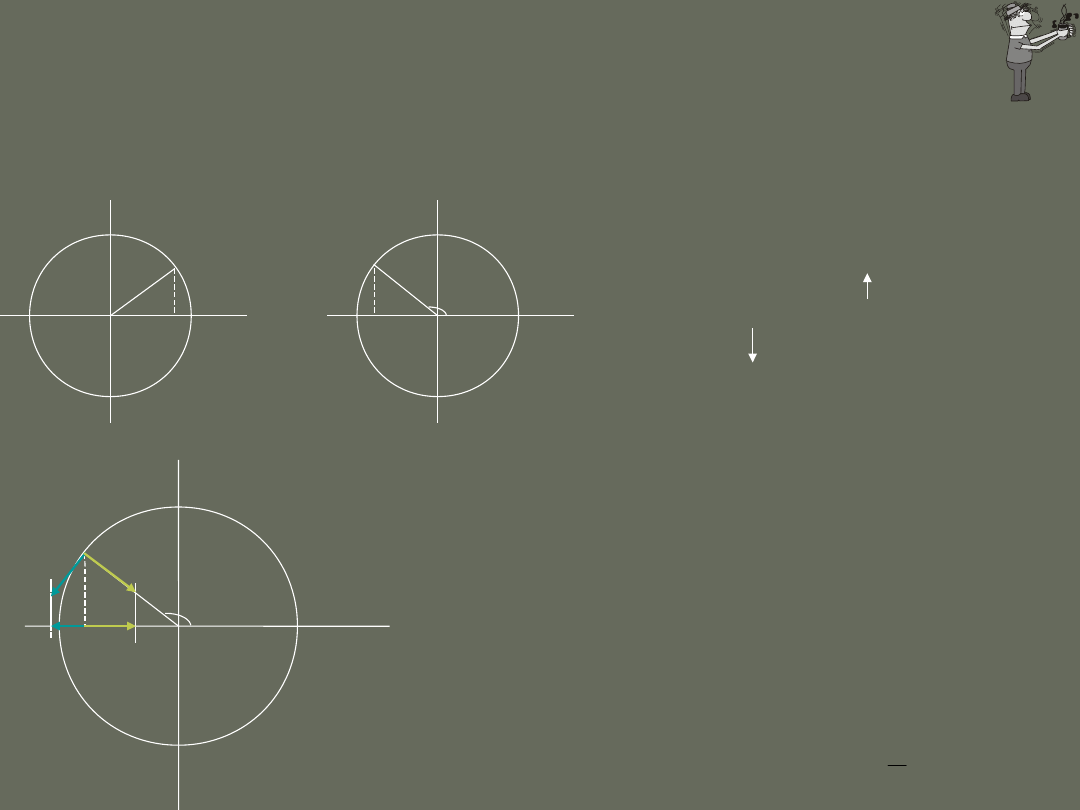
cos

x A

t

w j

=

+

x

y

P

R

0



t=0

 - faza początkowa

x

y

R

0

t+

t>0

(t+) – faza ruchu

amplituda równa promieniowi okręgu

częstość kątowa równa prędkości
kątowej ruchu po okręgu

P

x

y

R

0

t+

(

)

sin

x

v

A

t

w

w j

=-

+

v

x

a

x

(

)

2

cos

x

a

A

t

w

w j

=-

+

A



2

A

(

)

sin

y A

t

w j

=

+

Gdybyśmy rzutowali na oś y, to
równanie ruchu miałoby postać:

Jedyną różnicą w porównaniu z x
jest różnica faz.

(

)

cos

sin

2

t

t

p

w j

w j

�

�

+ -

=

+

�

�

�

�

Ruch harmoniczny

Ruch harmoniczny

związek z ruchem jednostajnym po

związek z ruchem jednostajnym po

okręgu

okręgu

Wykład

Wykład

3

3

2

2

x

y

v

v

v

A

w

=

+ =

2

2

2

x

y

a

a

a

A

w

=

+

=

(

)

(

)

2

2

2

2

2

2

cos

sin

r

x

y

A

t

A

t

A

w j

w j

=

+ =

+ +

+ =

Rzut ruchu jednostajnego po okręgu na dowolną jego średnicę daje

prosty ruch harmoniczny.

Jednostajny ruch po okręgu można przedstawić jako kombinację

dwóch ruchów harmonicznych prostych zachodzących wzdłuż linii

wzajemnie prostopadłych, mających tę samą amplitudę i częstość

lecz różniących się w fazie o 90°. Kiedy jedna składowa ma

maksymalne wychylenie, druga składowa znajduje się w położeniu

równowagi.

Wielkości charakteryzujące ruch jednostajny po okręgu o promieniu A.

Ruch harmoniczny

Ruch harmoniczny

składanie ruchów harmonicznych

składanie ruchów harmonicznych

Wykład

Wykład

3

3

(

)

(

)

cos

cos

y

y

x

x

y A

t

x A

t

w j

w j

=

+

=

+

(

)

(

)

cos

cos

y

y

x

x

t

A

y

x

A

t

w j

w j

+

� �

=� �

+

� �

y

x

j

j

=

1.

y

x

A

y

x

A

=

Równanie prostej ze współczynnikiem
nachylenia zależnym od amplitud
dwóch ruchów składowych

= 1

A

x

A

x

= 2

A

x

A

x

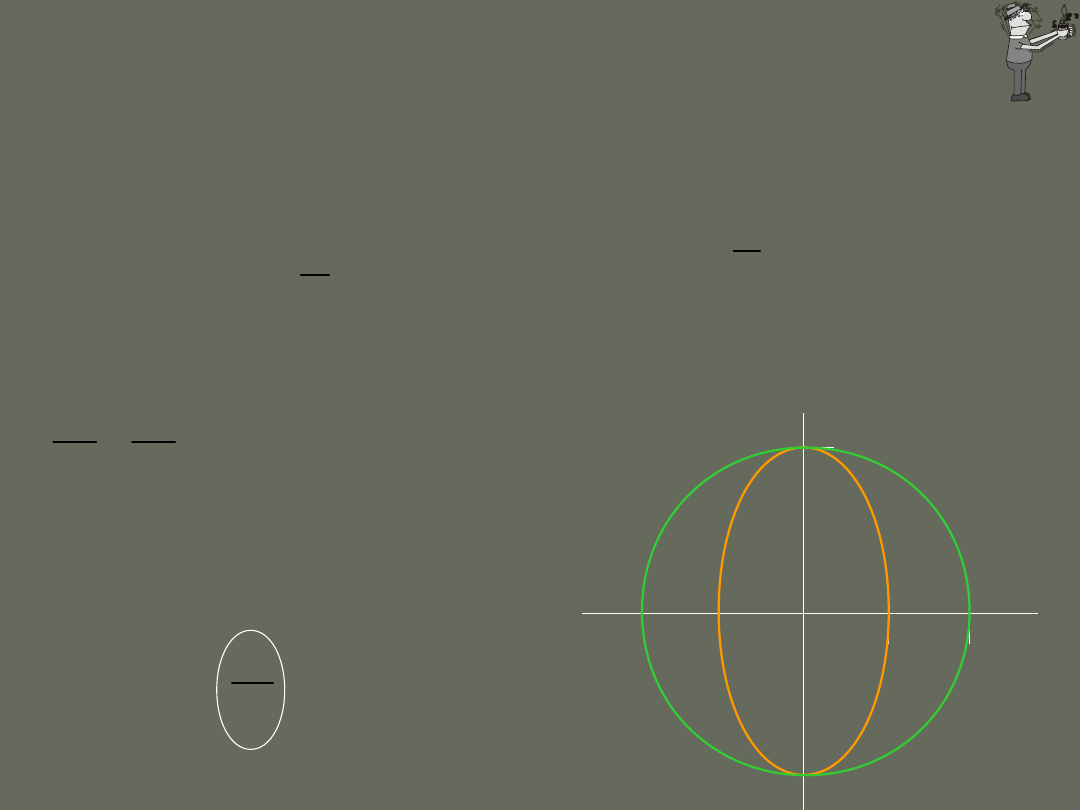
Ruch harmoniczny

Ruch harmoniczny

składanie ruchów harmonicznych

składanie ruchów harmonicznych

Wykład

Wykład

3

3

(

)

(

)

cos

sin

2

cos

y

x

y

x

x

x

y A

t

A

t

x A

t

p

w j

w j

w j

�

�

=

+ -

=

+

�

�

�

�

=

+

2

y

x

p

j

j

= -

2.

(

)

(

)

2

2

2

2

2

2

cos

sin

1

x

x

x

y

x

y

t

t

A

A

w j

w j

+

=

+

+

+

=

y

x

A

A

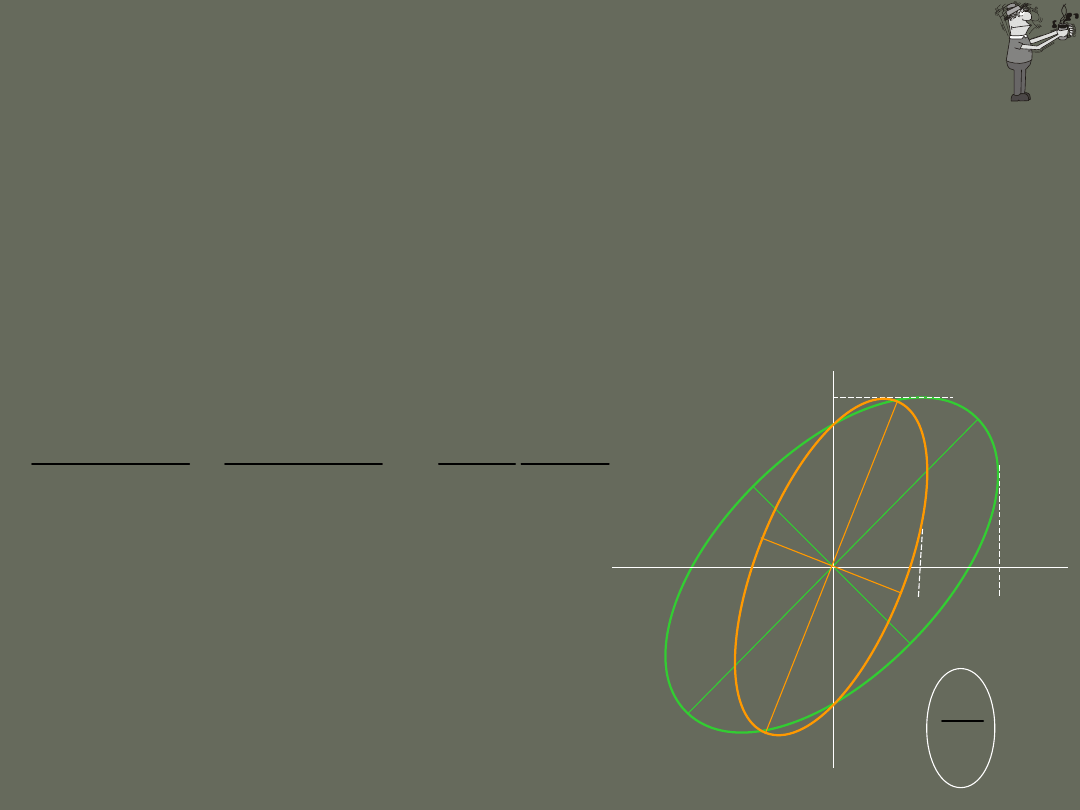
Równanie elipsy o półosiach będących
amplitudami dwóch ruchów składowych

= 2

A

x

A

x

A

x

A

x

= 1

= 1

A

x

A

x

Ruch harmoniczny

Ruch harmoniczny

składanie ruchów harmonicznych

składanie ruchów harmonicznych

Wykład

Wykład

3

3

(

)

(

)

( )

(

) ( )

(

)

(

)

cos

cos

cos

sin

sin

cos

y

x

y

x

x

x

x

y A

t

A

t

t

x A

t

w j

j

w j

j

w j

j

w j

=

+ -

=

+

+

+

=

+

Wyprowadzenie:

1.

Wstawić cosinus z drugiego równania do równania
pierwszego

2.

Zostawić po jednej stronie sinusy i podnieść obustronnie do
kwadratu

3.

Zamienić sinus kwadrat na jeden minus cosinus kwadrat i
podstawić cosinus z drugiego równania

4.

Zostawić po prawej stronie sinus kwadrat  a po lewej

stronie skorzystać z jedynki trygonometrycznej

5.

Podzielić obustronnie przez sinus kwadrat

(

)

(

)

2

2

2

2

2

cos

2

1

sin

sin

sin

y x

x

y

x

y

xy

A A

A

A

j

j

j

j

+

-

=

y

x

j

j

j

= -

3.

y

x

A

A

Równanie obróconej

elipsy

= 2

A

x

A

x

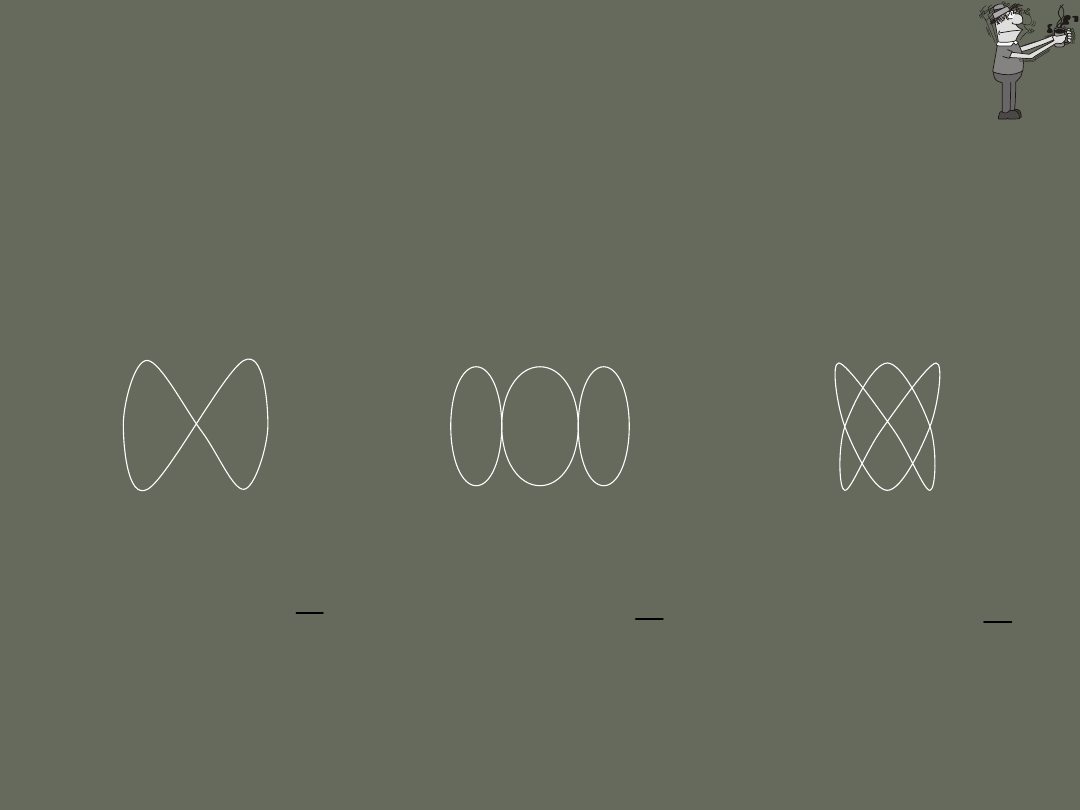
Ruch harmoniczny

Ruch harmoniczny

składanie ruchów harmonicznych

składanie ruchów harmonicznych

1

2

:

1:3

2

x

y

w w

p

j

j

j

=

=

-

=

Wykład

Wykład

3

3

1

2

:

1:2

2

x

y

w w

p

j

j

j

=

= -

=

We wszystkich rozważanych przypadkach okres drgania wypadkowego

równa się okresowi drgań składowych, ponieważ częstość kątowa była

stała.

Tory zakreślane prze punkty materialne odbywające dwa ruchy harmoniczne

wzajemnie prostopadłe noszą nazwę krzywych lub figur Lissajous.

1

2

:

2:3

3

x

y

w w

p

j

j

j

=

= -

=

Ruch harmoniczny tłumiony

Ruch harmoniczny tłumiony

2

2

F ma

dx

d x

kx b

m

dt

dt

=

-

-

=

2

2

2

2

0

2

0

2

0

d x b dx k

x

dt

m dt m

d x

dx

x

dt

dt

d

w

+

+

=

+

+

=

Wykład

Wykład

3

3

(

)

0

cos

t

x A e

t

d

w j

-

=

+

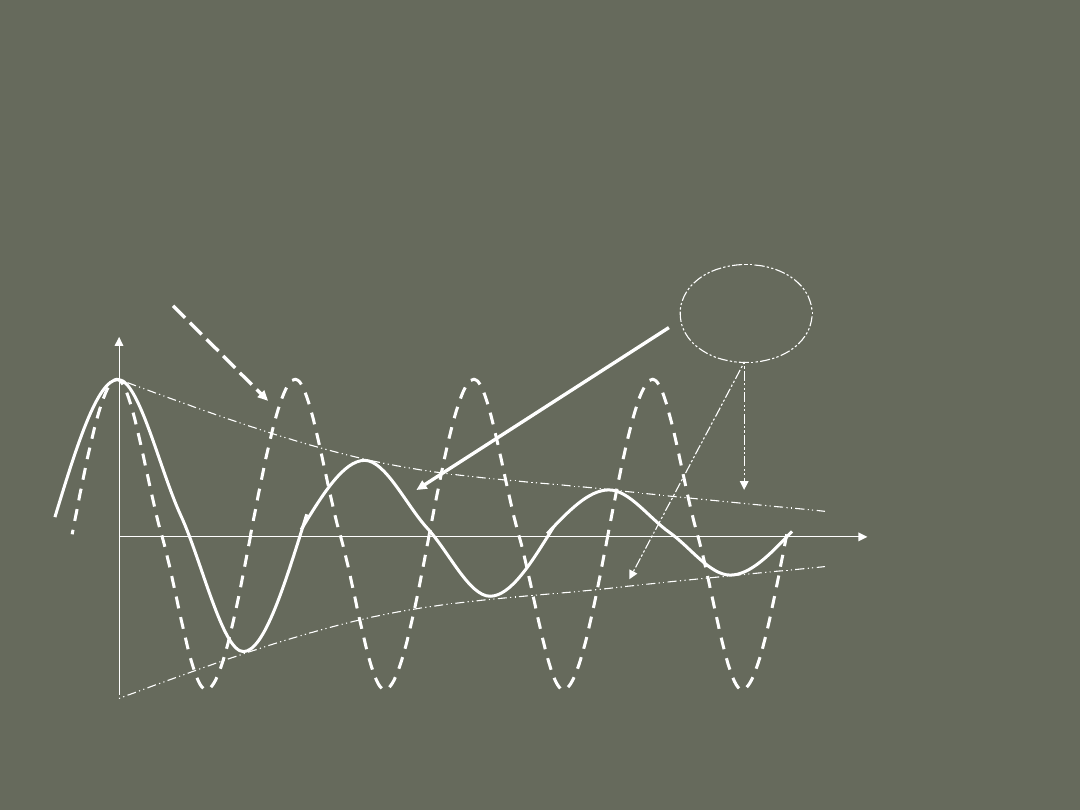
W wyniku działania tarcia amplituda drgań zmniejsza się stopniowo do

zera. Mówimy, że taki ruch jest tłumiony przez tarcie i nazywamy go

ruchem harmonicznym tłumionym.

Z drugiej zasady dynamiki Newtona

siła sprężystości
przywracająca
równowagę

siła hamująca
ruch jest
proporcjonalna
do prędkości i
skierowana do
niej przeciwnie

stała tłumienia

współczynnik oporu

częstość drgań
własnych, bez
tłumienia

początkowa
maksymalna
amplituda

częstość drgań
tłumionych

amplituda drgań
tłumionych zmienia
się wykładniczo

k

m

b

Ruch harmoniczny tłumiony

Ruch harmoniczny tłumiony

2

2

0

w

w

d

=

-

Wykład

Wykład

3

3

(

)

(

)

0

cos

0

t

x A e

t

d

w

j

-

=

+ =

(

)

(

)

0

0

cos

0

x A

t

w

j

=

+ =

x

t

2

2

0

d

w

<

W ośrodku o silnym
tłumieniu powstaje
ruch aperiodyczny.

warunek powstania
drgań tłumionych
periodycznych

Drgania wymuszone

Drgania wymuszone

cos

x A

t

w

=

Wykład

Wykład

3

3

( )

2

2

d x

kx F t

dt

=-

+

2

2

0

0

cos

cos

cos

m A

t m A

t F

t

w

w

w

w

w

-

=

+

Drgania wymuszone powstają gdy na oscylator działa siła zewnętrzna.

Równanie oscylatora ma wówczas postać:

Siła zewnętrzna może mieć
różną zależność funkcyjną
od czasu.

( )

( )

0

cos

F t

F

t

w

=

Siła o częstości różnej od
częstości własnej układu

(

)

0

2

2

0

F

A

m w

w

=

-

Masa m drga z tą samą częstością co siła, ale z
amplitudą zależną zarówno od częstości siły jak i od
częstości własnej oscylatora.

częstość
przyłożona

częstość
własna

Rezonans

Rezonans

(

)

sin

x A

t

w j

=

-

Wykład

Wykład

3

3

(

) ( )

2

2

2

2

0

0

d

b

d

w

w

w

w

�

�

-

+

�

�=

2

0

2

cos

d x

dx

kx b

F

t

dt

dt

w

=-

-

+

(

)

2

2

2

0

2

2

0

4

2

0

1

2

r

b

b

w w

w

w

w

w

-

-

+

=

=

-

(

)

0

2

2

2

2

2

2

2 2

0

0

arctan

F

b

A

m

b

w

j

w

w

w

w

w

=

=

-

-

+

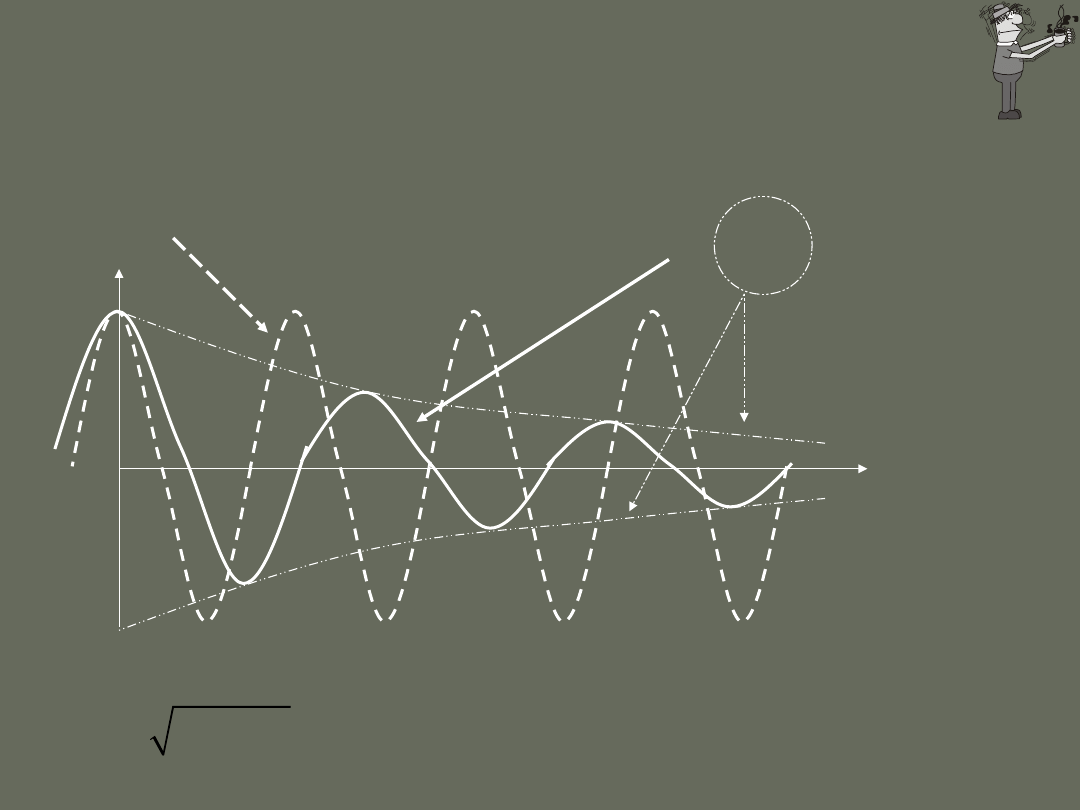
Drgania wymuszone osiągają maksymalną amplitudę A gdy wyrażenie

podpierwiastkowe ma minimum. Gdy pulsacja siły wymuszającej jest tak dobrana,

aby drgania wymuszone odbywały się z maksymalną amplitudą to mamy do

czynienia ze zjawiskiem rezonansu.

Częstość

rezonansowa

Rezonans

Rezonans

Wykład

Wykład

3

3

2

2

0

1

2

r

b

w

w

=

-

Częstość rezonansowa jest zawsze

mniejsza od częstości drgań własnych

układu. Różnica pomiędzy tymi

częstościami rośnie ze wzrostem

współczynnika oporu.

Dla układów o bardzo małym tłumieniu

można przyjąć, że pulsacja rezonansowa

siły wymuszającej jest równa pulsacji

drgań własnych.

Drgania elektromagnetyczne

Drgania elektromagnetyczne



Wprowadzenie

Wprowadzenie



Analiza jakościowa drgań elektromagnetycznych

Analiza jakościowa drgań elektromagnetycznych



Analiza ilościowa drgań elektromagnetycznych

Analiza ilościowa drgań elektromagnetycznych

•

Drgania w układach LC

Drgania w układach LC

•

Drgania w układach LRC

Drgania w układach LRC



Drgania elektromagnetyczne wymuszone

Drgania elektromagnetyczne wymuszone

•

Zjawisko rezonansu

Zjawisko rezonansu



Elektryczne obwody drgające otwarte

Elektryczne obwody drgające otwarte

Wykład 3

Wykład 3

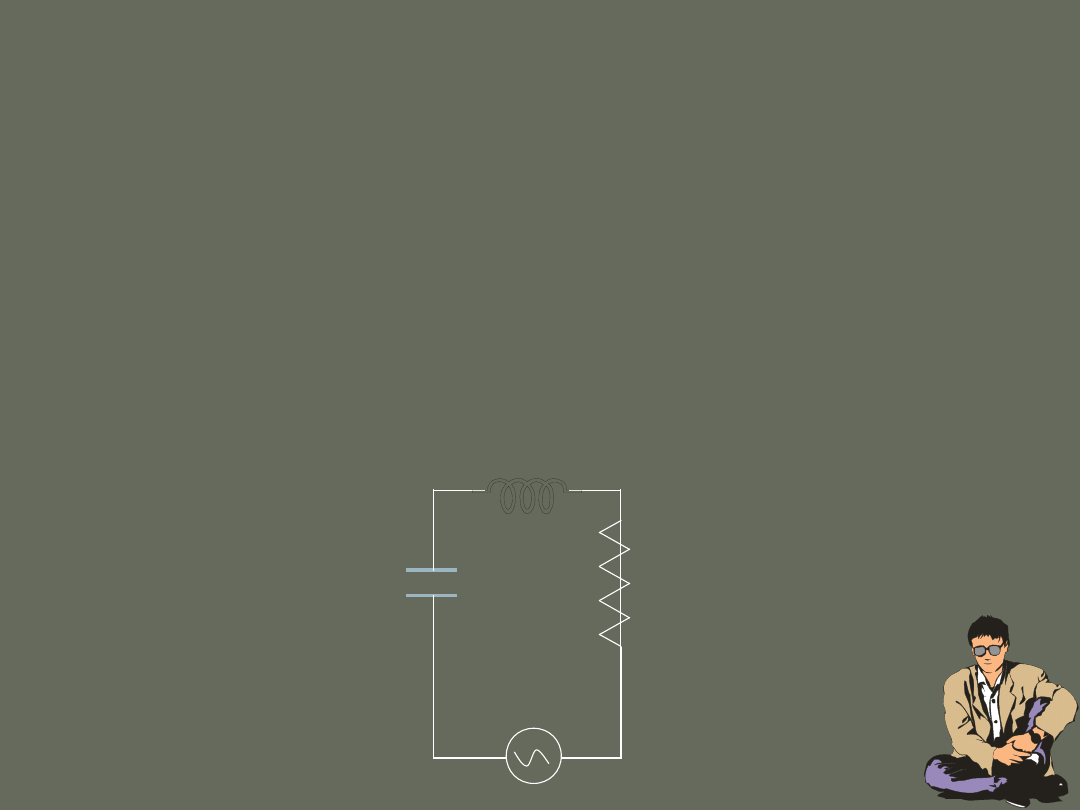
Wprowadzenie

Wprowadzenie

Wykład 3

Wykład 3

Każdy układ drgający może być opisany z punktu widzenia zasady zachowania

energii.

Drgania elektromagnetyczne powstają w obwodach elektrycznych typu LC/RLC i

mogą być scharakteryzowane kolejnymi przemianami energii pola

elektrycznego w energię pola magnetycznego i odwrotnie.

energia pola magnetycznego cewki

energia pola

elektrycznego

kondensatora

energia

termiczna

+

_

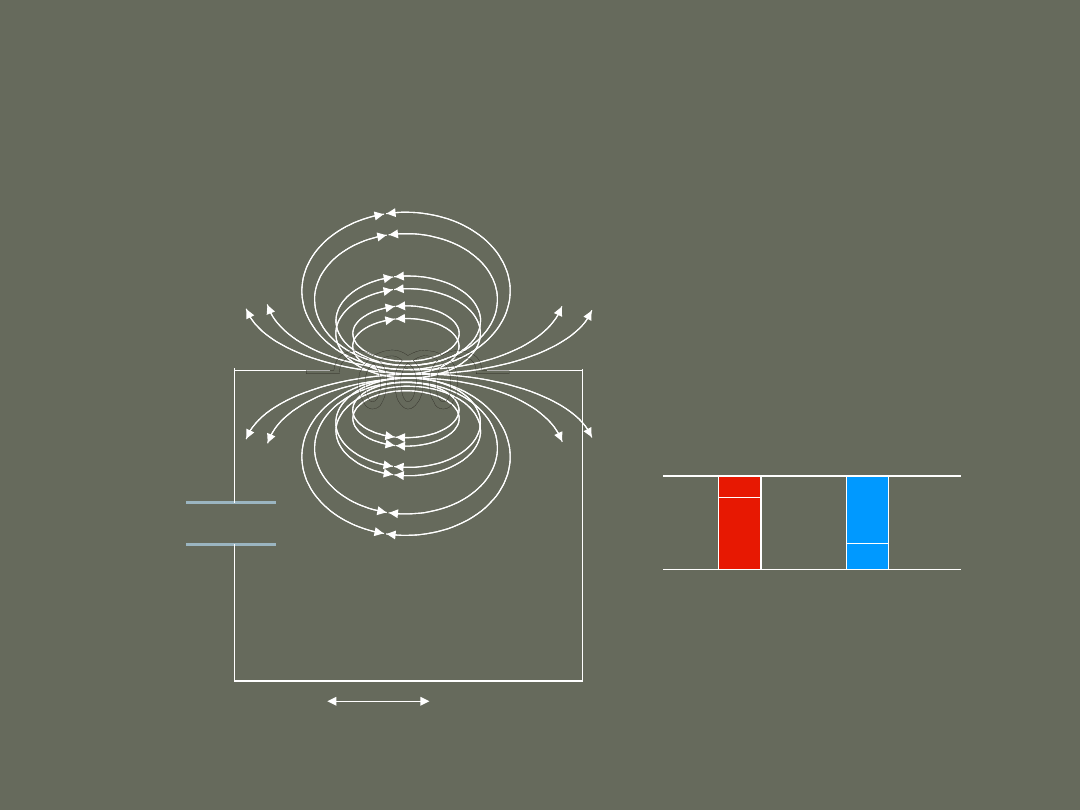
Analiza jakościowa drgań

Analiza jakościowa drgań

elektromagnetycznych

elektromagnetycznych

Wykład 3

Wykład 3

+

_

E

e

E

m

I= 0

+

_

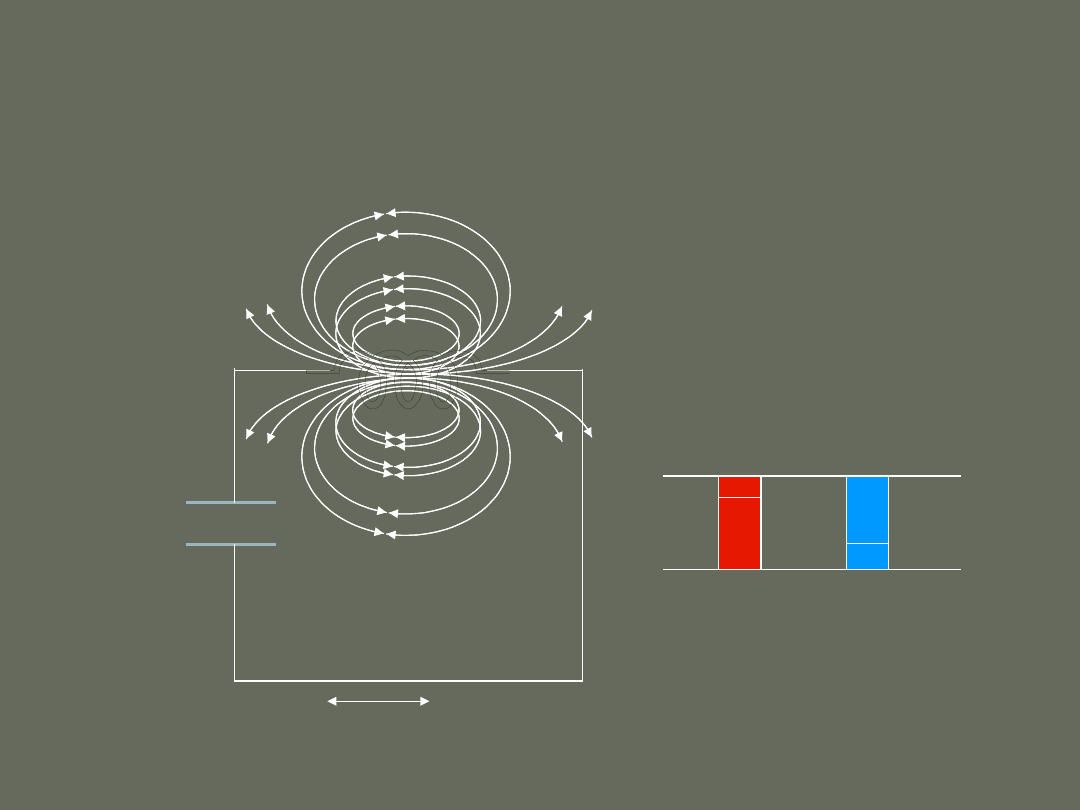
Analiza jakościowa drgań

Analiza jakościowa drgań

elektromagnetycznych

elektromagnetycznych

Wykład 3

Wykład 3

+

_

E

e

E

m

I= 0

t = 0

t = T/4

t = T/2

t = 3T/4

t = T

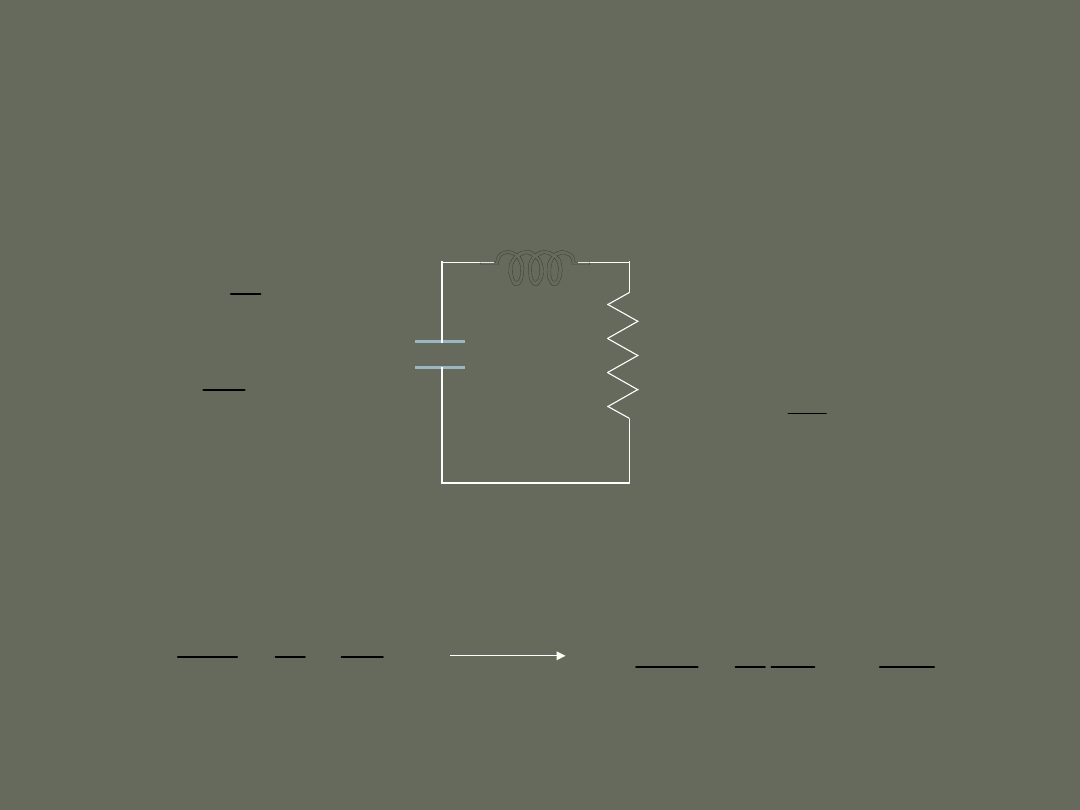
Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

Wykład 3

Wykład 3

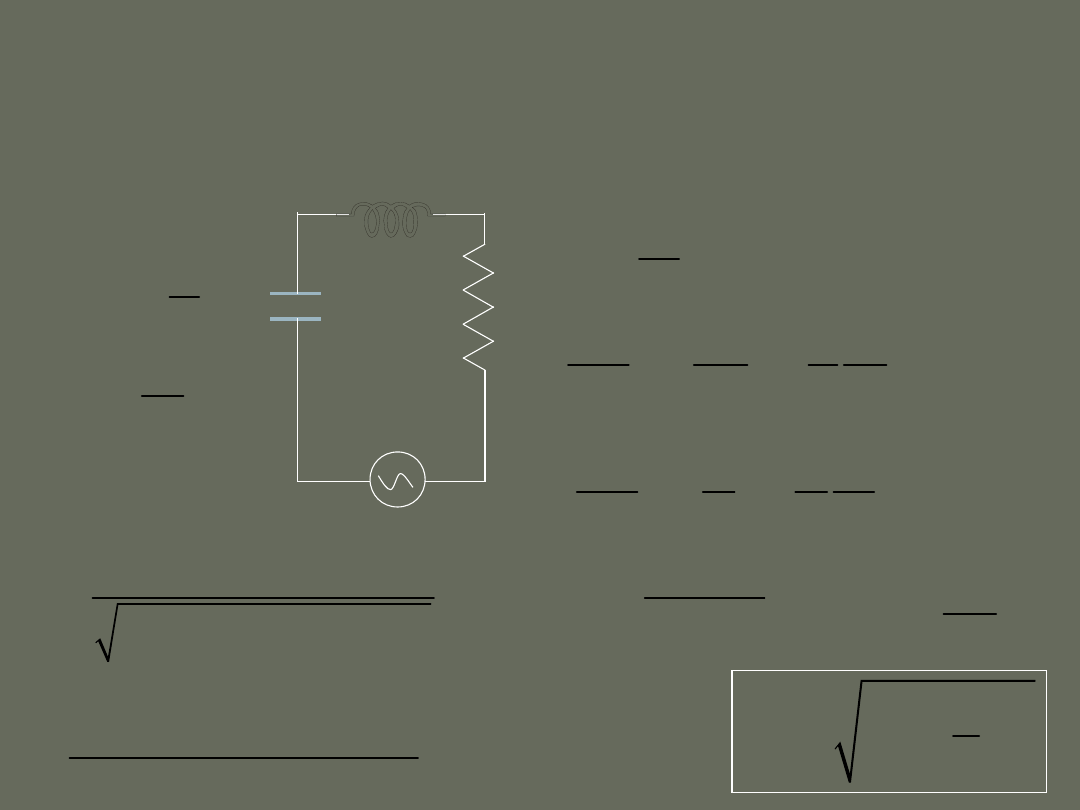
C

dI

L

U

IR

dt

-

=

+

L

C

R

II prawo Kirchhoffa

C

q

U

C

dq

I

dt

=

=

2

2

d q q dq

L

R

dt

C dt

-

= +

2

2

1

d q R dq

q

dt

L dt

LC

+

=-

Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

drgania w układzie LC

drgania w układzie LC

Wykład 3

Wykład 3

2

2

1

d q

q

dt

LC

=-

(

)

0

cos

Q

q

t

w

j

=

+

2

2

1

d q R dq

q

dt

L dt

LC

+

=-

2

0

w

częstość drgań

własnych

(

)

0

0

sin

dq

Q

t

dt

I

w

w

j

= =-

+

max

I

(

)

0

cos

A

x

t

w

j

=

+

2

2

d x

k

x

dt

m

=-

częstość drgań

własnych

2

0

w

(

)

0

0

sin

dx

A

t

dt

v

w

w

j

= =-

+

1

m

L

k

C

�

�

Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

drgania w układzie LC

drgania w układzie LC

Wykład 3

Wykład 3

2

1

2

k

E

mv

=

(

)

2

2

0

cos

2

e

Q

C

E

t

w

j

=

+

2

1

2

p

E

kx

=

2

1

2

m

E

LI

=

(

)

2

2

0

sin

2

m

Q

C

E

t

w

j

=

+

(

)

2

2

2

0

0

1

sin

2

m

L

t

E

Q

w

w

j

=

+

2

1 1

2

e

q

C

E

� �

= � �

� �

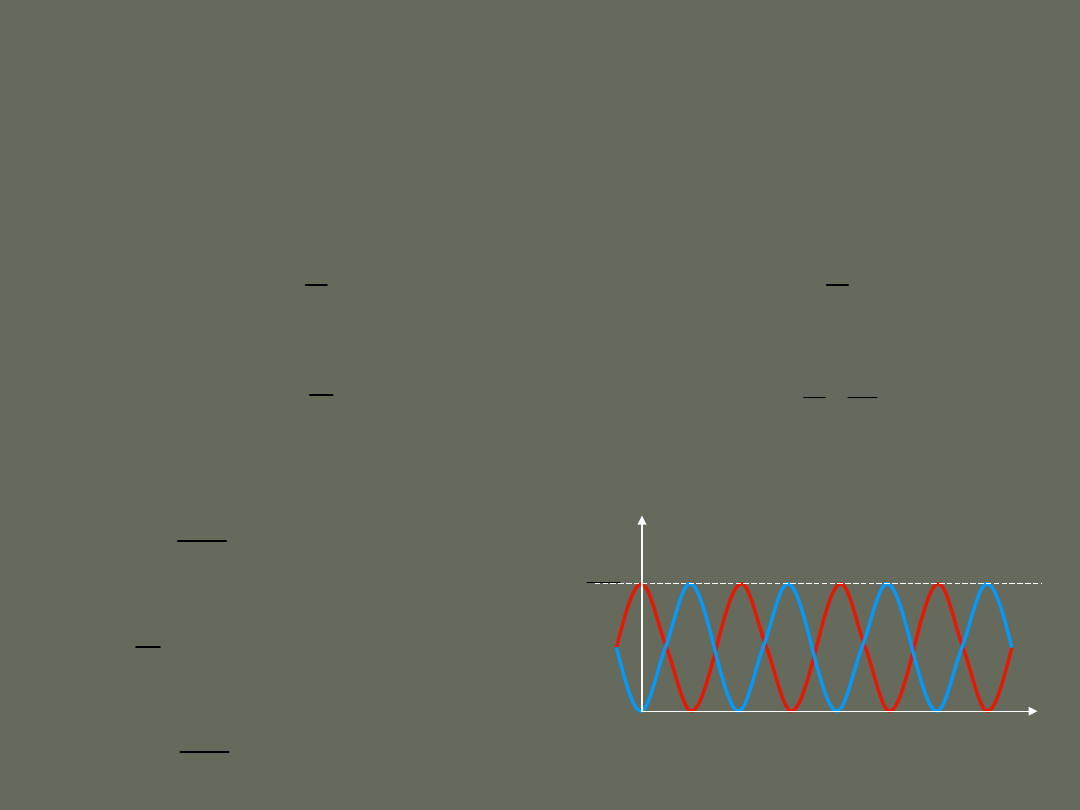
E

t

T/2

T

2

2

Q

C

(

)

m

e

E

E

E

=

+

kulka

cewka

sprężyna

kondensator

Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

drgania w układzie LC

drgania w układzie LC

(

)

max

0

0

sin

90

U

I

t

w

w

j

=-

+ -

Wykład 3

Wykład 3

(

)

(

)

max

0

max

0

0

sin

cos

U

I

t

dt I

t

w

j

w

w

j

=-

+

=

+

�

dU

I

dt

=

(

)

max

0

sin

I

I

t

w

j

=-

+

t

U, I

U

I

Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

drgania w układach kulka/sprężyna – LC

drgania w układach kulka/sprężyna – LC

Wykład 3

Wykład 3

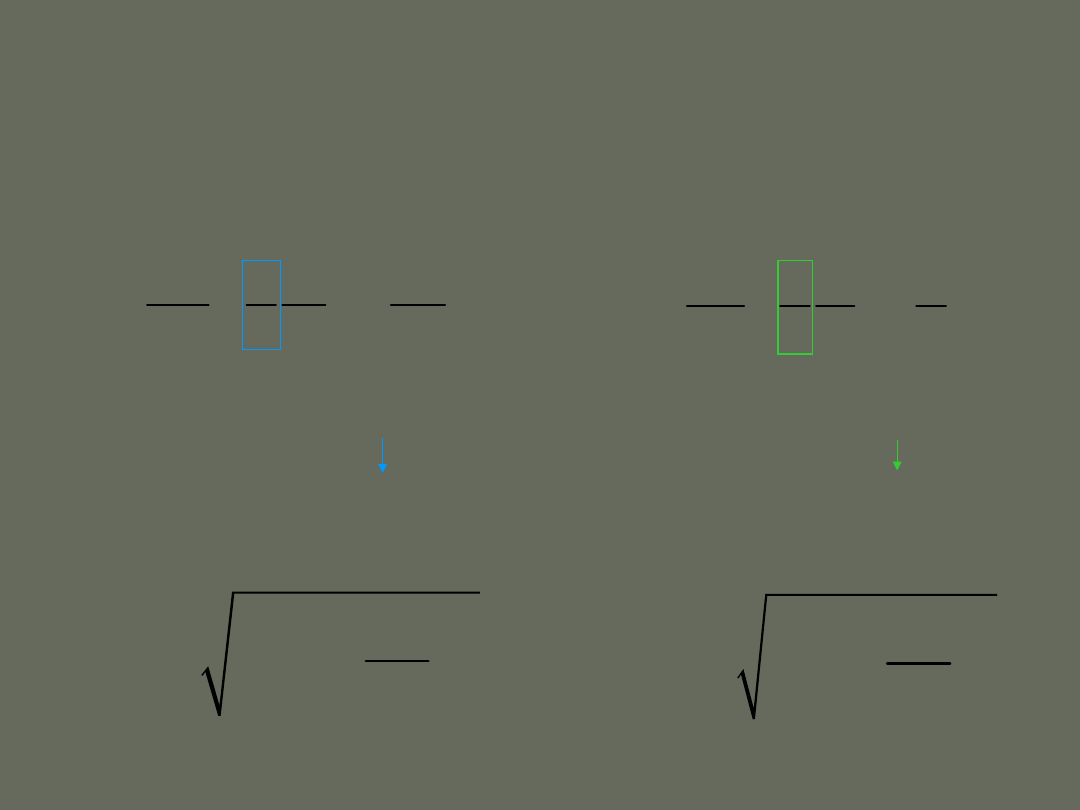
2

2

1

2

1

2

x

dx

dt

mv

kx

dv

m

kx

dt

k

m

=-

2

2

1

2

1 1

2

1

1

q

dq

dt

LI

q

C

dI

L

q

dt

C

LC

� �

� �

� �

=-

położenie  ładunek

prędkość  natężenie prądu

energia kinetyczna  energia magnetyczna

energia potencjalna  energia elektryczna

II prawo Newtona  II prawo Kirchhoffa

częstość  częstość

(

)

/2

cos

bt m

x Ae

t

w j

-

=

+

Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

drgania w układzie LRC

drgania w układzie LRC

2

2

d x b dx

k

x

dt

m dt

m

+

=-

Wykład 3

Wykład 3

2

2

1

d q R dq

q

dt

L dt

LC

+

=-

częstość drgań

tłumionych

2

2

0

2

b

m

w

w

� �

=

- � �

� �

(

)

/2

cos

Rt L

q Qe

t

w j

-

=

+

2

2

0

2

R

L

w

w

� �

=

- � �

� �

częstość drgań

tłumionych

(

)

0

cos

0

q Q

t

w

j

=

+ =

Analiza ilościowa drgań

Analiza ilościowa drgań

elektromagnetycznych

elektromagnetycznych

drgania w układzie LRC – drgania tłumione

drgania w układzie LRC – drgania tłumione

Wykład 3

Wykład 3

(

)

/2

cos

0

Rt

L

q Qe

t

w j

-

=

+ =

q

t

Drgania elektromagnetyczne

Drgania elektromagnetyczne

wymuszone

wymuszone

układ LRC z siłą elektromotoryczną

układ LRC z siłą elektromotoryczną

2

0

2

cos

d x

k

b dx

x

F

t

dt

m

m dt

=-

-

+

W

Wykład 3

Wykład 3

0

sin

C

dI

L

E

t U

RI

dt

-

+

W =

+

C

q

U

C

dq

I

dt

=

=

2

0

2

1

cos

d q

R dq

q

E

t

dt

LC

L dt

=-

-

+

W

0

cos

E E

t

=

W

C

L

R

(

)

sin

q Q

t

w j

=

-

(

) (

)

2

2

2

2

0

0

d

R

d

w

�

�

- W

+ W

�

�=

W

2

2

0

1

2

r

R

w

W =

-

(

)

0

2

2

2

2

2

2

2

2

0

0

arctan

E

R

Q

L

R

j

w

w

W

=

=

- W

- W

+ W

2

0

1

LC

w =