1

Równowagi kompleksowania w
roztworach

Są one zawsze sumą dwóch procesów:

redukcji i utlenienia; są więc
algebraiczną sumą reakcji
połówkowych red-ox, uzgodnionych
co do liczby przenoszonych
elektronów.

2

Równowagi kompleksowania w
roztworach

Rozważamy reakcje tworzenia związków kompleksowych

(koordynacyjnych) w roztworach.

Kompleksem (związkiem koordynacyjnym) nazywamy taki

związek, w którym występuje wiązanie koordynacyjne,

a więc związane z uwspólnieniem pary elektronowej

pochodzącej w całości od donora (liganda).

Akceptorami par elektronowych są metale i ich jony

(zwłaszcza metale grup przejściowych) zwane dalej

atomami (jonami) centralnymi; donorami (ligandami)

są jony lub cząsteczki, często organiczne, np. H

2

O,

NH

3

, aminy, kwasy karboksylowe.

Tak więc tworzenie się związku kompleksowego związane

jest z przeniesieniem (przyłączeniem) całych związków

chemicznych lub jonów wieloatomowych. Są to reakcje

równowagowe polegające na przeniesieniu cząsteczek

lub grup atomów.

3

Tworzenie związków
kompleksowych

Liczba par elektronowych jaką przyjmuje jon

(atom)

centralny

nazywa

się

liczbą

koordynacji

. Np. jony Cu

+2

z amoniakiem jako

ligandem mają liczby koordynacji 1, 2, 3 i 4.
Oznacza to, że w roztworze wodnym tworzenie
kolejnych kompleksów stanowi serię reakcji
następczych:
Cu

+2

+ NH

3

 [Cu(NH

3

)]

+2

[Cu(NH

3

)]

+2

+ NH3

 [Cu(NH

3

)

2

]

+2

[Cu(NH

3

)

2

]

+2

+ NH3  [Cu(NH

3

)

3

]

+2

[Cu(NH

3

)

3

]

+2

+ NH

3

 [Cu(NH

3

)

4

]

+2

które opisywane są kolejnymi

stałymi tworzenia

:

4

Tworzenie związków
kompleksowych





K

Cu NH

Cu

NH

1

3

2

2

3







[ (

)]

[

][

]









K

Cu NH

Cu NH

NH

2

3 2

2

3

2

3







[ (

) ]

[ (

)] [

]









K

Cu NH

Cu NH

NH

3

3 3

2

3 2

2

3







[ (

) ]

[ (

) ] [

]









K

Cu NH

Cu NH

NH

4

3 4

2

3 3

2

3







[ (

) ]

[ (

) ] [

]

5

Tworzenie związków
kompleksowych

Niekiedy

wygodniej

jest

operować

sumaryczną

stałą

tworzenia

danego

kompleksu,

zwaną

stałą

trwałości

kompleksu:







1

1

3

2

2

3









K

Cu NH

Cu

NH

[ (

)]

[

][

]







2

1

2

3 2

2

2

3

2











K K

Cu NH

Cu

NH

[ (

) ]

[

][

]

6

Tworzenie związków
kompleksowych







3

1

2

3

3 3

2

2

3

3



 







K K K

Cu NH

Cu

NH

[ (

) ]

[

][

]







4

1

2

3

4

3 4

2

2

3

4



  







K K K K

Cu NH

Cu

NH

[ (

) ]

[

][

]

7

Tworzenie związków
kompleksowych

ogólnie:

 
Stałe trwałości są stablicowane, zwykle w

postaci

ich

logarytmów

dziesiętnych

(log

i

).

 







n

i

i

N

n

n

K

Me L

Me L





1

[

( ) ]

[

][ ]

8

Tworzenie związków
kompleksowych

Niektóre związki kompleksowe tworzą się

bezpośrednio (bez kompleksów pośrednich),
np.:

kompleks cyjankowy żelaza(II),

[Fe(CN)

6

]

-4

(log

6

=24)

kompleks cyjankowy żelaza(III),

[Fe(CN)

6

]

-3

(log

6

=36)

kompleks cyjankowy niklu(II),

[Ni(CN)

4

]

-2

(log

4

=31.3)

kompleks cyjankowy cynku(II),

[Zn(CN)

4

]

-2

(log

4

=16.7)

9

Tworzenie związków
kompleksowych

Szczególnie przydatne bywają wzory na

ułamki

molowe

form

metalu

(wyprowadzone wprost z wyrażeń na stałe
tworzenia).

Jeżeli metal w roztworze może istnieć w

postaciach z 0, 1, 2, ..., n przyłączonymi
ligandami, to ułamek 

i

mówi, jaka jego

część (molowo) związana jest w kompleks z
i ligandami. Oczywiście



0

+

1

+... +

n

=1.

10

Tworzenie związków
kompleksowych









0

1

2

2

1

1







 

[ ]

[ ] ...

[ ]

L

L

L

n

n











1

1

1

2

2

1







 

[ ]

[ ]

[ ] ...

[ ]

L

L

L

L

n

n

11

Tworzenie związków
kompleksowych

.....................................

Wzory

te

są

przydatne

wtedy,

gdy

równowagowe znane jest stężenie liganda.











2

2

2

1

2

2

1







 

[ ]

[ ]

[ ] ...

[ ]

L

L

L

L

n

n











n

n

n

n

n

L

L

L

L







 

[ ]

[ ]

[ ] ...

[ ]

1

1

2

2

12

Wpływ pH na tworzenie się
związków kompleksowych

Wiele ligandów to słabe zasady: NH

3

, CN

-

, reszty

kwasów karboksylowych. Oznacza to, że w roztworze

wodnym ulegają one reakcji hydrolizy, która przesuwa

równowagę tworzenia kompleksów (bowiem z układu

ubywa formy będącej ligandem).

Jeżeli znamy równowagowe stężenie jonów H

+

w

układzie, można zastosować wzór

 

gdzie c

L

- całkowite stężenie ligandu, K

a

- stała dysocjacji

kwasowej kwasu sprzężonego z ligandem-zasadą.

 Łatwo zauważyć, że w takich wypadkach obniżanie pH

powoduje osłabienie kompleksujących własności

ligandów.

[ ]

[

]

L

K

K

H

c

a

a

L









13

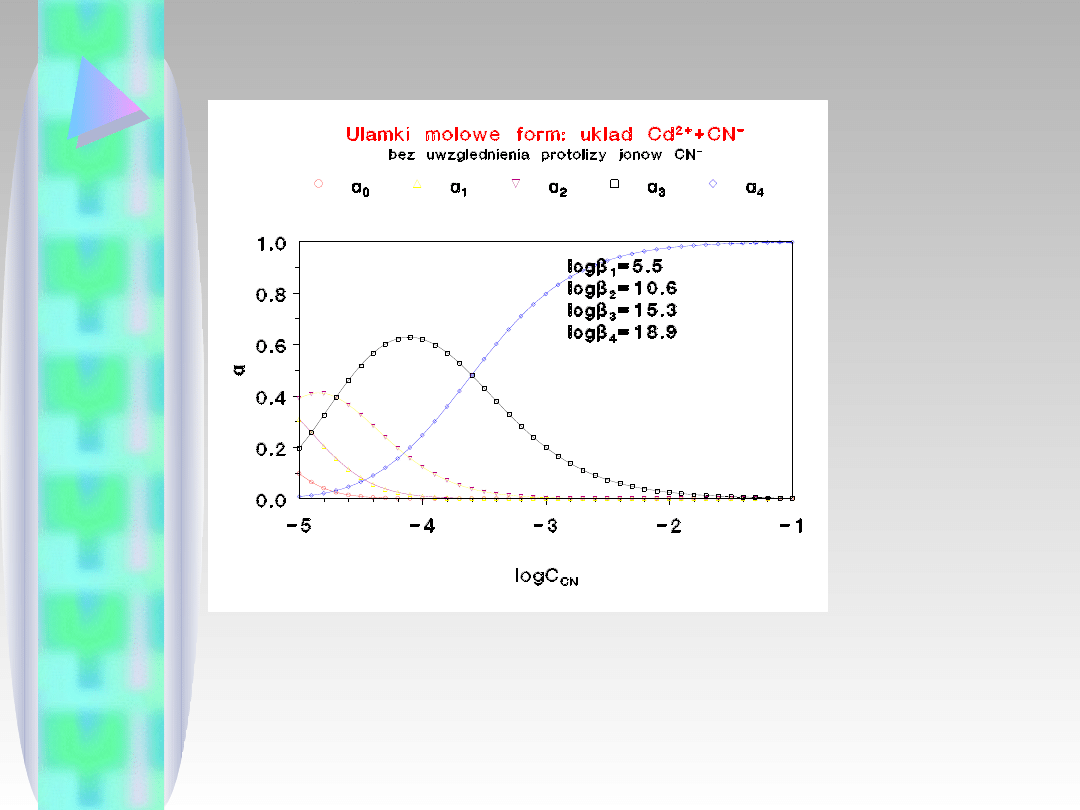
Diagramy tworzenia związków

kompleksowych

Typowy diagram, pozwalający określić niezbędny

nadmiar liganda, potrzebny do tego, żeby w roztworze

znajdował się przede wszystkim właściwy kompleks.

Jak widać nie dla każdego kompleksu jest to możliwe.

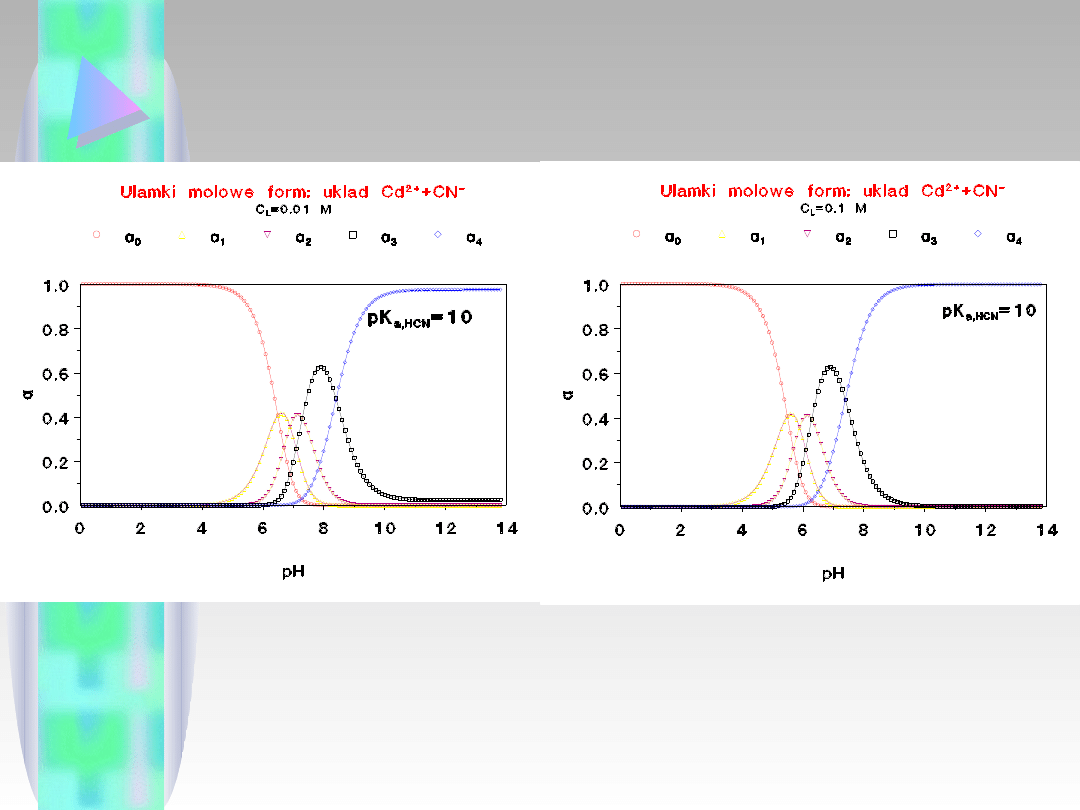
14

Diagramy tworzenia związków

kompleksowych

Jak widać, zmiana stężenia liganda niewiele wpływa

na rozkład form w funkcji pH.

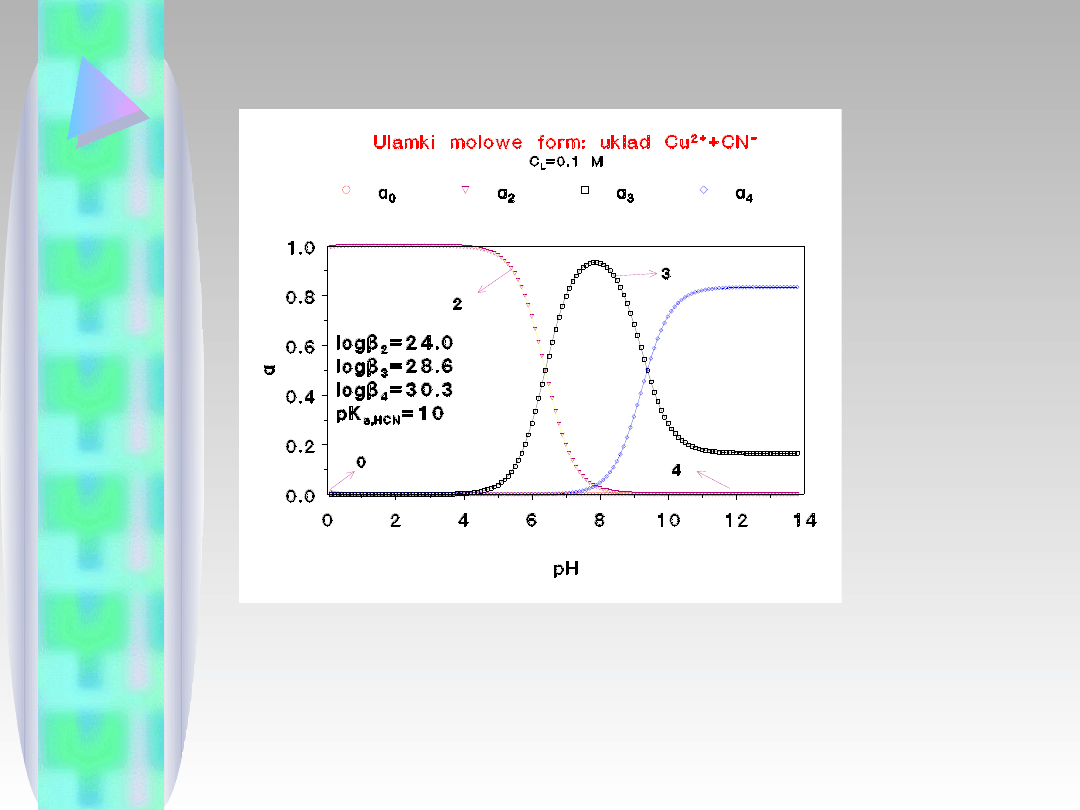
15

Diagramy tworzenia związków

kompleksowych

Proszę porównać te rozkłady z odpowiednim

wykresem dla kadmu. Są zupełnie różne. Na

kształt tych diagramów wpływ maja przede

wszystkim stałe trwałości.

16

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

Metody

iteracyjne

pozwalają

obliczyć

pierwiastek równania lub rozwiązać układ
równań.

W przypadku jednego równania należy je

najpierw sprowadzić do postaci x=f(x).

17

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

Zadanie:

rozwiąż równanie x-sinx=1 (x w

radianach).

Równanie nie jest rozwiązywalne analitycznie.

1.

Przekształcamy je do postaci x=sinx+1

2.

Wybieramy dowolną wartość x (np. 10). Jest

to nasze przybliżenie „zerowe”, x

0

.

3.

x

0

podstawiamy do prawej strony. Wynik

jest przybliżeniem nr 1, x

1

.

4.

x

1

podstawiamy do prawej strony. Wynik

jest przybliżeniem nr 2, x

2

.

5.

Procedurę powtarzamy aż x

n

różni się od x

n-1

o mniej niż zadana dokładność.

18

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

i (nr

iter.)

x

i

0
1
2

3
4
5

6

7
8
9

10
11
12

13

10.0000000000

0.4559788891
1.4403414011

1.9915028172
1.9128006336
1.9420843619

1.9318607990

1.9355213074
1.9342218938
1.9346845959

1.9345200154
1.9345785787
1.9345577428

1.9345651562

19

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

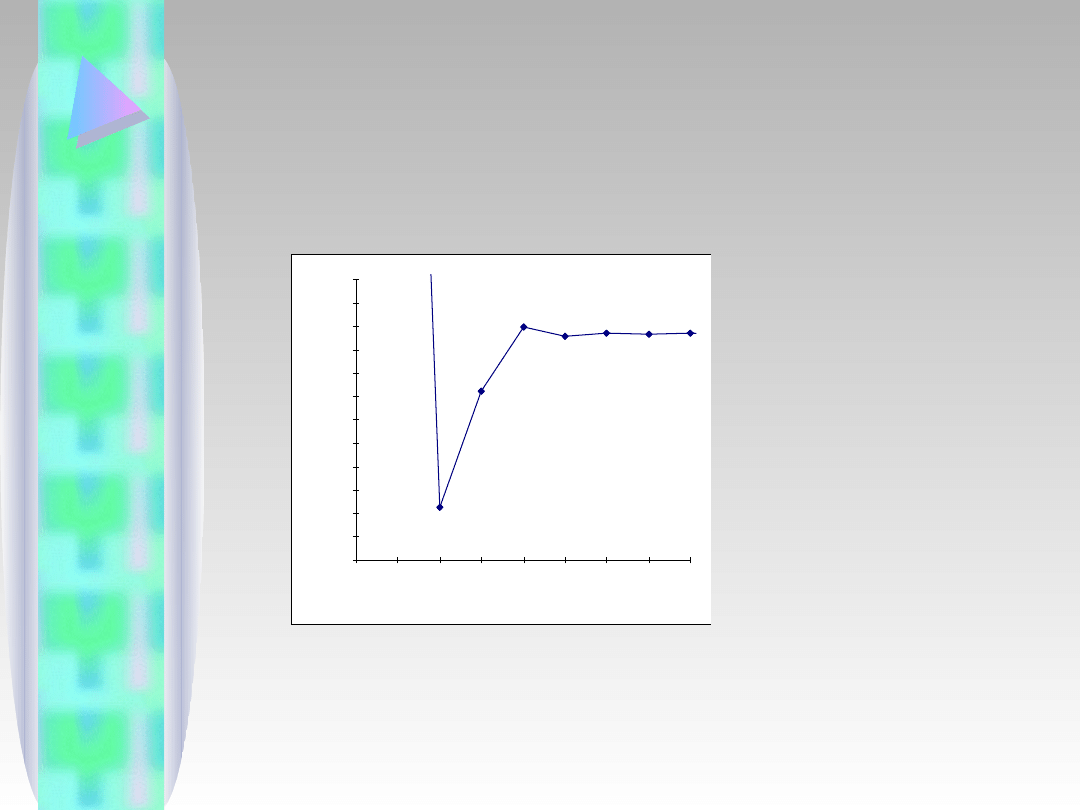
Już po 28 iteracjach wynik jest dokładny na 10.

miejscu po przecinku (x=1.9345632108).

Zwróćmy uwagę na oscylacje rozwiązań wokół

wartości dokładnej. Nie zawsze tak jest (iteracje

mogą być zbieżne jednostronnie lub nie być w

ogóle zbieżnymi). Zbieżność trzeba sprawdzić!

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

2.4

0

1

2

3

4

5

6

7

8

nr iteracji

w

a

rt

o

œ

æ

x

20

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

W

obliczeniach

analitycznych

metody

iteracyjne szczególnie nadają się do
rachunków związanych z równowagami
kompleksowania.

Zadanie:

Do 1 dm

3

0.01 M roztworu

Sn(NO

3

)

2

dodano 0.05 moli KCl. Oblicz

rozkład kompleksów chlorkowych cyny.
log

1

=1.5,

log

2

=2.2,

log

3

=2.0,

log

4

=1.5.



1

=31.62,

2

=158.5,

3

=100.0,

4

=31.62)

Reakcje uboczne pomiń.

21

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

Rozwiązanie analityczne, mocno przybliżone:
 Załóżmy, że tworzą się głównie kompleksy SnCl

+

(będzie to zaraz widoczne). Gdyby to była prawda,

to stężenie wolnych jonów chlorkowych powinno

wynosić [L]=0.05-0.01=

0.04

. Podstawiamy tę

wartość do wyrażeń na ułamki molowe form:



0

=1/(1 + 1.2648 + 0.2536 + 0.0064 + 0.000081) =

0.396



1

=0.501, 

2

=0.100, 

3

=0.00253, 

4

=0.0000321

 Widać,

że

wprawdzie

rzeczywiście

przeważa

kompleks SnCl

+

, ale wolnej formy Sn

2+

jest

niewiele mniej. Stawia to pod niejakim znakiem

zapytania nasze założenie i użytą wartość [L]=0.04

M.

22

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

Rozwiązanie iteracyjne:
Niech założenie że tworzą się wyłącznie kompleksy

SnCl

+

([L]=0.05-0.01=0.04)

będzie

naszym

„zerowym x-em”. Obliczenia z poprzedniego
rozwiązania, dające 

0

=0.396, 

1

=0.501, 

2

=0.100,



3

=0.00253, 

4

=0.0000321, pozwalają udokładnić

[L]:

 [L]=0.05-

(0.501+2*0.100+3*0.00253+4*0.0000321)*0.01

[L]=

0.0429

 Widać, że wprawdzie rzeczywiście przeważa kompleks

SnCl

+

, ale wolnej formy Sn

2+

jest niewiele mniej.

Stawia to pod niejakim znakiem zapytania nasze
założenie i użytą pierwotnie wartość [L]=0.04 M.

23

Zastosowania metody iteracyjnej w

obliczeniach chemicznych

Do następnego etapu bierzemy więc [L]=0.0429,

otrzymując:



0

=0.376,



1

=0.511,



2

=0.110,



3

=0.00297, 

4

=0.0000404

 
Różnica nie jest wielka (w tym wypadku). Powtórzmy

obliczenia jeszcze raz, na wszelki wypadek:

[L]=0.05-(0.511+2*0.110+3*0.00297+4*0.0000404)*0.01

[L]=0.0426

co daje 

0

=0.378, 

1

=0.510, 

2

=0.109, 

3

=0.00293,



4

=0.0000397 oraz [L]=

0.0426

.

 
Na żądanym poziomie dokładności (tutaj trzy cyfry

znaczące) obliczenia można zakończyć.