dr inż. Katarzyna Halicka

dr inż. Katarzyna Halicka

Politechnika Białostocka

Wydział Zarządzania

Katedra Informatyki Gospodarczej i Logistyki

Prognozowanie Gospodarcze, Ćwiczenia
3

Prognozowanie

Prognozowanie

Gospodarcze

Gospodarcze

Ćwiczenia 4

Składowe szeregów czasowych

Składowe szeregów czasowych

Każdy rzeczywisty szereg czasowy obrazujący

pewne zjawisko gospodarcze jest złożeniem
dwóch składowych:



składowej systematycznej, będącej

wynikiem oddziaływania stałego zestawu
bodźców na zmienną prognozowaną,



składowej przypadkowej (nieregularnej,

składnika losowego), będącej efektem
oddziaływania przyczyn
o charakterze losowym.

2

Prognozowanie gospodarcze

Składowe szeregów czasowych

Składowe szeregów czasowych

Składowa systematyczna występuje zazwyczaj w

postaci:



trendu

trendu – powolnych, regularnych i
systematycznych zmian określonego zjawiska,
obserwowanych w dostatecznie długim
przedziale czasu, wyraża on długookresową
skłonność do jednokierunkowych zmian (wzrostu
lub spadku) wartości badanej zmiennej;



stałego (średniego) poziomu

stałego (średniego) poziomu – wartości
prognozowanej zmiennej oscylują wokół
pewnego stałego poziomu;



składowej okresowej

składowej okresowej (periodycznej).

3

Prognozowanie gospodarcze

Składowe szeregów czasowych

Składowe szeregów czasowych

Składową okresową (periodyczną)

Składową okresową (periodyczną) można wyrazić w

postaci:



wahań cyklicznych – długookresowych, rytmicznych wahań
zmiennej wokół tendencji rozwojowych lub stałego przeciętnego
poziomu, wahania cykliczne (koniunkturalne) obrazują
powtarzające się po sobie okresy ożywienia i recesji w
gospodarce trwające od kilku do kilkunastu lat, starzenie się
powstawanie nowych technologii;



wahań sezonowych – wahań zmiennej wokół tendencji
rozwojowych lub stałego przeciętnego poziomu występujących
jako powtarzające się dość regularne zmiany ilościowe w
przebiegu zjawisk w tych samych jednostkach kalendarzowych
zamykające się w czasie nie przekraczającym jednego roku, ich
źródłem są na przykład zmiany pór i miesięcy roku, dni
tygodnia, cyklu dnia i nocy;

4

Prognozowanie gospodarcze

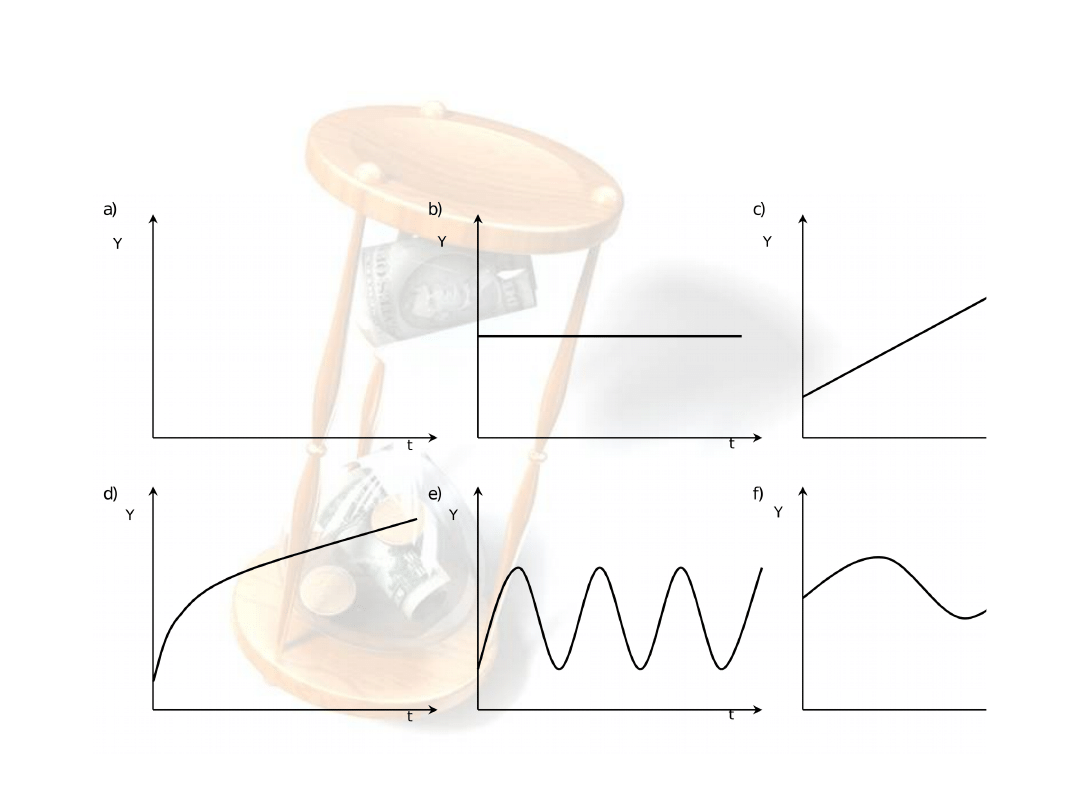
Graficzna prezentacja poszczególnych

Graficzna prezentacja poszczególnych

składowych szeregu czasowego

składowych szeregu czasowego

5

Prognozowanie gospodarcze

Relacje pomiędzy poszczególnymi komponentami szeregu

Relacje pomiędzy poszczególnymi komponentami szeregu



Postać

addytywna

addytywna

 

gdzie:
Y

t

- wartość zmiennej Y w momencie lub okresie t,

T

t

- wartość składowej systematycznej opisana funkcją trendu w

momencie lub okresie t,

S

t

- wartość składowej systematycznej wyrażona przez składnik

sezonowy w momencie lub okresie t,

C

t

- wartość składowej systematycznej wyrażona przez składnik

cykliczny w momencie lub okresie t,

E

t

- wartość składowej losowej w momencie lub okresie t.

6

Prognozowanie gospodarcze

t

t

t

t

t

E

C

S

T

Y









Relacje pomiędzy poszczególnymi komponentami szeregu

Relacje pomiędzy poszczególnymi komponentami szeregu



Postać

multiplikatywna:

multiplikatywna:



Postać

mieszana:

mieszana:

7

Prognozowanie gospodarcze

t

t

t

t

t

E

C

S

T

Y









t

t

t

t

t

S

E

C

T

Y









Dekompozycja szeregu czasowego

Dekompozycja szeregu czasowego

Wyodrębnienie elementarnych składowych
systematycznych i składowej przypadkowej z
analizowanego szeregu czasowego.

 Najpopularniejszym, najprostszym, skutecznym i
zarazem najmniej kosztownym sposobem dekompozycji
szeregów czasowych jest

analiza graficzna

analiza graficzna.

Pierwszym krokiem do przeprowadzenia dekompozycji
jest sporządzenie wykresu badanego szeregu
czasowego. Na jego podstawie prognosta identyfikuje
komponenty wchodzące w skład analizowanego szeregu.

8

Prognozowanie gospodarcze

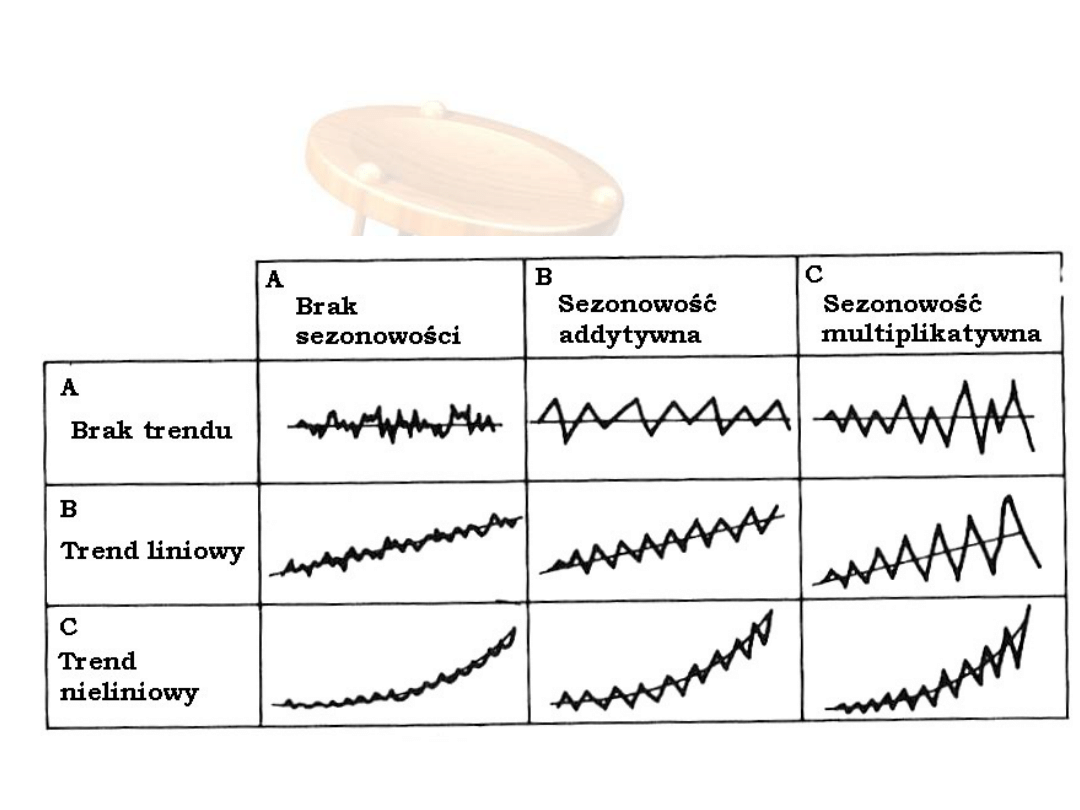
Kształt kilku typowych kombinacji składowych

Kształt kilku typowych kombinacji składowych

szeregów czasowych

szeregów czasowych

9

Prognozowanie gospodarcze

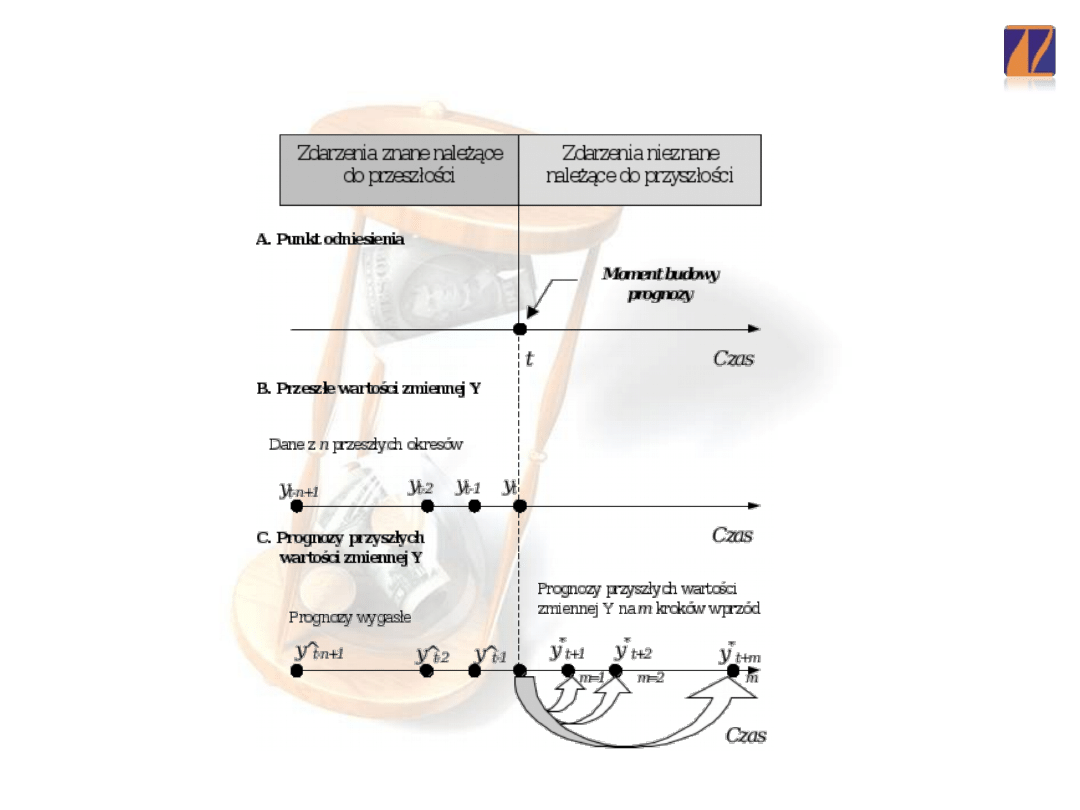
Prognozowanie na podstawie szeregów czasowych

Prognozowanie na podstawie szeregów czasowych

10

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Podstawowy model metody naiwnej

Podstawowy model metody naiwnej

Zgodnie z modelem podstawowym metody naiwnej,

przyszła wartość zmiennej prognozowanej przyjmuje
wartość zaobserwowaną w okresie poprzednim:

gdzie:
y

*t+1

– prognozowana wartość zmiennej Y

wyznaczona na

moment lub okres t+1,

y

t

– rzeczywista wartość zmiennej prognozowanej Y
w momencie lub okresie t.

11

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

t

t

y

y 



*

1

Podstawowy model metody naiwnej

Podstawowy model metody naiwnej

Podstawowa metoda naiwna oparta jest na modelu

błądzenia przypadkowego. Może być stosowana do
konstrukcji prognoz:



krótkookresowych

krótkookresowych,



na jeden krok w przód,

na jeden krok w przód,



w przypadku, gdy w szeregu czasowym występuje

składowa systematyczna w postaci

stałego

stałego

(przeciętnego) poziomu

(przeciętnego) poziomu oraz składnik losowy w postaci

niewielkich wahań przypadkowych

niewielkich wahań przypadkowych.

12

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Błąd

Błąd

ex post

ex post

prognozy

prognozy

13

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Podstawowym błędem wykorzystywanym do

oceny trafności jest bezwzględny błąd prognozy ex
post w czasie t. Błąd ten można zapisać za pomocą
następującej zależności:

gdzie:
y

t

- wartość zmiennej prognozowanej w chwili t,

y

*t

- prognoza na moment lub okres t.

W literaturze błąd ten często oznaczany jest jako

q

t

lub

e

t

*

-

t

t

t

y

y

q 

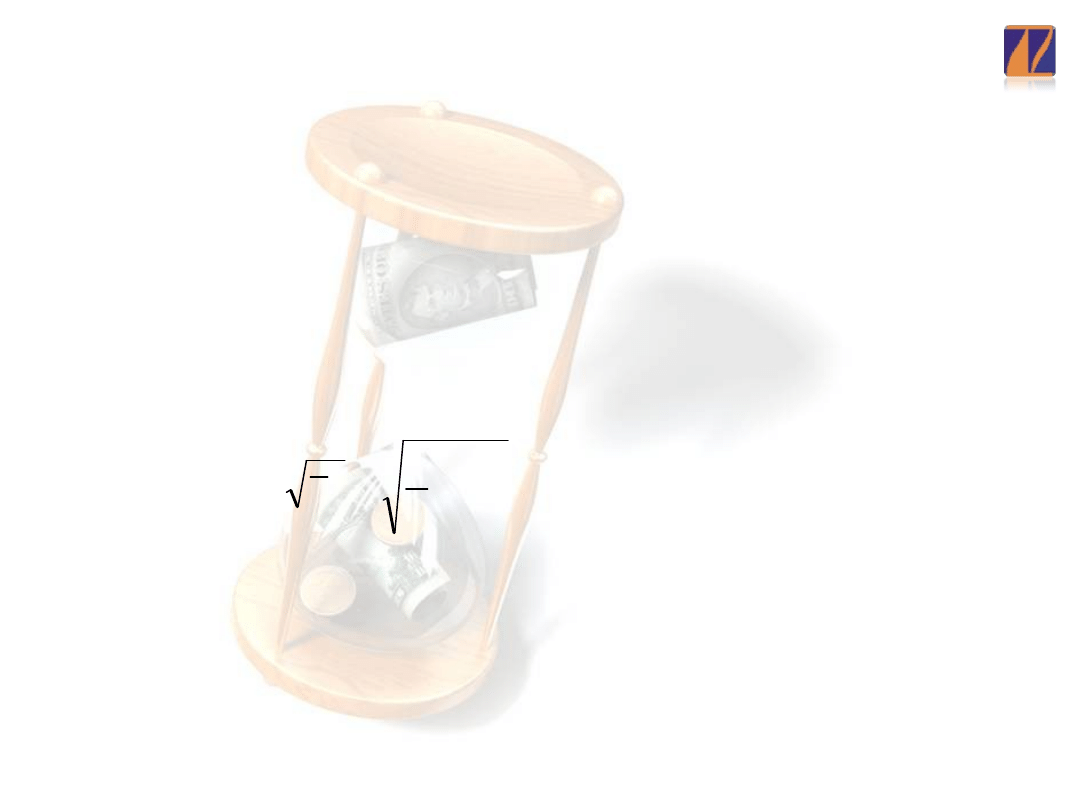
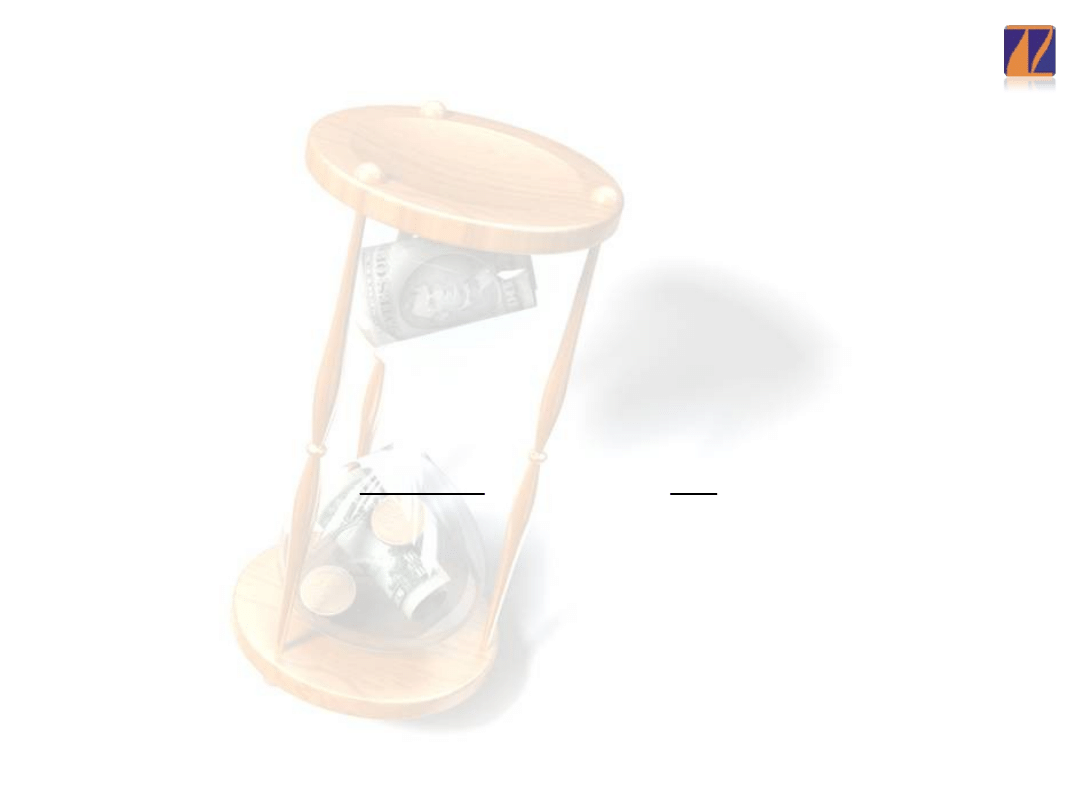
Pierwiastek ze średniego kwadratowego

Pierwiastek ze średniego kwadratowego

bezwzględnego błędu prognozy ex post

bezwzględnego błędu prognozy ex post

14

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Z uwagi na brak możliwości bezpośredniego

odniesienia błędów bezwzględnych do zmiennej
prognozowanej, w praktyce prognostycznej
wykorzystywany jest pierwiastek ze średniego
kwadratowego bezwzględnego błędu prognozy ex post).

Błąd średniokwadratowy, informuje o przeciętnych

odchyleniach prognoz od wartości rzeczywistych.

Wartość ta wyrażona jest w tych samych jednostkach co

zmienna prognozowana y

t

.









n

i

t

q

n

q

s

1

2

2

*

1

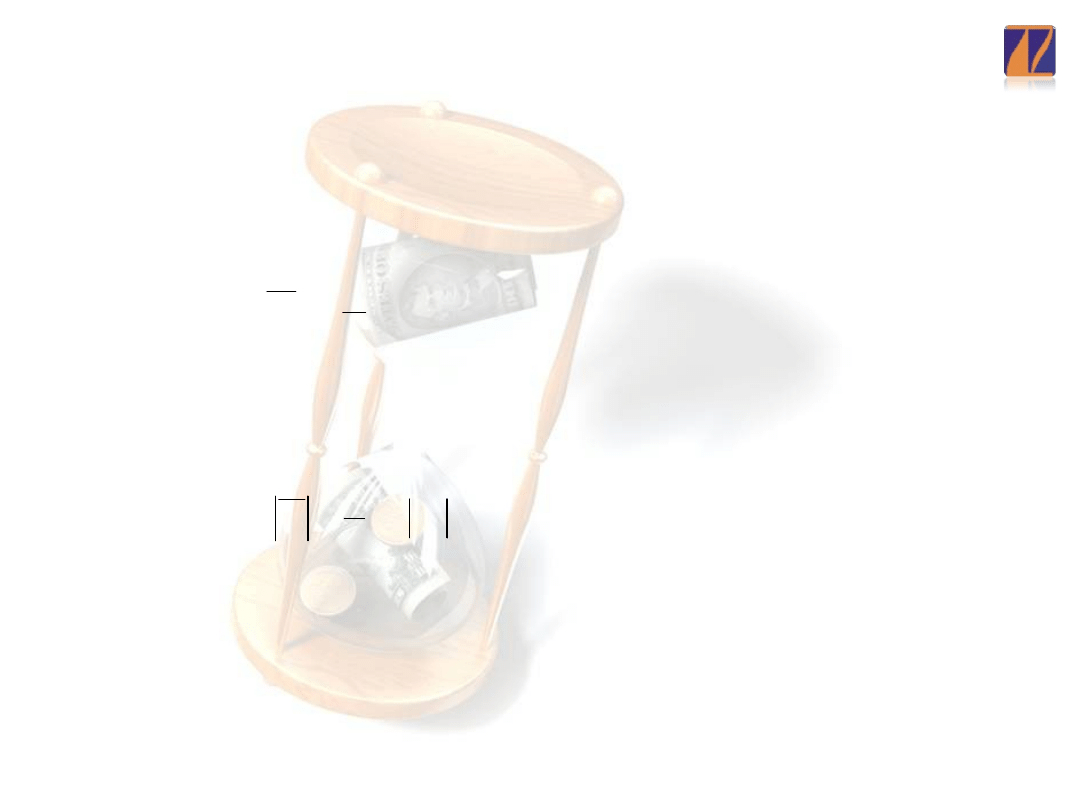
Względny błąd prognozy

Względny błąd prognozy

ex post

ex post

15

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Względny błąd prognozy ex post informuje o

wielkości odchylenia prognozy od wartości
rzeczywistej w czasie t. Odchylenie to wyrażone
jest w procentach wartości zmiennej
prognozowanej.

%

100

%

100

-

*











t

t

t

t

t

t

y

q

y

y

y

Średnie względne błędy prognozy

Średnie względne błędy prognozy

16

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Średni względny błąd prognozy

Wartość średnia modułu względnego błędu prognozy

Błędy te wskazują na przeciętne odchylenie prognoz

od wartości rzeczywistej, które wyrażone jest
najczęściej w procentach wartości zmiennej
prognozowanej.











n

i

t

n

1

1











n

i

t

n

1

1

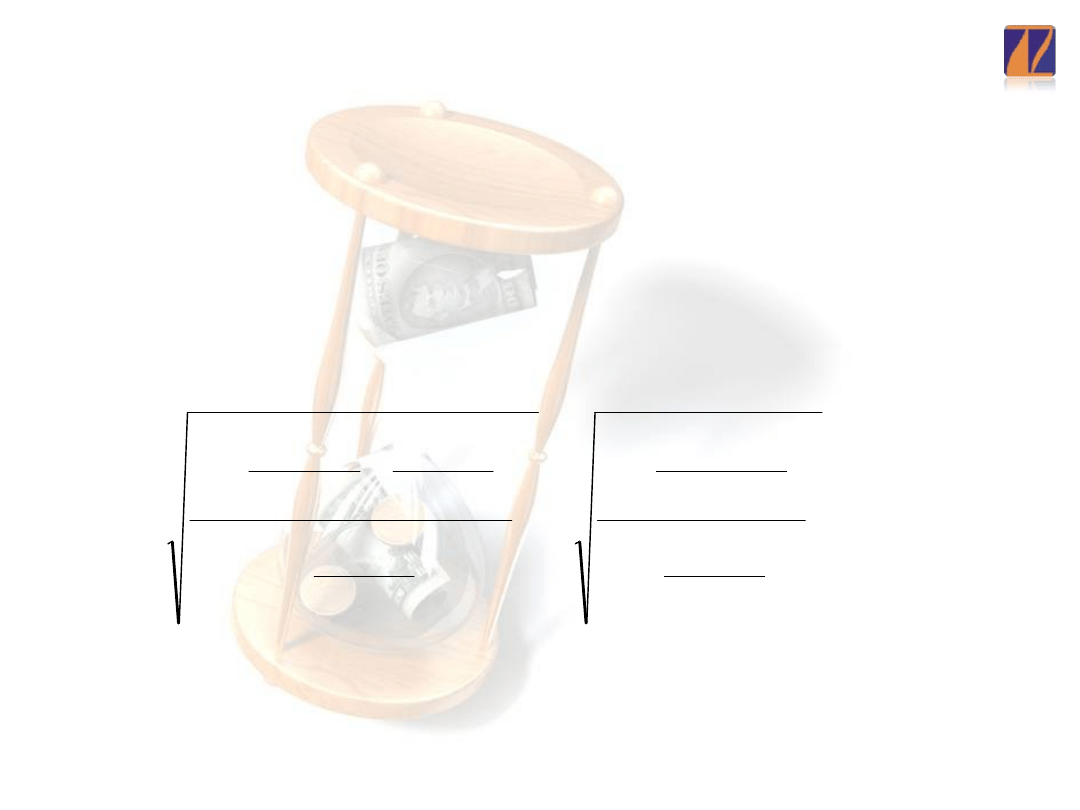
Współczynnik

Współczynnik

U Theila

U Theila

17

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Rola współczynnika U Theila. miernika

najczęściej sprowadza się do oceny porównawczej
(benchmarkingu) formalnych metod
prognostycznych z modelem naiwnym.
Współczynnika U można przedstawić za pomocą
następujących zależności:

2

1

1

2

1

1

1

1

*

1

2

1

1

2

1

1

1

1

*

1





































































































n

t

t

t

t

n

t

t

t

t

n

t

t

t

t

n

t

t

t

t

t

t

t

y

y

y

y

y

y

y

y

y

y

y

y

y

y

y

U

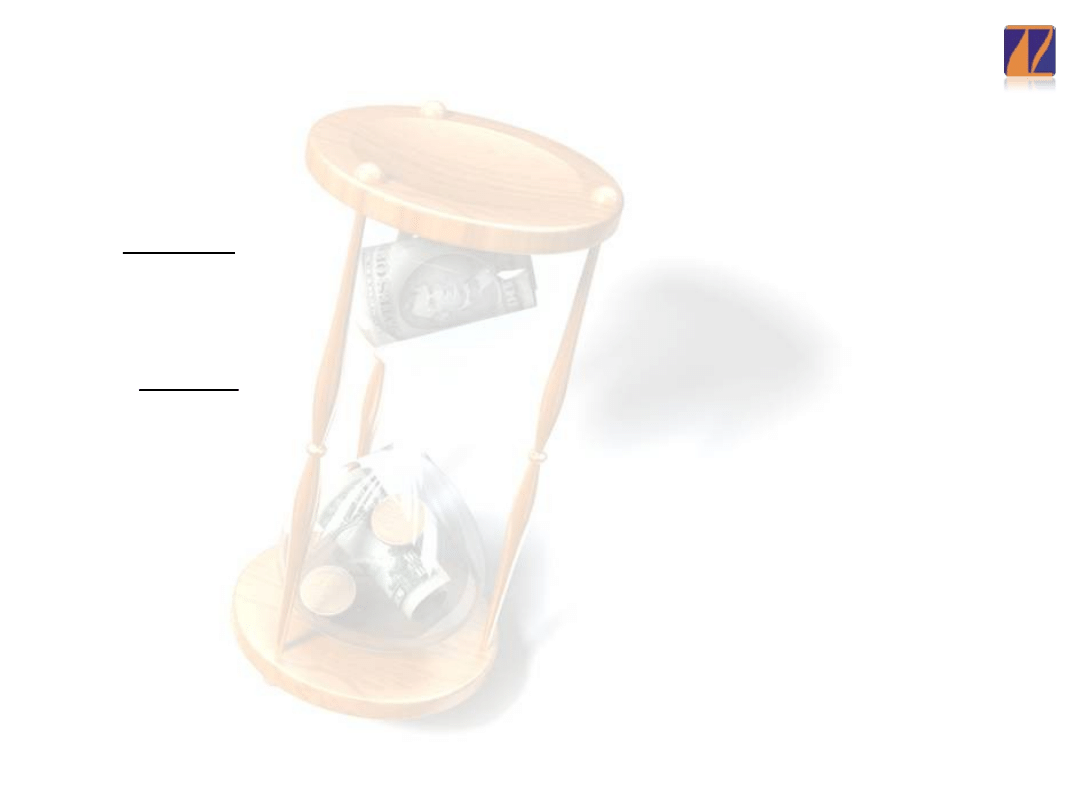
Współczynnik

Współczynnik

U Theila

U Theila

18

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

gdzie:
- względna zmiana prognozy,

- względna zmiana wartości

rzeczywistej.

 
Miernik ten pozwala na porównanie względnych

zmian prognozy i wartości rzeczywistych.

t

t

t

y

y

y 



*

1

t

t

t

y

y

y 

1

Współczynnik

Współczynnik

U Theila

U Theila

19

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Współczynnik U będzie równy zero wówczas, gdy

zbudowana prognoza będzie prognozą w 100%
trafną (błąd prognozy ex post równy zero).

Współczynnik U będzie równy jeden wówczas, gdy

prognozy zbudowane przy wykorzystaniu metody
formalnej będą równe wartościom rzeczywistym.

W przypadku, gdy względne zmiany prognozy

będą miału przeciwny kierunek niż względne zmiany
wartości rzeczywiste, wówczas współczynnik U
będzie przyjmował wartości większe od jedności.

Im większe są różnice pomiędzy wartościami

rzeczywistymi a prognozami tym współczynnik U
Theila przyjmuje coraz większe wartości.

Współczynnik

Współczynnik

U Theila

U Theila

20

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Przedział ufności prognozy

Przedział ufności prognozy

21

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Przedział ufności do prognozy ma postać:

gdzie:
z - wartość rozkładu t-Studenta dla s stopni

swobody i poziomie prawdopodobieństwa 1-a ,

s

*

- pierwiastek ze średniego kwadratowego

błędu prognoz ex post.

 





*

*

*

*

;

zs

y

zs

y

t

t





Przedział ufności prognozy

Przedział ufności prognozy

22

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Interpretując tak skonstruowany przedział

ufności można stwierdzić, że z
prawdopodobieństwem p prognoza będzie należała
do przedziału od do . Wielkość
tego przedziału odzwierciedla dokładność
oszacowania prognoz.

 
Duży przedział ufności do prognozy może

wskazywać na niską dokładność predykcji.

*

*

zs

y

t



*

*

zs

y

t



Przedział ufności prognozy

Przedział ufności prognozy

23

Politechnika Białostocka

Wydział Zarządzania

Prognozowanie gospodarcze

Wybrane wartości rozkładu t-Studenta

przy s = ∞

p=1-a

0,50

0,60

0,70

0,80

0,90

0,95

0,99

z

0,674 0,842 1,036 1,282 1,645 1,960 2,576

KONIEC