Regresja z predyktorami
dychotomicznymi
Regresja z predyktorami
dychotomicznymi
Zmienne jakościowe w
regresji
• Sprawdzamy, czy ciśnienie
skurczowe krwi zależy od wieku i płci
pacjentów
• Płeć (0-mężczyzna, 1 – kobieta)
• Wiek zmienna ilościowa
Wyniki analizy wariancji –
dopasowanie modelu
• Analiza wariancji okazała się istotna
statystyczne F(2, 66)=114,25; p<0,001
• Oznacza to, że model regresji jest dobrze
dopasowany do danych
Analiza wariancji
b
18009,779
2 9004,890
114,249
,000
a
5201,989
66
78,818
23211,768
68
Regresja
Reszta
Ogółem
Model
1
Suma
kwadratów
df
Średni
kwadrat
F
Istotność
Predyktory: (Stała), wiek, plec
a.
Zmienna zależna: cisnienie
b.
Współczynniki
• Oba predyktory okazały się istotne statystyczne a więc
wpływają na wartości zmiennej zależnej.
• Silniejszym predyktorem zmiennej zależnej jest wiek.
Zależność ta jest dodatnia i bardzo silna
• Zależność między płcią a ciśnieniem jest ujemna. Aby
zinterpretować tę wartość beta trzeba pamiętać jak
była kodowana zmienne niezależna. 0 to mężczyźni 1 to
kobiety a więc im wyższe wartości tym bardziej osoba
badana jest kobietą. A zatem im bardziej jest kobietą
tym ma niższe wartości ciśnienia.
Współczynniki
a
110,287
3,638
30,313
,000
-13,513
2,169
-,364
-6,229
,000
,956
,072
,780
13,366
,000
(Stała)
plec
wiek
Model
1
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Zmienna zależna: cisnienie
a.
Współczynniki
• Model można opisać za pomocą następującego równania:
• Ciśnienie=110,29 + 0,96*wiek-13,51* płeć
• Zwiększenie wieku o rok pociąga za sobą niewielki wzrost
ciśnienia o 0,956 jednostki
• W modelu dla mężczyzn otrzymujemy równanie
Ciśnienie=110,29 + 0,96*wiek
• Dla kobiet otrzymujemy równanie Ciśnienie=110,29 +
0,96*wiek – 13,51 = 0,96*wiek +96,77
Współczynniki
a
110,287
3,638
30,313
,000
-13,513
2,169
-,364
-6,229
,000
,956
,072
,780
13,366
,000
(Stała)
plec
wiek
Model
1
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Zmienna zależna: cisnienie
a.
Procent wyjaśnionej
wariancji
• Za pomocą modelu udaje się
wyjaśnić 77% wariancji zmiennej
zależnej
Model - Podsumowanie
,881
a
,776
,769
8,87795
Model
1
R
R-kwadrat
Skorygowane
R-kwadrat
Błąd
standardowy
oszacowania
Predyktory: (Stała), wiek, plec
a.
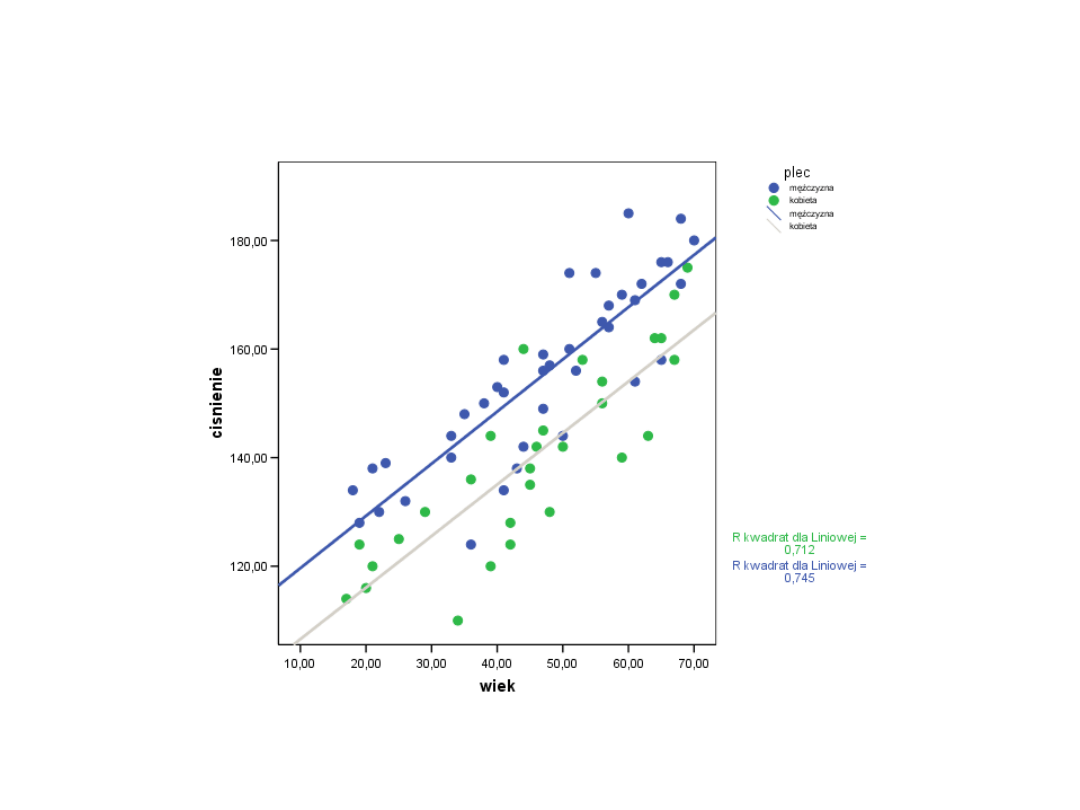
Linie regresji
Analiza regresji – zmienne
jakościowe
• Rozważmy następujący przykład (dane:
dummy.sav)
• Badanie wykonywane było w tzw
paradygmacie testu Stroopa ( liczy się tu czas
odczytywanie nazw np kolorów napisanych
różnymi kolorami np:
czerwony
,
czerwony
)
• Model 1: Jaką część czasów reakcji w teście
Stroopa możemy przewidzieć na podstawie
znajomość nastroju przed badaniem
(NASTRÓJ) i umiejętności komputerowych
(COMP) badanych?
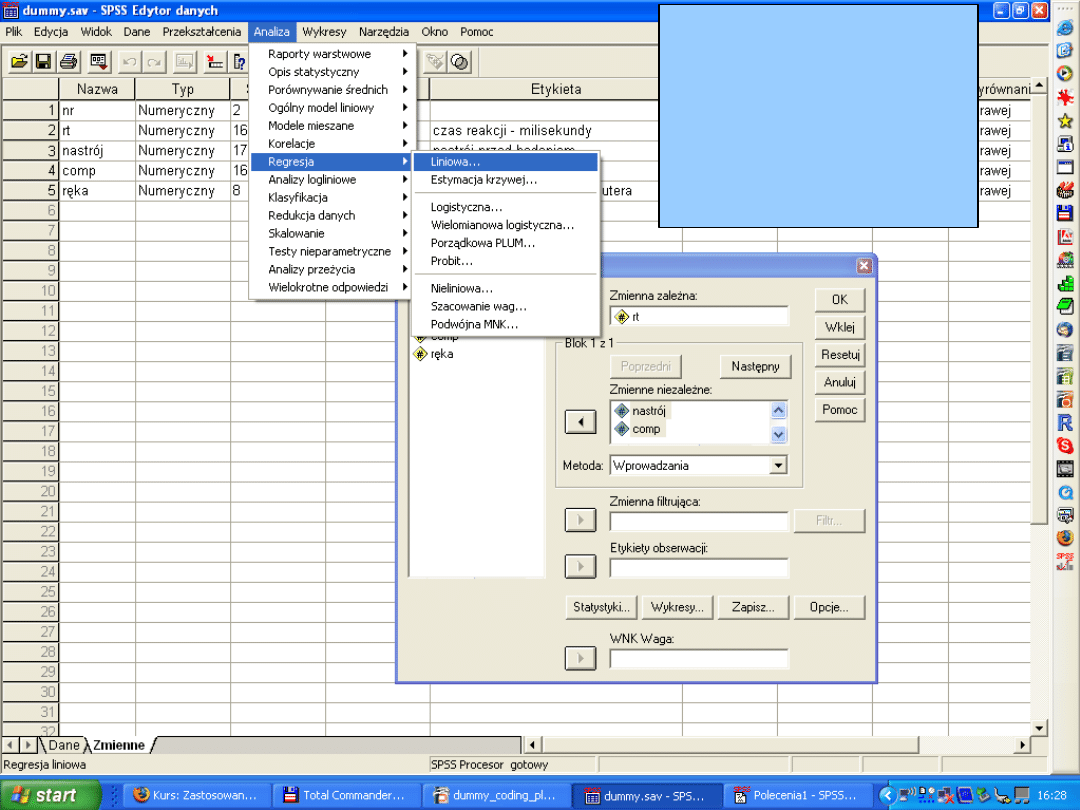
Model 1: Czy
możemy
przewidywać czas
reakcji na podstawie
znajomości nastroju i
umiejętności
komputerowych?
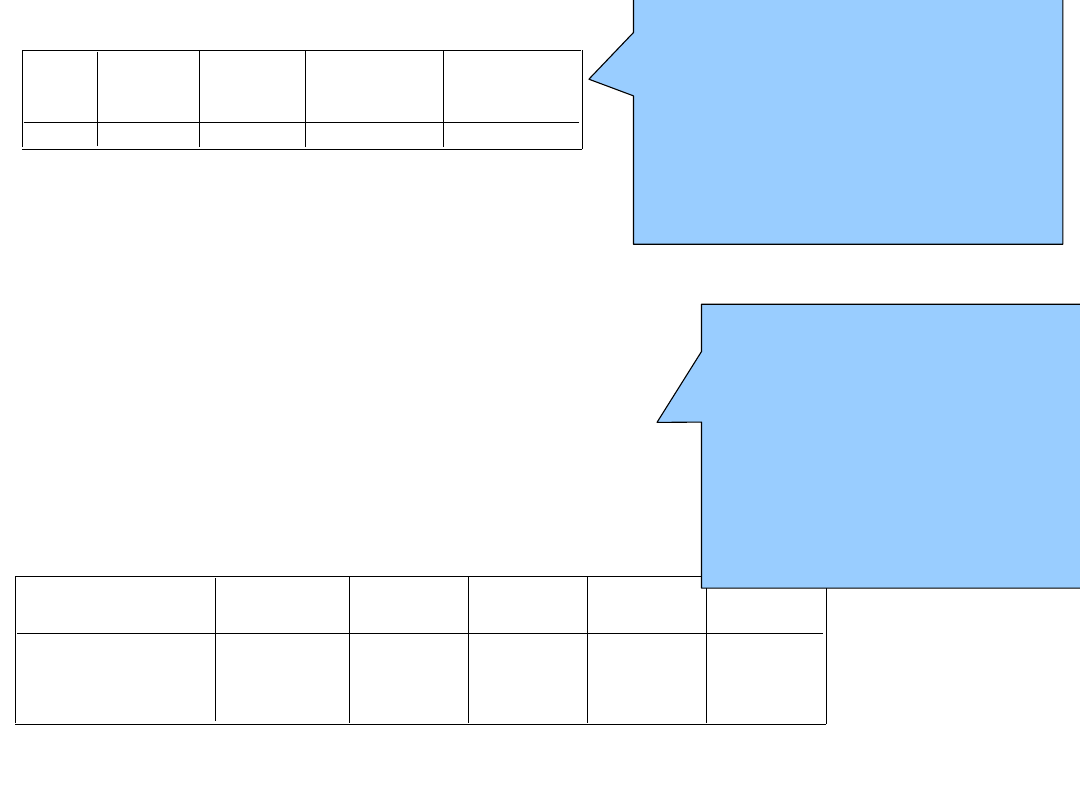
Analiza wariancji
b
2551338,9
2
1275669
599,002
,000
a
632508,286
297
2129,658
3183847,2
299
Regresja
Reszta
Ogółem
Model
1
Suma
kwadratów
df
Średni
kwadrat
F
Istotność
Predyktory: (Stała), umiejętności komputerowe, nastrój przed badaniem
a.
Zmienna zależna: czas reakcji - milisekundy
b.
Anova jest istotna –
możemy założyć, że
model jest liniowo
powiązany ze zmienną
zależną, oraz, że
kontroluje on więcej
zmienności czasów reakcji
niż czynniki które nie
kontrolujemy (błąd).
Model - Podsumowanie
b
,895
a
,801
,800
46,14821
Model
1
R
R-kwadrat
Skorygowane
R-kwadrat
Błąd
standardowy
oszacowania
Predyktory: (Stała), umiejętności komputerowe, nastrój
przed badaniem
a.
Zmienna zależna: czas reakcji - milisekundy
b.
R
2
= 0,800
Na podstawie Modelu 1
możemy przewidzieć aż do
80% zmienności czasów
reakcji, na podstawie
znajomości nastroju i
poziomu umiejętności
komputerowych.
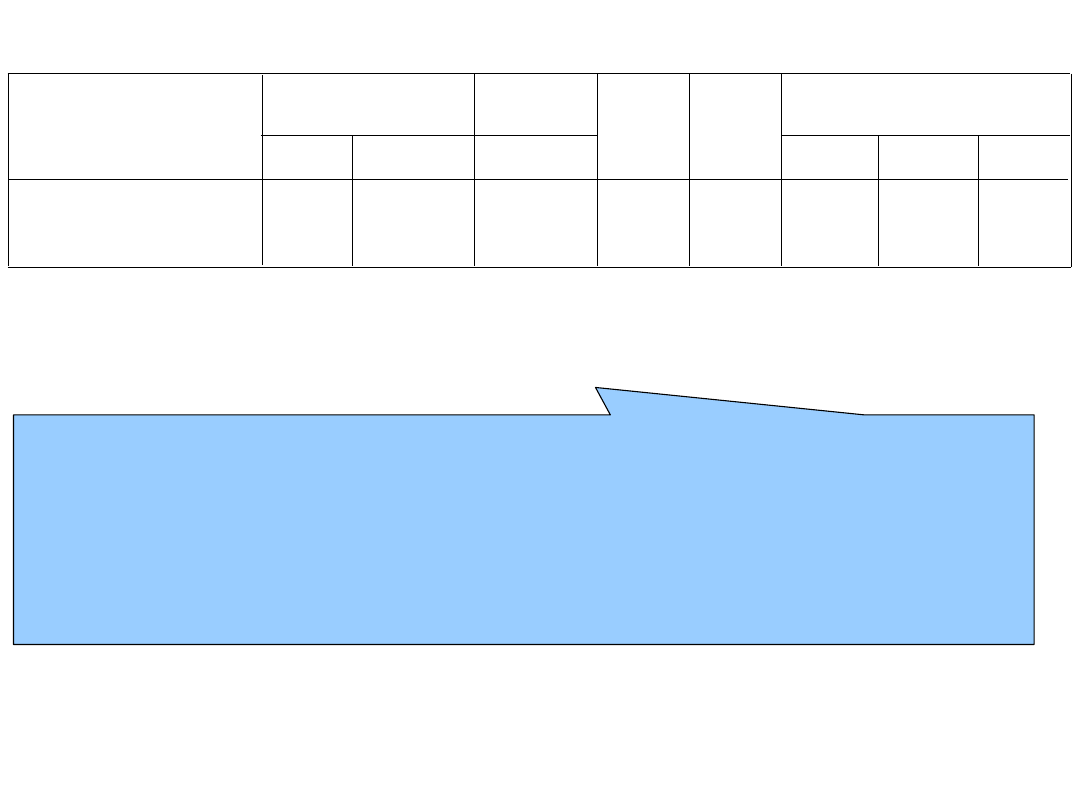
Czas reakcji (rt) = 42,6*nastrój + 65,8*umiejętności + 9621,8;
Umiejętności komputerowe są lepszym predyktorem (β=0,66) niż nastrój
(β=0,44). Obydwa predyktory są istotne
Czysta korelacja (cząstkowa) umiejętności komputerowych i czasów
reakcji r
cząstkowa
=0,81;nastroju i czasów reakcji r
cząstkowa
=0,68. Obydwa
predyktory są ze sobą powiązane oraz są powiązane ze zmienną zależną.
Współczynniki
a
9621,864
11,631
827,228
,000
42,605
2,628
,438
16,212
,000
,632
,685
,419
65,814
2,686
,663
24,500
,000
,791
,818
,634
(Stała)
nastrój przed badaniem
umiejętności
komputerowe
Model
1
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Rzędu
zerowego
Cząstkowa
Semicząs
tkowa
Korelacje
Zmienna zależna: czas reakcji - milisekundy
a.
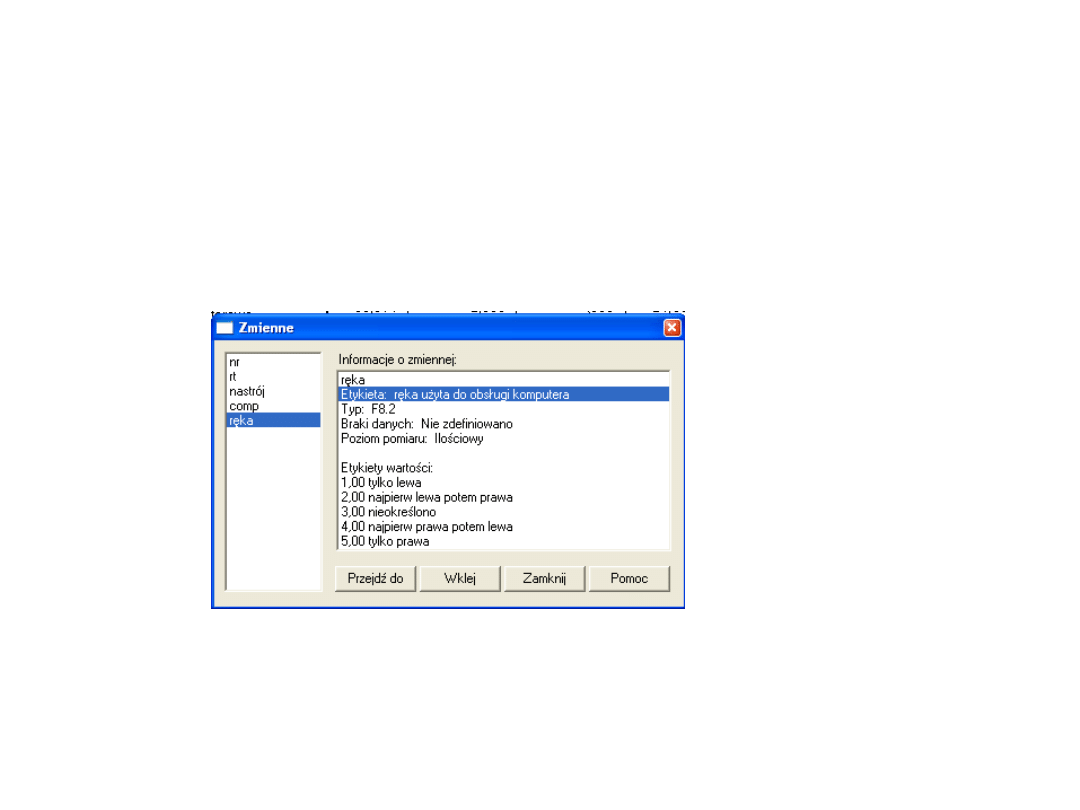
Analiza regresji ze zmienną
jakościową
• W naszym badaniu kontrolowaliśmy też to
przy pomocy której ręki reagowała osoba
badana
Jak widać zmienna RĘKA jest zmienną
nominalną (o pięciu kategoriach) – nie
możemy jej użyć w analizie regresji w tej
postaci
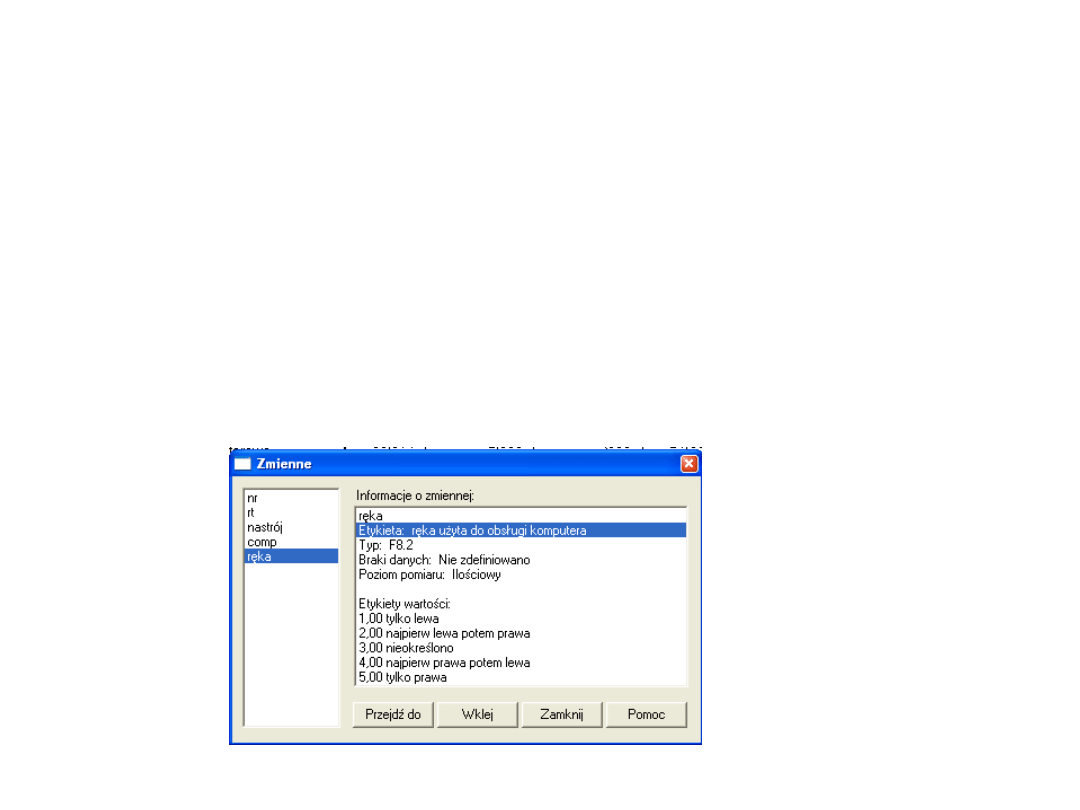
Rekodowanie zmiennej
jakościowej na
dychotomiczne
• Możemy przekodować RĘKĘ na zmienne
instrumentalne
• Przypuśćmy, że jesteśmy tylko zainteresowani
kontrolą takich przypadków, kiedy badani
reagowali tylko przy użyciu prawej lub lewej
ręki
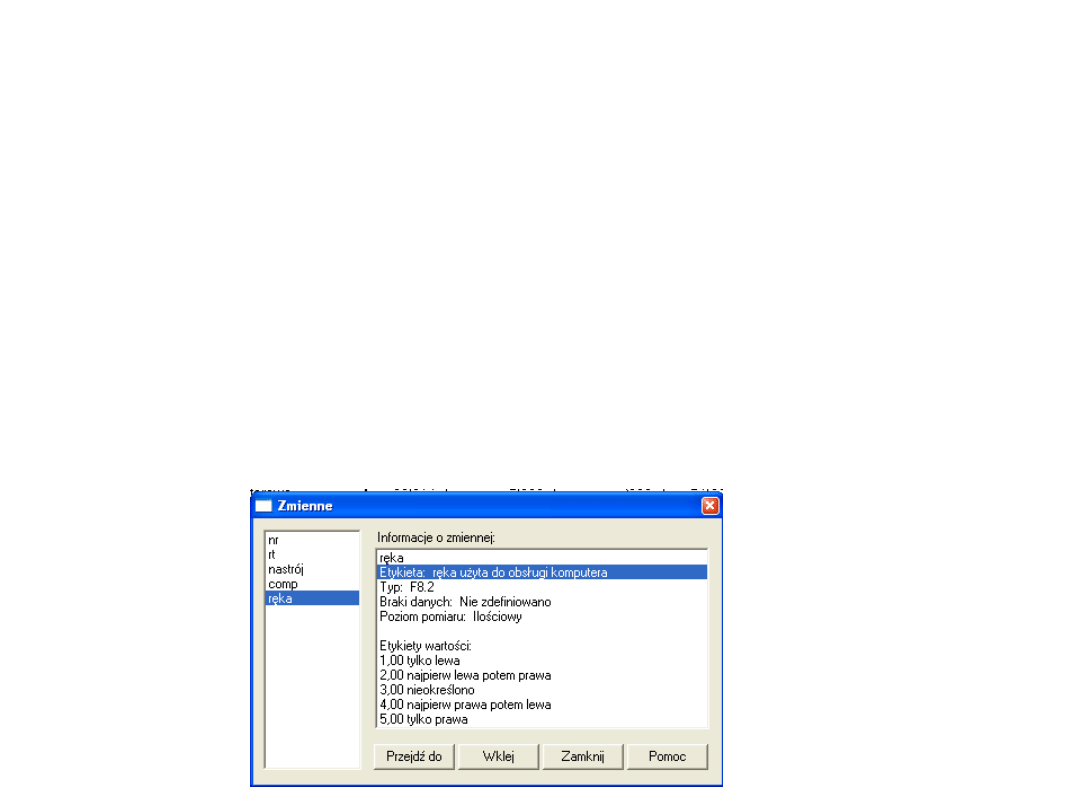
Zmienne instrumentalne
• Aby wykorzystać te informacje musimy
stworzyć dwie zmienne instrumentalne: LEWA
– osoba odpowiadała tylko przy użyciu lewej
ręki (i w żaden inny sposób); PRAWA – osoba
odpowiadała przy użyciu prawej ręki (i w
żaden inny sposób)
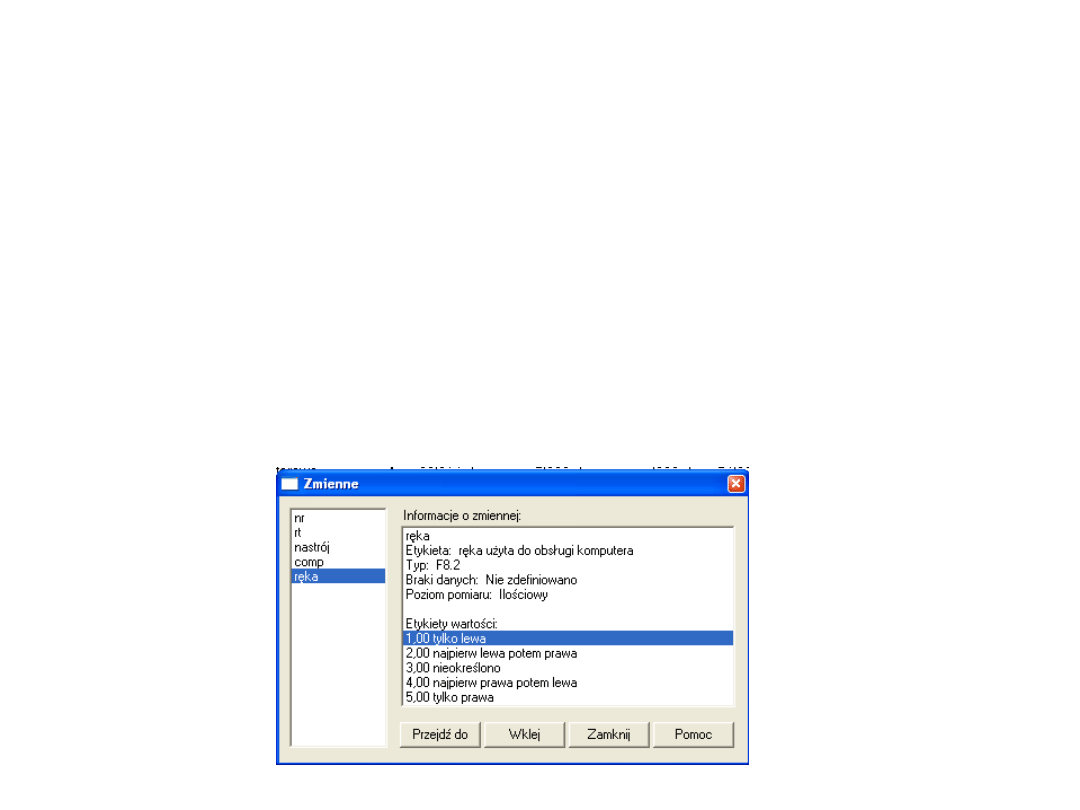
Zmienna „lewa”
• A więc, w nowej zmiennej LEWA, 1 otrzymają
te osoby, które odpowiadały tylko przy użyciu
lewej ręki (1 na zmiennej RĘKA), a 0
otrzymają te osoby, które odpowiadały w inny
sposób (2 – 5 na zmiennej RĘKA)
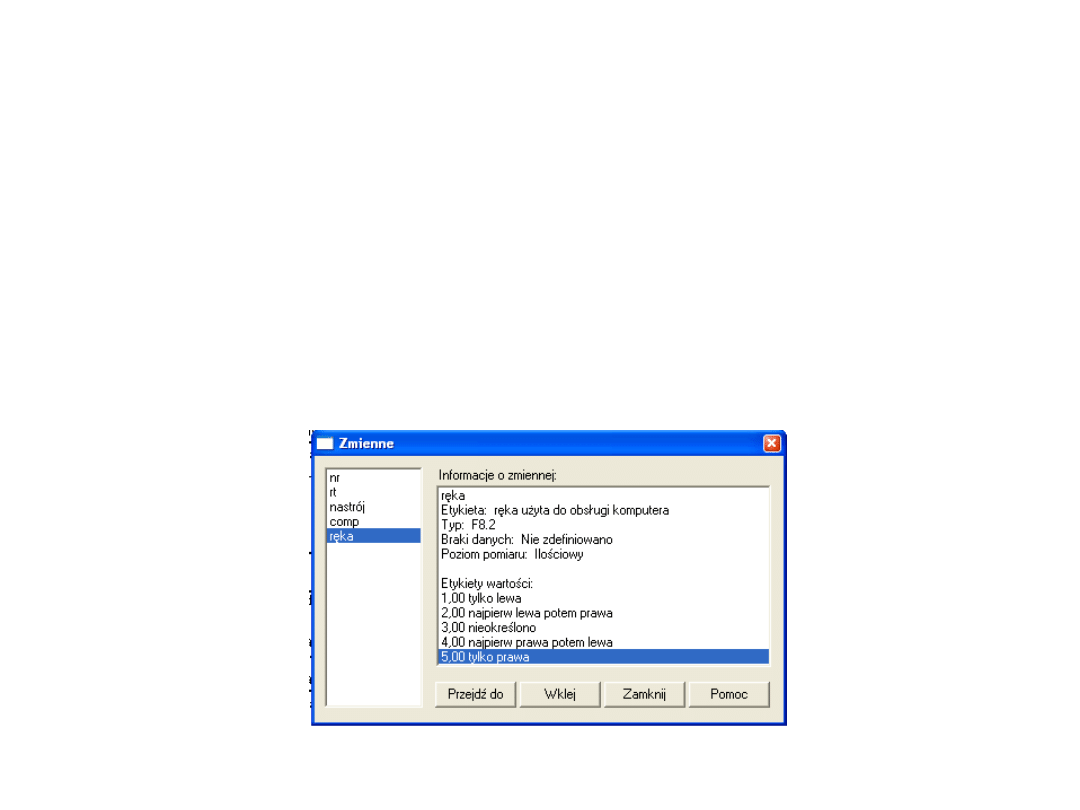
Zmienna „prawa”
• A więc, w nowej zmiennej PRAWA, 1 otrzymają
te osoby, które odpowiadały tylko przy użyciu
prawej ręki (5 na zmiennej RĘKA), a 0
otrzymają te osoby, które odpowiadały w inny
sposób (1 – 4 na zmiennej RĘKA)
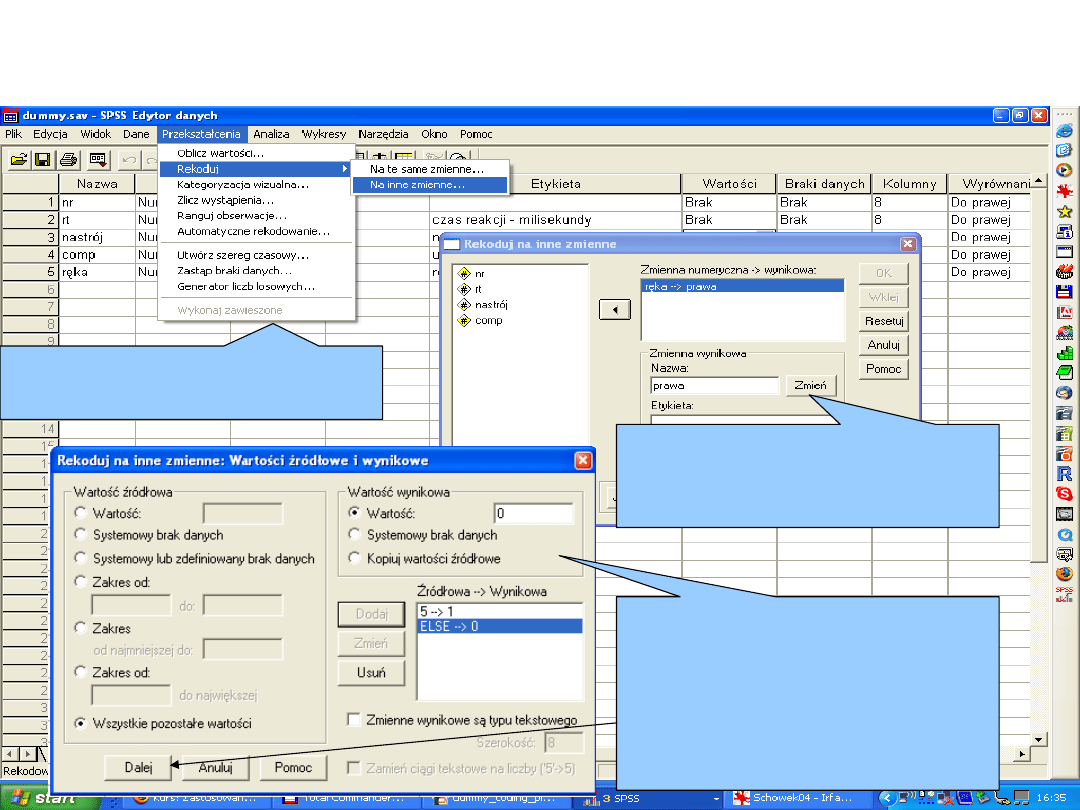
Rekodowanie zmiennej RĘKA na zmienną
instrumentalną PRAWA
Przekształcenia > Rekoduj
> na inne zmienne
Przenieś RĘKA. Określ
nazwę nowej zmiennej >
PRAWA > wciśnij zamień
Wartości źródłowe i
wynikowe. Rekodowanie:
5 -> 1 (ludzie odpowiadali
tylko przy użyciu prawej
ręki);
Pozostałe wartości -> 0
• Po przekodowaniu RĘKi na LEWA i PRAWA,
nowe zmienne możemy wykorzystać w
analizie regresji.
• Wprowadzimy je jako drugi blok poprzedniej
analizy aby sprawdzić czy kontrolowanie tego,
której ręki używali badani do reagowania
zwiększa moc eksplanacyjną poprzedniego
modelu!
• Model 2: Jaką część czasów reakcji w teście
Stroopa możemy przewidzieć na podstawie
znajomość nastroju przed badaniem
(NASTRÓJ), umiejętności komputerowych
(COMP) badanych oraz tego której ręki
używali do reagowania (LEWA i PRAWA)
Kolejność wprowadzania
zmiennych
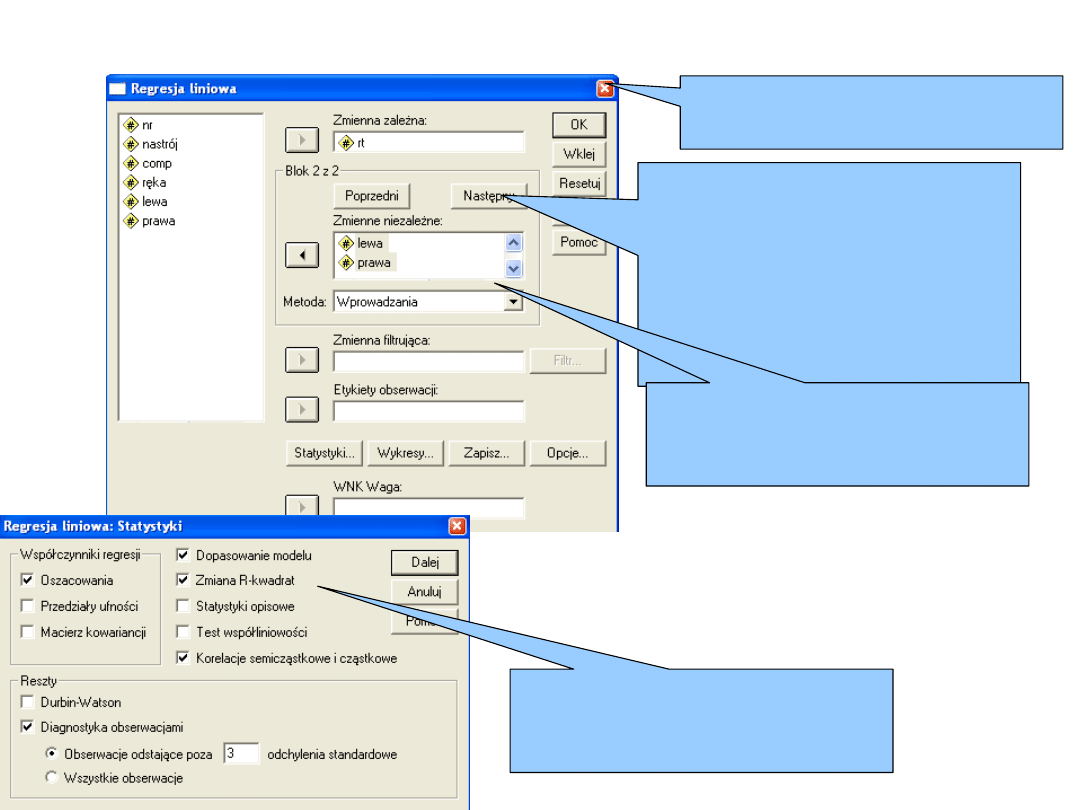
Reresja hierarchiczna
Analiza > Regresja >
Liniowa
Nie usuwaj nastroju i
umiejętności
komputerowych z listy
zmiennych niezależnych.
Zamiast tego wciśnij
NASTĘPNY
Statystyki. Wybierz:
Zmiana R kwadrat >
Dalej > OK
Przenieś: LEWA I PRAWA
do drugiego bloku
predyktorów
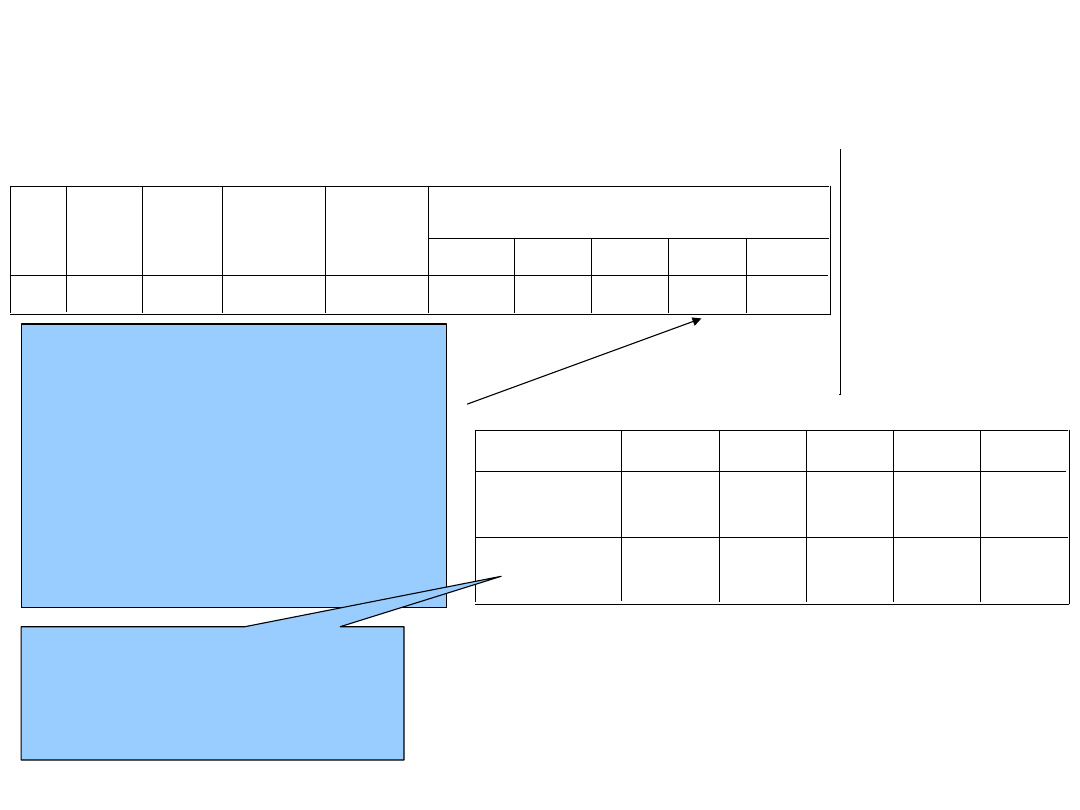
Analiza wariancji
c
2551338,9
2
1275669
599,002
,000
a
632508,286
297
2129,658
3183847,2
299
2584514,0
4
646128,5
318,033
,000
b
599333,139
295
2031,638
3183847,2
299
Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem
Model
1
2
Suma
kwadratów
df
Średni
kwadrat
F
Istotność
Predyktory: (Stała), umiejętności komputerowe, nastrój przed badaniem
a.
Predyktory: (Stała), umiejętności komputerowe, nastrój przed badaniem,
prawa, lewa
b.
Zmienna zależna: czas reakcji - milisekundy
c.
Model - Podsumowanie
c
,895
a
,801
,800
46,14821
,801
599,002
2
297
,000
,901
b
,812
,809
45,07369
,010
8,165
2
295
,000
Model
1
2
R
R-kwadrat
Skorygowane
R-kwadrat
Błąd
standardowy
oszacowania
Zmiana
R-kwadrat
Zmiana F
df1
df2
Istotność
zmiany F
Statystyki zmiany
Predyktory: (Stała), umiejętności komputerowe, nastrój przed badaniem
a.
Predyktory: (Stała), umiejętności komputerowe, nastrój przed badaniem, prawa, lewa
b.
Zmienna zależna: czas reakcji - milisekundy
c.
Regresja hierarchiczna – czy dodawanie
nowych zmiennych zwiększa wyjaśniającą
wartość poprzedniego modelu?
Tak! Nasz model (nr 2)
przewiduje istotnie więcej
wariancji czasów reakcji.
R
2
zmieniło się o ok 0,01
Teraz odczytujemy informacje
tylko dla modelu nr 2
(gdyby zmiana była
nieistotna to zostalibyśmy
przy modelu 1)
Anova dla modelu 2 jest
istotna!
F(4,295)=318; p<0,001;
R
2
=0,809
Współczynniki
a
9621,864
11,631
827,228
,000
42,605
2,628
,438
16,212
,000
,632
,685
,419
65,814
2,686
,663
24,500
,000
,791
,818
,634
9588,810
14,020
683,937
,000
43,609
2,593
,449
16,819
,000
,632
,700
,425
73,436
3,233
,739
22,716
,000
,791
,798
,574
26,072
7,687
,101
3,392
,001
-,357
,194
,086
-15,445
7,288
-,060
-2,119
,035
,345
-,122
-,054
(Stała)
nastrój przed badaniem
umiejętności
komputerowe
(Stała)
nastrój przed badaniem
umiejętności
komputerowe
lewa
prawa
Model
1
2
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Rzędu
zerowego
Cząstkowa
Semicząs
tkowa
Korelacje
Zmienna zależna: czas reakcji - milisekundy
a.
Czas reakcji = 43,6*nastrój + 73,4*umiejętności + 26*lewa - 15,4*prawa
+ 9588,8;
Umiejętności komputerowe okazały się najlepszym predyktorem
(β=0,74), następnie: nastrój (β=0,45); lewa (β=0,1) i prawa (β=-0,06).
Wszystkie predyktory były istotne. Czas reakcji wzrastał wraz z
poziomem nastroju, umiejętności komputerowych i był dłuższy przy
reagowaniu lewą ręką. Jeśli osoba odpowiadała przy pomocy prawej ręki,
czas reakcji skracał się (beta ujemna).
Czyste korelacje (cząstkowe):
of umiejętności i czas r
cząstkowa
=0,79;
of nastrój i czas r
cząstkowa
=0,70;
of lewa i czas r
cząstkowa
=0,19;
of prawa i czas r
cząstkowa
-0,12;
Efekty interakcyjne w regresji -obliczenia
1. Dwie zmienne niezależne (wyjaśniające)
2. Jedna zmienna zależna
Kroki
1. Zmienne niezależne: standaryzujemy
zmienne ilościowe, zmienne jakościowe
rekodujemy na dwuwartościowe o
wartościach –1 i 1 (centracja zmiennych).
2. Tworzymy nową zmienną – składnik
interakcyjny, który jest iloczynem
przekształconych zmiennych niezależnych
3. Robimy analizę regresji, gdzie w pierwszym
kroku wprowadzamy zmiennej niezależne a
w drugim kroku składnik interakcyjny.
Analiza wydruku
• Jeśli model ze składnikiem interakcyjnym jest
istotny statystycznie (istotna beta tego
składnika) to uznajemy, że mamy do
czynienia z efektem interakcyjnym i
przeprowadzamy analizę dodatkową
• Robimy dwie regresje osobno dla dwóch grup
(jeśli jeden z predyktorów jest jakościowy) lub
redukujemy jeden z predyktorów do zmiennej
dychotomicznej i robimy dwie regresje dla
dwóch grup osobno.
Efekty interakcyjne w regresji - przykład
Szukamy predyktorów depresji
Czy ilość wrażeń jakich dostarcza życie wiąże
się z poziomem depresji w dwóch grupach
płciowych
Szukamy efektu interakcyjnego tych dwóch
zmiennych: płeć i ilość wrażeń na zmienną
poziom depresji?
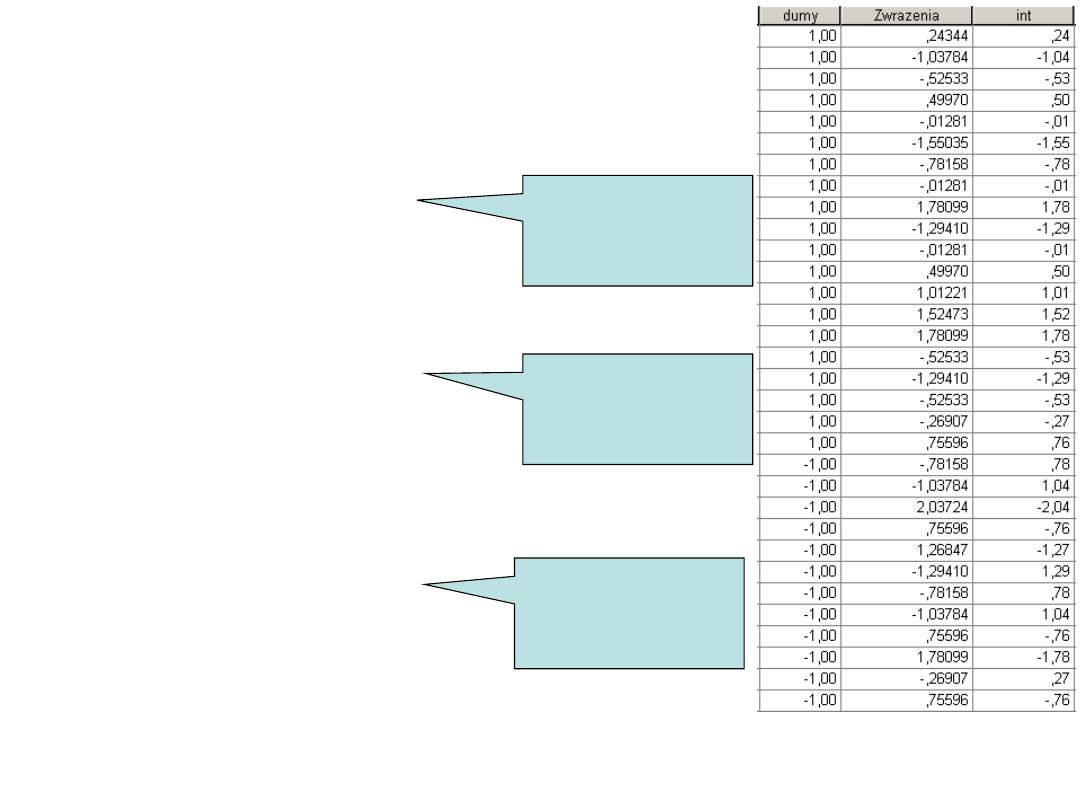
Rekodujemy zmienną płeć na
zmienną o wartościach -1 i 1
RECODE
płec
(0=-1) (1=1) INTO
dumy .
EXECUTE .
DESCRIPTIVES
VARIABLES=wrazenia
/SAVE
/STATISTICS=MEAN
STDDEV MIN MAX .
COMPUTE int = dumy *
Zwrazenia .
EXECUTE .
Rekodujemy
zmienną
jakościową
Standaryzujem
y zmienną
ilościową
Obliczamy
składnik
interakcyjny
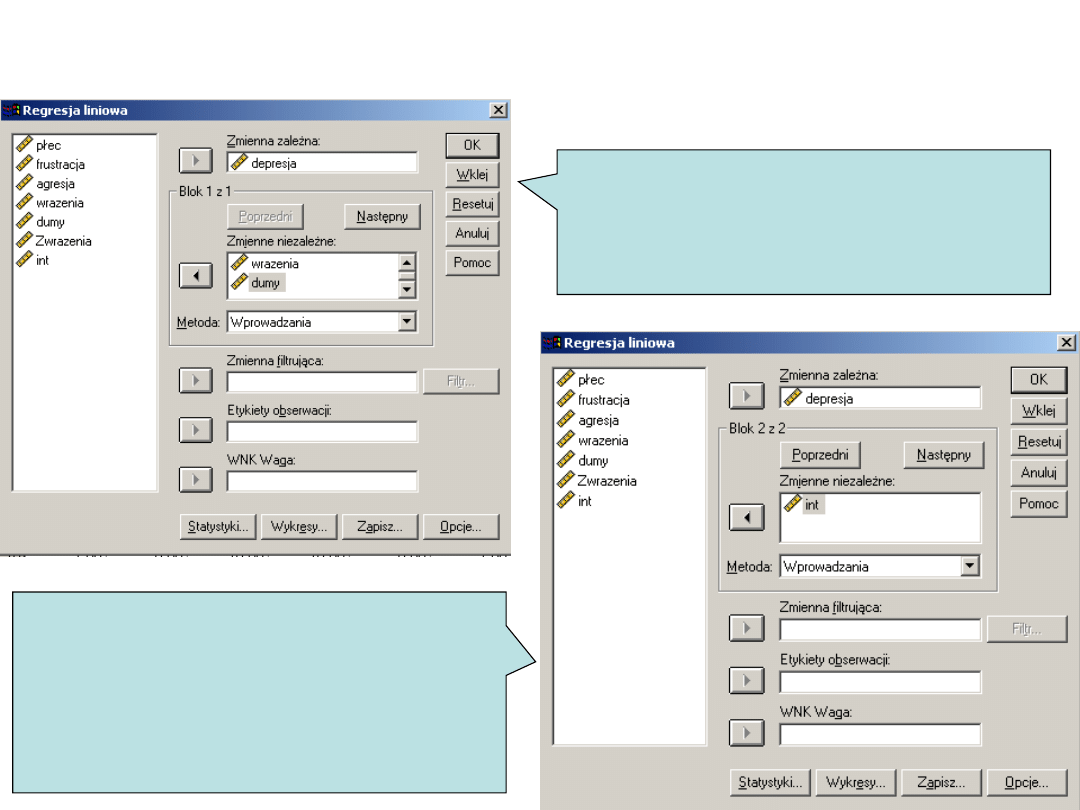
Analiza hierarchiczna
W pierwszym kroku
wprowadzamy predyktory
– rodzaj efektów
głównych
W drugim kroku
wprowadzamy składnik
interakcyjny – rodzaj
efektu interakcyjnego
Wydruk 1
Zmienne wprowadzone/usunięte
b
dumy,
wrazenia
a
.
Wprowad
zanie
int
a
.
Wprowad
zanie
Model
1
2
Zmienne
wprowadzone
Zmienne
usunięte
Metoda
Wszystkie wyspecyfikowane zmienne
zostały wprowadzone.
a.
Zmienna zależna: depresja
b.
Analiza wariancji
c
8,100
2
4,050
,283
,755
a
529,000
37
14,297
537,100
39
387,232
3
129,077
31,006
,000
b
149,868
36
4,163
537,100
39
Regresja
Reszta
Ogółem
Regresja
Reszta
Ogółem
Model
1
2
Suma
kwadratów
df
Średni
kwadrat
F
Istotność
Predyktory: (Stała), dumy, wrazenia
a.
Predyktory: (Stała), dumy, wrazenia, int
b.
Zmienna zależna: depresja
c.
Pierwszy model jest nieistotny
statystycznie a zatem nie mamy efektów
głównych wprowadzonych predyktorów.
Dopiero drugi model jest istotny
statystycznie a zatem mamy
prawdopodobnie do czynienia z istotną
interakcją
Wydruk 2 – współczynniki
Współczynniki
a
11,342
1,963
5,778
,000
,001
,155
,001
,004
,997
,450
,598
,123
,753
,456
11,137
1,059
10,511
,000
,014
,084
,015
,172
,864
,449
,323
,123
1,393
,172
3,119
,327
,840
9,543
,000
(Stała)
wrazenia
dumy
(Stała)
wrazenia
dumy
int
Model
1
2
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Zmienna zależna: depresja
a.
W drugim modelu mamy istotny statystycznie
współczynnik beta dla zmiennej oznaczającej
składnik interakcyjny. Ten współczynnik nie jest
interpretowalny. Najważniejsze, że jest istotna beta.
Uznajemy, że mamy istotną interakcję.
Analiza zależności osobno w
grupach płciowych
Współczynniki
a,b
20,317
1,904
10,673
,000
-,785
,151
-,775
-5,200
,000
(Stała)
wrazenia
Model
1
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Zmienna zależna: depresja
a.
Wybrano tylko te obserwacje, dla których płec = kobieta
b.
Współczynniki
a,b
1,956
,894
2,188
,042
,814
,070
,939
11,551
,000
(Stała)
wrazenia
Model
1
B
Błąd
standardowy
Współczynniki
niestandaryzowane
Beta
Współczynniki
standaryzowa
ne
t
Istotność
Zmienna zależna: depresja
a.
Wybrano tylko te obserwacje, dla których płec = mężczyzna
b.
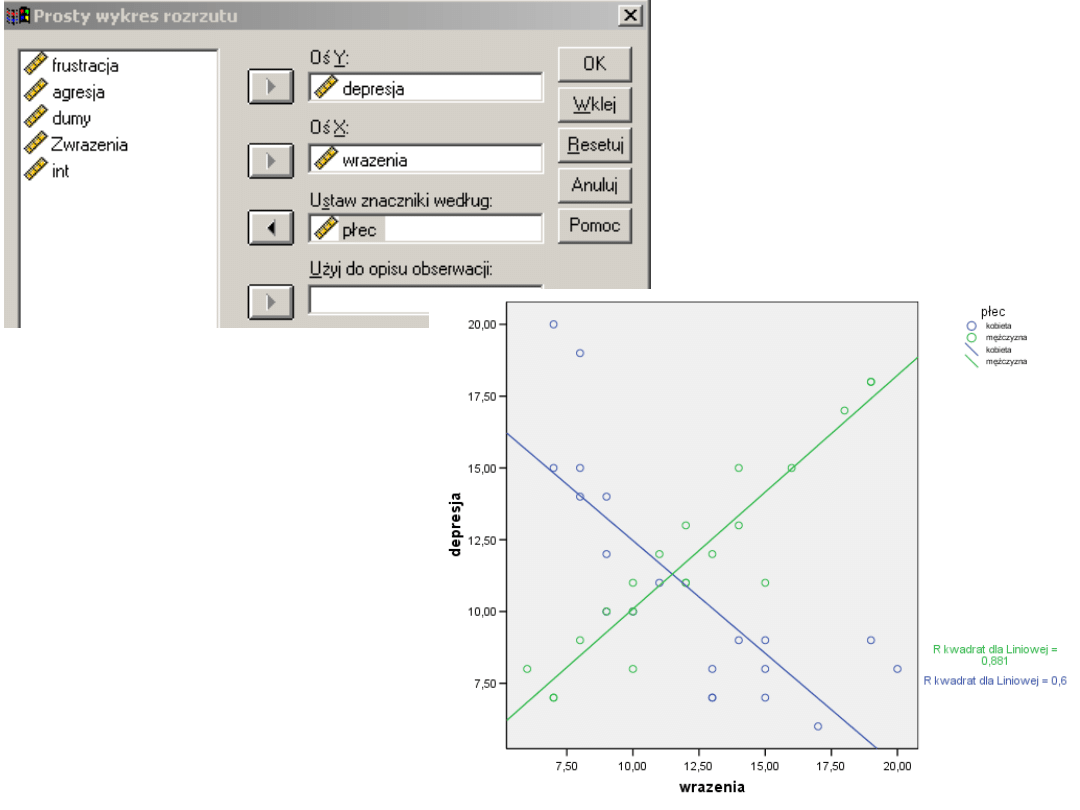
Wykres rozrzutu
Alternatywnie
• Mona też wykonać podział po
medianie dla zmiennej ilościowej i
wykonać następnie dwuczynnikową
analizę wariancji w schemacie
międzygrupowym a potem analizę
efektów prostych. Wyniki wyjdą
identyczne.
Założenia – analiza reszt
• Główne założenia analizy regresji
dotyczą reszt i dlatego jest to
najważniejsza analiza eksploracyjna
robiona w trakcie tej analizy
• Reszty surowe
• Reszty standaryzowane
• Odległości Cooka
• Statystyka Durbina - Watsona
Założenia
• Reszty mają rozkład normalny
• To założenie jest ważne nie dla metody najmniejszych
kwadratów ale dla szacowania parametrów. Jeśli
założenie to jest złamane to błędnie mogą zostać
oszacowane parametry regresji. Aby zrobić analizę
reszt musimy wybrać w oknie dialogowym analizy
regresji reszty niestandaryzowane
Reszty niestandaryzowane
• Jeśli wybierzemy reszty niestandaryzowane to
reszty te zostaną zapisane w pliku z danymi jako
dodatkowa zmienna. Aby sprawdzi normalność
tej zmiennej można narysować wykres KK albo
PP, jak również użyć testu Shapiro-Wilka
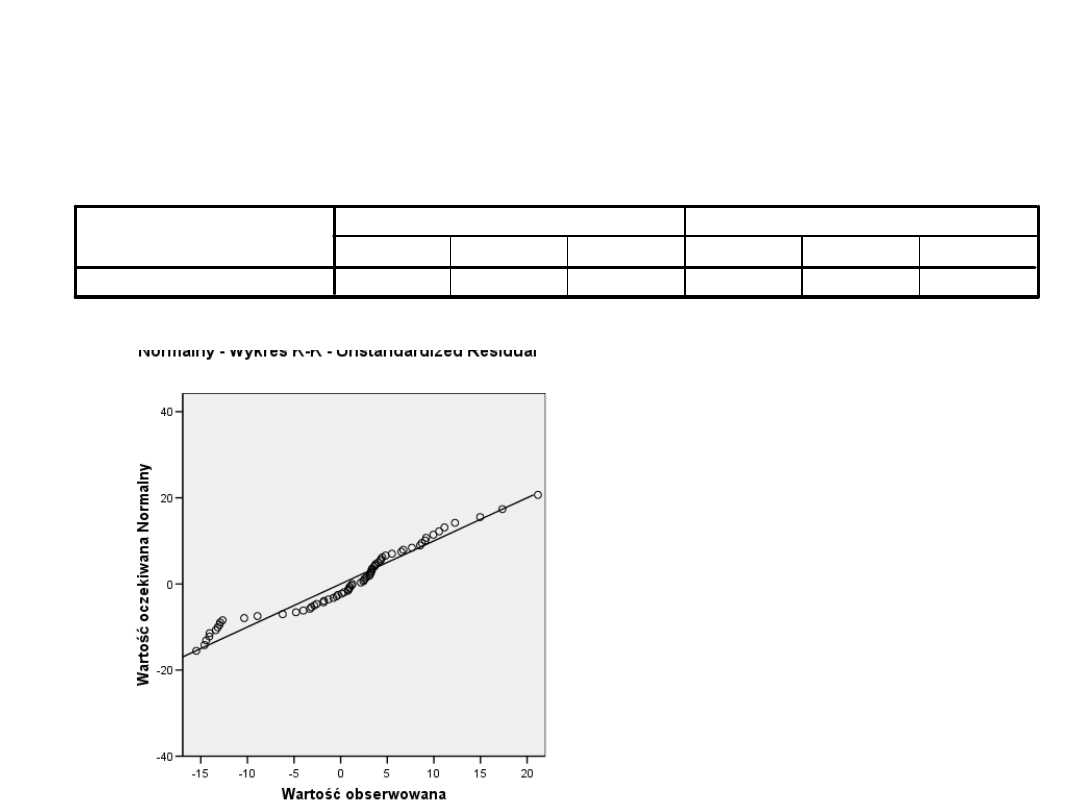
Wykres KK i test Shapiro-Wilka
• Rozkłady
reszt
odbiegają
od
normalnośc
i
Testy normalności rozkładu
,117
69
,020
,956
69
,016
Unstandardized Residual
Statystyka
df
Istotność Statystyka
df
Istotność
Kołmogorow-Smirnow
a
Shapiro-Wilk
Z poprawką istotności Lillieforsa
a.
Założenie o braku korelacji
reszt
O korelacji reszt mówi nam test
Durbina –Watsona. Test ten zakłada,
że reszty nie są skorelowane.
Aby poprawnie stosować ten test
muszą być spełnione następujące
warunki:
• Analizowany model musi mieć wyraz
wolny
• Składniki reszt muszą mieć rozkład
normalny
• Liczba obserwacji jest większa niż 15
Test Durbina -Watsona
• Statystyka d=<0,4>
• Gdy wartość bliska 2
to reszty są niezależne
•
(k to liczba
predyktorów, n to
liczba badanych)
Model - Podsumowanie
b
,881
a
,776
,769
8,87795
1,292
Model
1
R
R-kwadrat
Skorygowane
R-kwadrat
Błąd
standardowy
oszacowania
Statystyka
Durbina-
Watsona
Predyktory: (Stała), wiek, plec
a.
Zmienna zależna: cisnienie
b.
Obserwacje nietypowe
Przypadki nietypowe pojawiają się z dwóch powodów:
• Braki w modelu (nieuwzględnianie ważnej zmiennej
niezależnej w modelu) lub zła postać algebraiczna
modelu (model nieliniowy)
• Błąd pomiaru (zanieczyszczenie warunków przez
zmienne zakłócające)
Cele usuwania przypadków odstających:
• Określenie wad modelu (jego ograniczeń)
• Zachowanie spójności modelu przed
oddziaływaniem punktów nie należących do tego
modelu
Analiza zakresów zmiennych
• Wiele przypadków odstających powstaje
w wyniku błędnego wprowadzenia
zmiennych. Nawet jeśli zbieramy dane
w sposób elektroniczny nie sposób
wykluczyć pomyłki systemu, czy
zakłóceń jego funkcjonowania, które
mogą powodować pojawianie się
wartości zmiennych wykraczających
poza możliwy zakres skali.
Statystyki reszt – wyszukiwanie
przypadków odstających
• Standaryzowane reszty
• Odległości Cooka (różnica między beta dla modelu
z wyłączonym przypadkiem oraz włączonym
przypadkiem – miara wpływu danego przypadku na
równanie regresji. Wszystkie odległości powinny
być podobne. Ta, która odstaje od reszty znacząco
zmienia współczynniki regresji. Znacząco to znaczy
jest większa od 1.
• Wartości wpływu – określają w jakim stopniu dana
wartość modyfikuje wzór linii regresji
• Wartości wpływu większe od wartości 2(k+1)/N,
gdzie k to liczba predyktorów powinny być
dokładniej sprawdzane
Wybór statystyk odległości
Nietypowość
• Przykład lęk.sav
• Zrób eksplorację obu zmiennych.
Sprawdź na wykresie skrzynkowym,
czy nie ma przypadków odstających
• Przeprowadź analizę regresji. Narysuj
wykres rozrzutu, dopasuj linię i
przedział ufności
Nietypowość a wpływowość
• To co nietypowe dla poszczególnych
zmiennych nie musi być nietypowe dla
linii regresji.
• Niekiedy przypadki odstające w obrębie
zmiennej nie są wpływowe dla linii
regresji
• Lepiej wpływowość obserwacji określać
za pomocą statystyki siły wpływu niż
posługując się wykresem skrzynkowym.