Wykład 15a

Skorelowane predyktory

Zyski ze znajomości

analizy czynnikowej

Rada na skorelowane

predyktory

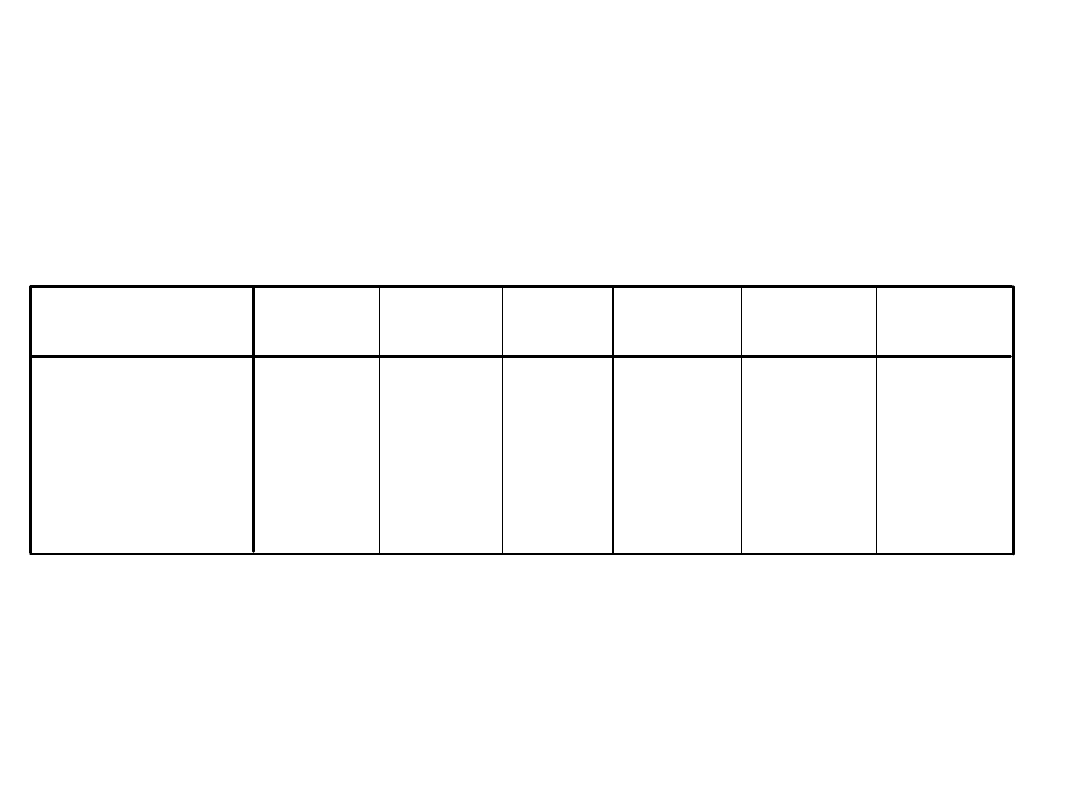
Analiza regresji – uwaga! skorelowane

predyktory

Korelacje

Korelacja Pearsona

1

,791**

,432**

,282**

,160**

,121*

,791**

1

,462**

,293**

,129*

,107

,432**

,462**

1

,230**

,089

,099

,282**

,293**

,230**

1

,745**

,750**

,160**

,129*

,089

,745**

1

,879**

,121*

,107

,099

,750**

,879**

1

NA2 lubie czytac ksiazki
NA3 uwielbiam poezje
NA4 fascynuje mnie teatr
NA5 bardzo lubie
ukladac rymowanki
NA6 pisze opowiadania
NA7 lubie rozwiazywac
krzyzowki

NA2 lubie

czytac ksiazki

NA3

uwielbiam

poezje

NA4

fascynuje

mnie teatr

NA5 bardzo

lubie ukladac

rymowanki

NA6 pisze

opowiadania

NA7 lubie

rozwiazywac

krzyzowki

Korelacja jest istotna na poziomie 0.01 (dwustronnie).

**.

Korelacja jest istotna na poziomie 0.05 (dwustronnie).

*.

lubie czytac

ksiazki

uwielbiam

poezje

fascynuje

mnie teatr

bardzo lubie

ukladac

rymowanki

pisze

opowiadania

lubie

rozwiazywac

krzyzowki

lu

bi

e

...

pi

sz

e

...

ba

rd

zo

lu

bi

...

fa

sc

yn

uj

e

...

uw

ie

lb

ia

m

..

.

lu

bi

e

cz

yt

a.

..

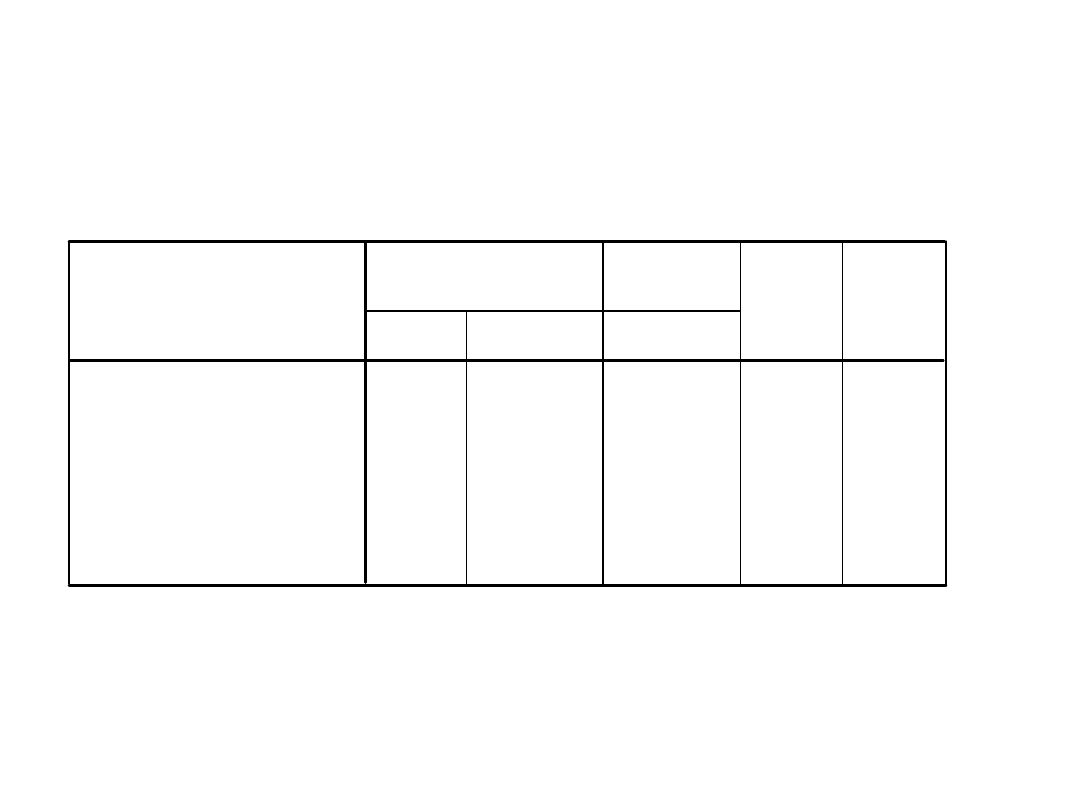
Które zmienne są istotnymi

predyktorami?

Współczynniki

a

-1,028

,148

-6,964

,000

,404

,039

,404

10,335

,000

,246

,040

,246

6,170

,000

,069

,027

,069

2,538

,012

,282

,039

,282

7,168

,000

,171

,052

,171

3,303

,001

,086

,052

,086

1,640

,102

(Stała)
NA2 lubie czytac ksiazki
NA3 uwielbiam poezje
NA4 fascynuje mnie teatr
NA5 bardzo lubie
ukladac rymowanki
NA6 pisze opowiadania
NA7 lubie rozwiazywac
krzyzowki

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: NA1 ocena z polskiego

a.

Ale można też inaczej…

• Być może te pojedyncze zmienne tworzą

pewne grupy skorelowanych zmiennych.

• Może „za ich plecami stoi” bardziej

podstawowy konstrukt psychologiczny i nie
warto tak bardzo szczegółowo rozpatrywać
tego zagadnienia.

• Prostota jest najbardziej elegancka w nauce



Robimy analizę czynnikową dla

predyktorów

1 krok –Ustalamy,

ile jest

skorelowanych

ze sobą wiązek

zmiennych

(rodzin)?

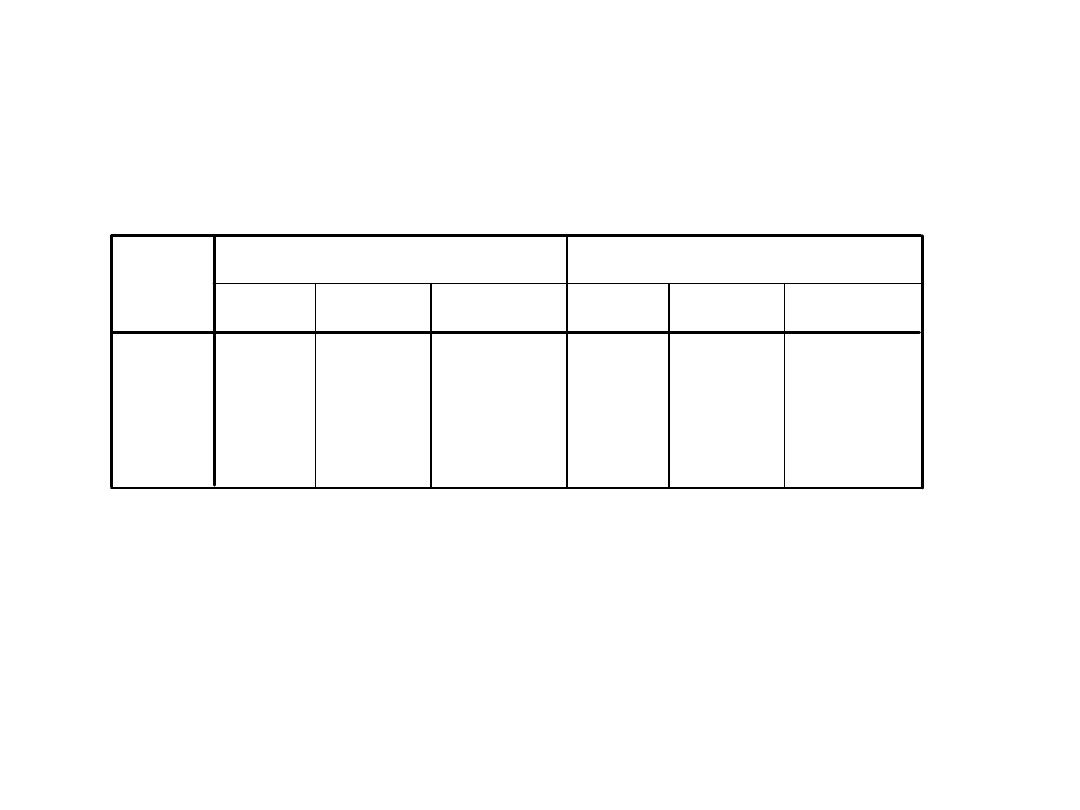
Kryterium Kaisera – wartość własna

czynnika większa od 1

Całkowita wyjaśniona wariancja

2,917

48,615

48,615

2,917

48,615

48,615

1,838

30,640

79,255

1,838

30,640

79,255

,652

10,863

90,118

,270

4,500

94,618

,204

3,403

98,021

,119

1,979

100,000

Składowa
1
2
3
4
5
6

Ogółem

% wariancji

%

skumulowany

Ogółem

% wariancji

%

skumulowany

Początkowe wartości własne

Sumy kwadratów ładunków po

wyodrębnieniu

Metoda wyodrębniania czynników - Głównych składowych.

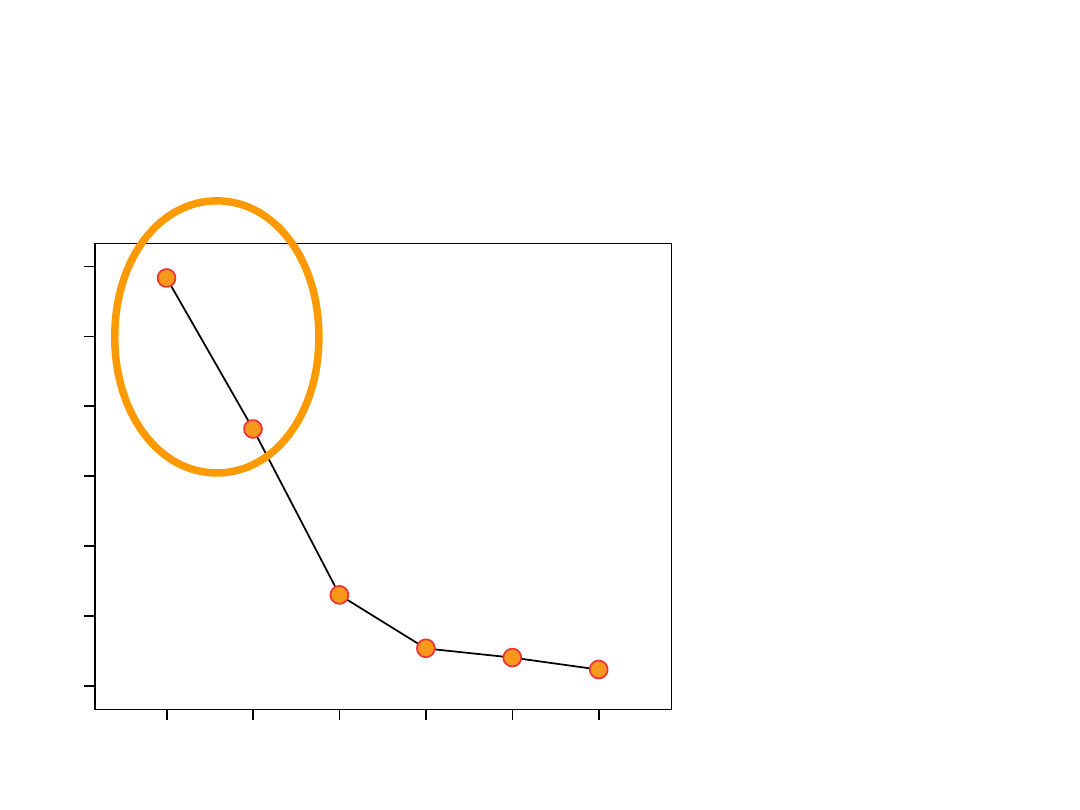
Kryterium 2 – Wykres osypiska

Dopóki wykres

jest stromy a
wartości
własne
powyżej
jedynki

1

2

3

4

5

6

Numer składowej

0,0

0,5

1,0

1,5

2,0

2,5

3,0

W

ar

to

ść

w

ła

sn

a

Wykres osypiska

Ile czynników?

• Wyniki kryterium Kaisera i wykresu

osypiska są zbieżne – uznajemy, że mamy

dwie wiązki silnie korelujących ze sobą

pytań.

• Dowiedzmy się teraz które dokładnie

pytania tworzą poszczególne wiązki…

• Krok 2 analizy czynnikowej

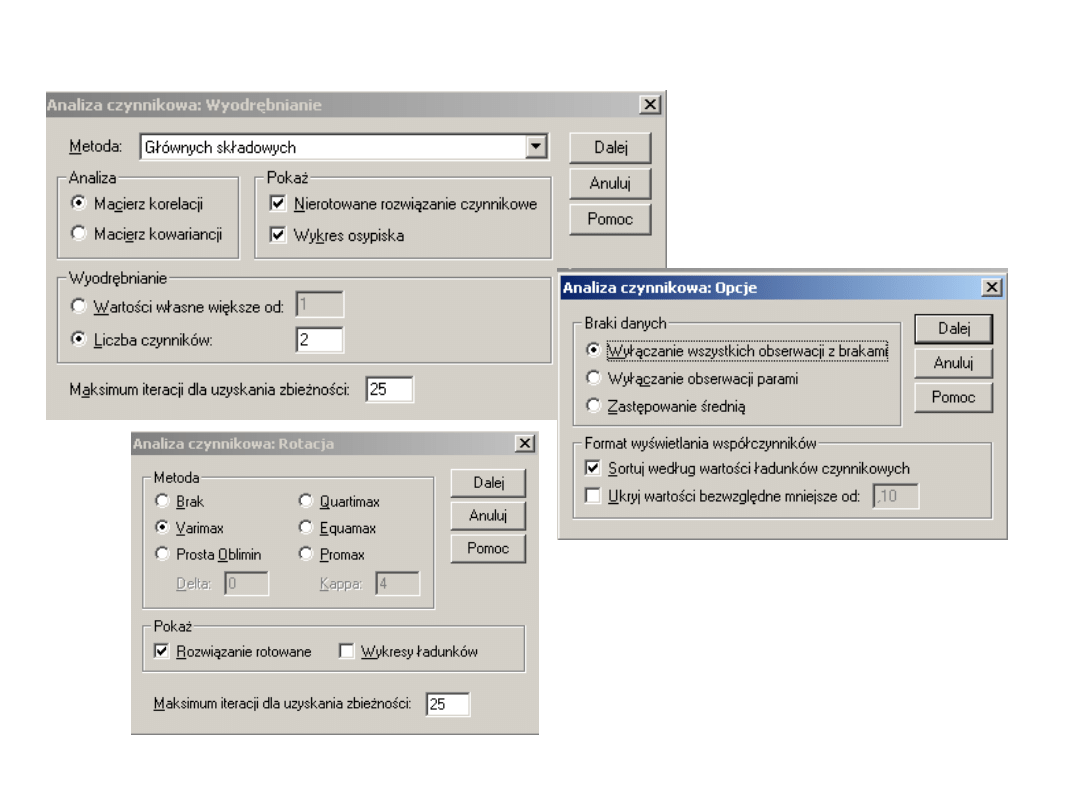
Klikamy…

Wyniki

• Czynnik 1 można

nazwać aktywną

postawą wobec

języka, czynnik 2

pasywną postawą

wobec języka.

• Możemy zatem

tak naprawdę

zrobić dwa

wskaźniki:

pasywna postawa

i aktywna

postawa

Macierz rotowanych składowych

a

,952

,021

,948

,044

,866

,250

,088

,906

,105

,891

,070

,706

NA7 lubie rozwiazywac
krzyzowki
NA6 pisze opowiadania
NA5 bardzo lubie
ukladac rymowanki
NA3 uwielbiam poezje
NA2 lubie czytac ksiazki
NA4 fascynuje mnie teatr

1

2

Składowa

Metoda wyodrębniania czynników - Głównych składowych.

Metoda rotacji - Varimax z normalizacją Kaisera.

Rotacja osiągnęła zbieżność w 3 iteracjach.

a.

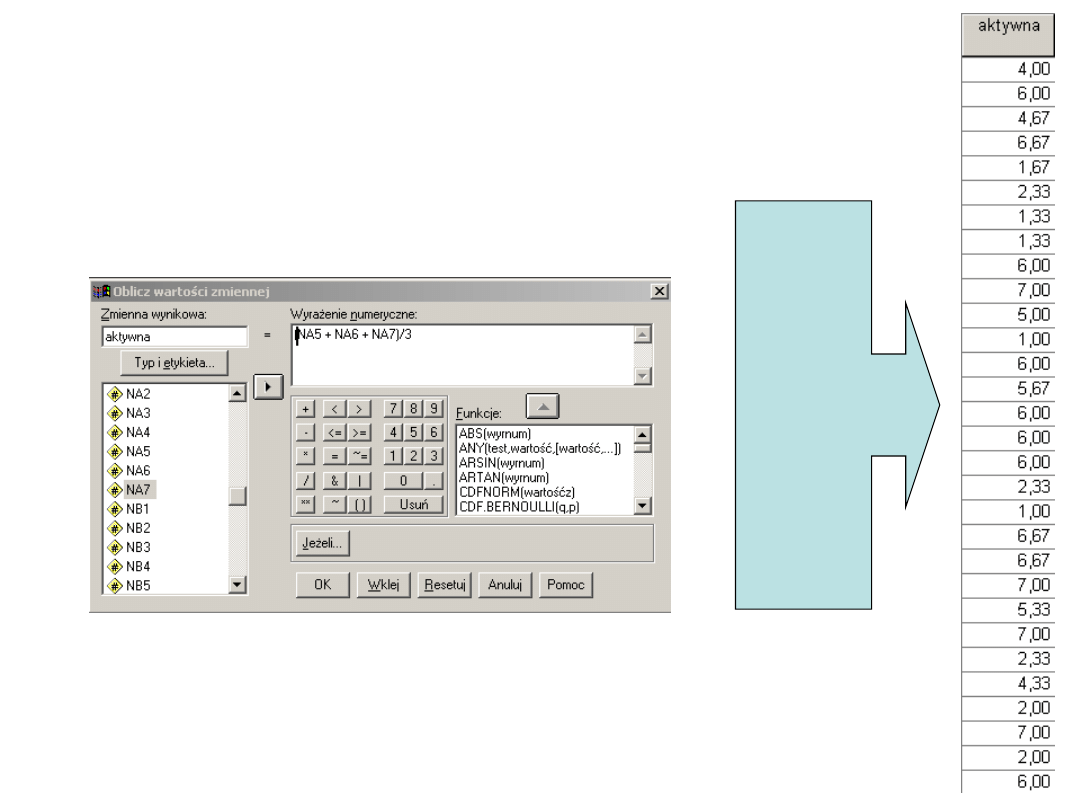
Jak zrobić wskaźniki? 1

• Wersja dla pracowitych

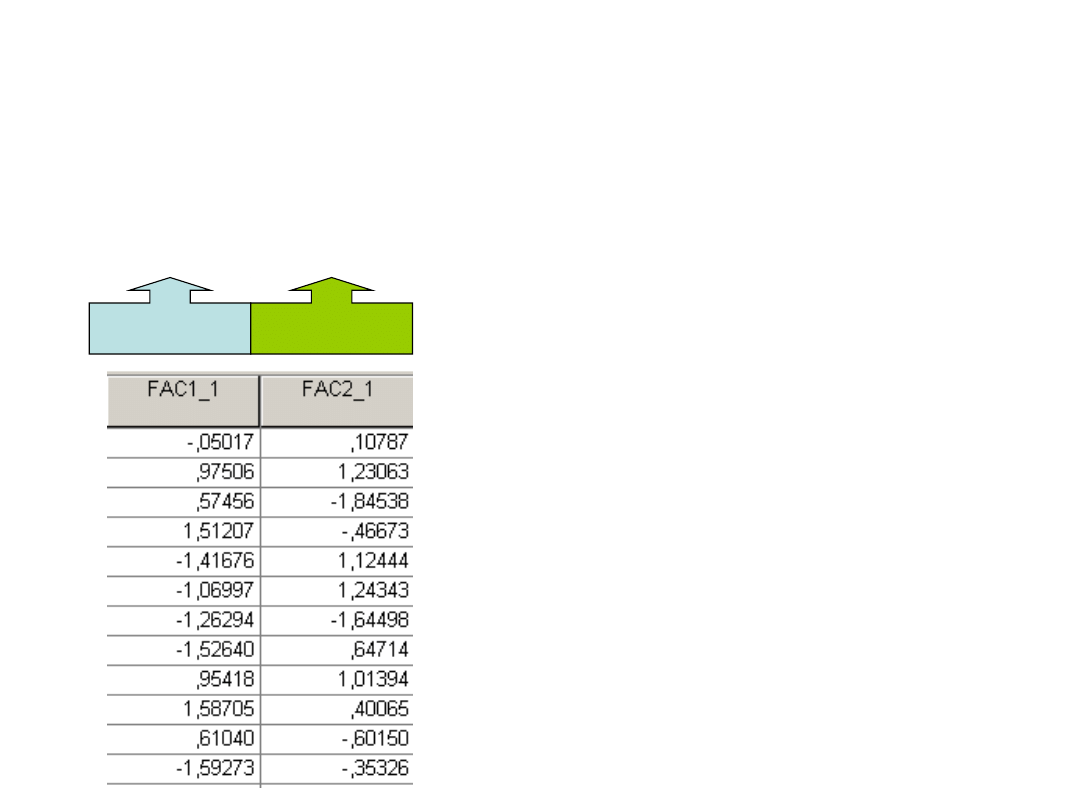
W danych

powstaje

nowa

zmienna

Jak zrobić wskaźniki 2?

• Wersja dla leniwych

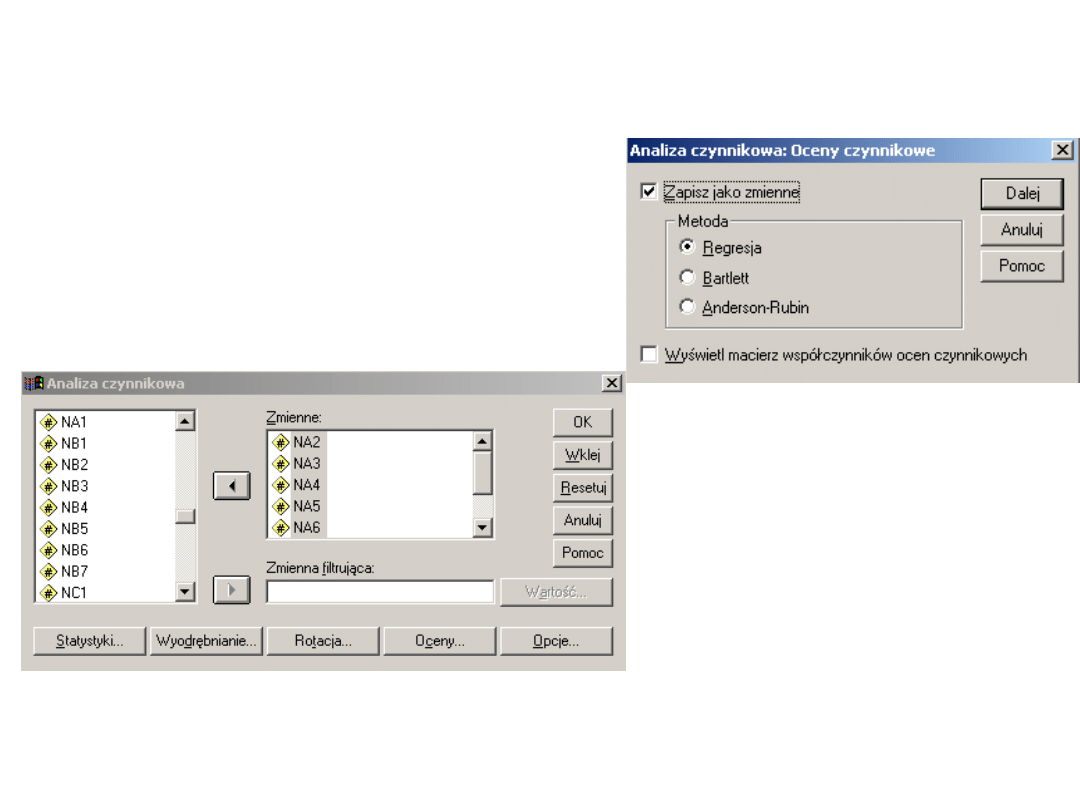
Podejście regresyjne

Macierz rotowanych składowych

a

,952

,021

,948

,044

,866

,250

,088

,906

,105

,891

,070

,706

NA7 lubie rozwiazywac
krzyzowki
NA6 pisze opowiadania
NA5 bardzo lubie
ukladac rymowanki
NA3 uwielbiam poezje
NA2 lubie czytac ksiazki
NA4 fascynuje mnie teatr

1

2

Składowa

Metoda wyodrębniania czynników - Głównych składowych.

Metoda rotacji - Varimax z normalizacją Kaisera.

Rotacja osiągnęła zbieżność w 3 iteracjach.

a.

1. Każda zmienna jest

standaryzowana

2. Następnie każda

wystandaryzowana zmienna
jest mnożona przez
współczynnik czynnikowy

3. Następnie zmienne są

uśredniane

4. Każde pytanie jest

uwzględniane przy czym siła
jego wpływu na wartość
całego wskaźnika jest
uzależniona od siły
powiązania z czynnikiem.
Słabe pytania słabo zmieniają
wskaźnik.

5. Powstały wskaźnik należy

interpretować w kategoriach
zmiennej wystandaryzowanej

Regresja

• Zmieniamy nazwy

zmiennym, tak, żeby nazwa

oddawała znaczenie

czynnika.

• Wprowadzamy te dwie

zmienne jako predyktory do

regresji

• Będziemy przewidywać

oceny z polskiego

Aktywne
poznawani
e języka

Bierne
poznawani
e języka

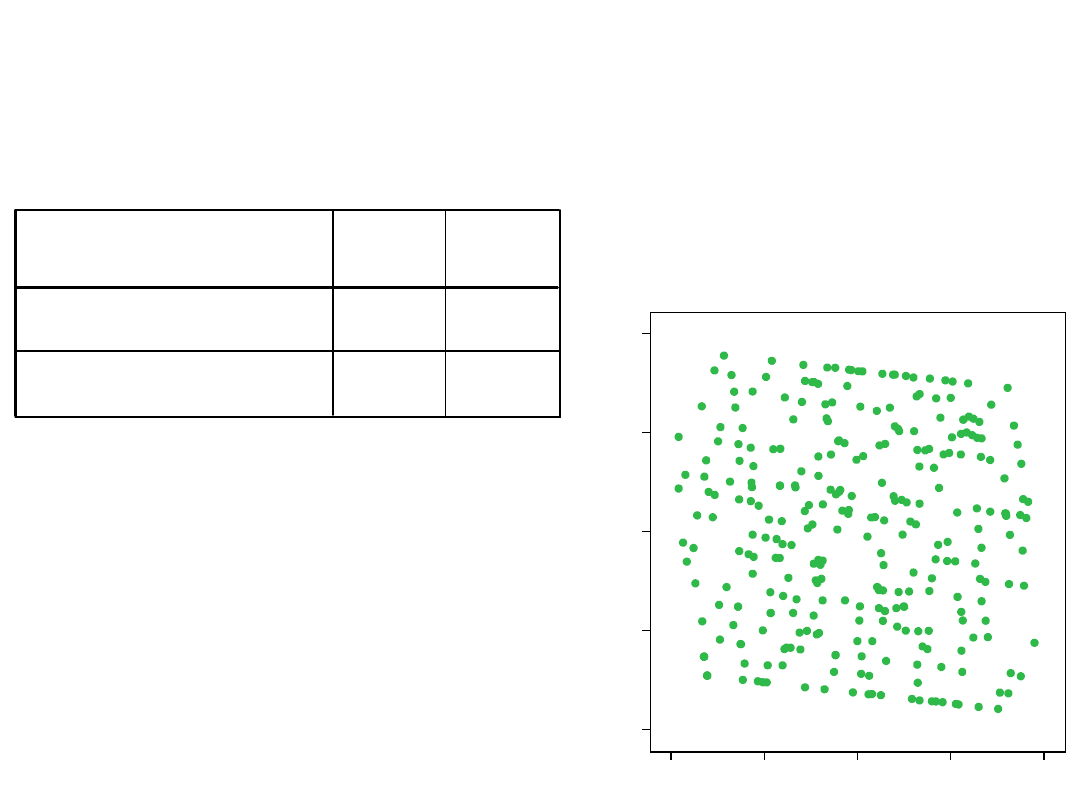
Sprawdzamy, czy predyktory są

skorelowane

Korelacje

1

,000

1,000

299

299

,000

1

1,000

299

299

Korelacja Pearsona
Istotność (dwustronna)
N
Korelacja Pearsona
Istotność (dwustronna)
N

aktywne aktywne
poznawanie jezyka

bierne bierne
poznawanie jezyka

aktywne

aktywne

poznawanie

jezyka

bierne bierne

poznawanie

jezyka

-2,00000

-1,00000

0,00000

1,00000

2,00000

bierne poznawanie jezyka

-2,00000

-1,00000

0,00000

1,00000

2,00000

ak

ty

w

n

e

p

o

zn

aw

an

ie

je

zy

ka

Dopasowanie

Analiza wariancji

b

966,627

2

483,314

652,137

,000

a

219,373

296

,741

1186,000

298

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), bierne bierne poznawanie jezyka, aktywne aktywne
poznawanie jezyka

a.

Zmienna zależna: NA1 ocena z polskiego

b.

Współczynniki

a

4,000

,050

80,343

,000

1,110

,050

,557

22,266

,000

1,418

,050

,711

28,434

,000

(Stała)
aktywne aktywne
poznawanie jezyka
bierne bierne
poznawanie jezyka

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: NA1 ocena z polskiego

a.

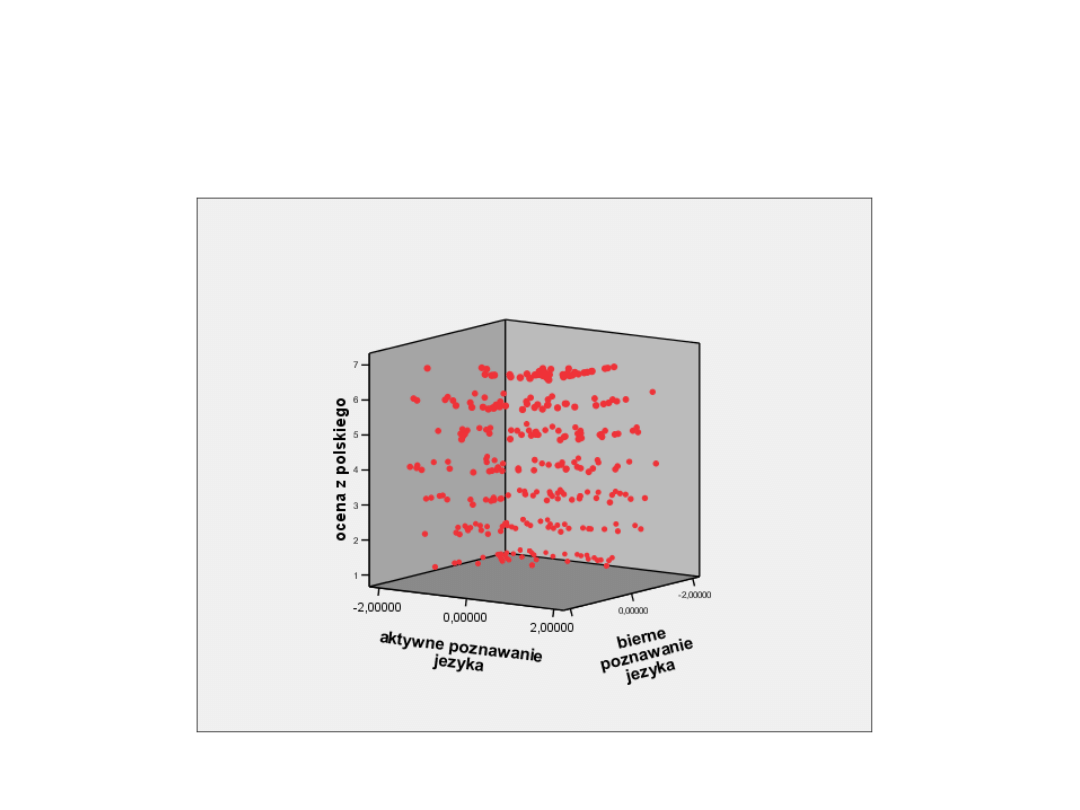
Wykres