1

ATESTACJA

APARATURY POMIAROWEJ

CZĘŚĆ 3.

ATESTACJA

APARATURY POMIAROWEJ

CZĘŚĆ 3.

Jednostka

prowadząca:

Instytut Metrologii i Inżynierii

Biomedycznej

Autor

prezentacji:

dr inż. Jerzy

Arendarski

2

Wzorcowanie

płytek wzorcowych, płytek

kątowych, kątowników

i płytek

interferencyjnych

Wzorcowanie

płytek wzorcowych, płytek

kątowych, kątowników

i płytek

interferencyjnych

3

Wzorcowanie (inaczej kalibracja) to zbiór

operacji ustalających, w określonych
warunkach,

relację między wartościami

wielkości mierzonej wskazanymi przez
przyrząd pomiarowy

...,

a odpowiednimi wartościami wielkości

realizowanymi przez wzorce jednostki miary

.

Uwaga:

Wynik wzorcowania pozwala na przypisanie wskazaniom

odpowiednich wartości wielkości mierzonej

lub na wyznaczenie poprawek wskazań.

4

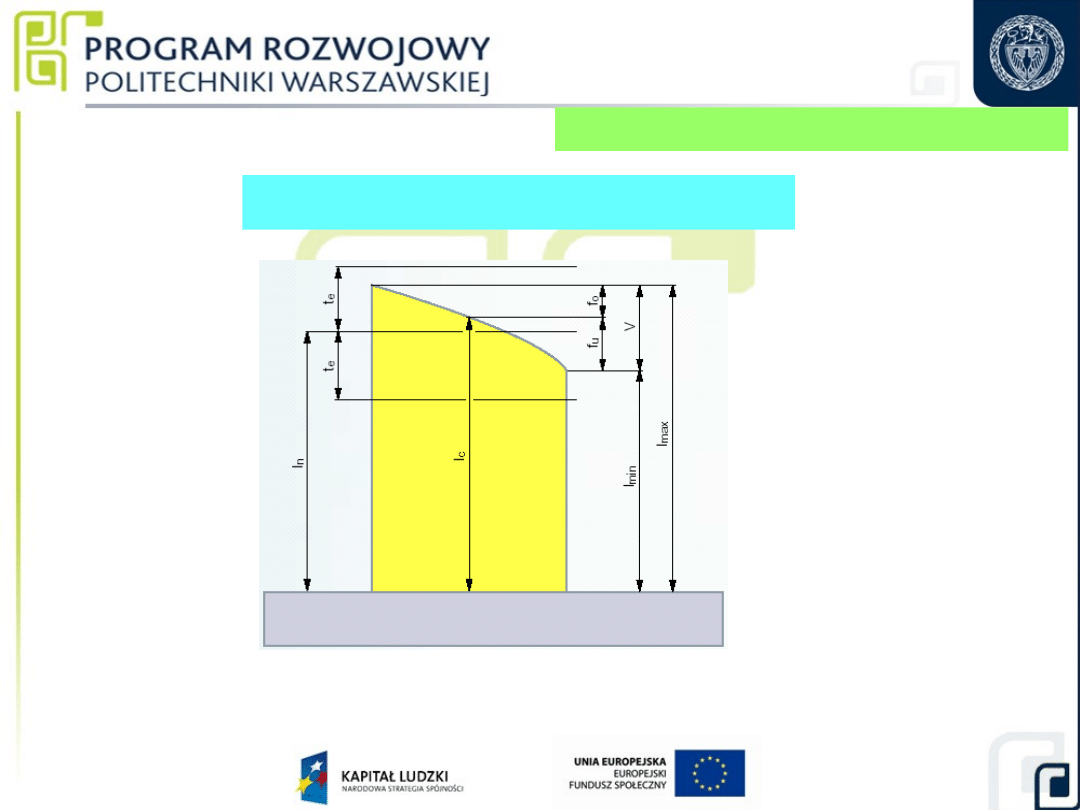
Wymiary płytki wzorcowej

Wzorcowanie płytek wzorcowych

f

o

= l

max

- l

c

f

u

= l

c

- l

min

ν = l

max

- l

min

= f

o

+ f

u

5

Długość płytki wzorcowej

odległość, w kierunku prostopadłym, między

każdym dowolnym punktem powierzchni
pomiarowej a powierzchnią płaską płytki
pomocniczej, z tego samego materiału i o

takiej

samej strukturze powierzchni, do której

druga

powierzchnia pomiarowa płytki wzorcowej
została przywarta.

(wg PN-EN ISO 3650)

Definicja długości płytki wzorcowej

6

1. Odchyłka długości w dowolnym

punkcie od długości nominalnej

Podstawowe właściwości płytki wzorcowej

2. Odchyłka płaskości powierzchni pomiarowej

3. Zakres rozrzutu długości

4. Przywieralność

PN-EN ISO 3650:2000 „Płytki wzorcowe”

7

Dopuszczalne odchyłki długości płytek

wzorcowych i dopuszczalna zmienność długości

Klas

a

Odchyłki graniczne

dop. t

e

Zakres rozrzutu

długości

ν

K

± (0,20 +0,004 l

n

)

μm

(0,05 +0,0002 l

n

) μm

0

± (0,10 +0,002 l

n

)

μm

(0,10 +0,0003 l

n

) μm

1

± (0,20 +0,004 l

n

)

μm

(0,16 +0,00045 l

n

)

μm

2

± (0,40 +0,008 l

n

)

μm

(0,30 +0,0007 l

n

) μm

Klasyfikacja i właściwości płytek wzorcowych

8

Dopuszczalne odchyłki płaskości powierzchni pomiarowych

Klasyfikacja i właściwości płytek wzorcowych

Długość

nominalna,

l

n

mm

Tolerancja płaskości t

f

µm

Klasa

K

0

1

2

0,5≤ l

n

≤

150

0,05

0,10

0,15

0,25

150> l

n

≤

500

0,10

0,15

0,18

0,25

500> l

n

≤

1000

0,15

0,18

0,20

0,25

9

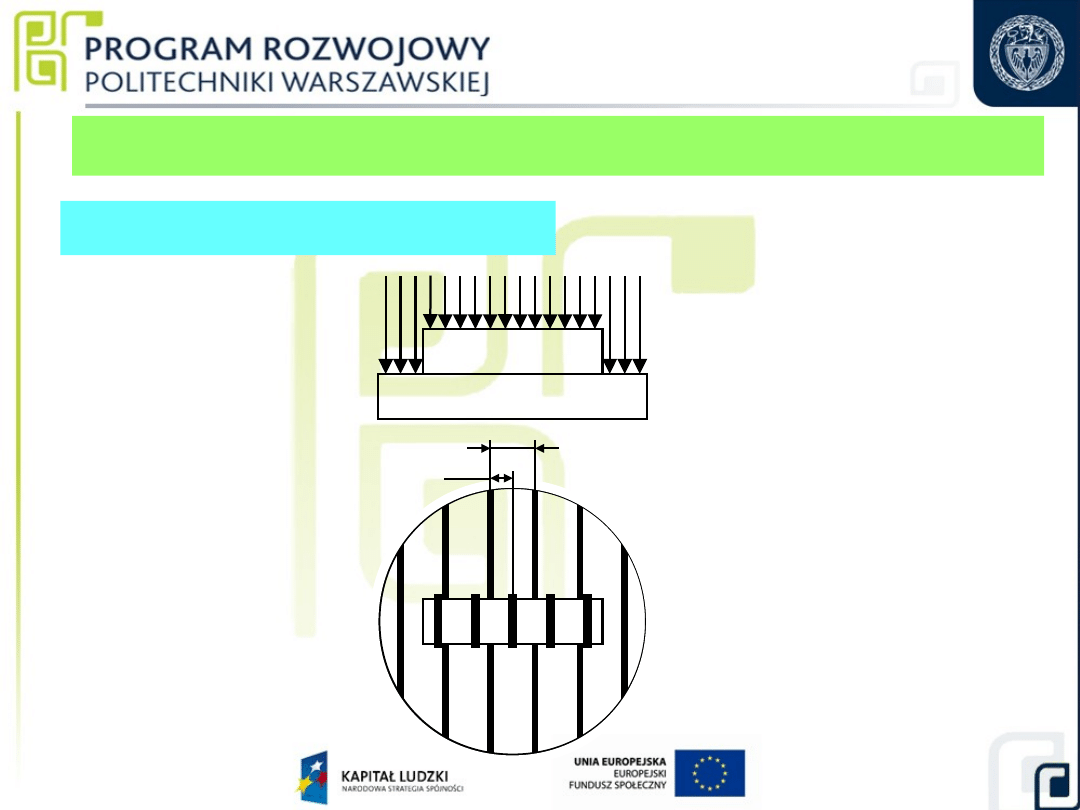
Przywieralność powierzchni pomiarowych

Klasyfikacja i właściwości płytek wzorcowych

Za kryterium oceny przywieralności przyjmuje się
obraz powierzchni pomiarowej po przywarciu do niej
szklanej płytki interferencyjnej, który powinien
odpowiadać wymaganiom podanym w tabeli poniżej:

klasa

płytki

wzorcow

ej

obraz interferencyjny

prążki

interferencyjne

odcienie

K, 0

nie dopuszcza się

nie dopuszcza się

1, 2

dopuszcza się

niewielkie jasne

plamy lub szare

odcienie

10

Właściwości materiału

Klasyfikacja i właściwości płytek wzorcowych

Stabilność wymiarowa

Klas

a

Największa dopuszczalna zmiana długości w

ciągu roku

K, 0 ± (0,02 m +0,25 x 10

-6

x l

n

)

1, 2

± (0,05 m +0,5 x 10

-6

x l

n

)

UWAGA

- l

n

wyrażona w milimetrach

Współczynnik rozszerzalności cieplnej stalowych płytek wzorcowych (10C ÷ 30 C)

powinien wynosić (11,5 ± 1,0) x 10

-6

K

-1

Współczynnik rozszerzalności cieplnej z niepewnością
powinien być podany
dla płytek klasy K, a dla pozostałych klas jeżeli materiał
jest inny niż stal.

11

Pomiary długości płytek wzorcowych klasy K

Metoda interferencyjna

M

ε

12

Wyposażenie pomiarowe i pomocnicze

Wzorcowanie płytek wzorcowych klas 0, 1 i 2

•

komplet płytek wzorcowych odniesienia klasy dokładności K

•

komplet płytek wzorcowych klasy dokładności 0 – wzorce robocze

•

płaskie płytki interferencyjne klasy I i klasy II

•

dwugłowicowy komparator do pomiarów porównawczych Mahr 826

•

kamień drobnoziarnisty Arkansas lub Missisipi

•

przyrząd do rozmagnesowywania płytek wzorcowych

•

zestaw do czyszczenia i konserwacji płytek wzorcowych

•

pęseta

13

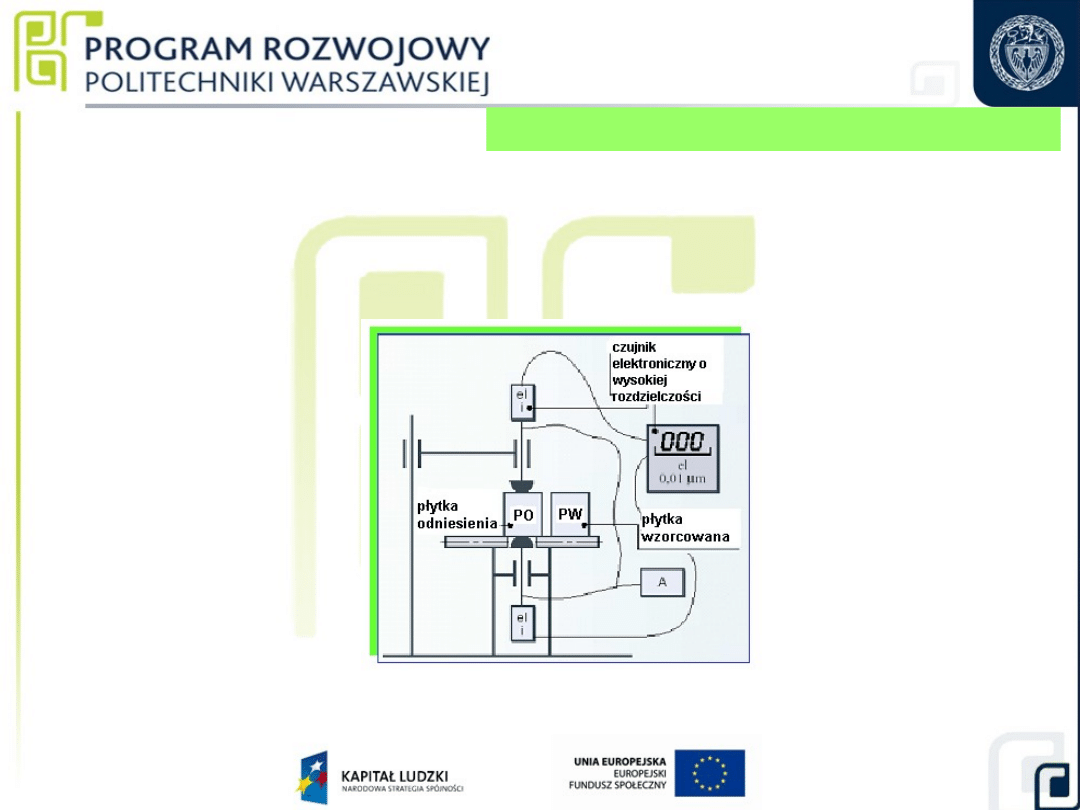
Pomiary długości płytek wzorcowych

metodą porównawczą (klasy: 0, 1 i 2)

Pomiary długości płytek wzorcowych

Schemat komparatora do pomiaru długości płytek

14

Komparator Mahr 826E

15

Budowa obsady z gniazdami dla porównywanych płytek

Komparator Mahr 826E

16

Manipulator do przemieszczania obsady z płytkami

Komparator Mahr 826E

17

Warunki środowiskowe

Dopuszczalne wartości zmian

temperatury

przy wzorcowaniu płytek wzorcowych

Klasa

płytki

wzorco

wa

-nej

Długość nominalna płytki wzorcowej

mm

do

2

Powyże

j 2

do 10

powyż

ej 10

do

100

do 2

powyż

ej 2

do 10

powyż

ej 10

do

100

odchylenie od

temperatury

otoczenia 20ºC

różnica temperatury

płytki wzorcowanej i

płytki odniesienia

ºC

0

±2

±1

±0,5

±0,2

±0,1

±0,05

1

±3

±2

±0,5

±0,3

±0,2

±0,1

2

±5

±3

±1

±0,5

±0,3

±0,1

18

Reklimatyzacja

Klasa

płytki

wzorco

wa

-nej

Długość nominalna płytki wzorcowej

mm

do

2

powyż

ej 2

do 5

powyże

j 5

do 10

powyż

ej 10

do 20

powyż

ej 20

do 50

powyż

ej 50

do

100

minuty

0

30

60

90

135

150

165

1

25

50

75

105

135

135

2

20

45

60

105

135

135

Czas potrzebny na wyrównanie temperatury płytek wzorcowych

19

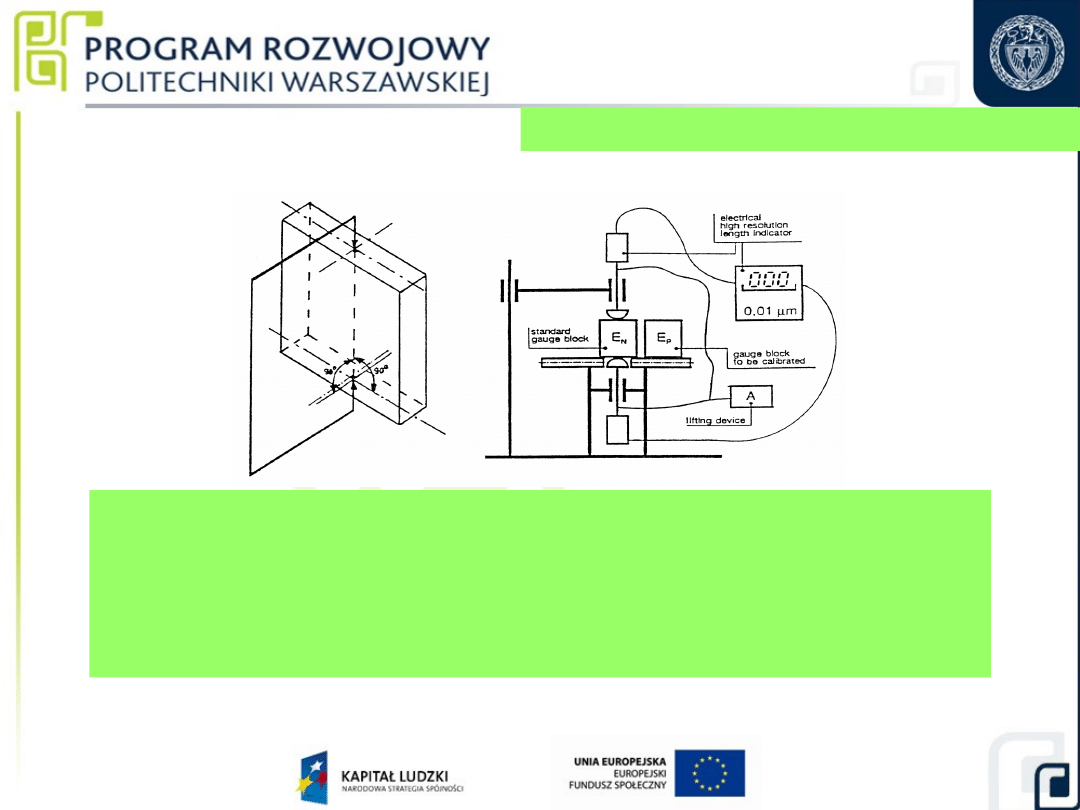
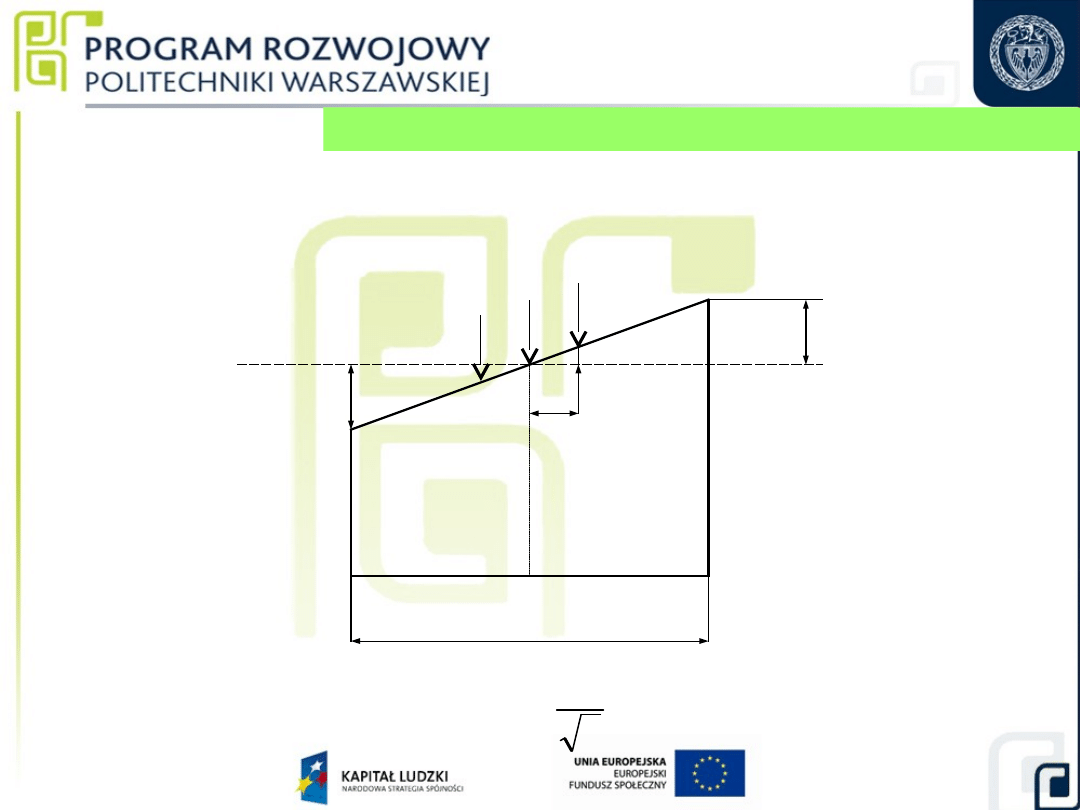
Długość płytki wzorcowej w dowolnym punkcie

–

może być interpretowana jako odległość między

punktem powierzchni pomiarowej, a punktem

przeciwległej powierzchni pomiarowej w kierunku

prostopadłym do płaszczyzny do niej przylegającej.

Pomiary długości płytek wzorcowych

(wg. PN-83/M-53101)

20

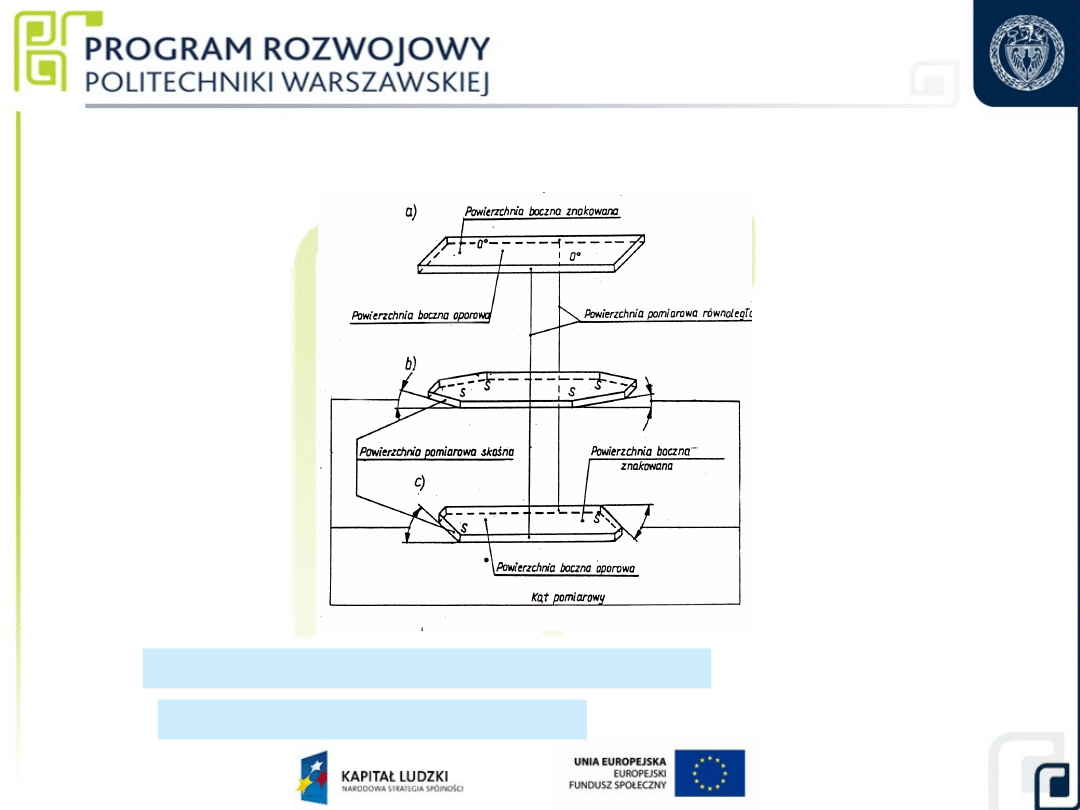
Punkty pomiarowe

Pomiary długości płytek wzorcowych

)

(

a

b

e

e

k

c







u

o

f

f

b

b

v









min

max

PO

+

1

PW

+

2

+

4

+

3

+

5

+

6

PO

+

a

PW

+

b

+

b

2

+

b

1

+

b

3

+

b

4

21

Pomiar odchyłki płaskości powierzchni pomiarowej

m

m

m

p





3

,

0

2









22

Płytka mierzona:

deklarowana klasa

dokładności 0;

porównywane płytki są

wykonane ze stali;

l

n

= 50 mm

;



t

ko

= (0  0,5)C

;



t

kw

=(0 

0,05)C

;

e

k

= - 0,08m

;

b-a = +0,12m

Niepewność pomiaru długości wybranej płytki wzorcowej

23

e

w

= (b – a) + e

k

Po uwzględnieniu poprawek wzór przyjmuje postać:

e

w

= (b-a) + e

k

+ P

t

+ P

b

+ P

d

+ P

ν

Otrzymuje się

równanie pomiaru

:

e

w

= (b - a) + e

k

+ l

n





t

ko

+ l

n



w



t

kw

+

P

b

+ P

d

+ P

ν

Po podstawieniu wzoru na poprawkę temperaturową

P

t

= [l

w

·



w

(t

o

– t

w

) – l

k



k

(t

o

– t

k

)]

Niepewność pomiaru długości wybranej płytki wzorcowej

24

gdzie:
c

1

= c

2

= c

7

= c

8

= c

9

= 1

c

3

= l

n

·



t

ko

= 0; c

4

= l

n



= 0; c

5

= l

n



t

kw

= 0; c

6

= l

n



w

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

2

2

9

2

2

8

2

2

7

2

2

6

2

2

5

2

2

4

2

2

3

2

2

2

2

2

1

r

d

b

kw

w

ko

k

w

P

u

c

P

u

c

P

u

c

t

u

c

u

c

t

u

c

u

c

e

u

c

a

b

u

c

e

u































Równanie niepewności standardowej złożonej przyjmuje postać:

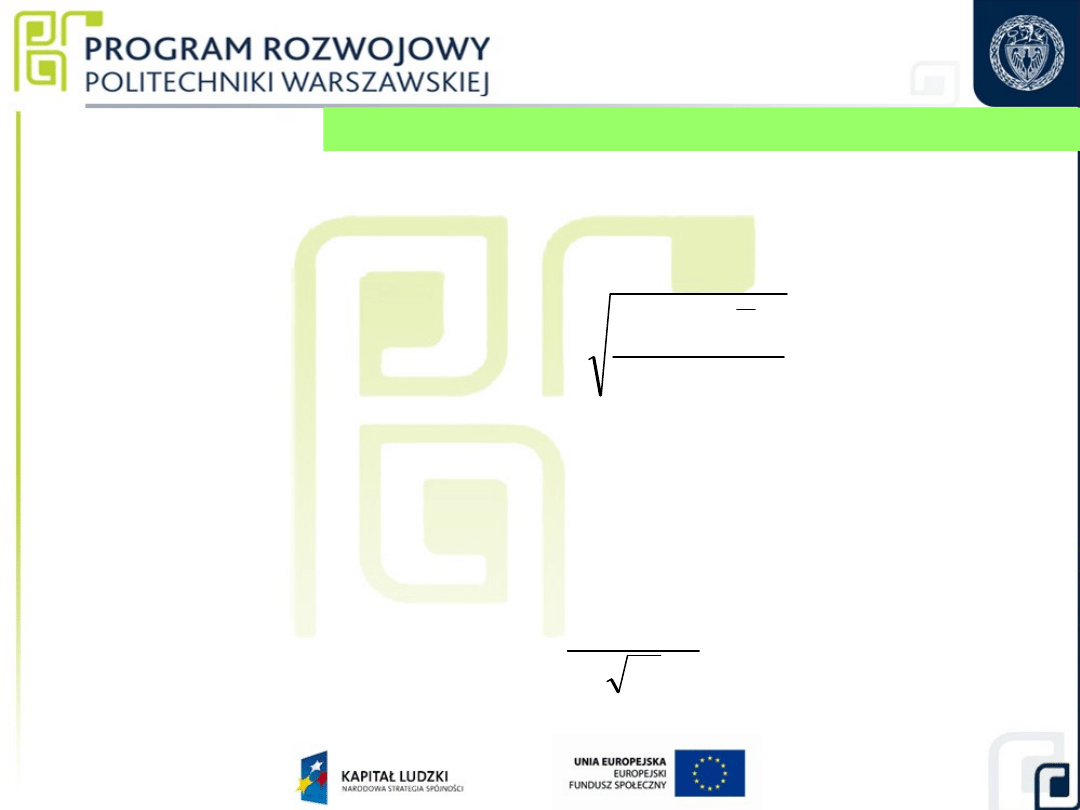
25

1. Niepewność standardowa pomiaru różnicy
długości
płytek u(b-a)



  





1

n











2

i

d

d

d

s

a

b

s

Otrzymaną wartość oznaczyć symbolem u

p

(b-a) i

traktować jako niepewność standardową połączoną przy
wzorcowaniu innych płytek
(o zbliżonym wymiarze nominalnym).









m

a

b

u

a

b

u

p







Obliczanie niepewności standardowych składowych

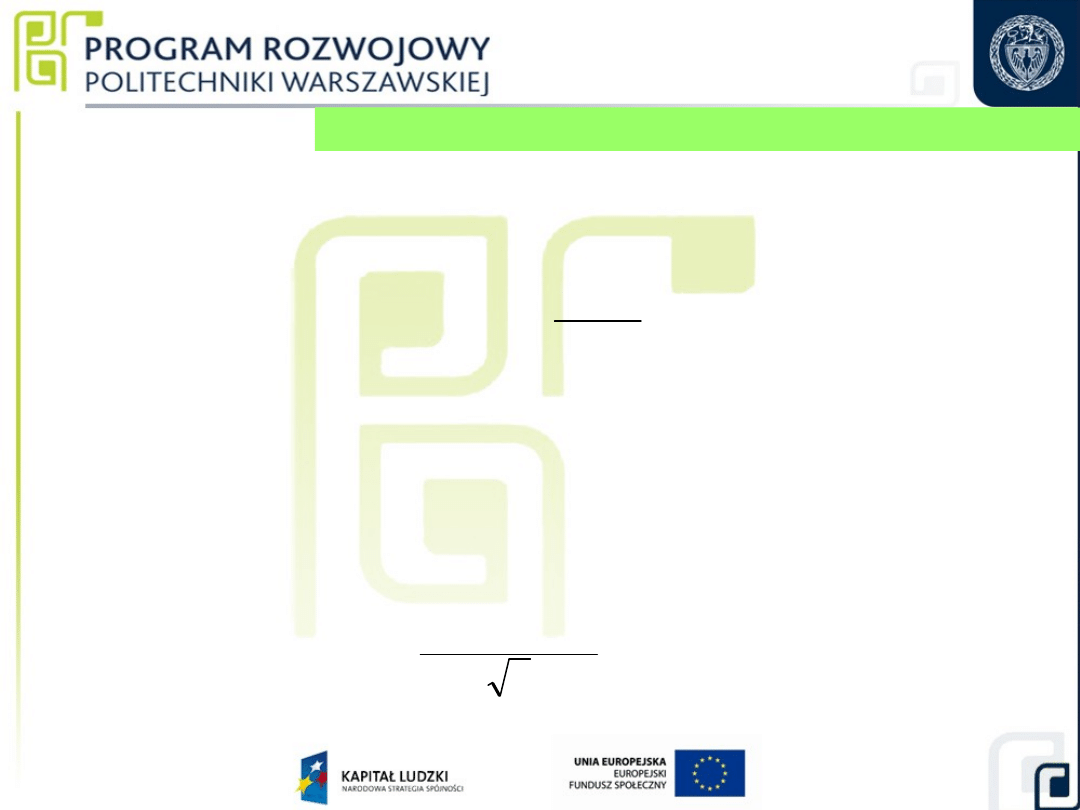
26

2. Niepewność standardowa pomiaru długości płytki
kontrolnej, u(e

k

).

 

 

k

e

U

e

u

k

k



3)

Niepewność

standardowa

różnicy

współczynników
rozszerzalności cieplnej, u(



).

 = (11,5  1,0) 10

-6

o

C

-1

 

1

6

1

6

C

10

0,82

6

C

10

2





















Δα

u

Obliczanie niepewności standardowych składowych

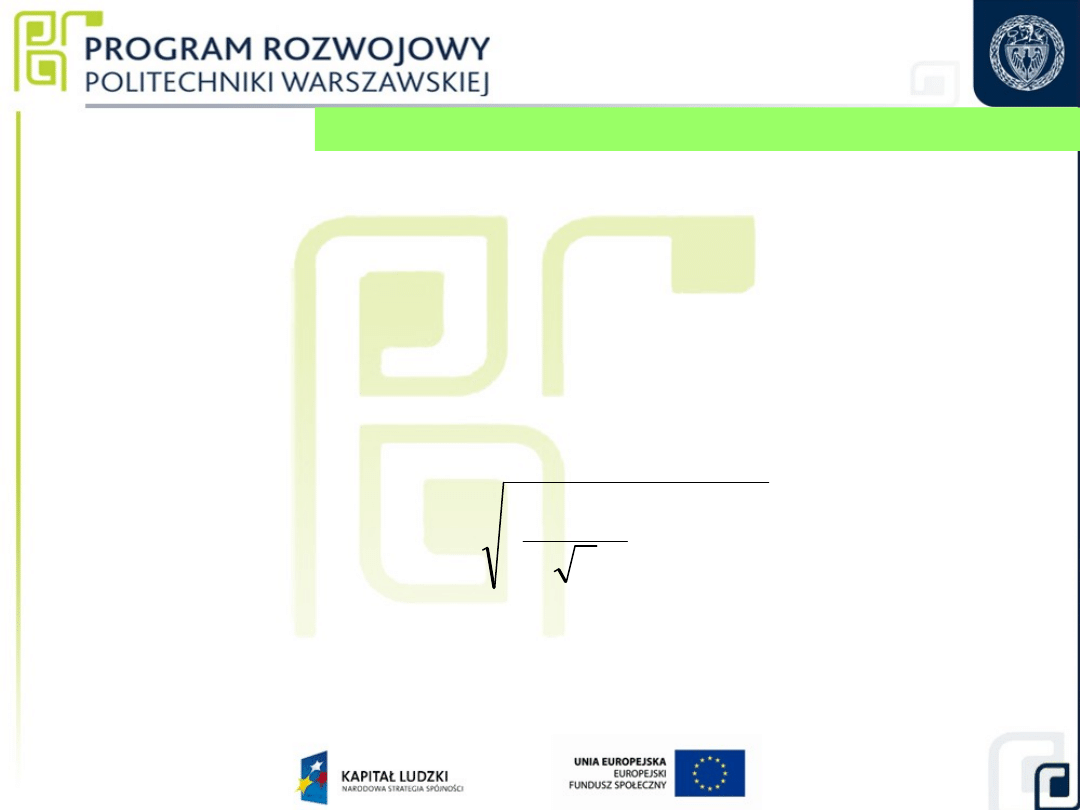
27

4. Niepewność standardowa odchylenia temperatury
płytki kontrolnej od temperatury otoczenia,
u(



t

ko

).

t = (20 



t

max

)

o

C





 

t

u

Δt

Δt

u

2

2

komax

ko

















2

Obliczanie niepewności standardowych składowych

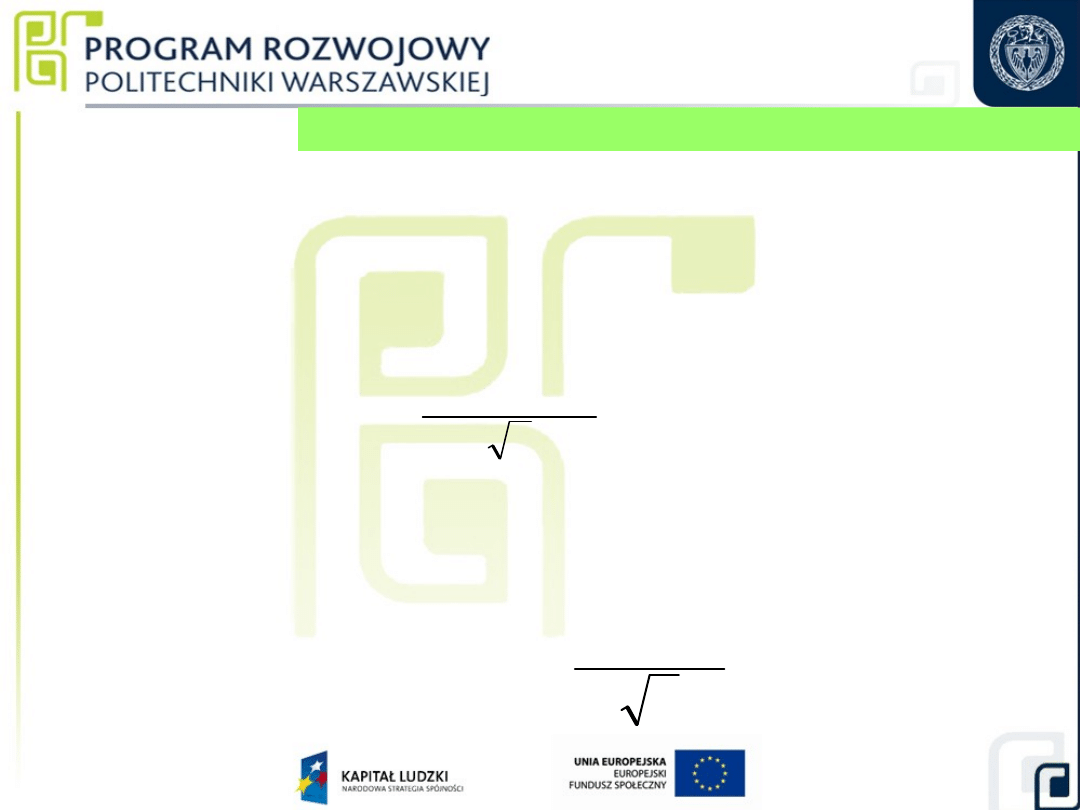
28

5. Niepewność standardowa współczynnika
rozszerzalności
cieplnej materiału płytki wzorcowanej, u(



w

)



= (11,5  1,0) · 10

-6

o

C

-1

 

1

6

1

6

C

10

0,58

3

C

10

1





















w

α

u

6. Niepewność standardowa różnicy temperatur
płytki
wzorcowanej i płytki kontrolnej, u(



t

kw

)





3

max

kw

kw

Δt

Δt

u



Obliczanie niepewności standardowych składowych

29

7. niepewność standardowa poprawki wskazania
przyrządu na płytce wzorcowanej, u(P

b

)

 

3

g

b

E

P

u



Obliczanie niepewności standardowych składowych

30

8. Obliczenie niepewności standardowej poprawki
na stabilność
materiału płytki kontrolnej, u(P

d

)

 

3

l

P

u

d





 

6

2 l

P

u

d





W normach podane są dopuszczalne roczne zmiany
długości płytek 



l

Obliczanie niepewności standardowych składowych

31

 

9. Obliczanie niepewności standardowej poprawki
na zmienność
długości płytki sprawdzanej, u(P

ν

)

9

0,5

ν

0,5

ν

h

0,5

 

3

h

P

u





Obliczanie niepewności standardowych składowych

32

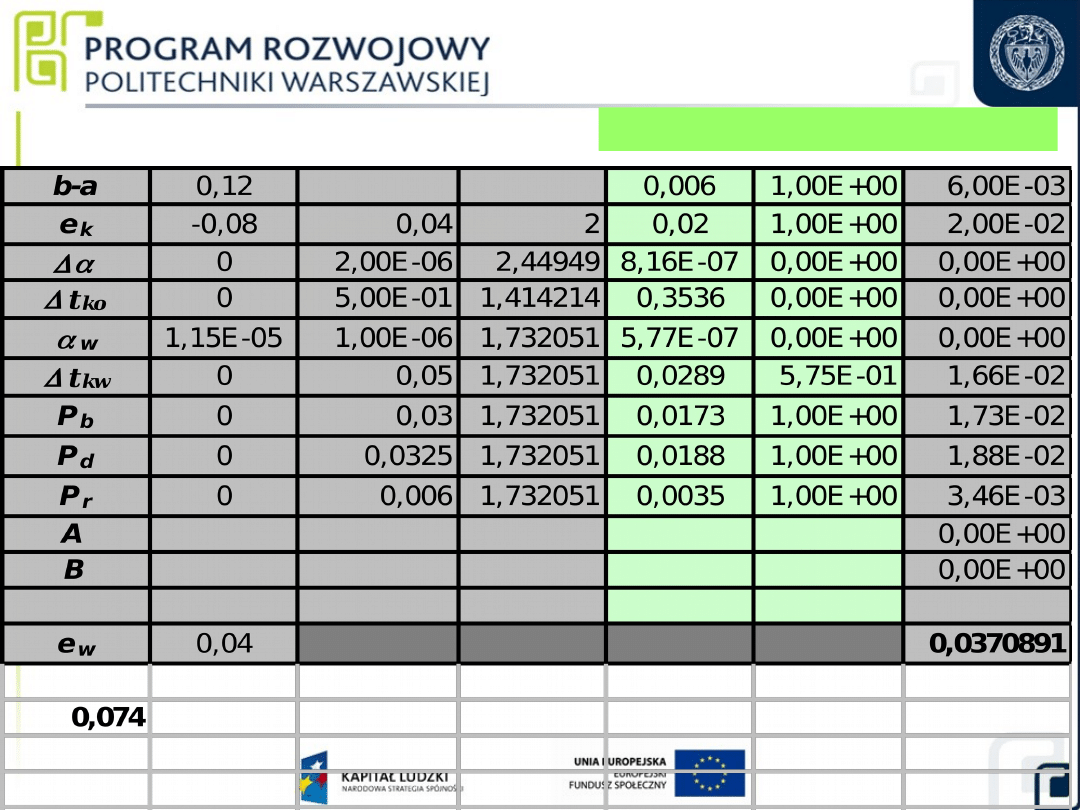
Budżet niepewności pomiaru

33

e

w

= (b - a) + e

k

+

l

n





t

ko

+

l

n



w



t

kw

+ P

b

+ P

d

+ P

r

)

(

)

(

)

(

)

(

)

(

2

2

2

2

2

2

2

2

2

ko

n

ko

n

ko

n

ko

n

t

u

u

l

t

u

l

u

t

l

t

l







































2
y

u

Składowe wyższego rzędu

)

(

)

(

0

0

)

(

2

2

2

ko

n

ko

n

t

u

u

l

t

l























2

y

u

)

(

)

(

)

(

ko

t

u

u

A

u











)

(

)

(

)

(

)

(

)

(

2

2

2

2

2

2

2

2

2

kw

w

n

kw

w

n

w

kw

n

kw

w

n

t

u

u

l

t

u

l

u

t

l

t

l































2
y

u

)

(

)

(

)

(

0

)

(

2

2

2

2

2

2

kw

w

n

kw

w

n

kw

w

n

t

u

u

l

t

u

l

t

l

























2
y

u

)

(

)

(

)

(

kw

w

t

u

u

B

u









34

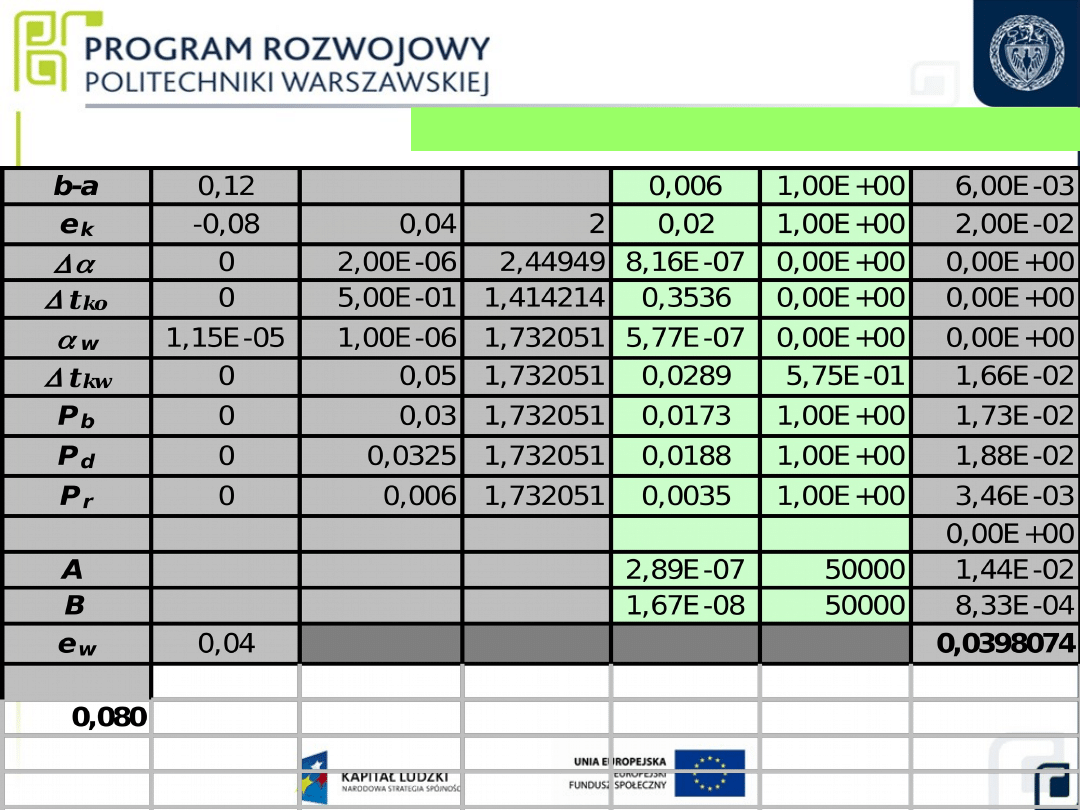
Budżet niepewności pomiaru (skorygowany)

35

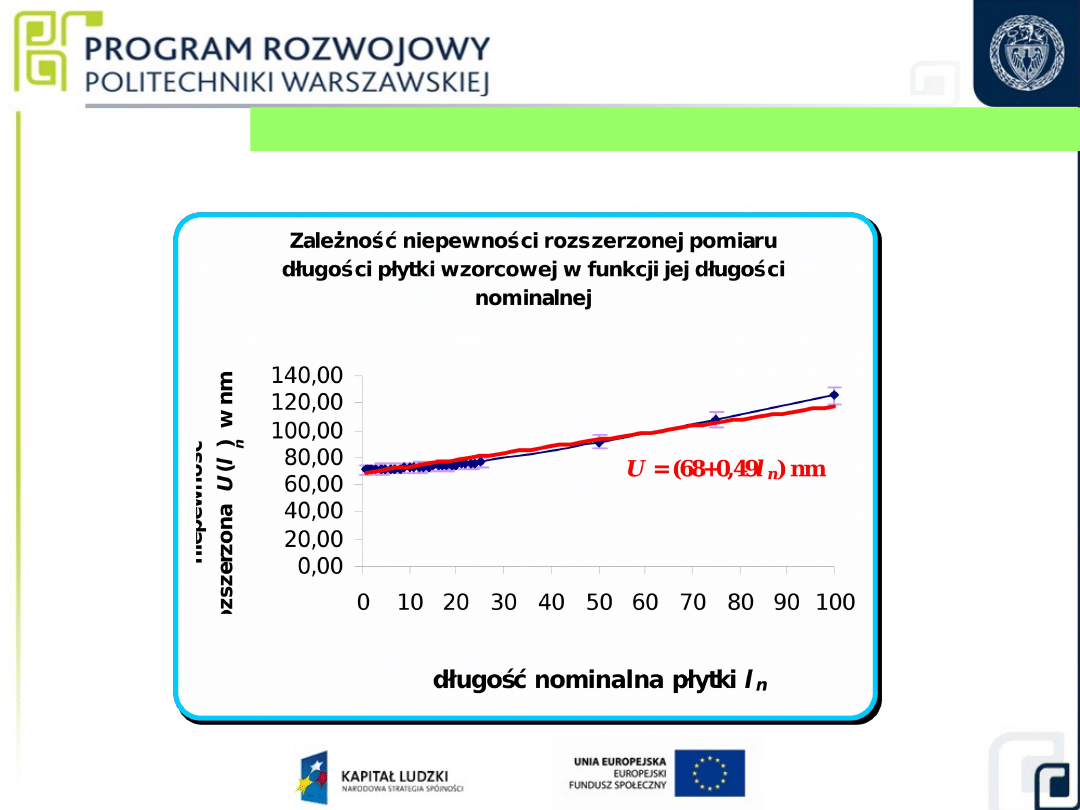
Niepewność pomiaru dla kompletu płytek wzorcowych

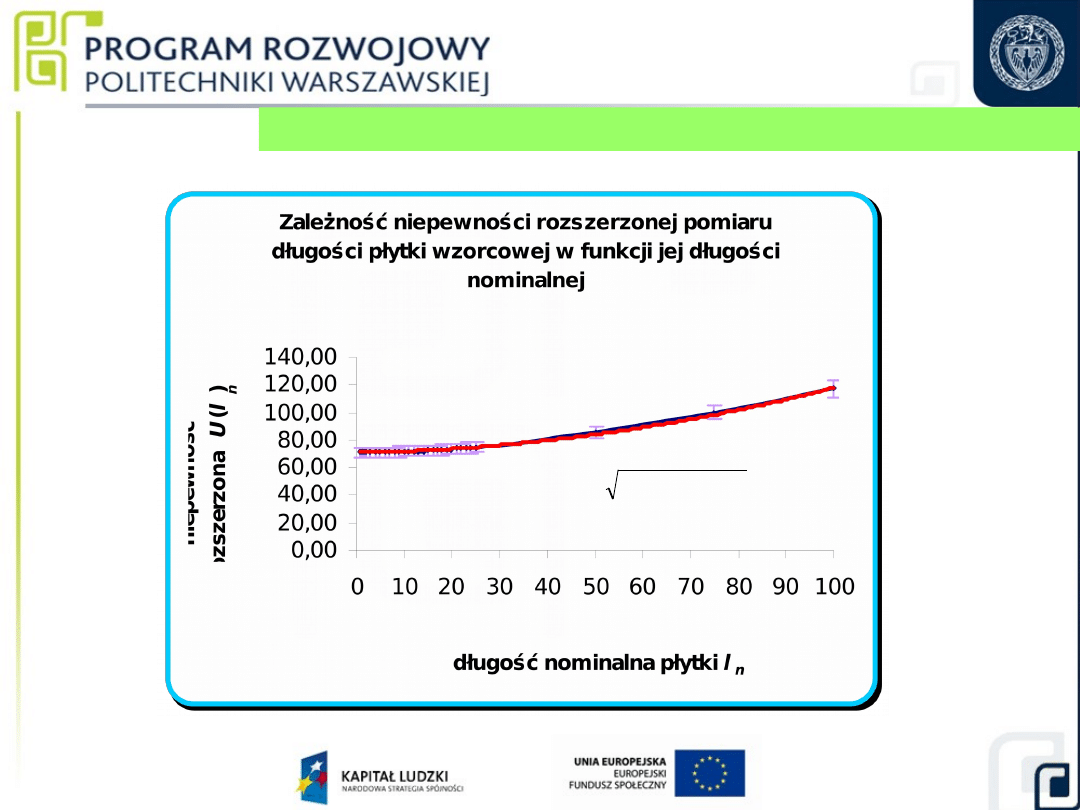
36

nm

l

0,93

70

U(l)

2

n

2

2







Niepewność pomiaru dla kompletu płytek wzorcowych

37

WZORCOWANIE PŁYTEK KĄTOWYCH

Praktyka szacowania niepewn.prez.1.doc

Niep_pom_przy wzorc_pp_1.xls

(wg PN-81/M-53108)

38

Płytka kątowa

– wzorzec kąta w kształcie wielościanu

o równoległych podstawach, przy czym dwie z jego
ścian stanowią powierzchnie pomiarowe równoległe.

Charakterystyki płytek kątowych

Kąty pomiarowe płytki zawarte są między
przedłużeniami powierzchni pomiarowych
równoległych, a odpowiednimi ścianami
wielościanu stanowiącymi powierzchnie pomiarowe
skośne (rys.)

W procesie wzorcowania najczęściej

mierzone są kąty

,

odchyłki płaskości powierzchni
pomiarowych

i

przywieralność powierzchni

pomiarowych

.

39

Pomiary kątów płytek kątowych są wykonywane

za pomocą goniometrów z autokolimatorami,

o wartości działki elementarnej 1˝ lub 2 ˝

Pomiary kątów w płytkach kątowych

Kąt płytki

α

m

oblicza się ze wzoru

definicyjnego:

α

m

= α

1

- α

2

gdzie:

α

1

, α

2

–

wskazania goniometru przy

nastawieniach autokolimatora
odpowiednio na pierwszej i na drugiej
powierzchni pomiarowej

40

Najczęściej wykonuje się dwa lub trzy

pomiary zmieniając za każdym razem

położenie płytki na stoliku przyrządu.

Pomiary kątów w płytkach kątowych

Wzór definicyjny przyjmuje postać:

)

(

2











1

m

Zmiana położenia płytki mierzonej względem
limbusa zapewnia
uzmiennienie błędów wskazań goniometru i
błędów wynikających
z ograniczonej rozdzielczości przyrządu.

41

Niepewność pomiaru kąta

Równanie pomiaru:

2

2

1

1

2

)

(

rg

wg

rg

wg

1

m

P

P

P

P



















gdzie:

P

wg1

– poprawka wskazania goniometru dla α

1

P

wg2

– poprawka wskazania goniometru dla α

2

P

wg1

i P

wg2

– poprawki kompensujące błędy rozdzielczości

Równanie niepewności standardowej złożonej:

)

(

)

(

)

(

)

(

)

(

)

(

2

2

2

2

1

2

1

2

2

rg

wg

rg

wg

m

P

u

P

u

P

u

P

u

u

u

















42

Budżet niepewności pomiaru

Niepewność
pomiaru kąta

Symbol
Wielko

ści

Estymat

a

wielkośc

i

Niepewno

ść

standardo

wa

Rozkład

prawdopodobień

stwa

Współczyn

nik

wpływu

Składowe

niepewnoś

ci

standardo

wej

złożonej

1

2

3

4

6

7

X

i

x

ipop

a

i

c

i

u

i

(Y)

α

u(

α)

normalny

1

u(

α)

P

wg1

0

u(P

wg1

)

trapezowy

1

u(P

wg1

)

P

rg1

0

u(P

rg1

)

prostokątny

1

u(P

rg1

)

P

wg2

0

u(P

wg2

)

trapezowy

-1

-u(P

wg2

)

P

rg2

0

u(P

rg2

)

prostokątny

-1

-u(P

rg2

)

α

m

α

m

u(α

m

)

Δα

43

Budżet niepewności pomiaru

Niepewność
pomiaru kąta

Symbol
Wielko

ści

Estymat

a

wielkośc

i

Niepewno

ść

standardo

wa

Rozkład

prawdopodobień

stwa

Współczynn

ik

wpływu

Składowe

niepewnośc

i

standardow

ej

złożonej

1

2

3

4

6

7

X

i

x

ipop

a

i

c

i

u

i

(Y)

10º01’01

”

0,50”

normalny

1

0,50”

P

wg1

0

0,88”

trapezowy

1

0,88”

P

rg1

0

0,29”

prostokątny

1

0,29”

P

wg2

0

0,88”

trapezowy

-1

- 0,88”

P

rg2

0

0,29”

prostokątny

-1

-0,29”

α

m

10º01’01

”

1,4”

Δα

U = 2,8˝

Błąd graniczny i niepewność wzorcowania goniometru(1,42;0,65)

44

Wzorcowanie kątowników płaskich

Wzorcowanie obejmuje czynności przygotowawcze
oraz określenie:

• odchyłek prostoliniowości krawędzi
pomiarowych
w kątownikach krawędziowych,

•

odchyłek płaskości powierzchni pomiarowych

w kątownikach powierzchniowych,

•

odchyłki kąta zewnętrznego,

•

odchyłki kąta wewnętrznego.

45

• Kątownik walcowy,

• komplet płytek wzorcowych kl. 1,

• komplet płytek wzorcowych stopniowanych co 1

m

• kontrolna płyta pomiarowa (400 x 400) mm

• mikrometry o zakresach pomiarowych: (0÷25)

mm i (25÷50) mm,

• suwmiarka cyfrowa o zakresie pom. (0÷250) mm,

Pomiar odchyłek kątów

Wyposażenie pomiarowe:

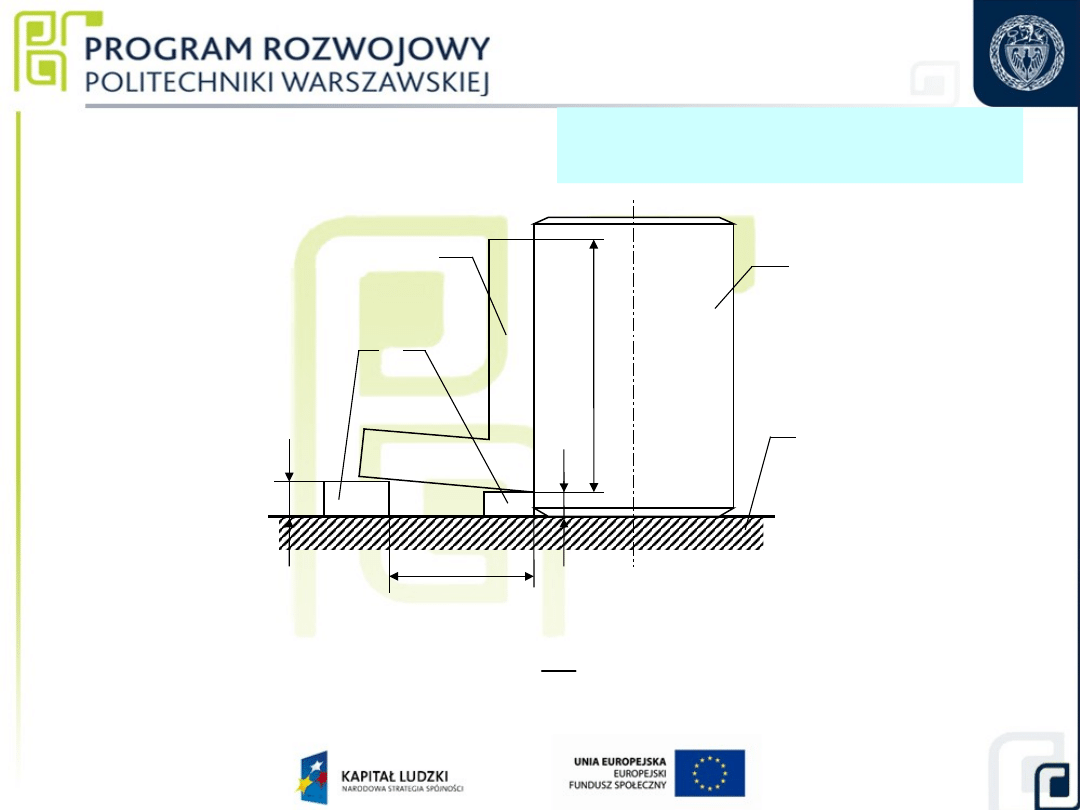
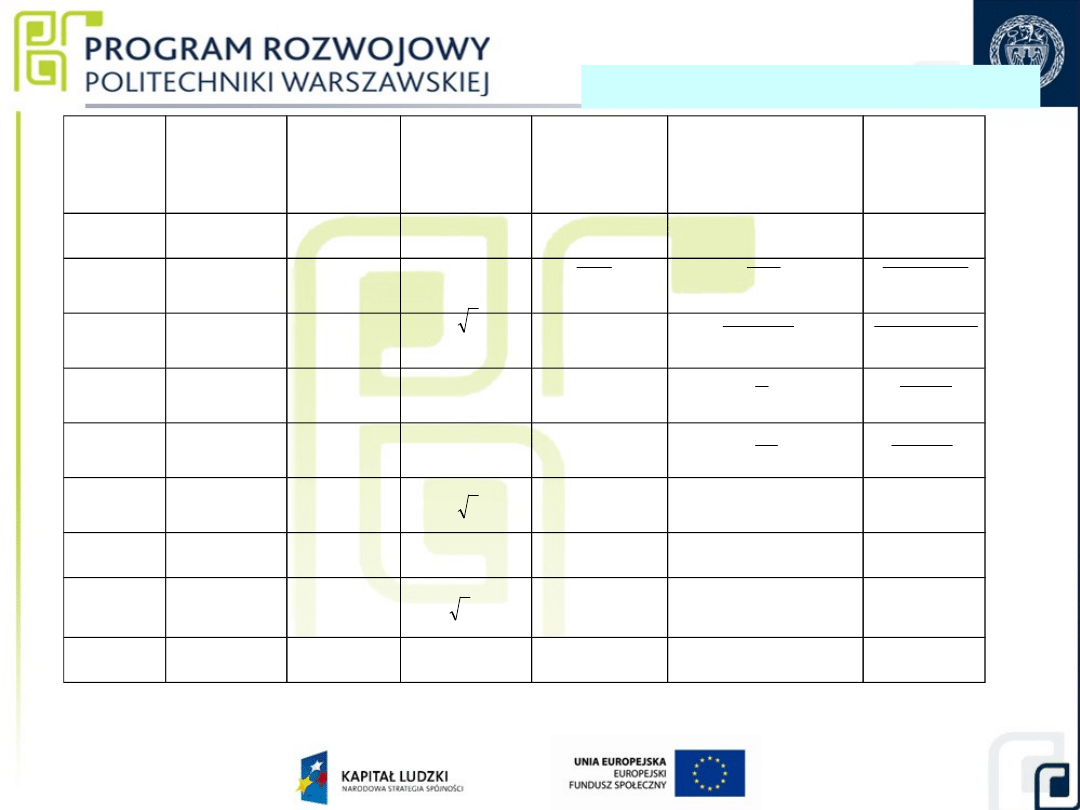
46

Pomiar odchyłki kąta
zewnętrznego

2

4

1

3

b

L

l

a

)

(

a

b

l

L

w

z







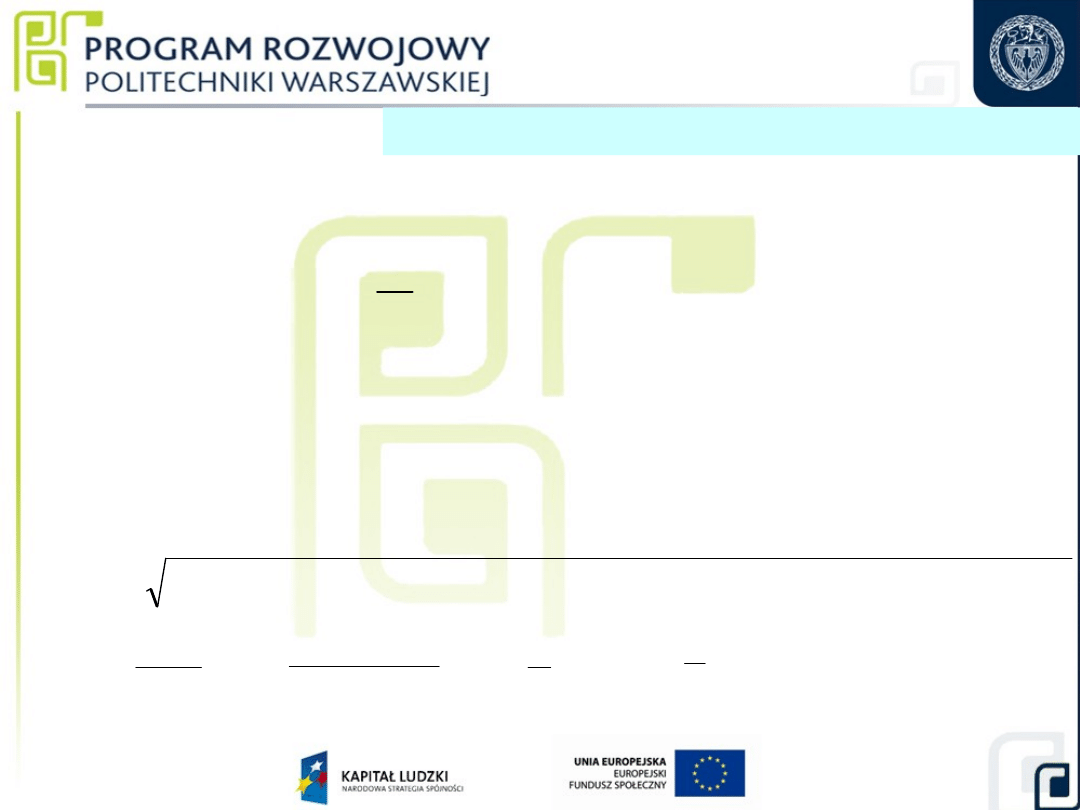
47

Szacowanie niepewności pomiaru odchyłki w

z

Równanie pomiaru:

sz

wz

z

P

P

)

a

b

(

l

L

w











P

wz

– poprawka kompensująca błąd kątownika walcowego

P

sz

– poprawka kompensująca błąd oceny szczeliny.

Równanie niepewności standardowej pomiaru:

)

P

(

u

c

)

P

(

u

c

)

a

(

u

c

)

b

(

u

c

)

l

(

u

c

)

L

(

u

c

)

w

(

u

sz

2

2

6

wz

2

2

5

2

2

4

2

2

3

2

2

2

2

2

1

z













l

a

b

c

1





2

2

l

)

a

b

(

L

c









l

L

c

3



l

L

c

4





;

;

;

c

5

= c

6

=1

48

3

Budżet niepewności pomiaru

symbol

wielkośc

i

oszacowa

nie

szerokoś

ć

połówko

wa

współczyn

nik

rozrzutu

niepewnoś

ć

standardo

wa

współczynnik

wpływu

składowe

niepewno

ści

złożonej

w

w

u(w)

c

i

c

i

·u(w)

L

…..

U(L)

2

l

…..

0,5

0,29

b

…..

-

-

u(b)

a

......

-

-

u(a)

P

wz

0

……

u

1

(P

wz

)

1

u

1

(P

wz

)

0

........

2

u

2

(P

wz

)

1

u

2

(P

wz

)

P

sz

0

0,0005

0,00029

1

0,00029

w

z

.........

-

-

-

-

u(w

z

)

2

U(L)

l

a

-

b

2l

a)

-

(b

U(L)

2

l

a)

-

(b

L

- 

2

l

a)

-

(b

0,29L

-



l

L

l

u(b)

L

l

L

-

3

3

l

u(a)

L

- 

49

Przykładowy budżet niepewności pomiaru

3

3

3

symbol

wielkoś

ci

oszacowa

nie

szerokoś

ć

połówko

wa

współczyn

nik

rozrzutu

niepewno

ść

standardo

wa

współczyn

nik

wpływu

składowe

niepewnośc

i złożonej

w

w

u(w)

c

i

c

i

·u(w)

L

250,04

0,06

2

0,03

-4,2E-05 -1,25E-06

l

120,15

0,5

1,73

0,29

8,681E-

05

2,52E-06

b

4,000

-

-

0,00026

2,08333

33

5,42E-04

a

4,005

-

-

0,00037

-

2,08333

3

-7,71E-04

P

wz

0

0,002

1,73

0,00115

1

1,15E-03

0

0,0005

2

0,00025

1

2,50E-04

P

sz

0

0,0005

1,73

0,00029

1

2,90E-04

w

z

-0,010

-

-

-

-

0,00153

5

U(w

z

) = 2· 0,001535 mm ≈ 0,003 mm = 3 m; w

z

= (-10 ±3) m

50

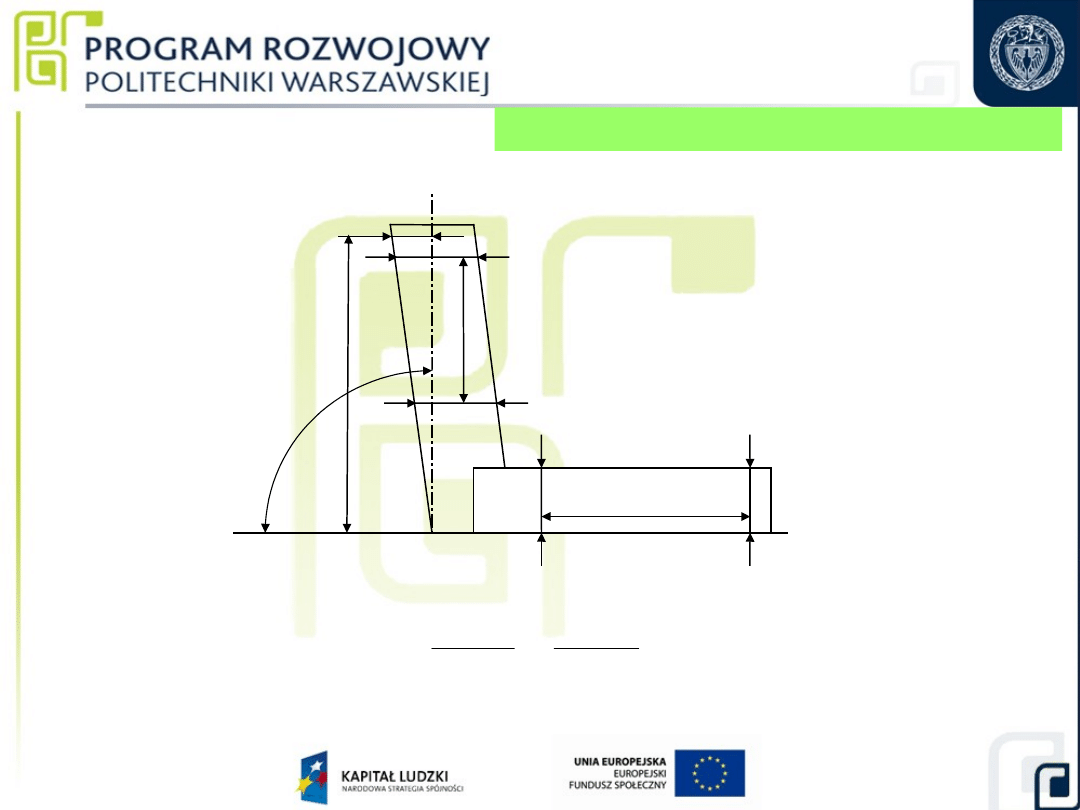
Pomiar odchyłki kąta wewnętrznego

b

l

2

l

1

a

L

w

z

90

◦

c

d

L

l

d

c

l

a

b

w

w

z

w

























2

1

51

Szacowanie niepewności pomiaru odchyłki w

w

Równanie pomiaru:

Równanie niepewności standardowej pomiaru:

;

;

;

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

2

2

8

2

2

2

7

2

2

6

2

2

5

1

2

2

4

2

2

3

2

2

2

2

2

1

L

u

c

l

u

c

d

u

c

c

u

c

l

u

c

a

u

c

b

u

c

w

u

c

w

u

z

w

















L

l

d

c

l

a

b

w

w

z

w

























2

1

1



1

c

1

2

l

L

c 

1

3

l

L

c





2

1

4

l

)

a

b

(

L

c







2

5

l

L

c 

2

6

l

L

c





2

2

7

l

)

d

c

(

L

c







2

1

8

l

d

c

l

a

b

c









52

z

w

w

w

symbo

l

wielko

ści

oszaco

wanie

szeroko

ść

połówk

owa

współczy

nnik

rozrzutu

niepew

ność

standar

dowa

współczy

nnik

wpływu

składowe

niepewności

złożonej

w

w

u(w)

c

i

c

i

·u(w)

-0,010

0,003

2

0,0015

1

1,50E-03

b

29,996

0,002

2

0,001

1,2502

1,25E-03

a

30,002

0,002

2

0,001

-1,2502

-1,25E-03

l

1

200,0

1,2

2

0,6

3,751E-

0,5

2,25E-05

c

30,005

0,002

2

0,001

2,5004

2,50E-03

d

29,996

0,002

2

0,001

-2,5004

-2,50E-03

l

2

100,0

1,2

2

0,6

-2,25E-

04

-1,35E-04

L

250,04

0,06

2

0,03

6E-05

1,80E-06

0,005

-

-

-

-

0,0042306

9

U(w

w

) = 8,5 m w

w

=

(5,0 ± 8,5) m

Przykładowy budżet niepewności pomiaru

53

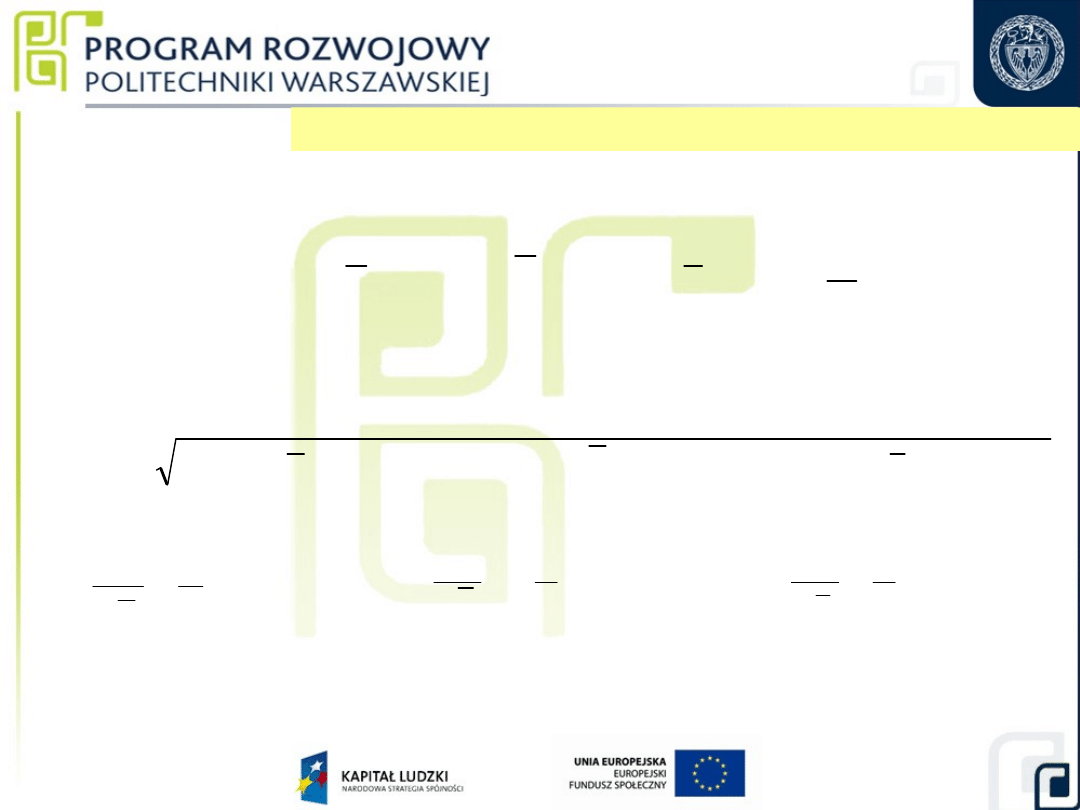
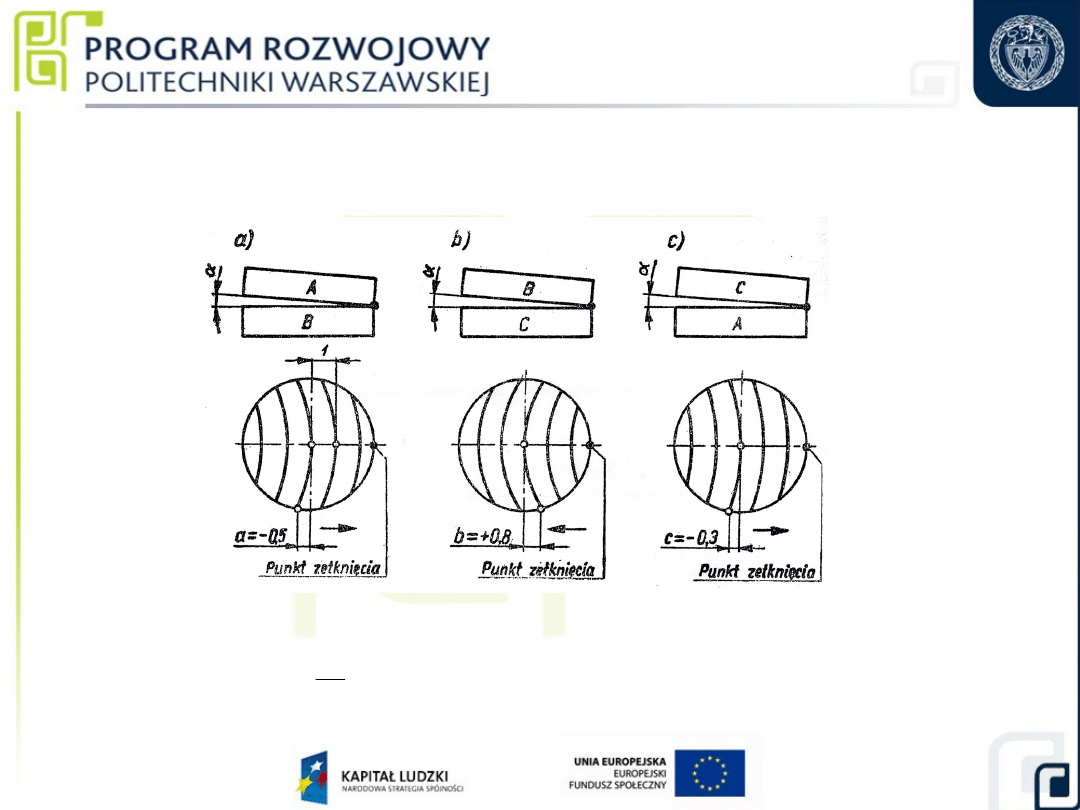
a = +
0,8

Punkt
zetknięci
a

α

Wzorcowanie płaskich płytek interferencyjnych

54

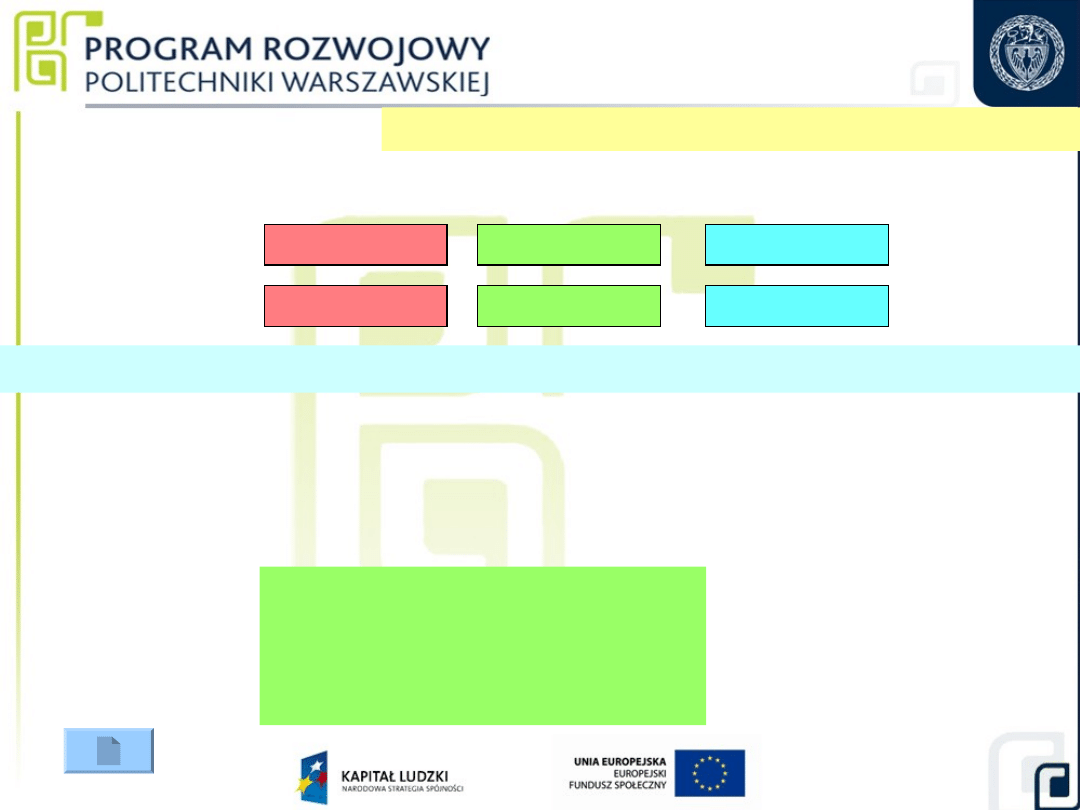
Metoda wzajemnego wzorcowania trzech płytek

Płytka A

Płytka B

Płytka B

Płytka C

Płytka A

Płytka C

a)

b)

c)

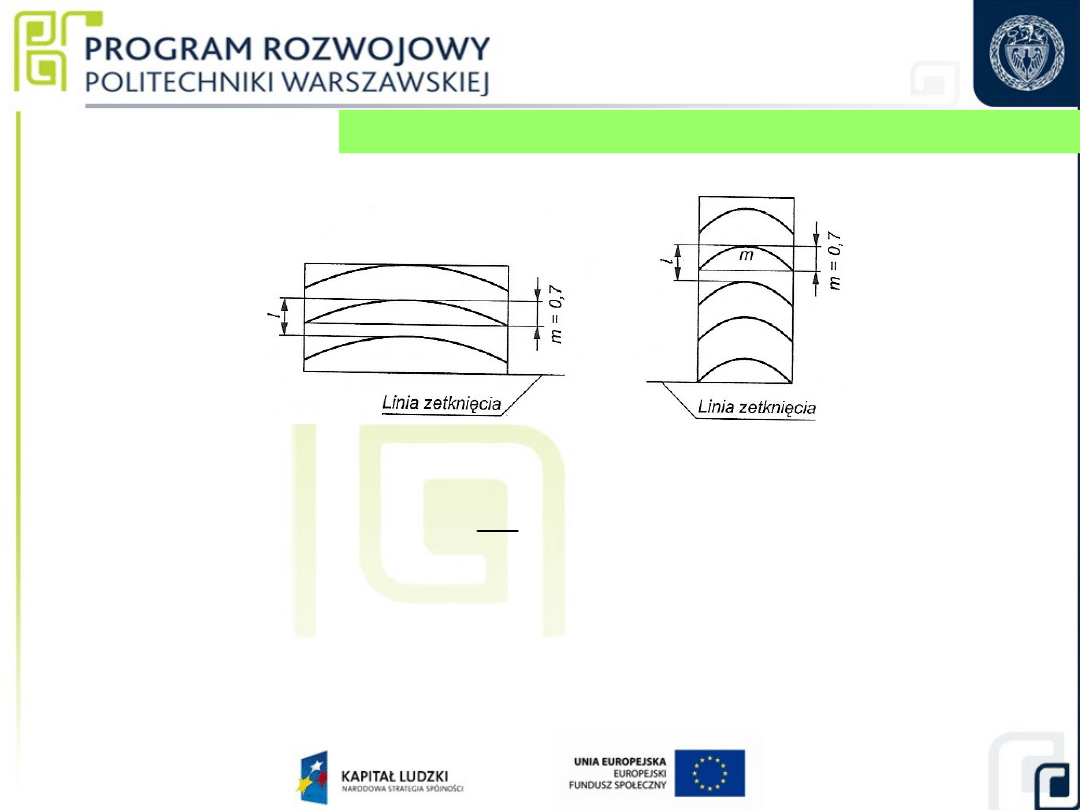
Kombinacje ułożenia płytek przy pomiarze odchyłek płaskości „metodą trzech”:

a) – układ do wyznaczenia strzałki ugięcia oznaczonej symbolem

a,

b) – układ do wyznaczenia strzałki ugięcia oznaczonej symbolem

b,

c) – układ do wyznaczenia strzałki ugięcia oznaczonej symbolem

c

.

p

a

= (a – b + c) · λ/4

p

b

= (a + b - c) · λ/4

p

c

= (- a + b + c) · λ/4

55

Równanie pomiaru:

Szacowanie niepewności pomiaru odchyłek płaskości





4

)

(

)

(

)

(

















r

r

r

a

P

c

P

b

P

a

p

Równanie niepewności standardowej pomiaru:

 

 

 

))

(

(

))

(

(

))

(

(

)

(

2

2

2

3

2

2

2

2

2

2

2

1

r

r

r

a

c

P

u

c

u

c

P

u

b

u

c

P

u

a

u

c

p

u



















m

a

p

c

a





15

,

0

4

1











m

b

p

c

b





15

,

0

4

2















m

c

p

c

c





15

,

0

4

3











56

Budżet niepewności pomiaru

i

X

i

x

)

(

i

x

u

i

c

)

(y

u

i

a

)

(a

u

m

a

u



15

,

0

)

( 

r

P

b

)

(b

u

m

b

u



15

,

0

)

( 

r

P

c

)

(c

u

m

c

u



15

,

0

)

(



r

P

a

p

)

(

a

c

p

u

Symbol

wielkości

Estymata
wielkości

Niepewno

ść

standardo

wa

Rozkład

prawdopodobień

stwa

Współczynn

ik

wrażliwości

Udział w

niepewności

złożonej

...

normalny

0,15 m

0

0,058

prostokątny

0,15 m

0,0087

m

...

normalny

0,15 m

0

0,058

prostokątny

0,15 m

0,0087

m

...

normalny

0,15 m

0

0,058

normalny

0,15 m

0,0087

m

57

Dziękuję za uwagę

58

P

t

= l

n

[



w

(t

o

-t

w

) -



k

(t

o

-t

k

)] =

= l

n

(



w

t

o

-



w

t

w

-



k

t

o

+



k

t

k

) =

= l

n

(-



k

t

o

+



w

t

o

+



k

t

k

-



w

t

k

+



w

t

k

-



w

t

w

) =

= l

n

[-t

o

(



k

-



w

) + t

k

(



k

-



w

) +



w

(t

k

–

t

w

)] =

= l

n

[(



k

-



w

) (t

k

– t

o

) +



w

(t

k

– t

w

)]

59

WZORCOWANIE PŁASKICH PŁYTEK

INTERFERENCYJNYCH

m

m

c

b

a

p

a







24

,

0

15

,

0

)

3

,

0

8

,

0

5

,

0

(

4

)

(





















