STRUKTURY RYNKU I ICH

REGULACJE

Wykład 5 i 6: Konkurencja

monopolistyczna i oligopol

Prowadzący zajęcia: dr inż. Edyta Ropuszyńska –

Surma

Politechnika Wrocławska

Wydział Informatyki i Zarządzania

Instytut Organizacji i Zarządzania

Wrocław

E-mail: edyta.ropuszynska-surma@pwr.wroc.pl

Plan wykładu

Konkurencja
monopolistyczna

Oligopol –
charakterystyka

Modele oligopolu –
klasyfikacja

Model Cournot’a,

Model złamanej
krzywej popytu

Strategie
współpracy

Teoria gier

National Geographyc

KONKURENCJA

MONOPOLISTYCZNA

Konkurencja monopolistyczna

model dużej grupy (large group

model)

Twórcą pracy o teorii konkurencji

monopolistycznej jest E. H. Chamberlin

(1899-1967). W swojej pracy na ten

temat, próbuje zrekonstruować teorię

wartości. Pisze: „Konkurencja

monopolistyczna (...) stanowi

wyzwanie dla tradycyjnego punktu

widzenia ekonomii, w której konurencja

i monopol są alternatywami, a

poszczególne ceny są do wyjaśnienia w

kategoriach jednej albo drugiej z nich”.

Konkurencja monopolistyczna

• Zauważył, że przez długi czas teoria ekonomiczna

utożsamiała w sposób luźny wolne przedsiębiorstwo z

konkurencją, ale gdy zbadał faktyczny wynik typowy

dla systemu wolnego przedsiębiorstwa, to znalazł w

nim nie czystą konkurencję, lecz konkurencję

monopolistyczną. Utrzymywał, że w wielu przypadkach

byłoby niemożliwe ustanowienie rynków doskonałej

konkurencji, i nawet kwestionował przydatność takich

rynków. Na przykład, nadmierna standaryzacja

produktów, która może być ich wynikiem,

niekoniecznie jest pożądana. „Różnice smaku,

pragnień, dochodów i lokalizacji nabywców, jak też

użytku, jaki nabywcy chcieliby zrobić z towarów,

wszystko to wskazuje na potrzebę różnorodności.”

Takie problemy, w jego odczuciu, dyktują zastąpienie

koncepcji „konkurencyjnego ideału” ideałem

zawierającym zarówno monopol, jak i konkurencję.

–

duża liczba uczestników rynku – liczba producentów na

rynku jest na tyle duża, że nie odczuwają oni związków

pomiędzy podejmowanymi przez siebie decyzjami ilościowo-

cenowymi.

–

zróżnicowanie produktu – producenci wytwarzają dobra,

które mają tyle cech wspólnych, że można je uznać za

bliskie substytuty. Jednakże każdy z producentów nadaje

swojemu produktowi cechy odróżniające go od wyrobów

innych producentów. Elementami wyróżniającymi mogą być

przykładowo: opakowanie, forma promocji rynkowej, zakres

usług związanych ze sprzedażą, lokalizacja, godziny

otwarcia. Zatem zróżnicowanie produktu stanowi bodziec

do podejmowania działań promocyjnych i marketingowych,

co się wiąże z dodatkowymi kosztami.

–

Możliwość kształtowania ceny przez producenta –

konkurent monopolistyczny jest cenotwórcą. Poprzez

nadanie swojemu produktowi cech odróżniających go od

innych produktów oferowanych na rynku producent

uzyskuje określona siłę monopolową wyrażającą się

możliwością kształtowania ceny.

–

Ceny czynników i technika produkcji są dane

–

Wejście do grupy i wyjście z niej jest wolne

–

Bariery wejścia na rynek i wyjścia z rynku do

pokonania w długim okresie – W długim okresie nie

ma przeszkód dla producentów zewnętrznych w

wejściu na rynek. W konsekwencji w punkcie

równowagi długookresowej konkurenci

monopolistyczni uzyskują zerowy poziom zysku

ekonomicznego, tzw. zysk normalny (podobnie jak

producenci działający w konkurencji doskonałej).

–

Duże wydatki na reklamę – aby nie zejść do roli

cenobiorców, konkurenci monopolistyczni muszą

różnicować swoje produkty. Promocja własnej marki w

warunkach silnej konkurencji ze strony innych

producentów oferujących zbliżony produkt wymaga

wysokich wydatków na reklamę.

–

Celem firmy jest maksymalizacja zysku zarówno w

krótkim, jak i w długim okresie

–

Doskonała informacja o rynku

–

Firma podejmuje decyzje tak, jakby znała krzywą

popytu własnego produktu oraz krzywe kosztów

–

Długi okres składa się z wielu identycznych i

niezależnych krótkich okresów; wynika z tego, że

maksymalizacja zysku w krótkim okresie prowadzi do

maksymalizacji zysku w długim okresie.

–

Krzywe kosztów i popytu są jednakowe dla

wszystkich uczestników grupy, a więc preferencje

konsumentów są równo rozłożone między

poszczególne produkty oraz zróżnicowanie produktu

nie prowadzi do różnicowania kosztów. Założenie to

zostało przyjęte, aby na jednym rysunku można było

pokazać równowagę firmy i całej grupy.

Konkurencja monopolistyczna

charakteryzuje się względnie dużą liczbą

producentów wytwarzających produkty
tego samego typu, ale posiadające
swoiste, indywidualne cechy, co
pozwala producentom odrębnie
ustalić ceny swych wyrobów.
Zakłada ona, nie tylko zróżnicowanie
produktów, ale również ograniczone
możliwości osiągania korzyści
skali.

Firmy konkurują ze sobą takimi
instrumentami, jak:

• jakość
• opakowanie
• reklama
• promocja
• znak firmowy
• zmiana wizerunku wyrobu
• itp.

Założenia modelu Chamberlin’a:

• w danej gałęzi produkcji działa tak dużo firm, że

każda z nich może uprawiać własną politykę bez

obawy przed działaniem odwetowym ze strony

pozostałych rywali;

• produkty tych firm są zróżnicowane, a nie

homogeniczne, nabywcy zaś przejawiają

preferencję w stosunku do wyrobów firmowych

określonych sprzedawców;

• dostęp do danej gałęzi produkcji jest swobodny, a

nowi producenci są w stanie podjąć produkcję

bliskich substytutów istniejących już produktów;

• krzywe popytu kosztów wszystkich działających w

danej gałęzi firm są takie same.

Krzywa popytu ulega przesunięciu wskutek zmian:

• cech wyróżniających produkt; strategii sprzedaży produktu
realizowanej przez firmę (np. opakowania);

• cen i cech substytutów wprowadzanych przez konkurentów z
grupy;

• cen i strategii sprzedaży wprowadzanych przez producentów z
innych grup

• usług i strategii sprzedaży konkurentów (np. zmiana warunków
gwarancji, „dodanie opcji z montażem u klienta”, itp.);

• gustów i dochodów konsumentów;

Wskutek zróżnicowania produktów producent nie jest cenobiorcą i ma

pewną siłę rynkową monopolu, ale jednocześnie napotyka silną

konkurencję w ramach własnej grupy produktowej. Konsumenci wykazują

pewną lojalność w stosunku do preferowanej marki, a producenci

ponoszą koszty działalności reklamowej i promocyjnej.

Konkurencja monopolistyczna

– funkcja popytu

•

Krzywa d*

przedstawia rzeczywistą sprzedaż

firmy przy różnych poziomach cen przy

uwzględnieniu reakcji u konkurentów. Krzywa

ta jest nazywana

krzywą rzeczywistej

sprzedaży

. Obniżce ceny wprowadzonej przez

daną firmę towarzyszą obniżki wprowadzone

przez pozostałe firmy. Krzywa d* pokazuje

skutki zmian ceny konkurentów na wielkość

sprzedaży danej firmy oraz udział danej firmy

w rynku i dlatego też jest nazywana

krzywą

udziału

w rynku. Ma ona tę samą

elastyczność cenową, co rynkowa krzywa

popytu przy każdym poziomie ceny.

•

Krzywa d* ma większe nachylenie niż krzywa

d, ponieważ sprzedaż rzeczywista po obniżce

ceny P jest mniejsza od oczekiwanej, co jest

spowodowane obniżkami wprowadzonymi

przez pozostałe firmy.

•

Ruch wzdłuż krzywej d* pokazuje zmiany w

rzeczywistej sprzedaży firm wskutek

wprowadzanych przez nie jednoczesnych i

niekoniecznie identycznych zmian ceny, przy

nie zmienionych udziałach w rynku.

Przesunięcie krzywej d* jest wynikiem wejścia

nowych firm na rynek lub wyjściem z rynku

firm dotychczas funkcjonujących i pokazuje

zmiany udziału firmy w zaspokajaniu popytu

rynkowego

Krzywa d – postrzegana krzywa
popytu przez firmę na rynku
konkurencji monopolistycznej (w
ramach grupy); krzywa
planowanej sprzedaży

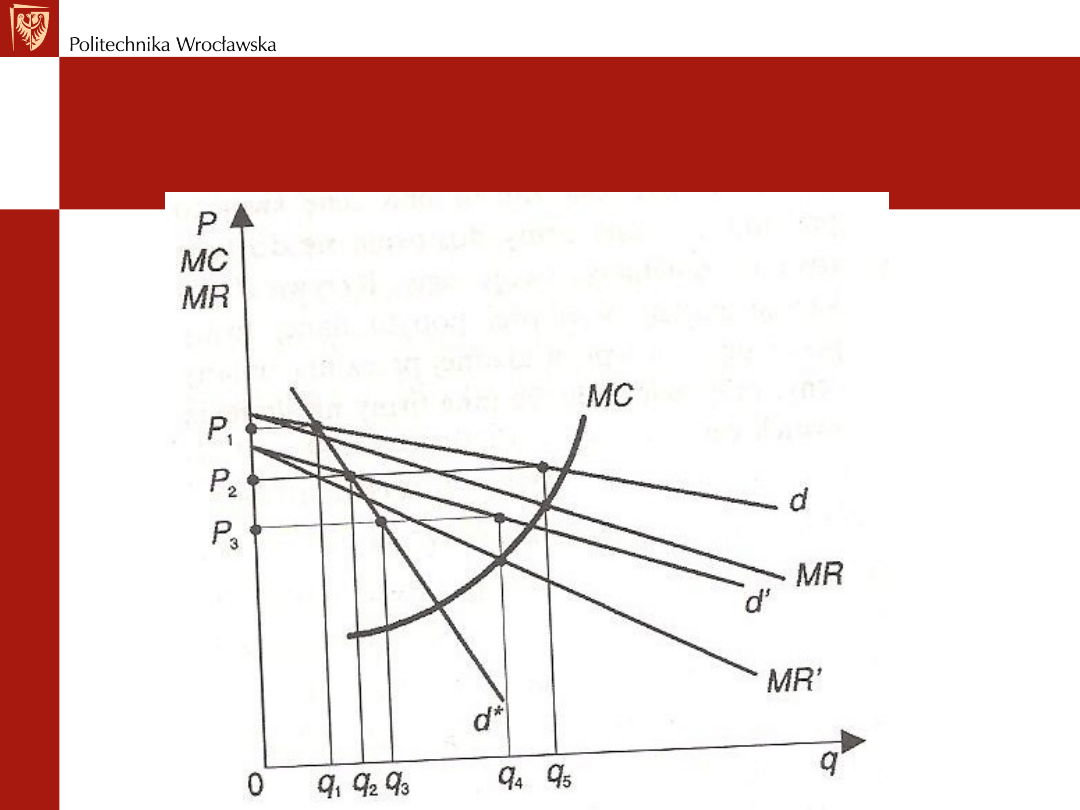
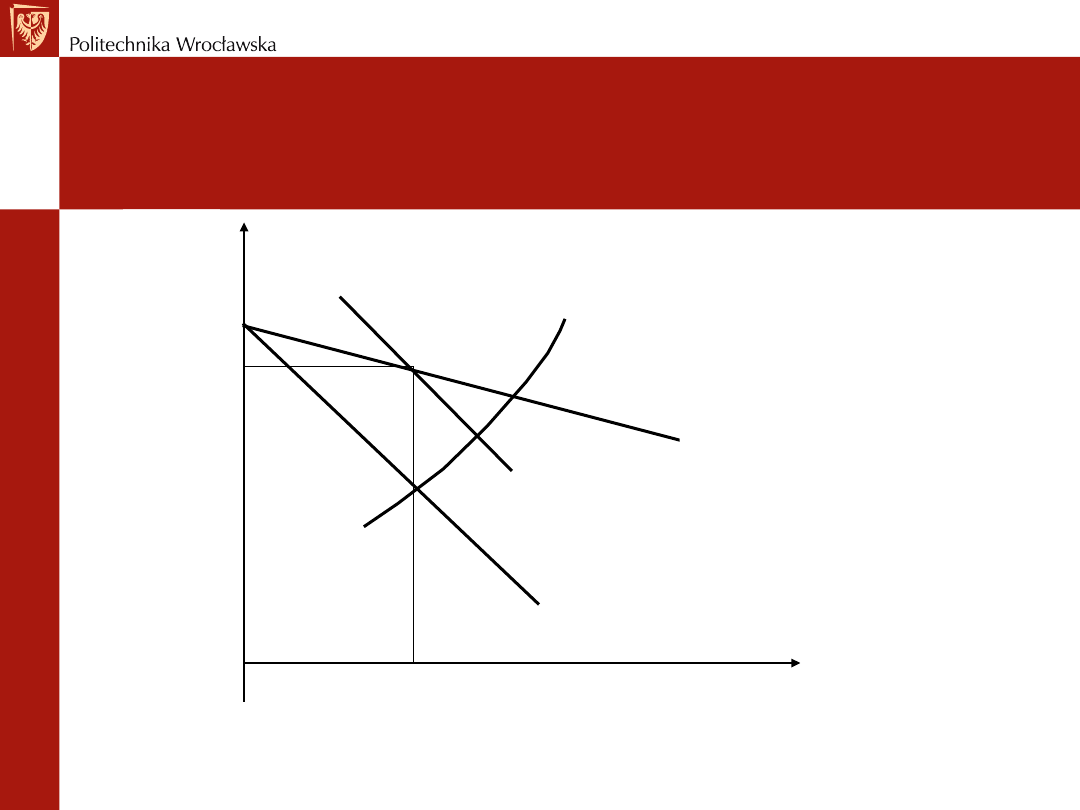
Dochodzenie do pkt. równowagi

w krótkim okresie

P
MR
MC

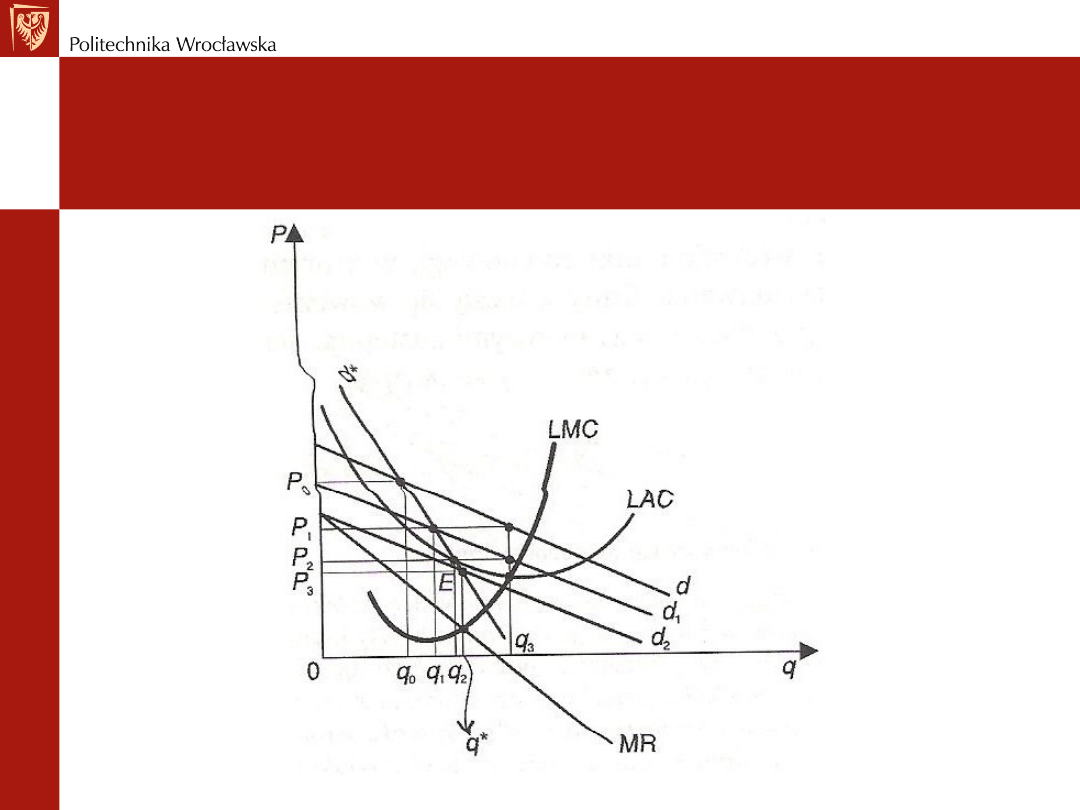
Osiąganie równowagi długookresowej
zał.: konkurencja cenowa, bez nowych
wejść i wyjść

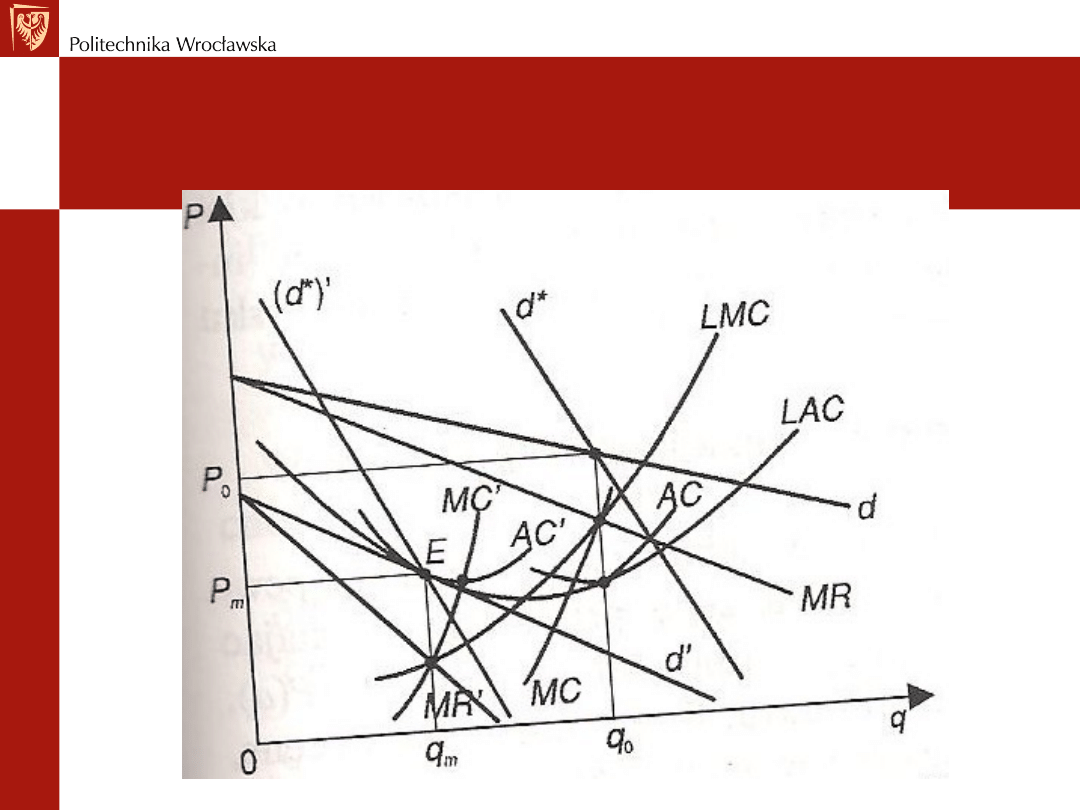
Równowaga długookresowa

OLIGOPOL

Charakterystyka oligopolu

• Jakie znasz

cechy
charakterystycz
ne oligopolu?

• Proszę podać

przykładowe
rynki
oligopolistyczne

• Dominującą cechą

jest współzależność

National Geographyc

Przykładowe rynki

• rynek cukru,
• telefonii komórkowych,
• samochodów - produkcja

KLASYFIKACJA MODELI
OLIGOPOLU

Modele oligopolu, w których

firmy działają niezależnie

Modele oligopolu, w których

firmy Współpracują

1. Firmy reagują

na zmiany

wielkości

produkcji u

konkurentów

2. Firmy

reagują na

zmiany ceny u

konkurentów

3. Kartele

4. Modele przywództwa

1.1. Model

Cournota

(duopol)
1.2. Model

Stockelberga

2.1. Model

Bertranda
2.2. Model

Edgewortha

(duopol)
2.2. Model P.

Sweezy’ego

(oparty na

złamanej

krzywej popytu)

3.1. Kartel

maksymalizują

cy wspólny

zysk
3.2. Kartel

dzielący rynek

4.1. Model firmy o

niskich kosztach
4.2. Model firmy-lidera

dominującej na rynku
4.3. Model przywództwa

cenowego

Źródło: na podsatwie Czarny E., Nojszewska E., Mikroekonomia, PWE, Warszawa 1997, s. 172

Model Cournota

Duopol - Szczególny przypadek oligopolu
przedstawiający rynek, na którym działają jedynie
dwaj producenci oferujący ten sam produkt.
Zależność między dwoma firmami oparta jest na
mechanizmach dotyczących wielkości produkcji lub
wyznaczeniu poziomu cen sprzedaży.
Modele duopolu:

– A. Cournota (1838r.),
– F. Y. Edgewortha (1925r.),
– E. Chamberlina

Model A. Cournota

Podstawowe założenia:
• Każda z firm traktuje wielkość produkcji konkurenta

jako daną,

• Przedsiębiorstwa mają te same koszty produkcji,
• Koszty krańcowe (MC=0),
• Produkt jednorodny i stosują tę samą cenę.

Model A. Cournota

Dana jest funkcja popytu

D= 90 – P

Gdy przychód marginalny jest
równy zero

MR = 0

, to

wielkość produkcji odpowiada
połowie popytu rynkowego dla
ceny równej zero (MC=MR, a
MC=0),

½ Q

dla

P= 0

Całkowita produkcja rynkowa
firmy 1 i 2

Q= Q

+ Q

= 90- P

P=90-Q
TR=QxP
TR=90Q-Q

MR = 90-2Q
MR=0

Q=45 i P=45

Model A. Cournota

Firma 1 wyznaczyła wielkość produkcji na poziomie Q

Popyt na produkty Firmy 2 wynosi:

= (90- Q

)- P

Uwzględniając popyt Q

Firma 2 wyznaczyła wielkość

produkcji maksymalizując zysk:





Powyższa zależność jest

funkcją reakcji

firmy 2 na

decyzje o wielkości produkcji jaką podjęła firma 1.

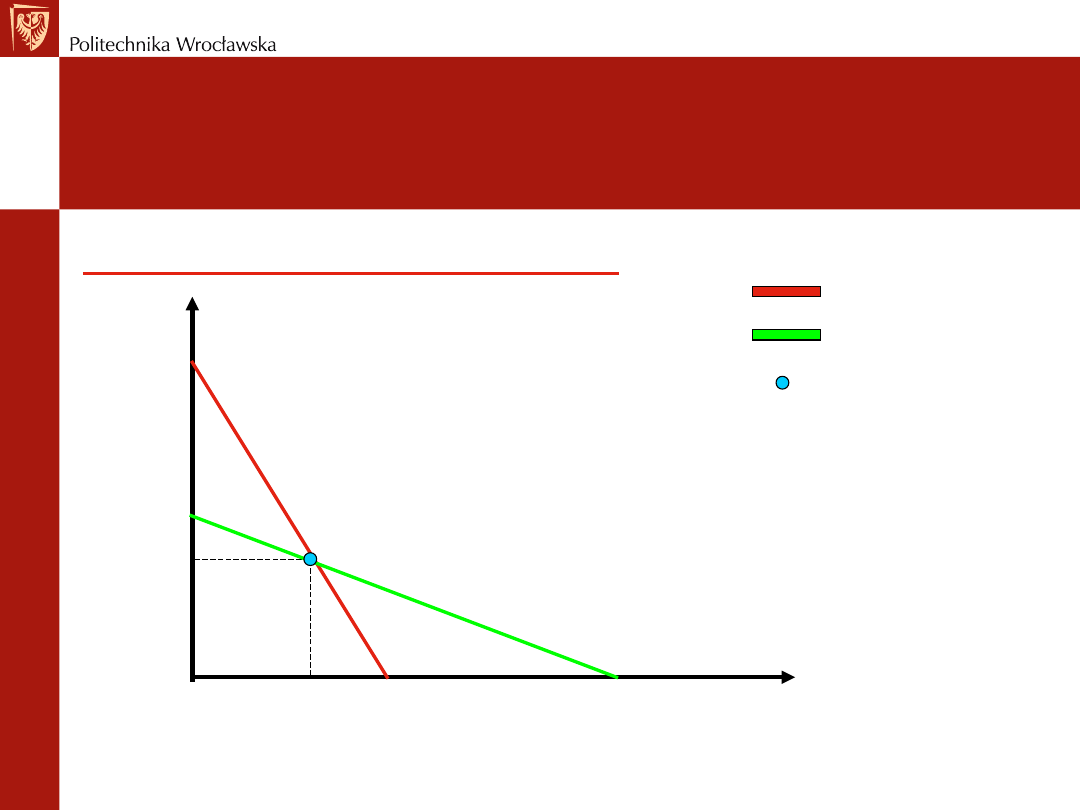
Model A. Cournota

Funkcje reakcji firm 1 i 2

Q dla firmy
1

Q dla firmy 2

0 30 45
90

Reakcja firmy
1

Reakcja firmy 2

Równowaga
Cournota

Duopol jest w równowadze, gdy:

= 1/3 0D

P = 1/3 0D

Model A. Cournota

Równowaga Cournota-

Punkt przecięcia

funkcji reakcji firm 1 i 2 na poczynania konkurentów.
Jest również punktem, w którym żadnemu z
przedsiębiorstw nie opłaca się zmieniać osiągniętej
produkcji.

Model duopolu Edgewortha -
założenia

• Produkt jednorodny
• wielkość produkcji to zmienna wynikowa
• Cena – to zmienna decyzyjna
• MC = 0
• Zdolności producentów są ograniczone
• Maksymalne wielkości produkcji

każdego z duopolistów < wielkość
popytu (sprzedaży) dla P=0 (równowaga
rynkowa)

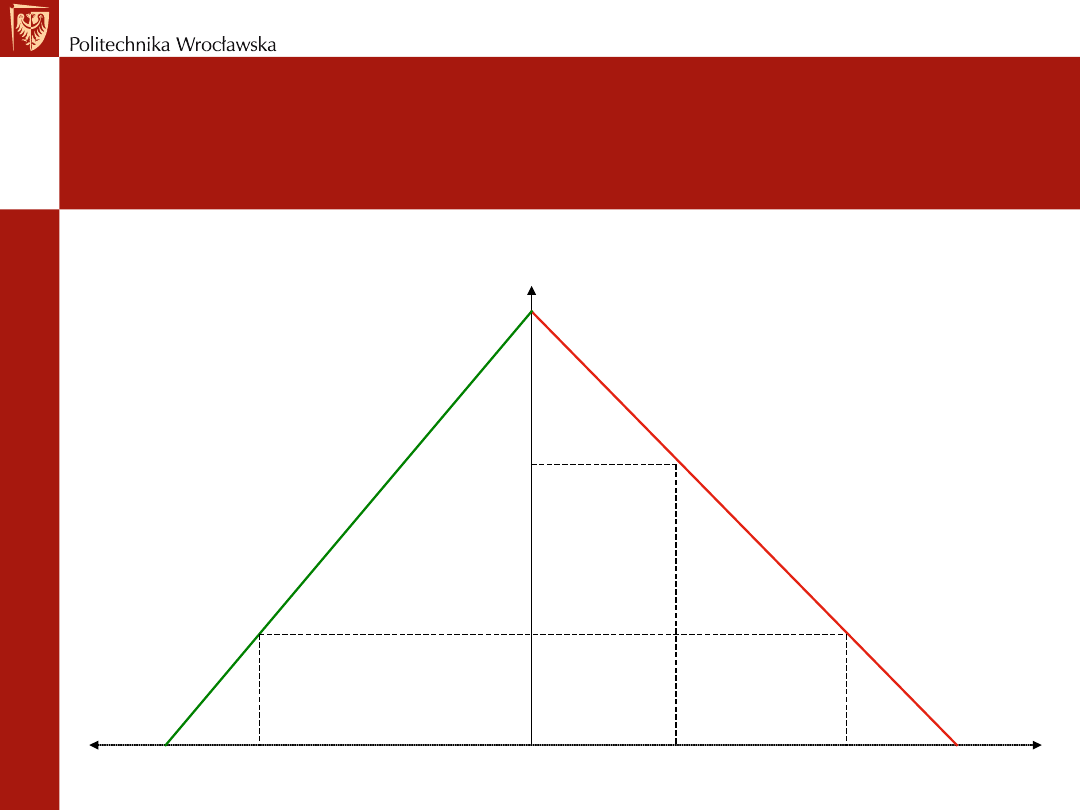
Model Edgewortha

Q1 maks

Q2maks

W celu maksymalizacji
zysku każdy duopolista
wyznacza

Odpowiednią cenę
sprzedaży zakładając, że
konkurent nie zmieni
swojej ceny

Wniosek:

Brak jednego rozwiązania
dotyczącego ceny i
wielkości równowagi

Cena jest wyznaczana
między jej poziomem
górnym (P1) i dolnym (P0)

Model duopolu Chamberlina -
założenia

• Każdy duopolista wyciąga wnioski na

podstawie nabytych doświadczeń i
reaguje odpowiednio na zmiany
decyzji konkurenta

Wnioski:

Każdy z duopolistów ma taki
sam udział rynkowy i
sprzedaje po Qe/2, a zysk
wynosi PeQe/2

Równowaga duopolu w
modelu Chamberlina jest taka
sama jak równowaga
monopolu pełnego.

Model
złamanej krzywej
popytu - założenia

• Dosyć sztywne ceny,
• Jeżeli jeden

oligopolista podnosi

cen, to inni nie

reagują (lub reagują

„słabo”),

• Jeżeli jeden

oligopolista obniża

cenę, to inni też ją

obniżają, chcąc

przyciągnąć

klientów

Wnioski:

Model wyjaśnia stabilność cen na
rynkach oligopolistycznych

Oligopol - współpraca

Oligopoliści stają przed dylematem czy

przyjąć strategię współdziałania,

porozumieć się i realizować wspólne cele,

czy walczyć z konkurencją o zagarnięcie jak

największej części rynku tylko dla siebie.

Formy współpracy w oligopolu:
• fuzja przedsiębiorstw działających na tym

samym lub innym rynku,

• porozumienie kartelowe (legalne i jawne),
• zmowa (nielegalna i tajna),

Oligopol - współpraca

• Syndykat – forma zjednoczenia monopolistycznego

ograniczająca samodzielność handlową należących
do niego firm, ale pozostawiająca ich samodzielność
prawną i wytwórczą.

• Trust – najwyższa forma zjednoczenia

monopolistycznego. Powstała z połączenia firm pod
wspólnym zarządem i radą nadzorczą. Firmy tracą
całkowicie swą samodzielność pod względem
handlowym, wytwórczym i prawnym. Natomiast
właściciele firm stają się udziałowcami trustu.

• Koncern – zjednoczenie wielkich firm, różnych

gałęzi przemysłu, firm handlowych i banków.

Oligopol - współpraca

W przypadku zawarcia efektywnego
porozumienia (kartelu) oligopol zachowuje się
podobnie jak wielozakładowy monopol — stara
się maksymalizować łączny zysk całej grupy.
Kartel – to grupa przedsiębiorstw, które zmówiły
się w celu:
 kontrolowania ceny,
 kontrolowania wielkości podaży,
 zapewnienia sobie zysku monopolowego.

OPEC [Organizacja Krajów Eksporterów Ropy Naftowej]

Oligopol - współpraca

Zmowa – to tajne porozumienie między

przedsiębiorstwami, które ma na celu uniknięcie
wzajemnej konkurencji. Może dotyczyć m. in.:

• ustalania cen,
• wielkości produkcji i sprzedaży,
• podziału rynków zbytu i zaopatrzenia,
• wspólnej akcji tworzenia barier wejścia dla nowych

konkurentów rzeczywistych bądź potencjalnych.

4,5 mln zł PKN Orlen i 1 mln zł Grupa Lotos – kary nałożone przez
UOKiK za zmowę, by wspólnie wycofac ze sprzedaży benzynę U-95.

Modele

przywództwa

Przywództwo cenowe
– występuje, gdy jedno z przedsiębiorstw

działających w branży dominuje nad innymi i
pozostałe firmy naśladują jego decyzje
cenowe.

Producent może osiągnąć przywództwo

•

gdy ma najniższe koszty produkcji.

•

gdy ma największą wielkość produkcji.

Konkurencja będzie musiała się dopasować albo

wypadnie z rynku.

Model przywództwa cenowego

Założenia:
1.Przedsiębiorstwo dominujące ustala
cenę na produkty dla całej gałęzi,
2.Małe przedsiębiorstwa nie mają
wpływu na cenę zachowują się
jakby prowadziły działalność gosp. W
konkurencji doskonałej (każde
wytwarza taką ilość, dla której ich
MC=P; gdzie P, to cena rynkowa).

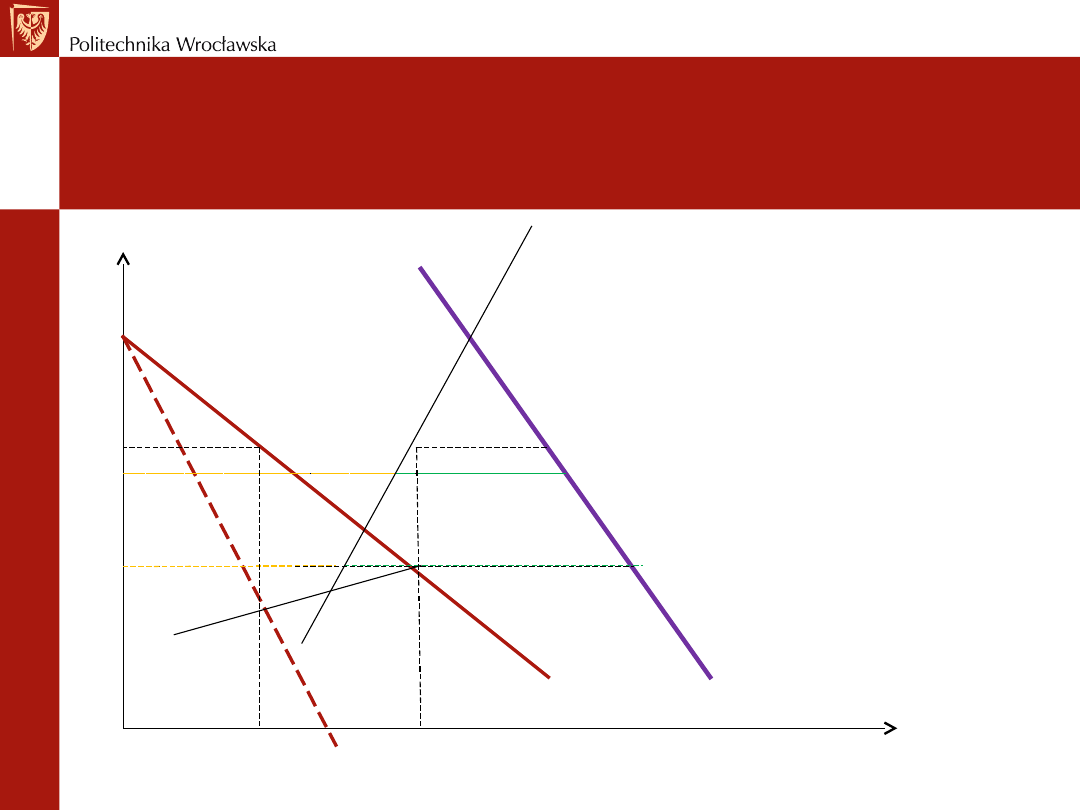
Model przywództwa cenowego

Qsm

Model przywództwa cenowego

Wnioski:
1.Krzywa popytu netto na produkty przedsiębiorstwa dominującego
odzwierciedla różnice między popytem gałęzi a podażą
wolnokonkurencyjnych małych przedsiębiorstw.
2.Im wyższa jest elastyczność cenowa podaży konkurentów
przedsiębiorstwa dominującego, tym bardziej elastyczny jest popyt
netto przedsiębiorstwa dominującego.
3.Nawet przedsiębiorstwo dominujące musi liczyć się z rywalami i nie
może swobodnie podwyższać ceny dóbr.

TEORIA

GIER

TEORIA

GIER

Co to jest teoria gier ?

• Teoria gier jest dziedziną zajmująca się

opisem różnych sytuacji, w których
uczestniczą podmioty świadomie podejmujące
pewne decyzje, w wyniku których następują
rozstrzygnięcia mogące zmienić ich położenie.

• Teoria gier zajmuje się przede wszystkim

sytuacjami konfliktowymi, ale również
sytuacjami, w których interesy graczy są
zgodne, ale ze względu na kłopoty w
porozumiewaniu się trudno im ustalić
jednolity sposób postępowania.

Matematyka w teorii gier

Matematyka jest wszechobecna w

teorii gier jako narzędzie, ale również
teoria gier inspiruje badania
matematyczne. Wiele dziedzin
matematyki, np. optymalizacja
wielokryteriowa, analiza nieliniowa, a
nawet podstawy matematyki, teoria
zbiorów, posiada twierdzenia
inspirowane odkryciami z zakresu
teorii gier.

Trochę historii…

• Rok 1944

to powszechnie uznana data

narodzin teorii gier.

Wydano

wówczas monografię Johna

von Neumanna i Oskara

Morgensterna "Teoria gier i

postępowanie

ekonomiczne„

• Rok 1994

Nagrodę Nobla z dziedziny

ekonomii otrzymują trzej

wybitni

specjaliści od teorii gier:

John Nash, John

Harsányi oraz

Reinhard Selten

Ostatnie 30 lat

to czas rosnącego

zainteresowania różnych nauk

teorią gier.

Teorię gier wykorzystuje się

głównie w: ekonomii, naukach

politycznych, socjologii,

psychologii, biologii, informatyce.

John Forbes Nash

Źródło: www.wikipedia.org

Kluczowe pojęcia :

Gracze i ich posunięcia.

Na rynku występuje przynajmniej dwóch graczy i ich działania inwestycyjne,

marketingowe oraz produkcyjno – cenowe są wzajemnie uzależnione.

Wyniki i wypłaty.

Wszystkim strategiom są przypisane odpowiednie wypłaty dla poszczególnych

graczy, które mogą mieć różną postać:

•

Pieniężną ( np. osiągnięte zyski, poniesione koszty)

•

Niepieniężną (np. zdobycze terytorialne, liczba zabitych żołnierzy wroga)

Strategia

Reguły gry i cele graczy.

Postępowaniem graczy rządzą formalne i nieformalne reguły gry. Mogą to być

przepisy prawne, powszechnie uznane zasady konkurencji i nieuczciwe

praktyki lub wrogie przejęcia, a także zasób

wiedzy analitycznej umożliwiającej śledzenie zachowań konkurencyjnych.

WAŻNE ZAŁOŻENIE:

Każdy gracz chce jak najlepiej dla siebie, czyli maksymalizuje swoje

zyski lub minimalizuje straty.

Ogólny podział gier :

Gry możemy podzielić według wielu

różnych kryteriów.

• jedno- i wieloetapowe
• z pełną i niepełną informacją
• z kompletną i niekompletną pamięcią
• jednorazowe i powtarzalne (skończony

lub nieskończony horyzont czasowy)

• z 2 graczami oraz z 3 i więcej

graczami

Gry o stałej sumie :

• Gry, w których suma wypłat obu graczy

jest stała, nazywamy

GRAMI O STAŁEJ

SUMIE

W grach takich znając wynik jednego

gracza możemy określić wynik drugiego
gracza.

• Szczególnym przypadkiem gier o stałej

sumie są

GRY O SUMIE ZEROWEJ

, w

których suma wypłat obu graczy jest
równa zero.

Gry macierzowe :

• Gry dwuosobowe o sumie zerowej - i o skończonej
liczbie strategii każdego gracza – to

GRY

MACIERZOWE-

ich nazwa stąd, że w każdej komórce tabeli

wystarczy wpisać jedną liczbę.

• Inne dwuosobowe gry ze skończoną liczbą

strategii każdego gracza nazywamy

GRAMI

DWUMACIERZOWYMI,

w każdej komórce tabeli

są dwie liczby, a macierz, której elementem są
pary liczb, to właściwie to samo, co para macierzy.

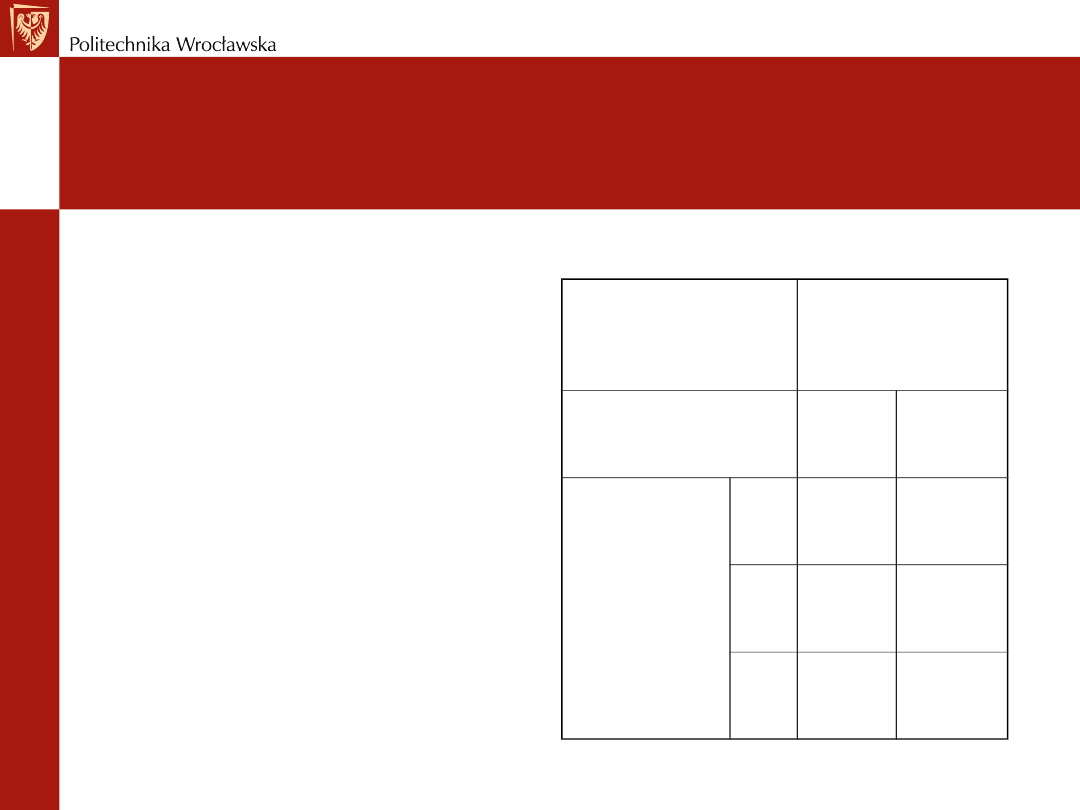
Przykład :

W tej grze bierze udział dwóch

graczy: Pan Wiersz i Pani

Kolumna. Pan Wiersz ma do

wyboru trzy strategie: A, B lub C,

zaś Pani Kolumna dwie - A lub B.

Zakłada się, że oboje gracze

równocześnie podejmują decyzje

o wyborze strategii. Wypłaty

(wygrane) Pana Wiersza można

odczytać na przecięciu

odpowiedniego wiersza i

kolumny. Ponieważ jest to gra o

sumie zerowej, nie trzeba

wypisywać wypłat Pani Kolumny

(są to po prostu przeciwieństwa

wypłat Pana Wiersza). Wypłaty

można traktować jako nagrody

pieniężne. Jeśli np. Pan Wiersz

wybierze strategię C, natomiast

Pani Kolumna strategię A, Pani

Kolumna wygra 5 (powiedzmy

dolarów) i tyle straci Pan Wiersz.

Pani

kolumna

Pan

Wiersz

-3

C -5

Gry jednoetapowe:

• Gra jednoetapowa

charakteryzuje się

tym, że gracze podejmują decyzje
jednocześnie (w tym samym momencie).
Gry jednoetapowe to jednocześnie gry z
niepełną informacją - każdy gracz
podejmuje decyzję nie znając decyzji
podjętych przez pozostałych graczy.

• UWAGA!

Przykładem gry wieloetapowej są

szachy

Przykład (dylemat więźnia)

Więzień 1 Więzień 2

zostali aresztowani za wspólnie dokonane

przestępstwo.

Policja ich przesłuchuje oddzielnie i mają do dyspozycji

następujące możliwości:

• przyznać się do winy

• nie przyznać się do winy.

Co może się zdarzyć?

• Jeśli żaden z nich nie przyzna się do winy, obydwaj dostaną 2

miesiące więzienia.

• Jeśli obydwaj przyznają się do winy, każdy zostanie skazany na

5 miesięcy więzienia.

• Jeśli jeden z nich przyzna się do winy, a drugi nie, wówczas ten,

który się przyzna, zostanie skazany na 1 miesiąc więzienia, a

ten, który się nie przyzna, dostanie karę 12 miesięcy więzienia.

Wypłaty

• Cel każdego gracza:

Maksymalizacja wypłaty, czyli jak najkrótszy pobyt w

więzieniu.

• Sytuacja konfliktowa:

Decyzja jednego gracza wpływa na wypłatę drugiego gracza.

Postać normalna

Gracz 1
Gracz 2

Przyznać się

Nie przyznać się

Przyznać się

(-5, -5 )

(-1, -12)

Nie przyznać się

(- 12, -1)

(-2, -2)

Strategia dominująca i

zdominowana

• Strategia dominująca

to najlepsza ze wszystkich możliwych

strategii, niezależnie od decyzji, jaką

podejmie drugi gracz.

• Strategia zdominowana

to taka strategia, względem której istnieje

strategia, która jest zawsze lepsza,

niezależnie od decyzji, jaką podejmie drugi

gracz.

(takich strategii może być wiele).

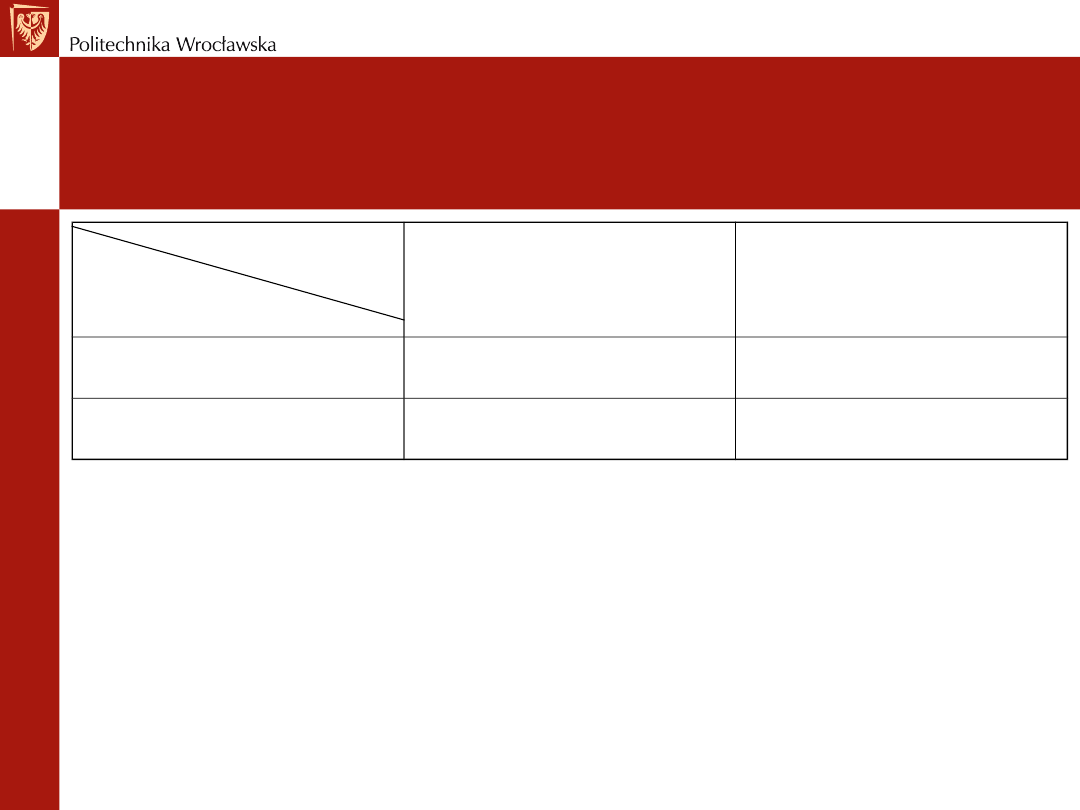
Dylemat więźnia (1)

• Jeżeli Gracz 1 przyzna się do winy,

Gracz 2 przyznając się zostanie skazany na 5 miesięcy więzienia, zaś

nie przyznając się zostanie skazany na 12 miesięcy więzienia.

Lepszym wyborem dla Gracz 2 jest zatem "przyznać się".

• Jeżeli Gracz 1 nie przyzna się do winy,

Gracz 2 przyznając się zostanie skazany na 1 miesiąc więzienia, zaś

nie przyznając się zostanie skazany na 2 miesiące więzienia. Również

teraz lepszym wyborem dla Gracza 2 jest "przyznać się”

Gracz

1
Gracz 2

Przyznać się

Nie przyznać się

Przyznać się

( -5, -5 )

( -1, -12)

Nie przyznać się

(- 12, -1)

(-2, -2)

Dylemat więźnia (2)

A zatem niezależnie od decyzji Gracza

1, zawsze dla Gracza 2 korzystniej jest
przyznać się do winy.

Decyzja o nie przyznaniu się do winy

zawsze będzie decyzją gorszą. Dla
Gracza 2 strategią dominującą będzie
«

przyznać się do winy

», natomiast «

nie

przyznać się do winy

» będzie

zdominowaną. Tak samo będzie dla
Gracza 1.

Strategia słabo dominująca i

mocno dominująca

Co jednak zrobić z taką sytuacją, gdy jakaś strategia nie jest

strategią dominującą, a jednocześnie pozwala na osiągnięcie

graczowi najwyższych wypłat, niezależnie od decyzji, jaką podjął

przeciwnik?

• STRATEGIE DOMINUJĄCE
*MOCNO DOMINUJĄCE
*SŁABO DOMINUJĄCE

• STRATEGIE ZDOMINOWANE
*MOCNO
*SŁABO

• Strategia słabo dominująca

to taka strategia, dla której nie istnieje

strategia lepsza przy dowolnej decyzji, jaką podjąłby drugi gracz.

• Strategia słabo zdominowana

to taka strategia, dla której istnieje (ą)

strategia (e), która (e) jest (są) zawsze nie gorsza (e), niezależnie od

decyzji, jaką podejmie drugi gracz.

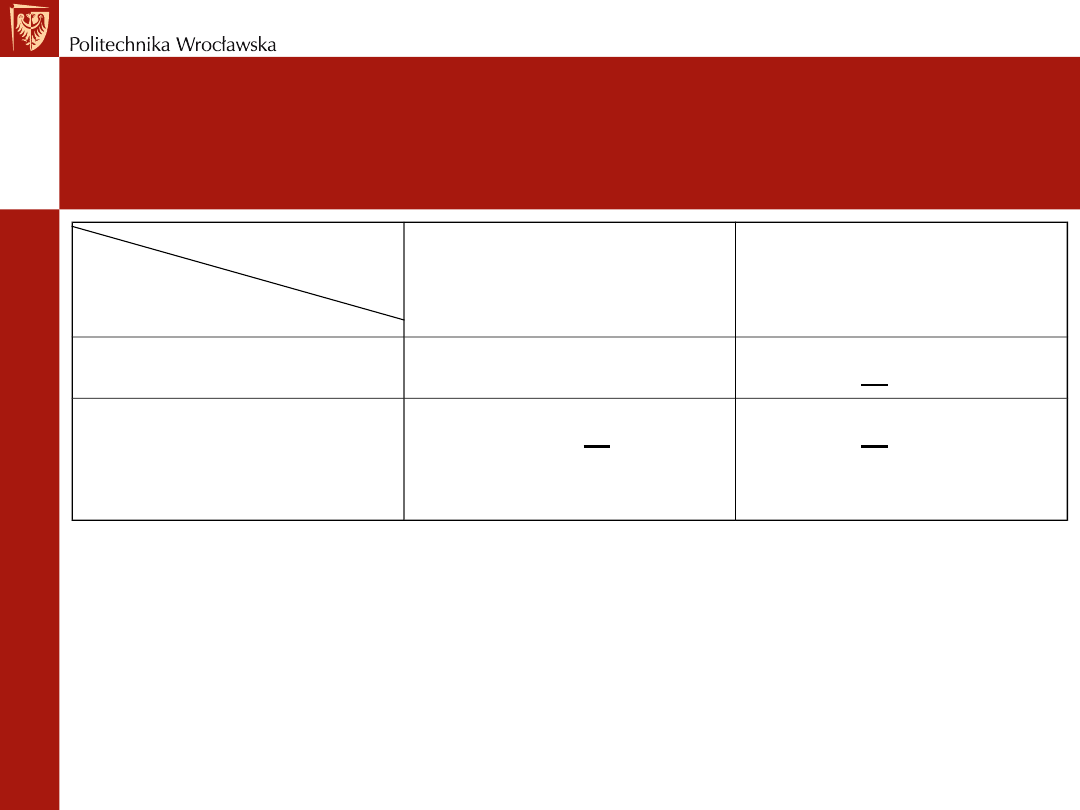
Przykład – mocna i słaba dominacja

Gracz

2
Gracz 1

Strategia C

Strategia D

Strategia A

(5; 2)

(6; 1)

Strategia B

(4; 3)

(6; 1)

Dla gracza 2

•

strategia C jest strategią mocnodominującą(2 > 1 i 3 > 1)

•

strategia D jest strategią mocnozdominowaną(1 < 2 i 1 < 3).

Dla gracza 1

• strategia A jest strategią słabodominującą(5 >= 4 i 6>= 6)
• zaś strategia B jest strategią słabozdominowaną(4 <= 5 i 6 <= 6).

Równowaga Nasha

• Równowaga Nasha

(zwana po prostu równowagą) to takie pary strategii,

które są najlepszymi odpowiedziami na siebie

nawzajem.

• Gdy w grze zostanie osiągnięta równowaga Nasha,

żaden z graczy nie może poprawić swojego wyniku

poprzez jednostronną zmianę wybranej strategii.

• W jednej grze może być kilka równowag Nasha.

• W równowadze Nasha wybór przez jednego z graczy
danej strategii jest najlepszą odpowiedzią na strategię
drugiego gracza i na odwrót, strategia drugiego gracza
jest najlepszą odpowiedzią na strategię pierwszego
gracza.

Dylemat więźnia (1)

• W „dylemacie więźnia” mieli strategię

dominującą „przyznać się”.

Równowagą Nasha w tej grze będzie zatem

kombinacja („

przyznać się

”, „

przyznać się

”).

• Gdy obaj gracze przyznają się do winy, żaden z

nich nie zwiększyłby swojej wypłaty zmieniając

jednostronnie strategię i nie przyznając się do

winy. Jeżeli bowiem więzień 1 przyzna się do

winy, najlepszą odpowiedzią więźnia 2 jest

także „przyznać się” i na odwrót, jeżeli więzień

2 przyzna się do winy, najlepszą odpowiedzią

więźnia 1 jest również przyznanie się do winy.

Dylemat więźnia (2)

• UWAGA !

Równowaga Nasha nie oznacza tego, że

obaj gracze osiągają największe możliwe

wypłaty.

Jak zauważyliśmy, gdyby obaj gracze nie

przyznali się do winy, uzyskaliby wyższe

wypłaty niż przyznając się do winy. Nie

jest jednak równowagą Nasha, bo takie

rozwiązanie zakłada współpracę obu

graczy (musieliby wybrać strategie

zdominowane!).

Strategie czysta i mieszana

• Strategia czysta

(inaczej strategia

prosta) to strategia, w której każdy

gracz dokonuje jednego wyboru z

prawdopodobieństwem 1 i trwa przy

nim. Jej przeciwieństwem jest strategia

mieszana, w której gracze podejmują

decyzje na podstawie rozkładu

prawdopodobieństwa.

• Strategia mieszana

to w teorii gier

strategia polegająca na wykonaniu

losowania, po czym podejmuje się

decyzje zależnie od wyniku losowania.

W każdej grze występuje

równowaga Nasha

W każdej grze (o skończonej liczbie graczy i

ruchów)

istnieje co najmniej jedna równowaga Nasha.

Jeżeli

nie ma równowagi w strategiach czystych, to na

pewno

występuje równowaga Nasha w strategiach

mieszanych.

Może się też zdarzyć, że w jakiejś grze

występują

zarówno równowagi Nasha w strategiach

czystych, jak i

mieszanych.

Możliwe układy równowagi w grze 2

x 2

Każda gra 2 x 2 ma jeden z wymienionych

poniżej układów równowag:

• jedną równowagę
• trzy równowagi (dwie w strategiach

czystych i jedną w strategiach

mieszanych)

• dwie równowagi (obie w strategiach

czystych)

• nieskończenie wiele równowag, w tym

dwie, trzy lub cztery w strategiach

czystych

Jak grać optymalnie?

Jakie działanie, najlepiej służące

osiągnięciu jego celów, powinien
podjąć gracz, kiedy rywalizuje z
innym graczem, którego
postępowanie jest podporządkowane
własnym interesom?

Teoria gier dostarcza następującej

odpowiedzi:

• W sytuacjach, w których konkurenci podejmują
działania niezależnie od siebie (a zatem

niemożliwa jest zmowa), każdy gracz powinien

stosować strategię zapewniającą osiągnięcie

równowagi. Strategia zapewniająca równowagę

pozwala zmaksymalizować wielkość wypłaty

każdego z graczy w warunkach określonych przez

wybór strategii dokonany przez przeciwnika.

Reguła powyższa oznacza, że każdy z graczy

powinien wybrać strategię zapewniającą

równowagę Nasha.

• Jeżeli jest kilka równowag Nasha, nie ma

powszechnie stosowanej reguły dotyczącej tego,

którą z równowag należy wybrać.

Reguła wyboru równowagi

Reguła najlepszej równowagi zaproponowana przez

Harsányi’ego i Seltena jest następująca:

• spośród wszystkich równowag gracze powinni wybrać
równowagę dominującą ze względu na wypłaty; (taka
równowaga, w której wypłata każdego z graczy jest
największa ze zbioru wypłat danego gracza we

wszystkich równowag Nasha)

• jeżeli nie ma równowagi dominującej ze względu na
wypłaty, gracze powinni wybrać równowagę

dominującą

ze względu na ryzyko (taka równowaga, która

odznacza się najmniejszym ryzykiem związanym z

wyborem poszczególnych strategii).