WSTĘP DO PROBLEMATYKI RYZYKA RYNKOWEGO, TECHNIKI

WSTĘP DO PROBLEMATYKI RYZYKA RYNKOWEGO, TECHNIKI

POMIARU RYZYKA.

POMIARU RYZYKA.

ZARZĄDZANIE RYZYKIEM

ZARZĄDZANIE RYZYKIEM

FINANSOWYM

FINANSOWYM

ODMIANY RYZYKA

ODMIANY RYZYKA

•

ryzyko dotyczące cen

ryzyko dotyczące cen

•

ryzyko stóp procentowych

ryzyko stóp procentowych

•

ryzyko walutowe

ryzyko walutowe

•

ryzyko płynności

ryzyko płynności

•

ryzyko bankructwa

ryzyko bankructwa

•

ryzyko kredytowe

ryzyko kredytowe

•

ryzyko stóp zwrotu

ryzyko stóp zwrotu

ZE WZGLĘDU NA

ZE WZGLĘDU NA

MOŻLIWOŚĆ

MOŻLIWOŚĆ

DYWERSYFIKACJI

DYWERSYFIKACJI

•

ryzyko

ryzyko

systematyczne

systematyczne

•

ryzyko

ryzyko

niesystematyczne

niesystematyczne

•

ryzyko operacyjne

ryzyko operacyjne

•

ryzyko finansowe

ryzyko finansowe

•

ryzyko projektów

ryzyko projektów

inwestycyjnych

inwestycyjnych

Ze względu na

Ze względu na

działalność

działalność

Różne kryteria

Różne kryteria

klasyfikacji

klasyfikacji

Ryzyko, zdefiniowane w słowniku

Ryzyko, zdefiniowane w słowniku

Webstera,

Webstera,

to „zagrożenie, niebezpieczeństwo,

to „zagrożenie, niebezpieczeństwo,

wystawienia na stratę lub szkodę

wystawienia na stratę lub szkodę

”

”

.

.

Ryzyko to prawdopodobieństwo

Ryzyko to prawdopodobieństwo

uzyskania dochodu mniejszego lub

uzyskania dochodu mniejszego lub

większego

większego

niż oczekiwany.

niż oczekiwany.

Cechy opisujące ryzyko:

Cechy opisujące ryzyko:



prawdopodobieństwo

prawdopodobieństwo



niepewność

niepewność



przyszłość

przyszłość

POMIAR RYZYKA

Wariancja rozkładu dyskretnego prawdopodobieństwa

Wariancja rozkładu dyskretnego prawdopodobieństwa

Wariancja jest miarą rozproszenia wyników możliwych

Wariancja jest miarą rozproszenia wyników możliwych

wokół wartości oczekiwanej: im większa wariancja tym

wokół wartości oczekiwanej: im większa wariancja tym

większe rozproszenie, a co za tym idzie ryzyko.

większe rozproszenie, a co za tym idzie ryzyko.

Pierwiastek z wariancji określa procentowe odchylenie.

Pierwiastek z wariancji określa procentowe odchylenie.

gdzie:

gdzie:

k

k

i

i

– jest i-tym możliwym wynikiem

– jest i-tym możliwym wynikiem

Pi – prawdopodobieństwo wystąpienia tego wyniku

Pi – prawdopodobieństwo wystąpienia tego wyniku

- oczekiwaną wartością k wyznaczoną na podstawie wzoru:

- oczekiwaną wartością k wyznaczoną na podstawie wzoru:

i

kˆ









n

1

i

i

i

p

k

kˆ









n

1

i

i

i

p

k

kˆ

















n

i 1

i

2

i

i

2

p

kˆ

k

σ

Wariancja

















n

i 1

i

2

i

i

2

p

kˆ

k

σ

Wariancja

W zasadzie jest prawdą, że im wyższy dochód

W zasadzie jest prawdą, że im wyższy dochód

oczekiwany, tym większe odchylenie. Nie zawsze

oczekiwany, tym większe odchylenie. Nie zawsze

rankingi oparte na odchyleniu standardowym dają jasny

rankingi oparte na odchyleniu standardowym dają jasny

obraz ryzyka. W przypadku gdy mamy różne odchylenia i

obraz ryzyka. W przypadku gdy mamy różne odchylenia i

różne wartości oczekiwane, przydatną staje się miara:

różne wartości oczekiwane, przydatną staje się miara:

współczynnik zmienności

współczynnik zmienności

t

kˆ

σ

V 

t

kˆ

σ

V 

Miara ta wyraża procentowe odchylenie od wartości oczekiwanej.

Miara ta wyraża procentowe odchylenie od wartości oczekiwanej.

W przypadku gdy nie znamy rozkładu

W przypadku gdy nie znamy rozkładu

prawdopodobieństwa oczekiwanych wartości, możemy

prawdopodobieństwa oczekiwanych wartości, możemy

posłużyć się danymi historycznymi pochodzącymi z

posłużyć się danymi historycznymi pochodzącymi z

próby. Wówczas poprzednie wzory przyjmują postać:

próby. Wówczas poprzednie wzory przyjmują postać:

Średnia wartość zmiennej =

Średnia wartość zmiennej =

Wariancja =

Wariancja =

n

k

k

n

1

i

t







n

k

k

n

1

i

t











1

n

k

k

σ

n

1

i

2

t

t

2















1

n

k

k

σ

n

1

i

2

t

t

2











Jeżeli założy się, że ryzyko powinno być określane

Jeżeli założy się, że ryzyko powinno być określane

na podstawie tylko elementów niepożądanych,

na podstawie tylko elementów niepożądanych,

czyli ujemnych odchyleń, to miarą ryzyka jest

czyli ujemnych odchyleń, to miarą ryzyka jest

semiwariancja, którą wyznacza się na podstawie

semiwariancja, którą wyznacza się na podstawie

wzoru:

wzoru:









n

1

i

2

i

i

2

d

p

SV









n

1

i

2

i

i

2

d

p

SV

gdzie:

gdzie:

SV

SV

2

2

– semiwariancja

– semiwariancja



















0

k

k

0,

0

k

k

,

k

k

d

i

i

i

i



















0

k

k

0,

0

k

k

,

k

k

d

i

i

i

i

1

n

d

SV

n

1

i

2

i

2









1

n

d

SV

n

1

i

2

i

2









lub

lub

GAP-ANALISYS - METODA LUKI

GAP-ANALISYS - METODA LUKI

Większość instytucji finansowych nadal stosuje

Większość instytucji finansowych nadal stosuje

metodologię „luki

metodologię „luki

”

”

okresów wymagalności do

okresów wymagalności do

oceny poziomu ekspozycji na ryzyko zmiany stóp

oceny poziomu ekspozycji na ryzyko zmiany stóp

procentowych.

procentowych.

Metoda ta pozwala zmierzyć „lukę

Metoda ta pozwala zmierzyć „lukę

”

”

między

między

kwotą aktywów wrażliwych na zmiany stóp

kwotą aktywów wrażliwych na zmiany stóp

procentowych (RSA) a kwotą zobowiązań

procentowych (RSA) a kwotą zobowiązań

wrażliwych na zmiany stóp procentowych (RSL),

wrażliwych na zmiany stóp procentowych (RSL),

tzn. aktywów i pasywów, których wartości ulegną

tzn. aktywów i pasywów, których wartości ulegną

zmianie w okresie luki.

zmianie w okresie luki.

luka = RSA - RSL

luka = RSA - RSL

Jeżeli przez

Jeżeli przez





r oznaczymy zmianę stóp

r oznaczymy zmianę stóp

procentowych w roku, to znając wartość luki,

procentowych w roku, to znając wartość luki,

możemy obliczyć zmianę dochodu odsetkowego:

możemy obliczyć zmianę dochodu odsetkowego:





NII = luka

NII = luka

x

x





r

r

Przykład:

Przykład:

Aktywa

Aktywa

(okresy wymagalności)

(okresy wymagalności)

Pasywa

Pasywa

(okresy wymagalności)

(okresy wymagalności)

3 miesiące lub

3 miesiące lub

mniej

mniej

100

100

3 miesiące lub

3 miesiące lub

mniej

mniej

400

400

6 miesięcy

6 miesięcy

100

100

6 miesięcy

6 miesięcy

300

300

12 miesięcy

12 miesięcy

400

400

12 miesięcy

12 miesięcy

200

200

Ponad 12

Ponad 12

miesięcy

miesięcy

100

100

Ponad 12

Ponad 12

miesięcy

miesięcy

100

100

100

100

0

0

100

100

0

0

W ciągu jednorocznego okresu luki

W ciągu jednorocznego okresu luki

aktywa i pasywa wrażliwe na zmiany

aktywa i pasywa wrażliwe na zmiany

stóp procentowych są następujące:

stóp procentowych są następujące:

•

aktywa o okresie wymagalności do 3

aktywa o okresie wymagalności do 3

miesięcy: 100

miesięcy: 100

•

aktywa o okresie wymagalności 6 miesięcy:

aktywa o okresie wymagalności 6 miesięcy:

100

100

•

aktywa o okresie wymagalności 12 miesięcy:

aktywa o okresie wymagalności 12 miesięcy:

400

400

•

pasywa o okresie wymagalności do 3

pasywa o okresie wymagalności do 3

miesięcy: 400

miesięcy: 400

•

pasywa o okresie wymagalności 6 miesięcy:

pasywa o okresie wymagalności 6 miesięcy:

300

300

•

pasywa o okresie wymagalności 12 miesięcy:

pasywa o okresie wymagalności 12 miesięcy:

200

200

Luka = RSA – RSL = 600 – 900 = -300

dla np.

dla np.





r = 5%

r = 5%





NII = -300 x 0,05 = -15

NII = -300 x 0,05 = -15

METODA ANALIZY

METODA ANALIZY

OKRESOWEJ - DURATION

OKRESOWEJ - DURATION

Stosowana jest przede wszystkim do oceny ryzyka

Stosowana jest przede wszystkim do oceny ryzyka

stopy procentowej inwestycji w papiery wartościowe o

stopy procentowej inwestycji w papiery wartościowe o

stałej stopie procentowej.

stałej stopie procentowej.

W metodzie tej próbuje się skwantyfikować ryzyko

W metodzie tej próbuje się skwantyfikować ryzyko

stopy procentowej za pomocą wartości przyszłych

stopy procentowej za pomocą wartości przyszłych

strumieni pieniężnych.

strumieni pieniężnych.

Przez durację rozumie się średni ważony

Przez durację rozumie się średni ważony

okres oczekiwania na wpływy środków

okres oczekiwania na wpływy środków

pieniężnych z danego instrumentu

pieniężnych z danego instrumentu

finansowego. Durację oblicza się zgodnie z

finansowego. Durację oblicza się zgodnie z

techniką obliczania wartości rynkowej

techniką obliczania wartości rynkowej

danego instrumentu finansowego.

danego instrumentu finansowego.

Stosowana jest przede wszystkim do oceny ryzyka

Stosowana jest przede wszystkim do oceny ryzyka

stopy procentowej inwestycji w papiery wartościowe o

stopy procentowej inwestycji w papiery wartościowe o

stałej stopie procentowej.

stałej stopie procentowej.

W metodzie tej próbuje się skwantyfikować ryzyko

W metodzie tej próbuje się skwantyfikować ryzyko

stopy procentowej za pomocą wartości przyszłych

stopy procentowej za pomocą wartości przyszłych

strumieni pieniężnych.

strumieni pieniężnych.

Przez durację rozumie się średni ważony

Przez durację rozumie się średni ważony

okres oczekiwania na wpływy środków

okres oczekiwania na wpływy środków

pieniężnych z danego instrumentu

pieniężnych z danego instrumentu

finansowego. Durację oblicza się zgodnie z

finansowego. Durację oblicza się zgodnie z

techniką obliczania wartości rynkowej

techniką obliczania wartości rynkowej

danego instrumentu finansowego.

danego instrumentu finansowego.

Wartość bieżąca instrumentu finansowego przy stałej

Wartość bieżąca instrumentu finansowego przy stałej

stopie dyskontowej jest określana wzorem:

stopie dyskontowej jest określana wzorem:

PV =

FV

t

1+r

(

)

t

t=1

n

å

a

PV =

FV

t

1+r

(

)

t

t=1

n

å

a

gdzie:

gdzie:

n – liczba okresów do terminu zapadalności,

n – liczba okresów do terminu zapadalności,

t – czas

t – czas

r – stopa dyskontowa

r – stopa dyskontowa

FV

FV

t

t

– wartość przyszła, czyli wpływy z odsetek i spłaty kapitału w okresie t

– wartość przyszła, czyli wpływy z odsetek i spłaty kapitału w okresie t

Natomiast durację można obliczyć następująco:

Natomiast durację można obliczyć następująco:

Natomiast durację można obliczyć następująco:

Natomiast durację można obliczyć następująco:

D =

t×PV

t

t=1

n

å

PV

t

t=1

n

å

D =

t×PV

t

t=1

n

å

PV

t

t=1

n

å

Duracja jest ilorazem, w którego liczniku

Duracja jest ilorazem, w którego liczniku

znajduje się suma ważona wartości

znajduje się suma ważona wartości

bieżących (przy czym wagami są

bieżących (przy czym wagami są

poszczególne okresy), a w mianowniku

poszczególne okresy), a w mianowniku

suma nie ważona wartości bieżących.

suma nie ważona wartości bieżących.

Duracja jest ilorazem, w którego liczniku

Duracja jest ilorazem, w którego liczniku

znajduje się suma ważona wartości

znajduje się suma ważona wartości

bieżących (przy czym wagami są

bieżących (przy czym wagami są

poszczególne okresy), a w mianowniku

poszczególne okresy), a w mianowniku

suma nie ważona wartości bieżących.

suma nie ważona wartości bieżących.

Przykład:

Przykład:

Dany jest instrument finansowy na 100 jednostek o

Dany jest instrument finansowy na 100 jednostek o

terminie 3 lata i oprocentowaniu 10%. Obliczyć durację.

terminie 3 lata i oprocentowaniu 10%. Obliczyć durację.

Bieżąca wartość instrumentu, będąca sumą wpływów

Bieżąca wartość instrumentu, będąca sumą wpływów

pieniężnych w poszczególnych okresach, wynosi:

pieniężnych w poszczególnych okresach, wynosi:



    

100

82,6446

8,2645

9,0909

r

1

110

r

1

10

r

1

10

PV

PV

PV

PV

3

2

3

2

1































    

100

82,6446

8,2645

9,0909

r

1

110

r

1

10

r

1

10

PV

PV

PV

PV

3

2

3

2

1





























Natomiast duracja:

Natomiast duracja:

D=

t

1

×FV

1

+t

2

×FV

2

+t

3

×FV

3

(

)

PV

å

=

1×9,0909+2×8,2645+3×82,6446

(

)

100

=2,7355

D=

t

1

×FV

1

+t

2

×FV

2

+t

3

×FV

3

(

)

PV

å

=

1×9,0909+2×8,2645+3×82,6446

(

)

100

=2,7355

Przeciętny okres oczekiwania na

Przeciętny okres oczekiwania na

wpływy z danego instrumentu

wpływy z danego instrumentu

finansowego wynosi więc ok.. 2,7 lat.

finansowego wynosi więc ok.. 2,7 lat.

POMIAR RYZYKA PŁYNNOŚCI.

POMIAR RYZYKA PŁYNNOŚCI.

Pewne ślady ryzyka finansowego widoczne są

Pewne ślady ryzyka finansowego widoczne są

już w bilansie. Ryzyko utarty płynności wiąże

już w bilansie. Ryzyko utarty płynności wiąże

się z niewypłacalnością podmiotu, tzn.

się z niewypłacalnością podmiotu, tzn.

nieuregulowaniem swych zobowiązań w

nieuregulowaniem swych zobowiązań w

terminie. Do pomiaru płynności mogą służyć

terminie. Do pomiaru płynności mogą służyć

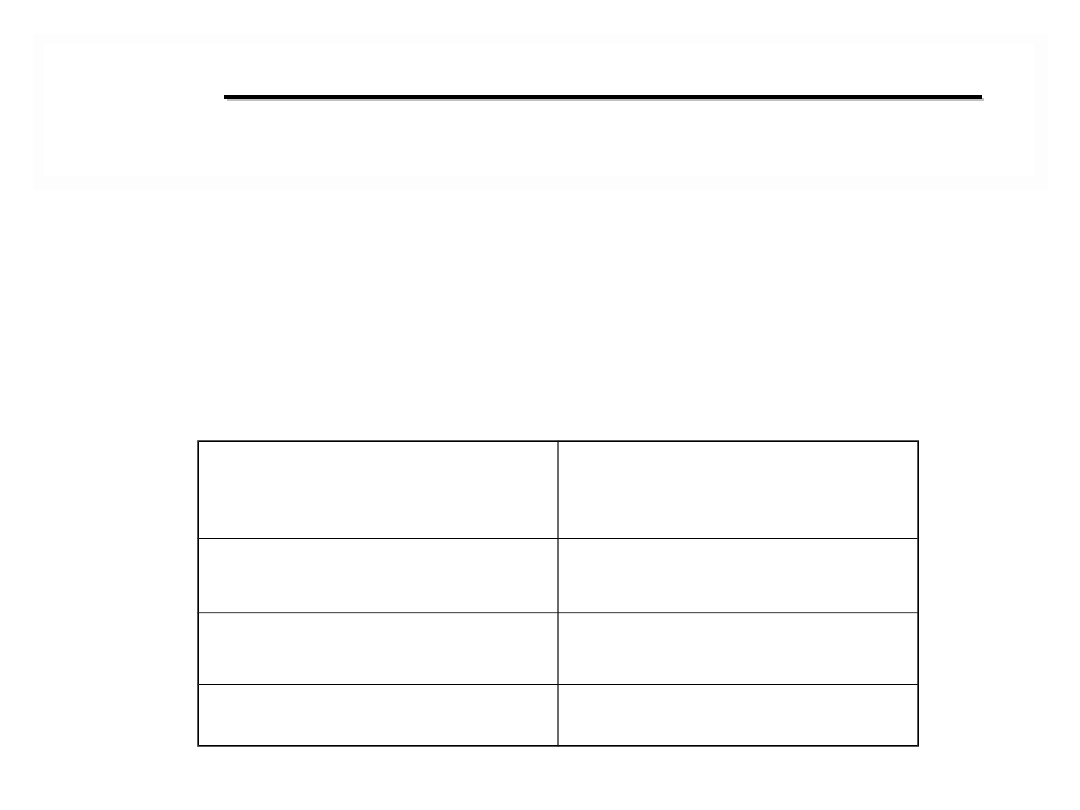
trzy podstawowe wskaźniki.

trzy podstawowe wskaźniki.

Wskaźnik

Optymalna

wielkość

Bieżąca płynność = m. obrotowy/zobow.

Bieżąca płynność = m. obrotowy/zobow.

krótkoterminowe

krótkoterminowe

(1,5-2,0)

Szybka płynność = m. obrotowy – zapasy/

Szybka płynność = m. obrotowy – zapasy/

zobow.

zobow.

krótkoterminowe

krótkoterminowe

(0,75-1,0)

Wysoka płynność = śr. pieniężne/

Wysoka płynność = śr. pieniężne/

zobow.

zobow.

krótkoterminowe

krótkoterminowe

(0,1-0,2)

ANALIZA SCENARIUSZY METODĄ

ANALIZA SCENARIUSZY METODĄ

ANALIZY RYZYKA WYŁĄCZNEGO.

ANALIZY RYZYKA WYŁĄCZNEGO.

Analizę tę wykorzystuje się przy preliminowaniu inwestycji. Wstępnie

Analizę tę wykorzystuje się przy preliminowaniu inwestycji. Wstępnie

formułuje się zestaw danych opisujących sytuację:

formułuje się zestaw danych opisujących sytuację:

•

złą

złą

•

przeciętną (najbardziej prawdopodobną)

przeciętną (najbardziej prawdopodobną)

•

dobrą

dobrą

Dla każdego scenariusza oblicza się NPV oraz określa

Dla każdego scenariusza oblicza się NPV oraz określa

prawdopodobieństwo zdarzenia. Podobnie jak przy tradycyjnym

prawdopodobieństwo zdarzenia. Podobnie jak przy tradycyjnym

odchyleniu standardowym obliczamy tutaj wartość oczekiwaną NPV

odchyleniu standardowym obliczamy tutaj wartość oczekiwaną NPV

jego odchylenie standardowe i współczynnik zmienności.

jego odchylenie standardowe i współczynnik zmienności.









n

1

i

i

i

NPV

p

NPV









n

1

i

i

i

NPV

p

NPV





2

n

1

i

i

NPV

NPV

NPV

p

σ















2

n

1

i

i

NPV

NPV

NPV

p

σ











NPV

σ

V

NPV

NPV



NPV

σ

V

NPV

NPV



Współczynnik zmienności może być

Współczynnik zmienności może być

porównany ze współczynnikiem zmienności

porównany ze współczynnikiem zmienności

przeciętnego aktywu, aby stwierdzić jakie

przeciętnego aktywu, aby stwierdzić jakie

jest względne ryzyko wyłączne projektu.

jest względne ryzyko wyłączne projektu.

Wady analizy scenariuszy:

Wady analizy scenariuszy:

•

Uwzględnia kilka osobnych wyników

Uwzględnia kilka osobnych wyników

(NPV) projektu, chociaż istniej

(NPV) projektu, chociaż istniej

nieskończona liczba możliwości,

nieskończona liczba możliwości,

•

Analiza scenariuszy zakłada, że

Analiza scenariuszy zakłada, że

zmienne traktowane jako niepewne

zmienne traktowane jako niepewne

są dodatni skorelowane,

są dodatni skorelowane,

•

Analiza scenariuszy przeszacowuje

Analiza scenariuszy przeszacowuje

wielkości graniczne NPV.

wielkości graniczne NPV.

SYMULACJA MONTE CARLO

SYMULACJA MONTE CARLO

Metoda ta służy jako narzędzie oceny

Metoda ta służy jako narzędzie oceny

poziomu ekspozycji firmy na ceny

poziomu ekspozycji firmy na ceny

finansowe oraz ceny na rynkach

finansowe oraz ceny na rynkach

towarowych w przyszłości.

towarowych w przyszłości.

Z doniesień prasy specjalistycznej

Z doniesień prasy specjalistycznej

wynika, że niektóre firmy zaczęły już

wynika, że niektóre firmy zaczęły już

stosować modele symulacyjne do badania

stosować modele symulacyjne do badania

wrażliwości dochodu przed

wrażliwości dochodu przed

opodatkowaniem na zmiany stóp

opodatkowaniem na zmiany stóp

procentowych, kursów walutowych oraz

procentowych, kursów walutowych oraz

cen surowców i towarów.

cen surowców i towarów.

Etapy budowy modelu:

Etapy budowy modelu:

1.

1.

Utworzenie modelu komputerowego,

Utworzenie modelu komputerowego,

zawierającego przepływy środków

zawierającego przepływy środków

2.

2.

Analityk musi określić rozkład

Analityk musi określić rozkład

prawdopodobieństwa każdej zmiennej

prawdopodobieństwa każdej zmiennej

objaśniającej obciążonej niepewnością, takiej

objaśniającej obciążonej niepewnością, takiej

jak ceny czy wolumen sprzedaży.

jak ceny czy wolumen sprzedaży.

3.

3.

Dalej program do symulacji dokonuje losowego

Dalej program do symulacji dokonuje losowego

wyboru każdej zmiennej obciążonej

wyboru każdej zmiennej obciążonej

niepewnością na podstawie jej ustalonego

niepewnością na podstawie jej ustalonego

rozkładu prawdopodobieństwa

rozkładu prawdopodobieństwa

4.

4.

Wybrana wartość każdej zmiennej obciążonej

Wybrana wartość każdej zmiennej obciążonej

niepewnością jest wówczas wykorzystana w

niepewnością jest wówczas wykorzystana w

modelu do określenia przepływów, a przepływy

modelu do określenia przepływów, a przepływy

te stosuje się do ustalenia NPV w każdym roku.

te stosuje się do ustalenia NPV w każdym roku.

5.

5.

Etapy 3 i 4 powtarza się wielokrotnie, które są

Etapy 3 i 4 powtarza się wielokrotnie, które są

następnie wykorzystane do zbudowania

następnie wykorzystane do zbudowania

rozkładu prawdopodobieństwa oraz jego

rozkładu prawdopodobieństwa oraz jego

wartości oczekiwanej i odchylenia

wartości oczekiwanej i odchylenia

standardowego.

standardowego.

Problemy w analizie Monte

Problemy w analizie Monte

Carlo:

Carlo:



Określenie rozkładu

Określenie rozkładu

prawdopodobieństwa zmiennych

prawdopodobieństwa zmiennych

stochastycznych i korelacji

stochastycznych i korelacji

rozkładów,

rozkładów,



Nawet gdy analiza jest

Nawet gdy analiza jest

ukończona, nie wyłania się

ukończona, nie wyłania się

zdecydowana podstawa do podjęcia

zdecydowana podstawa do podjęcia

decyzji,

decyzji,



Analiza scenariuszy i Monte Carlo

Analiza scenariuszy i Monte Carlo

nie biorą pod uwagę efektów

nie biorą pod uwagę efektów

zróżnicowania projektów

zróżnicowania projektów

wewnętrznych firmy, jak i portfeli

wewnętrznych firmy, jak i portfeli

inwestycyjnych inwestorów.

inwestycyjnych inwestorów.

RYZYKO RYNKOWE WG MODELU

SHARP’A



Najprostszym i najczęściej używanym modelem,

opisującym powiązanie zmian wartości akcji z
zachowaniem całego rynku, jest
jednowskaźnikowy model rynku (single-index
model), zaproponowany przez W. Sharpe'a.
Model ten znalazł zastosowanie w budowie
portfela papierów wartościowych. W modelu tym
zakłada się, że stopy zwrotu akcji zależą od
działania czynnika, który można określić jako
czynnik rynku. Czynnik ten może być wyrażony
indeksem giełdowym.



Model jednowskaźnikowy, zwany czasem również

Model jednowskaźnikowy, zwany czasem również

modelem jednoczynnikowym, można przedstawić w

modelem jednoczynnikowym, można przedstawić w

postaci następującego wzoru:

postaci następującego wzoru:

 

 

 

 

 

 

gdzie:

gdzie:

R

R

i

i

- stopa zwrotu akcji spółki,

- stopa zwrotu akcji spółki,

R

R

m

m

- stopa zwrotu wskaźnika rynku,

- stopa zwrotu wskaźnika rynku,





i

i

- wyraz wolny równania,

- wyraz wolny równania,





i

i

- współczynnik beta,

- współczynnik beta,





- składnik losowy.

- składnik losowy.

ε

R

β

α

R

m

i

i

i









ε

R

β

α

R

m

i

i

i









Ważną rolę odgrywa współczynnik kierunkowy prostej, zwany

Ważną rolę odgrywa współczynnik kierunkowy prostej, zwany

współczynnikiem beta. Współczynnik beta wskazuje, o ile

współczynnikiem beta. Współczynnik beta wskazuje, o ile

jednostek (punktów procentowych) w przybliżeniu wzrośnie

jednostek (punktów procentowych) w przybliżeniu wzrośnie

(spadnie) stopa zwrotu akcji, gdy stopa zwrotu wskaźnika rynku

(spadnie) stopa zwrotu akcji, gdy stopa zwrotu wskaźnika rynku

wzrośnie (spadnie) o jednostkę (jeden punkt procentowy).

wzrośnie (spadnie) o jednostkę (jeden punkt procentowy).

Współczynnik beta, może przyjmować różne wartości:

Współczynnik beta, może przyjmować różne wartości:

•

•

O <

O <





< l oznacza, że stopa zwrotu akcji w małym stopniu

< l oznacza, że stopa zwrotu akcji w małym stopniu

reaguje na zmiany zachodzące na rynku,

reaguje na zmiany zachodzące na rynku,

•

•





> l oznacza, że stopa zwrotu akcji w dużym stopniu reaguje

> l oznacza, że stopa zwrotu akcji w dużym stopniu reaguje

na zmiany zachodzące na rynku,

na zmiany zachodzące na rynku,

•

•





= 1 oznacza, że stopa zwrotu akcji zmienia się w takim

= 1 oznacza, że stopa zwrotu akcji zmienia się w takim

samym stopniu, jak stopa zwrotu rynku,

samym stopniu, jak stopa zwrotu rynku,

•

•





= 0 oznacza, że stopa akcji nie reaguje na zmiany rynku,

= 0 oznacza, że stopa akcji nie reaguje na zmiany rynku,

•

•





< 0 oznacza, że stopa zwrotu akcji reaguje na zmiany

< 0 oznacza, że stopa zwrotu akcji reaguje na zmiany

przeciwnie niż rynek.

przeciwnie niż rynek.

Współczynnik beta:

Współczynnik beta:



Jest miarą względnego ryzyka rynkowego

Jest miarą względnego ryzyka rynkowego



Jest wskaźnikiem wrażliwości rynku

Jest wskaźnikiem wrażliwości rynku

Współczynnik beta:

Współczynnik beta:



Jest miarą względnego ryzyka rynkowego

Jest miarą względnego ryzyka rynkowego



Jest wskaźnikiem wrażliwości rynku

Jest wskaźnikiem wrażliwości rynku

Do wyznaczenia współczynnika beta stosuje się

Do wyznaczenia współczynnika beta stosuje się

następujący wzór: 

następujący wzór: 

gdzie:

gdzie:

t - okres, na którego podstawie wyznacza się

t - okres, na którego podstawie wyznacza się

parametry modelu,

parametry modelu,

- średnia stopa zwrotu akcji,

- średnia stopa zwrotu akcji,

- średnia stopa zwrotu rynku,

- średnia stopa zwrotu rynku,

R

R

it

it

- stopa zwrotu akcji w okresie t,

- stopa zwrotu akcji w okresie t,

R

R

mt

mt

- stopa zwrotu rynku w okresie t

- stopa zwrotu rynku w okresie t

i

R

m

R



 























2

m

mt

N

1

i

i

it

m

mt

i

R

R

R

R

R

R

β



 























2

m

mt

N

1

i

i

it

m

mt

i

R

R

R

R

R

R

β

RYZYKO CAŁKOWITE WEDŁUG SHARPA.

RYZYKO CAŁKOWITE WEDŁUG SHARPA.

2

i

2
m

2

i

2

i

se

s

β

s







2

i

2
m

2

i

2

i

se

s

β

s







Zależnośc ta wskazuje, że ryzyko akcji (mierzone za pomocą

Zależnośc ta wskazuje, że ryzyko akcji (mierzone za pomocą

wariancji), tzw. Ryzyko całkowite (total risk), jest sumą dwóch

wariancji), tzw. Ryzyko całkowite (total risk), jest sumą dwóch

składników:

składników:



Ryzyko systematyczne

Ryzyko systematyczne

zwane

zwane

ryzykiem rynkowym

ryzykiem rynkowym

– pierwsza

– pierwsza

część wzoru

część wzoru



Ryzyko specyficzne

Ryzyko specyficzne

lub

lub

niesystematyczne

niesystematyczne

, mierzone wariancją

, mierzone wariancją

składnika losowego

składnika losowego

IM WYŻSZY WSPÓŁCZYNNIK BETA (CO DO

IM WYŻSZY WSPÓŁCZYNNIK BETA (CO DO

WARTOŚCI BEZWZGLĘDNEJ), TYM WYŻSZE JEST

WARTOŚCI BEZWZGLĘDNEJ), TYM WYŻSZE JEST

RYZYKO RYNKOWE

RYZYKO RYNKOWE

2

i

2
m

2
I

s

s

β 

- wariancja stopy zwrotu z rynku

- wariancja składnika losowego

2
m

s

2
m

s

2
ei

s

2
ei

s

Udział ryzyka rynkowego w

Udział ryzyka rynkowego w

ryzyku całkowitym

ryzyku całkowitym

MODEL E.I. ALTMANA W RYZYKU

MODEL E.I. ALTMANA W RYZYKU

BANKRUCTWA

BANKRUCTWA



Zbadał 33 przedsiębiorstwa, które

Zbadał 33 przedsiębiorstwa, które

zbankrutowały, oraz 33 firmy, należące do

zbankrutowały, oraz 33 firmy, należące do

podobnej branży i charakteryzujące się

podobnej branży i charakteryzujące się

dobrą kondycją finansową.

dobrą kondycją finansową.



Oszacowano 22 wskaźniki, z których

Oszacowano 22 wskaźniki, z których

wybrano 5 najbardziej przydatnych do

wybrano 5 najbardziej przydatnych do

oceny przewidywanej zdolności płatniczej:

oceny przewidywanej zdolności płatniczej:

ogolem

aktywa

pracujacy

kapital

X

1



ogolem

aktywa

pracujacy

kapital

X

1



ogolem

aktywa

zatrzymany

zysk

X

2



ogolem

aktywa

zatrzymany

zysk

X

2



ogolem

aktywa

niem

opodatkowa

przed

zysk

X

3



ogolem

aktywa

niem

opodatkowa

przed

zysk

X

3



obcych

kapitalow

rynkowa

wartosc

orstwa

przedsiebi

rynkowa

wartosc

X

4



obcych

kapitalow

rynkowa

wartosc

orstwa

przedsiebi

rynkowa

wartosc

X

4



ogolem

aktywa

sprzedaz

X

5



ogolem

aktywa

sprzedaz

X

5



Rzeczywiste wielkości tych wskaźników

Rzeczywiste wielkości tych wskaźników

pomnożone przez odpowiednie wagi

pomnożone przez odpowiednie wagi

dają globalny wskaźnik Z, służący

dają globalny wskaźnik Z, służący

ocenie sytuacji finansowej w

ocenie sytuacji finansowej w

następującej postaci:

następującej postaci:

5

4

3

2

1

X

1,0

X

0,6

X

3,3

X

1,4

X

1,2

Z





















5

4

3

2

1

X

1,0

X

0,6

X

3,3

X

1,4

X

1,2

Z





















Z > 2,99 – dobra kondycja

Z > 2,99 – dobra kondycja

finansowa,

finansowa,

Z < 1,81 – przedsiębiorstwa są

Z < 1,81 – przedsiębiorstwa są

bankrutami.

bankrutami.

Z > 2,99 – dobra kondycja

Z > 2,99 – dobra kondycja

finansowa,

finansowa,

Z < 1,81 – przedsiębiorstwa są

Z < 1,81 – przedsiębiorstwa są

bankrutami.

bankrutami.

PODSUMOWANIE



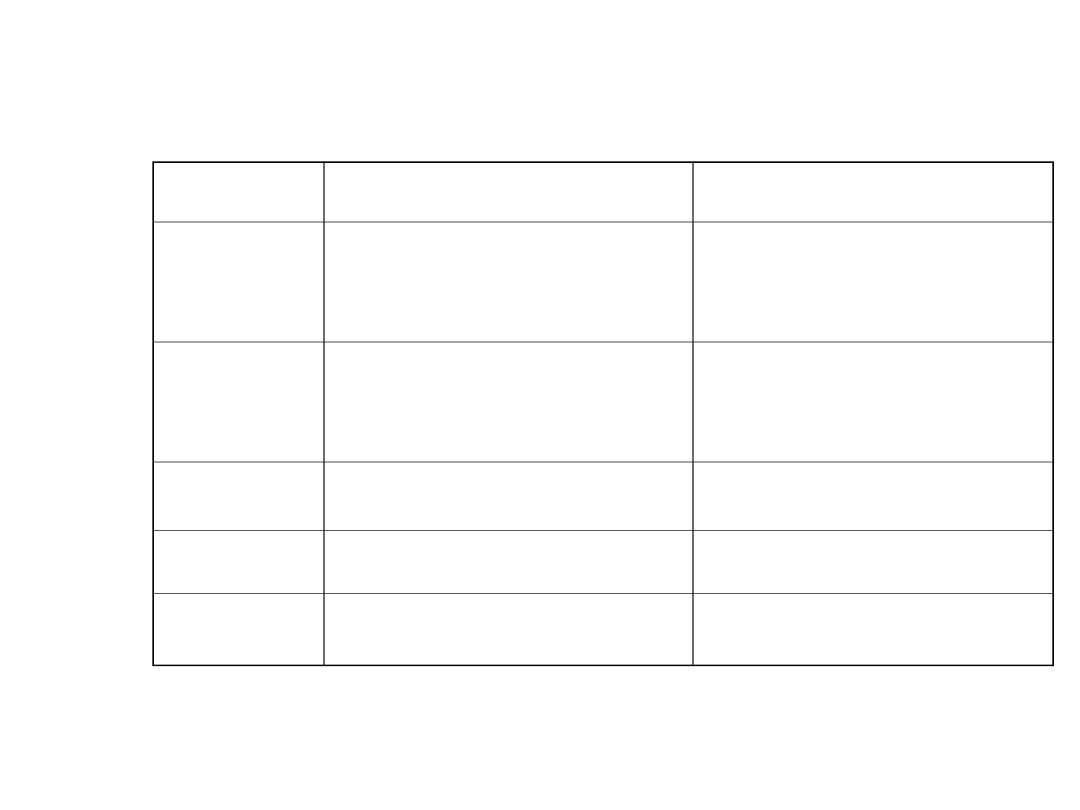
W zarządzaniu ryzykiem wykorzystuje się dwie grupy

W zarządzaniu ryzykiem wykorzystuje się dwie grupy

ogólnie nazwanych metod:

ogólnie nazwanych metod:



Metody oparte o podejście portfelowe, gdzie

Metody oparte o podejście portfelowe, gdzie

koncepcja Valeu at Risk jest powszechnie akceptowaną

koncepcja Valeu at Risk jest powszechnie akceptowaną

metodą. Wśród metod opartych o VaR wyróżnia się

metodą. Wśród metod opartych o VaR wyróżnia się

różnego rodzaju podejścia obliczeniowe różniące się

różnego rodzaju podejścia obliczeniowe różniące się

czasem symulacji i poziomem złożoności.

czasem symulacji i poziomem złożoności.



Metody koncentrujące się na sytuacjach

Metody koncentrujące się na sytuacjach

ekstremalnych. Korelacje występujące pomiędzy

ekstremalnych. Korelacje występujące pomiędzy

poszczególnymi instrumentami finansowymi znikają, a

poszczególnymi instrumentami finansowymi znikają, a

zmiany, jakie występują przy zmianach cen, niedają się

zmiany, jakie występują przy zmianach cen, niedają się

wytłumaczyć przy pomocy VaR. Ta grupa metod

wytłumaczyć przy pomocy VaR. Ta grupa metod

(Stress Test) ma za cel zapobieganie upadłości

(Stress Test) ma za cel zapobieganie upadłości

finansowej.

finansowej.

Cel

Cel

Metodologia

Metodologia

Value at

Value at

Risk

Risk



Alokacja aktywów

Alokacja aktywów

pomiędzy poszczególne

pomiędzy poszczególne

departamenty, zespoły

departamenty, zespoły

Pomiar kwantyla rozkładu z

Pomiar kwantyla rozkładu z

pomocą statystyki

pomocą statystyki

matematycznej

matematycznej



Analiza zyskowności w

Analiza zyskowności w

porównaniu do

porównaniu do

poniesionego ryzyka

poniesionego ryzyka

Stress Test

Stress Test

Funkcjonowanie

Funkcjonowanie

przedsiębiorstwa:

przedsiębiorstwa:

Analiza scenariuszy w

Analiza scenariuszy w

oparciu o:

oparciu o:



Zapobieganie bankructwo

Zapobieganie bankructwo



Historyczne sytuacje

Historyczne sytuacje



Stabilizacja wyników

Stabilizacja wyników

finansowych

finansowych



Makroekonomiczne

Makroekonomiczne

analizy

analizy