Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

Teoria Sterowania

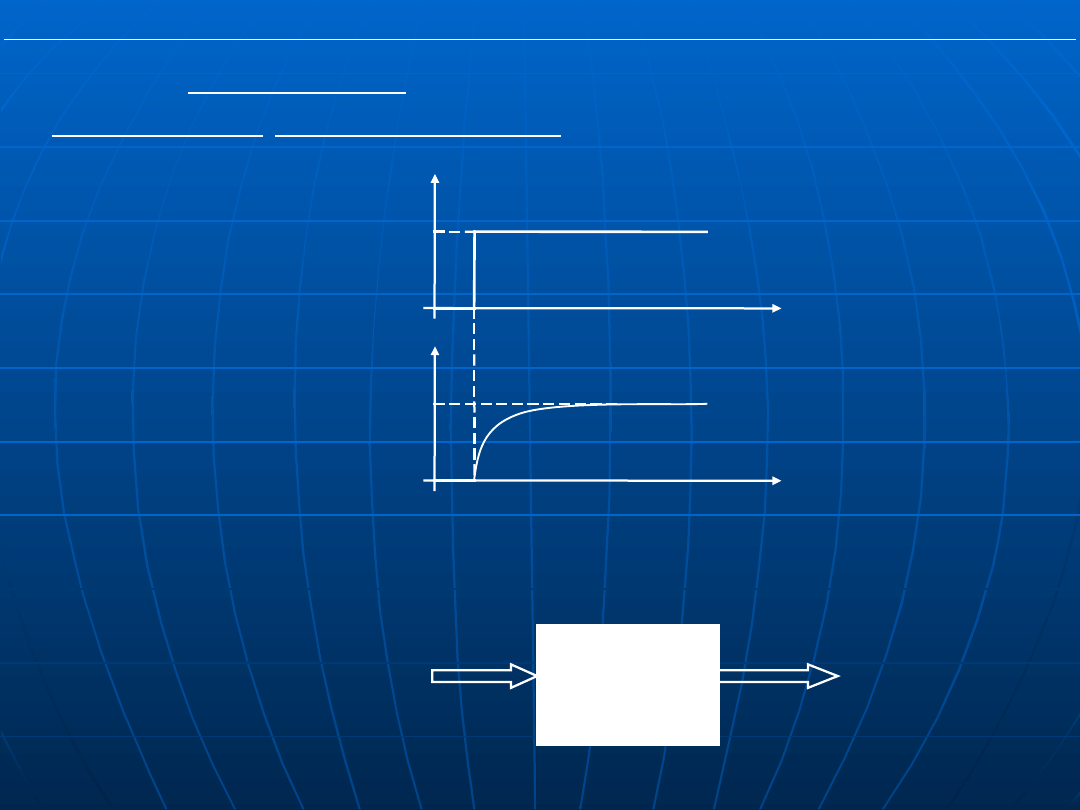
Układy dynamiczne ciągłe – opisywane zwykle
równaniami różniczkowymi. Charakteryzują się
występowaniem procesów przejściowych.

t

t

P

in

Θ

K·P

in

1) Opis za pomocą zmiennych stanu (wektora stanu)



























n

x

x

x



2

1

x

 

t

u

 

t

y

( , )

=

x f x u

&

Teoria Sterowania

Teoria Sterowania

 

 











u

x

g

y

u

x

f

x

,

,



układ n równań pierwszego rzędu

algebraiczne

równania wyjścia































p

n

n

n

p

n

p

n

u

u

u

x

x

x

f

x

u

u

u

x

x

x

f

x

u

u

u

x

x

x

f

x

,...

,

;

,...

,

,...

,

;

,...

,

,...

,

;

,...

,

2

1

2

1

2

1

2

1

2

2

2

1

2

1

1

1







































p

n

l

l

p

n

p

n

u

u

u

x

x

x

g

y

u

u

u

x

x

x

g

y

u

u

u

x

x

x

g

y

,...

,

;

,...

,

,...

,

;

,...

,

,...

,

;

,...

,

2

1

2

1

2

1

2

1

2

2

2

1

2

1

1

1



 

 

 























u

x

u

x

u

x

f

,

,

,

1

n

f

f



gdzie

Teoria Sterowania

Teoria Sterowania

Wybór zmiennych stanu dla danego układu może być różny.

Zwraca się uwagę na:

a) sens fizyczny i mierzalność zmiennych lub

b) wygodę opisu matematycznego.

Model liniowy

Du

Cx

y

Bu

Ax

x











p

l

n

l

p

n

n

n









D

C

B

A

;

;

;

Przykład: Napisać równania stanu dla























33

32

31

23

22

21

13

12

11

a

a

a

a

a

a

a

a

a

A























32

31

22

21

12

11

b

b

b

b

b

b

B





13

12

11

c

c

c



C

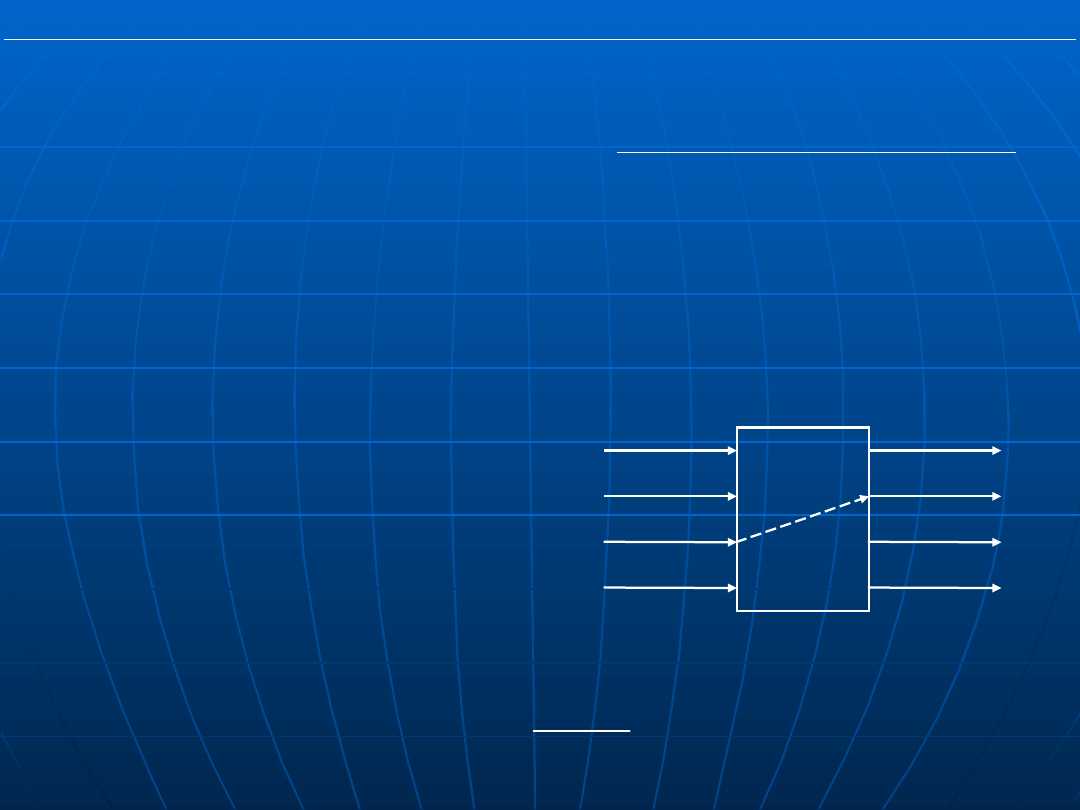
Wymiary macierzy (n nazywamy rzędem
układu):

Teoria Sterowania

Teoria Sterowania

 

t

u

 

t

y



C

D

A

B

( )

t

x

( )

t

x&

A – macierz stanu,
B – macierz wejścia,
C – macierz wyjścia,
D – macierz transmisyjna

Macierze zawierają stałe współczynniki dynamiczne
układu.

Teoria Sterowania

Teoria Sterowania

Macierz transmitancji:























)

(

)

(

)

(

)

(

)

(

1

1

11

s

G

s

G

s

G

s

G

s

lp

l

p











G

Transmitancja G

ij

(s) od j-tego wejścia do i-tego wyjścia

u

j

y

i

G

ij

(s)

( )

( )

( )

i

ij

j

Y s

G s

U s

=

Równania operatorowe dla liniowego układu wielowymiarowego
(

p wejść, l wyjść

):

1

1

( )

( )

( )

( )

( ) (

)

( )

( )

( )

( )

( )

(

)

( )

l p

s

s s

s

s

s

s

s

s

s

s

s

s

s

�

-

-

=

+

�

=

-

=

+

�

�

=

-

+

�

�

G

X

AX

BU

X

I A BU

Y

CX

DU

Y

C I A B D U

1 4 442 4 4 43

Przejście od równań stanu do

transmitancji

Teoria Sterowania

Teoria Sterowania

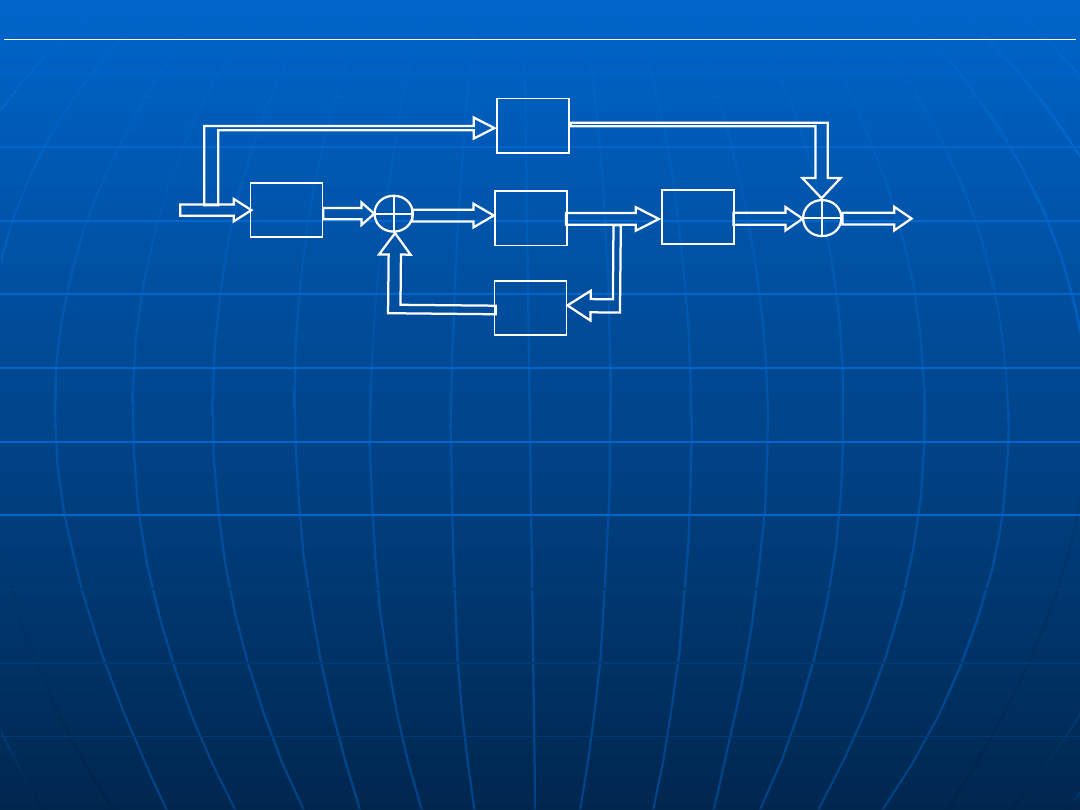
Przejście od transmitancji do równań

stanu

Jest to operacja o wyniku zależnym od wyboru zmiennych stanu.

Dzieląc licznik i mianownik transmitancji przez a

n

uzyskuje się

współczynnik =1 przy s

n

. Jeżeli w G(s) n=m, to dzieli się

wielomian licznika przez wielomian mianownika otrzymując
sumę współczynnika wzmocnienia K i transmitancji właściwej:

1

0

1

1

1

0

1

0

1

0

1

1

1

0

( )

( )

...

( )

( )

( )

- transmitancja właściwa,

( )

( )

...

( )

...

( )

( ) ...

( )

( )

( )
( )

1

( )

( )

...

w

m

m

w

n

n

n

m

m

m

m

n

n

n

n

G s

K G s

b s

bs b

Y s X s

G s

n>m

X s U s

s

a s

a s a

Y s

b s

bs b

Y s

b s X s

bsX s b X s

X s
X s

s X s

a s

U s

s

a s a

-

-

-

-

= +

+ + +

=

�

=

+

+ +

+

=

+ + + �

=

+ +

+

=

�

=-

+ +

+

1

0

( ) ...

( )

( )

( )

X s

a sX s a X s U s

- -

-

+

Teoria Sterowania

Teoria Sterowania

0

1

2

1

0

1

0

0

0

0

1

0

0

0

0

1

n

n

a

a

a

a

-

-

�

�

�

�

�

�

�

�

=

�

�

�

�

�

�

-

-

-

-

�

�

A

L

L

M

O

O

M

L

[

]

0

1

m

b b

b

=

B

L

0
0

1

��

��

��

=

��

��

��

C

M

[ ]

K

=

D

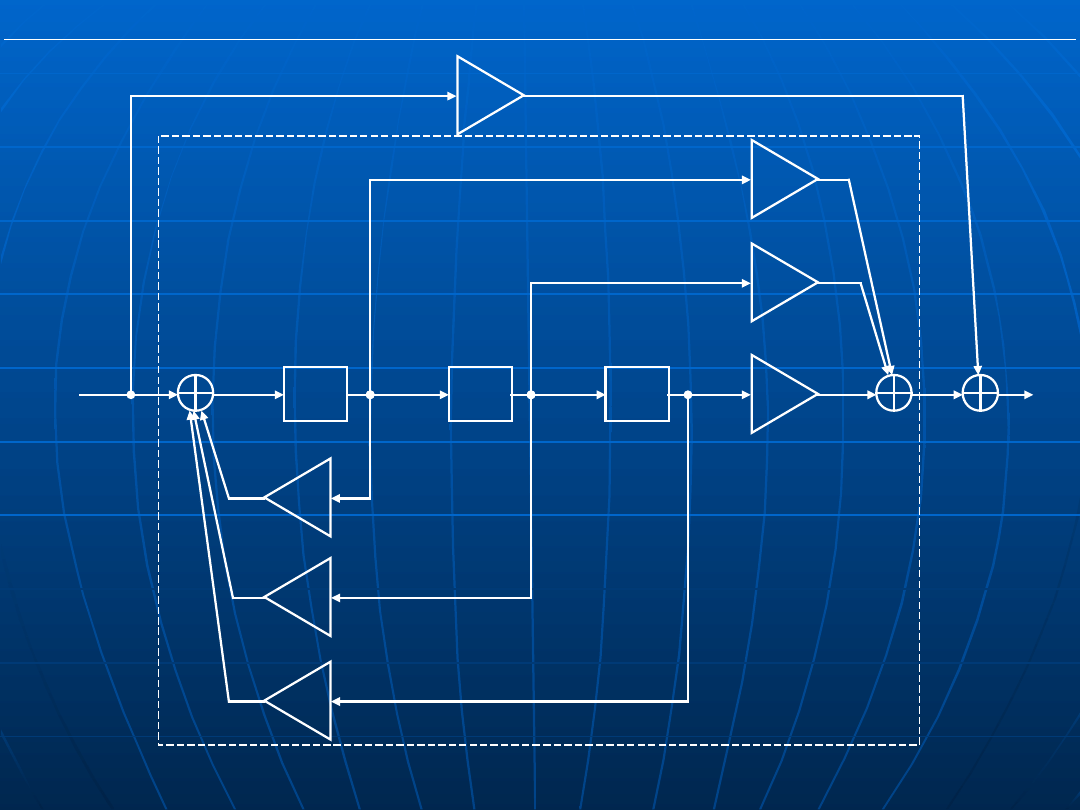
Przykład schematu dla
n=3:

2

2

1

0

3

2

2

1

0

( )

b s

bs b

G s

K

s

a s

a s a

+ +

= +

+

+

+

Teoria Sterowania

Teoria Sterowania

b

0

-

a

2







b

1

b

2

-a

1

-a

0

1

x x

=

y

2

x x

=

&

3

x x

=

&&

3

x x

=

&&& &

( )

X s

( )

sX s

2

( )

s X s

3

( )

s X s

u

( )

U s

( )

Y s

K

Teoria Sterowania

Teoria Sterowania