XIV. STEROWANIE

XIV. STEROWANIE

OPTYMALNE

OPTYMALNE

14.1. Zadania optymalizacji

14.1. Zadania optymalizacji

Sterowanie optymalne polega na szukaniu minimum lub maksimum:

- wielkości wyjściowej obiektu
lub jej funkcji

funkcji

(optymalizacja statyczna)

-

funkcjonału

funkcjonału

jako całki z funkcji (optymalizacja dynamiczna).

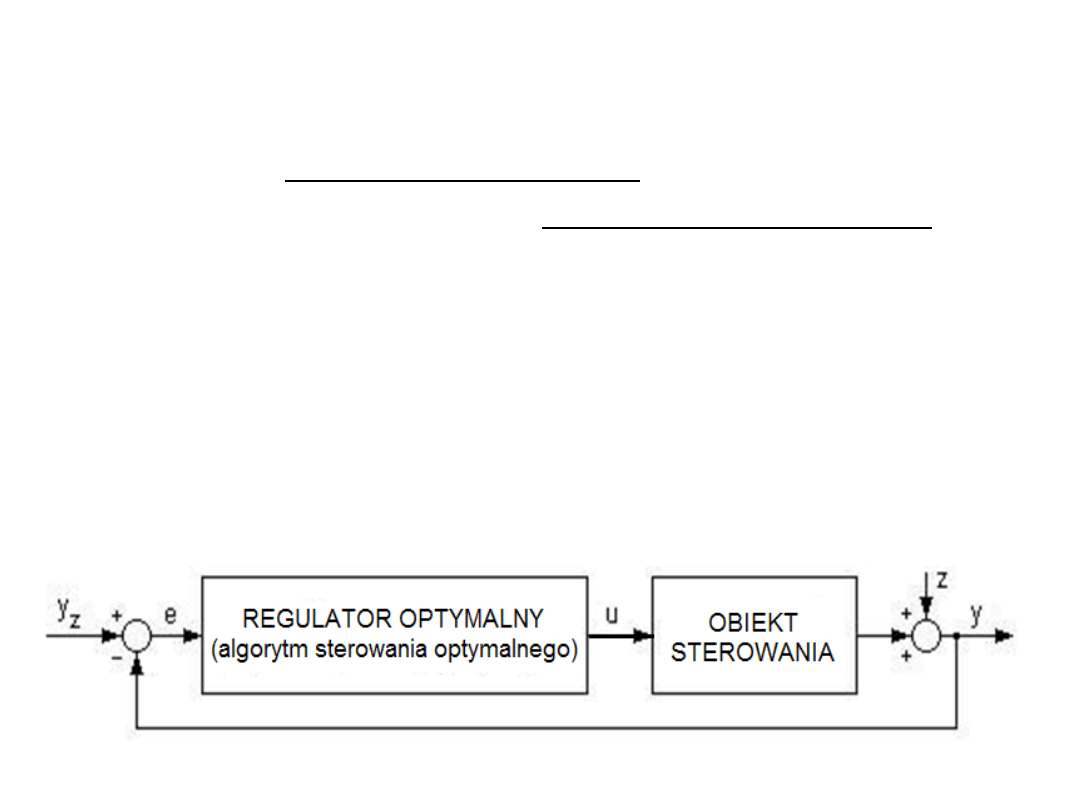
Sterowanie optymalne obiektem lub procesem technologicznym jest

realizowane w układzie zamkniętym przez regulator optymalny lub
algorytm sterowania optymalnego zapisany w pamięci
mikroprocesorowego sterownika programowalnego PLC
(Programmable Logic Controller):

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

2

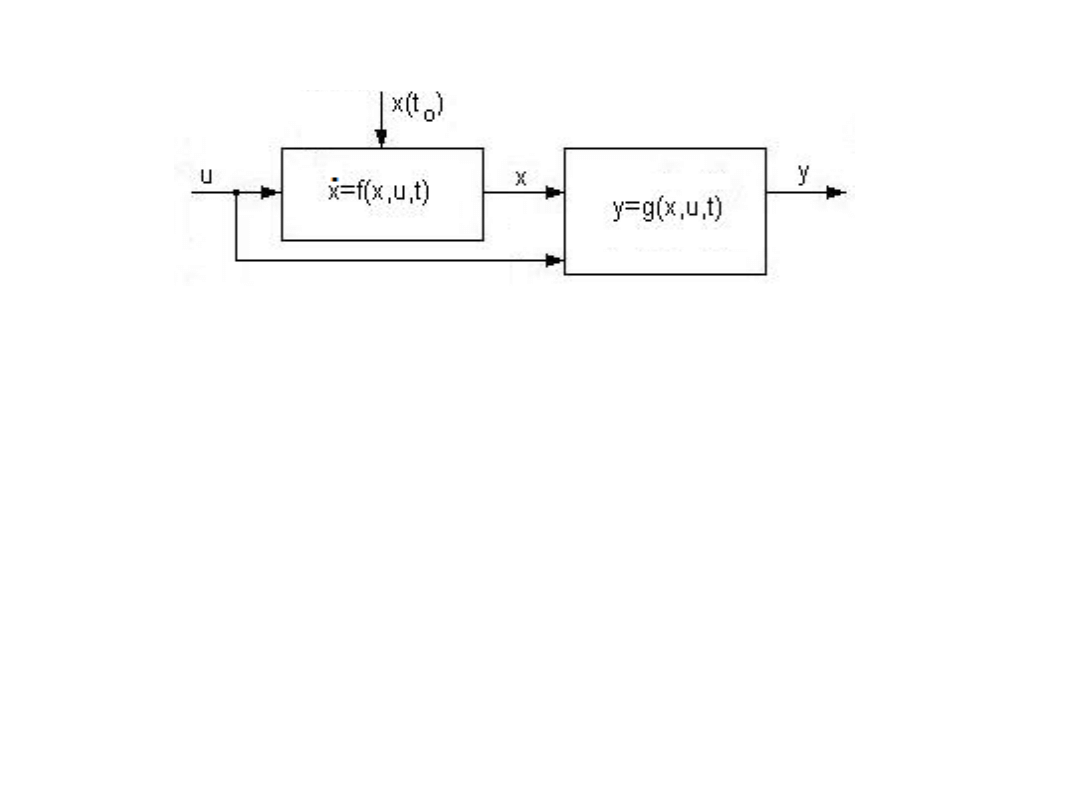
Obiekt lub proces sterowania opisany jest równaniami stanu i wyjścia:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

3

Przy syntezie regulatora optymalnego lub algorytmu sterowania

optymalnego wykorzystuje się różne metody optymalizacji.
Zadania optymalizacji dzieli się na:

•

optymalizację statyczną

optymalizację statyczną

, formułując zadanie jako

 programowanie liniowe,

 programowanie nieliniowe, np. kwadratowe,

•

optymalizację dynamiczną

optymalizację dynamiczną

, stosując

 metodę wariacyjną wykorzystującą równanie Eulera-
Lagrange’a,

 zasadę maksimum Pontriagina,

 zasadę optymalności Bellmana w postaci programowania
dynamicznego.

14.2. Optymalizacja statyczna

14.2. Optymalizacja statyczna

Sformułowanie zadania optymalizacji

statycznej

Zadanie optymalizacji statycznej można
sformułować jako znalezienie takiej optymalnej
wartości zmiennej x*, która minimalizuje lub
maksymalizuje funkcję celu sterowania jako
wskaźnika jakości sterowania optymalnego:

spełniając równocześnie układ ograniczeń:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

4

 

m

,...,

2

,

1

i

b

x

g

i

i









F = f(x) dla x = x

1

,

x

2

, ..., x

n

Rodzaje zadań optymalizacji
statycznej
Programowanie liniowe

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

5













n

1

j

j

j

n

1

x

c

x

,...,

x

f

F





0

x

m

,...,

2

,

1

i

b

x

a

x

,...,

x

g

j

i

j

n

1

j

ij

n

1

















2) F – funkcja celu sterowania nieliniowa,

g – ograniczenia liniowe:

• F jako funkcja addytywna

• F jako suma formy liniowej i kwadratowej stanowiąc

zadanie programowania kwadratowego:

 

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

6





 









 



m

1

i

n

1

j

j

i

ij

n

1

j

j

j

n

1

x

x

d

x

c

x

,...,

x

f

F

3) F – funkcja celu sterowania nieliniowa,
g – ograniczenia nieliniowe:





 

 

 

m

,...,

1

i

x

g

...

x

g

x

g

x

,...,

x

g

n

in

2

2

i

1

1

i

n

1

i









Programowanie nieliniowe

1) F – funkcja celu sterowania nieliniowa,
g – ograniczenia nieliniowe równościowe:
jako klasyczny problem optymalizacji
rozwiązywany metodą Lagrange’a

metodą Lagrange’a

.

 

i

i

b

x

g







 

 

 

n

n

2

2

1

1

n

1

x

f

...

x

f

x

f

x

,...,

x

f

F











Metody rozwiązywania zadań optymalizacji
statycznej
Metody analityczne

Klasyczne problemy optymalizacji statycznej

rozwiązywane są następującymi metodami
analitycznymi:

 Metoda Lagrange’a

Metoda Lagrange’a

optymalizacji z ograniczeniami

równościowymi

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

7





 

i

i

n

2

1

b

x

g

x

,...,

x

,

x

f

F





Funkcja Lagrange’a:

   

 



















m

1

i

i

i

i

x

g

b

x

f

,

x

L

gdzie wyrażenie pod  oznacza funkcję kary za

przekroczenie ograniczeń.

Lagrange Joseph
Louis (1736-1813)
Matematyk włoski.

Warunek konieczny optimum :

W celu wyznaczenia optymalnych wartości x

*

należy

rozwiązać (m+n) równań z n niewiadomymi x

j

oraz z m

niewiadomymi 

j

.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

8

 

 






































m

,..,

1

i

0

,

x

L

n

,..,

1

j

0

x

,

x

L

i

j

0

i





Metoda Kuhna i Tuckera

Metoda Kuhna i Tuckera

z ograniczeniami

nierównościowymi

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

9

 

 

















m

1

i

i

i

i

x

g

b

x

f

L











































0

L

0

x

L

x

0

L

0

x

L

i

i

j

j

i

j

0

x

j



0

i





j =1,..., n i
=1,..., m

Kuhn Harold William
(ur. 1925)
Amerykański matematyk.

Tucker Albert William
(1905-1995)
Amerykański matematyk.

 

i

i

b

x

g



Metody numeryczne

Metoda programowania liniowego SIMPLEX

Metoda programowania liniowego SIMPLEX

z zastosowaniem:

- do planowania produkcji (optymalne obciążenie sprzętu,

optymalny asortyment produkcji)

- do sporządzania mieszanek (stopy metali, diety, racjonalne cięcie

materiałów w stoczni lub fabryce odzieżowej, produkty
rafineryjne)

- w transporcie (optymalny plan przewozów, optymalizacja drogi

statku, optymalny manewr antykolizyjny).

 

 

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

10

 

 

m

n

mn

2

2

m

1

1

m

2

n

n

2

2

22

1

21

1

n

n

1

2

12

1

11

j

n

1

j

ij

j

j

2

2

1

1

b

x

a

...

x

a

x

a

b

x

a

...

x

a

x

a

b

x

a

...

x

a

x

a

x

a

x

g

x

c

...

x

c

x

c

x

f

F













































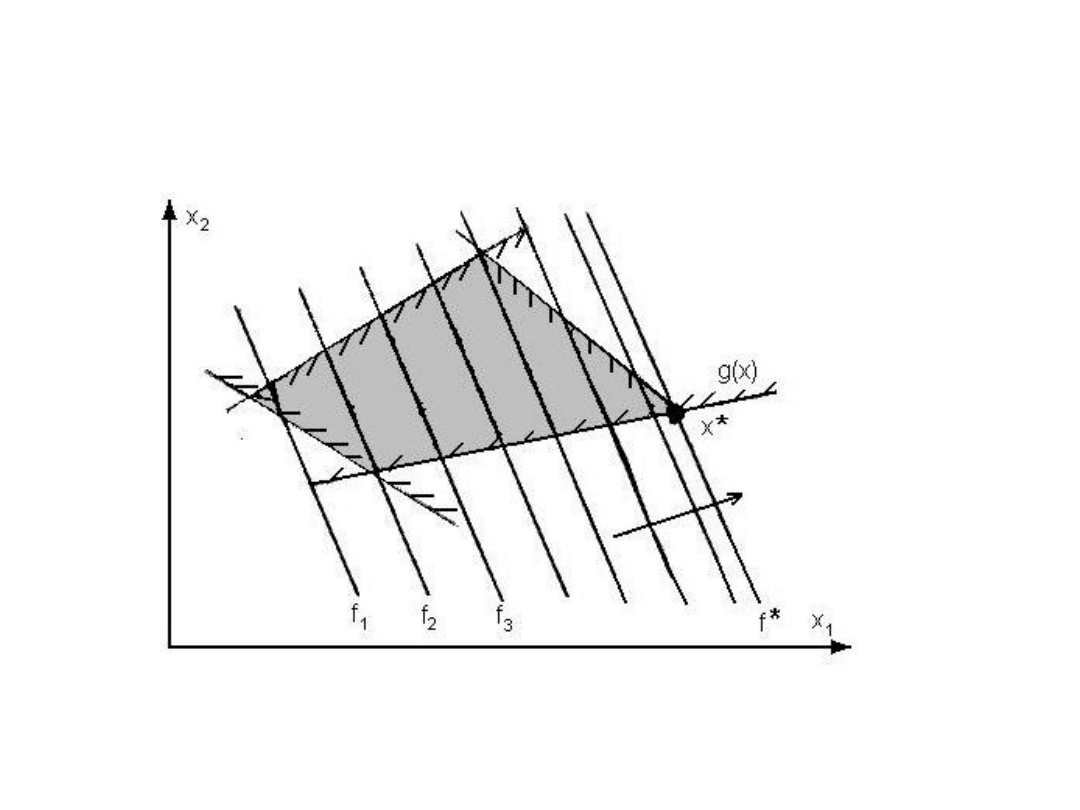
Graficzna prezentacja znajdowania optymalnego

rozwiązania metodą programowania liniowego:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

11

Metoda programowania kwadratowego

Metoda programowania kwadratowego

Wolfe’a

Metody bezgradientowe

Metody bezgradientowe

minimalizacji funkcji wielu

zmiennych bez ograniczeń: Rosenbrocka, Neldera i

Meada, Powella

Metody gradientowe

Metody gradientowe

minimalizacji funkcji wielu

zmiennych bez ograniczeń: największego spadku,

gradientu sprzężonego, Davidona

Metody funkcji kary

Metody funkcji kary

poszukiwania ekstremum funkcji celu

sterowania z ograniczeniami nierównościowymi przez

wprowadzenie: Rosenbrocka, Carolla, Powella.

 

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

12

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

13

W sytuacjach mijania się własnego statku ze spotkanym

obiektem istnieje nieskończenie wiele możliwych
manewrów zmianą kursu lub/i zmianą prędkości, z których
wybiera się rozwiązanie spełniające warunki optymalności.

Każdemu manewrowi przyporządkowuje się koszt uniknięcia

kolizji i wykorzystuje się sterowanie optymalne
minimalizujące ten koszt.

Można rozważać następujące kryteria optymalnego

manewru:

- straty drogi na wymijanie spotkanych statków

- odchylenie od zadanej trasy rejsu

- zużycie paliwa.

Przykład

Przykład

Wyznaczanie optymalnego manewru antykolizyjnego

Wyznaczanie optymalnego manewru antykolizyjnego

statkiem metodą programowania liniowego

statkiem metodą programowania liniowego

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

14

Ponadto przy wyborze sterowania należy uwzględnić
przepisy MPDM (Międzynarodowe Prawo Drogi
Morskiej) oraz nawodne i podwodne ograniczenia
nawigacyjne.
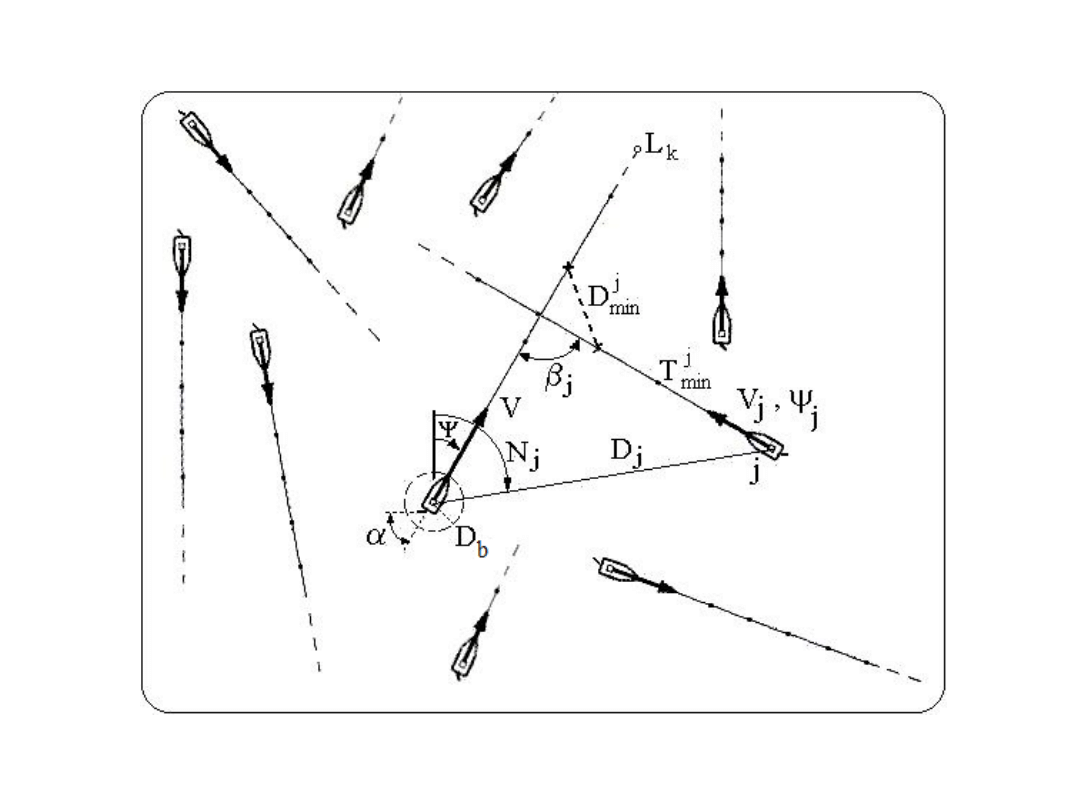
Charakter zapobiegania kolizjom statków wymaga
spełnienia podstawowego warunku:

b

j

min

D

D



j

min

D

-

najmniejsza odległość zbliżenia z j-tym

spotkanym statkiem, oceniona przez
radarowy system antykolizyjny ARPA

- bezpieczna odległość mijania w danych
warunkach widzialności na morzu, określana
przez nawigatora

b

D

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

15

Zakładając ruch prostoliniowy i jednostajny
statków, zadanie wyznaczenia optymalnego
manewru bezpiecznego w stosunku do
wszystkich j-tych spotkanych statków można
sprowadzić do obliczenia optymalnych wartości
kursu 

*

i prędkości V

*

własnego statku ze

statycznego zbioru ich dopuszczalnych wartości
w układzie współrzędnych (x

1

, x

2

).

Uwzględnienie dynamiki własnego statku
możliwe jest poprzez obliczenie i realizację
manewru z czasem wyprzedzenia t

w

.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

16

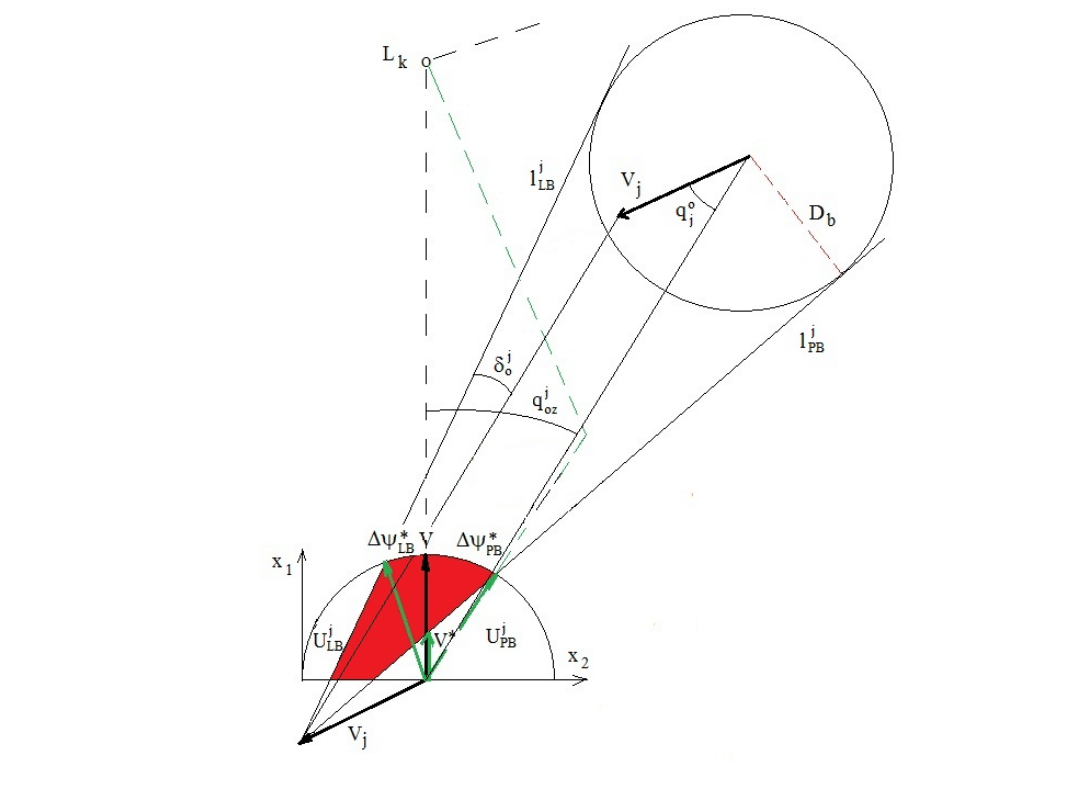
Obszar zabronionych manewrów
w stosunku
do jednego spotkanego obiektu

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

17

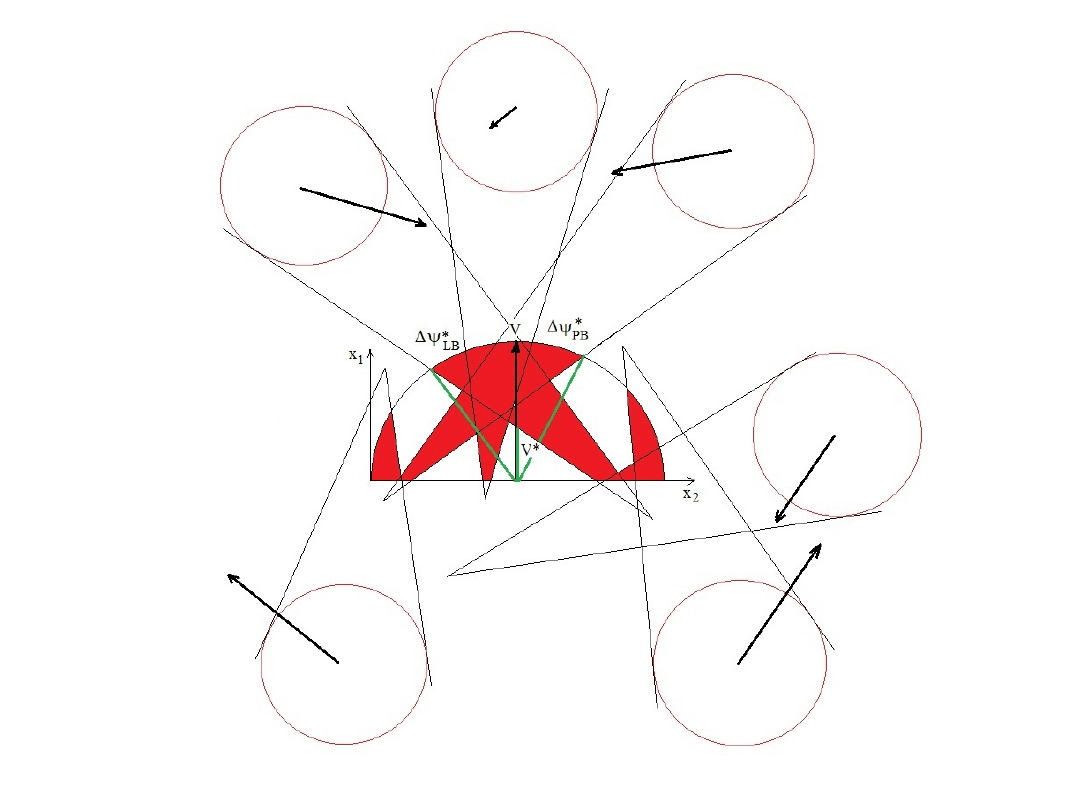
Obszar zabronionych
manewrów w
stosunku
do sześciu
spotkanych statków

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

18

Uwzględnienie reguł MPDM możliwe jest poprzez

odpowiedni wybór manewru ze zbioru:

Przedstawienie reguł MPDM w postaci odpowiednich

diagramów manewrowych opracowanych przez A.G.

Corbet, S.H. Hollingdale, E.S. Calvert i K.D. Jones

umożliwia sformułowanie pewnej funkcji logicznej Z

j

jako semantycznej interpretacji reguł MPDM.
Każdy rodzaj sytuacji zbliżenia statków jest opisany

zmiennymi logicznymi: A, B, C, D, E przyjmującymi

wartość 0 lub 1.

j

PB

j

LB

j

o

U

U

U





prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

19

A – spotkanie statku z dziobu lub z innego kierunku
B – zbliżanie się lub oddalanie spotkanego statku

C – mijanie się ze spotkanym statkiem z dziobu lub rufy
D – zbliżanie się spotkanego statku z dziobu lub z rufy
E – zbliżanie się spotkanego statku z PB lub LB
Zastosowanie tablicy Karnaugh’a prowadzi do minimalizacji funkcji

logicznej Z

j

do postaci:

Wartość funkcji Z

j

określa dla każdego spotkanego statku wybór

manewru na PB lub LB zależnie od reguł MPDM.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

20

Do wyznaczenia optymalnego manewru własnego statku w łącznym do wszystkich j
spotkanych statków dopuszczalnym obszarze sterowań:

można wykorzystać zasadę programowania liniowego, dającą się sformułować
następująco:
należy wyznaczyć składowe odpowiadające
i zapewniające maksymalny rzut wektora prędkości własnego statku na zadany kurs:

przy ograniczeniach:





*
2

*

1

x

,

x





*

V

*,



0

x

,

0

x

2

1





m

...,

,

2

,

1

i

,

b

x

a

x

a

i

2

2

i

1

1

i







max x

1



m

1

j

j

o

o

m

...,

,

2

,

1

j

U

U







prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

21

Pierwsze 7 ograniczeń wynika z liniowej aproksymacji

okręgu o promieniu V z dokładnością 1%, następne pary

ograniczeń przyporządkowane są liniom stycznym

do okręgu o promieniu D

b

odpowiednio z LB i PB.

Przy czym wartości współczynników ograniczeń wynoszą

dla
j-tego obiektu:

gdzie: Z

j

= -1 dla podzbioru U

LB

Z

j

= +1 dla podzbioru U

PB

j

PB

j

LB

l

i

l





j

o

j

j

oz

j

1

,i

7

Z

q

cos

Z

a















j

o

j

j

oz

j

2

,

i

7

Z

q

sin

Z

a





















j

o

j

j

oz

j

o

j

o

j

j

i

7

Z

q

cos

V

Z

q

sin

Z

b

















prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

22

Wartości kątów są jednoznaczną funkcją
parametrów ruchu j-tego spotkanego statku:
-prędkości V

j

-kursu 

j

-namiaru N

j

-odległości D

j

otrzymywanych z radarowego systemu antykolizyjnego
ARPA podczas automatycznego śledzenia

ech statków na

ekranie radaru.

j

o

o

j

j

oz

,

q

,

q



prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

23

Algorytm wyznaczania optymalnego bezpiecznego
manewru statkiem zawiera:
- biblioteczną procedurę programowania liniowego w
Optimization Toolbox MATLAB/SIMULINK
- procedurę reguł MPDM wyznaczającą wartość funkcji
logicznej Z

j

procedurę szeregowania spotkanych obiektów

według wartości ryzyka kolizji.

Rezultatem obliczeń są wartości:

-optymalnej prędkości V

*

i optymalnego kursu 

*

własnego

statku, zapewniających mijanie spotkanych statków w
bezpiecznej odległości D

b

-najmniejszych odległości mijania i czasu po
manewrze optymalnym w stosunku do każdego
śledzonego
j-tego spotkanego statku.

j

min

D

j

min

T

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

24

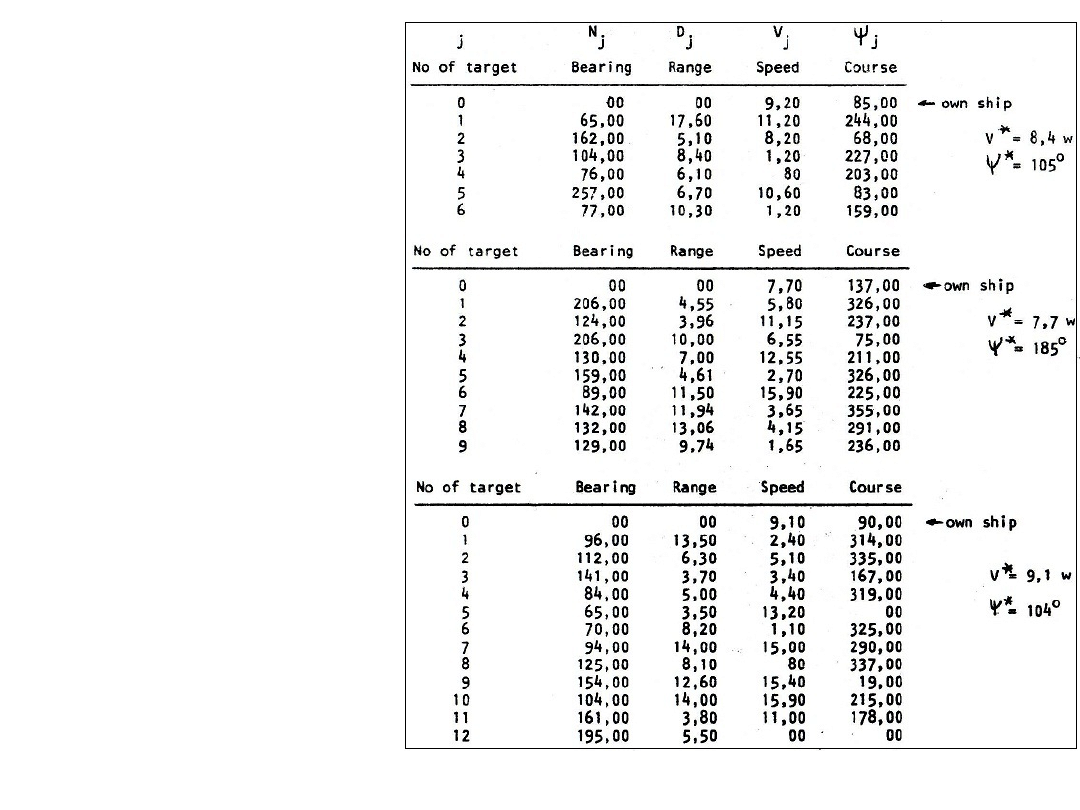
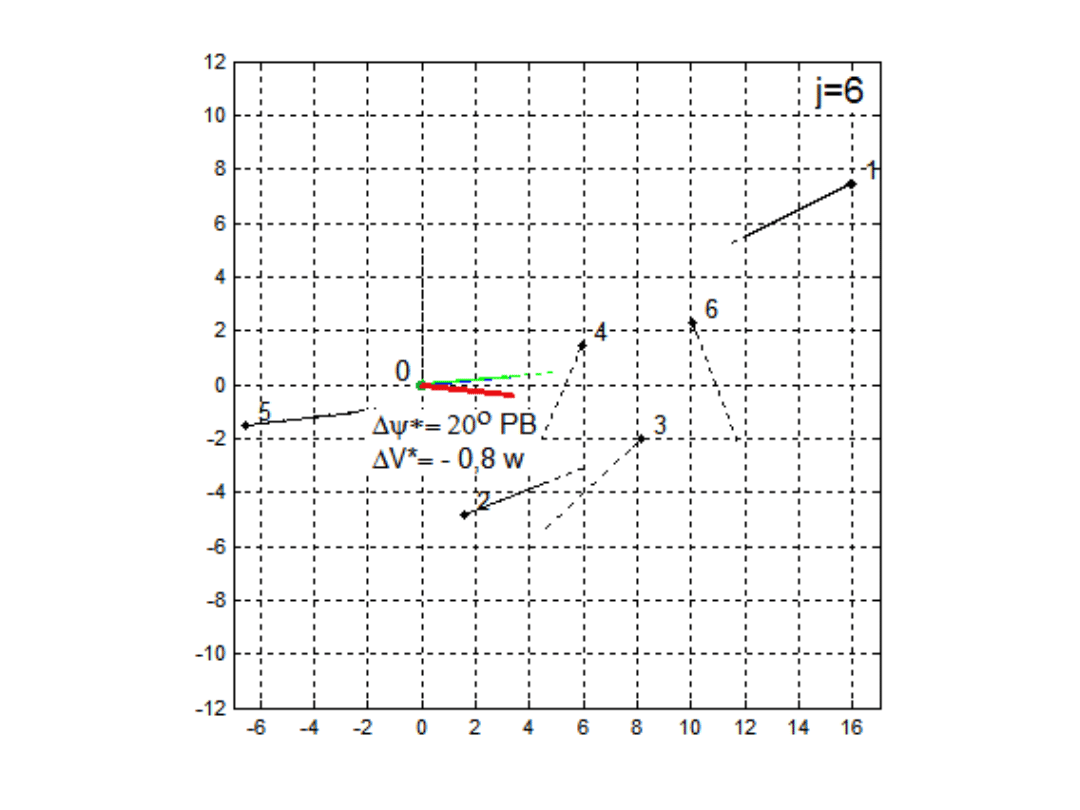
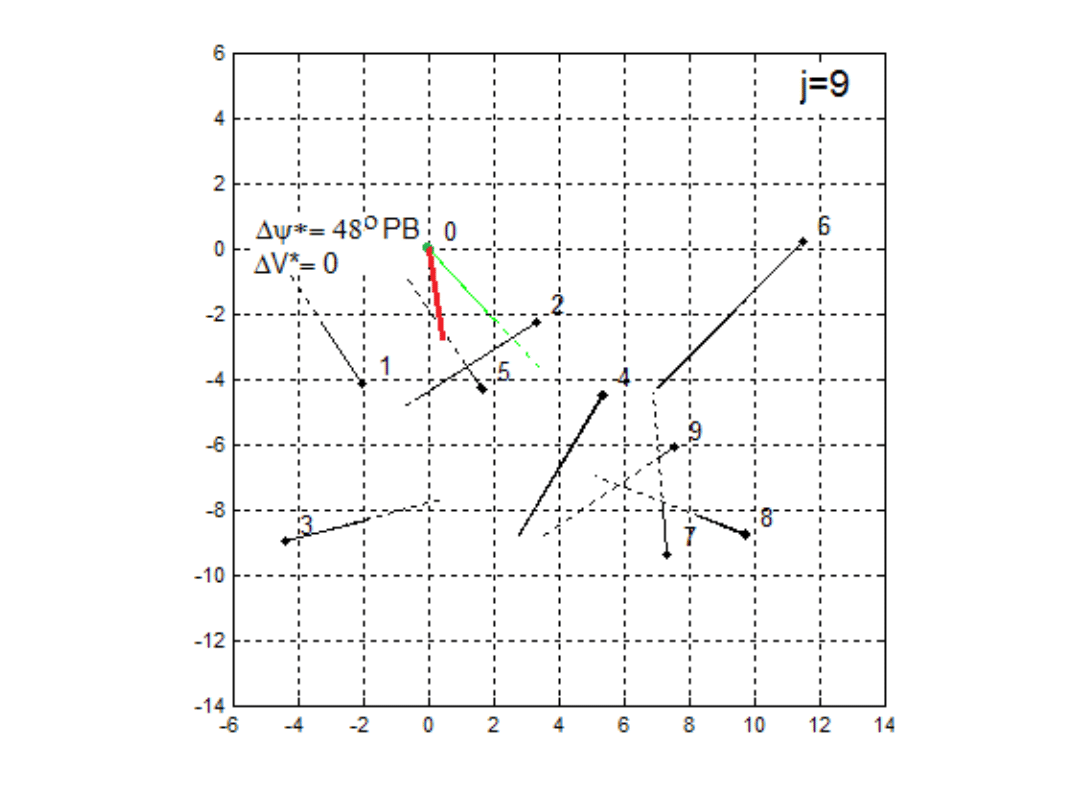
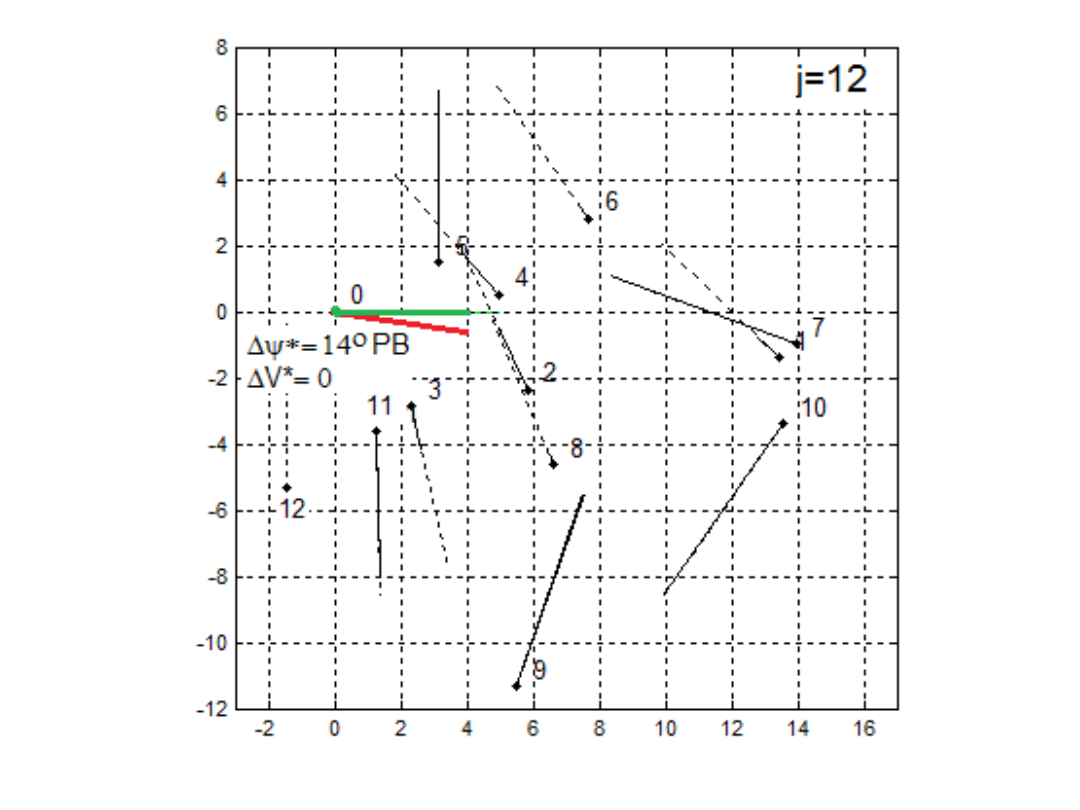
Wyniki obliczeń

optymalnego manewru
bezpiecznego

własnego statku
w sytuacjach
mijania się z:
j=6, j=9, j=12
spotkanymi statkami

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

25

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

26

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

27

14.3. Optymalizacja

14.3. Optymalizacja

dynamiczna

dynamiczna

Metoda wariacyjna

Dane jest równanie stanu:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

28





t

,

u

,

x

f

x 



oraz wskaźnik jakości
sterowania:









k

o

t

t

o

dt

t

,

u

,

x

f

I

przy: x(t

o

) = x

o

, x(t

k

)

= x

k

Rozróżnia się zadania z określonym stanem końcowym
oraz ze swobodnym stanem końcowym.

Warunek konieczny istnienia ekstremum wskaźnika
jakości dany jest w postaci równania

Eulera-Lagrange’a

:

0

u

f

u

f

dt

d

u

f

x

f

u

f

u

f

x

f

o

o

o



































przy warunku końcowym:

0

u

f

u

f

k

t

t

o













Euler Leonhard
(1707-1783)
Matematyk i
fizyk
szwajcarski.

Jeżeli:

to równanie Eulera-Lagrange’a przyjmie postać:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

29









k

o

t

t

o

dt

t

,

x

,

x

f

I



0

f

dt

d

f

'

ox

'

ox





przy warunku

0

f

k

t

t

'

ox





Jeżeli punkt końcowy leży na krzywej x = g(t) to warunek
końcowy nazywa się warunkiem transwersalności i
wyrażony jest przez zależność:

 

   





k

t

t

'

x

o

k

o

f

t

g

t

x

t

f













Zasada maksimum
Pontriagina

 

Wprowadza się pomocniczą
funkcję H zwaną hamiltonianem:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

30













t

,

u

,

x

f

t

,

u

,

x

f

t

,

,

u

,

x

H

n

1

i

i

i

o

 











gdzie: - zmienna sprzężona

i



Hamiltonian rozszerzony:





 

t

S

t

,

x

H

u

,

x

,

H

~

t

t



















Zmienne sprzężone stanowią
rozwiązanie równań
różniczkowych:





























H

dt

dx

x

H

dt

d

Pontriagin Lew
(1908-1988)
Matematyk

rosyjski.

W wieku 14 lat w
wyniku wypadku
stracił wzrok.

Według zasady maksimum sterowanie optymalne u*(t)
minimalizujące wskaźnik jakości sterowania:

maksymalizuje hamiltonian:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

31





dt

t

,

u

,

x

f

I

o

o















t

,

u

,

,

x

H

max

t

,

u

,

,

x

H

u









0

H

~

max

u



Zaletą

Zaletą metody jest łatwość zastosowania zasady
maksimum do optymalizacji procesów opisywanych dużą
liczbą zmiennych stanu, zaś

wadą

wadą złożoność obliczeń

przy uwzględnianiu ograniczeń stanu procesu.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

32

Przykład

Przykład

Wyznaczanie bezpiecznej trajektorii statku z

Wyznaczanie bezpiecznej trajektorii statku z

zastosowaniem zasady maksimum

zastosowaniem zasady maksimum

Według danych Lloyd’a ilość utraconego tonażu

spowodowanego kolizjami statków, w odniesieniu do
wszystkich strat poniesionych w wyniku zatonięcia,
pożaru, zaginięcia czy rozbicia, wynosi w
poszczególnych latach od kilku do kilkunastu procent.

Zakłada się, że około połowę tych strat można uniknąć

stosując lepsze metody komputerowo wspomaganego
bezpiecznego sterowania ruchem statku, szczególnie
spośród metod teorii sterowania automatycznego –
optymalizacji statycznej i dynamicznej z
ograniczeniami stanu oraz metod sztucznej inteligencji.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

33

Problem poszukiwania efektywnych metod zapobiegania

kolizjom statków nabrał szczególnego znaczenia wraz ze

zwiększeniem wielkości, prędkości i liczby statków

uczestniczących w przewozach morskich.

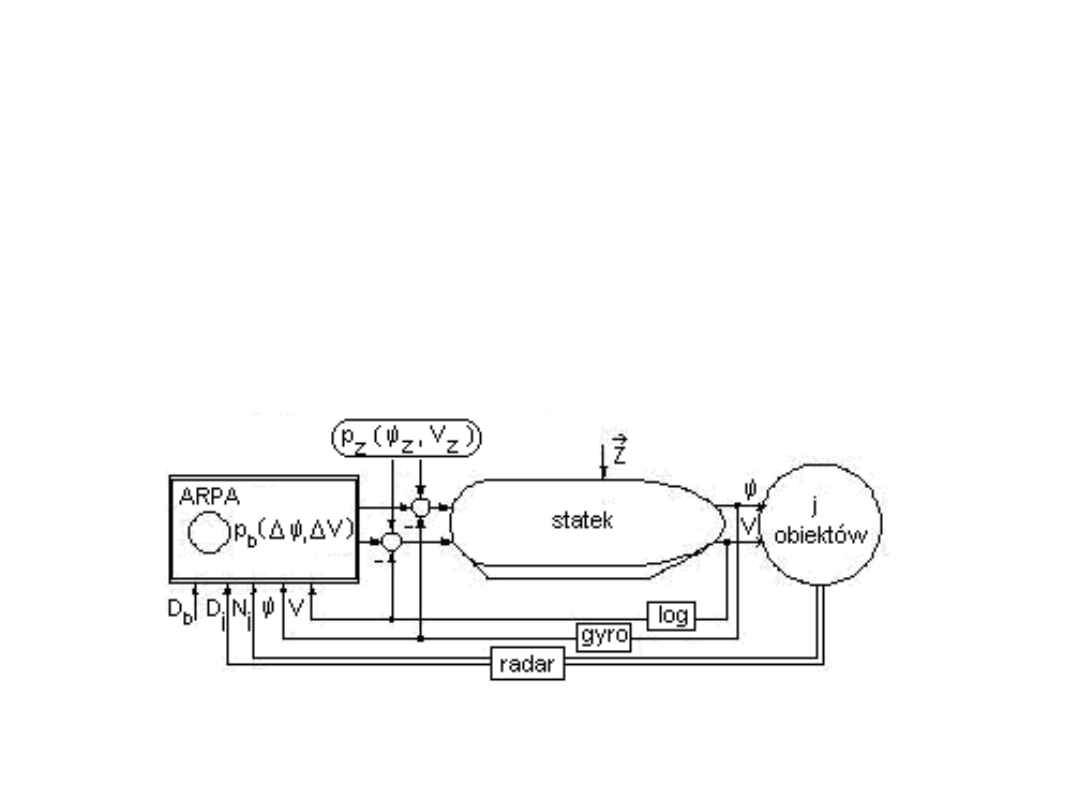
Niewątpliwy wkład do zwiększenia bezpieczeństwa żeglugi

wniosło najpierw zastosowanie radaru, a później

mikrokomputerowego systemu antykolizyjnego ARPA

(Automatic Radar Plotting Aids),

Rys. 1.Struktura systemu bezpiecznego sterowania
statkiem

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

34

System ARPA umożliwia automatyczne śledzenie 20

spotkanych „j” obiektów, wyznaczenie ich parametrów
ruchu (prędkości V

j

, kursu ψ

j

, odległości D

j

, namiaru N

j

) i

elementów zbliżenia

(odległości , czasu ) oraz ocenę ryzyka kolizji r

j

.

Jednak zakres funkcji standardowego systemu ARPA kończy

się na symulacji wybranego przez nawigatora manewru
zmiany kursu Δψ lub prędkości ∆V w stosunku do ich
zadanych wartości 

z

i V

z

aby zachować bezpieczną

odległość mijania D

b

.

Problem wyboru tego manewru jest bardzo trudny ze

względu na dużą złożoność procesu sterowania,
mającego własności: dynamiczne, nieliniowe,
wielowymiarowe, niestacjonarne i rozgrywające.

j

min

D

j

min

T

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

35

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

36

W praktyce metody wyboru manewru przyjmują postać
odpowiednich algorytmów sterowania,
zaprogramowanych w pamięci sterownika
mikroprocesorowego, tworzącego opcję systemu
antykolizyjnego ARPA lub symulatora szkoleniowego w
laboratorium uczelni morskiej.
Uwzględnienie kinematyki i dynamiki statku prowadzi do
równań stanu procesu sterowania jego ruchem:



max

u







gdzie: x

1

, x

2

– współrzędne położenia statku, x

3

=  – kurs statku,

x

4

= - prędkość kątowa zwrotu statku, x

5

= t – czas, -

względne

wychylenie steru

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

37

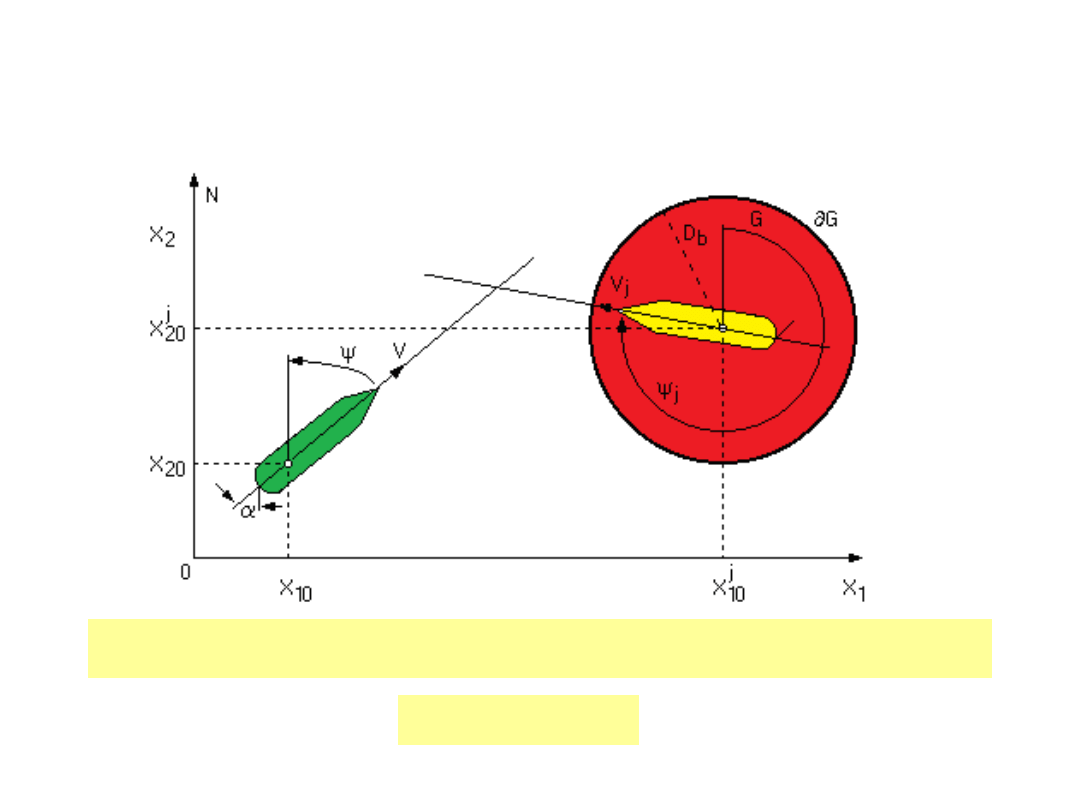
Ograniczenia stanu i sterowania

Ograniczenia stanu i sterowania

Ograniczenia stanu wynikające z konieczności zachowania

bezpiecznej odległości mijania D

b

postać koła:

 



 



0

x

cos

x

V

x

x

sin

x

V

x

D

x

g

2

j

20

j

5

j

2

2

j

10

j

5

j

1

2

b























 

0

1

u

u

g

2









prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

38

Wska

Wska

ź

ź

nik jakości sterowania

nik jakości sterowania

Oprócz kryterium bezpieczeństwa istotne jest kryterium

ekonomiczne związane z najmniejszymi stratami drogi
na bezpieczne wymijanie spotkanych statków, które
można sprowadzić do problemu sterowania
czasooptymalnego:









k

o

k

o

t

t

t

t

o

dt

dt

f

I

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

39

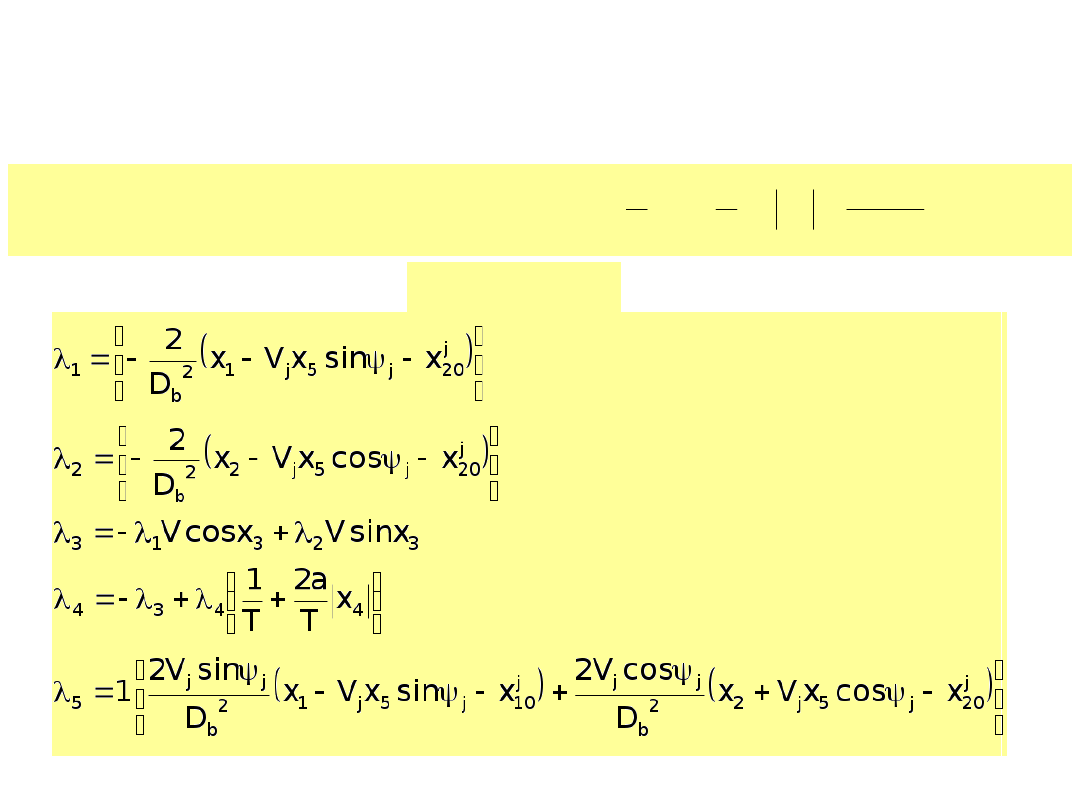
Hamiltonian i równania sprzężone

Hamiltonian i równania sprzężone

dla zasady maksimum z funkcją kary

dla zasady maksimum z funkcją kary

gdzie:
f

o

– funkcja celu sterowania

L – funkcja kary

x

g

l

x

f

x

f

o

o





























































g

0

g

g

l

2

Jeżeli  dąży do zera to wyznaczone sterowanie zbliża się do

optymalnego z uwzględnieniem ograniczeń.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

40

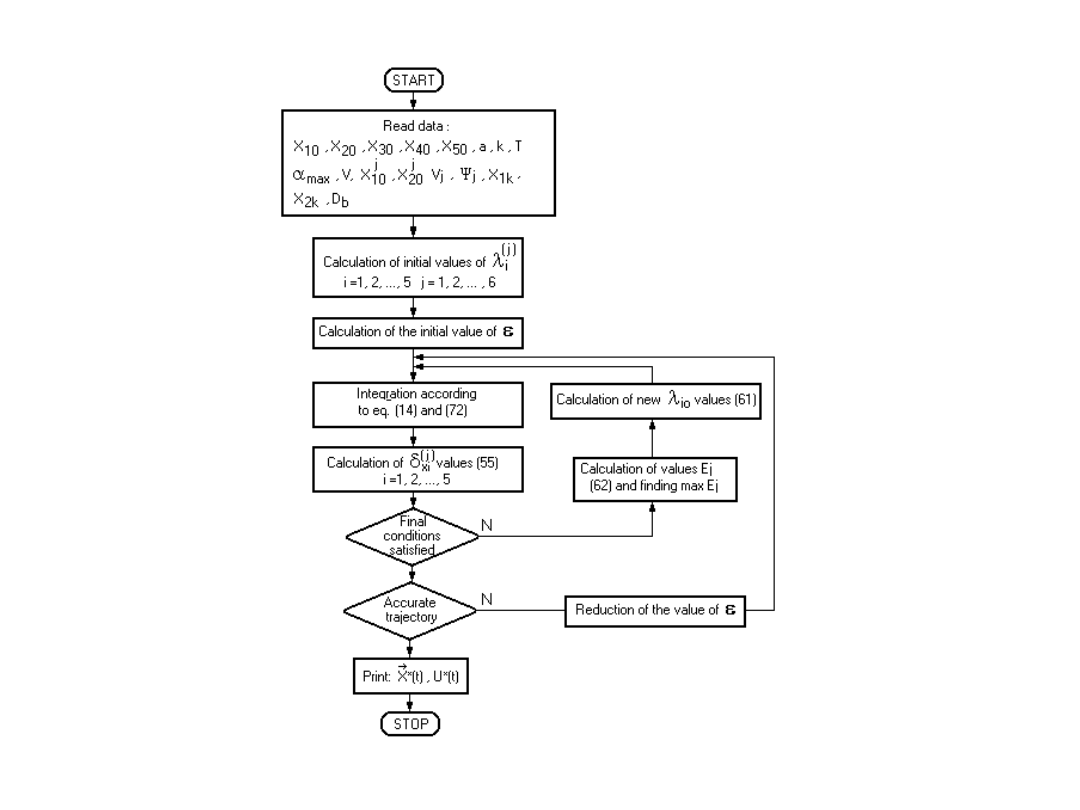
Hamiltonian i równania sprzężone

Hamiltonian i równania sprzężone

Sterowanie optymalne wynika z warunku maksimum
hamiltonianu:

 

4

sign

t

u







L

u

T

k

x

x

T

a

x

T

1

x

x

cos

V

x

sin

V

H

5

max

4

4

4

4

4

3

3

2

3

1

o















































prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

41

Algorytm wyznaczania trajektorii

Algorytm wyznaczania trajektorii

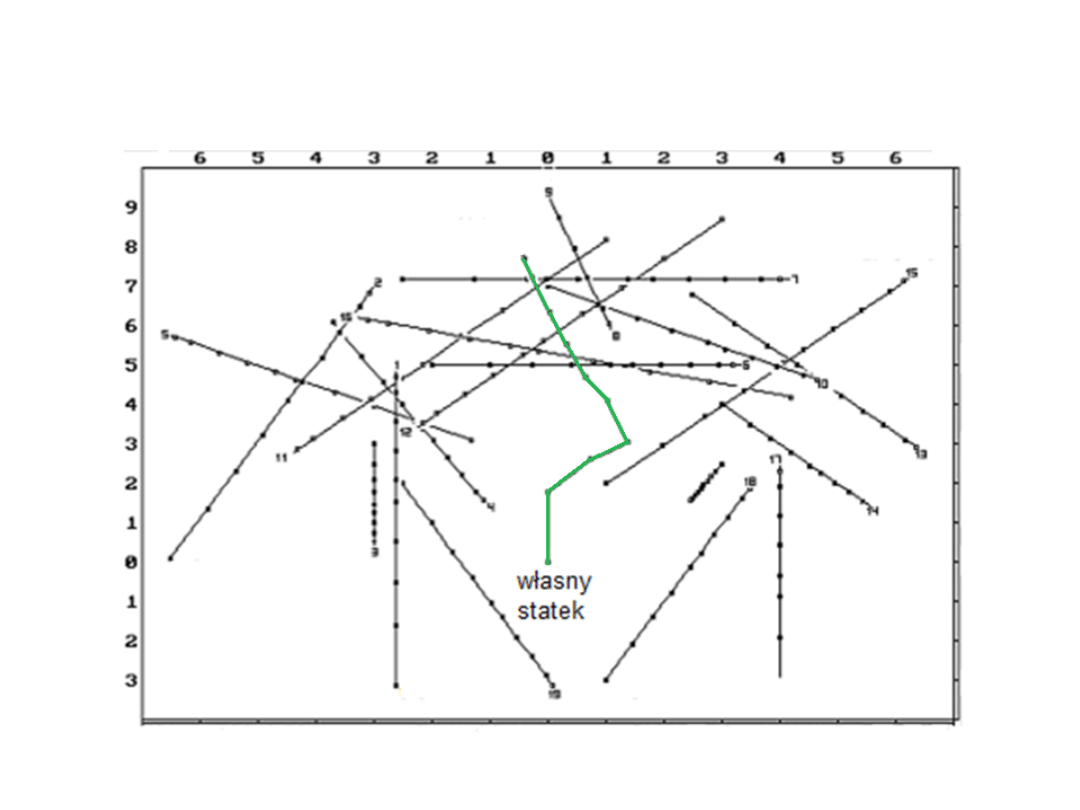
prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

42

Trajektoria bezpieczna i optymalna własnego statku

w sytuacji mijania się z 20 spotkanymi statkami u ujścia

Tamizy

Zasada optymalności

Zasada optymalności

Bellmana

Bellmana

 

Sterowanie optymalne od danej chwili t do chwili

końcowej t

k

zależy tylko od aktualnego stanu procesu,

a nie zależy od poprzednich stanów.

Dla równania stanu procesu:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

43





t

,

u

,

x

f

x 



oraz wskaźnika jakości sterowania:





dt

t

,

u

,

x

f

I

o

o







który

ma

przyjąć

wartość

optymalną:





 

t

,

x

S

dt

t

,

u

,

x

f

min

I

min

o

o









Richard
Ernest
Bellman

(1920-1984)

Matematyk
amerykański.

Równanie funkcyjne Bellmana, opisujące zasadę optymalności,
przyjmie następującą postać analityczną:

Rozwiązanie dyskretne zasady optymalności jako

programowanie dynamiczne ma postać:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

44



 



0

x

S

t

,

u

,

x

f

t

,

u

,

x

f

min

t

S

o

u

























przy równaniu stanu procesu w postaci dyskretnej





   





k

,

k

u

,

k

x

f

1

k

x





Programowanie dynamiczne w odróżnieniu od rachunku

wariacyjnego pozwala znaleźć optymalne sterowanie jako funkcję

współrzędnych stanu procesu tj. rozwiązać problem syntezy

zamkniętego układu sterowania ze sprzężeniem zwrotnym.

Zaletą

Zaletą

metody jest łatwość uwzględniania ograniczeń stanu procesu.

Wadą

Wadą metody jest ograniczona możliwość zastosowania do większej

liczby zmiennych stanu konkretnego procesu sterowania.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

45

Uwzględnienie kinematyki i dynamiki statku prowadzi do równań

stanu procesu sterowania jego ruchem, które w postaci
dyskretnej przyjmują postać:

(1)

gdzie: x

1

= x, x

2

= y, x

3

=, x

4

= , x

5

=V, x

6

= , x

7

= t, u

1

=

m

, u

2

= n/n

m



V

Przykład

Przykład

Wyznaczanie bezpiecznej trajektorii statku z

Wyznaczanie bezpiecznej trajektorii statku z

zastosowaniem

zastosowaniem

programowania dynamicznego z

programowania dynamicznego z

neuronowymi ograniczeniami stanu procesu

neuronowymi ograniczeniami stanu procesu

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

46

Występujące ograniczenia wynikają z konieczności

uwzględnienia fizycznych ograniczeń wielkości
charakteryzujących proces:

uwzględnienia rzeczywistych ograniczeń nawigacyjnych:

oraz zapewnienia bezpiecznego mijania się z „j”
spotkanym
obiektem z jednoczesnym uwzględnieniem zaleceń
przepisów prawa drogi morskiej:

(4)

(3)

(5)

(2)

1

u

0

,

1

u

2

1







max

6

max

5

max

4

V

x

0

,

V

x

0

,

x

0























0

x

,

x

g

2

1

n







0

x

,

x

,

x

g

7

2

1

j



prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

47

Zależność g

j

określa obszar zagrożenia kolizyjnego tzw. domenę

statku (z ang. ship’s domain), przyjmując postać koła, paraboli,
elipsy lub sześciokąta.

Domeny statków mają zmienny kształt zależny od względnej

prędkości spotkanego obiektu oraz ryzyka kolizji i są

generowane przez sztuczną sieć neuronową wykorzystując

Neural Network Toolbox MATLAB.

W praktyce stan procesu jest kontrolowany na bieżąco przez

urządzenia systemu antykolizyjnego ARPA (radar, żyrokompas,

log, mierniki prędkości kątowej i obrotowej).

Warunki początkowe procesu wyznacza rozmaitość Θ ํ, określona

w trakcie inicjacji automatycznego śledzenia przez system ARPA

ruchu spotkanych obiektów:

(6)

(7)

0

x

,

0

x

,

V

x

,

0

x

,

x

,

y

x

,

x

x

o

7

o

6

o

o

5

o

4

o

o

3

o

o

2

o

o

1

















prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

48

Ze względu na warunki końcowe wyróżnia się dwa
rodzaje zadań sterowania:
- z ustalonym punktem końcowym trajektorii w sytuacji

kierowania ruchem statku na wodach ograniczonych

-

z ustalonym kursem końcowym na wodach otwartych

Dodatkowo uwzględnia się kryterium optymalności w
postaci najmniejszych strat drogi na bezpieczne
wymijanie obiektów, które przy stałej prędkości statku
prowadzi do sterowania czasooptymalnego:

(10

)

(11

)

(12

)





k

k

oK

oK

y

,

x

L

L 

o

K

5

K

6

K

4

o

K

3

V

x

,

0

x

x

,

x



















k

0

k

0

t

t

t

t

dt

V

Vdt

I

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

49

Algorytm OPTDYN

Algorytm OPTDYN

wyznaczania bezpiecznej trajektorii statku

w sytuacji kolizyjnej metodą

programowania dynamicznego

z neuronowymi ograniczeniami stanu

procesu

Zasada optymalności Bellmana określa podstawową

własność strategii optymalnej – niezależnie od stanu i
decyzji początkowych pozostałe decyzje muszą tworzyć
strategie optymalne z punktu widzenia stanu wynikłego z
pierwszej decyzji.

Można wykazać, że proces zapobiegania zderzeniom

statków spełnia warunki dualności, dlatego trajektorię
optymalną statku w sytuacji kolizyjnej wyznacza się
rozpoczynając obliczenia od pierwszego etapu, a
następnie przesuwając się ku ostatniemu.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

50

Optymalny czas przepłynięcia przez statek k etapów
wyniesie:

(13

)

Optymalny czas przejścia k etapów jest funkcją
stanu układu na końcu (k–1) etapu oraz
sterowania na (k–2) etapie.
Przechodząc od pierwszego do ostatniego etapu
wzór określa równanie funkcyjne Bellmana dla
procesu sterowania statkiem poprzez zmianę
kąta wychylenia steru oraz prędkości obrotowej
śruby.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

51

Ograniczenia zmiennych stanu oraz wielkości
sterujących tworzą w algorytmie wyznaczania
dynamicznej bezpiecznej trajektorii statku
oddzielną procedurę obliczeniową.
Uwzględnienie ograniczeń wynikających z
zachowania bezpiecznej odległości zbliżenia oraz
zaleceń prawa drogi polega na sprawdzeniu, czy
zmienne stanu nie przekroczyły ograniczeń w
każdym rozważanym węźle i odrzuceniu węzłów,
w których przekroczenie to zostało wykryte.

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

52

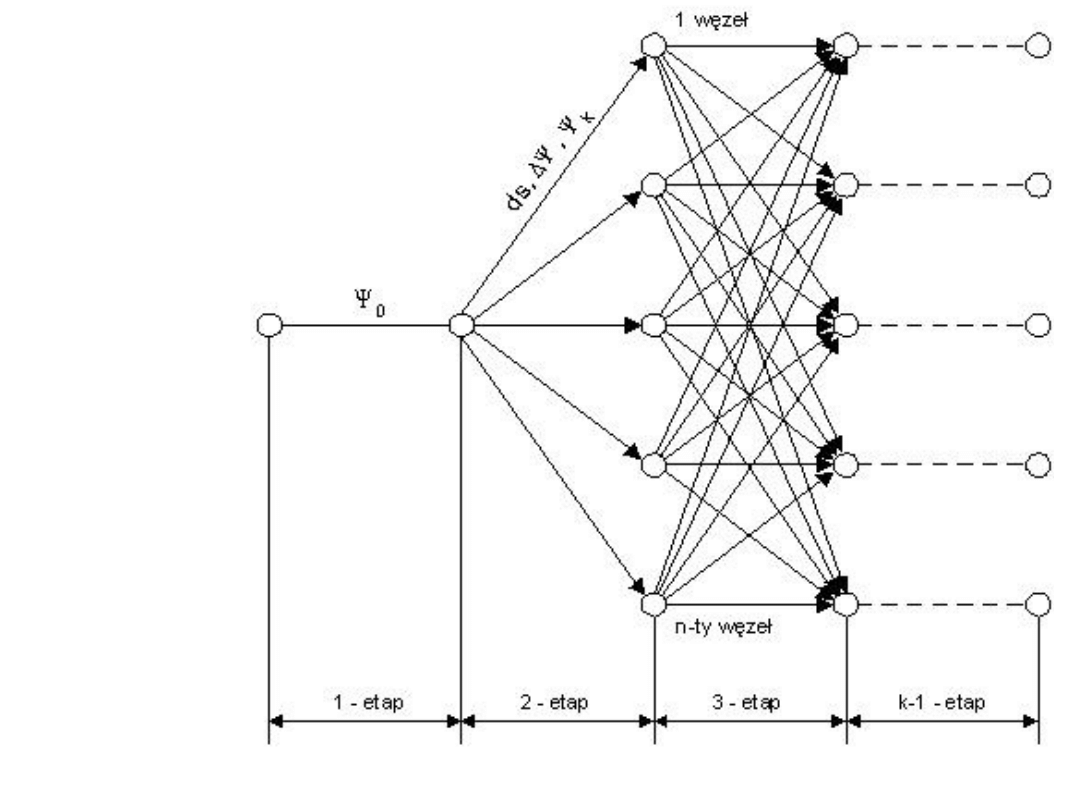
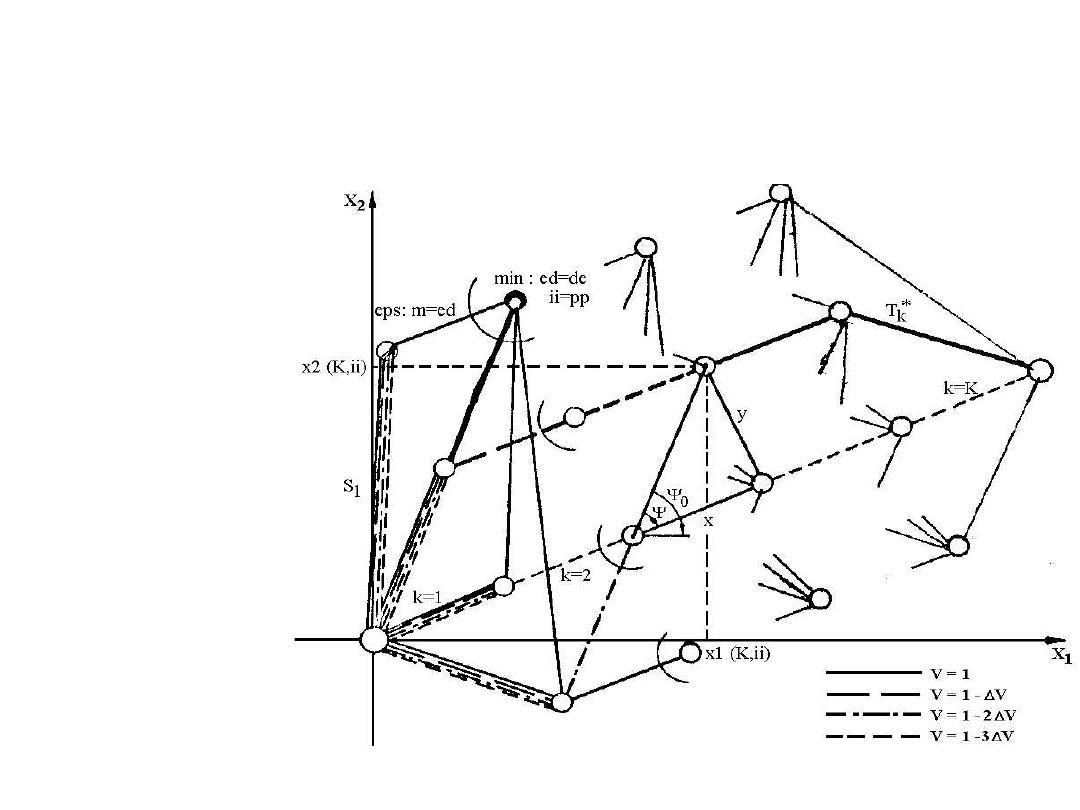
Podział
drogi statku
na
k etapów
i
n węzłów:

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

53

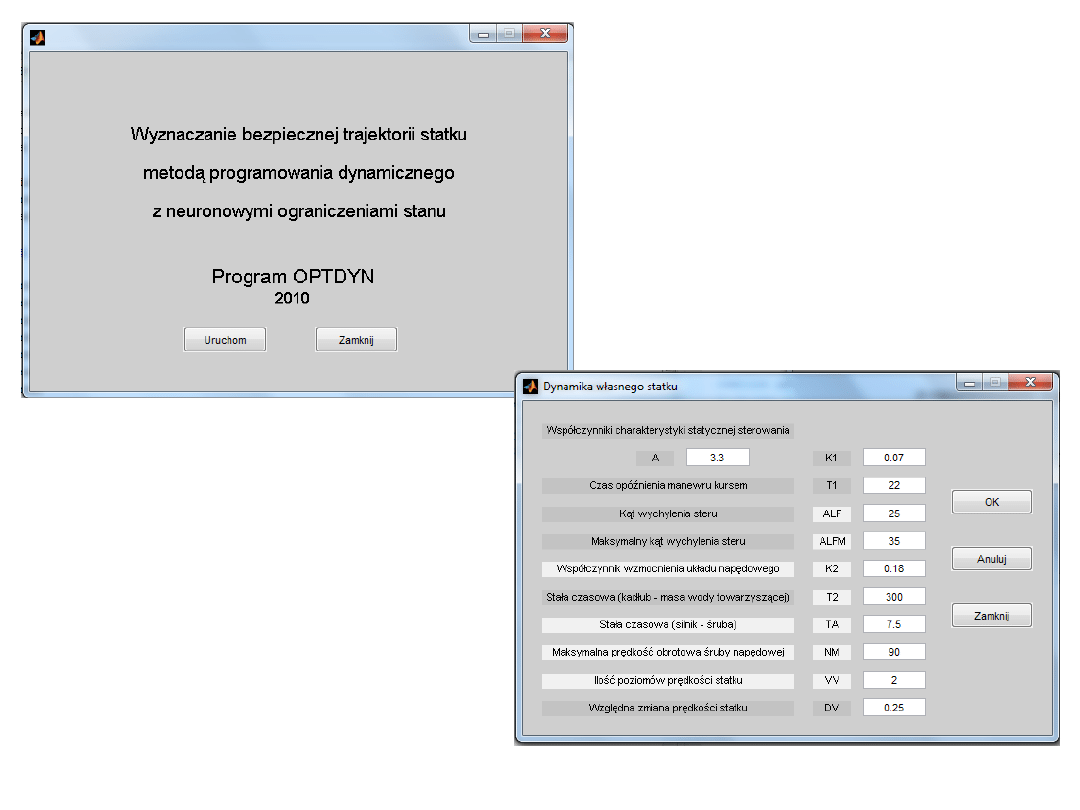
Wyznaczenie
bezpiecznej
trajektorii
z
uwzględnienie
m
zmian
prędkości
własnego
statku

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

54

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

55

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

56

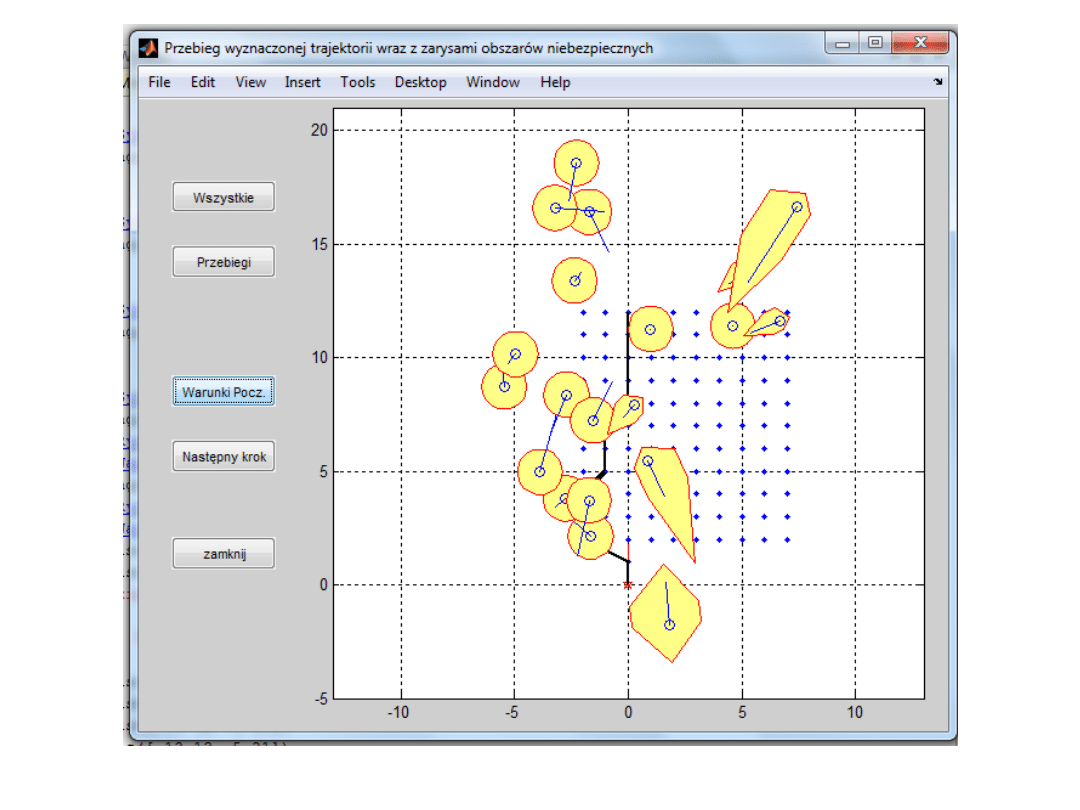
prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

57

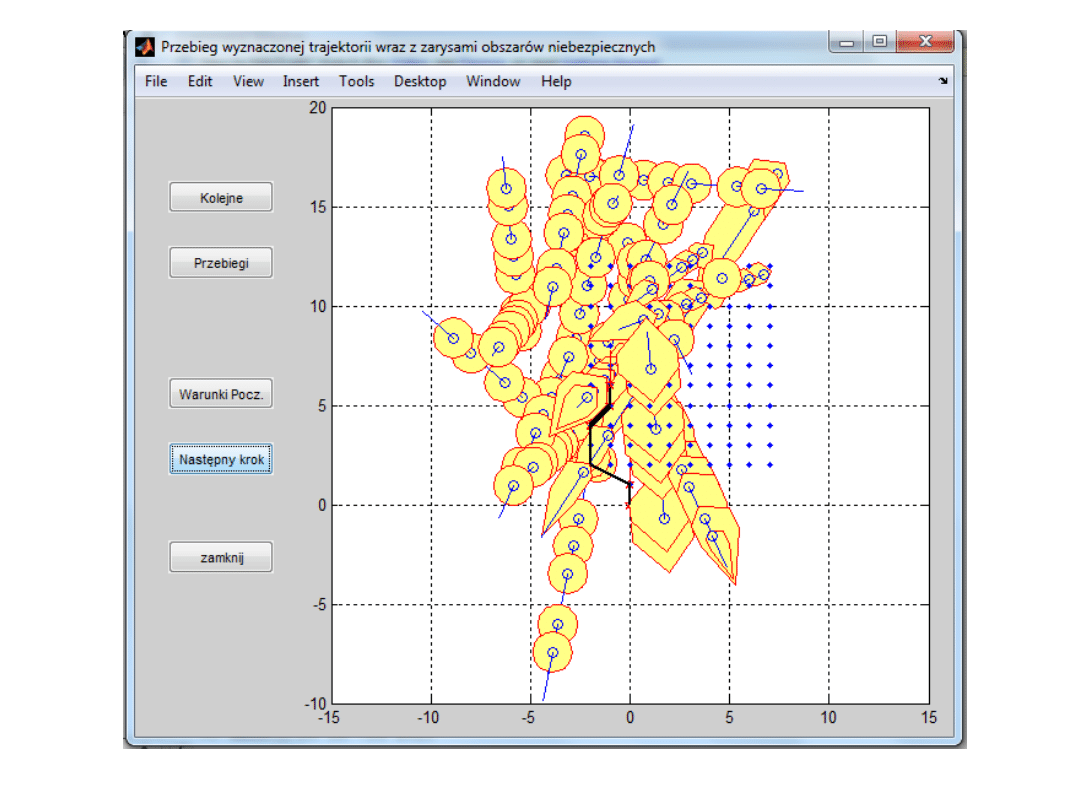
prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

58

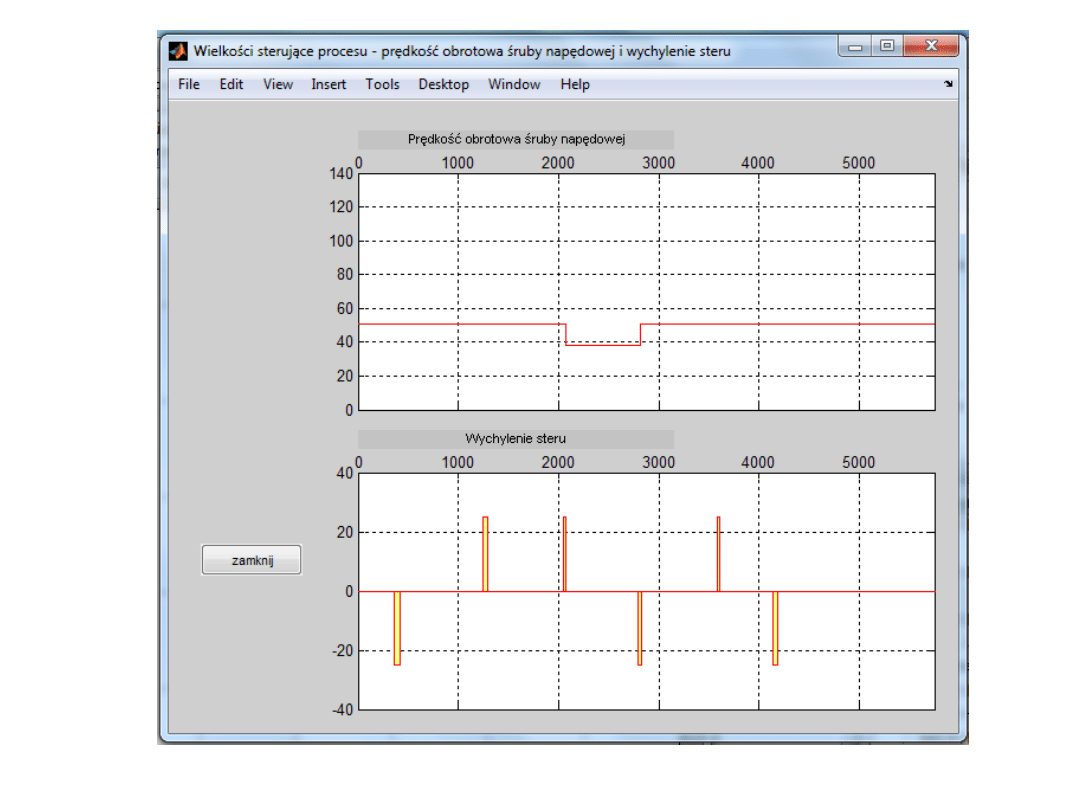
prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

59

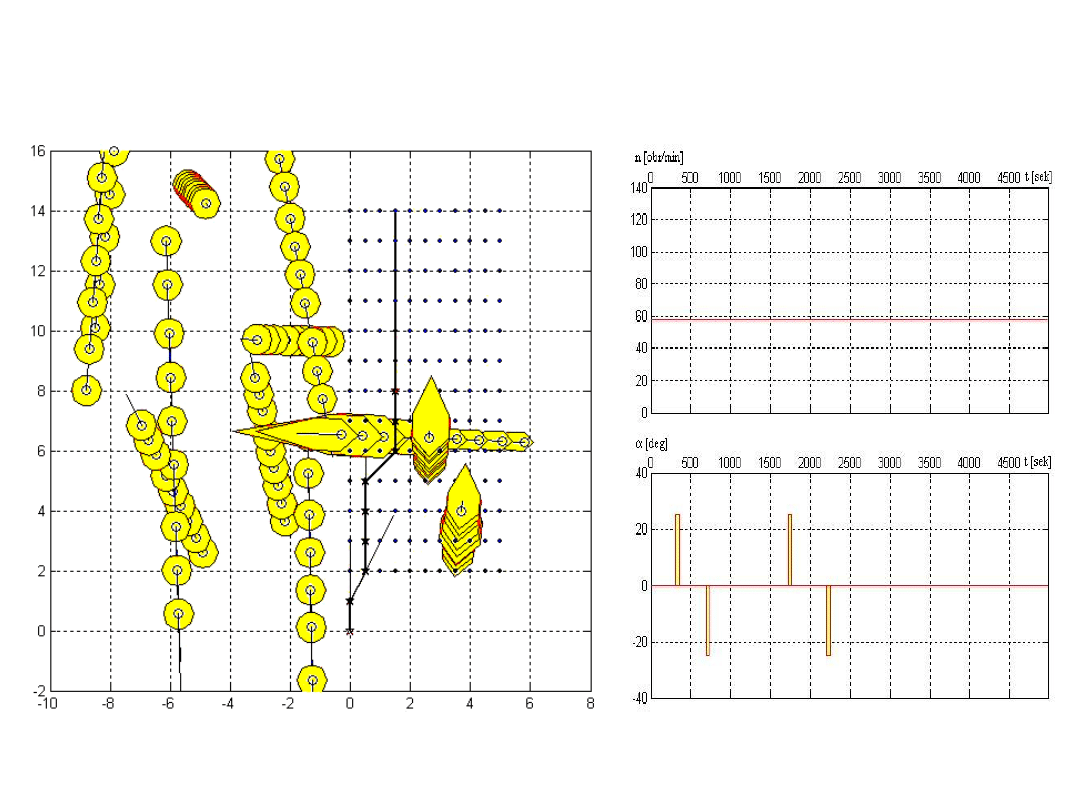
prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

60

Symulacja bezpiecznej trajektorii statku w warunkach dobrej

widzialności na morzu, j=12, D

b

= 0,5 Mm, t*

k

= 4982 sek

prof. Józef Lisowski

PODSTAWY AUTOMATYKI_XIV_Sterowanie

optymalne

61

Symulacja bezpiecznej trajektorii statku w warunkach

ograniczonej widzialności na morzu, j=12, D

b

= 3 Mm t*

k

= 6685 sek