1

Algorytmy i struktury danych, temat 1

Algorytmy i struktury danych



Wprowadzenie

dr hab.inż. ANDRZEJ WALCZAK, prof.WAT

WAT, 2008

Algorytmy i struktury

danych

Temat 2:rekurencja i iteracja

3

Algorytmy i struktury danych, temat 1

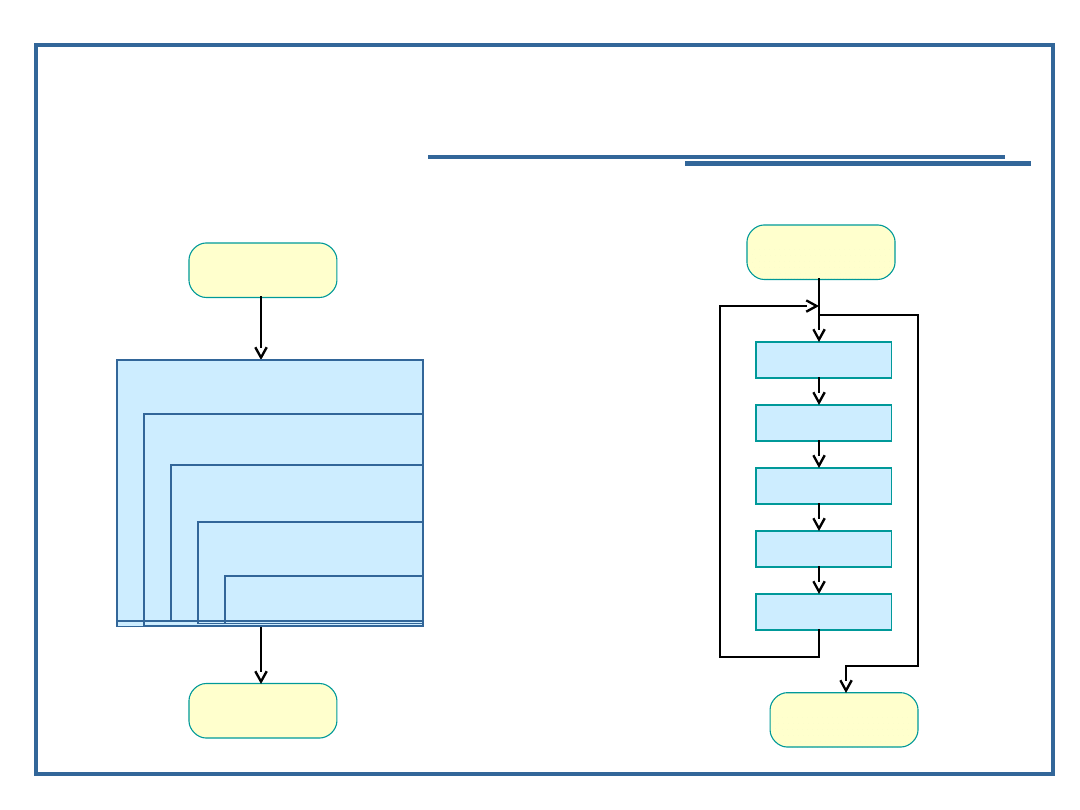
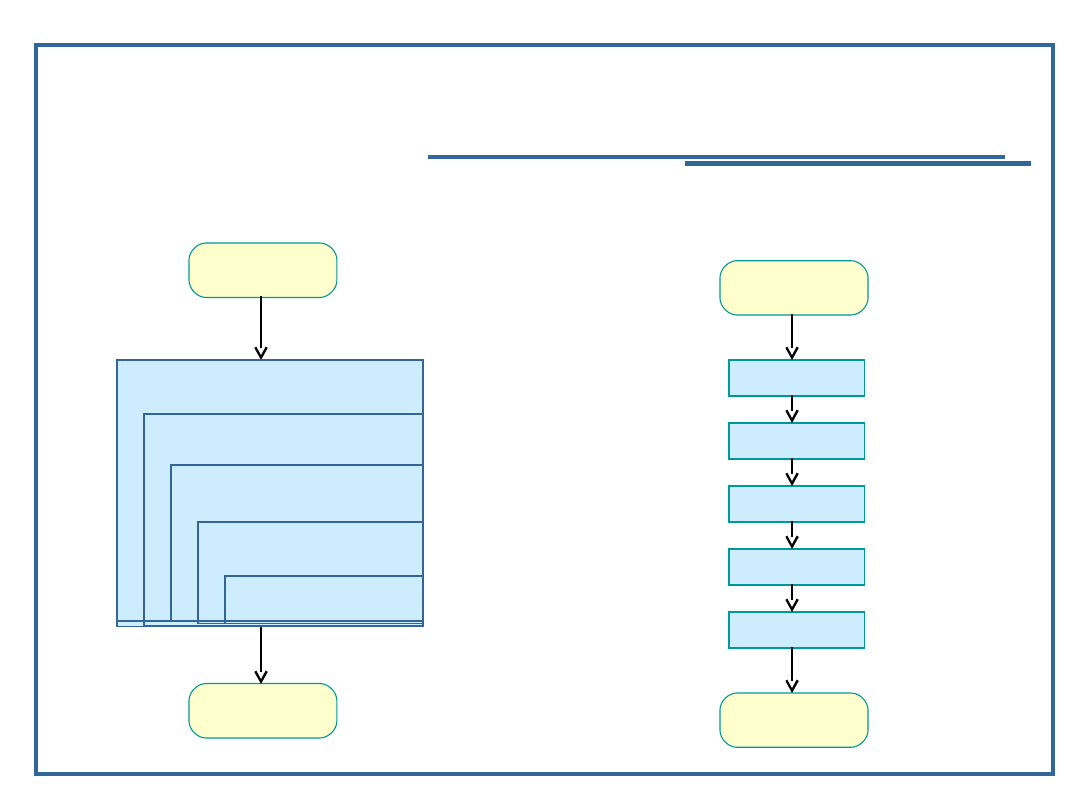
Klasyfikacja algorytmów, cd.

algorytmy rekurencyjne, algorytmy iteracyjne

Algorytm rekurencyjny: Algorytm iteracyjny:

START

STOP

Krok_1

Krok_2

Krok_3

Krok_4

Krok_5

START

STOP

Krok_1

Krok_2

Krok_3

Krok_4

Krok_5

4

Algorytmy i struktury danych, temat 1

Przykład obliczania silni dla n=5,

Algorytm rekurencyjny: Algorytm sekwencyjny

(podobna zasada obowiązuje dla iteracji):

START

STOP

= 1

= 1* 2

= 2 * 3

= 6 * 4

= 24 * 5

START

STOP

= 5 * 4!

= 4 * 3!

3 * 2!

2 * 1!

1

= 4 * 3!

= 3 * 2!

= 2 * 1!

= 1

5

Algorytmy i struktury danych, temat 1

Wywołanie funkcji rekurencyjnej



Rekurencja oznacza wywołanie funkcji (procedury)
przez tę samą funkcję



Ważne jest, aby kolejne wywołania funkcji (procedury)
rekurencyjnej były realizowane dla kolejnych wartości
parametrów formalnych w taki sposób, aby nie doszło
do zjawiska „nieskończonej pętli rekurencyjnych
wywołań funkcji”

6

Algorytmy i struktury danych, temat 1

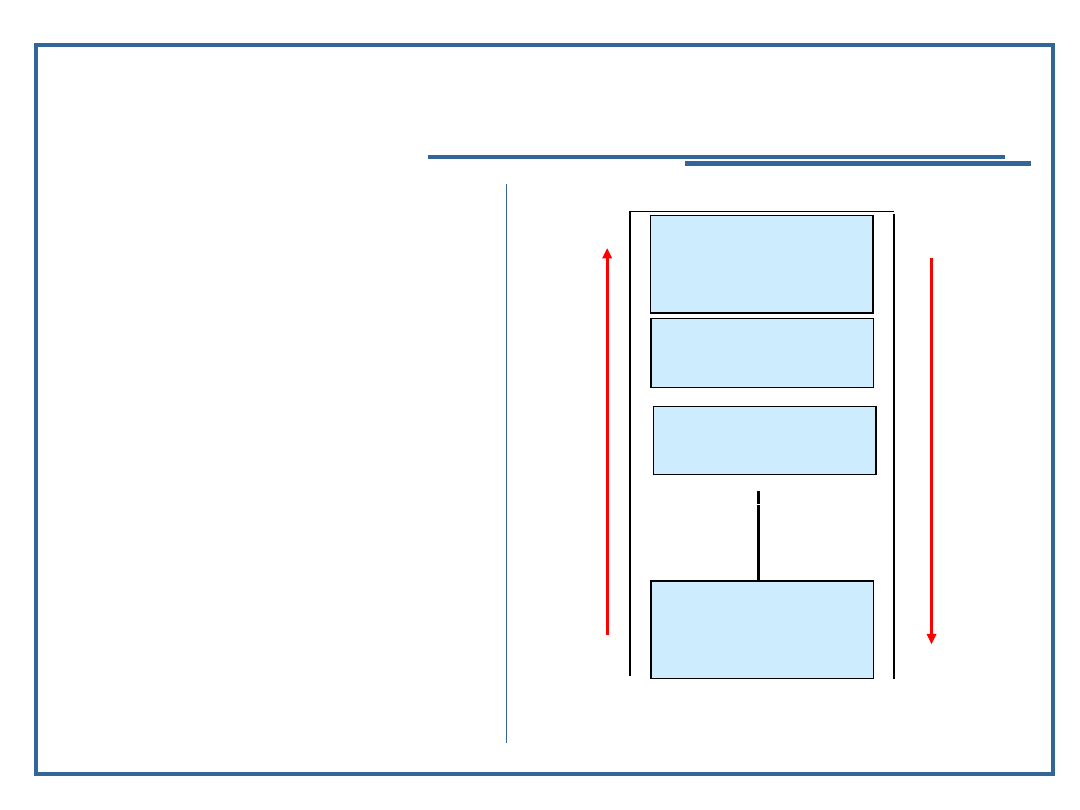
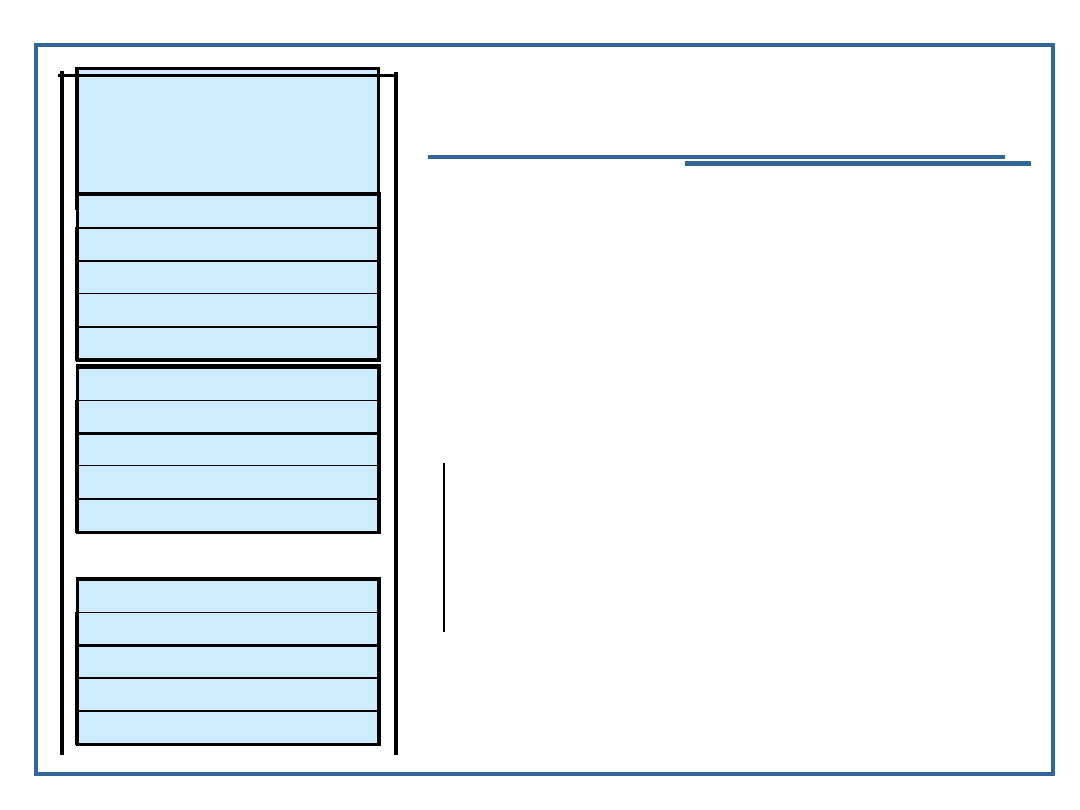
Wywołanie funkcji rekurencyjnej



Kolejne wywołania
funkcji rekurencyjnej są
związane z odkładaniem
na stosie programu
kolejnych rekordów
aktywacji procedury



W wyniku kończenia
działania
poszczególnych funkcji
na kolejnych poziomach
rekurencji kolejne
rekordy aktywacji są
zdejmowane ze stosu

Pierwszy

poziom

rekurencji

Drugi poziom

rekurencji

Trzeci poziom

rekurencji

Ostatni

poziom

rekurencji

Dno stosu

programu

Wierzchołek

stosu

k

o

le

jn

e

w

yw

o

ła

n

ia

r

e

k

u

re

n

c

yj

n

e

zw

a

ln

ia

n

ie

s

to

su

i

z

w

ro

t

p

a

ra

m

e

tr

ó

w

p

o

m

ię

d

zy

k

o

le

jn

ym

i

p

o

zi

o

m

a

m

i

re

k

u

re

n

c

ji

7

Algorytmy i struktury danych, temat 1

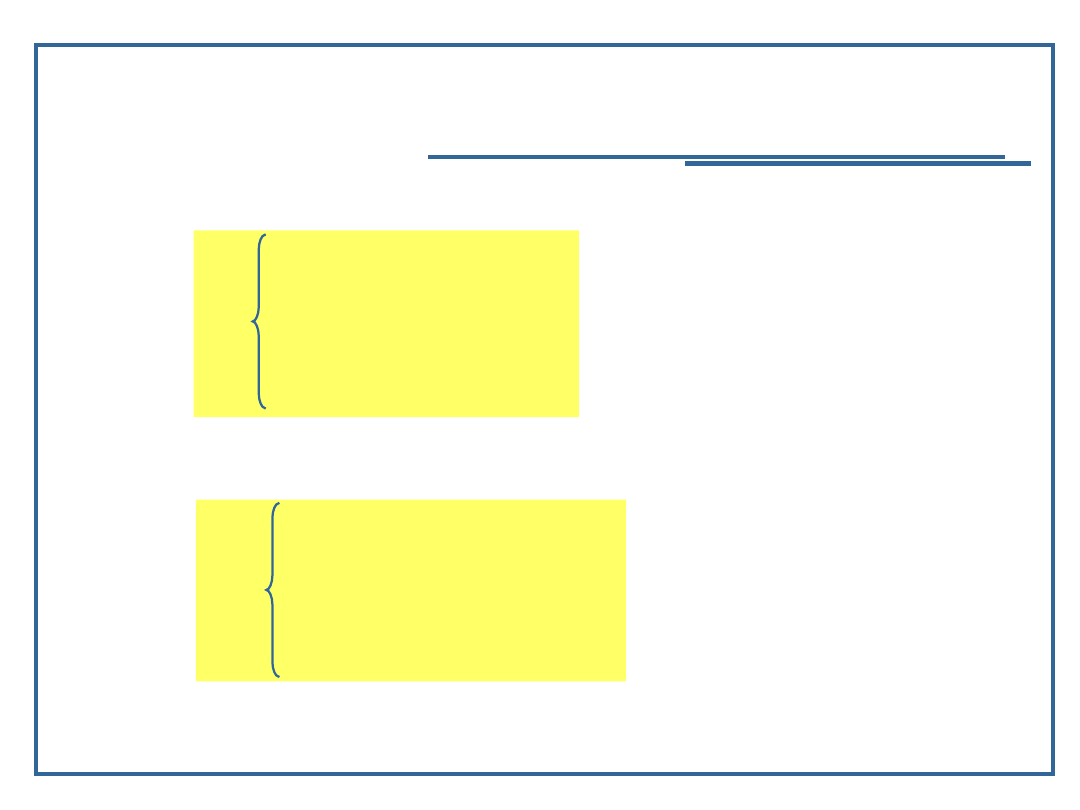
Stos programu w

wywołaniach

rekurencyjnych –

przykład C/C++

Adres powrotu do

systemu

operacyjnego

Dno stosu programu

Adres powrotu z funkcji

Zwracana wartość

Parametry przez adres

Parametry przez wartość

Zmienne lokalne

Adres powrotu z funkcji

Zwracana wartość

Parametry przez adres

Parametry przez wartość

Zmienne lokalne

Adres powrotu z funkcji

Zwracana wartość

Parametry przez adres

Parametry przez wartość

Zmienne lokalne

funkcja main()

funkcja f1

funkcja f2

funkcja fN

• Stos programu w

wywołaniach

rekurencyjnych jest

bardziej eksploatowany

niż wtedy, gdy

wywołania nie są

rekurencyjne
Kolejne poziomy

rekurencji wymagają

odkładania na stosie

programu kolejnych

rekordów aktywacji

funkcji
W przypadku procedur

mechanizm obsługi

stosu jest analogiczny.

Różnica polega na tym,

że adres do zwracanej

wartości jest „void”

8

Algorytmy i struktury danych, temat 1

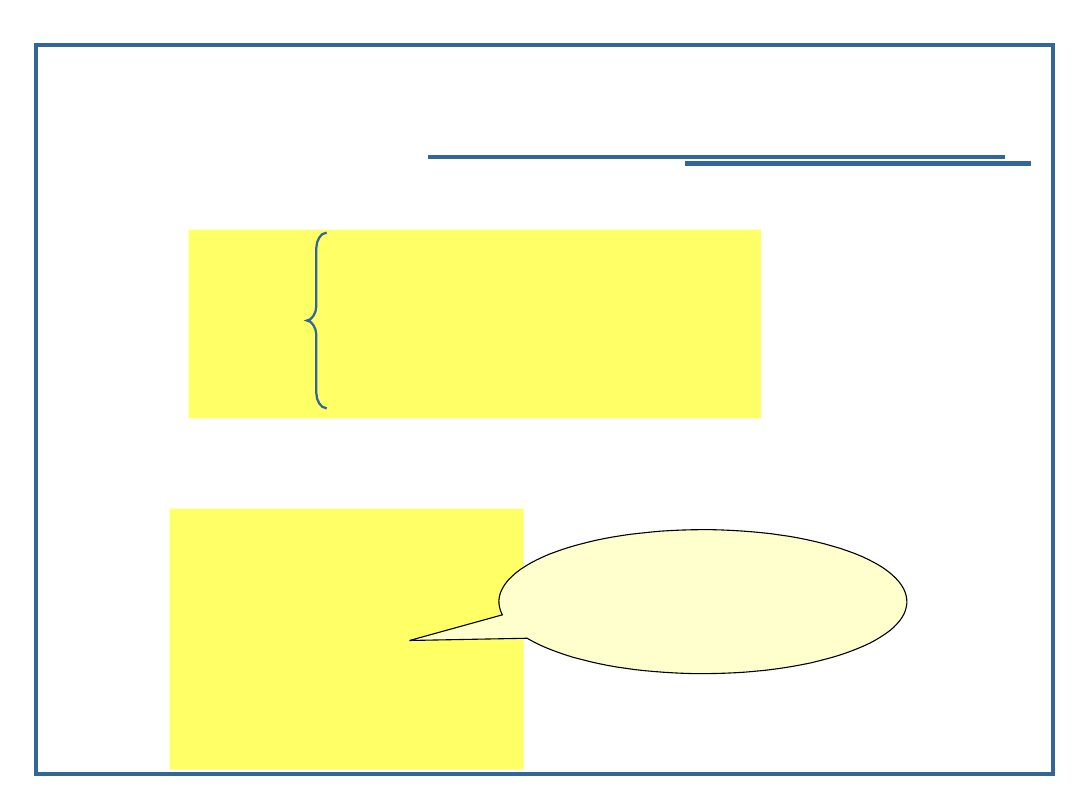
Przykłady funkcji rekurencyjnych



Znana już funkcja „silnia”:

1,

dla n=0

(warunek zakończenia rekurencji)

n!=

n*(n-1)!

dla n>0



Definicja ciągu liczb wymiernych:

1,

dla n=0

(warunek brzegowy, zakończenia)

f(n)=

f(n-1) + (1/f(n-1)), dla n>0,

określa ciąg o wartościach:

1, 2, 5/2, 29/10, 941/290, 969581/272890,.................

9

Algorytmy i struktury danych, temat 1

Funkcja rekurencyjna – ciąg liczb

Fibonacciego



Ciąg liczb Fibonacciego jest wyliczany wg formuły:

n,

dla n<2

Fib(n)=

Fib(n-2) + Fib(n-1) dla n>=2



Rekurencyjna implementacja w języku C:

long intFib (int n)

{

if (n<2)

return n;

else

return Fib(n-2) + Fib (n-1);

}

Czy na pewno stos

programu

„wytrzyma” taką

realizację funkcji

rekurencyjnej Fib?

10

Algorytmy i struktury danych, temat 1

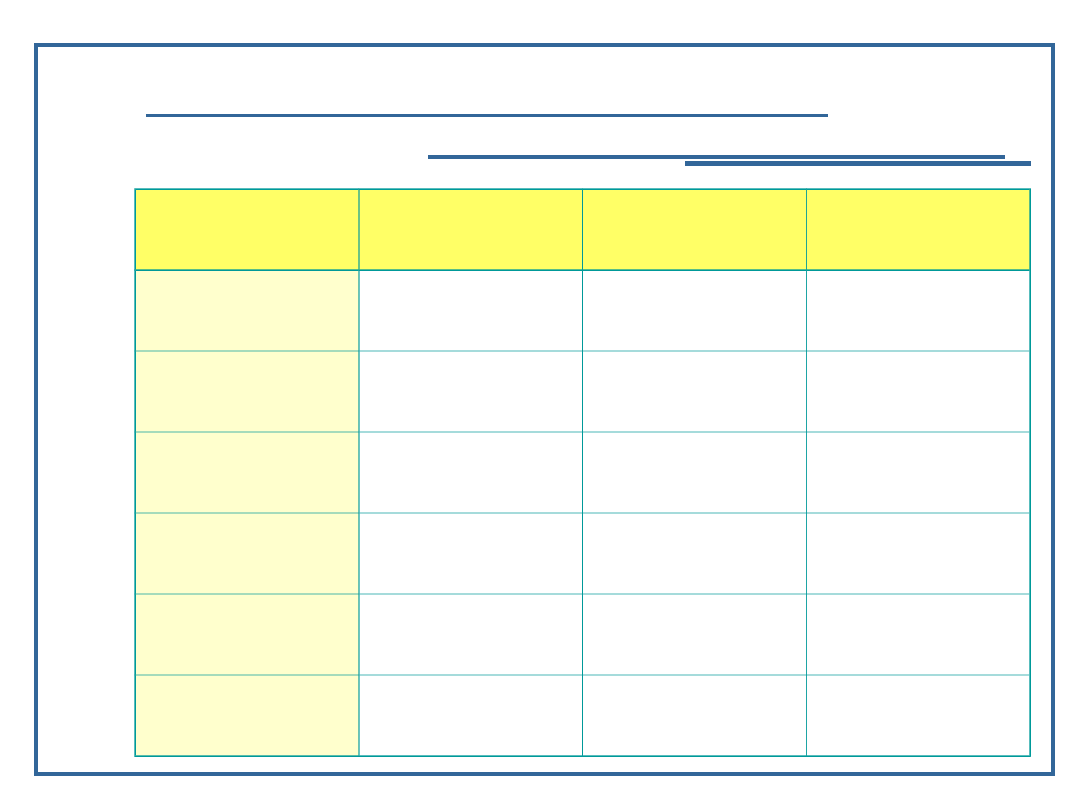
Efektywność rekurencyjnego

wykonania funkcji Fibonacciego

n

Fib(n+1)

Liczba

dodawań

Liczba

wywołań

6

13

12

25

10

89

88

177

15

987

986

1 973

20

10 946

10 945

21 891

25

121 393

121 392

242 785

30

1 346 269

1 346 268

2 692 537

11

Algorytmy i struktury danych, temat 1

Efektywność rekurencyjnego

wykonania funkcji Fibonacciego, cd.



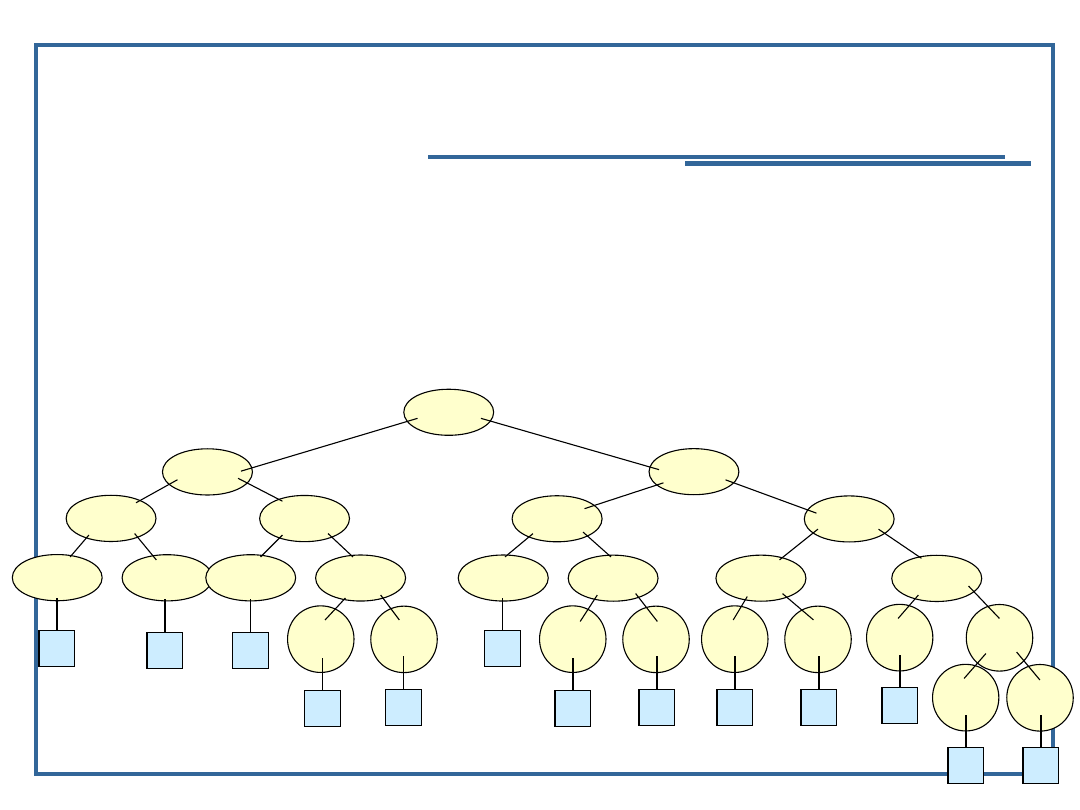
Okazuje się więc, że rekurencyjna implementacja funkcji Fibonacciego
jest niezwykle nieefektywna. Stos programu nie jest praktycznie w
stanie zrealizować tego algorytmu już dla liczb większych od 9.
Oznacza to, że program ma zbyt dużą „złożoność pamięciową”.



Przykład: drzewo wywołań dla F(6):

F(6)

F(5)

F(4)

F(2)

F(0)

F(1)

F(3)

F(1)

F(2)

F(3)

F(1)

F(2)

F(4)

F(2)

F(3)

F(
0)

F(
1)

F(
0)

F(
1)

F(
0)

F(
1)

F(
1)

F(
2)

F(
0)

F(
1)

0

1

0

1

1

0

1

0

1

0

1

1

1

12

Algorytmy i struktury danych, temat 1

Iteracyjne wykonanie rekurencyjnej

funkcji Fibonacciego



Bardziej efektywna jest iteracyjna implementacja funkcji Fibonacciego. Nie przepełniamy wtedy stosu programu i wykonujemy mniejszą liczbę przypisań wartości niż w
implementacji rekurencyjnej, dla której liczba dodawań wynosi Fib(n+1)-1, natomiast liczba przypisań jest równa: 2*Fib(n+1)-1.



Przykład implementacji metodą iteracyjną funkcji Fibonacciego:

long int IteracyjnyFib(int n)
{ register int i=2, last=0, tmp; long int current =1;
if (n<2)
return n;
else {
for ( ; i<=n; ++i) {
tmp = current;
current += last;
last = tmp;
}
return current;
}
}

13

Algorytmy i struktury danych, temat 1

Efektywność iteracyjnego

wykonania rekurencyjnej funkcji

Fibonacciego

n

Liczba przypisań

dla algorytmu

iteracyjnego

Liczba przypisań

(wywołań) dla

algorytmu

rekurencyjnego

6

15

25

10

27

177

15

42

1 973

20

57

21 891

25

72

242 785

30

87

2 692 537

14

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne

Jeśli procedura

P

zawiera bezpośrednie odwołanie do

samej siebie, to

P

nazywa się procedurą

bezpośrednio

rekurencyjną

.

Jeśli

P

zawiera odwołanie do innej procedury

Q

, która

zawiera bezpośrednie lub pośrednie odwołanie do

P

, to

P

nazywa się procedurą

pośrednio rekurencyjną

.

15

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne



Charakterystyczną cechą funkcji (procedury) rekurencyjnej jest to, że

wywołuje ona sama siebie. Druga cechą rekursji jest jej dziedzina,

którą mogą być tylko liczby naturalne.



Najłatwiej zrozumiec mechanizm dzialania rekursji na przykładzie

silni: rekurencyjny wzór na obliczenie n! zapisuje sie w ten sposób: n!

=n*(n-1)!



Ze wzoru tego wynika, ze aby obliczyc np. 4!, nalezy najpierw

obliczyc 3!. Ale zeby obliczyc 3! trzeba obliczyc 2! itd. az dojdziemy

do 0!, które jak wiemy wynosi 1.



Sposób obliczenia 4! wyglada wiec nastepujaco:



4!=4*3!=4*3*2!=4*3*2*1!=4*3*2*1*0!=4*3*2*1*1=24



Przykladowa implementacja funkcji rekurencyjnej obliczajacej n!

wyglada tak:



function silnia(n:integer):integer;



begin



if (n=0)or(n=1) then silnia:=1 else



silnia:=n*silnia(n-1);



end;

16

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne – ciąg

Fibonacciego

 































1

2

1

1

1

0

0

N

dla

N

F

N

F

N

dla

N

dla

N

F

17

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne – ciąg

Fibonacciego

złożoność rekurencji Fibonacciego

0

5

10

15

20

1

2

3

4

5

6

zmiennych

o

p

e

ra

c

ji

18

Algorytmy i struktury danych, temat 1

Ciąg Fibonacciego – rozwiązanie

iteracyjne



Bardziej efektywna jest iteracyjna implementacja funkcji

Fibonacciego. Nie przepełniamy wtedy stosu programu i

wykonujemy mniejszą liczbę przypisań wartości niż w

implementacji rekurencyjnej, dla której liczba dodawań wynosi

Fib(n+1)-1, natomiast liczba przypisań jest równa: 2*Fib(n+1)-1.



Przykład implementacji metodą iteracyjną funkcji Fibonacciego:

long int IteracyjnyFib(int n)
{ register int i=2, last=0, tmp; long int current =1;

if (n<2)

return n;

else {

for ( ; i<=n; ++i) {

tmp = current;

current += last;

last = tmp;

}

return current;

}

}

19

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne wykonane

iteracyjnie



Wniosek z poprzedniego slajdu brzmi: nawet przy
naturalnie rekurencyjnej formie matematycznej
możliwa jest iteracyjna metoda wykonania. Możliwość
jej wykonania tkwi w strukturze logicznej instrukcji
języka programowania.

20

Algorytmy i struktury danych, temat 1

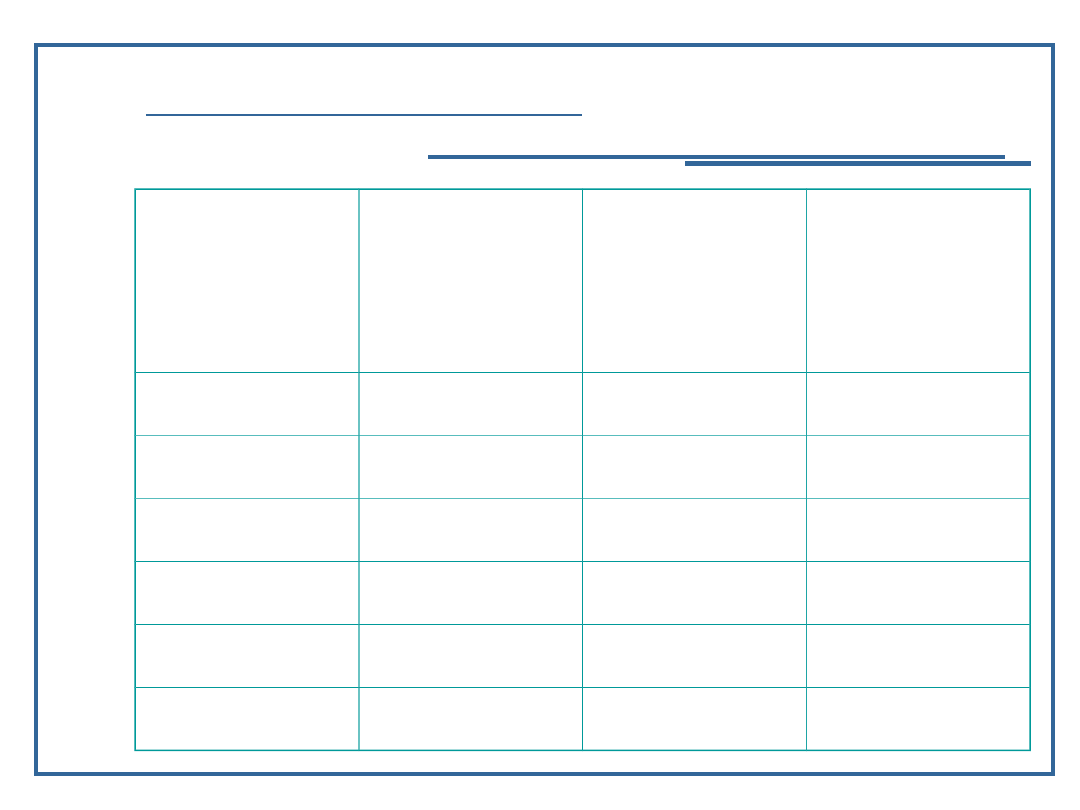
Efektywność iteracyjnego wykonania

rekurencyjnej funkcji Fibonacciego

n

Liczba

przypisań dla

algorytmu

iteracyjnego

Liczba

przypisań

(wywołań) dla

algorytmu

rekurencyjneg

o

porównanie

6

15

25

25/15=5/3

10

27

177

15

42

1 973

20

57

21 891

25

72

242 785

30

87

2 692 537

~30949

21

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne



Nie należy jednak unikać rekurencyjnego
rozwiązywania problemów za wszelką cenę. Istnieje
wiele algorytmów skutecznie funkcjonujących w formie
rekurencyjnej. Jednym z przykładów skutecznego
algorytmu rekurencyjnego jest tzw. schemat Hornera
do obliczania wartości liczbowej wielomianu n-tego
stopnia p(x) przy zadanej wartości zmiennej
niewiadomej x.

22

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne



Przykład.



Oblicz w zadanym
punkcie x wartość
wielomianu :

 

3

2

2

1

3

0

a

x

a

x

a

x

a

x

p









23

Algorytmy i struktury danych, temat 1

Algorytmy rekurencyjne



Zgodnie ze wzorem mamy tutaj ogólnie tzn. bez danych
liczbowych 6 mnożeń i 3 dodawania tj. dziewięć operacji.



Rozwiązanie Hornera: podaną sumę wyrazów możemy
wyliczyć wg rozbicia na iloczyny co daje trzy mnożenia i trzy
dodawania:

 









3

2

1

0

a

x

a

x

a

x

a

x

p









24

Algorytmy i struktury danych, temat 1

Podsumowanie:



Poznaliśmy podstawowe pojęcia algorytmów
rekurencyjnych



Następny wykład:



poznamy na nim między innymi definicję struktury
danych

i przykłady różnych struktur danych

dziękuję za uwagę