Wiesław WSZOŁEK

Wiesław WSZOŁEK

Akademia Górniczo-

Akademia Górniczo-

Hutnicza

Hutnicza

Podstawy

Podstawy

Automatyki

Automatyki

Wykład 5

Wykład 5

Charakterystyki

częstotliwościowe

Wykład 5

Wykład 5

Charakterystyki

częstotliwościowe

2

Sygnał harmoniczny

podawany na wejście

elementu liniowego jest istotny ze względu na:



dość częste występowanie w wielu układach,



możliwość

rozkładu

innych

sygnałów

o

charakterze okresowym na szereg Fouriera
złożony z funkcji harmonicznych.

Ogólny symbol graficzny elementu

liniowego

Charakterystyki
częstotliwościowe

Element

liniowy

y(t)

x(t)

3

Sygnał harmoniczny w postaci zespolonej
można zapisać jako:

 



 

t

j

e

A

t

j

t

A

t

x











1

1

sin

cos

)

(







gdzie:
A

1

- pulsacja sygnału (T - okres
drgań)

T





2



Przy takim sygnale wejściowym, odpowiedź y(t)
elementu ma również charakter harmoniczny.

 

 





 









 

 







































t

j

e

A

t

j

t

A

t

y

2

2

sin

cos

)

(

- amplituda
sygnału

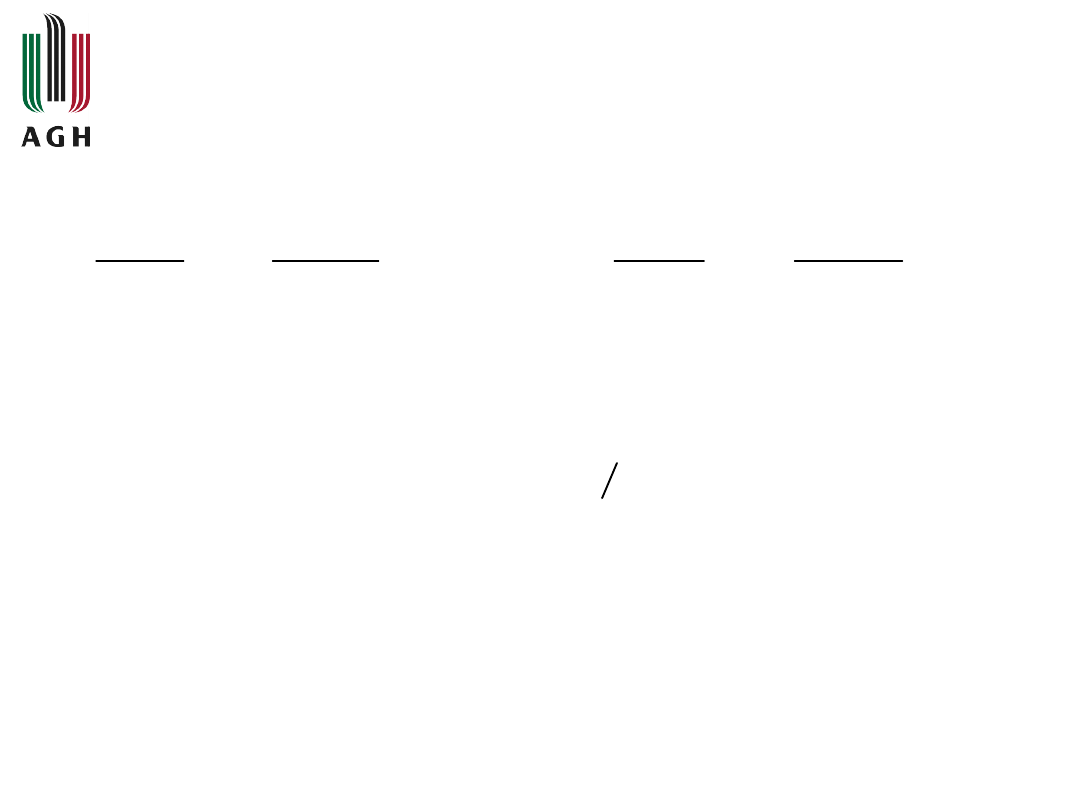
4

Podstawiając wyżej wymienione
równania

do

równania

różniczkowego

)

(

)

(

)

(

)

(

...

)

(

)

(

0

1

1

1

0

1

1

1

t

x

b

dt

t

x

d

b

dt

t

x

d

b

t

y

a

dt

t

y

d

a

dt

t

y

d

a

m

m

m

m

m

m

n

n

n

n

n

n

























można wyznaczyć

stosunek amplitud

sygnałów

wyjściowego i wejściowego

 

 







1

2

)

(

A

A

M



 

 

 





 

 

 





 

 



















































t

j

t

j

n

n

t

j

n

n

e

A

a

e

A

j

a

e

A

j

a

2

0

2

1

1

2



 

 

 

 

 

t

j

t

j

m

m

t

j

m

m

e

A

b

e

A

j

b

e

A

j

b

















1

0

1

1

1

1















oraz

przesunięcie fazowe

(



) między tymi

sygnałami

5

 

 

 

 

 

 

 

)

(

1

2

0

1

1

0

1

1



















j

G

e

A

A

a

j

a

j

a

b

j

b

j

b

j

n

n

n

n

m

m

m

m





























Wielkość G(j



) nazywana jest

transmitancją

widmową

.

Pojęcie transmitancji widmowej związane jest z
przekształceniem Fouriera, które przyporządkowuje
funkcjom czasu f(t), funkcje pulsacji G(j



) wg

zależności:













dt

e

t

f

j

G

t

j





)

(

)

(

zwaną

całką Fouriera

.

Przekształcając

6

Transmitancję widmową wyznaczyć można
także

na

podstawie

transmitancji

operatorowej stosując podstawienie





j

s

s

G

j

G





)

(

)

(

Z zależności wynika, że transmitancja widmowa jest
wektorem, którego

moduł M(



)

dla każdej pulsacji



,

jest

stosunkiem

amplitudy

sygnału

wyjściowego

do

amplitudy

sygnału

wejściowego

,

 

 









1

2

)

(

)

(

A

A

M

j

G





 

 









j

G

arg

a

argumentem



(



)

przesunięcie fazowe

sygnału

wyjściowego

względem

sygnału

wejściowego

.

7

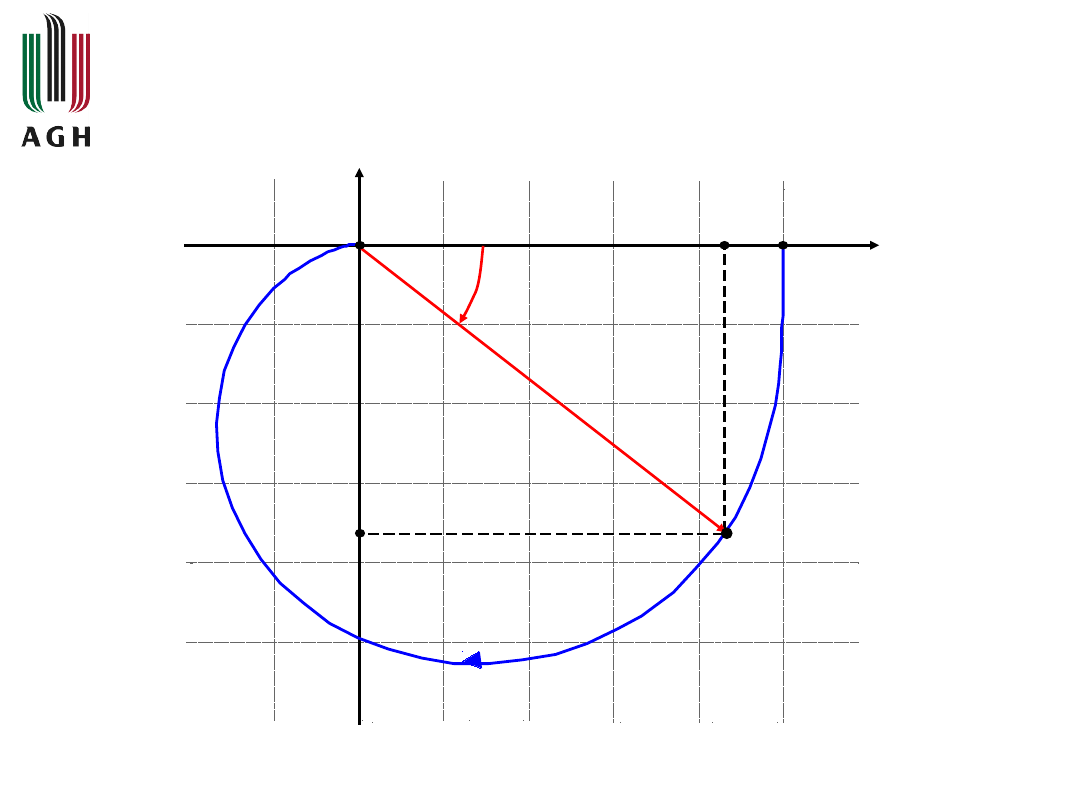
Przykładowy przebieg charakterystyki amplitudowo-
fazowej

Charakterystyka amplitudowo-
fazowa

P()

Q()

=

=0

P(

1

)

Q(

1

)

M(

1

)

(

1

)



1

8

Charakterystyki amplitudowo-fazowe układów
rzeczywistych, dla których stopień wielomianu
licznika transmitancji jest

niższy

od stopnia

wielomianu mianownika,

dążą do początku

układu współrzędnych











gdy

,

0

)

( j

G

Korzystając z równania

 









j

e

M

j

G

)

(

)

(



)

(

)

(

)

(







jQ

P

j

G













sin

cos

j

e

j



transmitancję

widmową

można

zapisać

w

następującej postaci

9

gdzie

 











cos

)

(

)

(

Re

)

(

M

j

G

P





 











sin

)

(

)

(

Im

)

(

M

j

G

Q





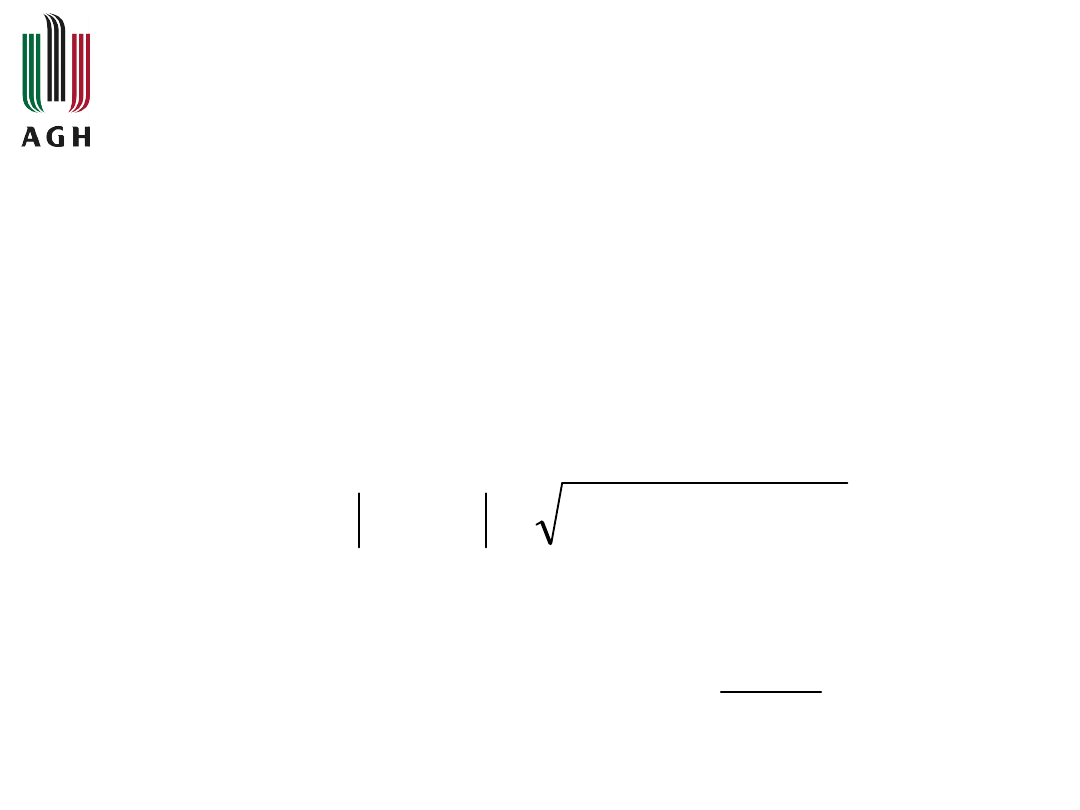
Ponadto na podstawie charakterystyki amplitudowo-
fazowej można napisać

)

(

)

(

)

(

)

(

2

2









Q

P

j

G

M







 

)

(

)

(

tg

)

(

arg











P

Q

arc

j

G





oraz

10

)

(

log

20

)

(

log

20

)

(







M

j

G

L





Charakterystyki
logarytmiczne



logarytmiczna charakterystyka amplitudowa

przedstawia
wykres

zależności

między

logarytmem

dziesiętnym modułu transmitancji widmowej
M(



) i logarytmem dziesiętnym pulsacji



.

Logarytm z modułu transmitancji widmowej M(



)

podaje się w dB.



logarytmiczna

charakterystyka

fazowa

przedstawia

natomiast

wykres

zależności

argumentu



(



) od logarytmu dziesiętnego

pulsacji



.

11

Załóżmy,
że

 

 

















2

1

)

(

)

(

oraz

)

(

)

(

2

2

1

1

j

j

e

M

j

G

e

M

j

G





 

 























2

1

)

(

)

(

)

(

)

(

)

(

2

1

2

1







j

e

M

M

j

G

j

G

j

G

)

(

)

(

)

(

2

1







M

M

M



 

 

 













2

1





duże

znaczenie

praktyczne

charakterystyk

logarytmicznych

wynika

z

łatwości

określania charakterystyki wypadkowej
układu

, złożonego ze znanych elementów

liniowych

połączonych

szeregowo

.

Wypadkowa transmitancja widmowa G(j



)

takiego

układu

jest

równa

iloczynowi

transmitancji elementów składowych.

wtedy

stąd

12

 

)

(

log

20

)

(

log

20

)

(

)

(

log

20

2

1

2

1











M

M

M

M

L







 

 

)

(

log

20

oraz

)

(

log

20

2

2

1

1









M

L

M

L





)

(

)

(

)

(

2

1







L

L

L





 

 

 













2

1





Na podstawie równania

)

(

log

20

)

(

log

20

)

(







M

j

G

L





przyjmujemy

oznaczając

równania charakterystyk logarytmicznych układu
można zapisać jako

13

L()



20

15

10

5

0

10

-1

10

0

10

1

()



0

-45

-90

10

-1

10

0

10

1

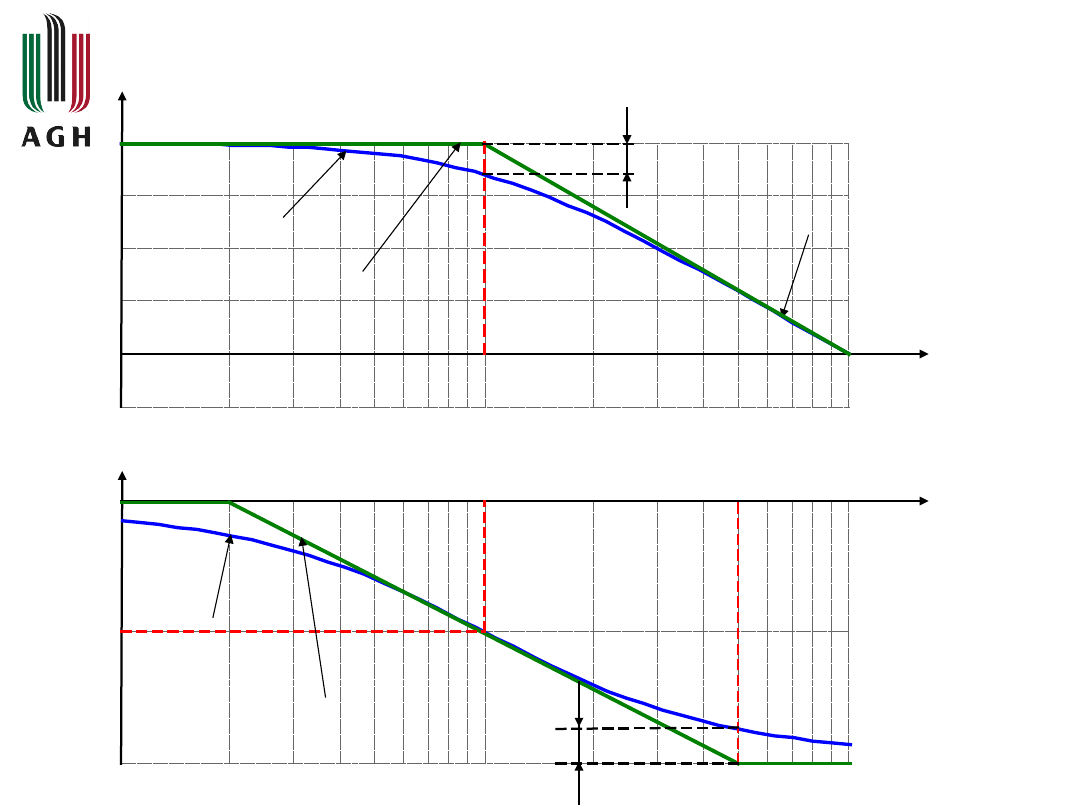
Przykładowe przebiegi charakterystyk

logarytmicznych

dokładna

-20 dB/dek

przybliżona



s

3 dB



s

1/5

s

5

s

przybliżona

dokładna

11

14

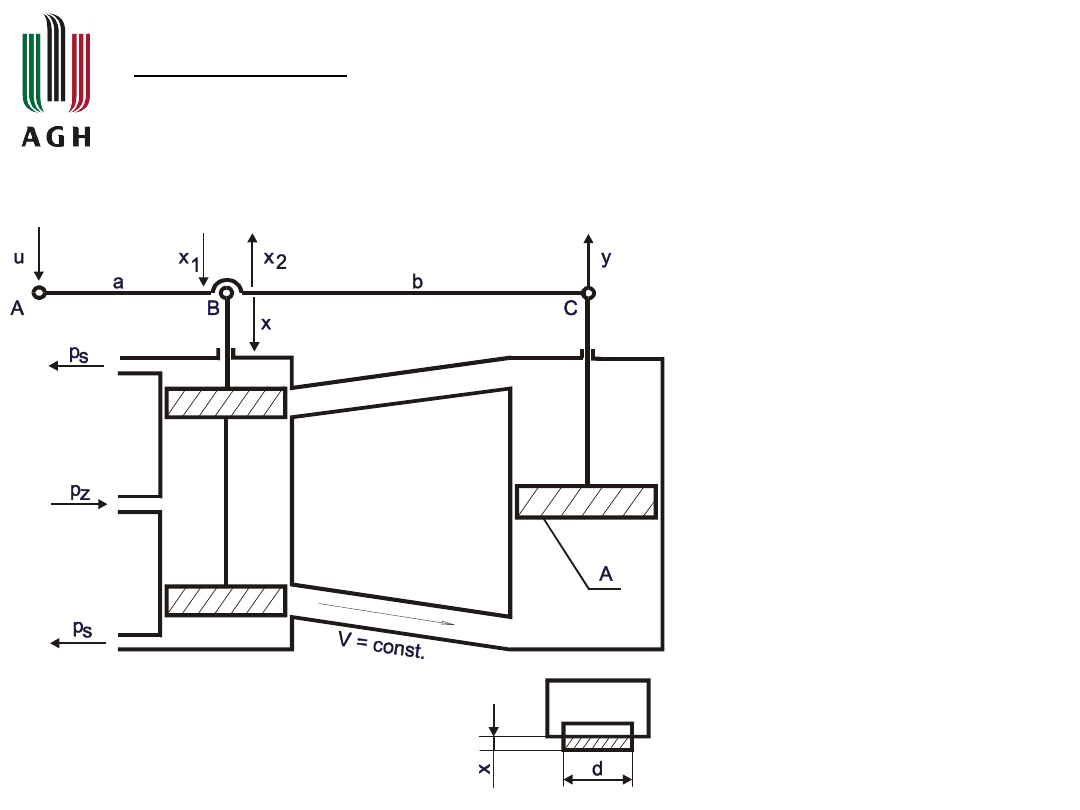
Przykład 1

Sporządzić

charakterystyki

częstotliwościowe

(amplitudowo-fazową, logarytmiczne: amplitudową i
fazową)

układu

automatyki,

którego

schemat

przedstawiono na poniższym rysunku:

gdzie:
d, x - wymiary okienka,
v

-

prędkość

przepływu oleju w
okienku,

A

-

powierzchnia

tłoka siłownika,

P

z

-

ciśnienie

zasilania
(p

z

= const),

P

s

-

ciśnienie

spływu
(p

s

= const).

u

–

przesunięcie

dźwigni (wejście)

y

–

przesunięcie

tłoczyska

siłownika

(wyjście)

15

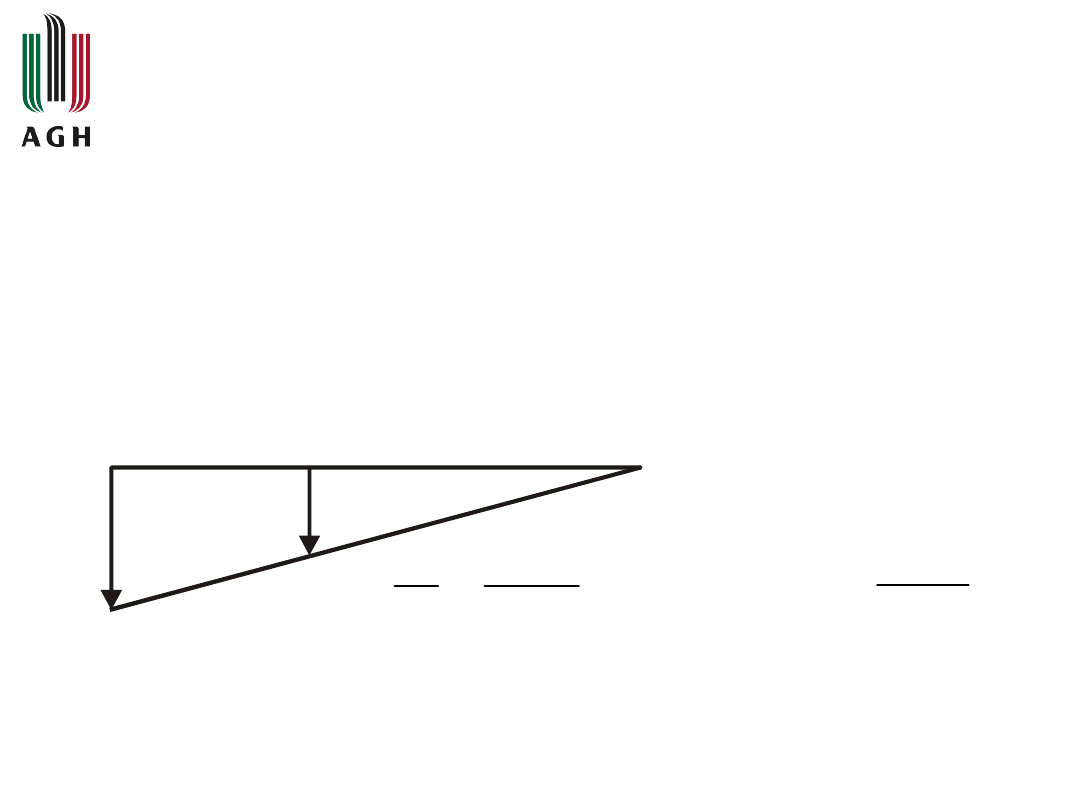
Wykorzystując zasadę superpozycji działanie dźwigni
można przedstawić jako złożenie przesunięć
składowych, pokazanych na rysunkach poniżej

A a B b C

u

x

1

Dla małych kątów wychyleń dźwigni:

b

a

u

b

x





1

u

b

a

b

x





1

stąd

Dźwignia dwustronna

gdzie:

x

1

- przesunięcie dźwigni przy obrocie wokół

punktu C

a)

16

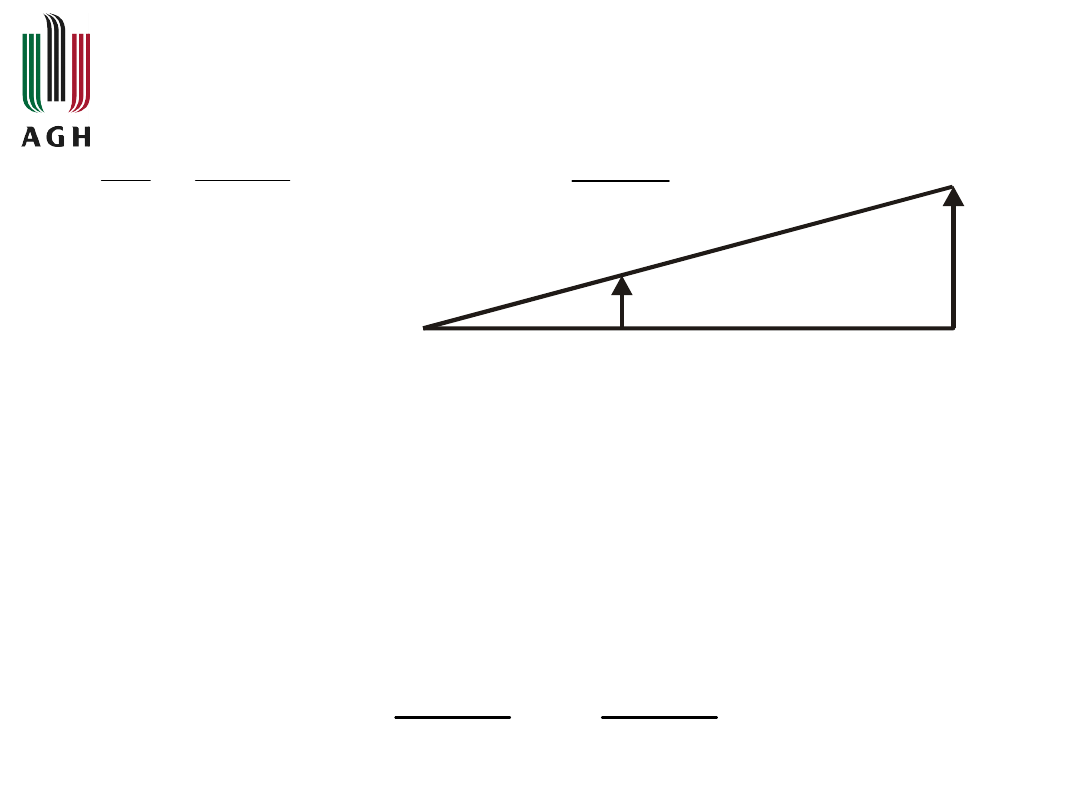
2

1

x

x

x





stąd

b

a

y

a

x





2

y

b

a

a

x





2

A a B b C

y

x

2

gdzie:

x

2

- przesunięcie dźwigni przy obrocie wokół

punktu A

Wypadkowe przesunięcie

punktu B dźwigni

można zapisać jako:

Podstawiając równania na x

1

i x

2

do powyższego

równania otrzymamy:

y

b

a

a

u

b

a

b

x









b)

17

Zmiana objętości oleju pod tłokiem siłownika
wynosi

Q

dt

dy

A



Objętościowe natężenie przepływu Q oleju przez
suwak







 x

d

Q

gdzie: d·x - powierzchnia przepływu oleju

v - prędkość przepływu.

Porównując

powyższe

wzory

i

oznaczając

v

d

A

T





1

otrzymamy

x

dt

dy

T



1

Siłownik hydrauliczny

18

Wyznaczenie

transmitancji

operatorowej

układu

Stosując przekształcenie Laplace’a do równań
opisujących

działanie

dźwigni

i

siłownika

otrzymamy

)

(

)

(

)

(

s

Y

b

a

a

s

U

b

a

b

s

X









)

(

)

(

1

s

X

s

sY

T



Po podstawieniu otrzymamy

)

(

)

(

1

s

U

b

a

b

s

Y

b

a

a

s

T





















i

1

)

(

)

(

)

(

1

1

















s

a

b

a

T

a

b

b

a

a

s

T

b

a

b

s

U

s

Y

s

G

stąd

gdzie:

a

b

K 

a

b

a

T

T





1

1





Ts

K

19





jT

K

)

j

(

G





1

2

2

2

2

2

2

1

1

1

)

1

(

1

1

1

)

(



















T

KT

j

T

K

T

jT

K

jT

jT

jT

K

j

G

























Wyznaczenie

transmitancji

widmowej

układu

Podstawiając do równania na transmitancję
operatorową s=j



otrzymamy

 

2

2

1

)

(

Re







T

K

P

j

G







 

2

2

1

)

(

Im









T

KT

Q

j

G









gdzie:

Część rzeczywistą i urojoną transmitancji widmowej
można obliczyć mnożąc licznik i mianownik
powyższej zależności przez

liczbę

sprzężoną z

mianownikiem

:

20

 

 

 

0

2

2













KP

P

Q

Wyznaczenie charakterystyki amplitudowo-

fazowej

Z
równań

 

2

2

1





T

K

P





 

2

2

1







T

KT

Q







wynika równanie charakterystyki amplitudowo-
fazowej

Po uzupełnieniu znoszącymi się wyrażeniami
otrzymamy

 

 

 

0

4

4

2

2

2

2











K

K

KP

P

Q







 

 

4

2

2

2

2

K

K

P

Q



















i

21

Wartości P(



) i Q(



) można również wyznaczyć ze

wzorów

T

1

2

K

2

K



 

2

2

1





T

K

P





 

2

2

1







T

KT

Q







i

dla różnych wartości



z przedziału (0, +



) i

zestawić dane w

tabeli.

K

0

0

0

0





)

(



P

)

(



Q

Jest to

równanie okręgu

o promieniu K/2, o

środku leżącym w punkcie [K/2, j0]. Ze wzoru
wynika, że część urojona transmitancji widmowej
jest ujemna dla



> 0.

22

Q()

P()

0 =

=0

2

K



T

1





Charakterystyka amplitudowo-fazowa układu

2

K

23

Wykorzystując

wykładniczy

zapis liczb zespolonych i

równanie

 



















j

T

jarc

T

arc

j

j

e

M

e

T

K

e

T

Ke

jT

K

j

G

)

(

1

1

1

)

(

tg

2

2

tg

2

2

0

















2

2

1





T

K

)

(

M





Wyznaczenie logarytmicznej charakterystyki
amplitudowej

 









j

e

M

j

G

)

(

)

(



transmitancję widmową omawianego układu można
zapisać jako

Równanie charakterystyki amplitudowej można więc zapisać w
postaci

)

(

)

(

)

(

)

(

2

2









Q

P

j

G

M







Równanie to można także wyznaczyć ze wzoru

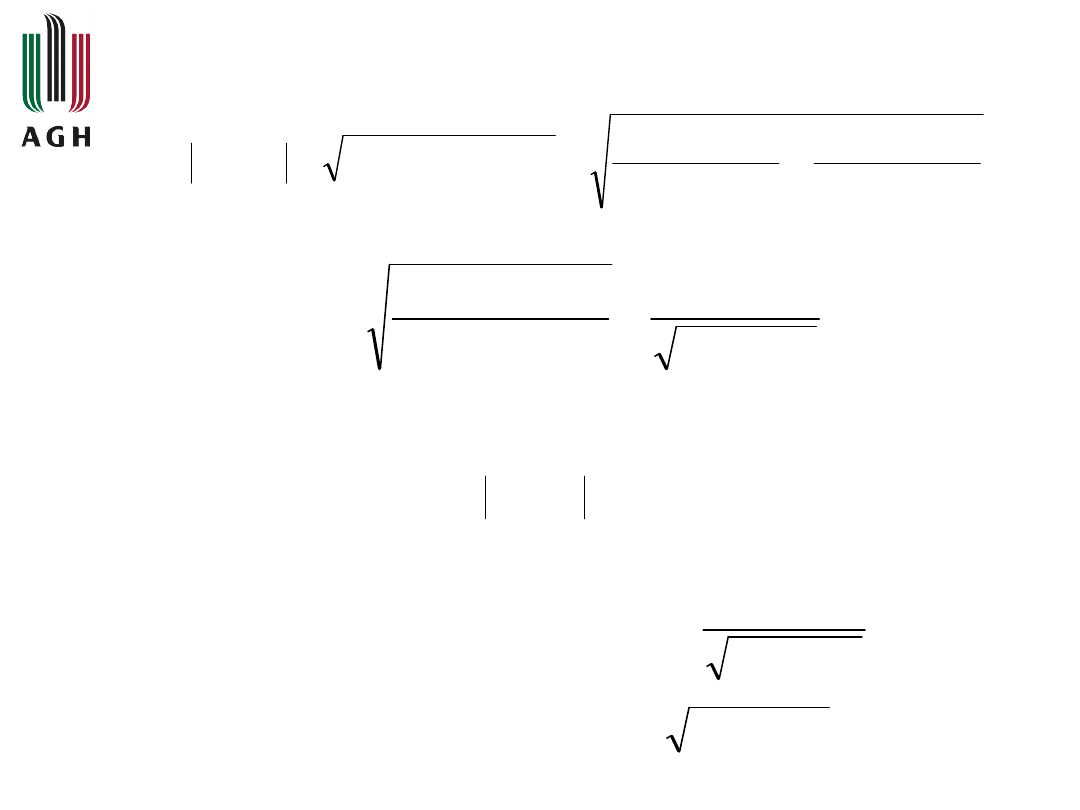
24

2

2

2

2

2

2

2

2

2

2

2

2

)

1

(

)

1

(

)

(

)

(

)

(

)

(















T

T

K

T

K

Q

P

j

G

M















2

2

2

2

2

2

2

2

1

)

1

(

)

1

(

)

(









T

K

T

T

K

M











Chcąc wyrazić moduł M(



) w decybelach, korzystamy z

równania

2

2

1

log

20

)

(

log

20

)

(







T

K

M

L







2

2

1

log

20

log

20

)

(





T

K

L







)

(

log

20

)

(

log

20

)

(







M

j

G

L





Otrzymujemy

25

Częstotliwość graniczna nazywana jest

częstotli-wością sprzęgającą.

Ponieważ

wykreślenie

charakterystyki

według

powyższego wzoru jest pracochłonne, można użyć

charakterystyk

asymptotycznych

,

które

są

przybliżeniem

charakterystyk

rzeczywistych.

Powstają w ten sposób charakterystyki logarytmiczne

aproksymowane

odcinkami linii prostych.

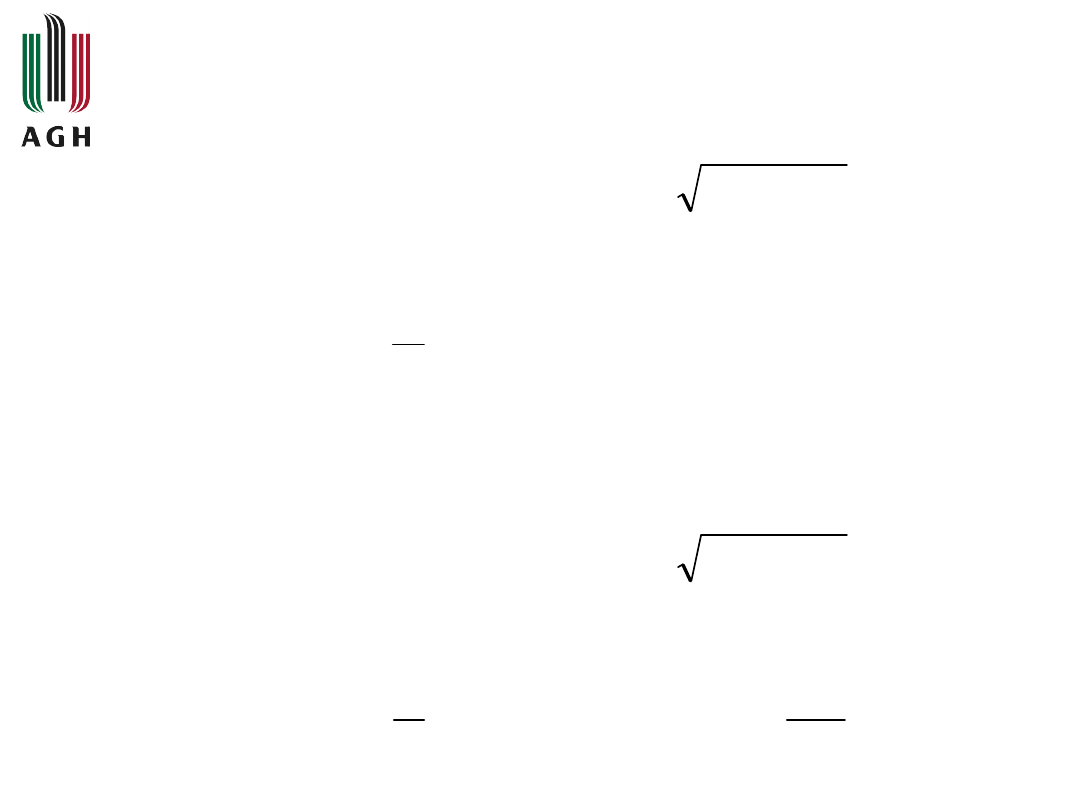
T

1





T

s

1





Cały zakres częstotliwości dzielimy na dwie
części:



Dla T

2



2

>> 1

czyli

T

1







Dla T

2



2

<< 1

czyli

26

Dla

pierwszego

zakresu częstotliwości, można w

równaniu

Dla

drugiego

zakresu częstotliwości, można w

równaniu

pominąć jego drugi składnik, stąd

2

2

1

log

20

log

20

)

(





T

K

L







pominąć jedynkę pod pierwiastkiem, stąd

2

2

1

log

20

log

20

)

(





T

K

L







K

L

T

log

20

)

(

1









dla







T

K

L

T

log

20

)

(

1





dla

27

Ponieważ

oś

odciętych

logarytmicznej

charakterystyki

amplitudowej ma podziałkę logarytmiczną, równaniom

T

s

1





K

T

KT

L

s

log

20

log

20

)

(







20

log

20

10

log

20

log

20

10

log

20

)

10

(











K

K

T

KT

L

s



odpowiadają na wykresie

odcinki linii prostej

. Wstawiając do

drugiego równania dwie dowolne wartości



, wyznaczamy

nachylenie tego odcinka charakterystyki względem osi
odciętych.

K

L

T

log

20

)

(

1

















T

K

T

K

L

T

log

20

log

20

log

20

)

(

1









Przykładowo dla
mamy

20

)

(

)

10

(







s

s

L

L





[dB/dek]

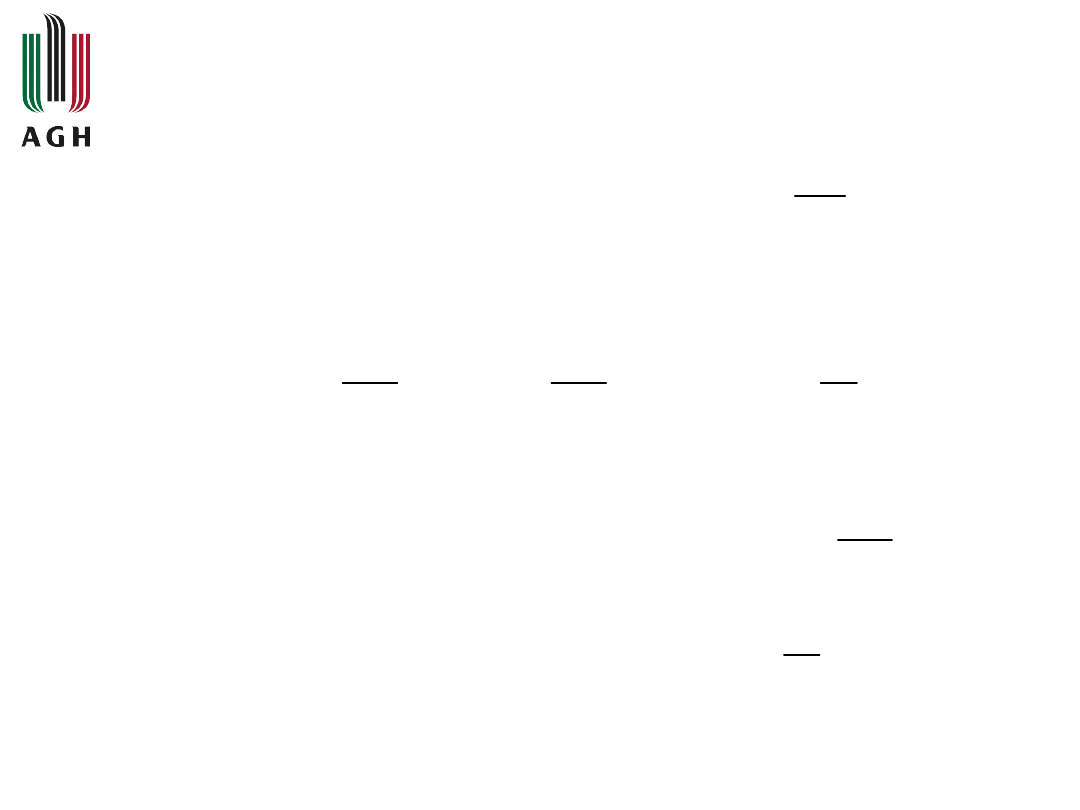
28

Prosta o równaniu

T

K

T

K

T

K

















1

0

log

20

przecina więc oś odciętych przy pulsacji i
obniża się o 20 dB/dek (występuje dziesięciokrotny
wzrost pulsacji).

T

K





przecina oś odciętych przy pulsacji



dla której

L()=0, czyli







T

K

T

K

L

log

20

log

20

log

20

)

(







Charakterystyka określona równaniem







T

K

T

K

L

log

20

log

20

log

20

)

(







29







T

arctg

)

(





















T

arc

T

K

T

KT

arc

P

Q

arc

tg

1

1

tg

)

(

)

(

tg

)

(

2

2

2

2















Wyznaczenie logarytmicznej
charakterystyki fazowej

Na podstawie równań

można napisać, że

 









j

e

M

j

G

)

(

)

(



 



















j

T

jarc

T

arc

j

j

e

M

e

T

K

e

T

Ke

jT

K

j

G

)

(

1

1

1

)

(

tg

2

2

tg

2

2

0

















Równanie to można także wyznaczyć ze
wzoru

30

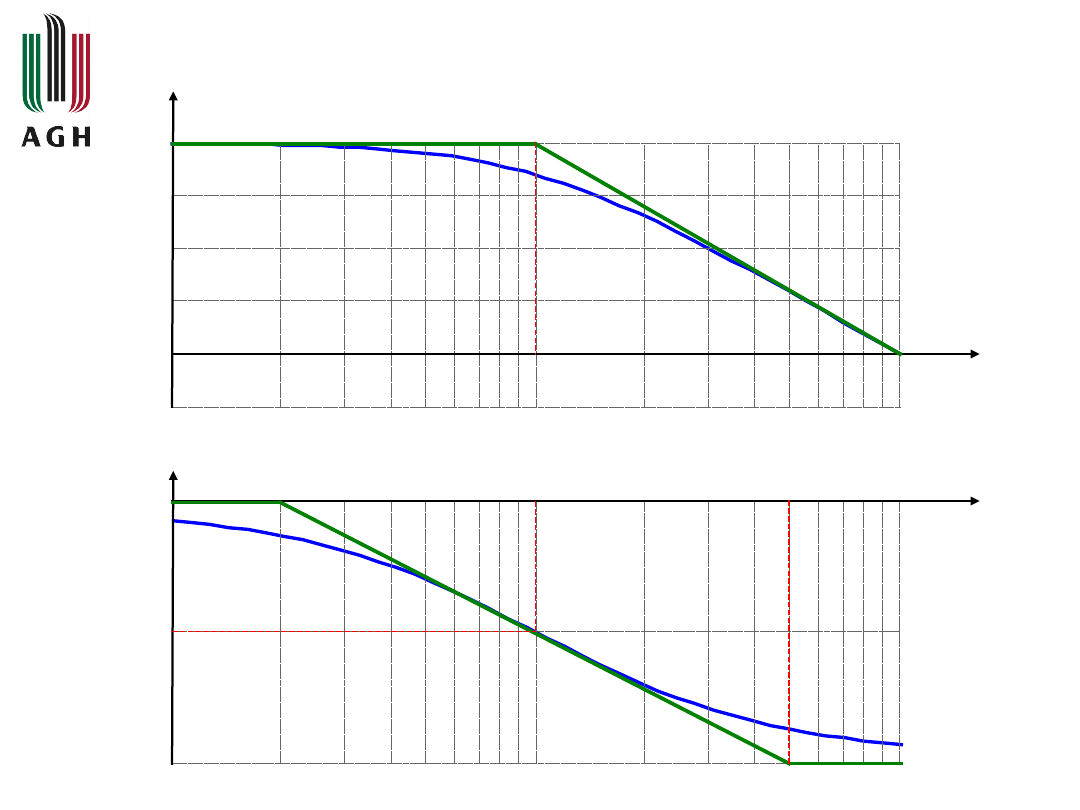
Dla różnych wartości



z przedziału (0, +



) można

wyznaczyć wartość



(



) na podstawie wzoru

T

1



 





4





2





i zestawić dane w

tabeli







T

arctg

)

(







0

0

31

L()



20

15

10

5

0

10

-1

10

0

10

1

()



0

-45

-90

10

-1

10

0

10

1

Charakterystyki logarytmiczne układu



s



s

1/5

s

5

s

32

s

T

s

T

s

G

2

1

1

)

(











j

j

j

G





1

2

)

(

Przykład 2

Wyznaczyć

charakterystyki

częstotliwościowe

(amplitudowo-fazową, logarytmiczne: amplitudową i
fazową) elementu o transmitancji:

gdzie T

1

= 2[s], T

2

= 1[s]

Wyznaczenie transmitancji widmowej



podstawiamy s=j



do równania na transmitancję

operatorową



obliczamy część rzeczywistą i urojoną transmitancji

widmowej

2

2

2

2

2

1

2

1

2

1

2

2

1

1

1

2

)

(

















































j

j

j

j

j

j

j

G

33

2

2

1

2

)

(











P

2

1

2

)

(











Q

Wyznaczenie

charakterystyki

amplitudowo-

fazowej

Wyznaczamy wartości P(



) i Q(



) z powyższych

równań dla różnych wartości



z przedziału (0, +



) i

zestawiamy dane w tabeli.



)

(



P

)

(



Q

0

0

0

1

1

1



2

0

34

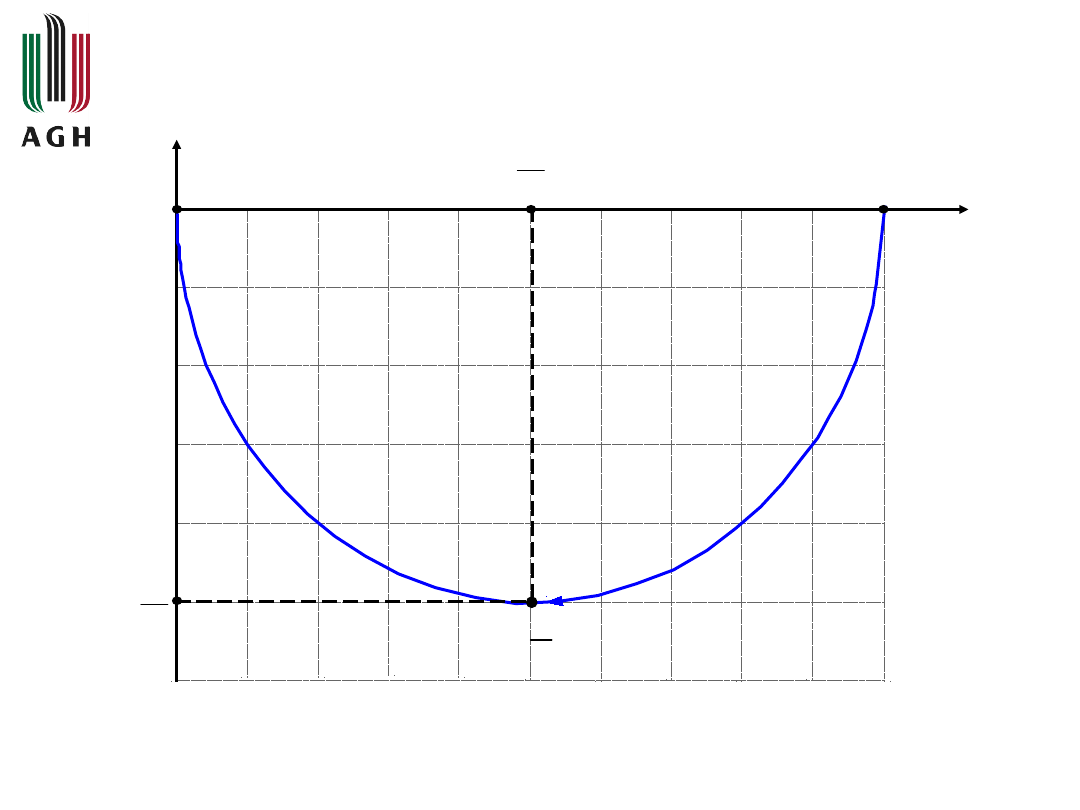
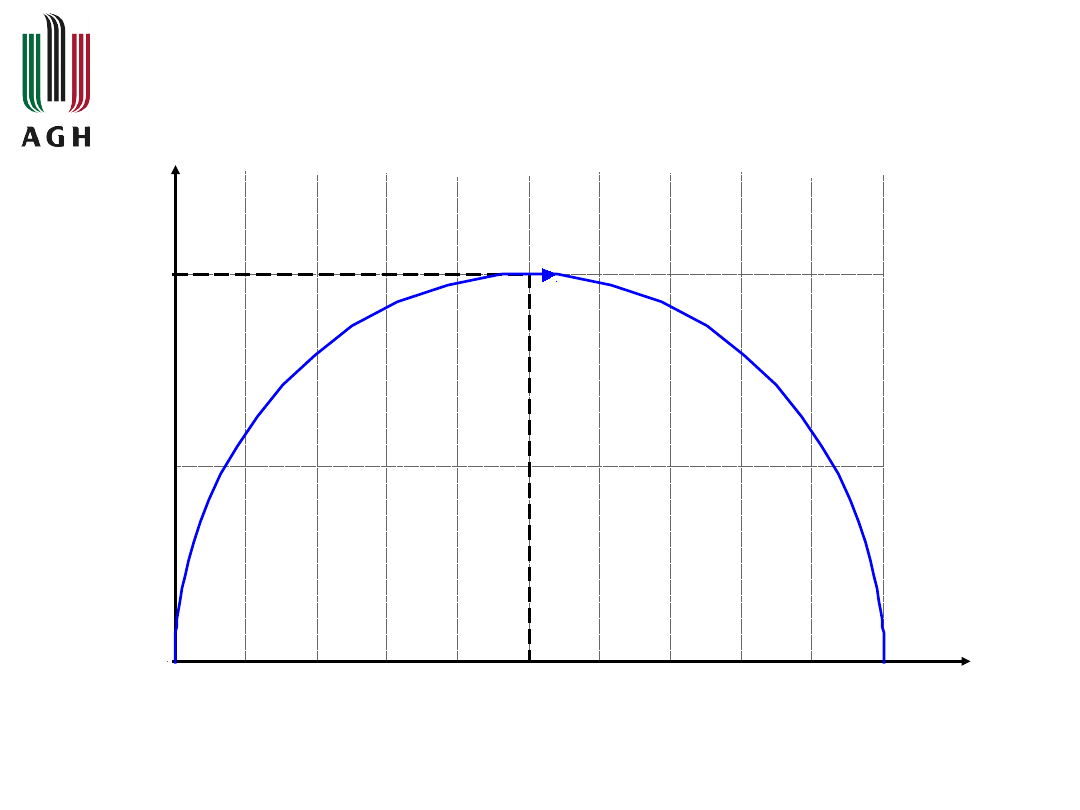
Charakterystyka amplitudowo-fazowa

=

=

0

1

Q()

P()

0

2

1

=1

35

Transmitancję widmową G(j



) można zapisać

jako:

)

tg

90

(

2

tg

2

90

1

2

1

2

1

2

)

(



















arc

j

arc

j

j

e

e

e

j

j

j

G















stąd równanie charakterystyki amplitudowej

2

1

2

)

(











M

Wyznaczenie logarytmicznej
charakterystyki amplitudowej

lub wyznaczone z
równania:

)

(

)

(

)

(

)

(

2

2









Q

P

j

G

M







2

2

2

2

2

4

2

2

)

1

(

4

)

1

(

4

)

(

)

(

)

(



























Q

P

M

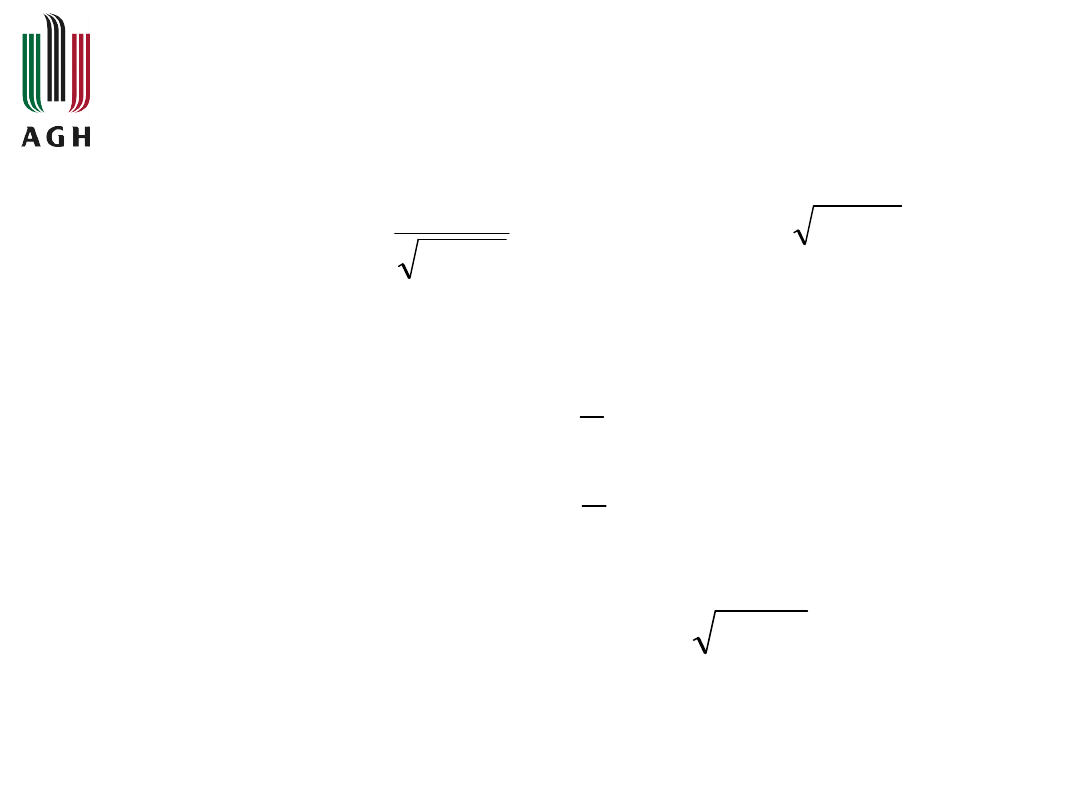
2

2

2

2

2

1

2

)

1

(

)

1

(

4

)

(























M

36

Chcąc wyrazić M(



) w decybelach korzystamy z

poniższego wzoru

2

2

1

log

20

2

log

20

1

2

log

20

)

(





















L

T

1





Aby wyznaczyć charakterystyki asymptotyczne cały
zakres częstotliwości dzielimy na dwie części:



dla



2

>> 1

czyli

T

1





Dla pierwszego zakresu częstotliwości, można w
równaniu

pominąć jego drugi składnik, stąd

2

1

log

20

2

log

20

)

(













L







2

log

20

)

(

,

1





L

dl
a



dla



2

<< 1

czyli

37

dB

L

6

2

log

20

)

(







Prosta o równaniu

2

1

1

2

0

2

log

20

















Dla drugiego zakresu częstotliwości, można w
równaniu

2

1

log

20

2

log

20

)

(













L

pominąć jedynkę pod pierwiastkiem, stąd

przecina oś odciętych przy pulsacji



, dla której

L(



)=0, czyli





2

log

20

)

(



L













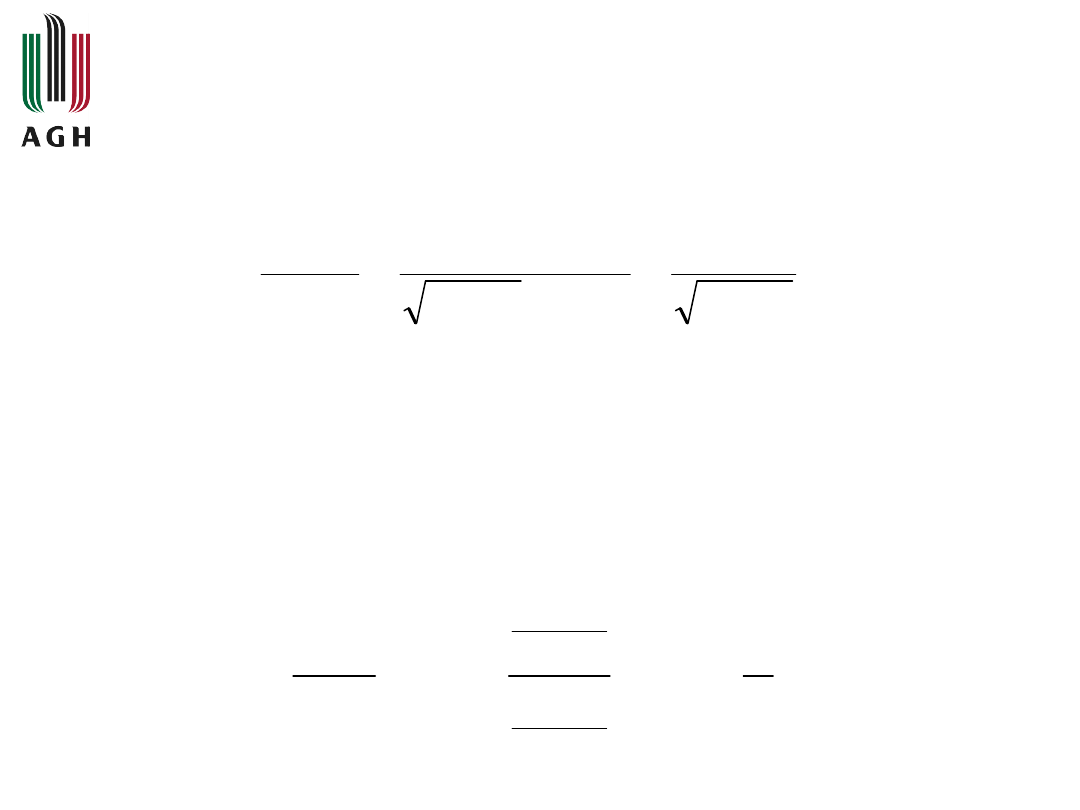
2

log

20

log

20

2

log

20

)

(

,

1









L

dl
a

38

Na podstawie
równania

 







tg

90 arc





Równanie to można także wyznaczyć ze
wzoru





















tg

90

1

tg

1

2

1

2

tg

)

(

)

(

tg

)

(

2

2

2

arc

arc

arc

P

Q

arc















Wyznaczenie

logarytmicznej

charakterystyki fazowej

)

tg

90

(

2

tg

2

90

1

2

1

2

1

2

)

(



















arc

j

arc

j

j

e

e

e

j

j

j

G















można napisać

39



 





2



4





0

1

0

Dla różnych wartości



z przedziału (0, +



) można

wyznaczyć wartość



(



) na podstawie wzoru

i zestawić dane w tabeli







T

arctg

)

(





40

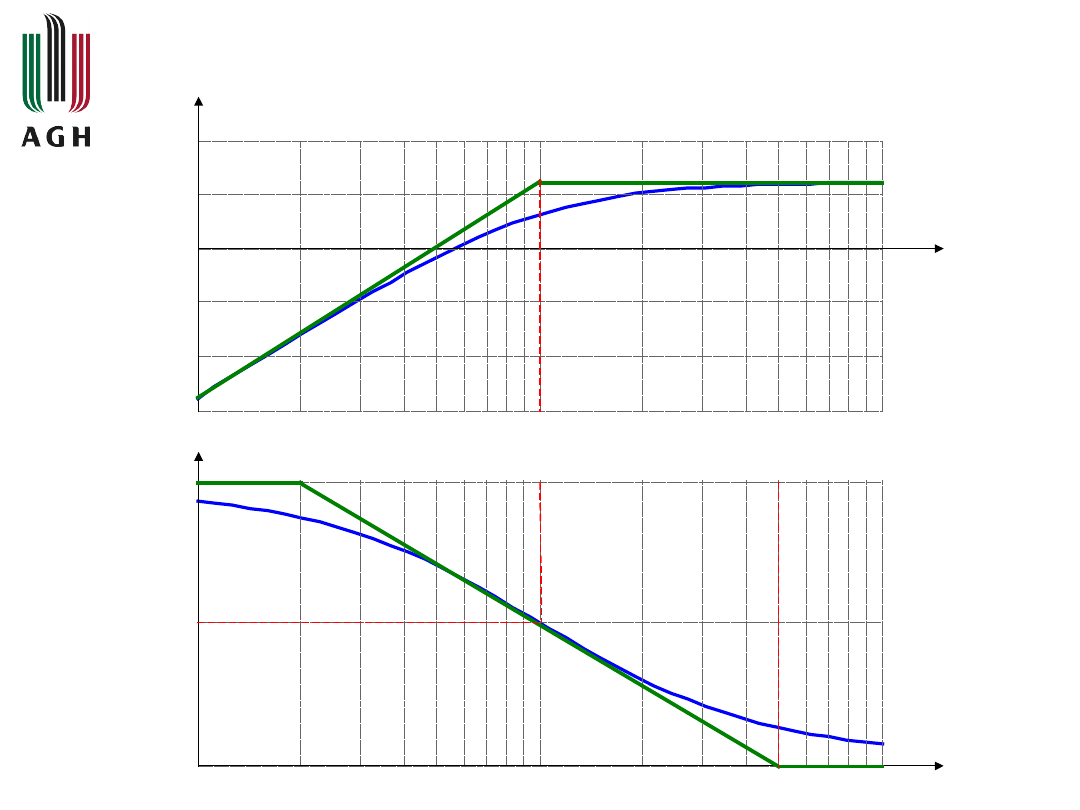
Przybliżoną logarytmiczną charakterystykę
fazową

można

wyznaczyć

stosując

aproksymację trzyodcinkową

.

Na podstawie częstotliwości sprzęgającej 

s

wyznaczamy dwie częstotliwości pomocnicze


1

=1/5

s

= 0.2[1/s] i 

2

=5

s

= 5[1/s] i

rysujemy trzy odcinki aproksymujące.

41

L()



10

5

0

-
5

-10

10

-1

10

0

10

1

-15

()



0

45

90

10

-1

10

0

10

1



s

1/5

s

5

s

Charakterystyki logarytmiczne układu



s

42

Generowanie

charakterystyk

częstotliwościowych
w programie MATLAB

Dana

jest

transmitancja

układu

oscylacyjnego

1

)

(

2

2

1







s

T

s

T

K

s

G

którą przedstawiamy w przestrzeni roboczej
MATLAB-a w następujący sposób

- licznik transmitancji
- mianownik transmitancji

Generowanie charakterystyki amplitudowo-fazowej

nyquist(l,

m)

Generowanie charakterystyk logarytmicznych:
amplitudowej i fazowej

l=[K

]

m=[T

1

T

2

1]

bode(l,m)