P

K

M

I

wytrzymałość

zmęczeniowa

Wytrzymałość - obciążenie

• Wytrzymałość doraźna – obciążenia

statyczne (było)

• Wytrzymałość zmęczeniowa –

obciążenia zmienne w czasie (np.
wielokrotne zginanie metalowego
pręta)

Współczynniki bezpieczeństwa ?

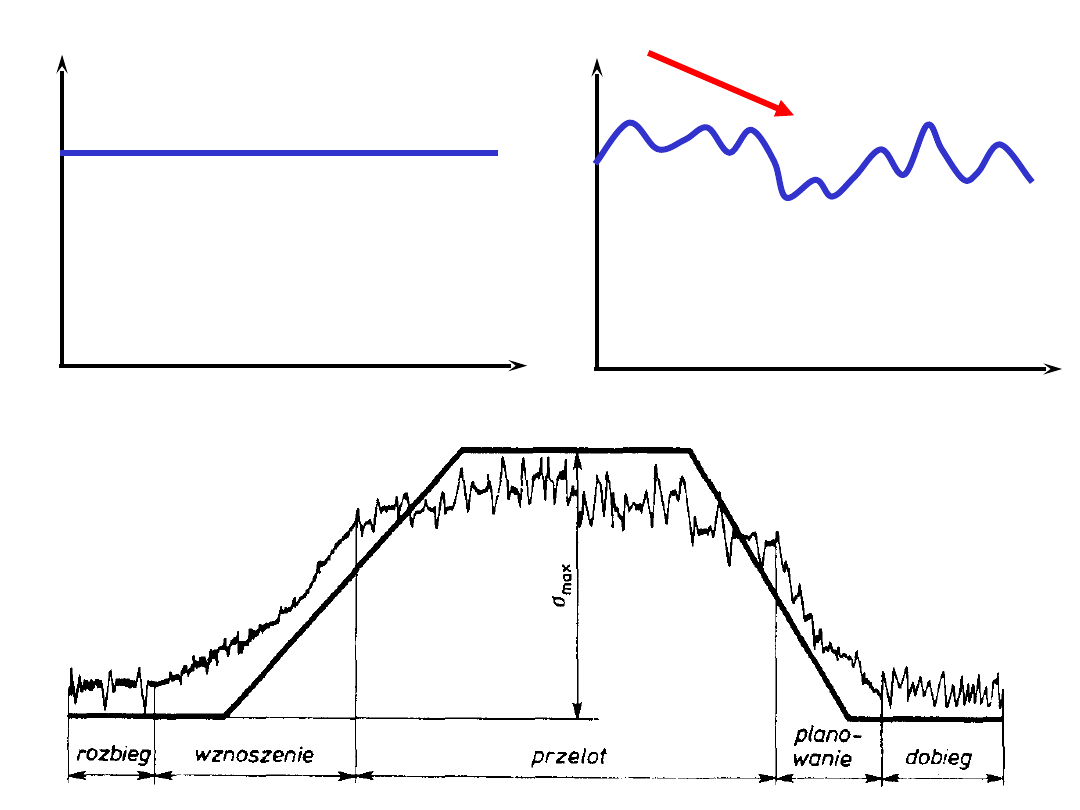
naprężenia zmienne w czasie – przyczyna zmęczenia !

t

σ

t

σ

Naprężenia zmienne w
czasie

Naprężenia stałe w
czasie

Samolot –
obciążenia
losowe

Zginanie zmęczeniowe

szyny

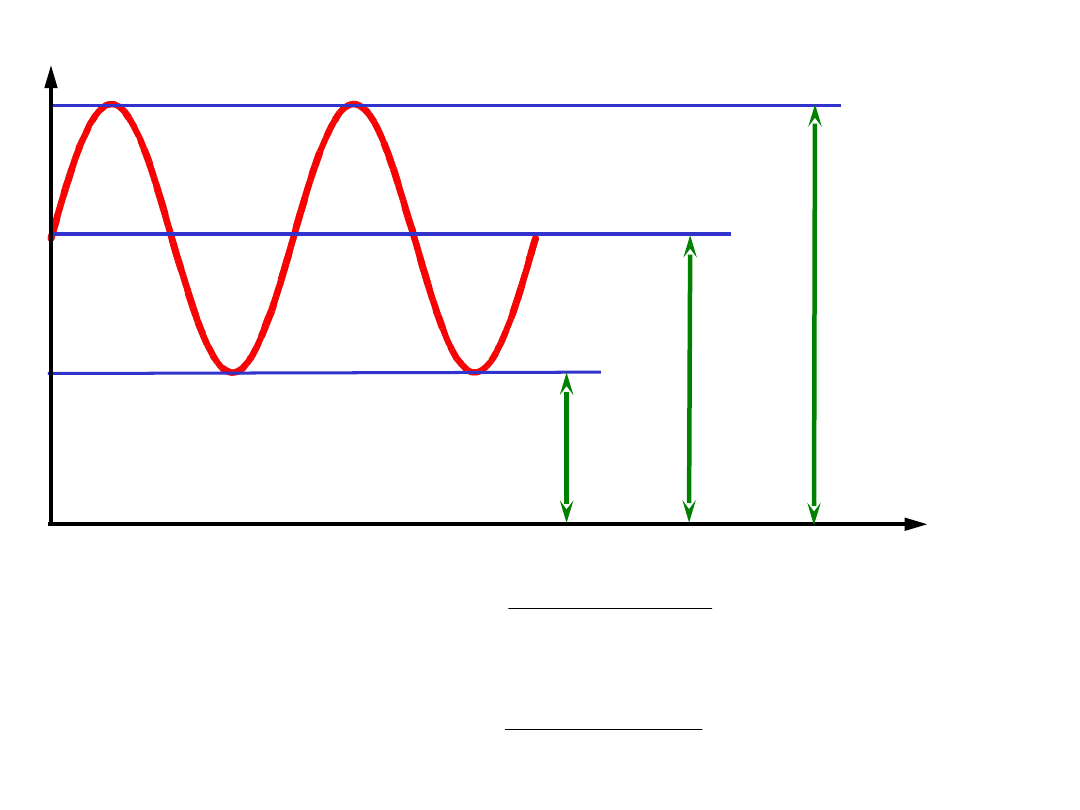
naprężenia zmienne okresowe – np. sinusoidalnie zmienne

t

σ

σ

min

σ

m

σ

max

2

min

max











m

2

min

max











a

naprężenia średnie

amplituda naprężeń

Okres T [s] lub
częstotliwość f [Hz]

Przykład

1,2,3

Przykłady

• Obracająca się zginana oś (wał a

oś ?)

T i f ?

• inne

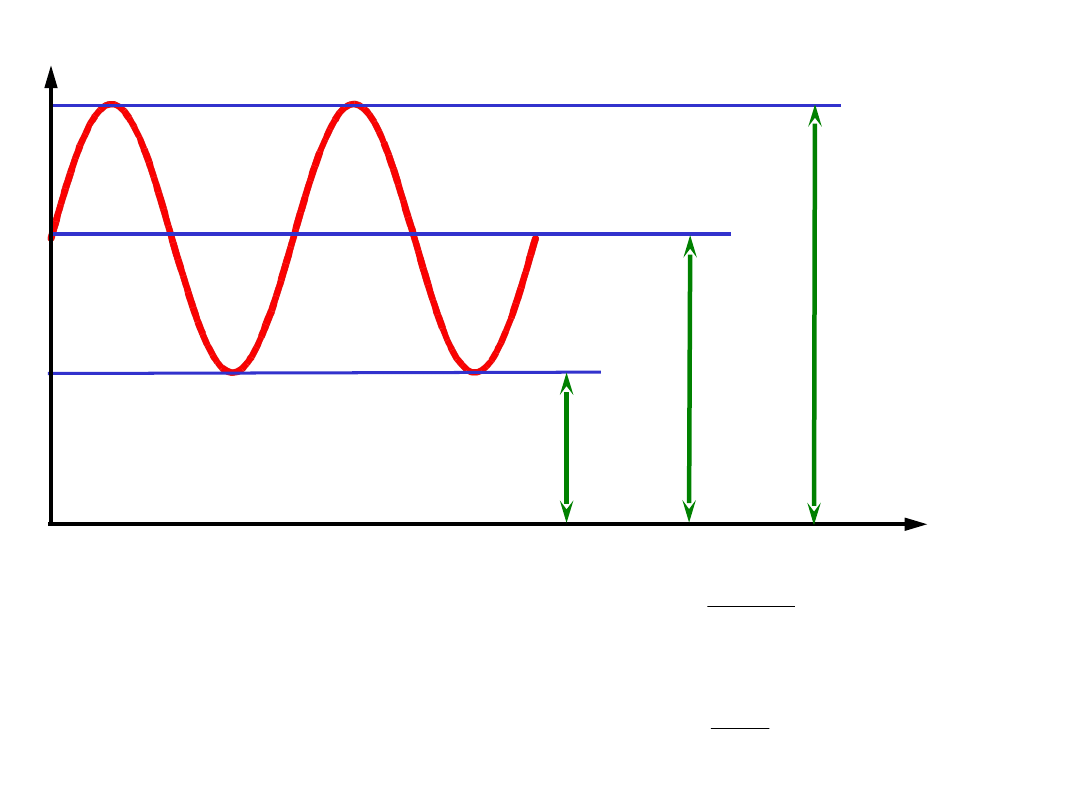
naprężenia zmienne

t

σ

σ

min

σ

m

σ

max

max

min







R

a

m









współczynnik asymetrii cyklu

współczynnik stałości
obciążenia

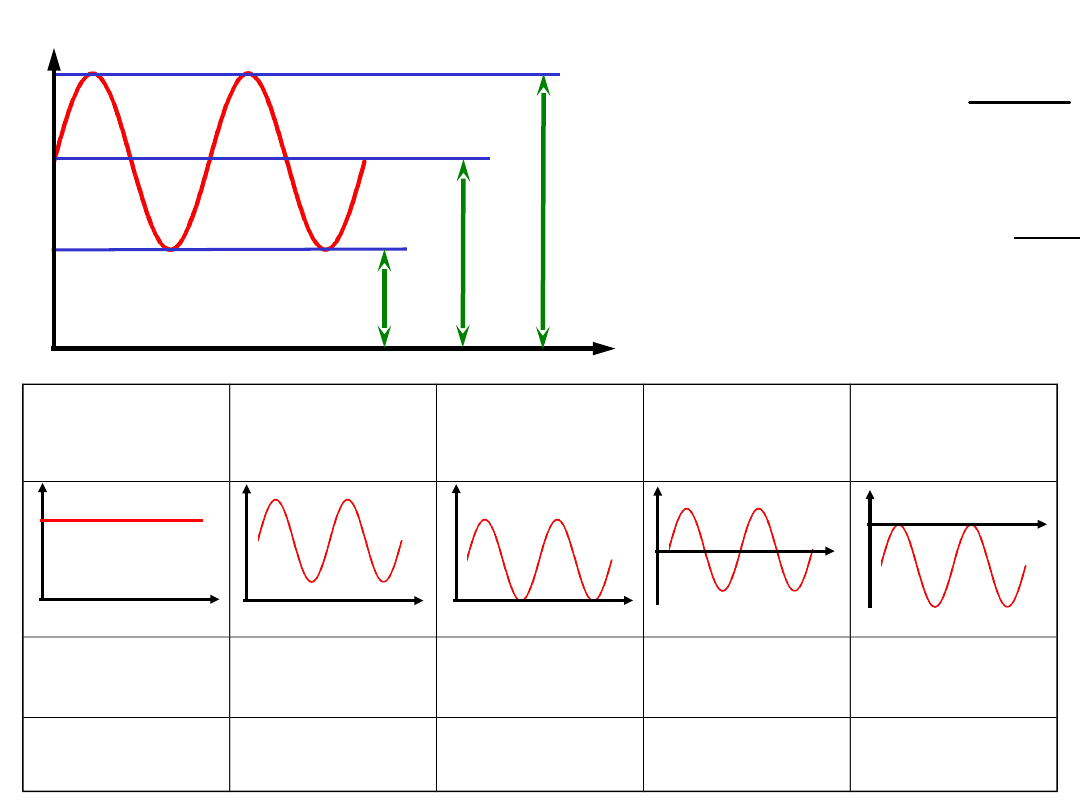
t

σ

σ

min

σ

m

σ

max

naprężenia zmienne

naprężenia

stałe

jednostronny

dodatni

odzerowo

tętniący

dodatni

wahadłowy

odzerowo

tętniący

ujemny

max

min







R

a

m









R = +1

 = +

0 < R <

1

1 <  <

+

R = 0

 = 1

R = -1

 = 0

R = ±

 = -1

Asymetria
cyklu:

Współczynnik
stałości
obciążenia

Związki R -  ?

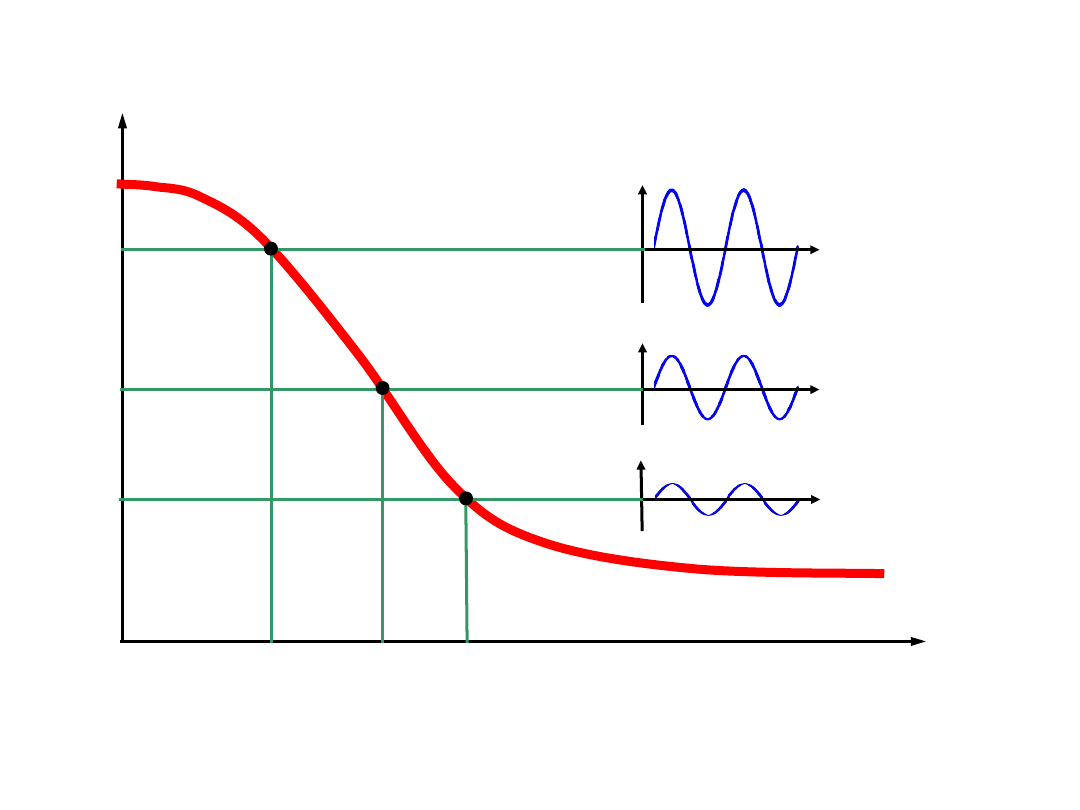
wykres Wöhlera – najczęściej cykle wahadłowe

N

σ

a

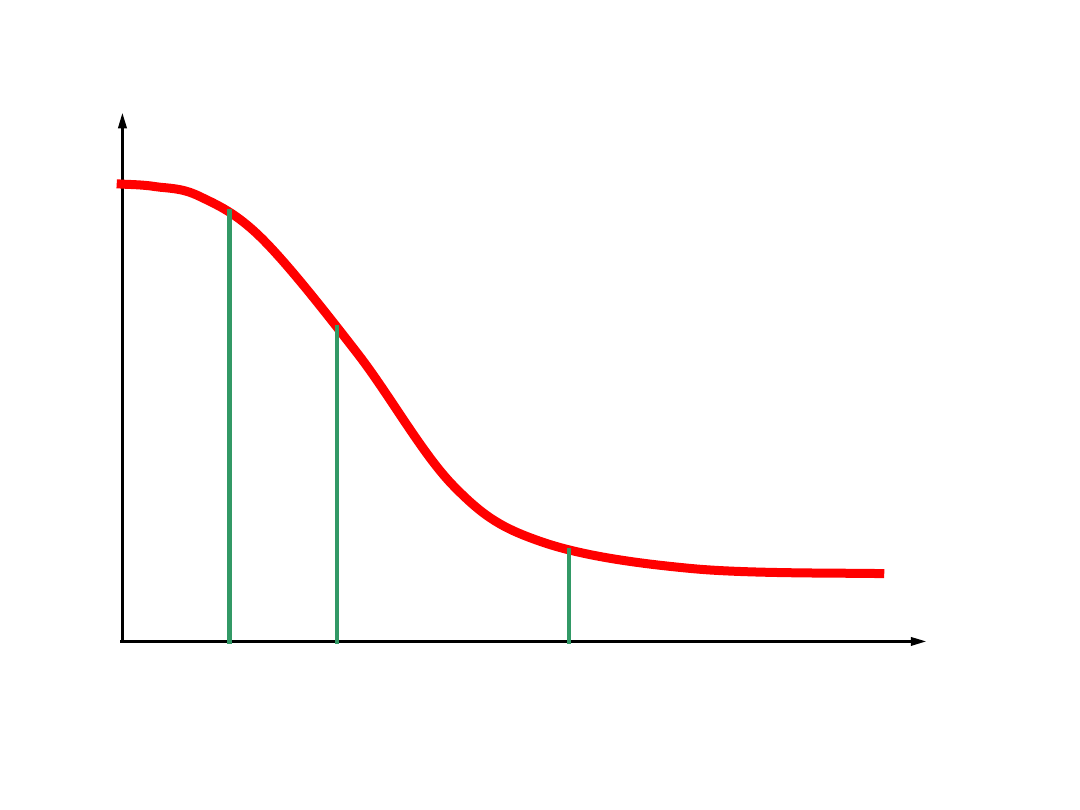
wykres Wöhlera

N

1/4

10

3

10

4

10

7

I

II

III

IV

I - w. quasi-
statyczna

II - w. niskocyklowa

III - w.
wysokocyklowa

IV - w.
nieograniczona

1·10

7

- stal

1·10

8

- metale nieżelazne

σ

a

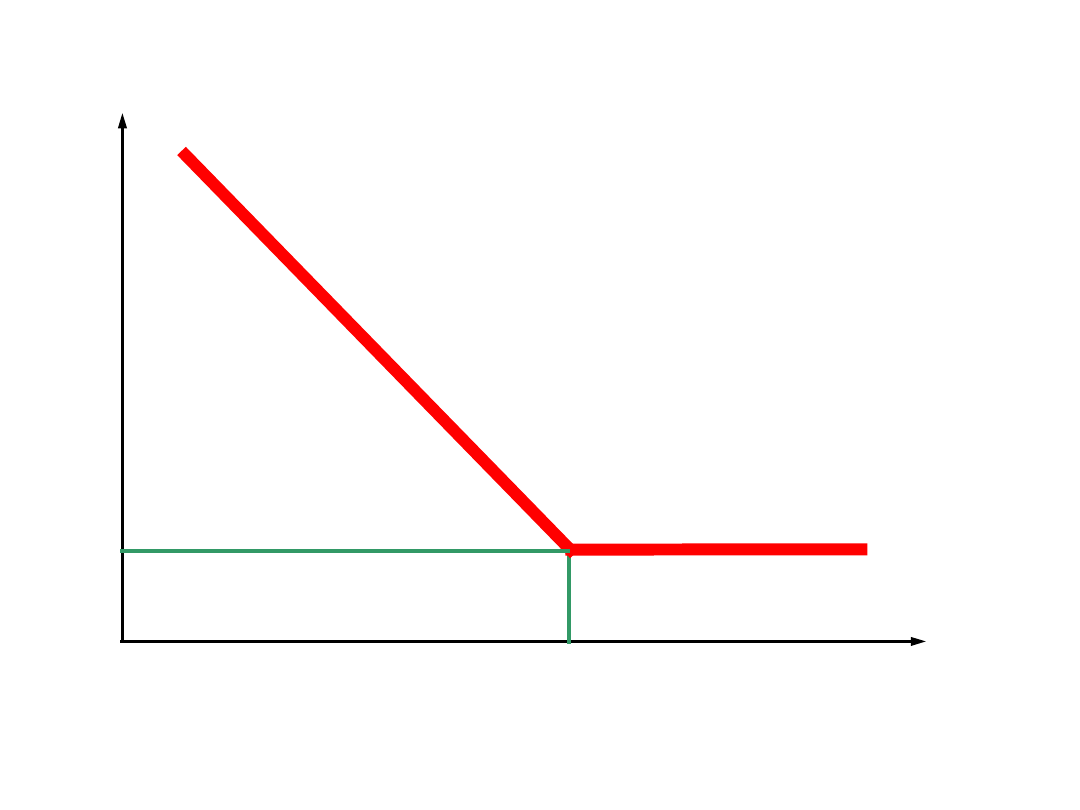
wykres Wöhlera

Log N

σ

a

10

3

Z

g

Z

g0

- zginanie

wahadłowe

Z

gj

- zginanie

odzerowe

Z

s0

- skręcanie

wahadłowe

Z

sj

- skręcanie

odzerowe

Z

rc

- rozciąganie-

ściskanie

wahadłowe

Z

rj

- rozciąganie

odzerowo tętniące

Z

cj

- ściskanie

odzerowo tętniące

Z

g

– granica zmęczenia

N

0

Nieograniczona wytrzymałość zmęczeniowa

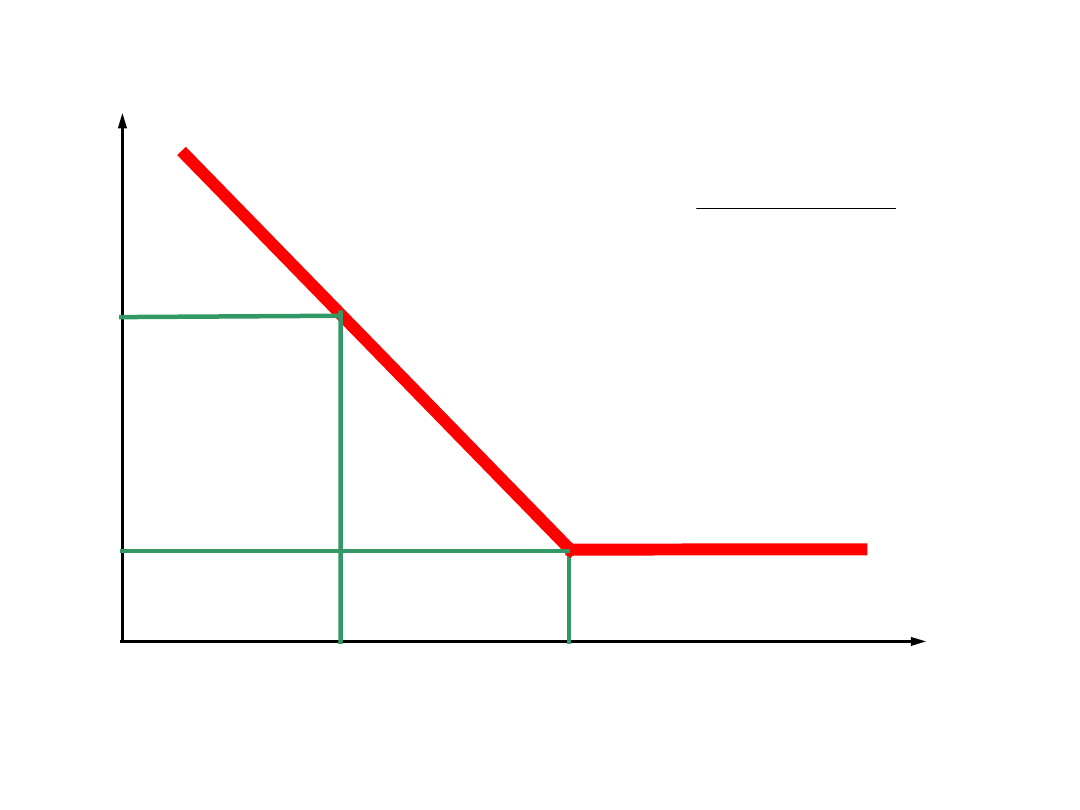
wykres Wöhlera

Log N

10

3

N

0

Z

g

Z

g

– granica zmęczenia

N

σ

a

0

log

log

N

k

Z

N

k

g

a









N

N

Z

k

g

a

log

log

0









stal 45 (C45) – wahadłowe zginanie:

σ

a

= 350 MPa

N = 10

5

Z

g

= 280 MPa

N

0

=

1,2·10

6

k=65

Równanie nachylonej prostej:

Współczynnik
:

σ

a

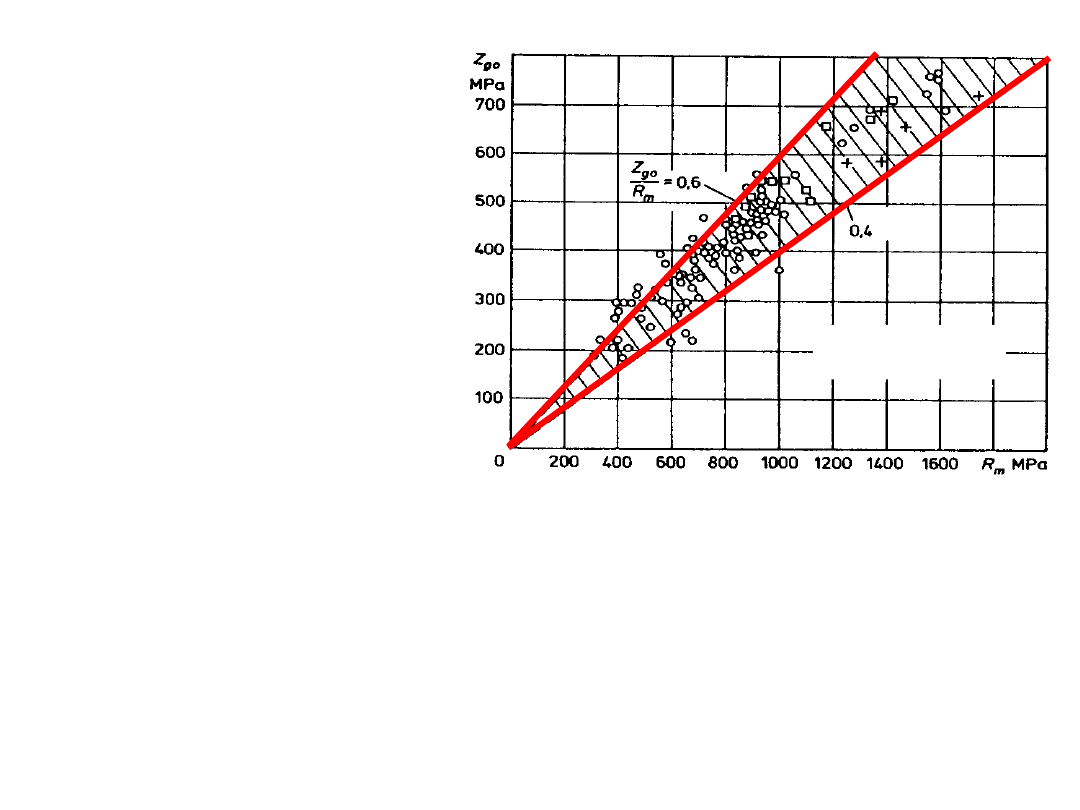
granica zmęczenia – stale konstrukcyjne

przybliżone wartości granic zmęczenia:

stale węglowe i stopowe obrabiane cieplnie:

Z

g0

=0,45·R

m

Z

gj

=0,7·R

m

Z

rc

=0,33·R

m

Z

rj

=(0,55÷0,63)·R

m

Z

s0

=0,25·R

m

Z

sj

=(0,45÷0,5)· R

m

zginanie

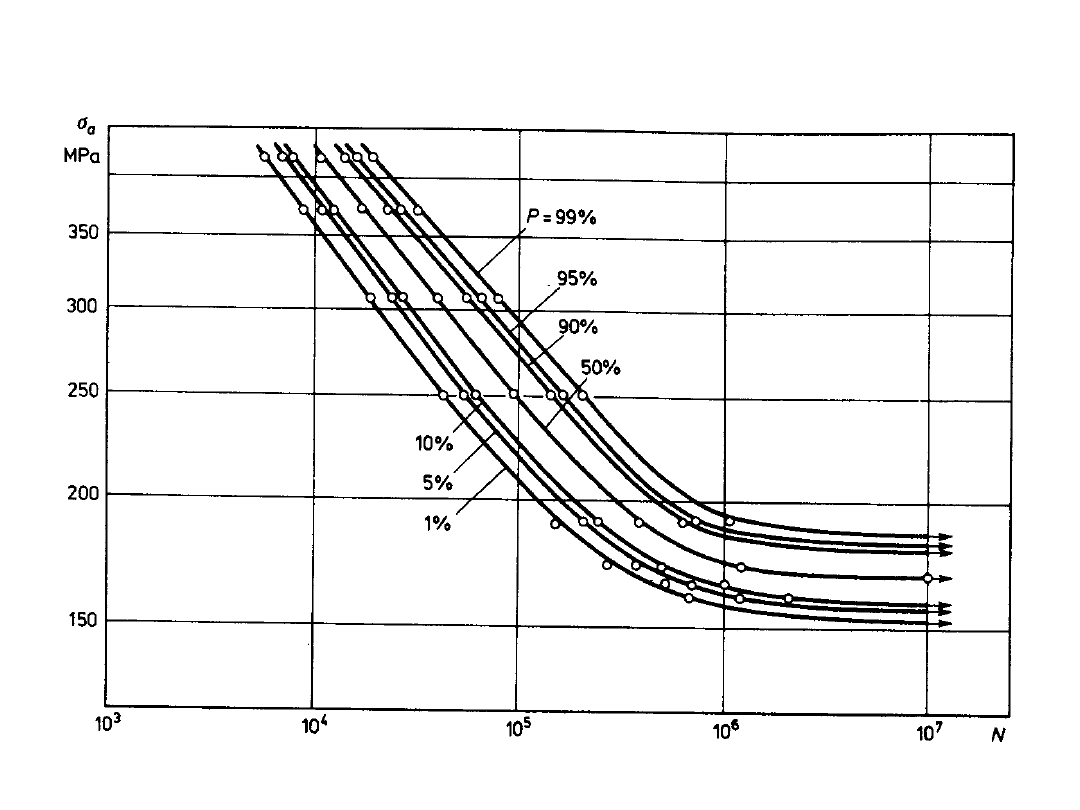
granica zmęczenia – ujęcie probabilistyczne (duże rozrzuty !) – zginane próbki
stal C45

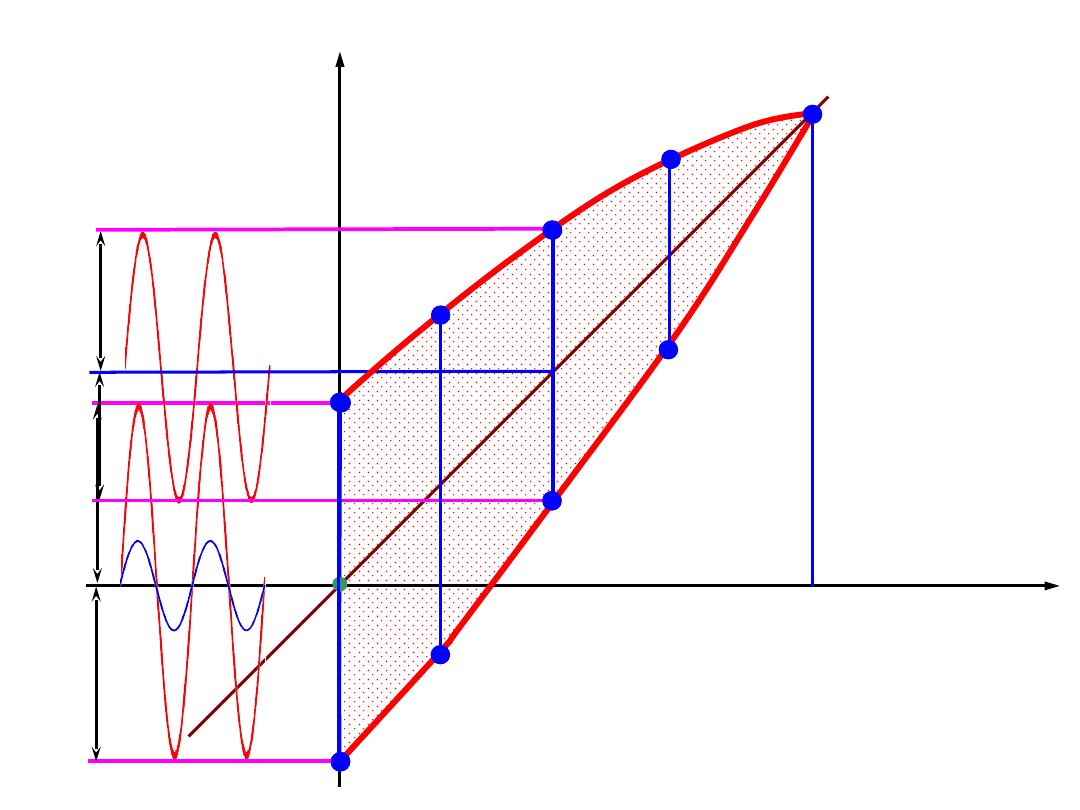
wykres zmęczeniowy Smitha – uwzględnia naprężenia średnie

– opisuje właściwości materiałowe -

zmęczeniowe

σ

m

σ

m

σ

max

σ

min

σ

max

σ

min

σ

m

σ

m

R

m

σ

max

σ

min

Zg

const

m





Granice zmęczenia
z wykresów

Wöhlera

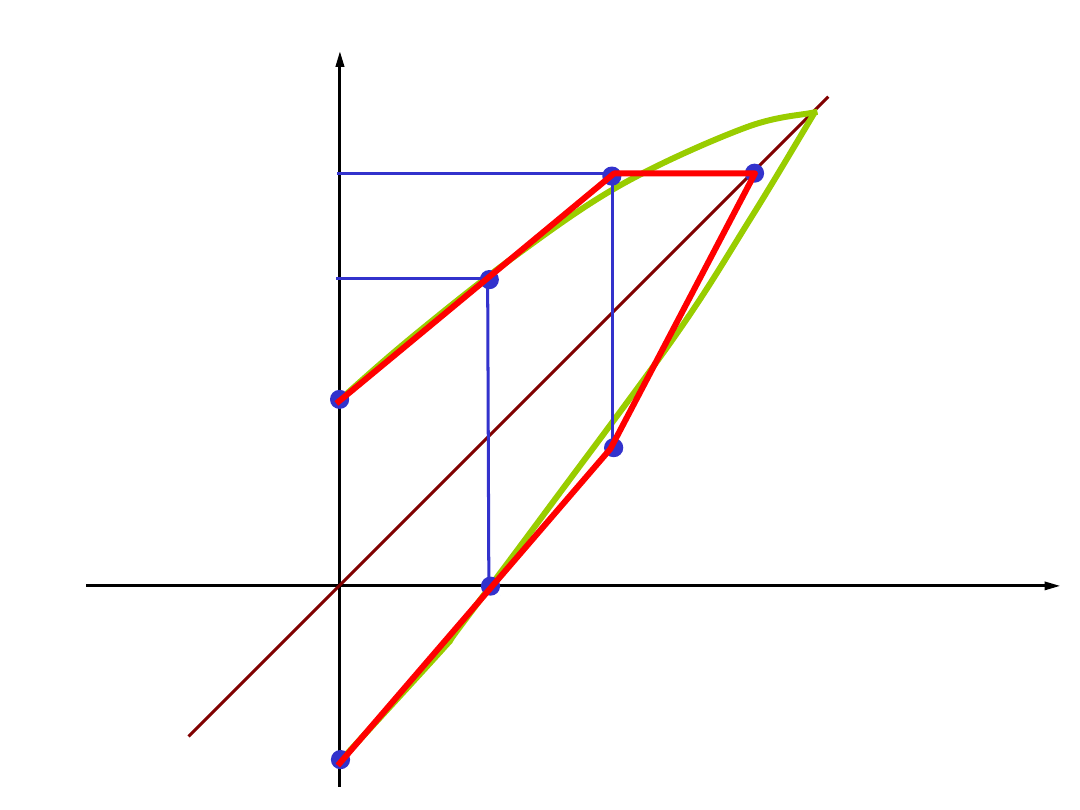
wykres zmęczeniowy Smitha - uproszczony

σ

m

R

e

Z

r

c

Z

rj

Z

rj

/2

σ

max

σ

min

Zg

Jakie
dane ?

Jakie N ?

Jakie R ?

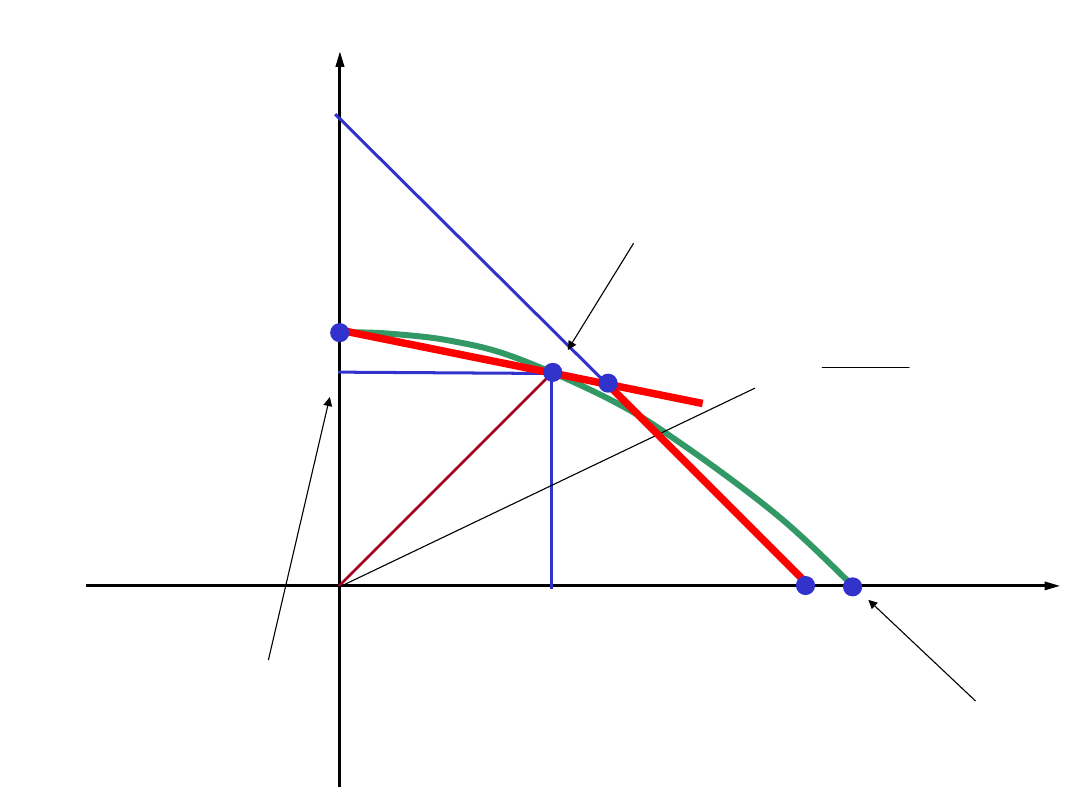
wykres zmęczeniowy Haigha

σ

m

σ

a

R

e

Z

r

c

Z

rj

/2

Z

rj

/2

R

e

R

m

const

R





max

min





Obciążenie
wahadłowe

Obciążenie
statyczne

Obciążenie odzerowo-
tętniące

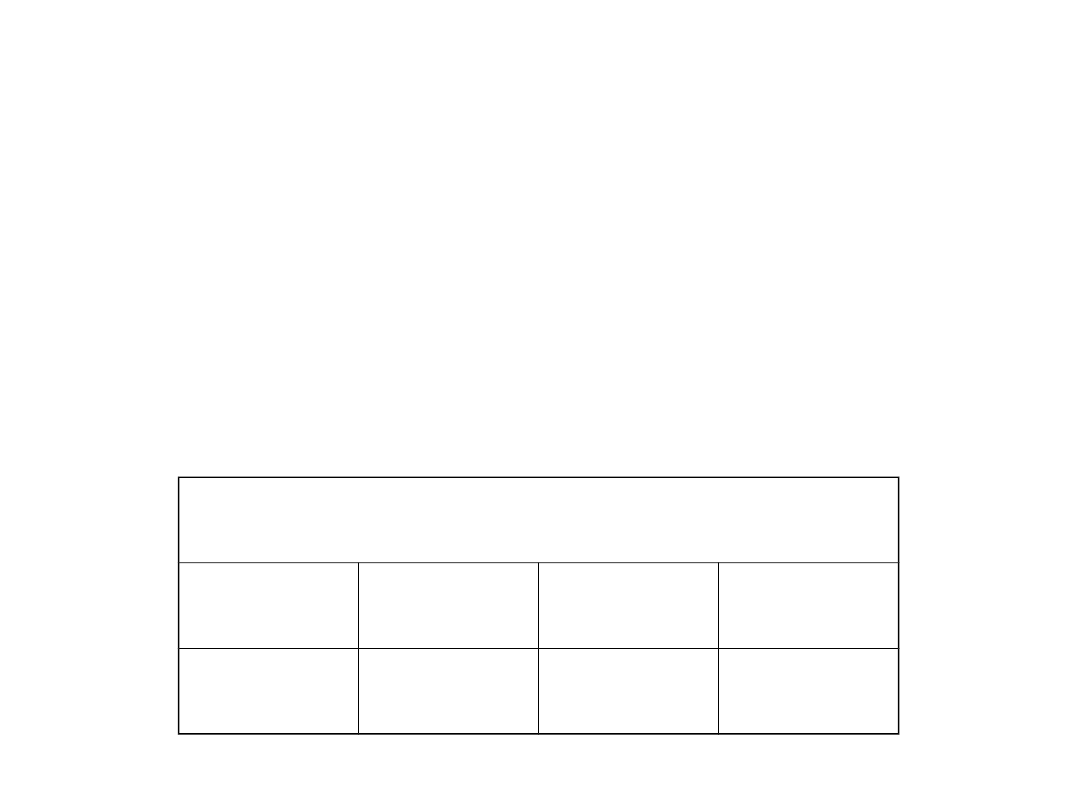
Zadanie 1

– wykres Smitha

1. Narysować wykres Smitha wg stałych materiałowych

podanych w tabeli.

2. Obliczyć dopuszczalne amplitudy naprężenia σ

a1

oraz σ

a2

tak, aby element miał nieograniczoną

wytrzymałość zmęczeniową.

własności mechaniczne [MPa]

R

m

R

e

Z

g0

Z

gj

650

430

280

470

Element ze stali 45 poddany jest czystemu zginaniu, przy
czym naprężenie średnie wynosi σ

m1

=100 MPa lub

σ

m2

=350 MPa.

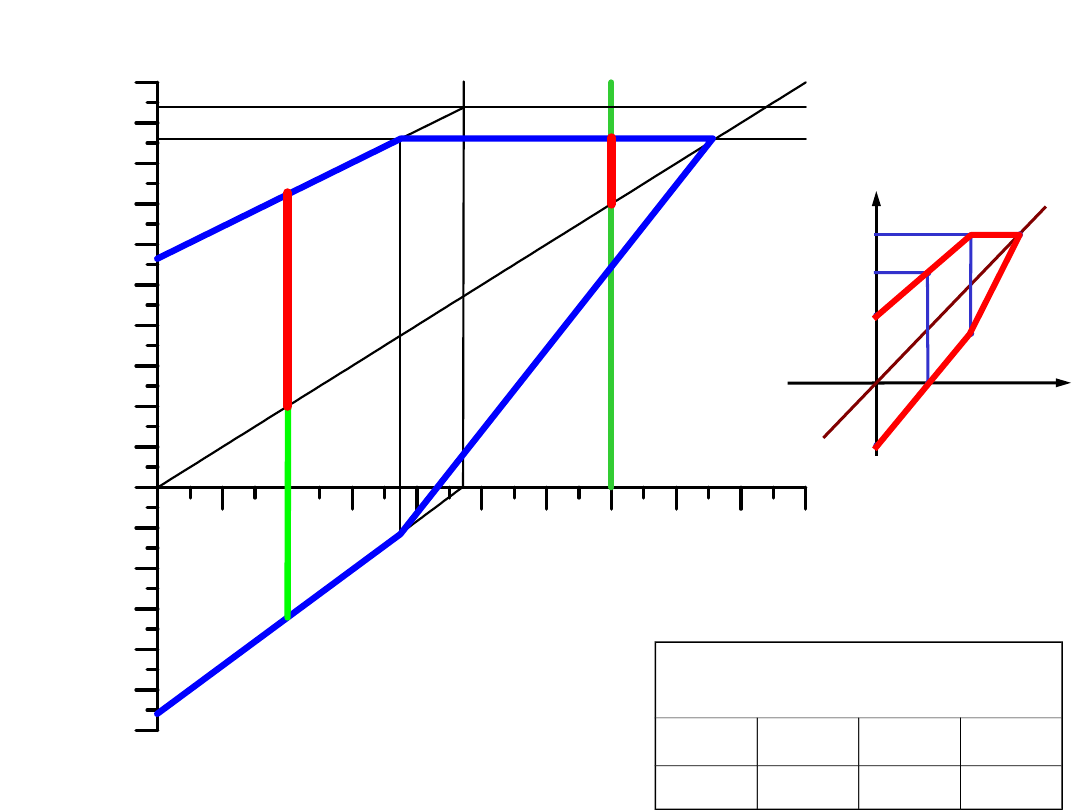
Zadanie 1

– wykres Smitha

własności mechaniczne

[MPa]

R

m

R

e

Z

g0

Z

gj

650

430

280

470

σ

m

R

e

Z

rc

Z

rj

Z

rj

/2

σ

max

σ

min

5 0

1 0 0

1 5 0

2 0 0

2 5 0

3 0 0

3 5 0

4 0 0

4 5 0

5 0 0

- 3 0 0

- 2 5 0

- 2 0 0

- 1 5 0

- 1 0 0

- 5 0

0

5 0

1 0 0

1 5 0

2 0 0

2 5 0

3 0 0

3 5 0

4 0 0

4 5 0

5 0 0

R

e

Z

gj

Z

gj

/2

Z

g0

-Z

g0

σ

m2

σ

a2

σ

a1

σ

m1

σ

m

Z

g

log N

σ

Z

g

brak
pęknięć

pęknięcie
krytyczne

wzrost
pęknięcia

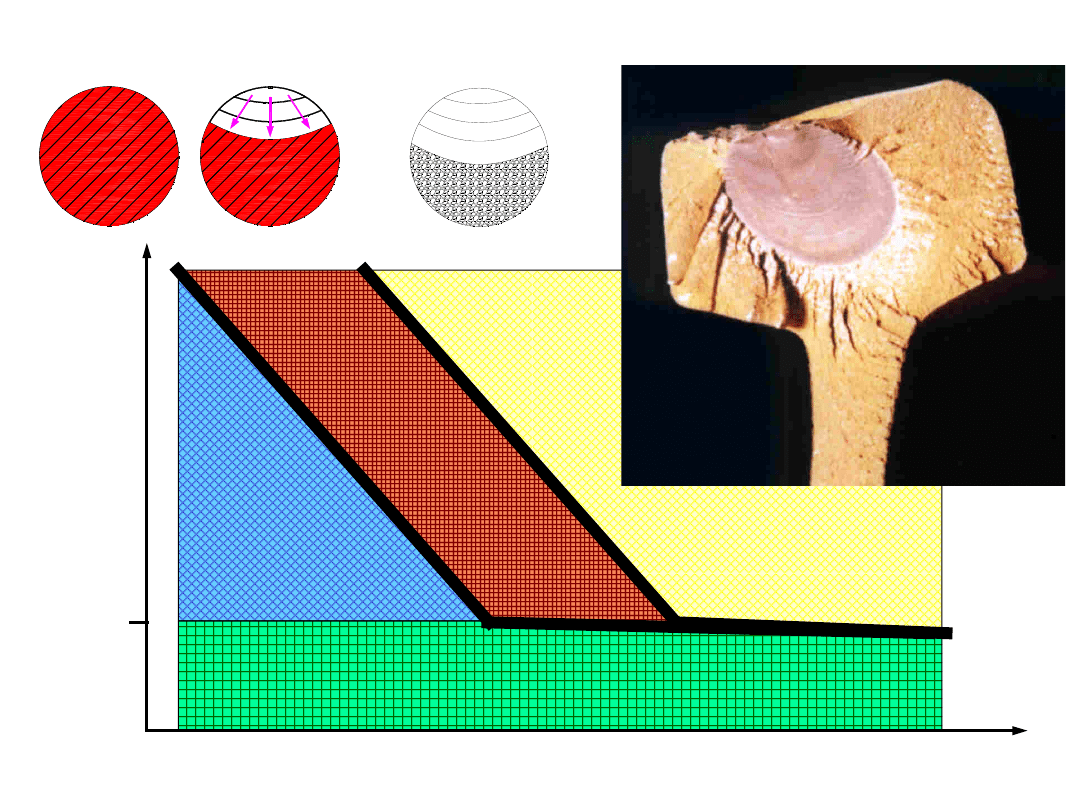
proces zniszczenia zmęczeniowego

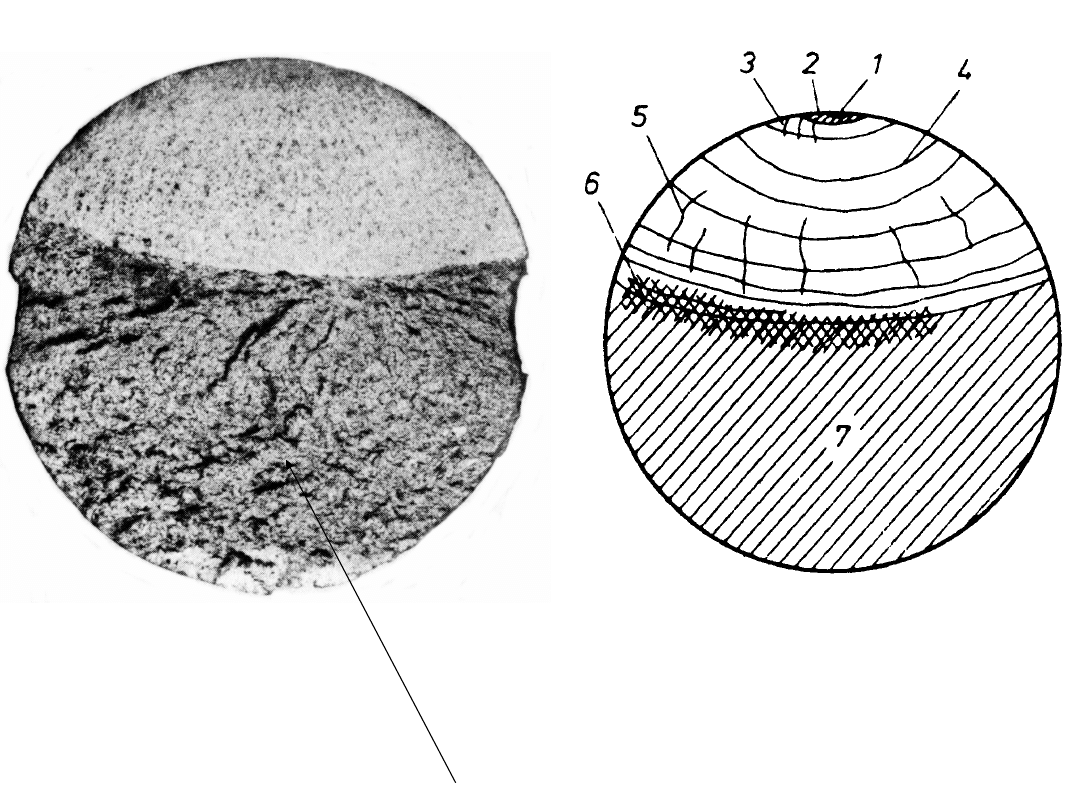
proces zniszczenia zmęczeniowego – przełom zmęczeniowy

1 - ognisko
2 - strefa przyogniskowa
3 - uskoki pierwotne
4 - prążki zmęczeniowe
5 - uskoki wtórne
6 - strefa przejściowa
7 - strefa resztkowa

gładkie

Właściwości zmęczeniowe

• Współczynnik kształtu

α

k

(wałek z

karbem)

• Współczynnik działania karbu

β

k

(wrażliwość materiału na działanie
karbu

η

k

- materiał kruchy i plastyczny)

• Współczynnik wielkości przedmiotu

ε

• Współczynnik obróbki powierzchni

β

p

•

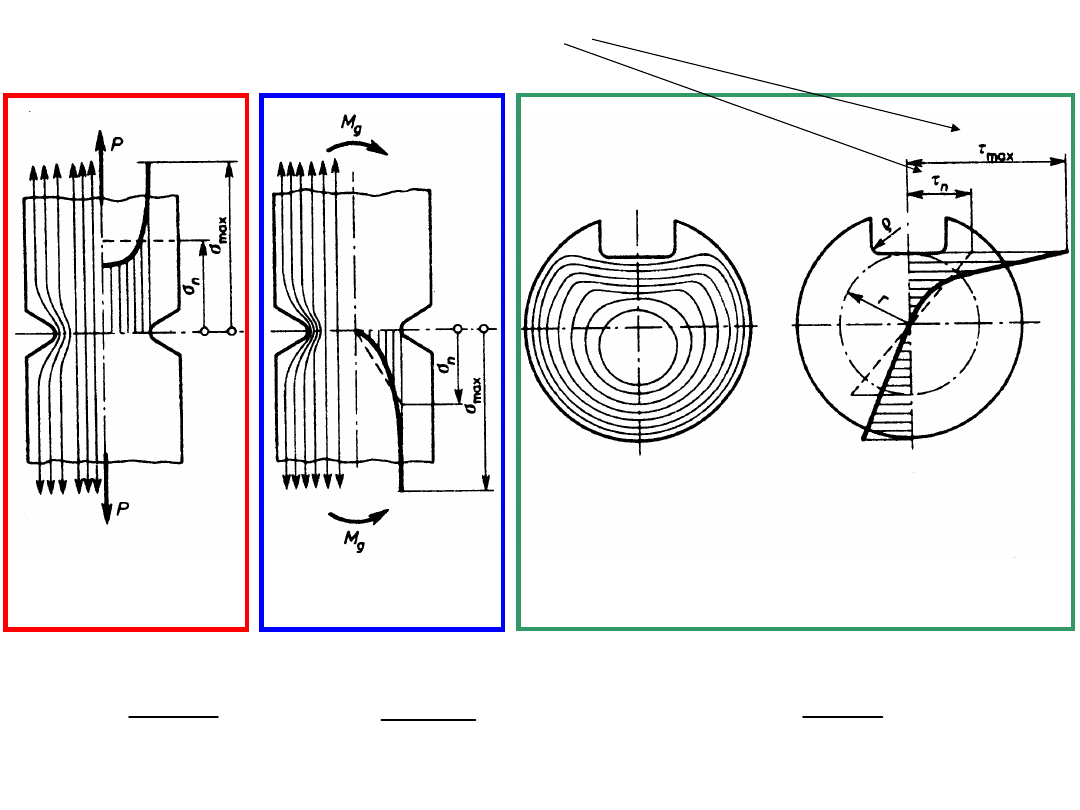
współczynnik kształtu – karb – zmiana rozkładu naprężeń (spiętrzenie) !
Zmęczenie

Rowki, otwory, wycięcia, gwinty …

rozciąganie

zginanie

skręcanie

n

k







max



n

k







max



n

k







max



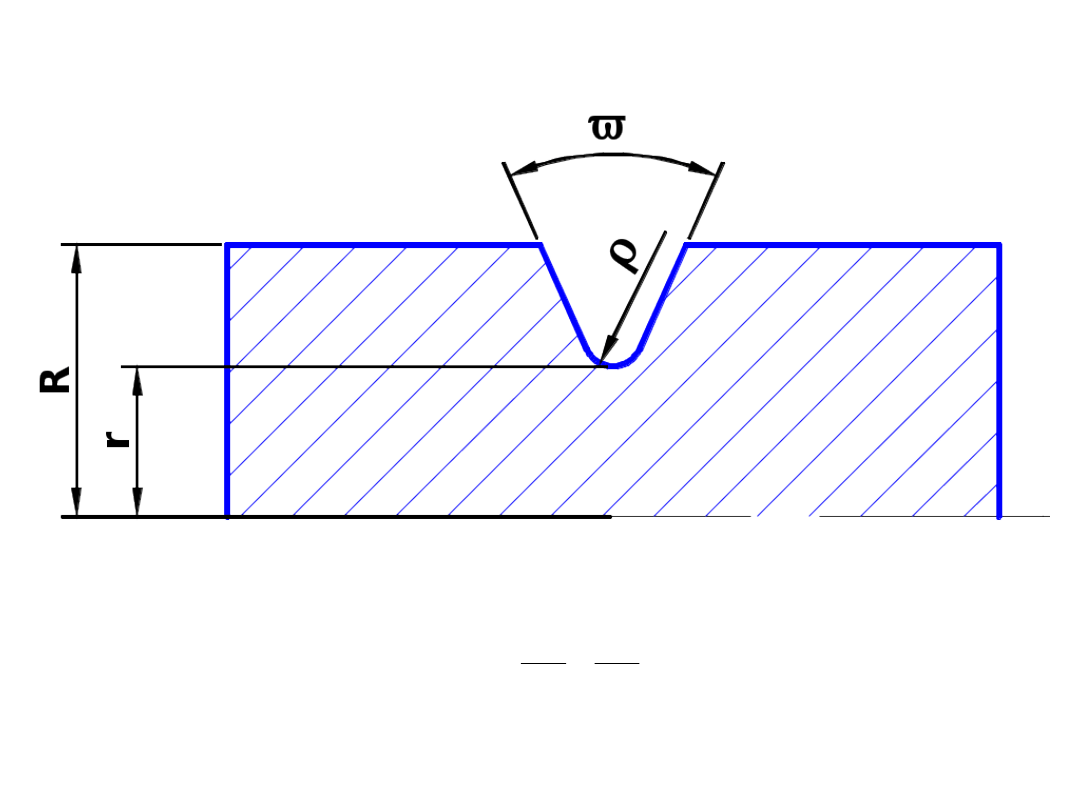
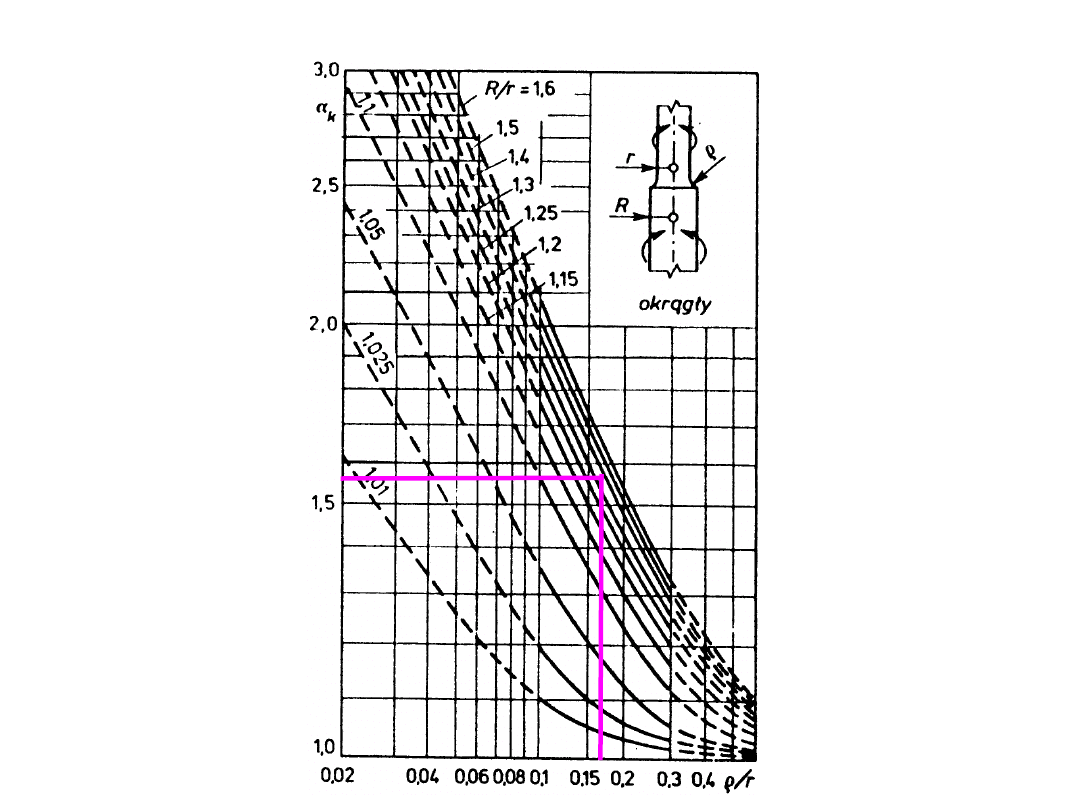
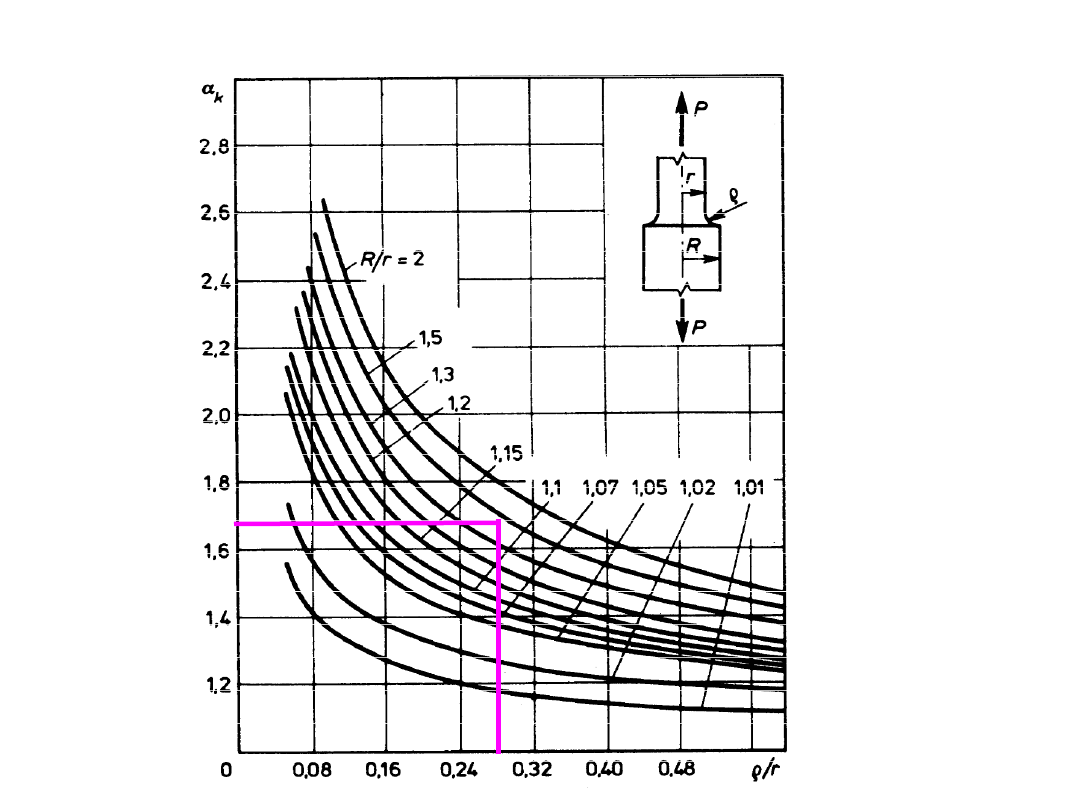
współczynnik kształtu – zależny wyłącznie od geometrii karbu





















,

,

r

R

r

f

k

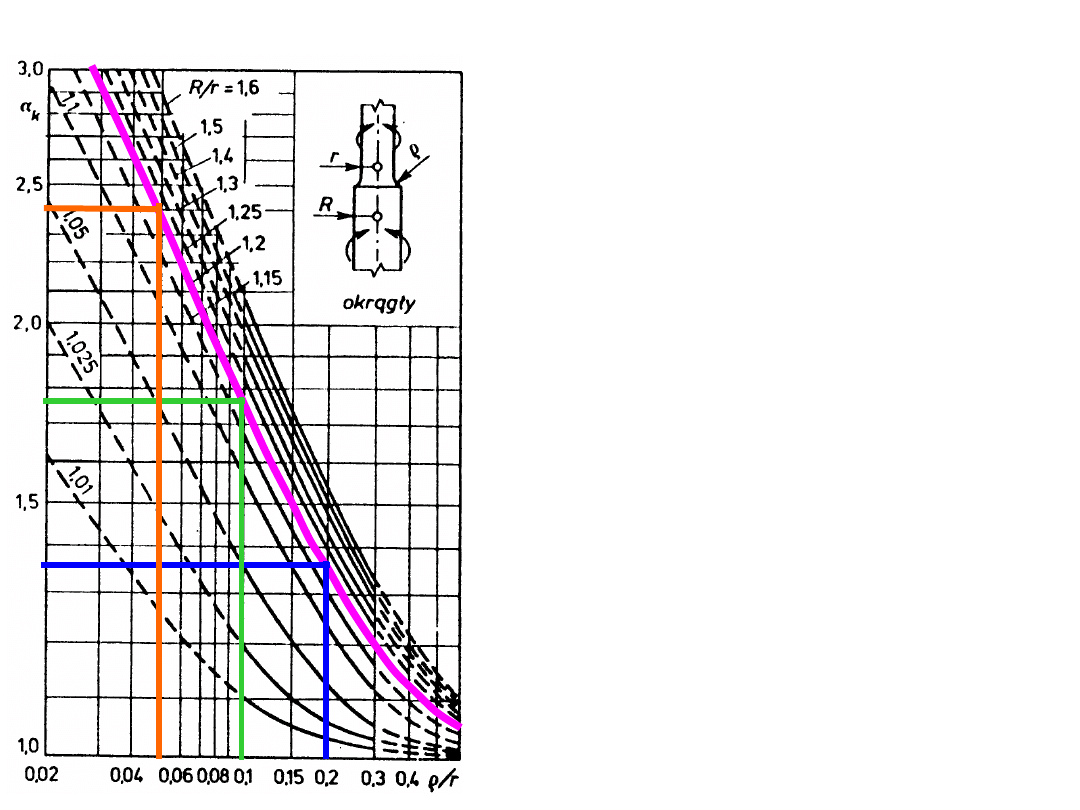
współczynnik kształtu

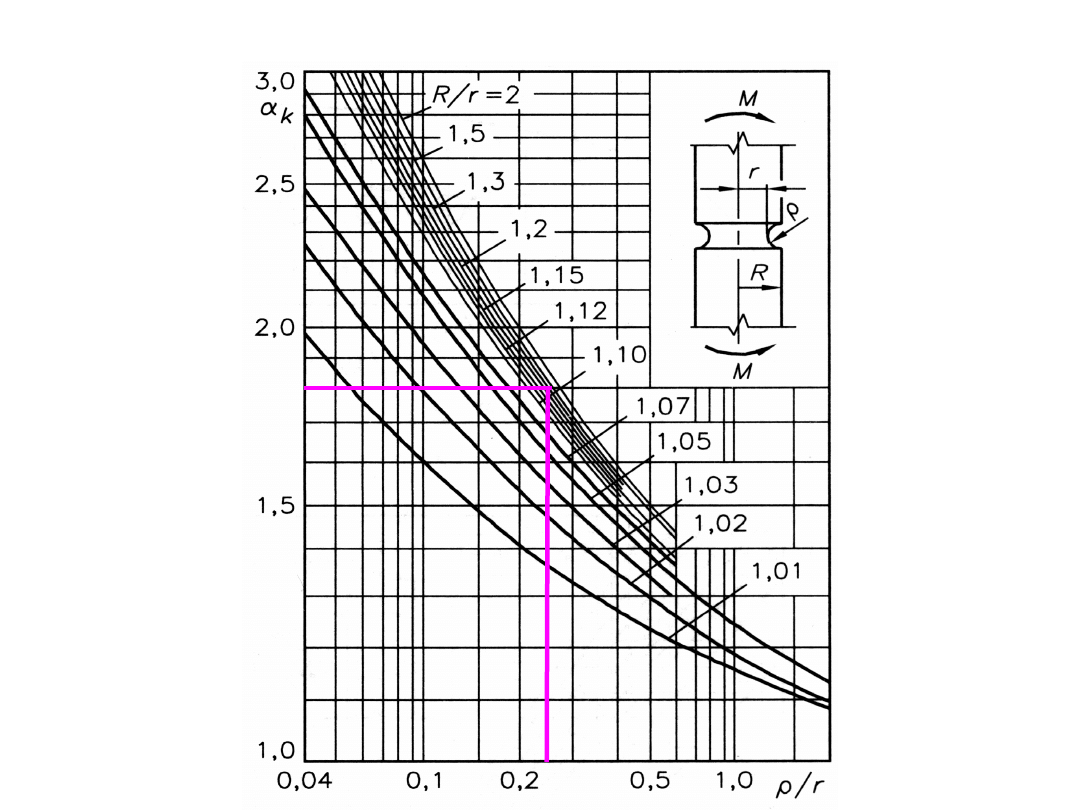
skręcanie pręta

okrągłego

z odsadzeniem

R = D/2 = 24 mm

r = d/2 = 20 mm

R/r = 24/20 = 1,2

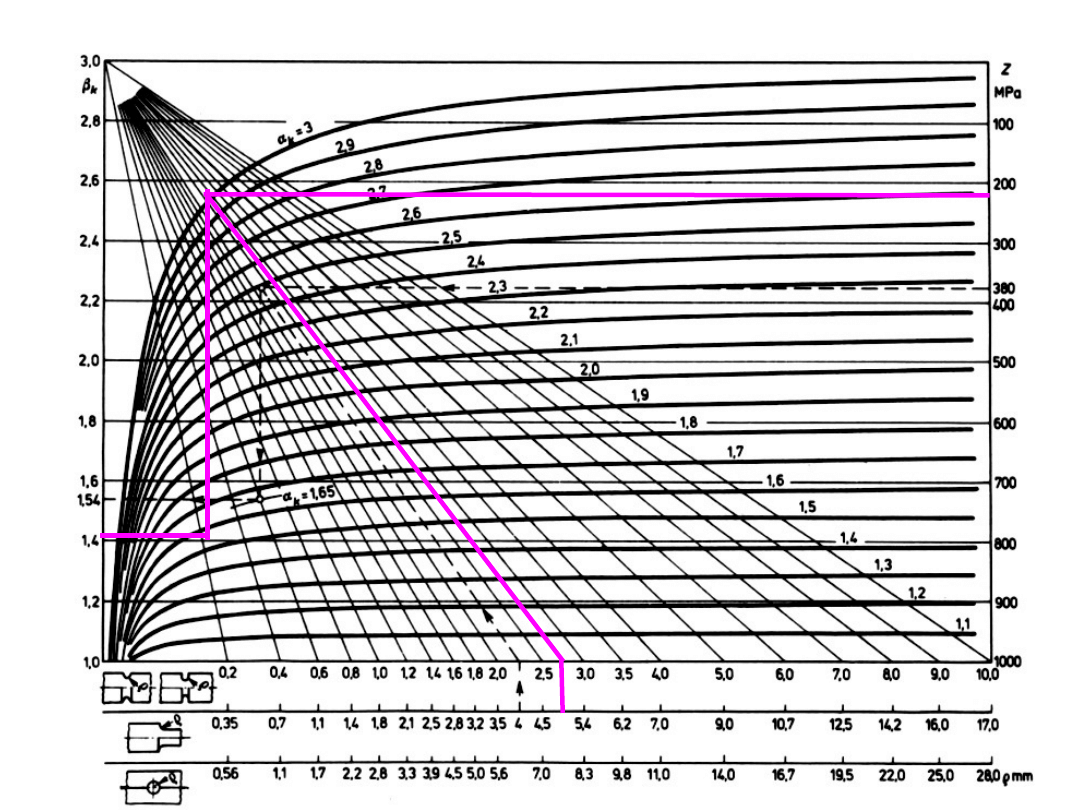
ρ = 4 mm ρ/r = 4/20 = 0,2 α

k

=

1,35

ρ = 2 mm ρ/r = 2/20 = 0,1 α

k

=

1,76

ρ = 1 mm ρ/r = 1/20 = 0,05 α

k

=

2,4

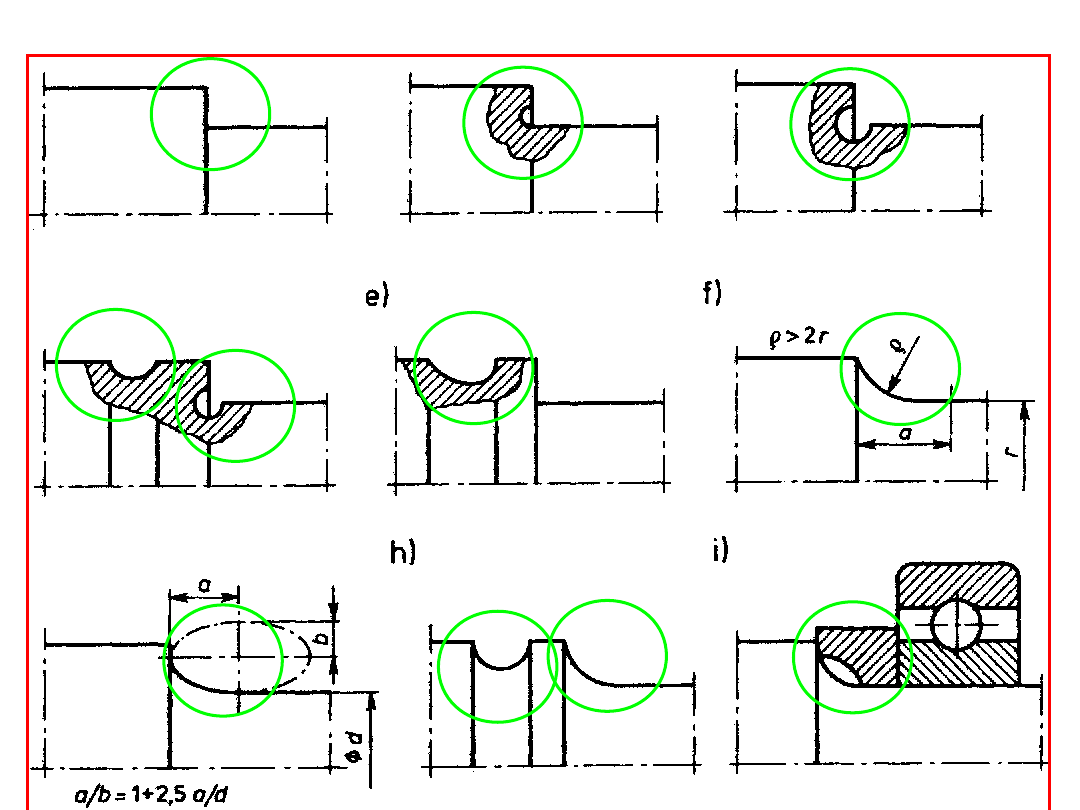
Zmniejszenie wpływu karbu (współczynnika kształtu) – odciążenie – przykłady

wgłębieni
e

wgłębieni
e

rowek
odciążający

rowek
odciążający

zaokrąglenie

zaokrąglenie
eliptyczne

rowek i zaokrąglenie

pierścień dystansowy

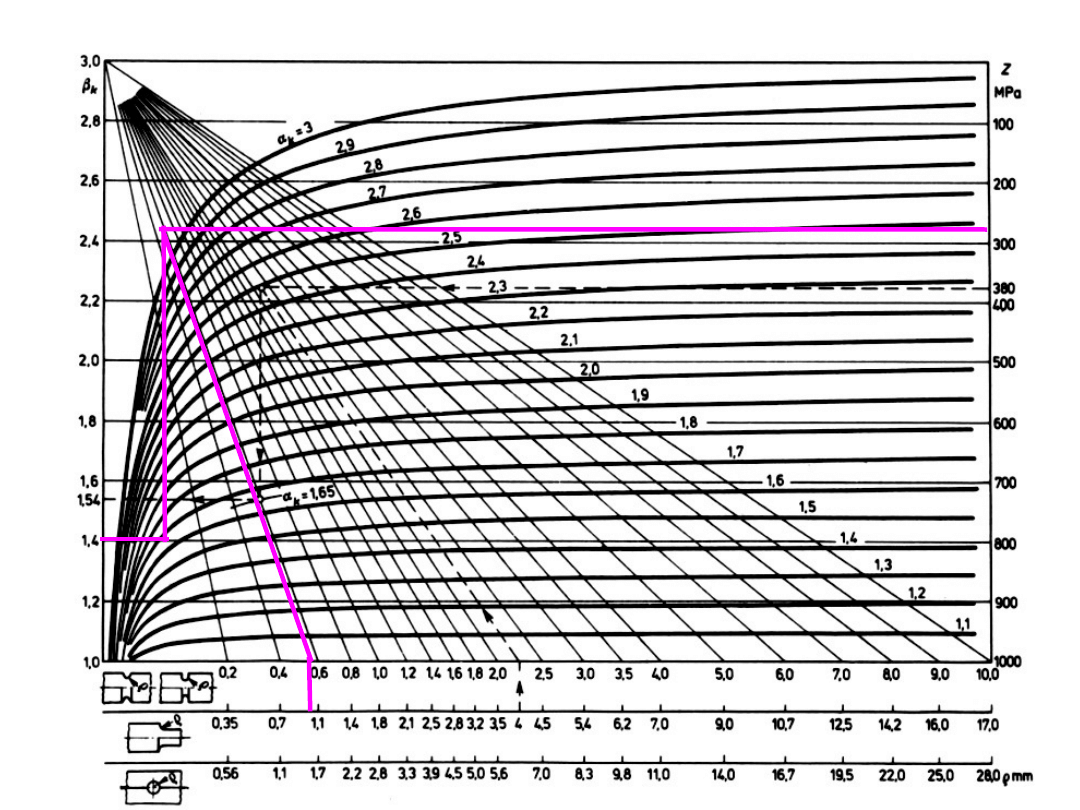
współczynnik działania karbu - model

k

gł

k

Z

Z





Z

gł

- granica zmęczenia próbki

gładkiej

Z

k

- granica zmęczenia próbki z

karbem





1

1







k

k

k







η

k

- współczynnik
wrażliwości materiału na
działanie karbu

η

k

= 1 dla materiałów doskonale

sprężystych i doskonale
kruchych

η

k

= 0 dla materiałów doskonale

plastycznych

np. żeliwo

η

k

bliskie zeru

Z wykresów lub ze wzoru lub będzie
podany:

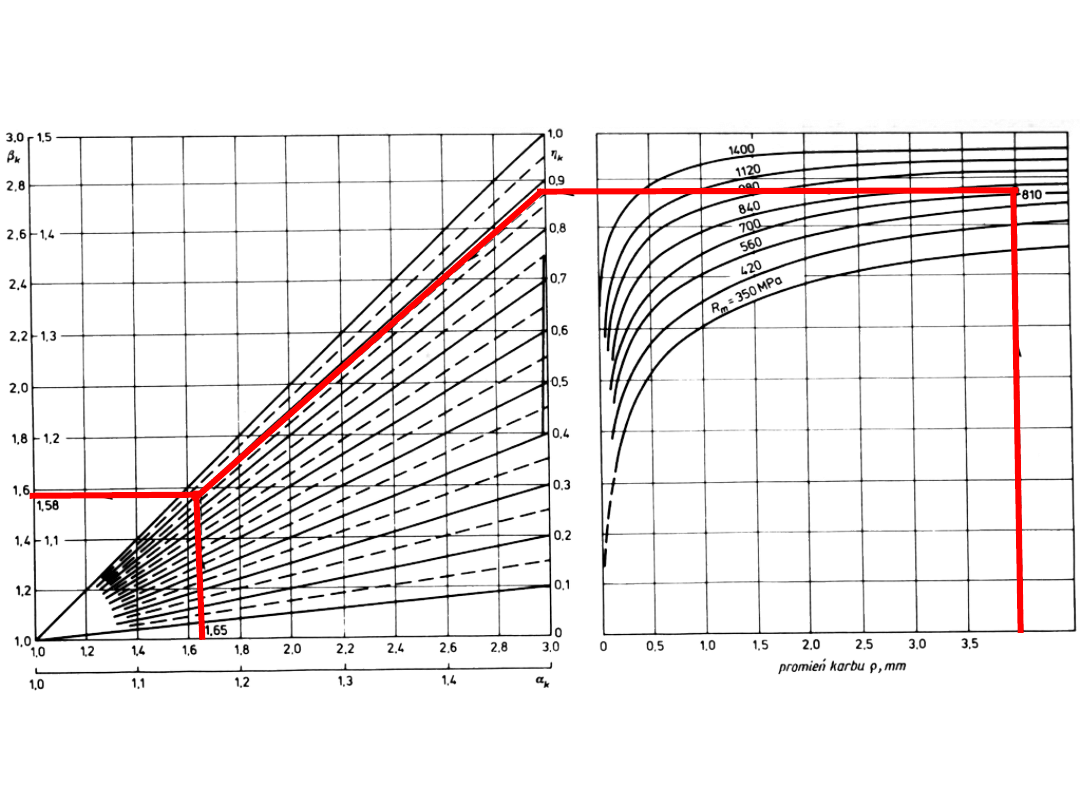
współczynnik działania karbu

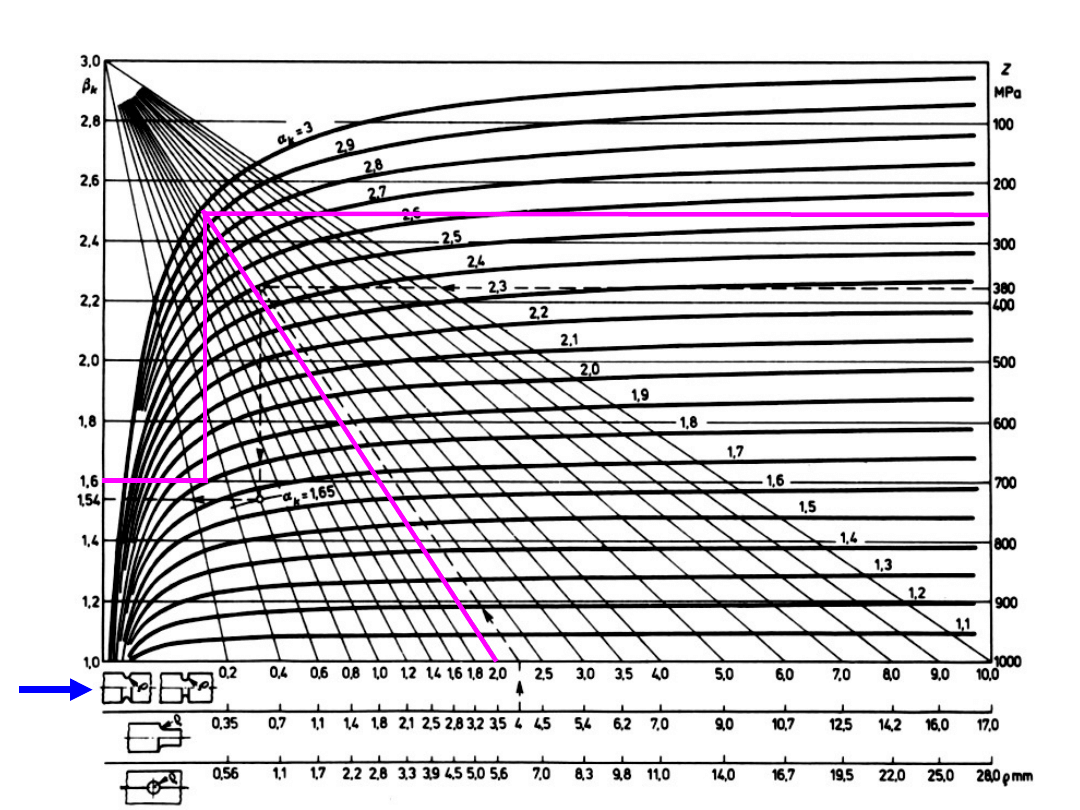
ρ

R

m

η

k

α

k

β

k

4

810

0,875

1,65

1,58

Stal C45 o Rm = 810
MPa

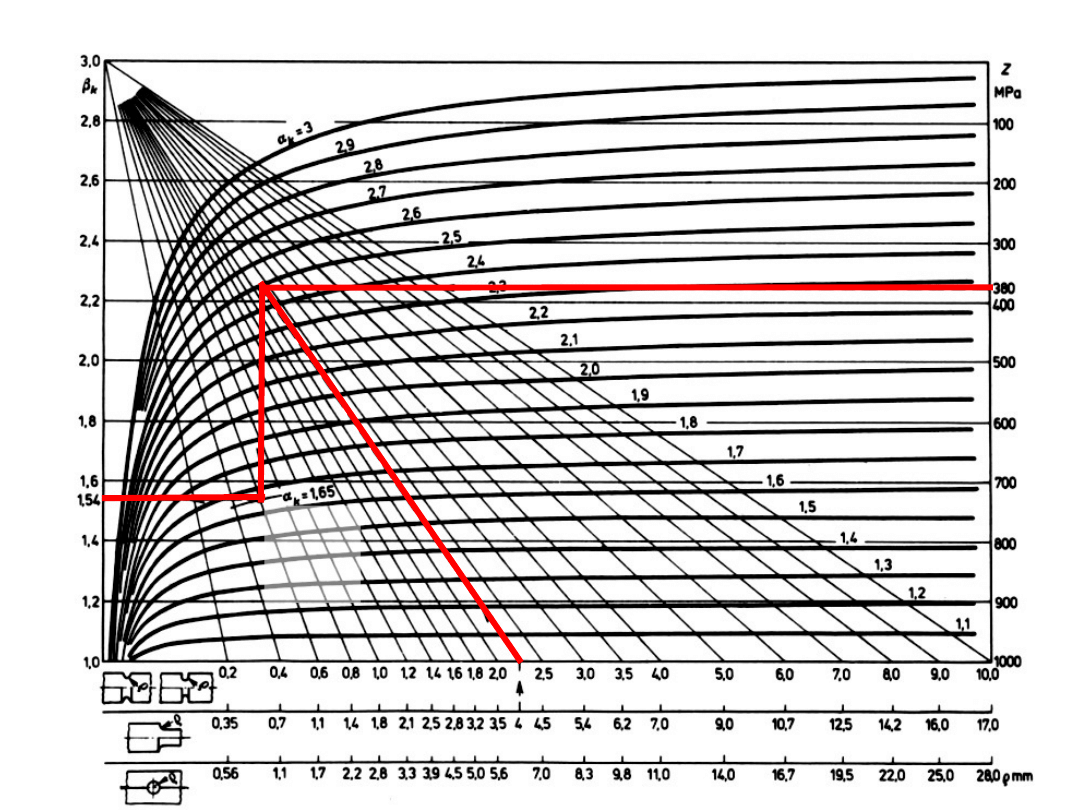
współczynnik działania karbu – obciążenie wahadłowym zginaniem wałka

ρ

Z

α

k

β

k

4

380

1,6
5

1,5
4

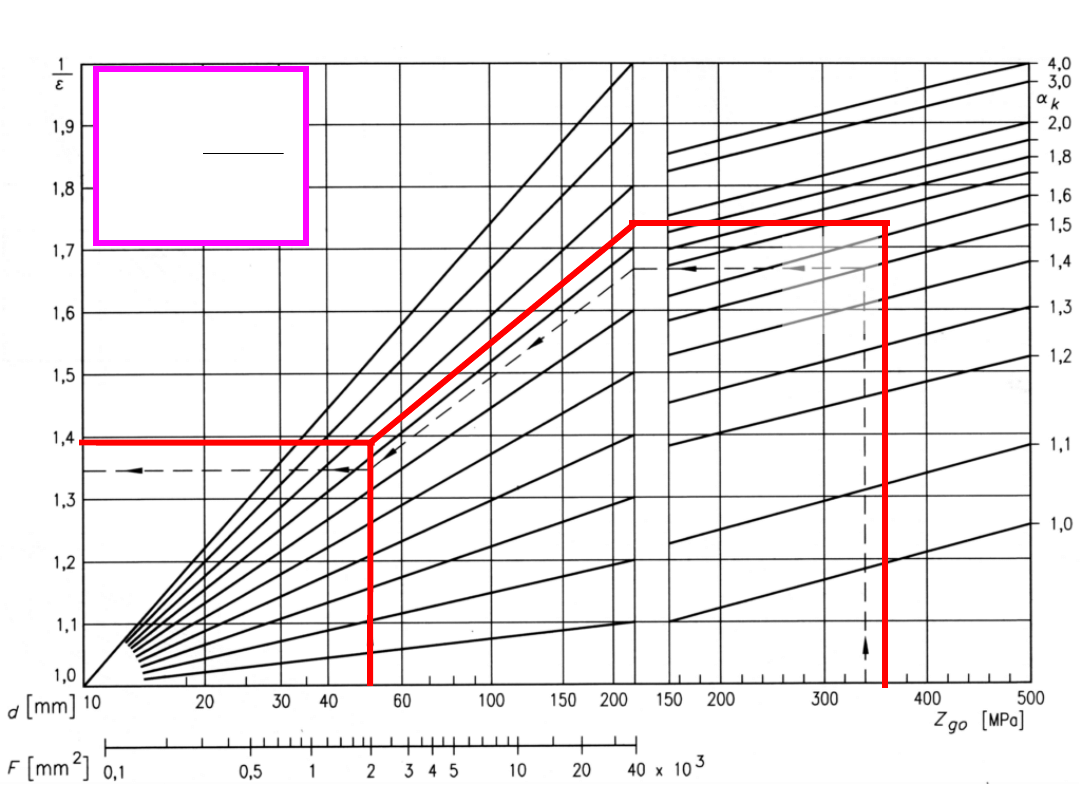
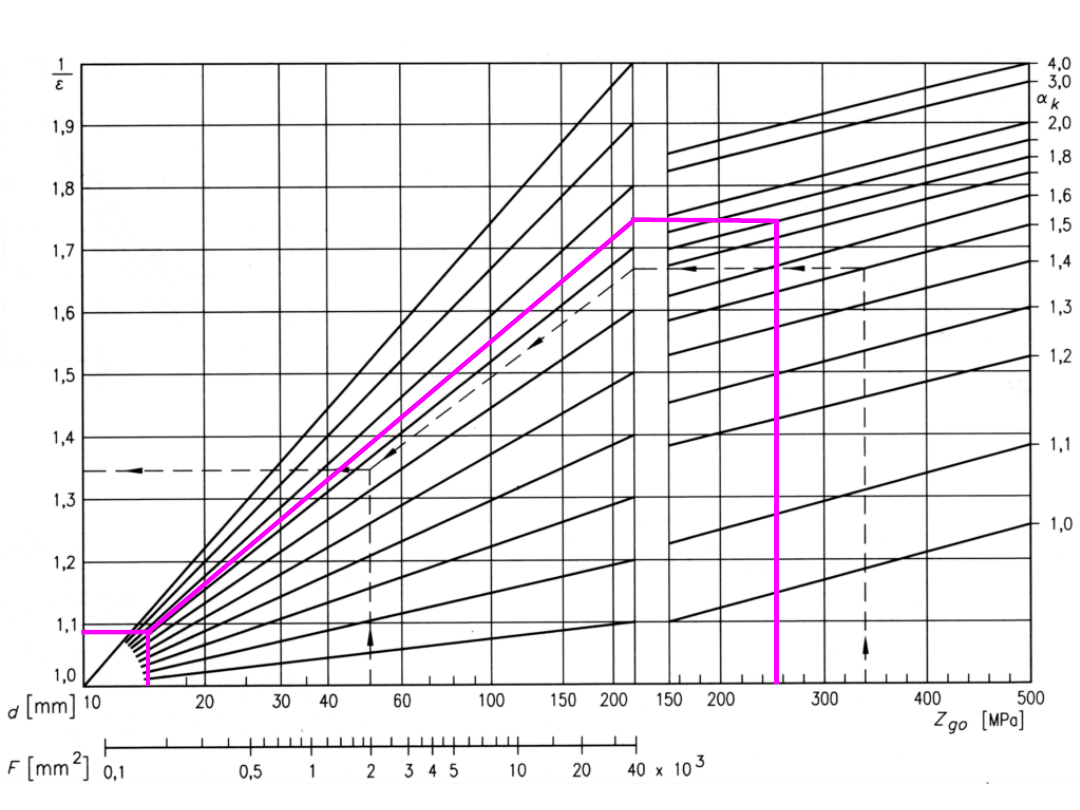
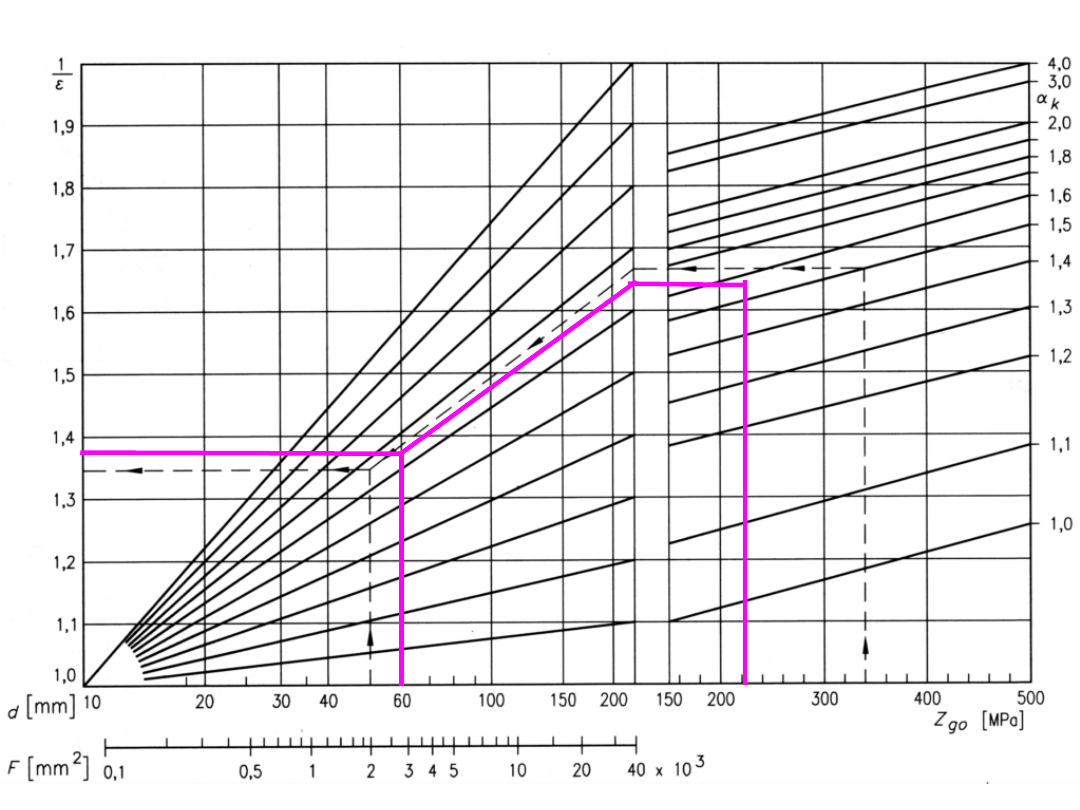
współczynnik wielkości przedmiotu (stal konstrukcyjna) w odniesieniu do
wałka Φ10 mm

d

Z

α

k

1/ε

50

380

1,6
5

1,3
9

10

Z

Z

d





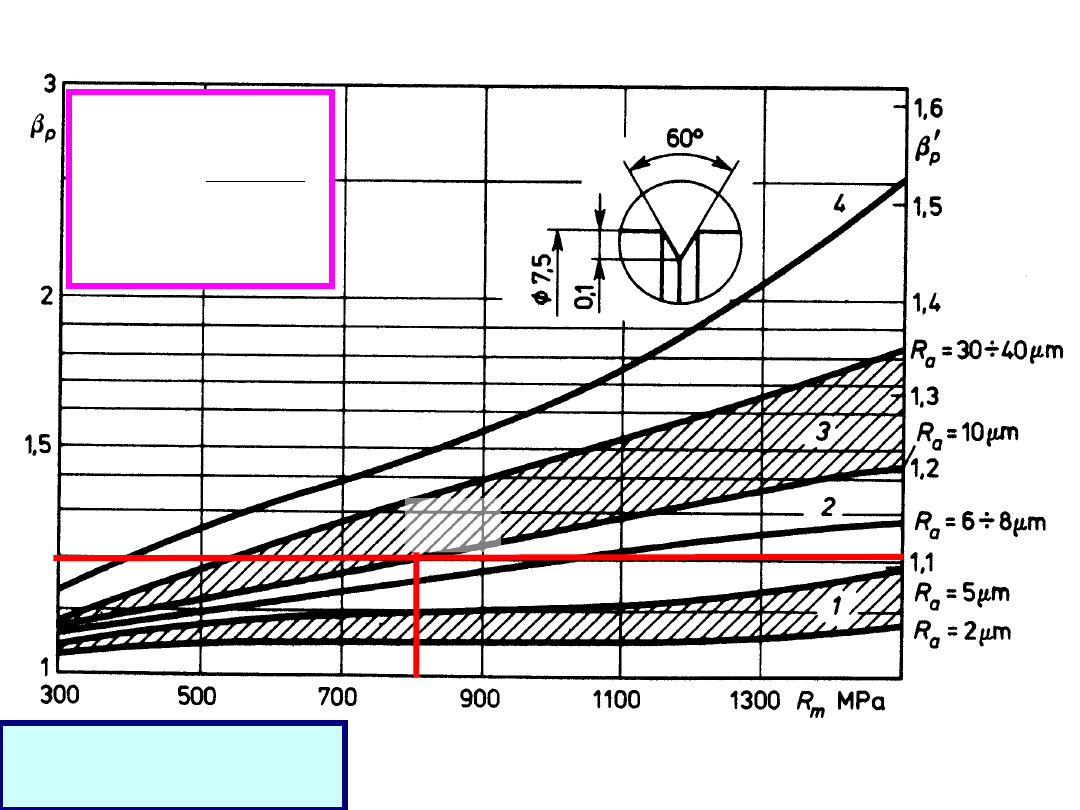
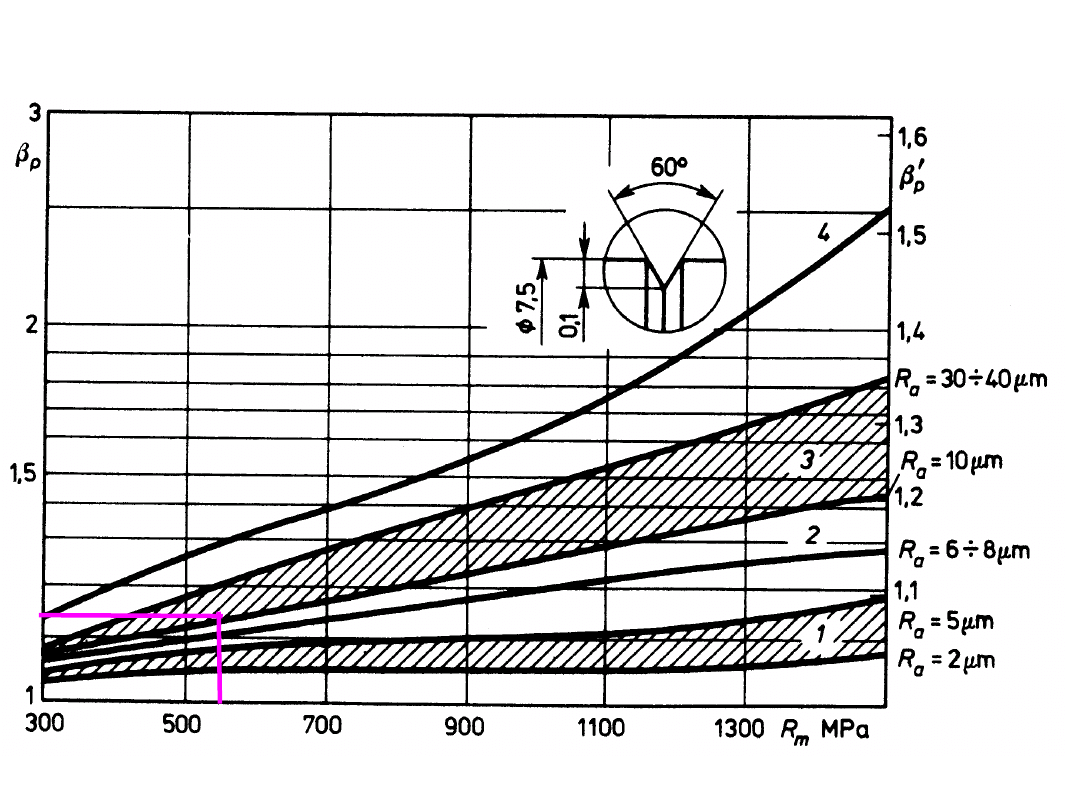
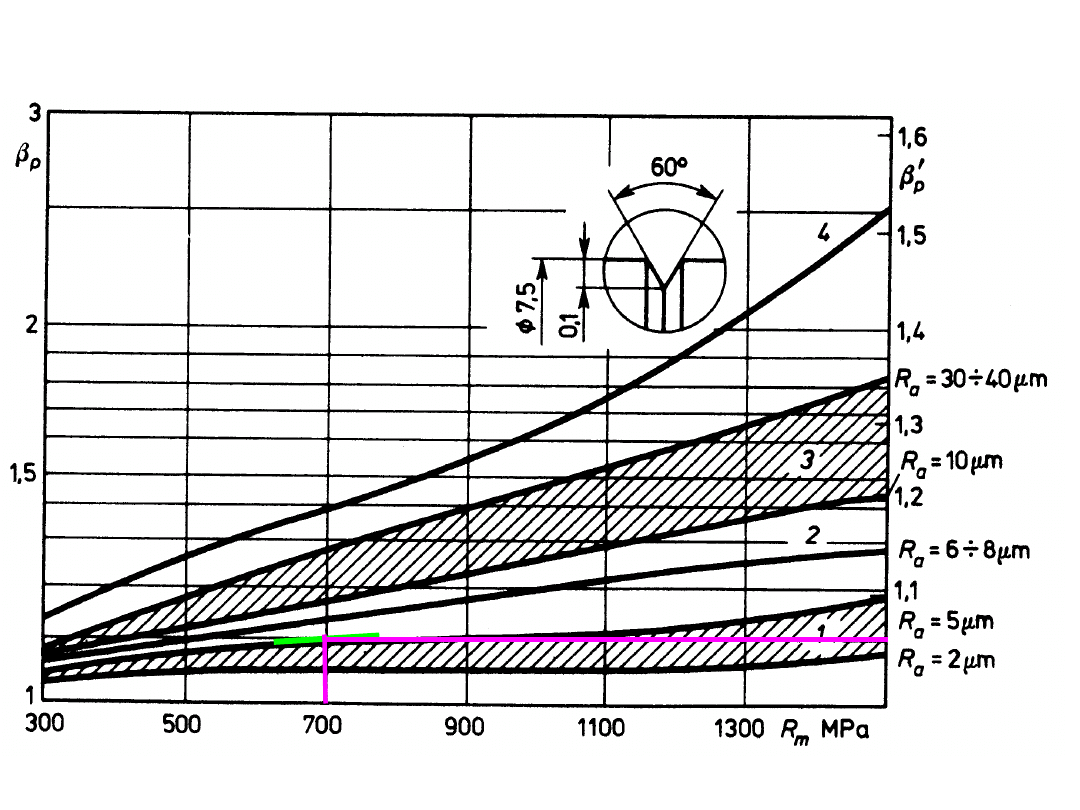
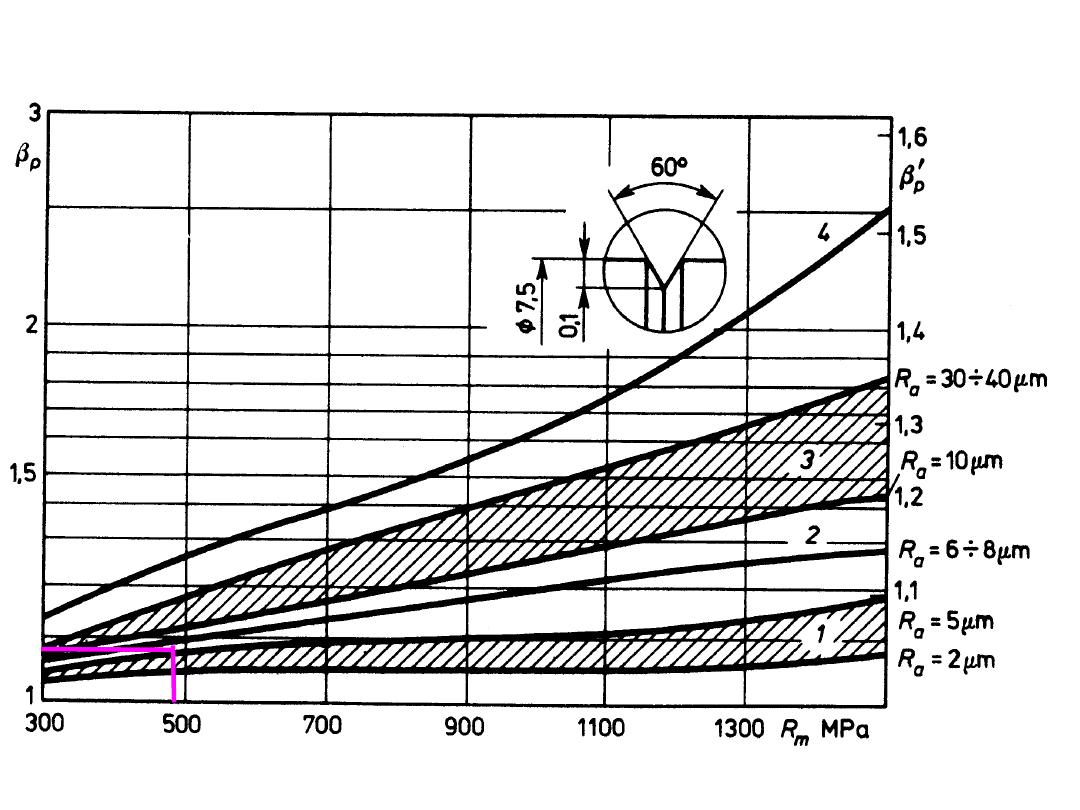
współczynnik obróbki powierzchni (odniesienie – próbka polerowana)

R

a

β

p

obr

pol

p

Z

Z





810

10

1,2

1,1

β

p

’

rozciąganie/skręcanie i
zginanie

skręcanie

1







p

k







współczynnik wpływu obróbki powierzchni

obr

k











obróbka

rodzaj

próbki

średnica [mm]

β

obr

kulowanie

gładka

7-20

0,77-0,91

30-40

0,91-0,93

z karbem

7-20

0,40-0,70

30-40

0,57-0,90

azotowanie

gładka

8-15

0,80-0,87

30-40

0,87-0,90

z karbem

8-15

0,33-0,52

30-40

0,50-0,77

obr

obr

Z

Z





Naprężenia nominalne i

zastępcze













a

z

a

współczynniki bezpieczeństwa – cykle symetryczne

a

az

Z

Z



















δ - współczynnik bezpieczeństwa
Z - granica zmęczenia
ε - współczynnik wielkości przedmiotu
β - współczynnik działania karbu i
powierzchni
σ

a

- nominalna amplituda obciążenia

przyjmowana wartość współczynnika bezpieczeństwa δ

δ

przypadek

1,3÷1,5

wykorzystanie wyników badań eksperymentalnych

1,5÷1,7

zwykła dokładność obliczeń, elementy niewielkie,
dobra technologia wykonania

1,7÷2,0

zwykła dokładność obliczeń, elementy duże lub o
średniej technologii wykonania

2,0÷3,0

obliczenia orientacyjne, ciężkie warunki pracy,
elementy odlewane

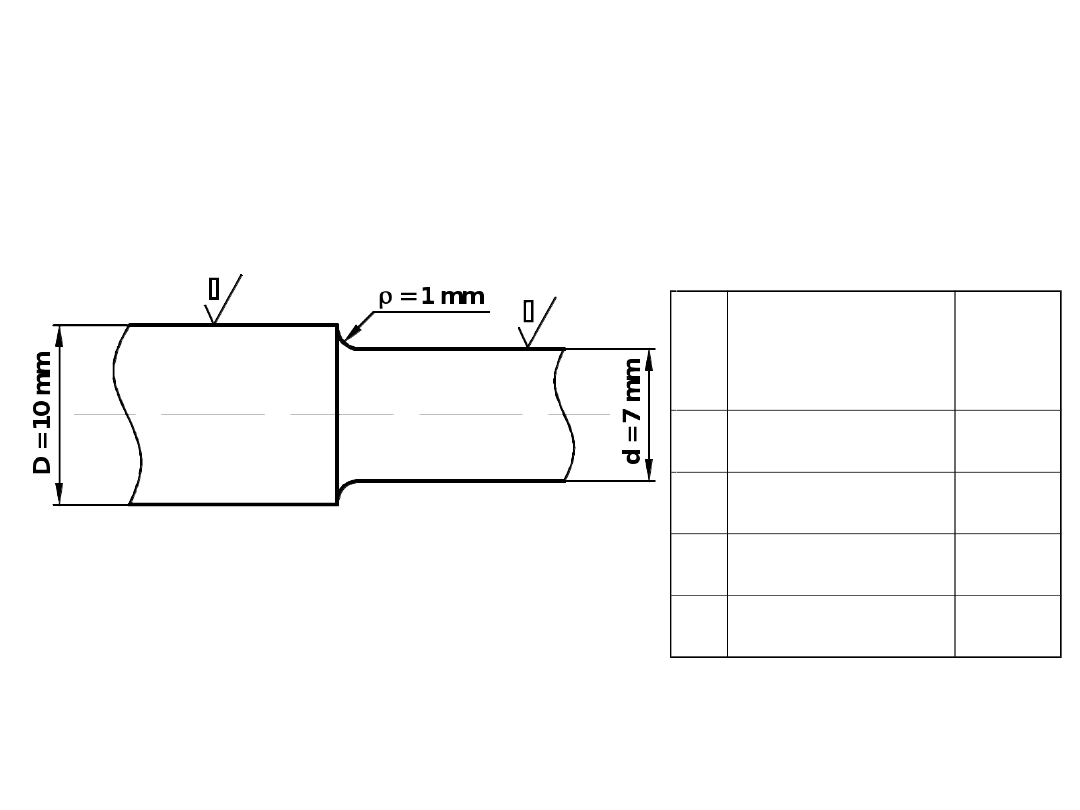
ZADANIE 1 - współczynniki bezpieczeństwa – cykle symetryczne

Wyznaczyć współczynnik bezpieczeństwa δ

1

dla pręta ze stali C35

(normalizowanej) o średnicy D

=

20 mm obciążonego wahadłowo

zmiennym momentem zginającym o amplitudzie M

=50 Nm.

Własności stali: Z

g0

=255 MPa, R

m

=

550 MPa. Określić współczynnik

bezpieczeństwa δ

2

jeśli na pręcie wykonany zostanie karb obrączkowy

o promieniu ρ

=

2 mm, przy czym średnica pręta ulega w tym miejscu

zmniejszeniu do d

=

15 mm. Wał został dokładnie wytoczony, wartość

R

a

=

10μm.

a

Z















1







p

k







32

3

d

M

W

M

x

a











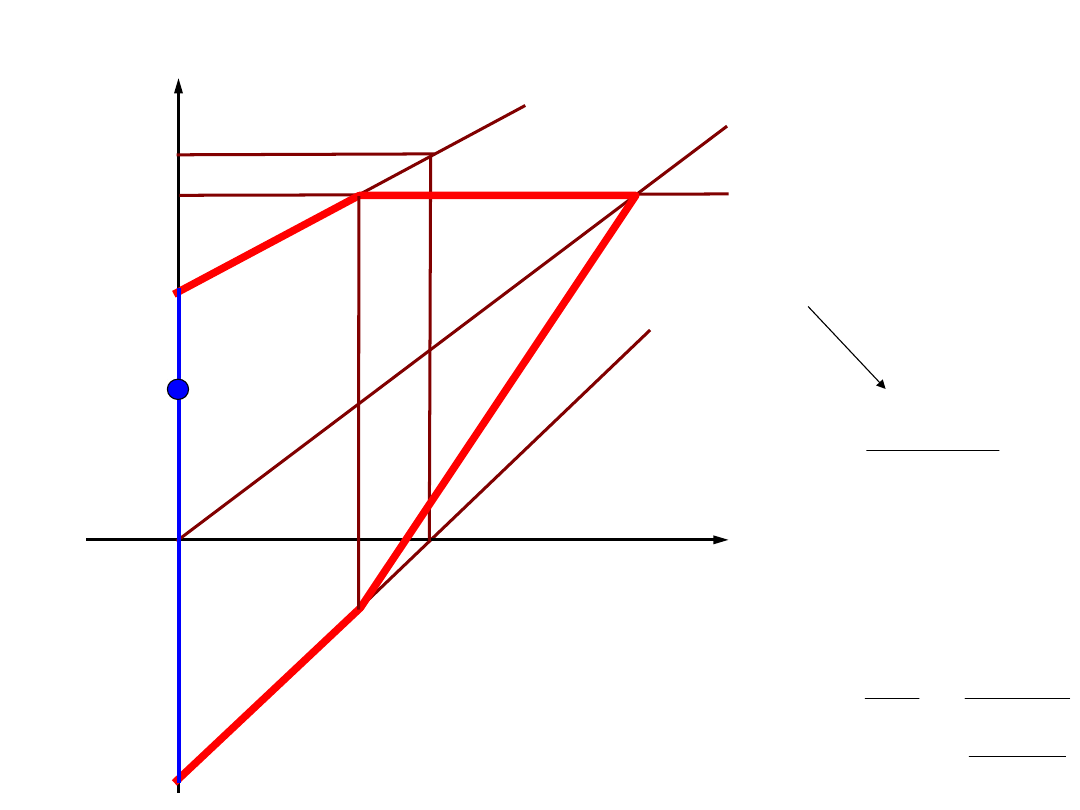
σ

m

R

e

Z

go

Z

gj

Z

rj

/2

-Z

rc

a

Z















1







p

k







32

3

d

M

W

M

x

a











σ

a z

Z = Z

go

A

ZADANIE 1 - współczynniki bezpieczeństwa – cykle symetryczne

ZADANIE 1 - współczynniki bezpieczeństwa – cykle symetryczne

ZADANIE 1 - współczynniki bezpieczeństwa – cykle symetryczne

ZADANIE 1 - współczynniki bezpieczeństwa – cykle symetryczne

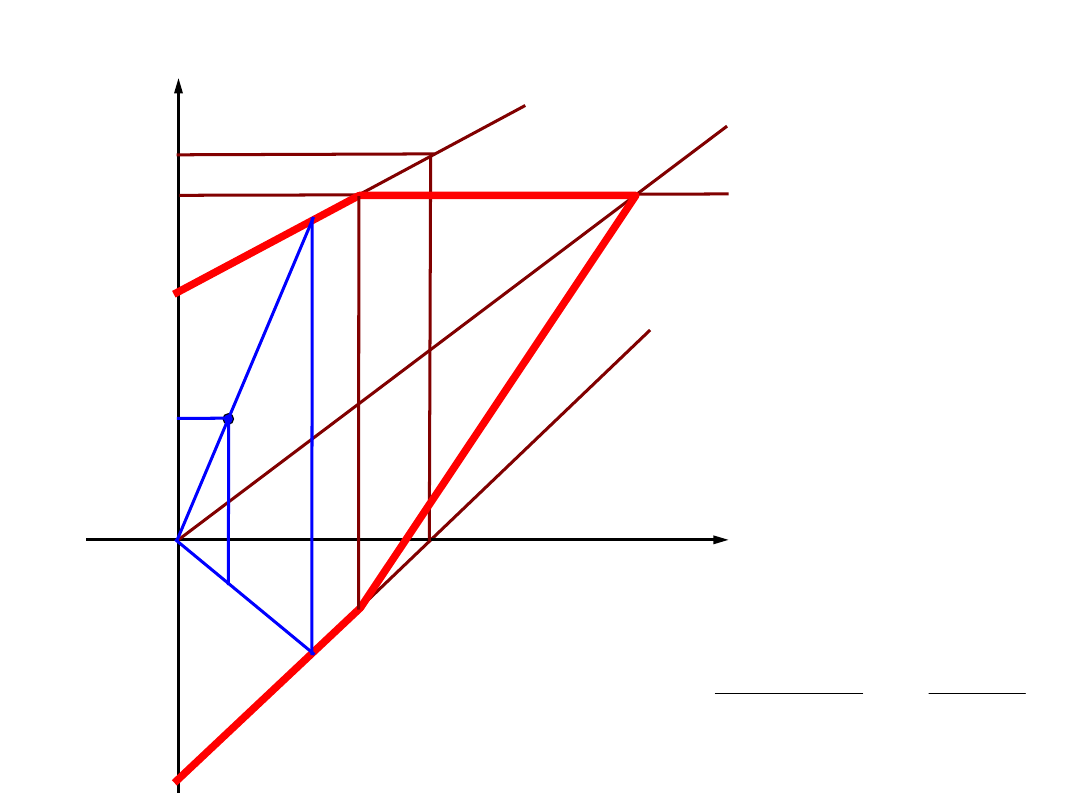
współczynniki bezpieczeństwa – cykle niesymetryczne – wsp. bezp.
zmęczeniowy

σ

m

R

e

Z

r

c

Z

rj

Z

rj

/2

σ

max

σ

min

-Z

rc

A

A’
’

A

0

A’

L

L

0

L’
’

L’

'

'

max

max

AA

LL

A

L











Założenie: dla R = const

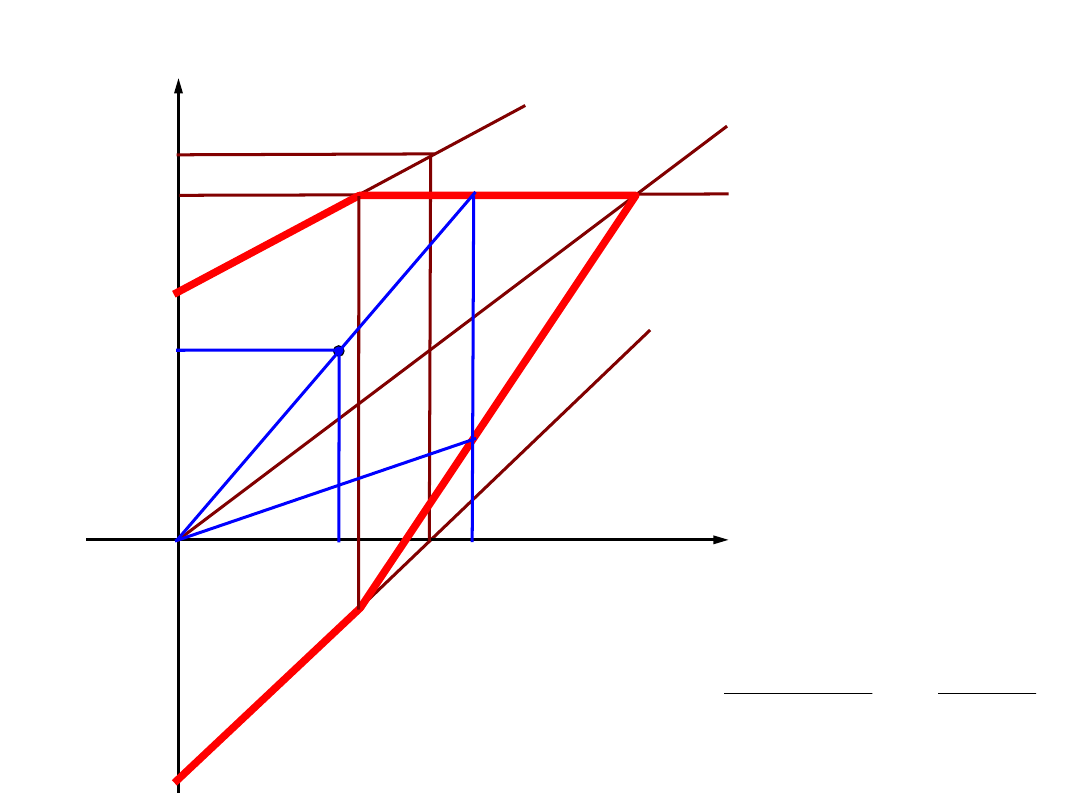
współczynniki bezpieczeństwa – cykle niesymetryczne – wsp. bezp.
plastyczny

σ

m

R

e

Z

r

c

Z

rj

Z

rj

/2

σ

max

σ

min

-Z

rc

B

B’
’

B

0

B’

P

P

0

P’’

P’

'

'

max

max

BB

PP

B

P

e











Dla R =
const

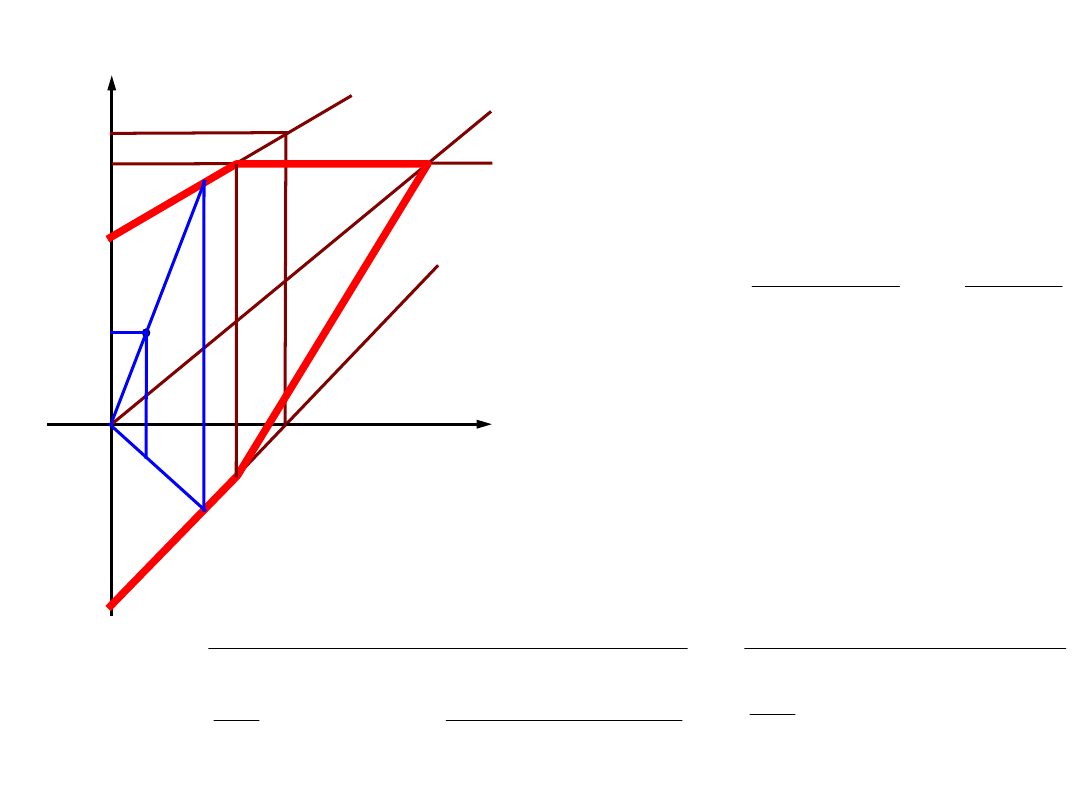
współczynniki bezpieczeństwa – cykle niesymetryczne – wsp. bezp.
zmęczeniowy

σ

m

R

e

Z

rc

Z

rj

Z

rj

/

2

σ

ma

x

σ

min

-Z

rc

A

A’

L

L’

'

'

max

max

AA

LL

A

L















































m

a

rc

rj

rj

rc

m

a

rc

Z

Z

Z

Z

Z

2

Dla R =
const

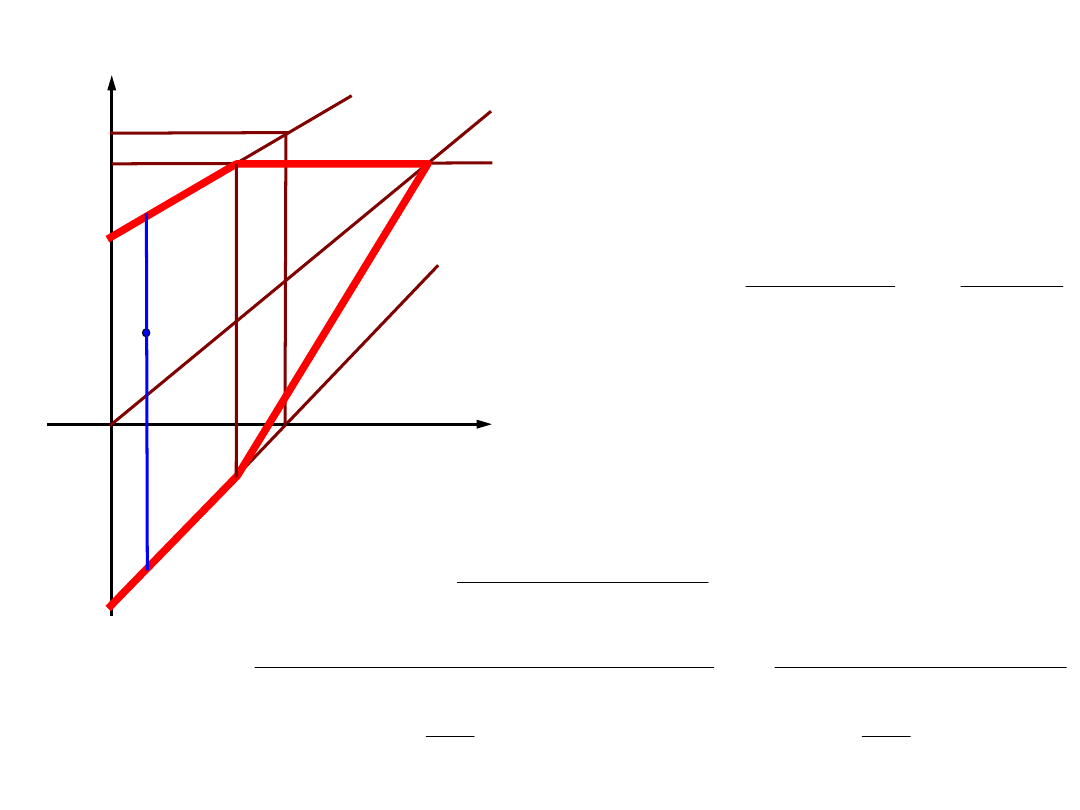
współczynniki bezpieczeństwa – cykle niesymetryczne – wsp. bezp.
zmęczeniowy

σ

m

R

e

Z

rc

Z

rj

Z

rj

/

2

σ

ma

x

σ

min

-Z

rc

C

C’=S
’

S

'

'

max

max

CC

SS

C

S











a

m

rc

a

rj

rj

rc

m

rc

Z

Z

Z

Z

Z





































2

Dla σ

m

=

const

ZADANIE 2 - współczynniki bezpieczeństwa – cykle niesymetryczne

Wał obciążony jest momentem skręcającym M = M

m

± M

a

=

5000±2000

Nm.

W pewnym miejscu jego średnica zmienia się z D = 80 mm na d = 60
mm, przy czym wykonane jest tam odsadzenie o promieniu ρ = 5
mm.

1. Narysować wykres Smitha jeżeli dane stali C55 z której wykonano

wał są następujące: Z

s0

= 225 MPa; Z

sj

= 405 MPa; R

e

= 320 MPa;

R

m

= 700 MPa.

2. Określić dopuszczalną chropowatość wału jeżeli współczynnik

bezpieczeństwa ma być nie mniejszy niż δ = 1,45. W przypadku
przeciążenia współczynnik asymetrii cyklu pozostaje stały.

16

3

d

M

a









ZADANIE 2 - współczynniki bezpieczeństwa – cykle niesymetryczne

ZADANIE 2 - współczynniki bezpieczeństwa – cykle niesymetryczne

ZADANIE 2 - współczynniki bezpieczeństwa – cykle niesymetryczne

ZADANIE 2 - współczynniki bezpieczeństwa – cykle niesymetryczne

hipoteza kumulacji uszkodzeń

N

σ

σ

1

σ

2

σ

3

σ

4

σ

5

n

1

n

2

n

3

n

4

n

5

N

1

N

2

N

3

N

4

N

5

= 

hipoteza Palmgrena-
Minera:









k

i

i

i

N

n

D

1

1

ZADANIE 3 – kumulacja uszkodzeń

Okrągłe cięgno pokazane na rysunku obciążone jest naprężeniami
blokami wg. tabeli. Obliczyć maksymalną liczbę bloków do
zniszczenia, jeżeli granica zmęczenia wynosi Z

g

=280 MPa przy N

0

=

1,2·10

6

cykli, zaś dla σ

x

= 350 MPa zmniejsza się do N

x

= 10

5

.

Pozostałe

stałe

materiałowe:

R

e

=

290

MPa,

R

m

= 480 MPa.

lp

.

amplituda

obciążenia

[kN]

liczb

a

cykli

1

10,5

10

2

7,5

300

3

8,5

80

4

9

50





ZADANIE 3 – kumulacja uszkodzeń

ZADANIE 3 – kumulacja uszkodzeń

ZADANIE 3 – kumulacja uszkodzeń

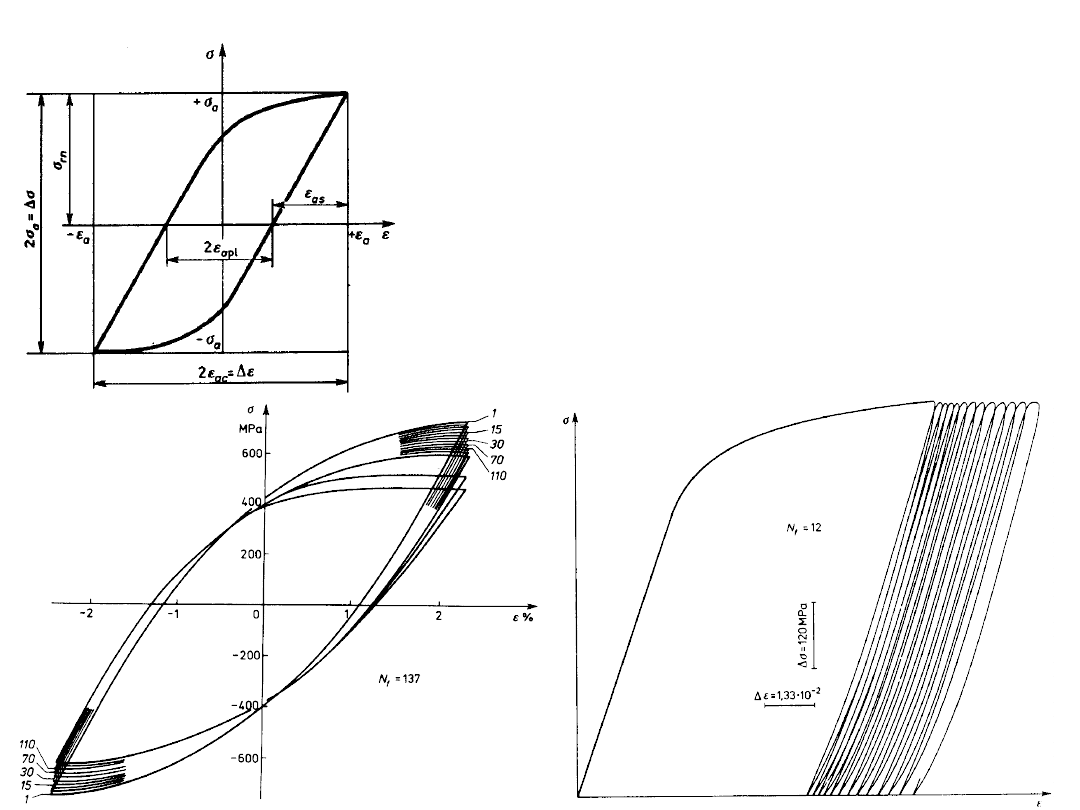
wytrzymałość niskocyklowa

ε

ac

- amplituda odkształcenia

całkowitego

ε

apl

- amplituda odkształcenia

plastycznego

ε

as

- amplituda odkształcenia

sprężystego

wytrzymałość niskocyklowa

N

ε

apl

N

σ

a

σ

a

=

const

ε

apl

=

const

materiał wykazujący:

umocnienie

,

osłabienie

,

stabilność