2004-12-12

1

WYTRZYMAŁOŚĆ

WYTRZYMAŁOŚĆ

CZĘŚCI MASZYN

CZĘŚCI MASZYN

Obliczenia wytrzymałościowe

2

MASZYNA

(jej części)

Obciążenia

mechaniczne

,

cieplne oraz

chemiczne

oddziaływani

e

środowiska

KONSTRUKTOR

(projektant)

OTOCZENIE

(czynniki

zew.)

3

Obciążenia mechaniczne mogą doprowadzić
maszynę lub jej części do:

• zniszczenia,
• uszkodzenia,
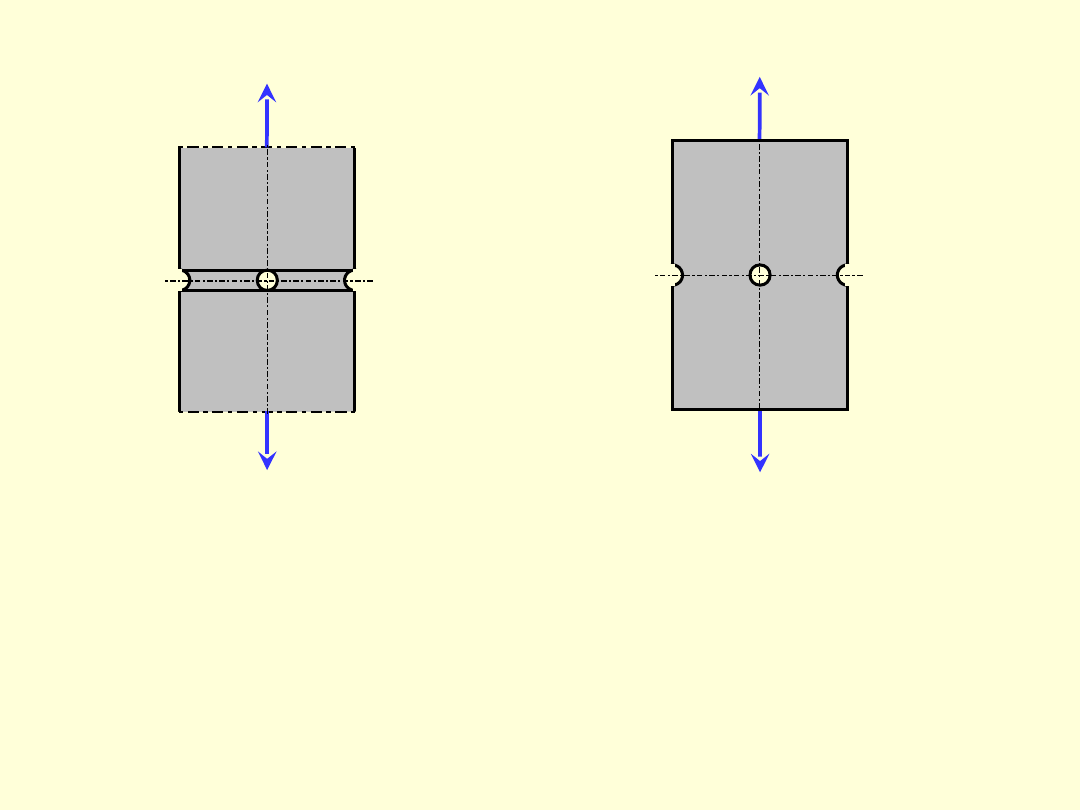
• innej zmiany uniemożliwiającej dalszą

eksploatacje.

4

RODZAJE OBCIĄŻEŃ

RODZAJE OBCIĄŻEŃ

Obciążenie części maszyny może być

stałe

(statyczne) lub

zmienne

, odpowiednio do

tego, czy siła obciążająca daną część (albo
moment siły) ma wartość i kierunek działania

niezmienny

czy

zmienny

. Doświadczenie

wyniesione z użytkowania maszyn i urządzeń
wykazuje, że wszystkie metale są mniej
wytrzymałe w przypadku obciążeń zmiennych
niż przy obciążeniach statycznych.

Obciążenia

występujące

najczęściej

w

konstruk-cjach to obciążenia o charakterze
sinusoidalnym.

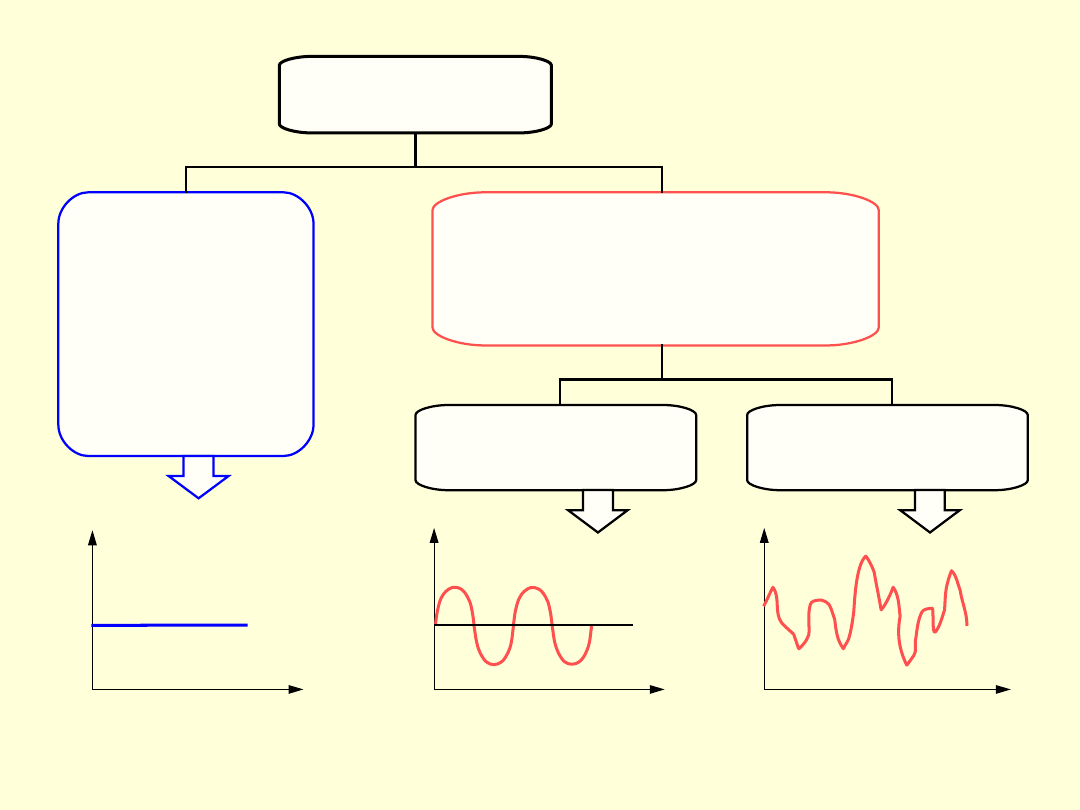
5

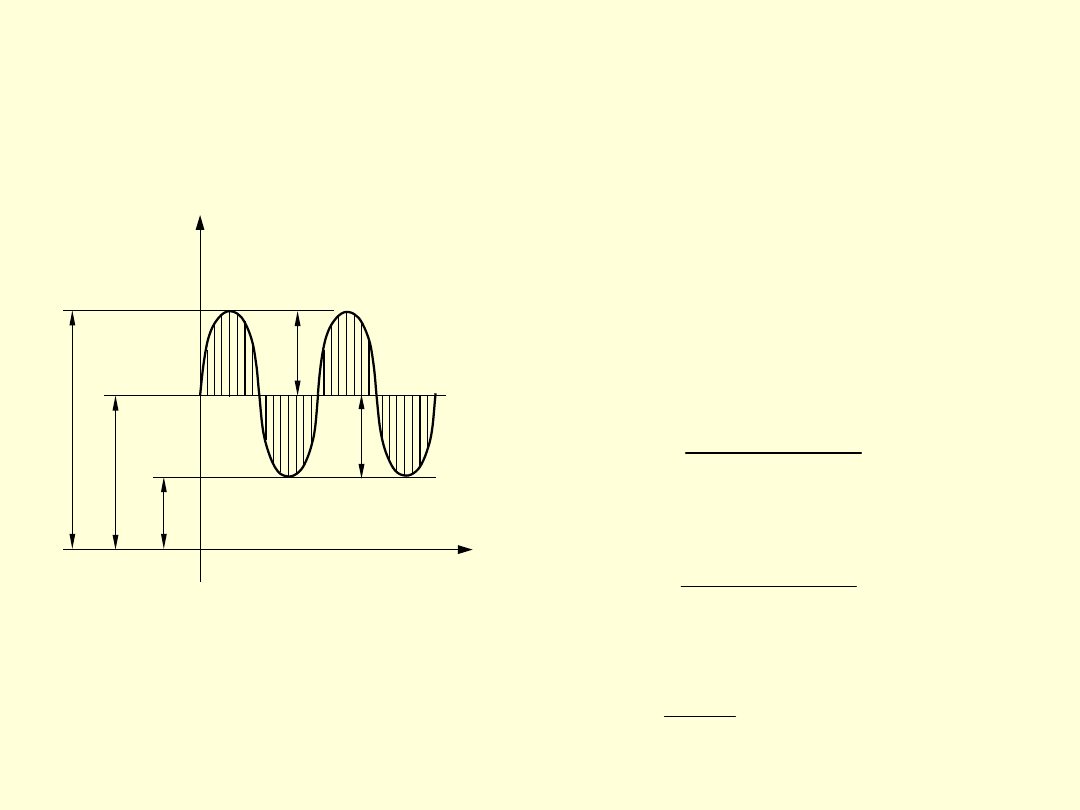
OBCIAŻENIA

OBCIAŻENIA

STAŁE

STAŁE

to takie, które
nie ulegają
zmianom
podczas
pewnego
dostatecznie
długiego czasu
pracy maszyny

ZMIENNE

ZMIENNE

są to obciążenia zmieniające
się
w czasie, przy czym
charakter
zmienności może być
różnorodny

P(t)

t

Obciążenia ustalone

Obciążenia ustalone

(cykliczne)

(cykliczne)

Obciążenia

Obciążenia

nieustalone

nieustalone

t

P(t)

t

P(t)

6

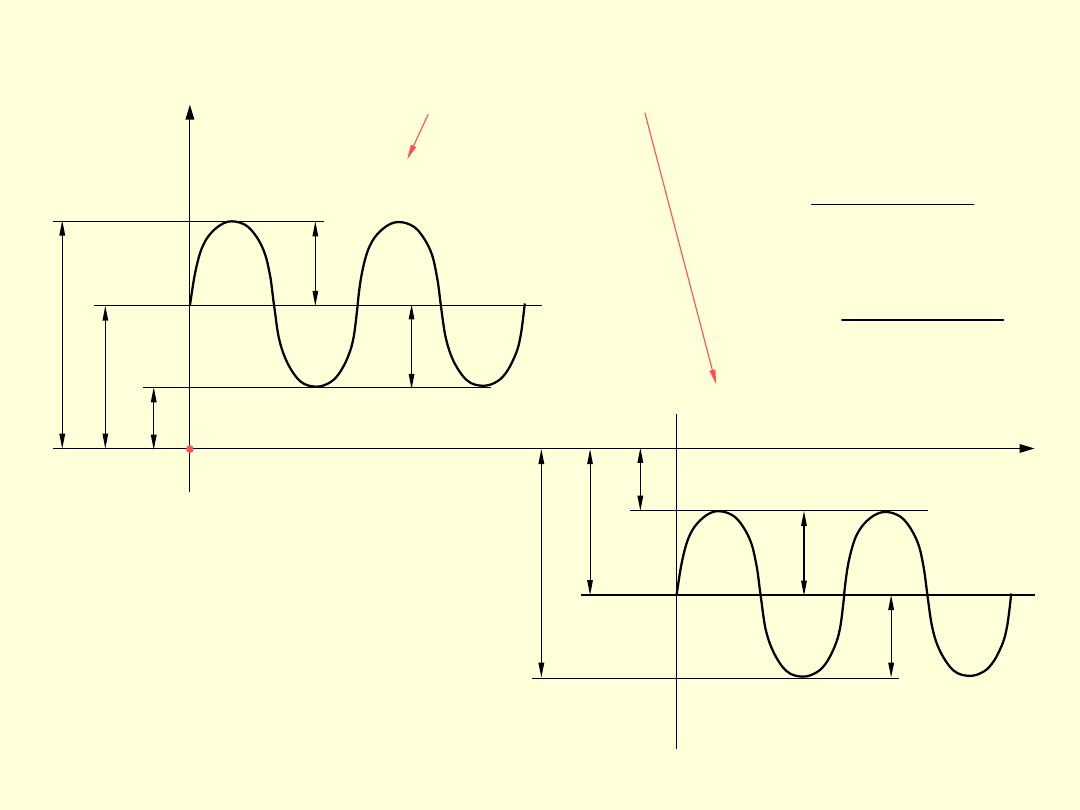
Obciążenia jednostronnie

zmienne (tętniące)

Obciążenia obustronnie

zmienne (wahadłowe)

Obciążenia ustalone

Obciążenia ustalone

(cykliczne)

(cykliczne)

t

P

P

m

a

x

P

m

in

T

obciążenia

odzerowo

tętniące

P

m

a

x

0

t

P

0

obciążenia

jednostronne

(+
)

(–
)

obciążenia

dwustronne

P

m

in

7

obciążenia jednostronne

t

P

P

m

P

m

in

P

m

a

x

P

a

(+
)

tętniące
rozciąganie

t

P

m

P

m

a

x

P

m

in

P

a

(-
)

tętniące

ściskanie

P

a

P

a

2

P

P

P

min

max

m





2

P

P

P

min

max

a





a

m

min

P

P

P





a

m

max

P

P

P





0

8

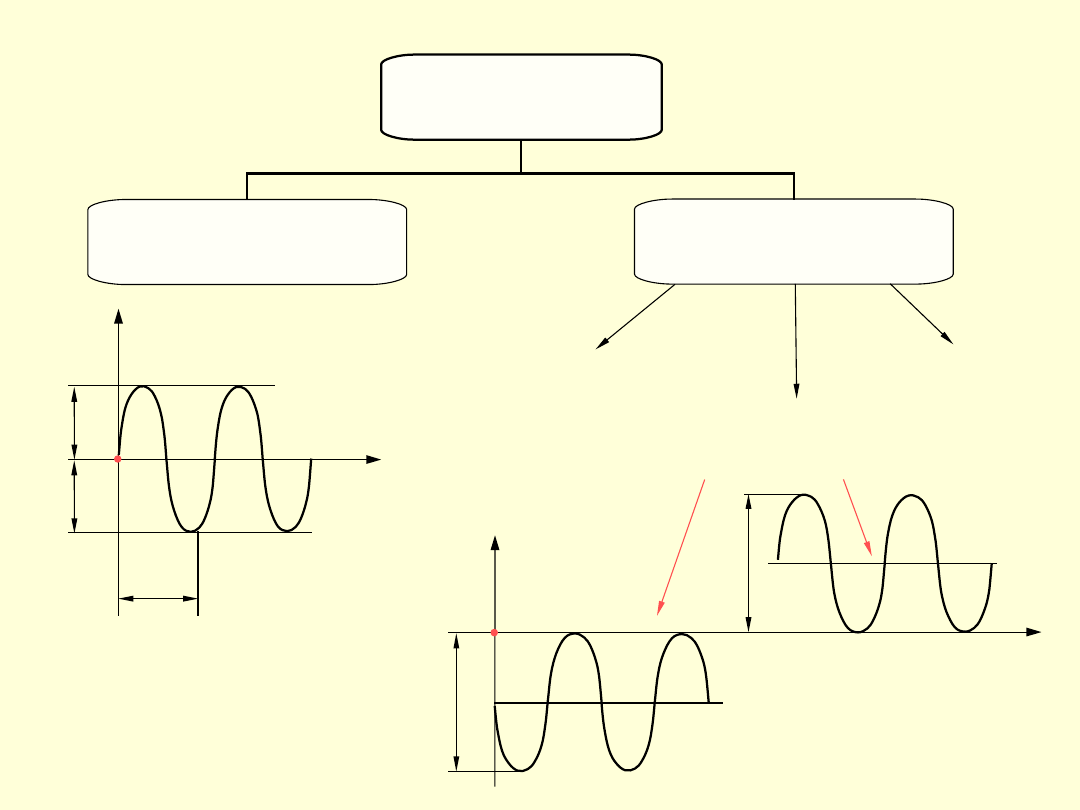
Obciążenia

obustronnie

zmienne

(wahadłowe) - są to obciążenia, których
wartość zmienia się od pewnej dodatniej
wartości maksymalnej

P

max

do pewnej ujemnej

wartości minimalnej

P

min

, przy czym wartości

bezwzględne

P

max

i

P

min

są równe.

Obciążenia odzerowo tętniące - są to
obciążenia, których wartość zmienia się
podczas jednego okresu od zera do wartości
maksymalnej i ponownie do zera.
Ponieważ obciążenia okresowe mogą mieć
różny przebieg, w celu ich sklasyfikowania
wprowadza się pojęcia: obciążenia średniego

P

m

oraz amplitudy obciążenia

P

a

.

9

NAPRĘŻENIA

NAPRĘŻENIA

Naprężenie - jest to miara sił wewnętrznych
powstałych w ciałach odkształcalnych pod
wpływem oddziaływań zewnętrznych (np.
obciążeń siłami).

Jednostką naprężenia w układzie SI jest

0

r

r

F

P



















2

m

N

Pa

W najprostszym przypadku rozciągania pręta
siłą skierowaną wzdłuż osi pręta

P

r

,

naprężenie równa się stosunkowi tej siły do
pola przekroju poprzecznego pręta

F

0

:

10

t

sin

σ

σ

σ

a

m









Zmiana naprężeń w funkcji czasu zazwyczaj
ma charakter sinusoidalny:

Naprężenia

można

rozłożyć

na

dwie

składowe:

• naprężenia normalne



n

–  do płaszczyzny

przekroju,

• naprężenie styczne



s

– leżące w tej płaszczyźnie.

P

r

P

r



n



s



s

11

WIELKOŚCI CHARAKTERYZUJĄCE CYKLE

NAPRĘŻEŃ ZMĘCZENIOWYCH

• maksymalne naprężenie cyklu



max

• minimalne naprężenie cyklu



min

• naprężenie średnie



m

• amplituda cyklu naprężeń



a

• współczynnik asymetrii

R





m



m

in



m

a

x

0

t

2

min

max

m











2

min

max

a











a

m

min











a

m

max













a



a

max

min

R







12

a

m









Podczas pracy maszyny przejście z jednego
stanu naprężeń do innego może odbywać się
na różne sposoby. Na przykład przy
zachowaniu:

• stałego stosunku naprężeń średnich



m

do

amplitudy naprężeń



a

, wyrażonego

współczyn-nikiem



(kappa):

• stałego naprężenia maksymalnego



max

=

const

; (w pewnych okolicznościach pracy

maszyny naprężenia średnie



m

mogą być

ustalone, natomiast zmieniać się może
amplituda cyklu naprężeń



a

- zachodzi to

w przypadku nakłada-nia się obciążeń
stałych ze zmiennymi.

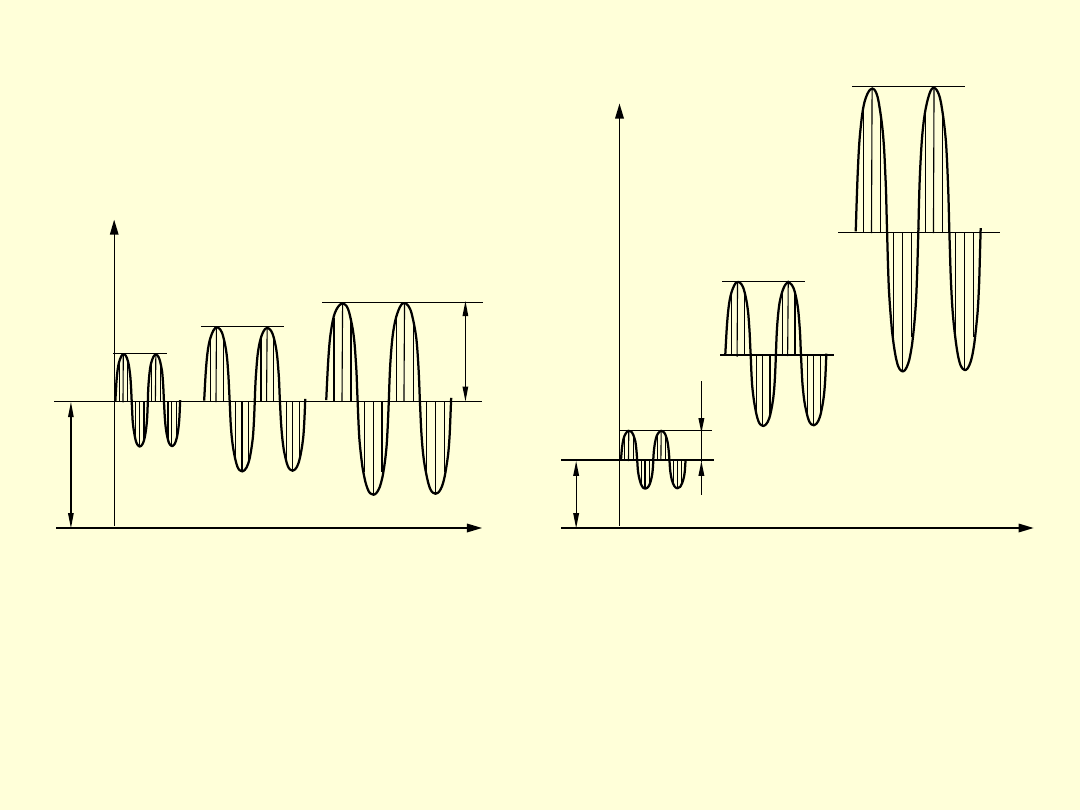
13



t



m



a

Naprężenia zmienne

przy



m

= const

.



t



m

Naprężenia zmienne przy

stałym stosunku



.



a

14

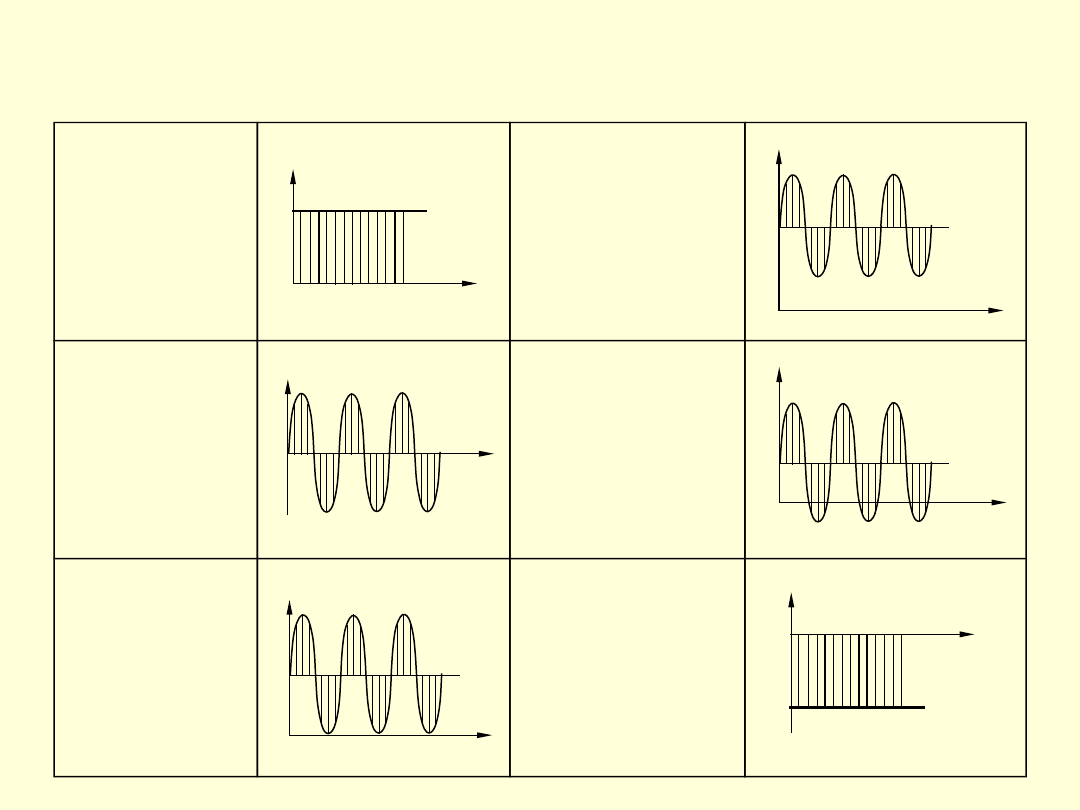
RÓŻNE CYKLE NAPRĘŻEŃ

ZMĘCZENIOWYCH

naprężenie

stałe (+)

cykl

jednostronny

(+)

cykl

wahadłowy

cykl

dwustronny

cykl

odzerowo

tętniący (+)

naprężenia

stałe (–)









κ

1

R











κ

1

1

R

0

1

κ

0

R





0

κ

1

R





t

0

t

0

t

0

t

0

1

κ

0

1

R

0









t

0









κ

1

R

t

0

15

Cykl naprężeń zmiennych, to przebieg zmian
naprężenia okresowo zmiennego, którego
wartość zmienia się w sposób ciągły w czasie
jednego okresu zmiany. Rozróżnia się
następujące

rodzaje

cykli

naprężeń

zmęczeniowych (rys.):

• wahadłowy symetryczny (4),
• wahadłowy niesymetryczny (3 i 5),
• odzerowo dodatni (6) lub ujemny (2).
• tętniący dodatni (7) lub ujemny (1),

16

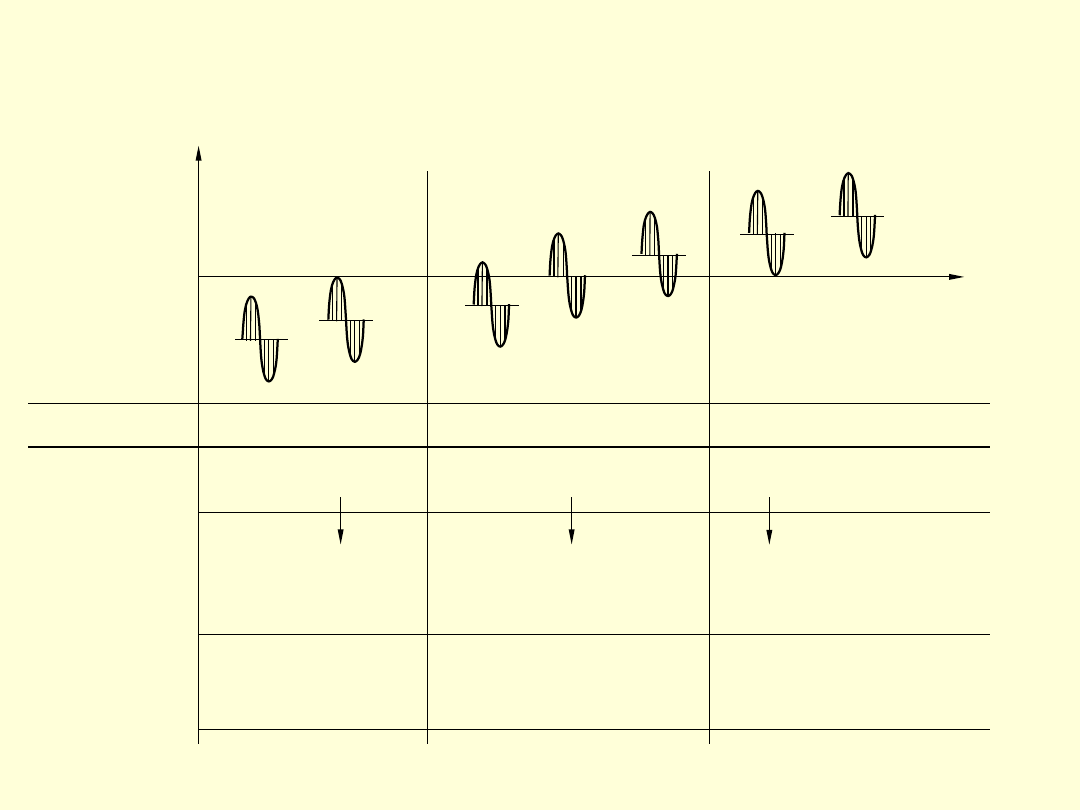
RODZAJE CYKLI NAPRĘŻEŃ ZMIENNYCH

Naprężenia

ujemne

Naprężenia

dodatnie

Naprężenia o

zmiennym

znaku

Tętniące

ściskanie

Tętniące

rozciąganie

Cykl

wahadłowy

t



(+)

(–)

Lp

1

2

3

4

5

6

7

Z

c

Z

cj

Z

c

Z

ro

Z

r

Z

rj

Z

r

Oznaczenie

granic

zmęczenia

17

0

r

r

F

P





RODZAJE NAPRĘŻEŃ

RODZAJE NAPRĘŻEŃ

• nominalne (

obliczeniowe

)

-

• rzeczywiste (

pomiarowe

)

• dopuszczalne -

• graniczne -

R

er

r

x

R

k 

m

0,2

e

R

,

R

,

R

R

e

r

R

e

g

R

e

s

18

ZASADY OKREŚLANIA DOPUSZCZALNYCH

NAPRĘŻEŃ I WSPÓŁCZYNNIKÓW

BEZPIECZEŃSTWA PRZY OBCIĄŻENIACH

STATYCZNYCH





n

2

1

Q

R

x

x

x

f

x

,...,

,

)

,

(



x

1

– jednorodność materiału (technologia),

x

2

– dokładność zachowania wymiarów,

x

3

– ważność przedmiotu,

x

4

– pewność założeń (dokładność i metody

obliczeń),

Orientacyjne

wartości

naprężeń

dopuszczalnych

bez

wyznaczania

współczynników

bezpieczeństwa

można

odczytać z tabel.

19

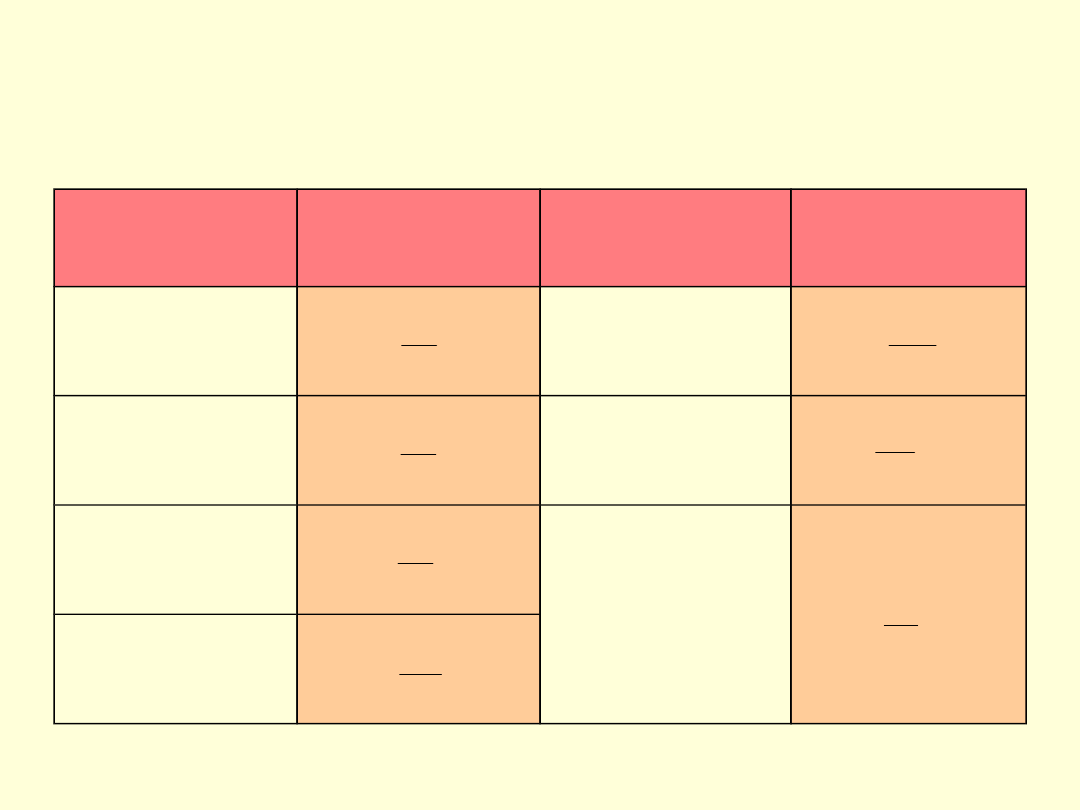
NAPRĘŻENIA DOPUSZCZALNE

k

(r,c,t,g,s,w,o)

 granicy plastyczności

R

e

;

 granicy plastyczności

R

0,2

;

 wytrzymałości na rozciąganie (doraźna)

R

m

;

Naprężenia dopuszczalne są obliczane na
podstawie:

Q

e

r

x

R

k 

R

m

r

x

R

k 

dla materiałów

plastycznych z wyraźną

granicą plastyczności

Q

r

x

R

k

0,2



dla materiałów

plastycznych bez

wyraźnej granicy

plastyczności

dla materiałów

kruchych (np. żeliwo)

20

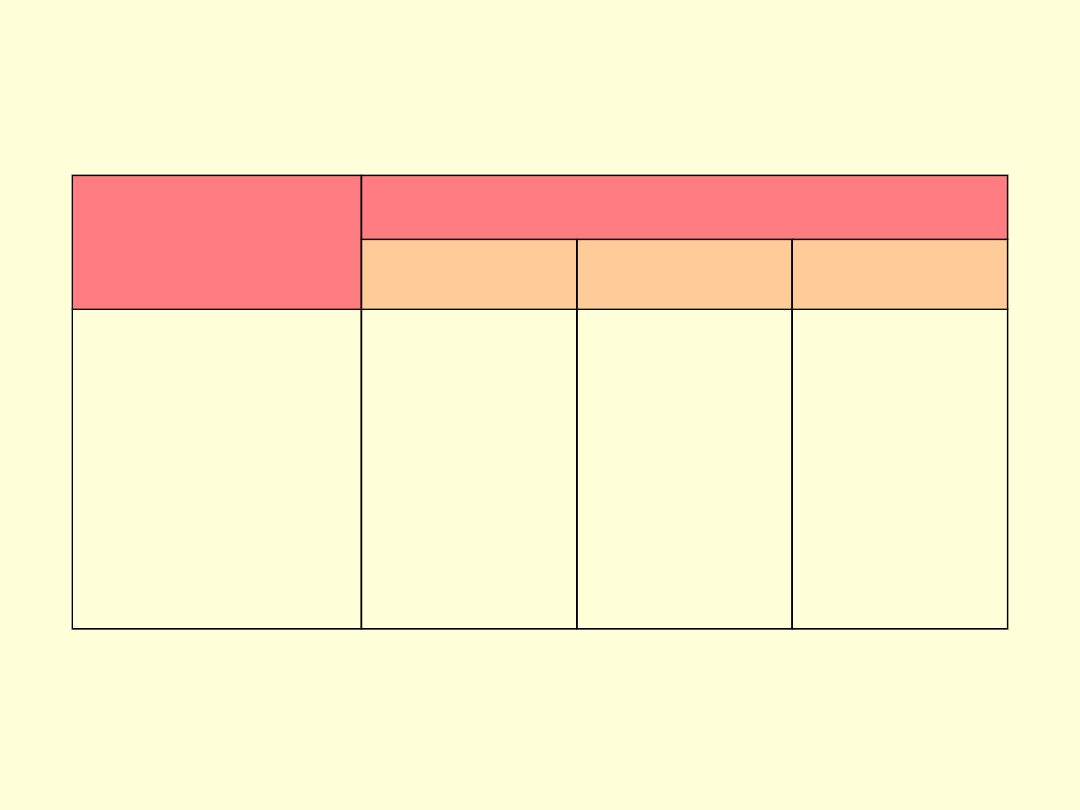
PODSTAWOWE ZALEŻNOŚCI

WYTRZYMAŁOŚCIOWE PRZY OBCIAZENIACH

STATYCZNYCH

Rodzaj

obciążenia

Zależność

Rodzaj

obciążenia

Zależność

rozciąganie

skręcanie

ściskanie

wyboczenie

ścinanie

nacisk

powierzchnio
wy

zginanie

r

0

r

r

k

F

P







c

0

c

c

k

F

P







g

x

g

g

k

W

W







t

0

t

t

k

F

P







s

0

s

s

k

W

M







0

1

0

k

F

P

p





c

w

w

k

F

P











0

21

Materiał

Współczynnik bezpieczeństwa

x

Q

x

R

x

Z

*

Stale
Staliwo
Żeliwo szare
Mosiądze
Brązy
Stopy aluminium
Stopy magnezu

2÷2,3
2÷2,3

-

3

3,5
3,9
3,9

-
-

3,5

-
-
-
-

3,5÷4
3,5÷4

3
5

4,5

6
6

Wartości współczynników bezpieczeństwa

(przeciętne)

* x

Z

– współczynnik bezpieczeństwa przy obciążeniach

zmęczeniowych

22

N

N

1

N

2

N

3

N

4



3



2



1

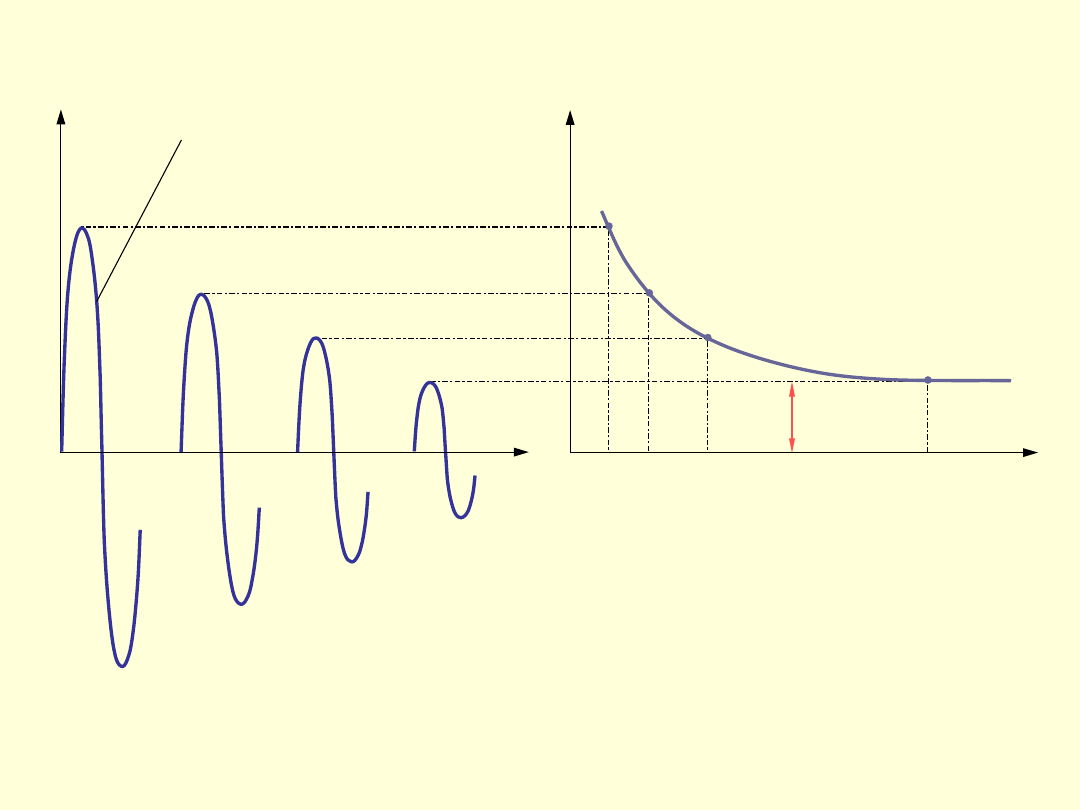
Wykres zmęczeniowy Wöhlera





Z

0



4

N

N

1

cykli wahadłowych

o

wartości naprężenia
maksymalnego



1

23

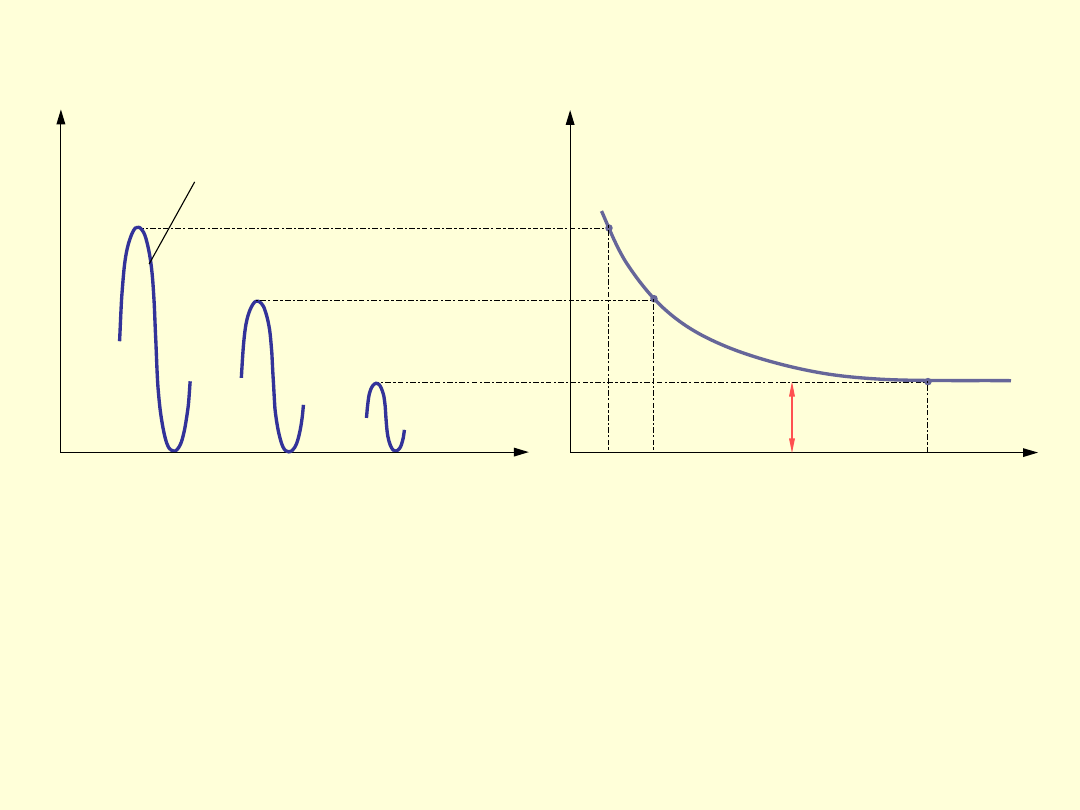
N



1





N

N

1

cykli odzerowo tętniących

(+)

o wartości naprężenia

maksymalnego



1



2



3

N

1

N

2

N

3

Z

j

a

m

Z









24

Wykres zmęczeniowy Wöhlera dostarcza
informacji

dotyczącej

wytrzymałości

zmęczeniowej dla określonego rodzaju widma
obciążeń.

Szereg tego typu wykresów sporządzonych
dla różnych wartości R (



) daje pełny obraz

własności zmęczeniowych danego materiału.

Najdogodniejszą formą ilustracji własności
zmęczeniowych

danego

materiału

są

sporządzane

na

podstawie

wykresów

Wöhlera odpowiednie wykresy zmęczeniowe,
wśród których najbardziej rozpowszechnione
są wykresy Smitha i Haigha.

25



m



max



min

Z

0

A

B

Z

0

Z

rj

½

Z

rj

D

C

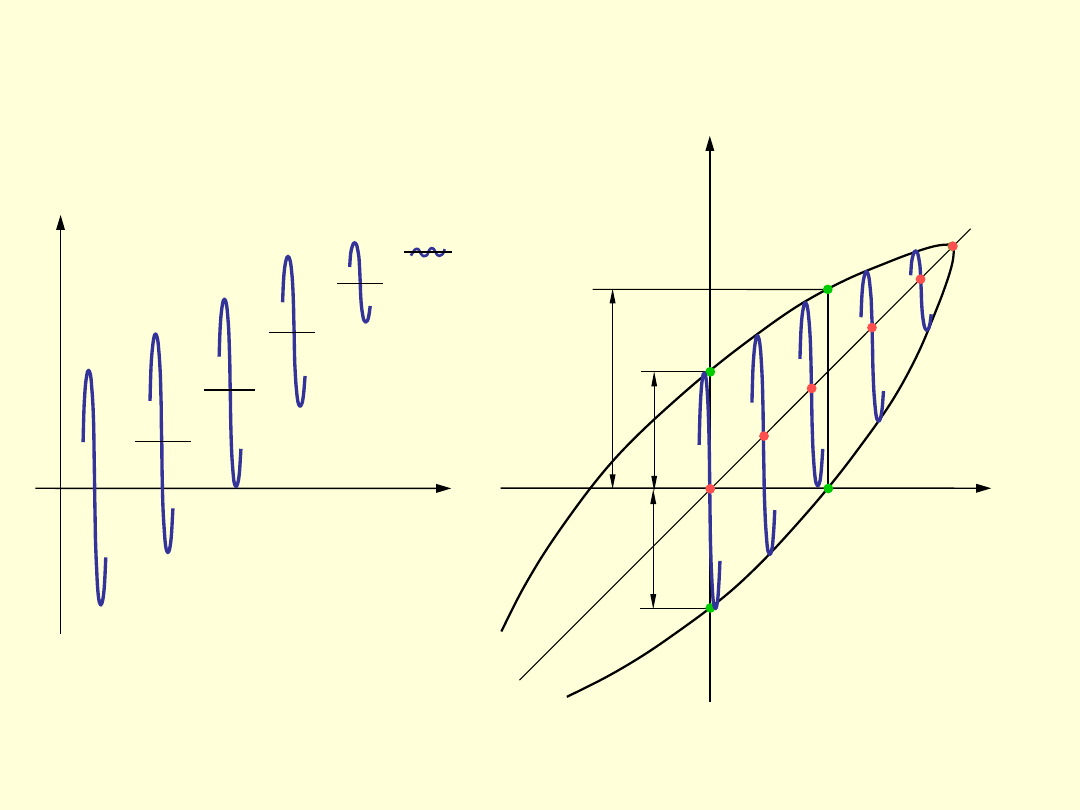
Uproszczony wykres zmęczeniowy
Smitha.



26

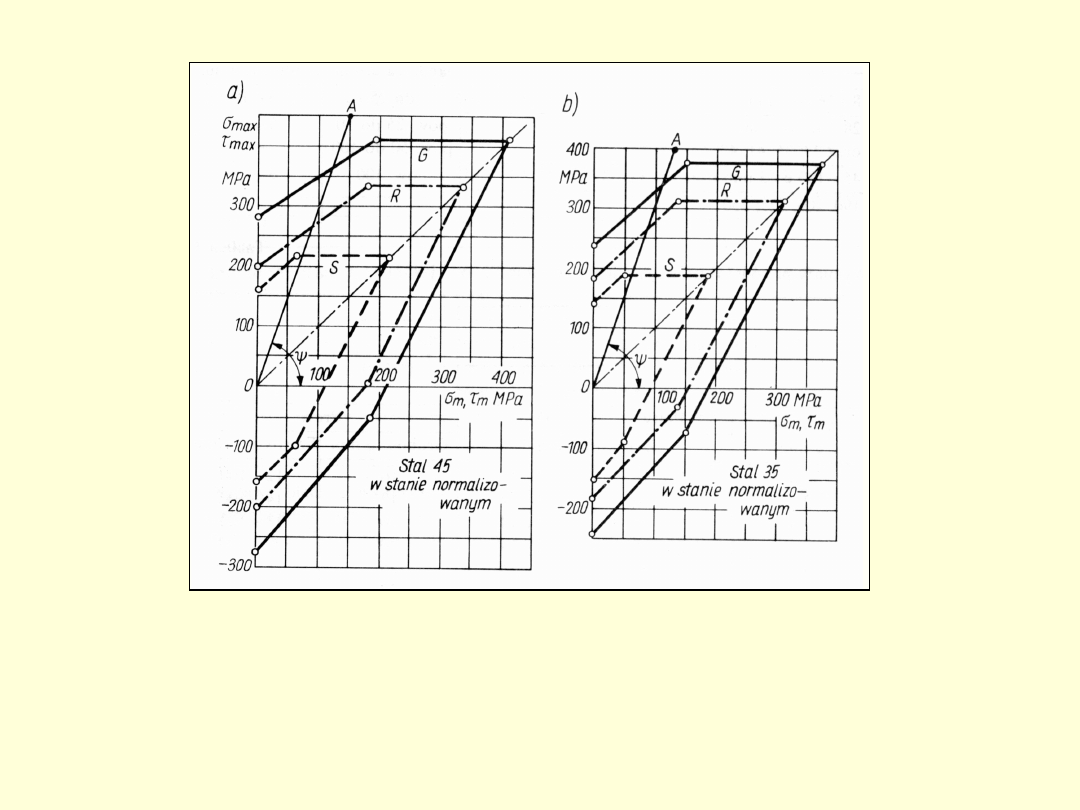
Praktyczne wykresy Smitha przy obciążeniach

rozciągająco - ściskających (R), zginajuących (G), i

skręcających (S);

a) dla St 45, b) dla St 35

27

W

praktyce

najczęściej

stosuje

się

uproszczone wykresy Smitha. Wykonuje się
je dla materiałów plastycznych (stali).

Uproszczony wykres Smitha sporządza się w
oparciu o znajomość trzech wartości:

Z

0

,

Z

j

,

R

e

(odczytuje się je z tablic).

Wykres ten sporządza się w układzie
współrzęd-nych



m

-



max(min)

. Na osi pionowej

odkłada się

Z

0

otrzymując punkty

A

i

B

,

następnie na osi poziomej odkłada się ½

Z

j

uzyskując punkt

C

oraz punkt

D

o

współrzędnych ½

Z

j

,

Z

j

. Punkty te łączy się

liniami

AD

i

BC

.

28

WPŁYW KSZTAŁTU PRZEDMIOTU W

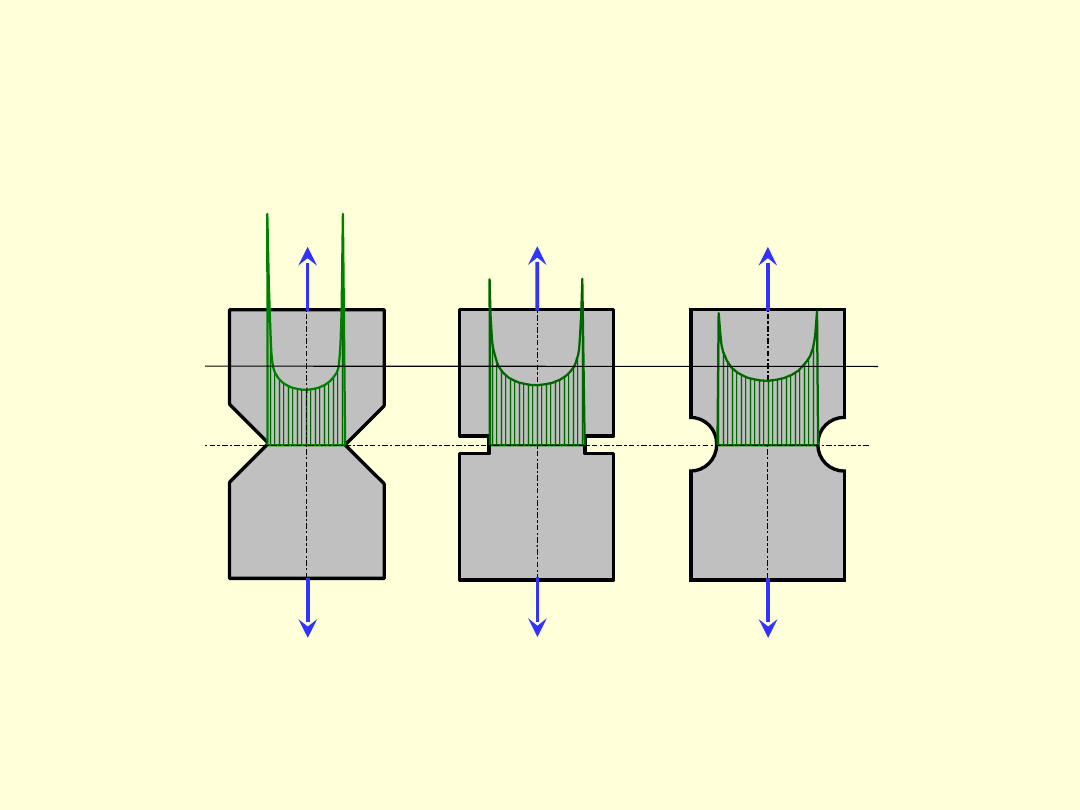
PRZYPADKU OBCIĄZEŃ STAŁYCH

Rozkład naprężeń w próbkach

rozciąganych o różnych rodzajach i

różnej głębokości karbu

P

r

P

r

P

r

P

r

P

r

P

r

29

W przekroju osłabionym karbem (otwór,
podcięcie, nagła zmiana przekroju) występuje
spiętrzenie

naprężeń,

zwane

również

działaniem karbu.

Stopień spiętrzenia spowodowanego zmianą
kształtu przedmiotu przy założeniu, że
przedmiot jest:

• idealnie gładki,
• wykonany z materiału izotropowego,
• wykonany

z

materiału

idealnie

sprężystego,

określa się tzw. współczynnikiem kształtu



K

.

30

n

m

K











m

- naprężenia maksymalne związane z istnieniem

zmian kształtu przedmiotu



n

- naprężenia nominalne obliczone według

konwencjonal-nych wzorów

Spiętrzenie naprężeń ma inny przebieg w
przypadku rozciągania, a zupełnie inny dla
zginania lub skręcania.

(1)

31

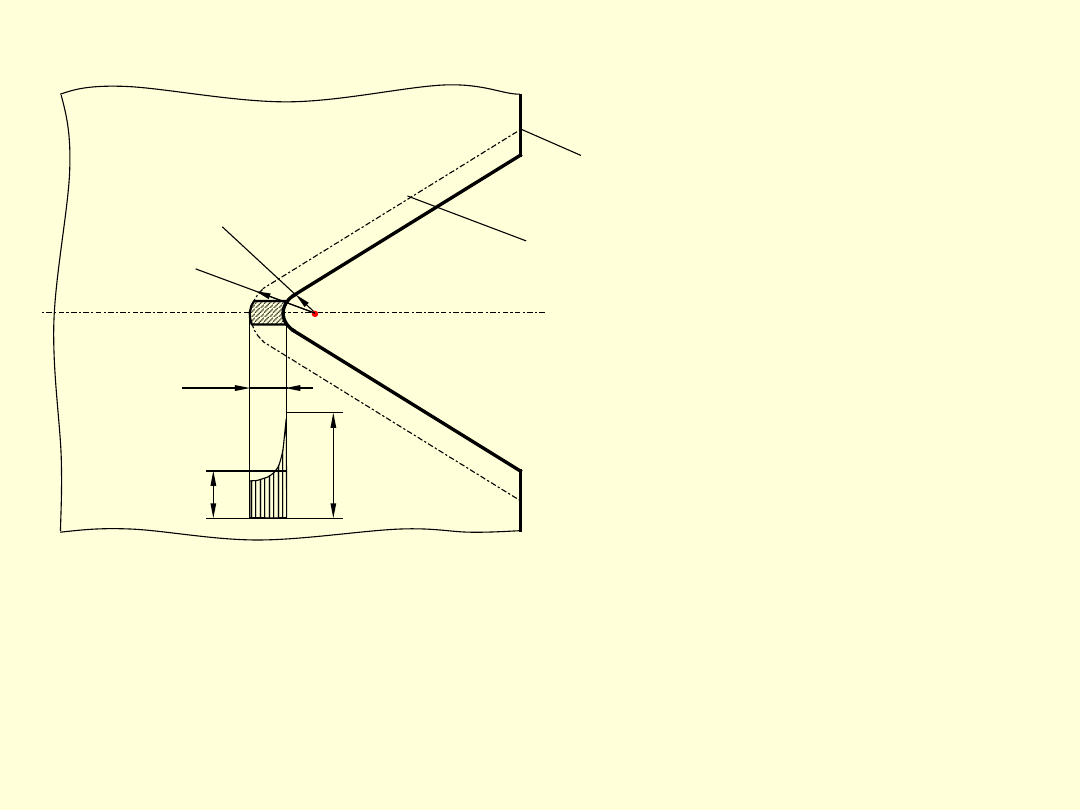
DZIAŁANIE KARBU W PRZYPADKU

OSTRYCH PODCIĘĆ

Wartości liczbowe współczyn. kształtu określonych
wzorem (1) dla konkretnych kształtów i wymiarów
przedmiotów

można

otrzymać

ze

wzorów

teoretycz-nych lub z badań doświadczalnych. W
przypadku łagodnych zmian kształtu badania
doświadczalne wykazują zgodność z wynikami
uzyskanymi na drodze teoretycznej. W przypadku
ostrych podcięć teoretyczne obliczenia wykazują,
że dla bardzo małych promieni karbu (



 0

)

naprężenia w miejscu podcięcia powinny rosnąć
nieograniczenie (



m

 

), natomiast wyniki badań

doświadczalnych wykazują tam mniejszy stopień
spiętrzenia.

32

1 – rzeczywisty zarys

karbu

2 – obliczeniowy zarys

karbu



max

- naprężenia

maksymalne
teoretyczne



śr

- naprężenia

rzeczywiste

s

2

1





k



m

a

x



śr

33

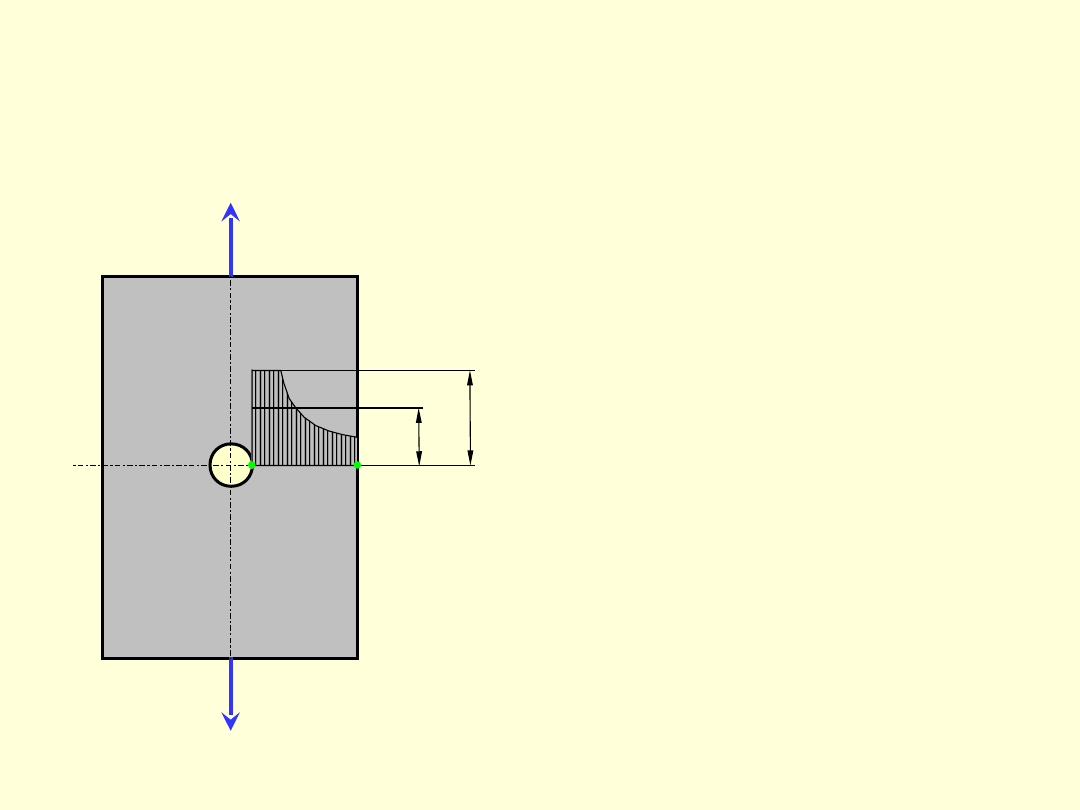
Wyjaśnienie tego zjawiska podał Neuber
opierając się na założeniu, że materiał
rzeczywisty

nie

stanowi

jednorodnego

continum

(którego

dotyczą

wzory

sprężystości) i na dnie karbu należy wyobrazić
sobie cząstkę materiału o grubości

s

, w której

nie zachodzi już dalsze spiętrzenie naprężeń,
lecz utrzymuje się stałe dla cząstki naprężenie



śr

. W otoczeniu dna karbu materiał

rzeczywisty zachowuje się tak, jakby promień



dna karbu był większy od promienia

rzeczywistego (konstrukcyjnego)



k

i wynosił:

m

k













m

– promień minimalny zależny od własności

materiału (odczytujemy z wykresu)

34

WPŁYW KILKU KARBÓW

WYSTĘPUJĄCYCH JEDNOCZEŚNIE

W przypadku jednoczesnego działania kilku
karbów można ich wpływ ująć jednym
współczynnikiem kształtu



k

obliczonym na

podstawie

współczynników

cząstkowych



k1

,



k2

,...,



ki

, ze wzorów przybliżonych:

o ile naprężenia maksymalne spowodowane
łącznym działaniem karbów nie przekroczą
granicy plastycz-ności

R

e

.

,

3

2

1























k

k

k1

k

ki

n

i

i

k

1

n













lub

e

n

k

max

R













35

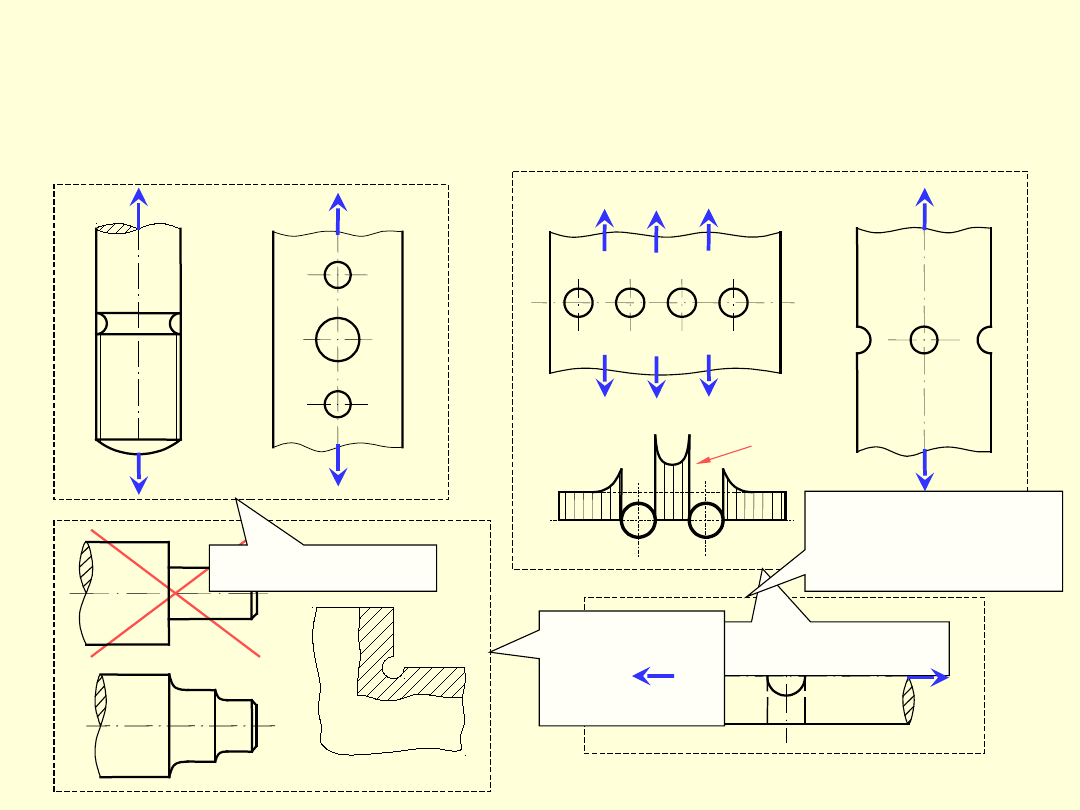
Karby nakładające
się

P

r

P

r

Karby nie

oddziaływujące na siebie

P

r

P

r

36

WPŁYW DOKSZTAŁCEŃ PLASTYCZNYCH

MATERIAŁU NA SPIĘTRZENIE NAPRĘŻEŃ

Po przyłożeniu siły

P

r

naprężenia w punkcie

A

osiągną

granicę

plastycz-ności

R

e

i

wówczas,

przy

dalszym wzroście siły

P

r

w

kolejnych

punktach
przyłożonych

w

pobliżu

punktu

A

naprężenia

osiągną

granicę plastycz-ności
R

e

, powstanie stan

przedstawiony

na

rysun-ku.

P

r

P

r



śr

R

e

A

B

37

Ponieważ w pobliżu punktu

B

naprężenia nie

osiągnęły granicy plastyczności R

e

, przeto w

przekroju

A-B

nie nastąpiło płynięcie całego

płaskownika.

Jeżeli

zatem

naprężenia

nominalne

nie

przekroczyły

naprężeń

dopuszczalnych

k

r

, to płaskownik nie wydłużył

się nadmiernie. Po usunięciu siły

P

r

w

płaskowniku pozostaną naprężenia wstępne;
w miejscach położonych w pobliżu punktu

A

naprężenia rozciągające, a pobliżu punktu

B

–

ściskające. Z chwilą ponownego przełożenia
siły

P

r

we wszystkich miejscach płaskownika

materiał będzie się zachowywał sprężyście.

38

Tak więc dla materiałów plastycznych
podanych

działaniu

obciążeń

stałych

spiętrzenie naprężeń nie powoduje istotnych
zmian w warunkach pracy. Z tego względu w
obliczeniach

wytrzymałościowych

dotyczących

obciążeń

stałych

wpływu

spiętrzenia

naprężeń

w

materiałach

plastycznych nie uwzględnia się.

39

WPŁYW KSZTAŁTU PRZEDMIOTU W

PRZYPADKU OBCIĄŻEŃ ZMIENNYCH

Zazwyczaj wytrzymałość zmęczeniowa

Z

jest

niższa od granicy plastyczności R

e

i nawet

przy niedużym zmiennym obciążeniu w
pobliżu karbu naprężenia maksymalne mogą
przekroczyć wytrzymałość zmęczeniową

Z

.

Wówczas pojawiają się mikro-pęknięcia -
nowe ogniska, co znów powoduje spiętrzenie
naprężeń i związane z tym coraz to szybsze
rozprzestrzenianie się szczeliny zmęcze-
niowej,

a

w

następstwie

uszkodzenie

elementu.

40

Zmęczeniowy współczynnik działania karbu



k

„współczynnik karbu” określa się ze wzoru:

k

bk

k

Z

Z





Z

k

– wytrzymałość zmęczeniowa gładkich próbek z

karbem,

Z

bk

- wytrzymałość zmęczeniowa gładkich próbek bez

karbu.

Uzyskanie właściwej wartości współczynnika
karbu



k

jest niezmiernie pracochłonne,

połączone

z

przeprowadzaniem

długotrwałych

badań

zmęcze-niowych.

Szukano dróg umożliwiających w miarę
dokładne oznaczenie współczynnika



k

w

zależnoś-ci od innych, łatwiejszych do
wyznaczenia wielkości.

41

Najszersze

zastosowanie

znalazło

wprowadzenie tzw. współczynnika wrażliwości
materiału na działanie karbu



k

(eta):

1

1

k

k

k













Na

podstawie

wyników

badań

doświadczalnych stwierdzono, ze określony
powyższym wzorem współczynnik wrażliwości
 wynosi:

• dla szkła



k

=1

• dla stali w stanie ulepszonym cieplnie



k

=0,7÷1,0

• dla stali w stanie surowym



k

=0,5÷0,9

• dla stali w stanie wyżarzonym



k

=0,4÷0,8

• dla żeliwa szarego



k

=0

(2)

42

Szkło i wysokowytrzymałe stale hartowane są
więc bardzo wrażliwe na działanie karbu
(



k

=1), a więc dla tych materiałów



k





k

.

Wyniki badań doświadczalnych wykazały, że
współczynnik wrażliwości



k

z wystarczającą

dla

praktyki

dokładnością

może

być

traktowany jako stała materiałowa, zależna
np. dla stali od wytrzymałości zmęczeniowej
Z

go

(przedstawiane jest to w postaci

wykresów).

Na podstawie zależności (2) współczynnik
karbu obliczać można ze wzoru:





1

1

k

k

k













43

WPŁYW STANU POWIERZCHNI NA

WYTRZYMAŁOŚĆ ZMĘCZENIOWĄ

Współczynnik karbu



k

dotyczy próbek o

gładkich powierzchniach (polerowanych). Aby
uwzględnić wpływ chropowatości powierzchni,
należałoby przeprowadzić ponowne badania
zmęczeniowe

na

próbkach

o

danej

chropowatości powierzchni, gdyż nierówności
powierzchni powstałe na skutek obróbki
skrawaniem lub w toku procesów walcowania,
albo odlewania w znacznych stopniu obniżają
własności zmęczeniowe materiałów. Wpływ
stanu warstwy wierzchniej elementu na
spietranie naprężeń wyraża się za pomocą
współczynnika stanu powierzchni



p

.

44

Współczynnik stanu powierzchni



p

:

p

gł

p

Z

Z





Z

gł

- wytrzymałość zmęczeniowa próbki gładkiej,

Z

p

- wytrzymałość zmęczeniowa próbki o danym

stanie powierzchni.

Wartość liczbowa



p

odczytujemy z wykresów.

W przypadku skręcania współczynnik
stanu po-wierzchni jest znacznie mniejszy niż
dla pozostałych przypadków obciążeń.

45

ZMĘCZENIOWY WSPÓŁCZYNNIK

SPIĘTRZENIA NAPRĘZEŃ



Łączne działanie karbu ujęte współczynnikami



k

i



p

określa wzór:

p

k













k

- współczynnik działania karbu,



p

- współczynnik stanu powierzchni charakteryzujący

zmianę granicy zmęczenia w zależności od
chropowatości i stanu powierzchni elementu.

1

p

k













lub

46

PRZYKŁADY ZMNIEJSZANIA WPŁYWU

KARBU NA DRODZE KONSTRUKCYJNEGO

KSZTAŁTOWANIA

Karby

szeregowe

Karby

równoległe



Kształtowani

e przejść na

wałkach

Karby

przenikające się

(zazwyczaj

przeciążające)

47

WPŁYW WIELKOŚCI PRZEDMIOTU

Warstwa powierzchniowa wykazuje znaczenie
większą wytrzymałość w porównaniu do
rdzenia, a ponieważ badamy próbki o
znormalizowanych średnicach d=8 należy
uwzględniać wielkość przedmiotu.

Z

Z

8





Z

8

- wytrzymałość zmęczeniowa uzyskana dla

próbek gładkich o średnicach 7÷10mm,

Z - wytrzymałość zmęczeniowa, jaką uzyskano by

dla gładkich dużych próbek (o średnicach
równych średnicy przedmiotu).

48

OBLICZANIE ZMĘCZENIOWYCH

WSPÓŁCZYNNIKÓW BEZPIECZEŃSTWA

W

elementach

poddanych

długotrwałym

obciążeniom

zmiennym

nie

można

w

maszynach dopuścić do powstawania naprężeń
równych Z, gdyż w przypadku zaistnienia
minimalnego

bodaj

wzrostu

naprężeń

spowodowanego np. drganiami maszyny lub
innymi czynnikami trudnymi do przewidzenia i
wyeliminowa-nia – po przepracowaniu pewnej
liczby

cykli

element

maszyny

uległby

zniszczeniu

zmęczeniowemu.

Aby

się

zabezpieczyć przed taką ewentualnością,
należy

naprężenia

maksymalne



max

,

wynikające

z

obliczeń

(nawet

bardzo

dokładnych), dać mniejsze od wytrzymałości
zmęczeniowej Z.

49

Stosunek wytrzymałości zmęczeniowej Z do
naprężeń

maksymalnych

nazywamy

zmęczenio-wym

współczynnikiem

bezpieczeństwa

x

z

:

max

Z

Z

Z

x





Występujące

w

powyższym

wzorze

naprężenie



Zmax

dotyczy

maksymalnej

wartości

umownych

naprężeń

zmęczeniowych dla cyklu pracy danego
elementu i nazywa się je rzeczywistym
zmęcze-niowym naprężeniem maksymalnym.
Oblicza się je według zasad znanych z
wytrzymałości materiałów z uwzględnieniem
działania karbu



i wielkości przedmiotu



.

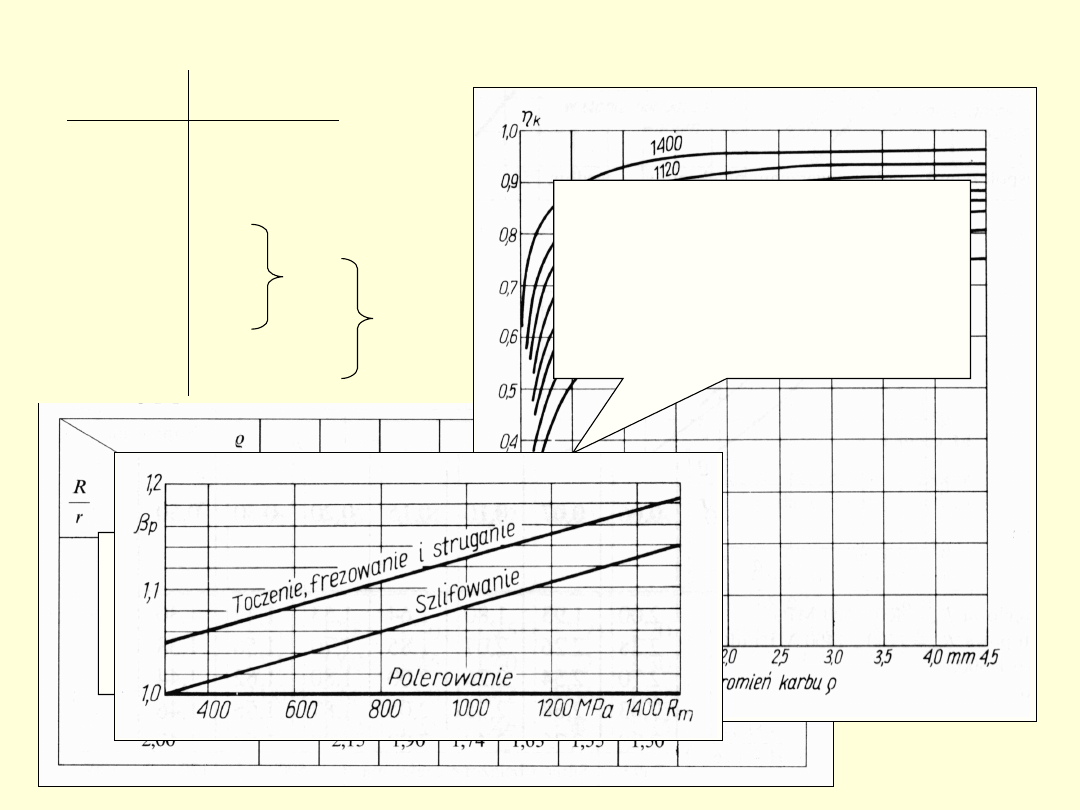
50

k



p





k





k



x

z

tablice lub

wykresy

wartości

obliczone

Przykładowe wartości

współczynnika kształtu



k

przy rozciąganiu

próbki okrągłej z

odsadzeniem

Wykres wartości

współczynnika

wrażliwości

materiału na

działanie karbu



k

Przykładowe wartości

współczynnika stanu

powierzchni



p

w

zależności od

chropowatości

powierzchni (rodzaju

obróbki)

51

WSPÓŁCZYNNIK BEZPIECZEŃSTWA x

Z

PRZY CYKLU SYMETRYCZNEM

Dla cyklu wahadłowego zmęczeniowy
współczynnik bezpieczeństwa oblicza się ze
wzoru:

a

0

z

Z

x















a

– amplituda naprężeń nominalnych obliczona z

konwencjonalnych wzorów,

W tym przypadku



a

=



max

.

Dla cyklu wahadłowego:

a

aZ

Z



















max

52

WSPÓŁCZYNNIK BEZPIECZEŃSTWA

PRZY CYKLACH NIESYMETRYCZNYCH

Wartość wytrzymałości zmęczeniowej Z dla
cykli niesymetrycznych nie może być
jednoznacznie określona, gdyż takiemu
samemu cyklowi naprężeń odpowiadać
mogą

różne

wartości

wytrzymałości

zmęczeniowej Z.

Dany cykl naprężeń charakteryzuje się
napręże-niem średnim



m

oraz amplitudą

naprężeń

zmęczeniowych



aZ

,

więc

zmęczeniowe

napręże-nie

maksymalne

wynosi:

aZ

m

Zmax











53

Amplitudę naprężeń zmęczeniowych



aZ

oblicza się analogicznie jak w przypadku cykli
symetrycznych:

a

aZ















naprężenie maksymalne po podstawieniu:

m

a

Z



















max

gdzie:



a

– amplituda naprężeń nominalnych

obliczona

z

konwencjonalnych

wzorów

bez

uwzględnienia



i



.

Ostatecznie

zmęczeniowy

wsp.

bezpieczeństwa

x

Z

:

max

Z

Z

Z

x





m

aZ

Z









m

a

Z

















54

Dla



=const

, czyli w przypadku stałego

stosunku

amplitudy

obciążenia

a do

obciążenia średniego



m

, wsp. x

Z

można

wyrazić zależnością:

przy

czym

otrzymana

wartość

należy

porównać z wartością ze wzoru:



























1

Z

Z

2

Z

x

j

0

m

a

0

Z









m

a

e

Z

R

x















