Mechanika Gruntów

Mechanika Gruntów

(stan naprężenia)

(stan naprężenia)

WYKŁAD NR 4

Plan wykładu

Plan wykładu



Wstęp - stan naprężenia w gruncie

Wstęp - stan naprężenia w gruncie



Naprężenia pierwotne

Naprężenia pierwotne



Naprężenia efektywne

Naprężenia efektywne



Naprężenia od sił zewnętrznych

Naprężenia od sił zewnętrznych



Rozkład naprężeń pod fundamentami

Rozkład naprężeń pod fundamentami

A

N

lim

0

A













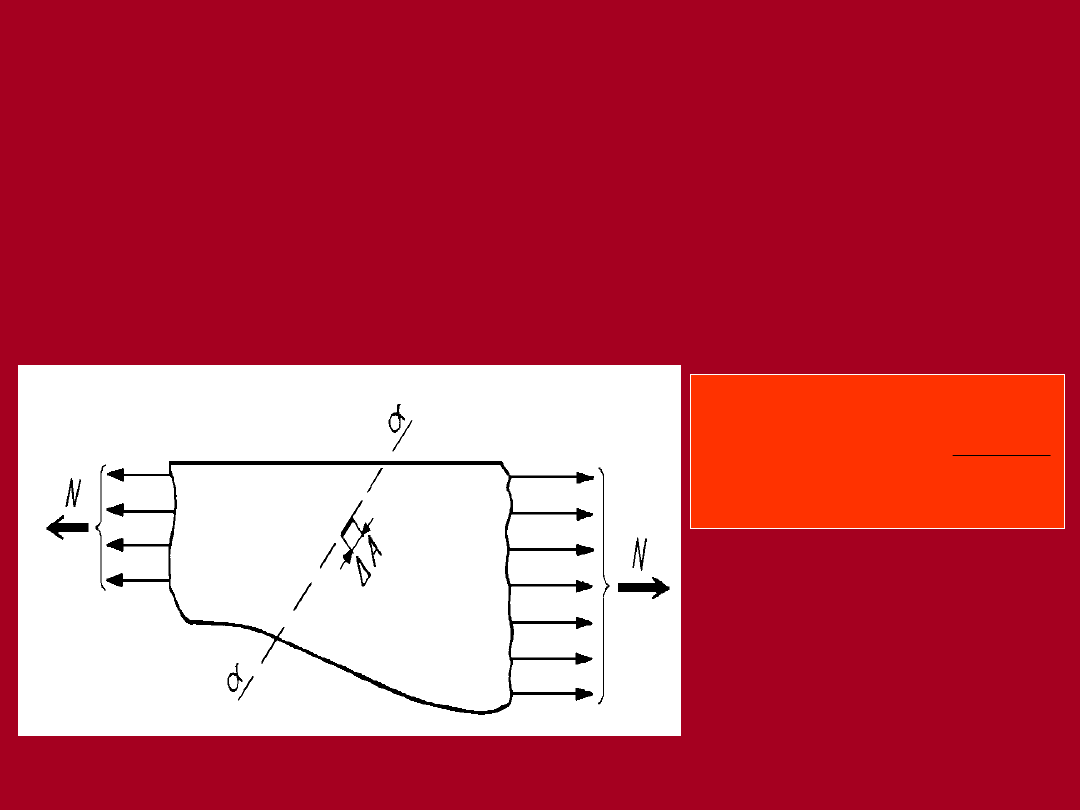
Stan naprężenia - definicja

Stan naprężenia - definicja

Naprężenie

Naprężenie

-

-

graniczna wartość siły działającej na

graniczna wartość siły działającej na

nieskończenie mały element pola przekroju ciała do

nieskończenie mały element pola przekroju ciała do

powierzchni tego pola:

powierzchni tego pola:

gdzie: σ - naprężenie

gdzie: σ - naprężenie

N - siła

N - siła

A - pole przekroju

A - pole przekroju

x

y

z



xz



yz



zz



yy



xy



zy



xx



yx



zx

z

x

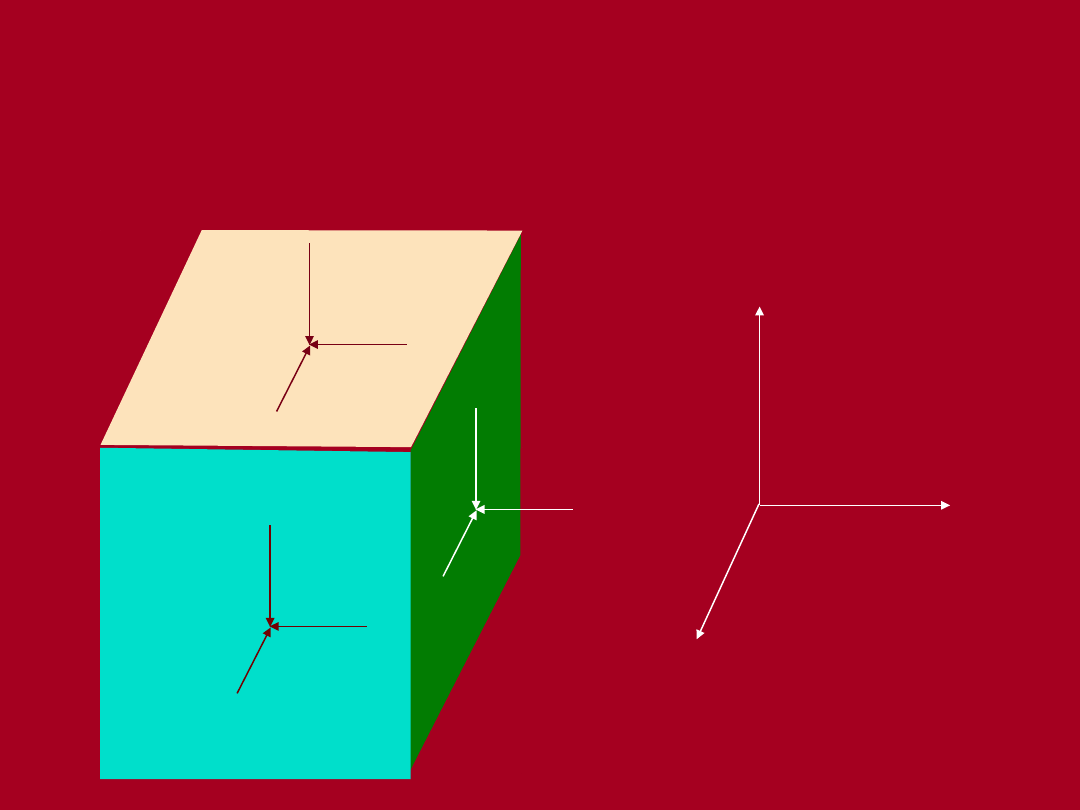
Składowe tensora naprężenia

Składowe tensora naprężenia







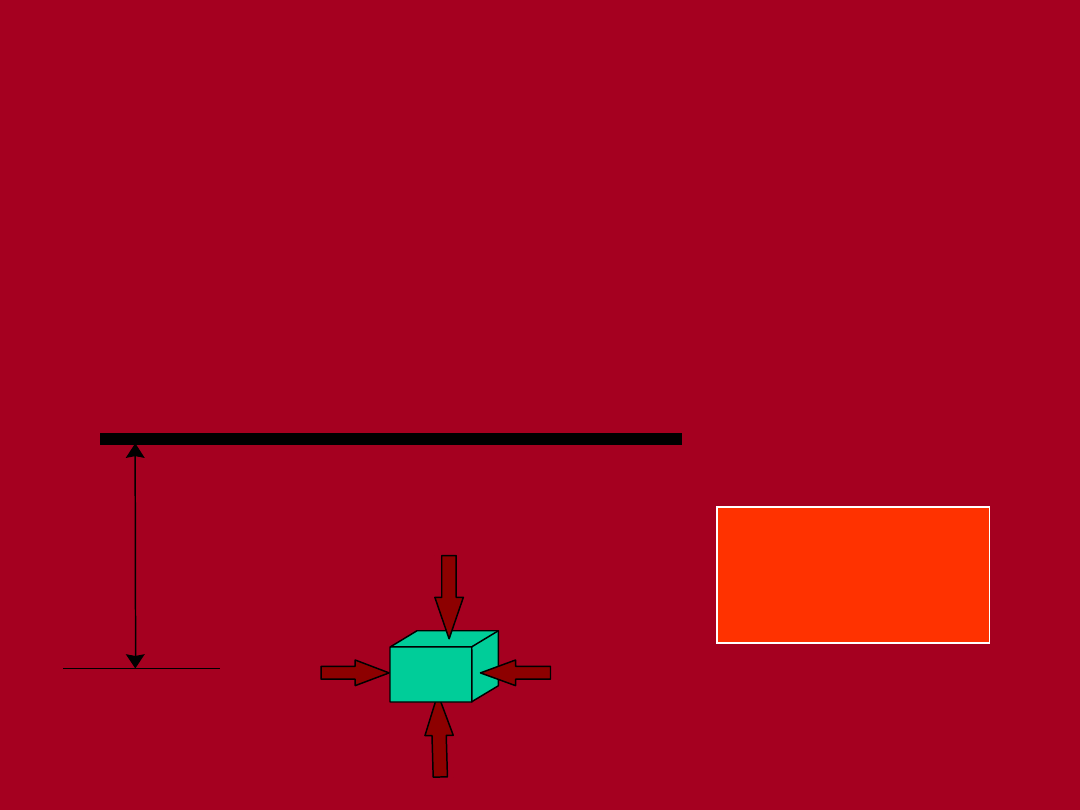
z

z

składowa pionowa naprężenia

składowa pionowa naprężenia

,

,







x

x

składowa pozioma naprężenia

składowa pozioma naprężenia



z

Z



x

Stan naprężenia - definicja

Stan naprężenia - definicja





x

x

≠

≠





z

z

Plan wykładu

Plan wykładu



Wstęp - stan naprężenia w gruncie

Wstęp - stan naprężenia w gruncie



Naprężenia pierwotne

Naprężenia pierwotne



Naprężenia efektywne

Naprężenia efektywne



Naprężenia od sił zewnętrznych

Naprężenia od sił zewnętrznych



Rozkład naprężeń pod fundamentami

Rozkład naprężeń pod fundamentami

Naprężenia pierwotne

Naprężenia pierwotne



Określają „naturalny” stan naprężenia w

Określają „naturalny” stan naprężenia w

gruncie wynikający z działania sił grawitacji

gruncie wynikający z działania sił grawitacji



Naprężenia pierwotne oznaczamy

Naprężenia pierwotne oznaczamy

indeksem

indeksem

ρ

ρ

przy symbolu naprężenia:

przy symbolu naprężenia:

σ

σ



Naprężenia pionowe:

Naprężenia pionowe:

σ

σ

z

z

ρ

ρ



Naprężenia poziome:

Naprężenia poziome:

σ

σ

x

x

ρ

ρ

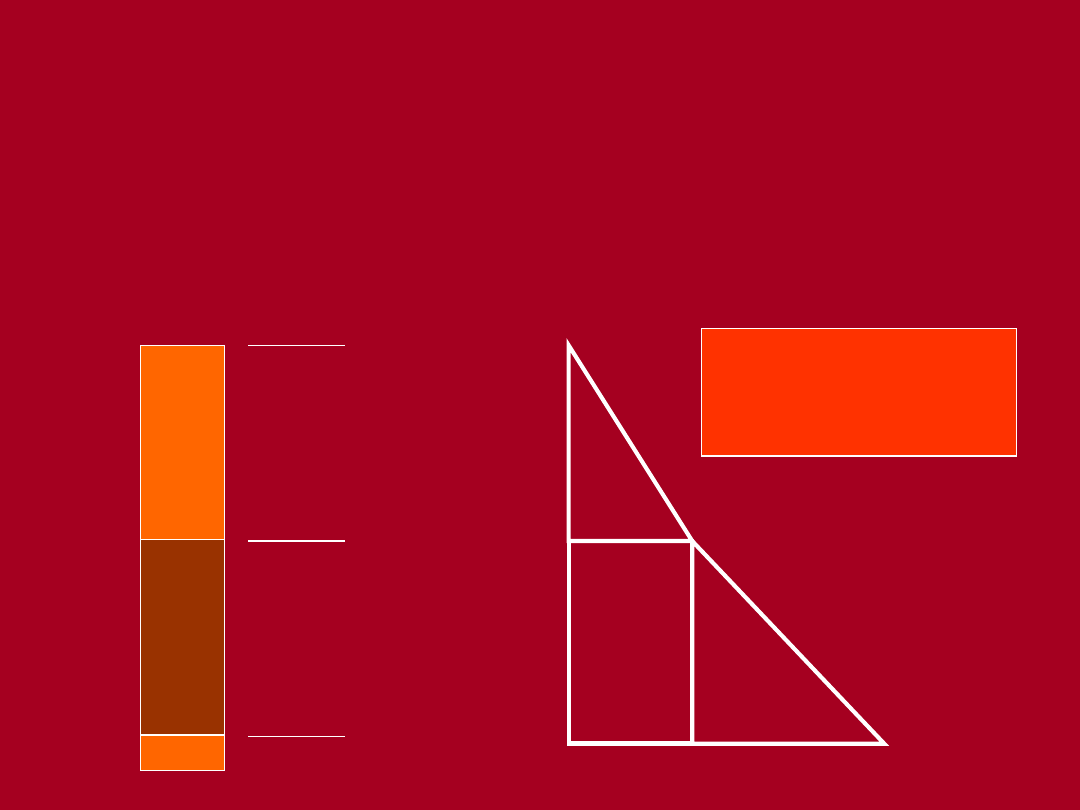
0 m

5 m

9 m

 = 16 kN/m

3

 = 18 kN/m

3

80 kPa

152
kPa

80

72



zρ

Naprężenia pierwotne pionowe

Naprężenia pierwotne pionowe

(przykład - grunt suchy)

(przykład - grunt suchy)



zρ

= Σ γ

i



h

i

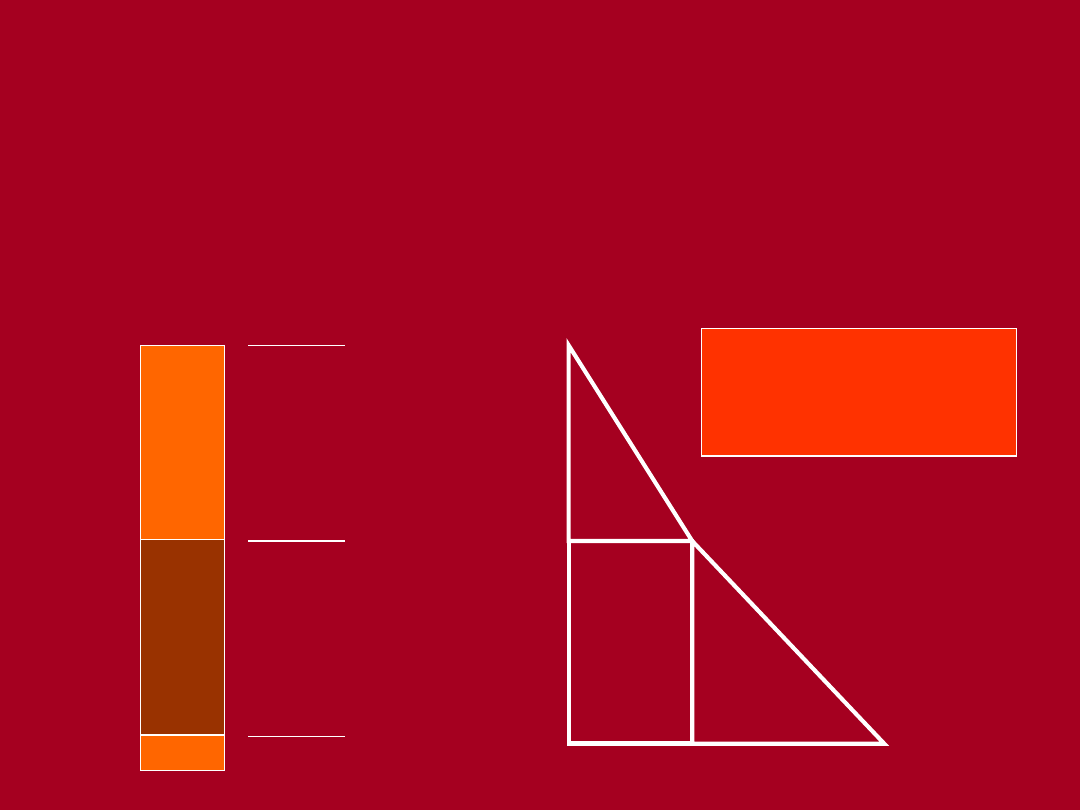
0 m

5 m

9 m

γ = 16
kN/m

3

K

0

= 0.4

 = 18 kN/m

3

K

0

= 0.5

32 kPa

68 kPa

32

36



xρ



xρ

= K

0





zρ

Naprężenia pierwotne poziome

Naprężenia pierwotne poziome

(przykład - grunt suchy)

(przykład - grunt suchy)



K

K

0

0

=

=

f

f

(

(

rodzaj gruntu

rodzaj gruntu

,

,

e

e

, OCR)

, OCR)



OCR = overconsolidation ratio

OCR = overconsolidation ratio



Dla gruntów normalnie skonsolidowanych

Dla gruntów normalnie skonsolidowanych

wzór

wzór

Jaky

Jaky

’ego

’ego

(1944):

(1944):

K

K

0

0

= 1 – sin

= 1 – sin

(

(





)

)

gdzie

gdzie





- kąt tarcia wewnętrznego gruntu

- kąt tarcia wewnętrznego gruntu

Współczynnik parcia

Współczynnik parcia

spoczynkowego K

spoczynkowego K

0

0

RODZAJ GRUNTU

RODZAJ GRUNTU

K

K

o

o

Piaski w stanie luźnym

Piaski w stanie luźnym

NC

NC

0.6

0.6

Piaski zagęszczone NC

Piaski zagęszczone NC

0.35

0.35

Gliny

Gliny

NC

NC

(Skandynawia)

(Skandynawia)

0.5 – 0.6

0.5 – 0.6

London clay OCR = 3.5

London clay OCR = 3.5

1.0

1.0

London clay OCR = 20

London clay OCR = 20

2.8

2.8

K

K

0

0

przykładowe wielkości

przykładowe wielkości

Plan wykładu

Plan wykładu



Wstęp - stan naprężenia w gruncie

Wstęp - stan naprężenia w gruncie



Naprężenia pierwotne

Naprężenia pierwotne



Naprężenia efektywne

Naprężenia efektywne



Naprężenia od sił zewnętrznych

Naprężenia od sił zewnętrznych



Rozkład naprężeń pod fundamentami

Rozkład naprężeń pod fundamentami

wykres ciśnienia obojętnego

wykres naprężeń

efektywnych

piezometr

u=(h

1

+h

2

)

w

u=(h

2

+z)

w

’=z’

’=h

1



’

=’+

u

=g



w

=

w

g

m

n

h

1

h

2

z

1

1

2

2

3

3

a)

b)

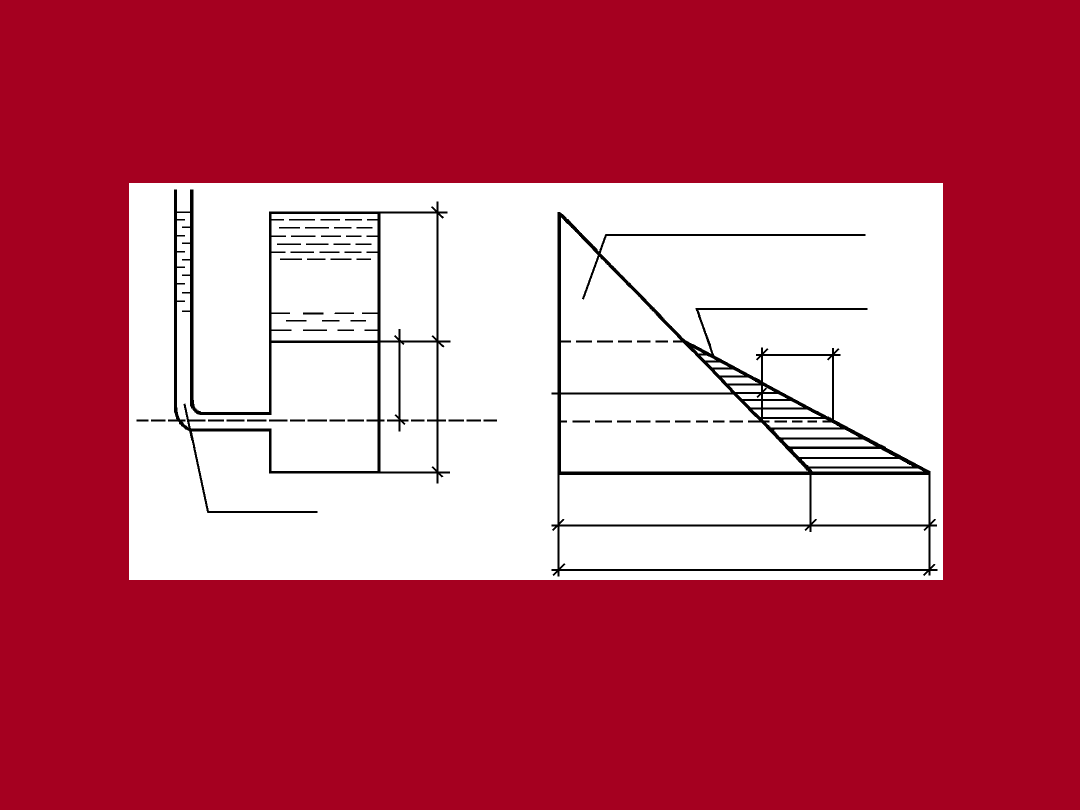
Naprężenia całkowite i

Naprężenia całkowite i

efektywne

efektywne

Rozkład naprężeń w gruncie:

Rozkład naprężeń w gruncie:

a) cylinder z gruntem obciążonym

a) cylinder z gruntem obciążonym

wodą

wodą

b) wykres naprężeń

b) wykres naprężeń

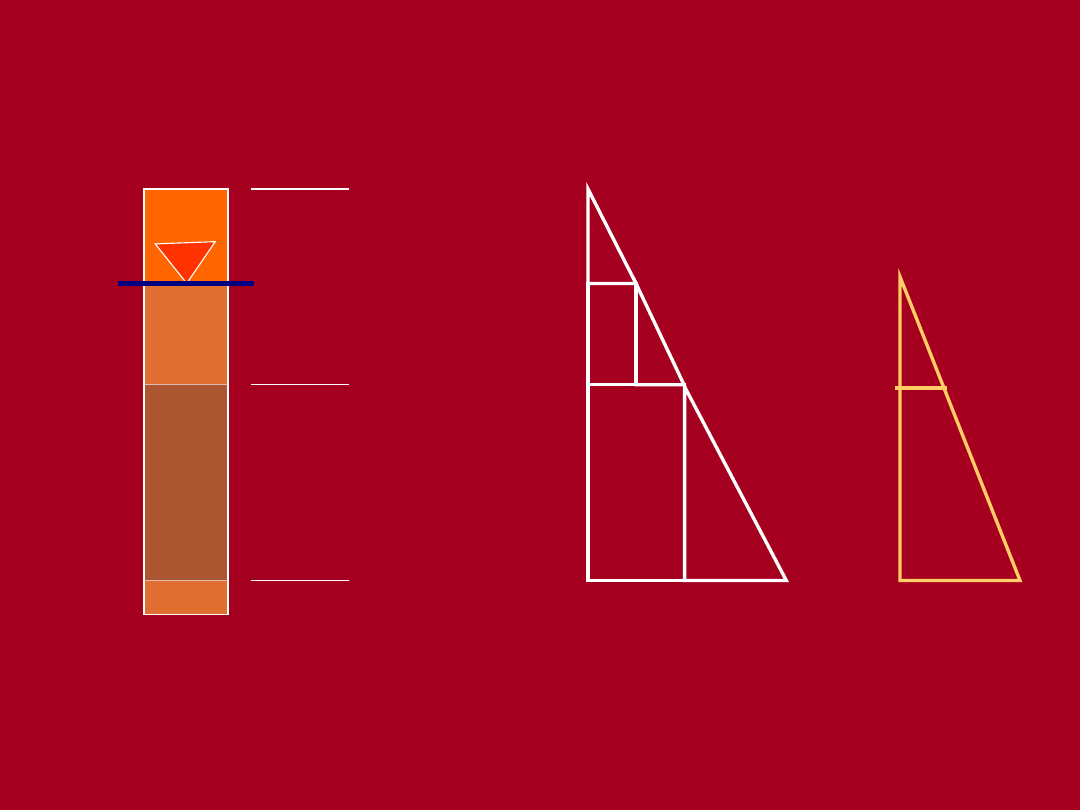
0 m

5 m

9 m

 = 16 kN/m

3



sr

= 20 kN/m

3

86 kPa

166 kPa

86

80



z



sr

= 18 kN/m

3

2 m

u

68.6 kPa

29.4

32 kPa

u - ciśnienie wody w porach

Zw.
wody



z

naprężenie

całkowite





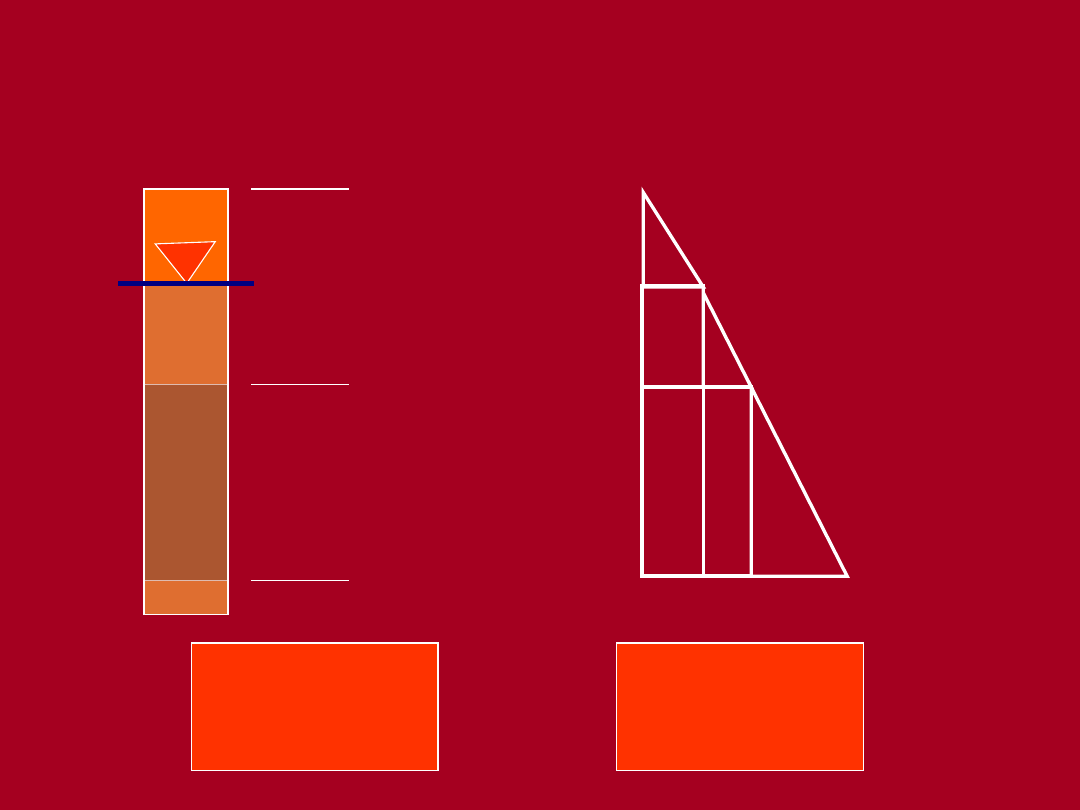
z

= 

z

-

u

0 m

5 m

9 m

2 m

56.6 kPa

97.4 kPa

32 kPa

Zw.

wody

 = 16 kN/m

3





= 10.2

kN/m

3





= 8.2

kN/m

3



 =



sr

-



w

86
kPa

166 kPa

86

80



z

u

68.6 kPa

29.4

32 kPa

56.6
kPa

97.4 kPa

32 kPa

’

z

=

+

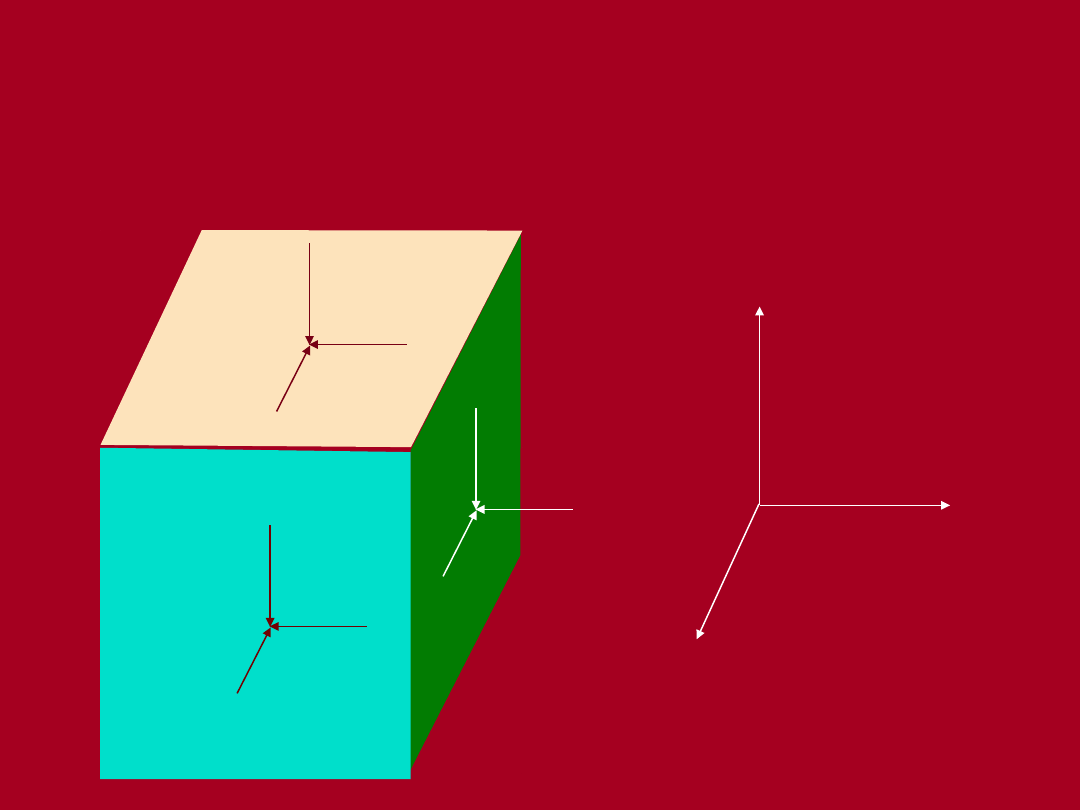
x

y

z



xz



yz



zz



yy



xy



zy



xx



yx



zx

z

x

Składowe tensora

Składowe tensora

naprężenia

naprężenia

Ogólna zasada

Ogólna zasada

naprężeń efektywnych Terzaghi’ego

naprężeń efektywnych Terzaghi’ego

 



 

 



 

 



 

























xx

xx

w

yz

yz

yy

yy

w

zx

zx

zz

zz

w

xy

xy

u
u
u

;
;
;

Naprężenia całkowite

Naprężenia całkowite

i efektywne

i efektywne

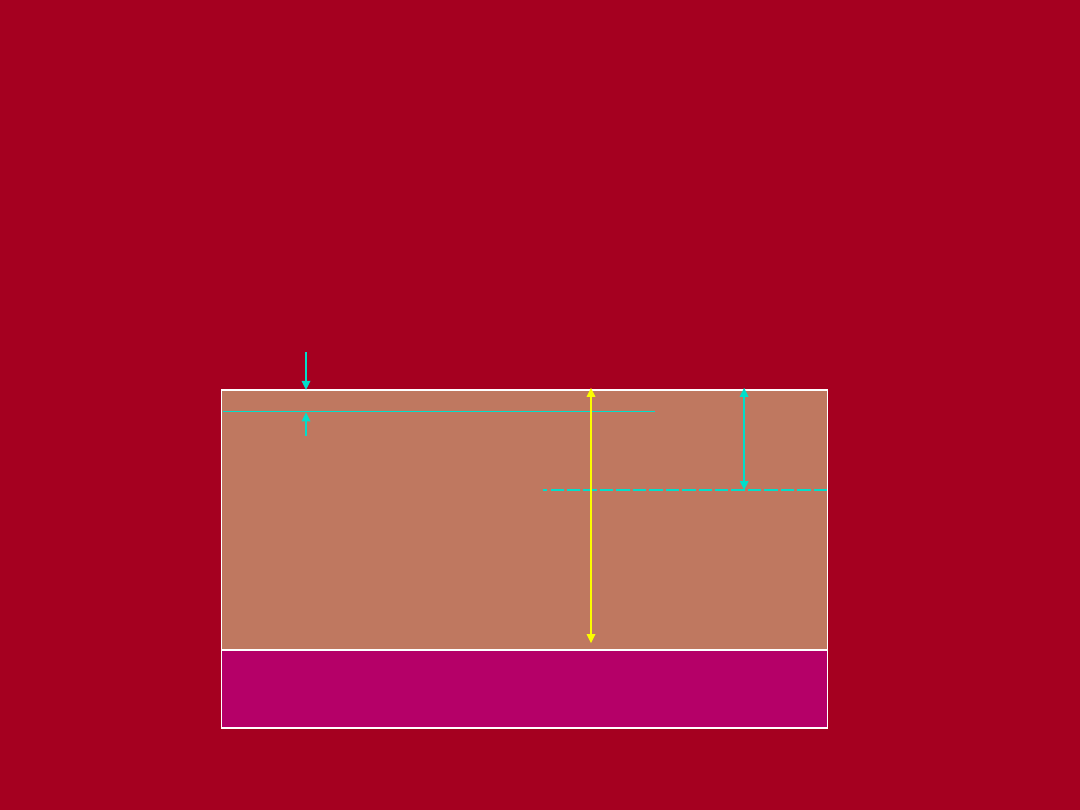
Piasek
drobny

Ił pylasty

Początkowe
ZWG

10
m

Obniżone
ZWG

5 m

1 m

Naprężenia efektywne – przykład nr

Naprężenia efektywne – przykład nr

2

2

γ = 20kN/m

3

γ’ = 12kN/m

3

K

0

= 0.4

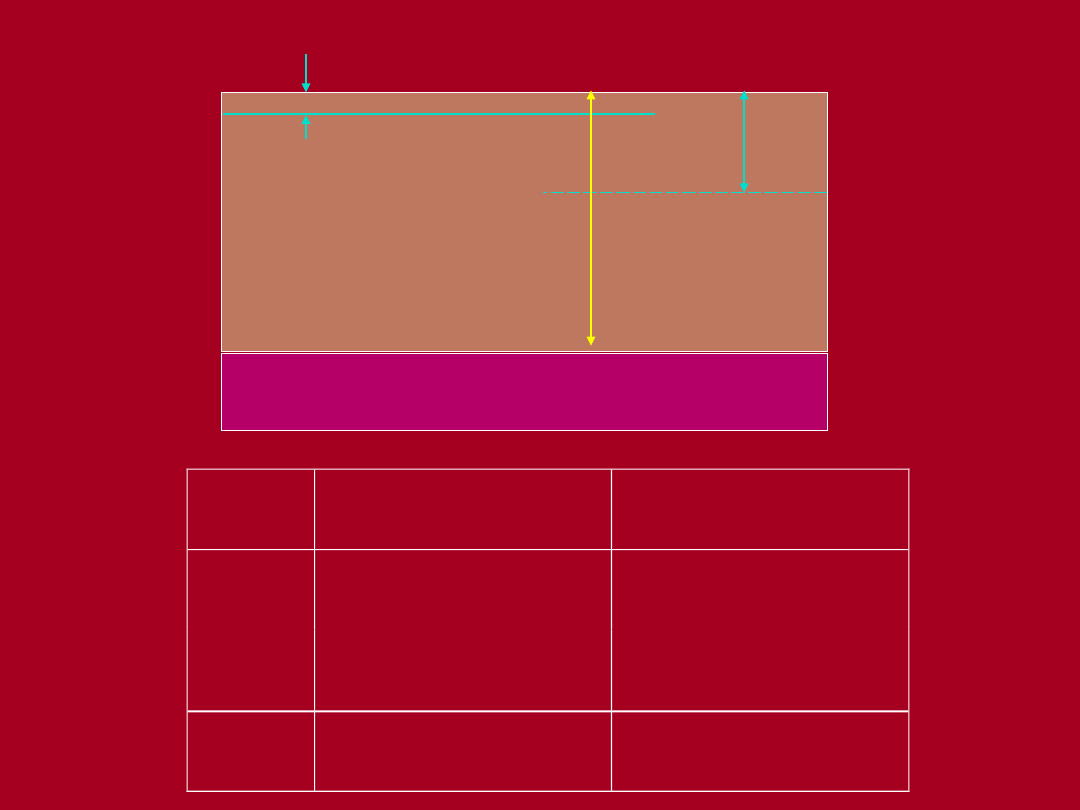
Piasek
drobny

Ił pylasty

Początkowe
ZWG

Obniżone
ZWG

1 m



z

u



z

´

Początkowe
ZWG

128+88.2=216.2
kPa

160+49= 209.0
kPa

99.8= 88.2

kPa

59.8= 49.0

kPa

120+912= 128

kPa

520+512= 160

kPa

5 m

Obniżone ZWG

γ = 20kN/m

3

γ’ = 12kN/m

3

K

0

= 0.4

10
m

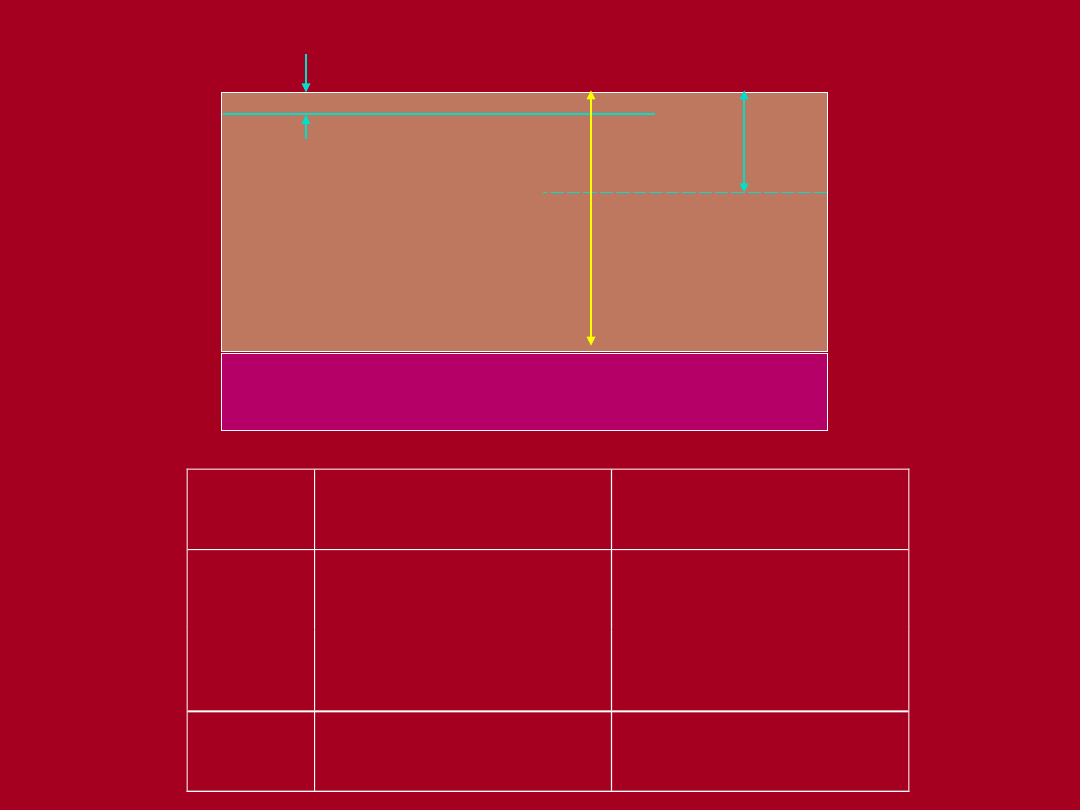
Piasek
drobny

Ił pylasty

Początkowe
ZWG

Obniżone
ZWG

1 m



x

u



x

´

Początkowe
ZWG

51.2+88.2=139.4
kPa

64+49= 113.0
kPa

99.8= 88.2

kPa

59.8= 49.0

kPa

1280.4= 51.2

kPa

1600.4= 64.0

kPa

5 m

Obniżone ZWG

γ = 20kN/m

3

γ’ = 12kN/m

3

K

0

= 0.4

10
m

Plan wykładu

Plan wykładu



Wstęp - stan naprężenia w gruncie

Wstęp - stan naprężenia w gruncie



Naprężenia pierwotne

Naprężenia pierwotne



Naprężenia efektywne

Naprężenia efektywne



Naprężenia od sił zewnętrznych

Naprężenia od sił zewnętrznych



Rozkład naprężeń pod fundamentami

Rozkład naprężeń pod fundamentami

Zasad

Zasad

a

a

superpozycji

superpozycji

przy

przy

działaniu

działaniu

wielu sił

wielu sił

skupionych

skupionych

Q

1

Q

2

M



1





2

q

Q

M

M



q

=f(q

)



q

=f(Q)

Naprężenie od dwóch sił
skupionych

Naprężenie od obciążenia
ciągłego

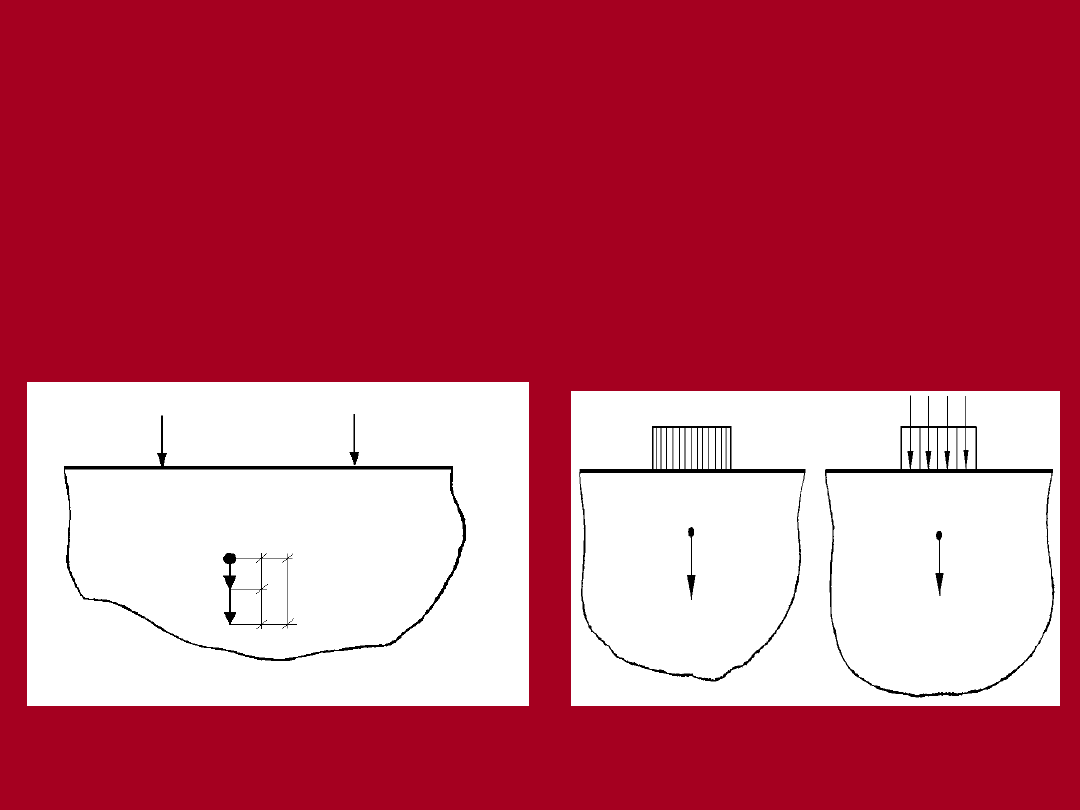
Naprężenie powstałe wskutek

Naprężenie powstałe wskutek

działania obciążeń

działania obciążeń

zewnętrznych

zewnętrznych

qz

z

z

















qz

z

z

z





















Jeżeli przyłożymy obciążenie nie na powierzchni, lecz

Jeżeli przyłożymy obciążenie nie na powierzchni, lecz

na pewnej głębokości - po wykonaniu wykopu,

na pewnej głębokości - po wykonaniu wykopu,

naprężenie całkowite

naprężenie całkowite

σ

σ

z

z

w dowolnym punkcie

w dowolnym punkcie

wyznacza się jako sumę naprężenia pierwotnego

wyznacza się jako sumę naprężenia pierwotnego

geostatycznego

geostatycznego

σ

σ

γz

γz

zmniejszonego o odciążenie

zmniejszonego o odciążenie

wykopem

wykopem

∆σ

∆σ

γz

γz

:

:

Zgodnie z zasadą superpozycji naprężenie całkowite

Zgodnie z zasadą superpozycji naprężenie całkowite

σ

σ

z

z

w gruncie jest sumą naprężenia pierwotnego

w gruncie jest sumą naprężenia pierwotnego

σ

σ

γz

γz

i

i

naprężenia od obciążenia zewnętrznego

naprężenia od obciążenia zewnętrznego

σ

σ

qz

qz

:

:

Rozkład naprężenia w gruncie od

Rozkład naprężenia w gruncie od

pionowej siły skupionej

pionowej siły skupionej

(rozwiązanie Boussinesq’a 1885)

(rozwiązanie Boussinesq’a 1885)



Ośrodek gruntowy jest jednorodny i izotropowy

Ośrodek gruntowy jest jednorodny i izotropowy

(tzn. działanie jednakowych naprężeń w

(tzn. działanie jednakowych naprężeń w

dowol

dowol

-

-

nym kierunku powoduje jednakowe odkształcenia

nym kierunku powoduje jednakowe odkształcenia



Grunt jest materiałem sprężystym, tzn. podlega

Grunt jest materiałem sprężystym, tzn. podlega

prawu Hooke’a

prawu Hooke’a



Naprężenia rozchodzą się promieniście od punktu

Naprężenia rozchodzą się promieniście od punktu

przyłożenia siły

przyłożenia siły



Nie uwzględnia się ciężaru własnego gruntu

Nie uwzględnia się ciężaru własnego gruntu



Obowiązuje zasada superpozycji

Obowiązuje zasada superpozycji

Rozkład naprężenia w gruncie od

Rozkład naprężenia w gruncie od

pionowej siły skupionej

pionowej siły skupionej

(rozwiązanie Boussinesq’a 1885)

(rozwiązanie Boussinesq’a 1885)



Pionowo działając

Pionowo działając

a

a

siła powoduje obniżenie się

siła powoduje obniżenie się

półkuli o dowolnym promieniu ze środkiem

półkuli o dowolnym promieniu ze środkiem

w

w

punkcie zaczepienia

punkcie zaczepienia

s

s

iły o jednakową

iły o jednakową

wartość „

wartość „

s

s

”

”

s

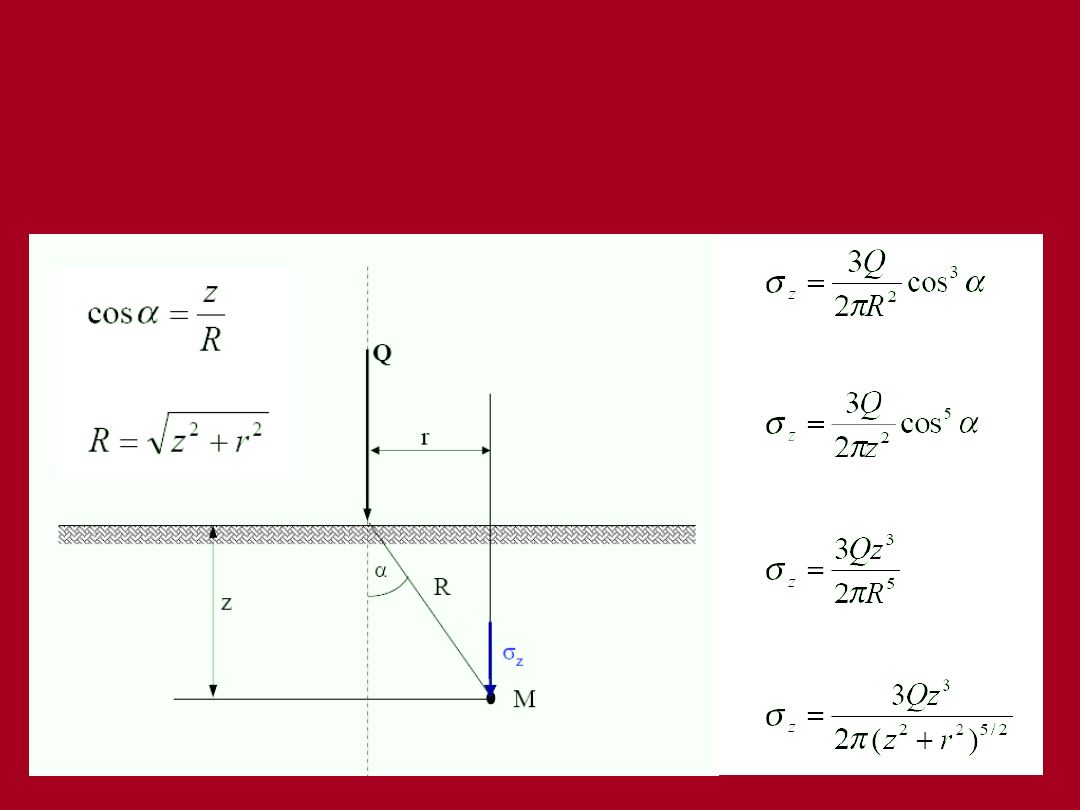
Rozwiązanie Boussinesq’a

Rozwiązanie Boussinesq’a

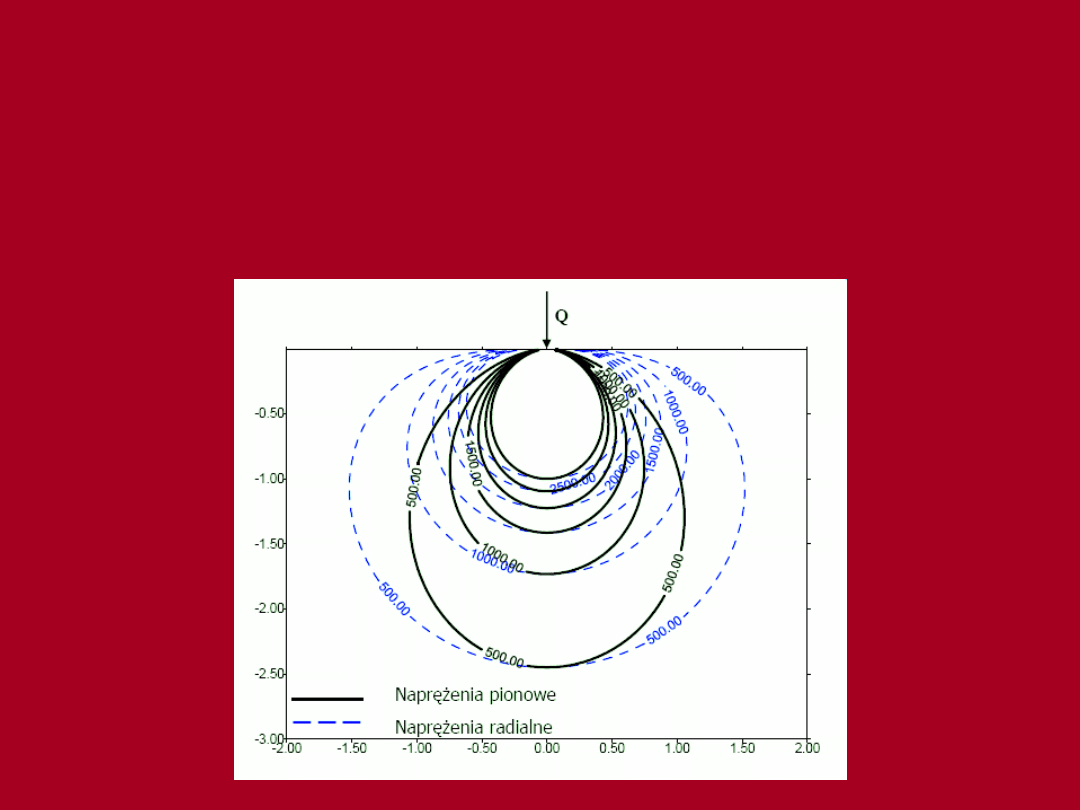
Rozwiązanie Boussinesq’a

Rozwiązanie Boussinesq’a

Izobary naprężeń w półprzestrzeni sprężystej

Rozwiązanie Boussinesq’a

Rozwiązanie Boussinesq’a

Izobary naprężeń w półprzestrzeni sprężystej

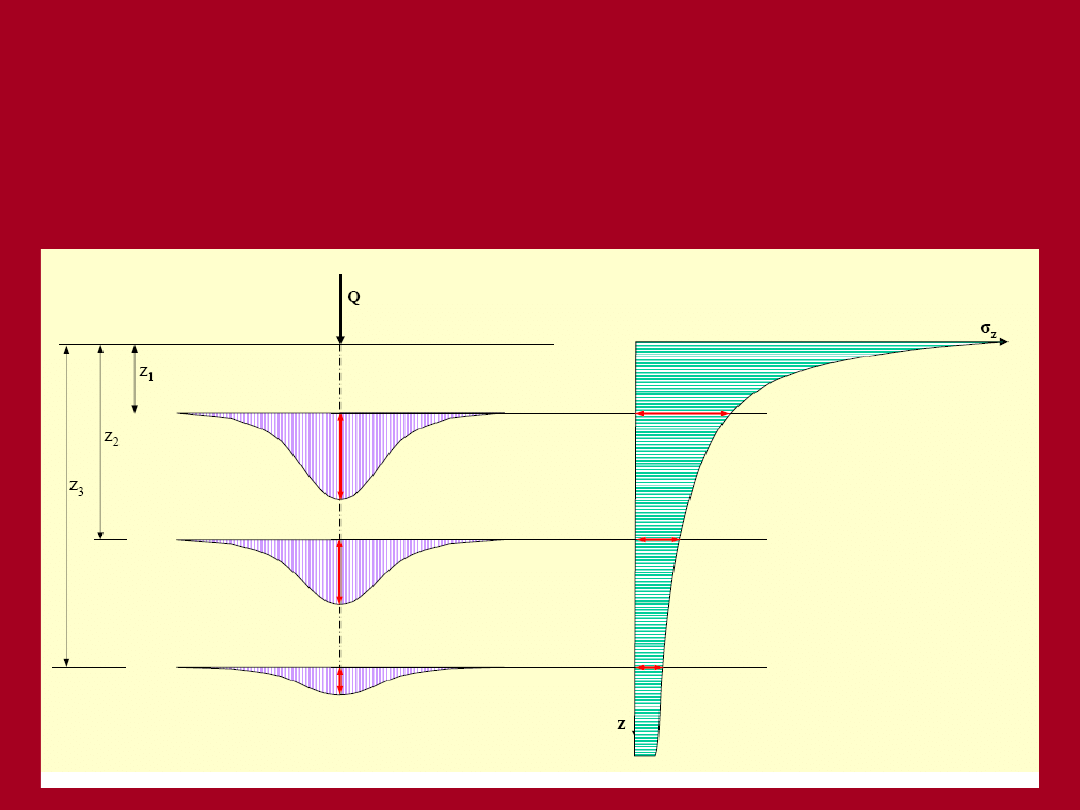
Rozwiązanie Boussinesq’a

Rozwiązanie Boussinesq’a

rozkład naprężeń pionowych w osi „z” krzywa zaniku
naprężeń

Rozwiązanie Boussinesq’a

Rozwiązanie Boussinesq’a

rozkład naprężeń pionowych w linii „a” krzywa zaniku
naprężeń

2

2

2

3

)

(

2

z

x

Pz

z









2

2

2

2

)

(

2

z

x

z

Px

x









)

(

2

2

2

z

x

P

y











2

2

2

2

)

(

2

z

x

xz

P

xz











P

Obciążenie rozłożone

Obciążenie rozłożone

równomiernie:

równomiernie:













)

2

sin(

sin

)

2

cos(

sin

)

2

cos(

sin





















































s

zx

s

x

s

z

q

q

q

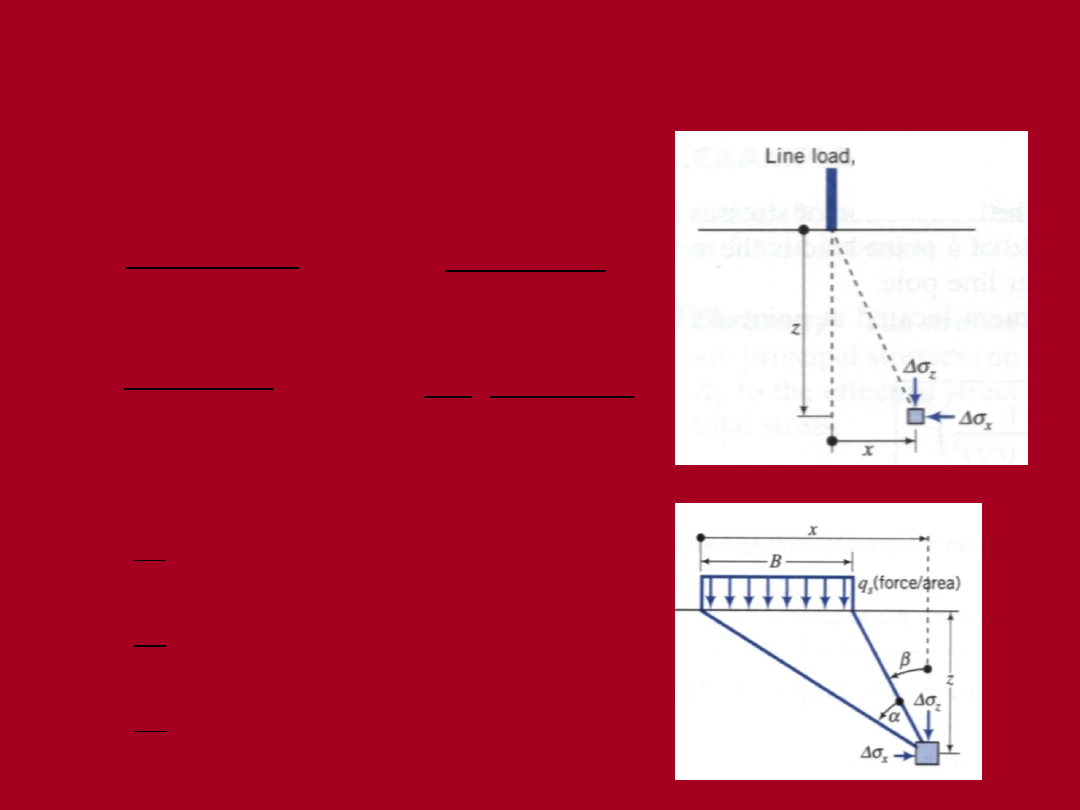
Rozwiązanie

Rozwiązanie

Flamanta

Flamanta

(obciążenie

(obciążenie

pasmowe)

pasmowe)





































































B

z

q

R

R

B

z

B

x

q

B

x

q

s

zx

s

x

s

z

2

2

cos

1

2

2

sin

2

1

ln

2

sin

2

1

2

2

2

1

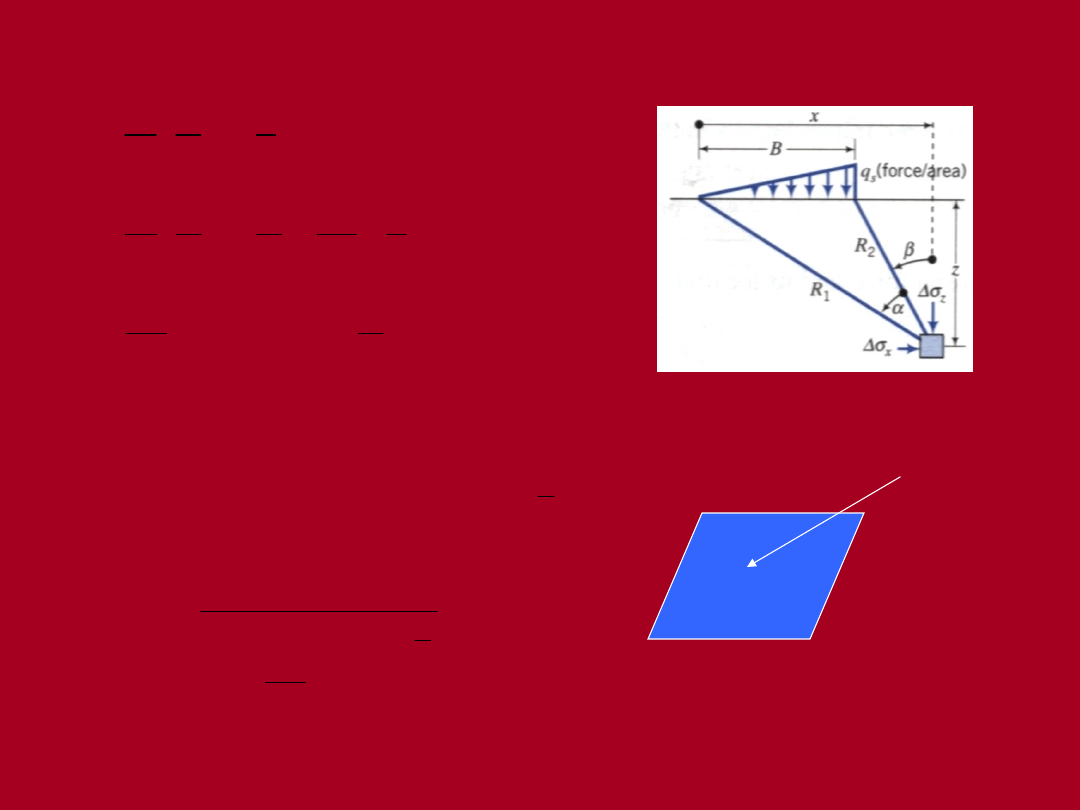
Obciążenie trójkątne:

Obciążenie trójkątne:

Naprężenie pionowe pod środkiem

Naprężenie pionowe pod środkiem

równomiernego obciążenia

równomiernego obciążenia

prostokątnego

prostokątnego

:

:



















































































L

B

L

B

z

z

B

q

84

.

0

6

.

2

62

.

0

38

.

1

2

1

1

1



obciążenie q

B

L

2

5

2

2

z

z

r

1

z

2

Q

3



































Q

Q

L=mL

i

B=nB

i

Q=qL

i

B

i

z

r

R

1



z

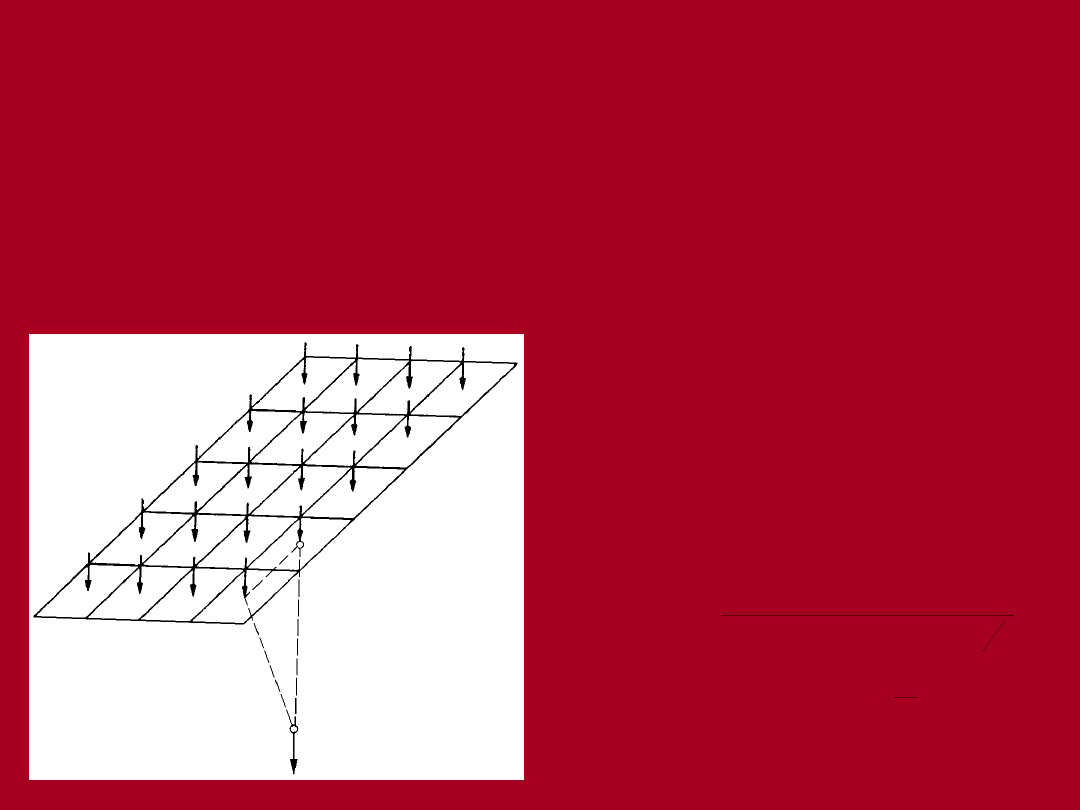
Rozkład naprężenia w gruncie

Rozkład naprężenia w gruncie

od działania obciążenia

od działania obciążenia

ciągłego

ciągłego

Obszar obciążony dzieli się na

Obszar obciążony dzieli się na

mniejsze elementy, w środku

mniejsze elementy, w środku

elementów przykłada się

elementów przykłada się

zastępcze siły skupione.

zastępcze siły skupione.

Wartość naprężenia pionowego

Wartość naprężenia pionowego

normalnego

w

dowolnym

normalnego

w

dowolnym

punkcie ośrodka gruntowego

punkcie ośrodka gruntowego

obciążonego wyznacza się na

obciążonego wyznacza się na

podstawie wzoru

podstawie wzoru

Boussinesq’a

Boussinesq’a

:

:

Zastosowanie superpozycji do

Zastosowanie superpozycji do

wyznacza-nia naprężenia od

wyznacza-nia naprężenia od

obciążenia ciągłego.

obciążenia ciągłego.

d

z

dQ

y

x

M

0

B

z

r

L

dy

dx

2

5

2

2

z

z

r

1

z

2

dQ

3

d































































L

0

B

0

2

2

2

2

z

2

5

z

y

x

1

z

2

qdxdy

3

Metoda punktów narożnych

Metoda punktów narożnych

Naprężenie pionowe w

Naprężenie pionowe w

rozpatrywanym punkcie M od

rozpatrywanym punkcie M od

obciążenia ciągłego działającego

obciążenia ciągłego działającego

w

w

obszarze A wynosi:

obszarze A wynosi:

Na danym obszarze

Na danym obszarze

A

A

wydziela się

wydziela się

nieskończenie mały element o polu

nieskończenie mały element o polu

dA

dA

= dx dy.

= dx dy.

Elementarna siła

Elementarna siła

dQ =

dQ =

qdA

qdA

wywołuje w rozpatrywanym

wywołuje w rozpatrywanym

punkcie

punkcie

M

M

na głębokości

na głębokości

z

z

poniżej

poniżej

powierzchni

półprzestrzeni

powierzchni

półprzestrzeni

elementarne naprężenie:

elementarne naprężenie:

z/B



n

10,

0

8,0

6,0

4,0

2,0

0

0,05

0,15

0

0,10

0

0,20

0

0,25

0

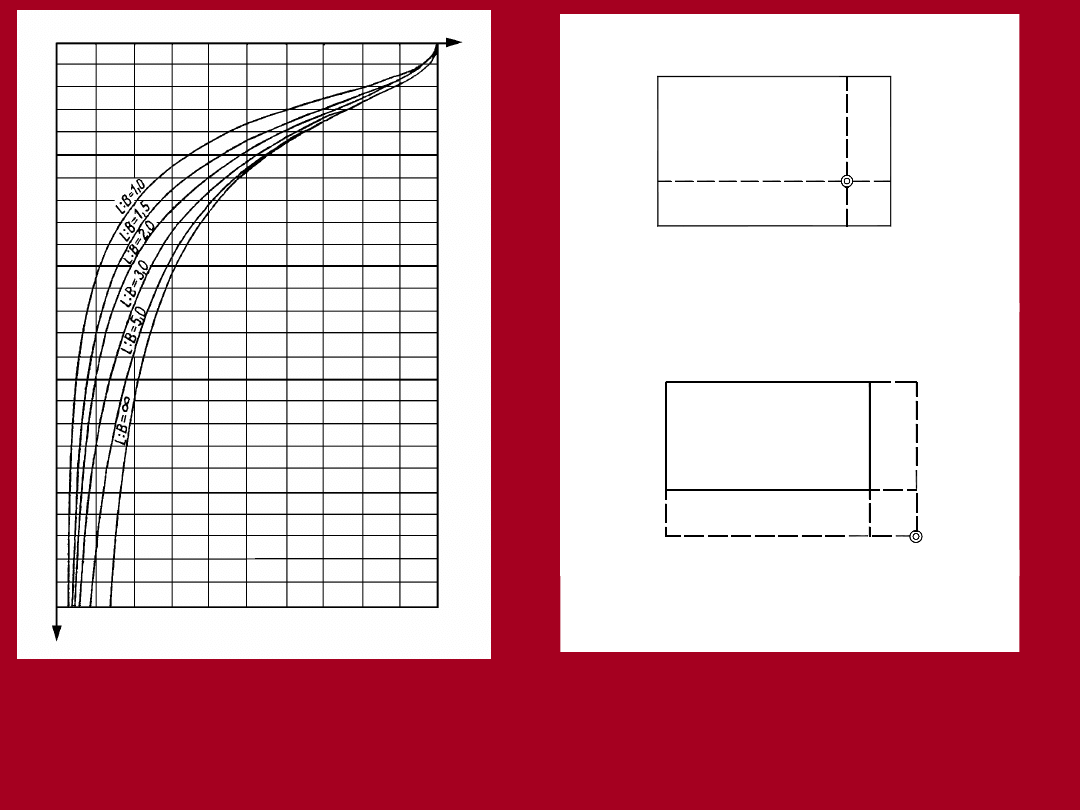
Nomogram

Nomogram

do

do

wyznaczania

wyznaczania

współczynnika η

współczynnika η

n

n

A

B

C

D

M

E

F

G

H

A

M

G

H

D

B

E

F

C





q

MGCH

n

EMHD

n

FBGM

n

AFME

n

zq

























q

CFMG

n

DFMH

n

BEMG

n

AEMH

n

zq





















a)

b)

Zastosowanie

metody

punktów

Zastosowanie

metody

punktów

narożnych do obliczania naprężeń w

narożnych do obliczania naprężeń w

dowolnym

punkcie

podłoża:

dowolnym

punkcie

podłoża:

a) naroże wewnątrz obciążonego

a) naroże wewnątrz obciążonego

obszaru,

obszaru,

b) naroże na zewnątrz obciążonego

b) naroże na zewnątrz obciążonego

obszaru.

obszaru.

Naprężenie pionowe pod
środkiem

prostokątnego

obszaru

obciążo-nego,

wyznaczamy ze wzoru:

q

z

0







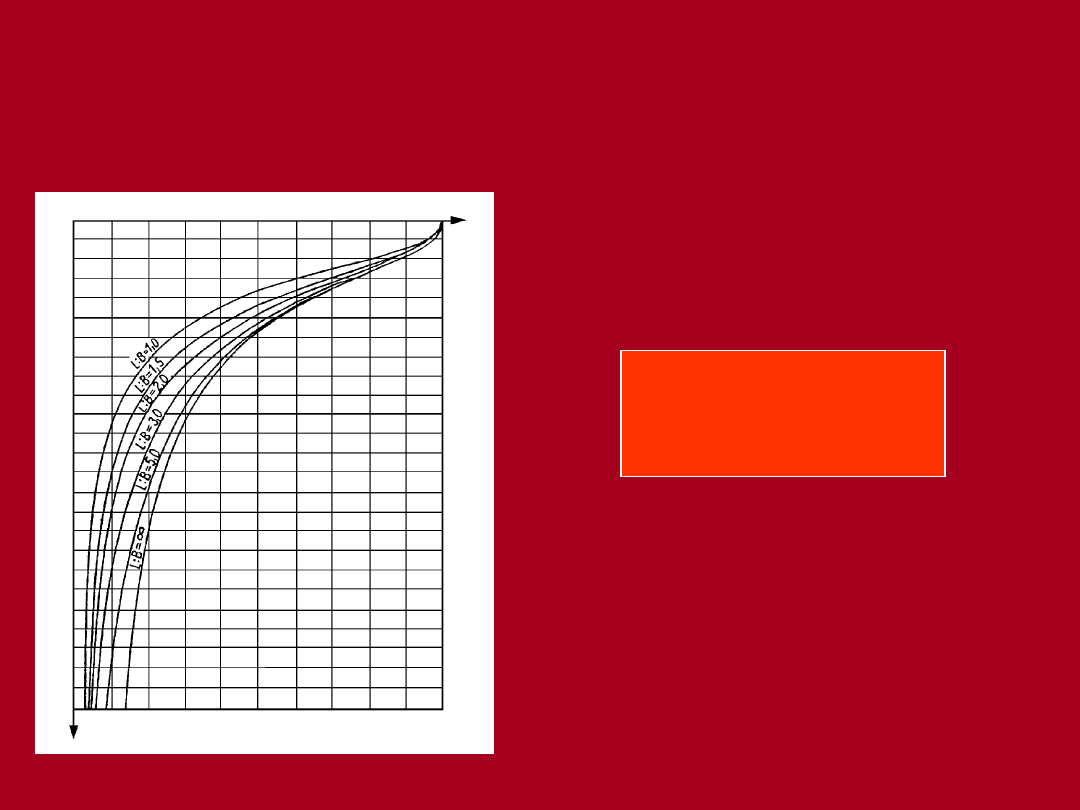
z/B



0

5,0

4,0

3,0

2,0

1,0

0

0,2

0,4

0,6

0,8

1,0

Nomogram η

Nomogram η

0

0

Metoda punktów

Metoda punktów

środkowych

środkowych

1

5

0

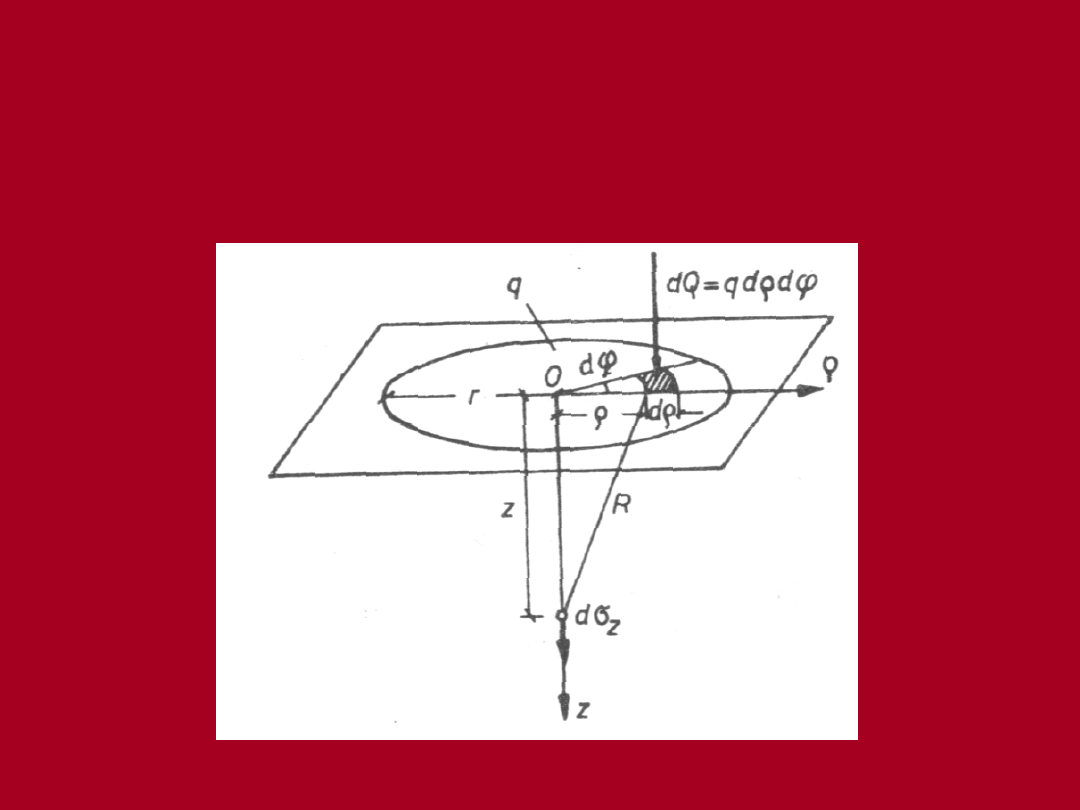
Naprężenia pionowe pod

Naprężenia pionowe pod

środkiem obszaru kołowego

środkiem obszaru kołowego

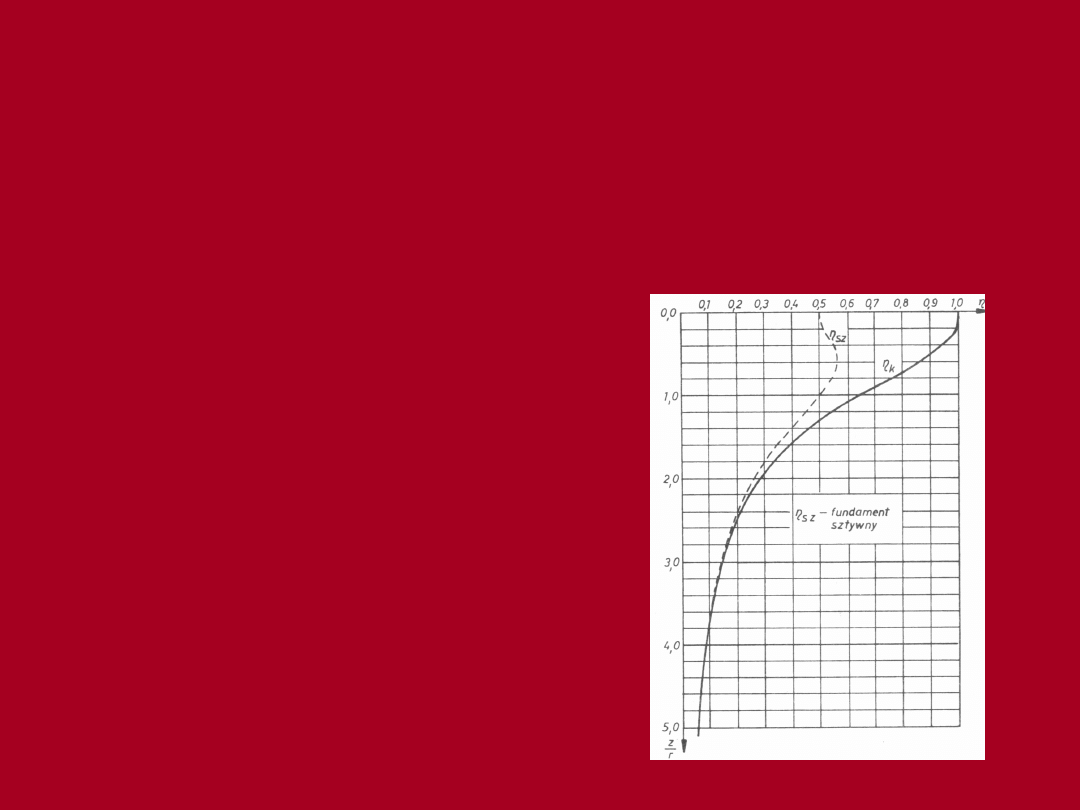
k

z

q







Naprężenia pionowe pod

Naprężenia pionowe pod

środkiem obszaru kołowego

środkiem obszaru kołowego

czyli:



Nomogram Newmarka

Nomogram Newmarka

(metoda pól

(metoda pól

wpływowych)

wpływowych)

umożliwia wyznaczanie

umożliwia wyznaczanie

rozkładu naprężenia pod dowolnie

rozkładu naprężenia pod dowolnie

obciążoną powierzchnią, którą dzieli się

obciążoną powierzchnią, którą dzieli się

współśrodkowymi okręgami o promieniach

współśrodkowymi okręgami o promieniach

r

r

i

i

na n promieni równoważnych pod

na n promieni równoważnych pod

względem wartości wzbudzonego przez

względem wartości wzbudzonego przez

każde z nich naprężenia pionowego pod

każde z nich naprężenia pionowego pod

środkiem tych kół.

środkiem tych kół.

Nomogram Newmarka

Nomogram Newmarka

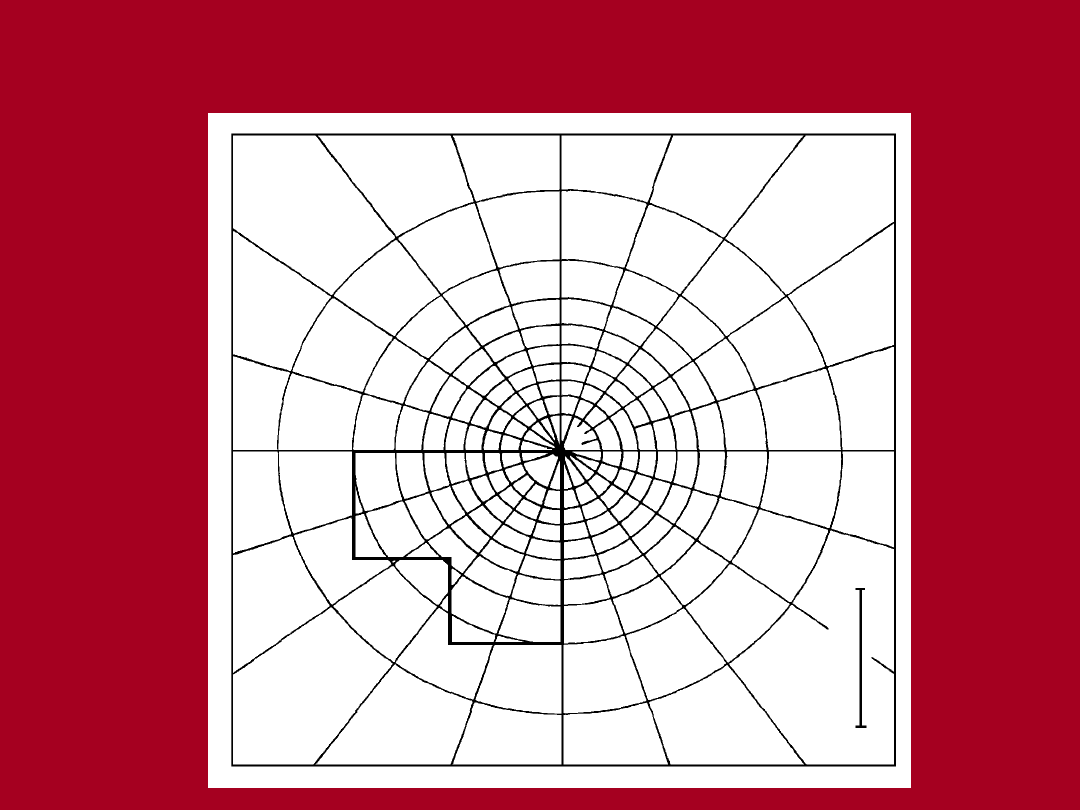
w

w

=0,005

z

n

M

0

2 3 4 5

6

7

8

9

1

Nomogram Newmarka

Nomogram Newmarka



Wykreślenie nomogramu polega na przyjęciu liczby

Wykreślenie nomogramu polega na przyjęciu liczby

n

n

okręgów i obliczenie ich promieni. Następnie dzieli

okręgów i obliczenie ich promieni. Następnie dzieli

się powierzchnię kół na

się powierzchnię kół na

m

m

wycinków. Otrzymuje się

wycinków. Otrzymuje się

m*n

m*n

pól równoważnych, które nazywa się polami

pól równoważnych, które nazywa się polami

wpływu. Współczynnik wpływu jednego pola wynosi:

wpływu. Współczynnik wpływu jednego pola wynosi:



Nomogram Newmarka umożliwia wyznaczenie

Nomogram Newmarka umożliwia wyznaczenie

naprężenia pionowego od obciążenia równomiernie

naprężenia pionowego od obciążenia równomiernie

rozłożonego

rozłożonego

q

q

na dowolnej powierzchni ze wzoru:

na dowolnej powierzchni ze wzoru:

q

W

I

w

p

z





nm

1

m

W

'

k

w







Nomogram Newmarka

Nomogram Newmarka



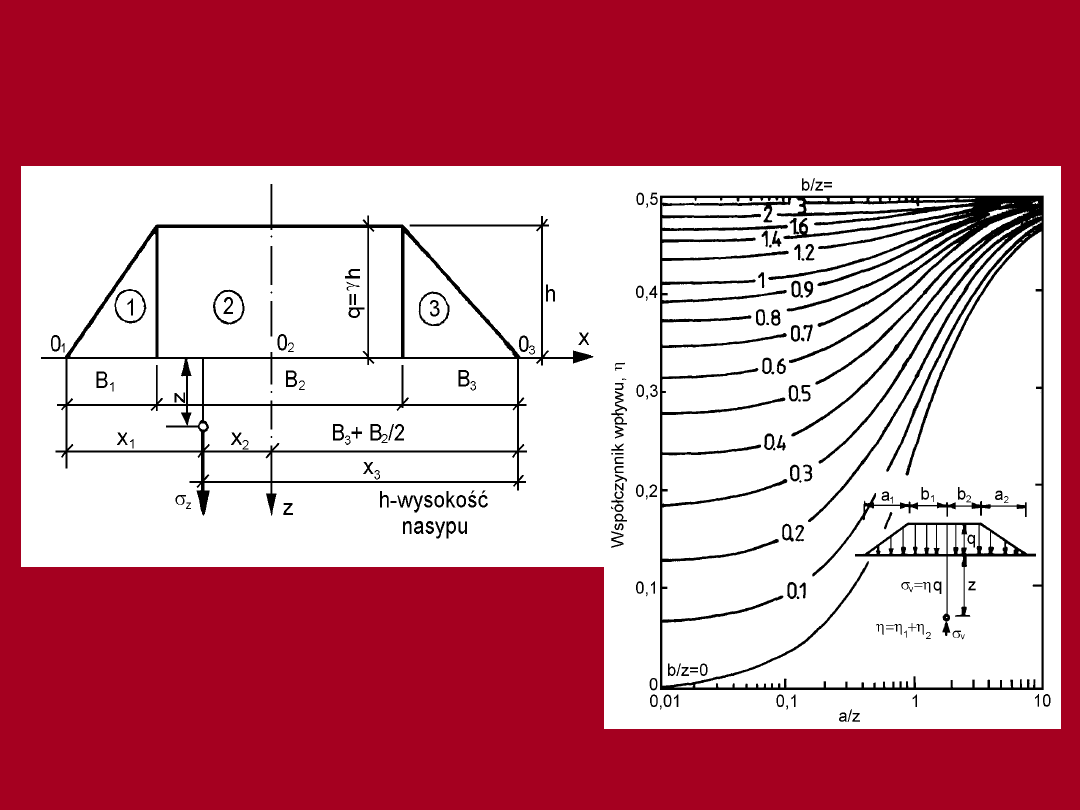
a)

Schemat do wyznaczania naprężenia
pionowego σ

z

w podłożu gruntowym

pod nasypem

b)

Rozkład naprężeń pod nasypami

Rozkład naprężeń pod nasypami

nomogram do wyznaczania
współczynnika η

Naprężenie w dowolnym punkcie podłoża jest równe
sumie naprężeń od obciążenia równomiernego
pasmowego i obciążenia pasmowego w postaci dwóch
prostokątnych trójkątów a mianowicie:





q

z

z

z

z

3

2

1

3

2

1



























gdzie: η

2

- współczynnik odpowiadający obciążeniu

pasmowemu o rozkładzie prostokątnym,

η

1

i η

3

- współczynnik odpowiadające

obciążeniu pasmowemu o rozkładzie trójkątnym

q

- obciążenie od nasypu (q = γ h).

Rozkład naprężeń pod nasypami

Plan wykładu

Plan wykładu



Wstęp - stan naprężenia w gruncie

Wstęp - stan naprężenia w gruncie



Naprężenia pierwotne

Naprężenia pierwotne



Naprężenia efektywne

Naprężenia efektywne



Naprężenia od sił zewnętrznych

Naprężenia od sił zewnętrznych



Rozkład naprężeń pod fundamentami

Rozkład naprężeń pod fundamentami

Rozkład naprężeń pod

fundamentami



Najczęściej stosuje się metodę punktów

Najczęściej stosuje się metodę punktów

środkowych przyjmując uproszczenie, że

środkowych przyjmując uproszczenie, że

naprężenia pionowe w poziomie

naprężenia pionowe w poziomie

posadowienia fundamentu i na głębszych

posadowienia fundamentu i na głębszych

poziomach są rozłożone równomiernie.

poziomach są rozłożone równomiernie.



W niektórych przypadkach przy obliczaniu

W niektórych przypadkach przy obliczaniu

osiadań różnych punktów tej samej budowli

osiadań różnych punktów tej samej budowli

stosuje się metodę punktów narożnych.

stosuje się metodę punktów narożnych.

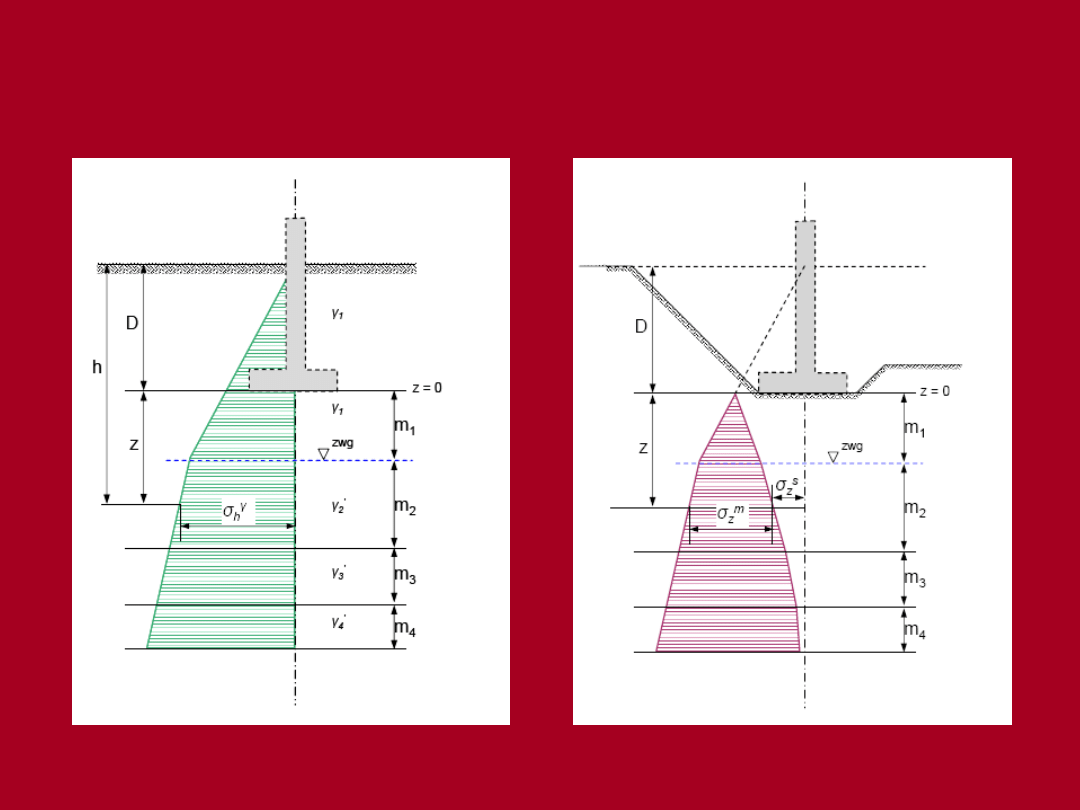
Stan pierwotny w gruncie

Stan pierwotny w gruncie

Stan po wykonaniu wykopu

Stan po wykonaniu wykopu

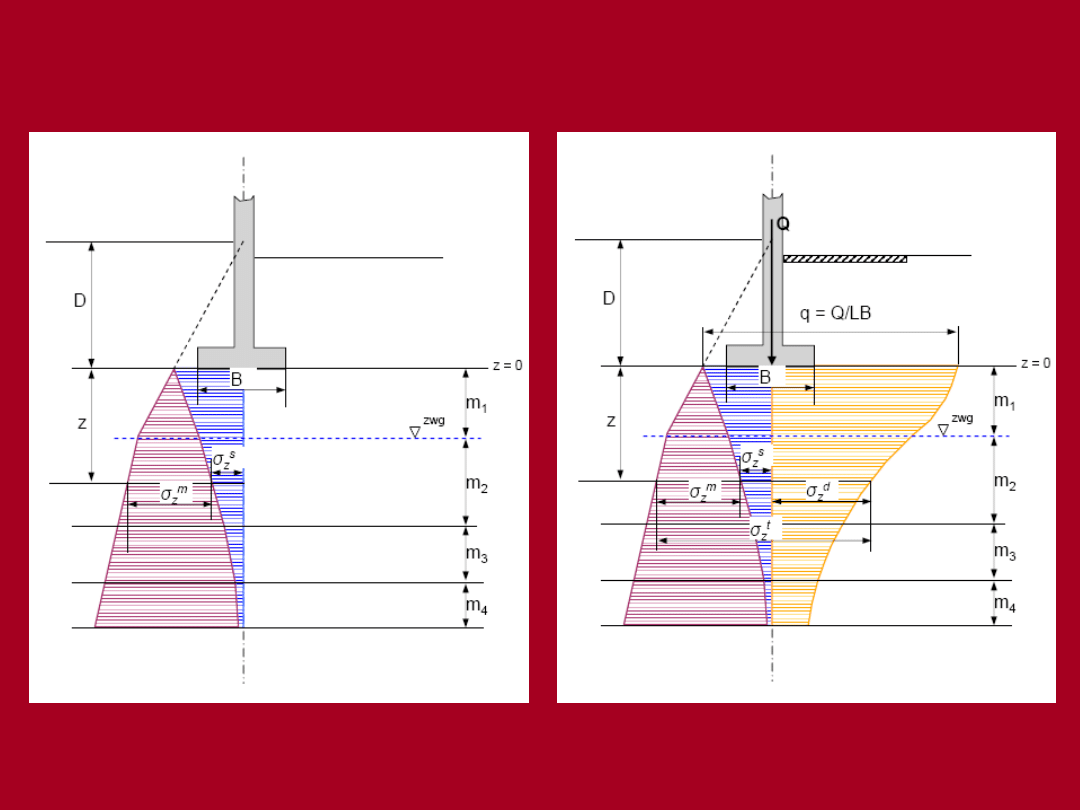
Stan po zasypaniu wykopu

Stan po zasypaniu wykopu

Stan po wykonaniu konstrukcji

Stan po wykonaniu konstrukcji



Obciążenia są przykładane przeważnie nie na

Obciążenia są przykładane przeważnie nie na

powierzchni terenu, lecz na pewnej głębokości

powierzchni terenu, lecz na pewnej głębokości

po wykonaniu wykopu. W takich przypadkach

po wykonaniu wykopu. W takich przypadkach

uwzględnia się odciążenie gruntu

uwzględnia się odciążenie gruntu

spowodowane wykopem.

spowodowane wykopem.



Wpływ odciążenia wykopem na naprężenie w

Wpływ odciążenia wykopem na naprężenie w

głębszych warstwach oblicza się podobnie jak

głębszych warstwach oblicza się podobnie jak

przy obciążaniu podłoża z tym, że odciążanie

przy obciążaniu podłoża z tym, że odciążanie

uwzględnia się ze znakiem ujemnym i

uwzględnia się ze znakiem ujemnym i

przyjmuje, że działa ono w poziomie dna

przyjmuje, że działa ono w poziomie dna

wykopu.

wykopu.

Rozkład naprężeń pod

Rozkład naprężeń pod

fundamentami

fundamentami

Za tydzień ciąg dalszy…

Za tydzień ciąg dalszy…











n

2

2

2

2

2

2

2

2

2

2

2

2

2

zn

q

z

B

L

z

LB

tg

arc

z

B

L

z

B

z

L

z

2

B

L

LBz

2

q



























gdzie:
η

n

- współczynnik wyznaczany z nomogramu w

zależności od
stosunku L:B (długość obszaru obciążonego do

jego szerokości)
oraz od stosunku z:B (zagłębienie punktu

poniżej powierzchni
do szerokości),

q - obciążenie ciągłe.

Metoda punktów narożnych

Metoda punktów narożnych

umożliwia wyznaczanie

umożliwia wyznaczanie

naprężenia pionowego oraz sumy naprężeń głównych

naprężenia pionowego oraz sumy naprężeń głównych

pod narożem prostokątnego obciążonego obszaru

pod narożem prostokątnego obciążonego obszaru

według wzoru:

według wzoru:

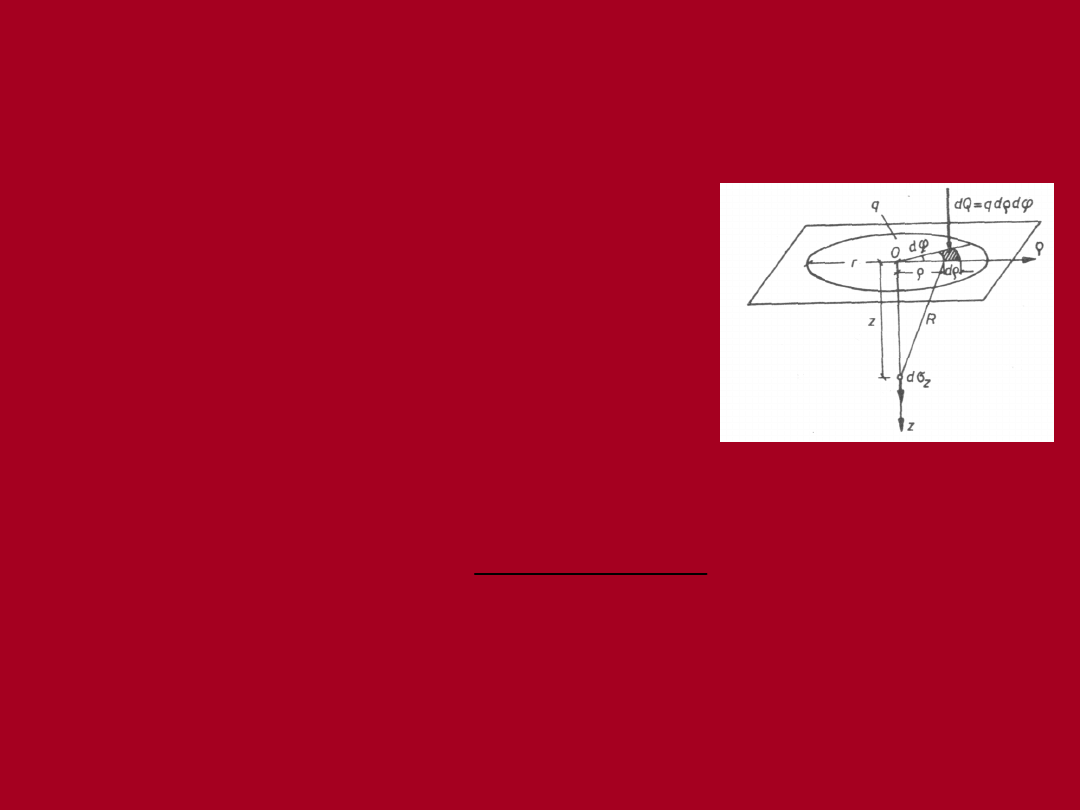
Zgodnie z rysunkiem na
elementarne pole dA działa
elementarna siła:







d

d

q

qdA

dQ





Zgodnie z rozwiązaniem Boussinesq’a
elementarne naprężenie pionowe pod
środkiem obszaru kołowego wynosi:

5

2

2

3

R

d

d

qz

d

z













Całkowite naprężenie pionowe pod środkiem
obszaru będzie więc równe:

Naprężenia pionowe pod środkiem

Naprężenia pionowe pod środkiem

obszaru kołowego

obszaru kołowego

Uwzględniając, że:







d

2

RdR

2

,

z

R

2

2

2







otrzymujemy:



















































































2

3

2

r

z

z

3

3

r

z

z

4

3

z

z

r

1

1

1

q

R

3

1

qz

3

R

dR

qz

3

2

2

2

2















r

0

5

3

r

0

2

0

5

3

r

0

2

0

z

z

R

d

qz

3

R

2

d

d

qz

3

d





















Naprężenia pionowe pod

Naprężenia pionowe pod

środkiem obszaru kołowego

środkiem obszaru kołowego

Przy wyznaczaniu

naprężenia punktowego

, pod

którym wyznacza się naprężenie σ

z

, należy umieścić

w środku nomogramu kontur obciążonego obszaru w
skali odpowiadającej danemu zagłębieniu: 1: (z/z

n

).

Następnie oblicza się liczbę pól zakrytych na
nomogramie obszarem obciążonym. wg wzoru:

2

cz

c

P

I

I

I





gdzie:

I

c

- liczba pól mieszczących się całkowicie wewnątrz konturów

fundamentów

I

cz

- liczba pól przykrytych częściowo obszarem obciążonym

Nomogram Newmarka

Nomogram Newmarka