Funkcje wielu
zmiennych

dr Tomasz
Kowalski

Wykład 26

Slajd nr 2 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przestrzeń euklidesowa R

n

Przestrzenią euklidesową n-wymiarową R

n

nazywać będziemy zbiór wszystkich
uporządkowanych układów n liczb rzeczywistych
(x

1

, x

2

, x

3

, …, x

n

).

Jeżeli P = P (p

1

, p

2

, p

3

, …, p

n

) i Q = Q (q

1

, q

2

,

q

3

, …, q

n

) są punktami przestrzeni R

n

, to

odległość między tymi punktami oznaczać
będziemy d(P,Q) i określać wzorem:

2

2

2

1

1

2

2

( , )

(

)

(

)

... (

) .

n

n

d P Q

q

p

q

p

q

p

=

-

+

-

+ +

-

Układ (x

1

, x

2

, x

3

, …, x

n

) nazywamy wtedy punktem

przestrzeni R

n

, liczby x

1

, x

2

, x

3

, …, x

n

–

współrzędnymi punktu.

Slajd nr 3 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przestrzeń euklidesowa R

2

R

2

jest przestrzenią uporządkowanych par liczb

rzeczywistych, tradycyjnie zapisywanych jako (x, y).

2

2

2

1

2

1

( , )

(

)

(

) .

d P Q

x

x

y

y

=

-

+

-

Dla dwóch punktów P = P(x

1

, y

1

) i Q = Q(x

2

, y

2

) tej

przestrzeni mamy

Slajd nr 4 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przestrzeń euklidesowa R

3

R

3

jest przestrzenią uporządkowanych trójek liczb

rzeczywistych, tradycyjnie zapisywanych jako (x, y,
z).

2

2

2

2

1

2

1

2

1

( , )

(

)

(

)

(

) .

d P Q

x

x

y

y

z

z

=

-

+

-

+

-

Dla dwóch punktów P = P(x

1

, y

1

, z

1

) i Q = Q(x

2

, y

2

,

z

2

) tej przestrzeni mamy

Slajd nr 5 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Funkcja n zmiennych

Funkcją n zmiennych x

1

, x

2

, x

3

, …, x

n

określoną w

zbiorze D nazywamy przyporządkowanie każdemu
punktowi P(x

1

, x

2

, x

3

, …, x

n

) tego zbioru dokładnie

jednej liczby rzeczywistej z.

Piszemy wówczas:

1

2

( , ,..., ).

n

z f x x

x

=

Zbiór D nazywamy wówczas dziedziną funkcji,
x

1

, x

2

, x

3

, …, x

n

–  argumentami , z –  wartością

funkcji .

Jeżeli funkcja zadana jest wzorem, a zbiór D nie
jest wyraźnie określony, to za dziedzinę uważać
będziemy zbiór punktów przestrzeni , dla
których f(x

1

, x

2

, x

3

, …, x

n

) ma sens liczbowy i

nazywać dziedziną naturalną funkcji.

Slajd nr 6 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Funkcje dwóch i trzech
zmiennych

W przypadku funkcji dwóch zmiennych zmienne
niezależne oznaczać będziemy literami x i y, w
przypadku trzech zmiennych – literami x, y, z.

Funkcje oznaczać będziemy odpowiednio
przez: z = f(x,y) oraz u = f(x,y,z) .

Slajd nr 7 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

2

3

( , )

.

f x y

xy x

y

= + +

Dana jest funkcja określona
wzorem:

Obliczyć: a) f(–2,3) , b) f(x,2) , c) f(1,y) .

a) Przyjmując we wzorze danej funkcji x = –2, y =
3 otrzymujemy

2

3

( 2,3) ( 2) 3 ( 2)

3

25.

f -

= - �+ -

+ =

b) Podstawiając do wzoru y = 2 i pozostawiając
bez zmian zmienną x mamy

2

3

2

( ,2)

2

2

2

8.

f x

x

x

x

x

= �+ + = + +

c) Podstawiając do wzoru x = 1 i pozostawiając
bez zmian zmienną y mamy

2

3

3

(1, ) 1

1

1.

f

y

y

y

y

y

= � + + = + +

Slajd nr 8 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Wnioski z przykładu

Jeżeli w funkcji dwóch zmiennych z = f(x,y)
jednej ze zmiennych nadać stałą wartość,
to uzyskamy funkcję jednej tylko (tej drugiej)
zmiennej.

Jeżeli w funkcji n zmiennych n – 1 zmiennym
nadać stałe wartości, to uzyskamy funkcję
jednej tylko zmiennej.

Slajd nr 9 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Interpretacja geometryczna
dziedziny

Dziedzinę funkcji dwóch zmiennych można
interpretować geometrycznie jako podzbiór
płaszczyzny, a dziedzinę funkcji trzech
zmiennych – jako podzbiór przestrzeni
trójwymiarowej.

Slajd nr 10 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

-4 -3 -2 -1

1

2

3

4

-3

-2

-1

1

2

3

4

5

x

Y

O

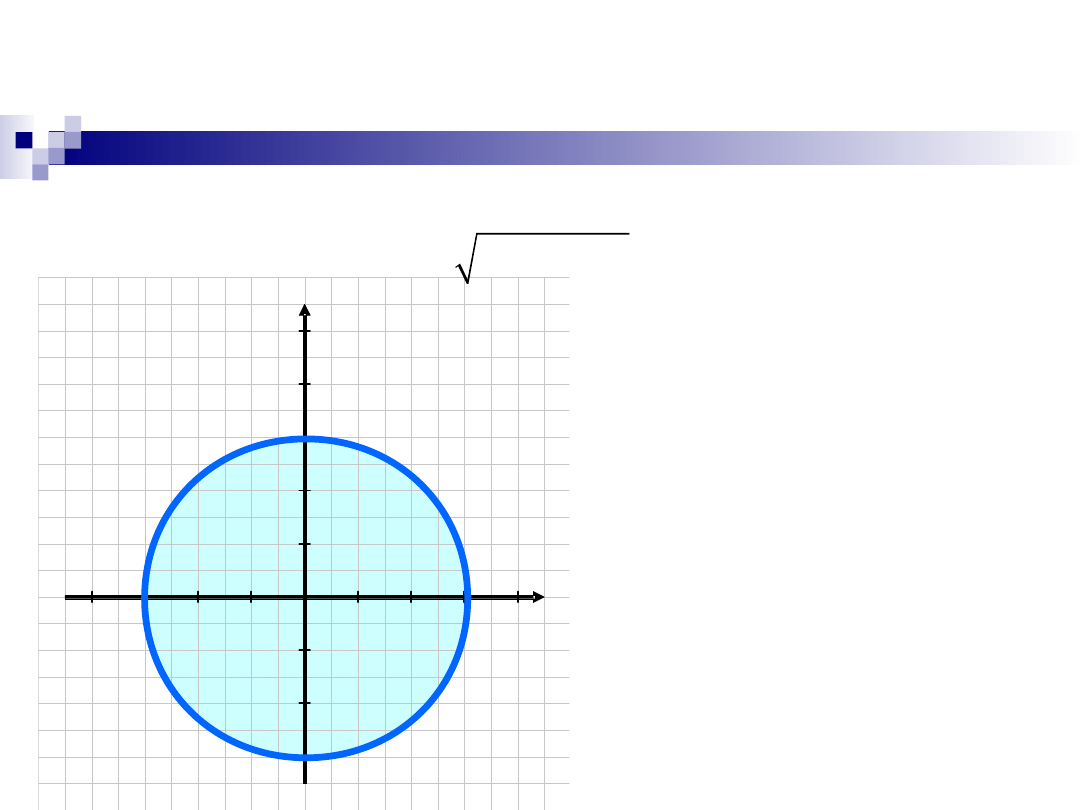
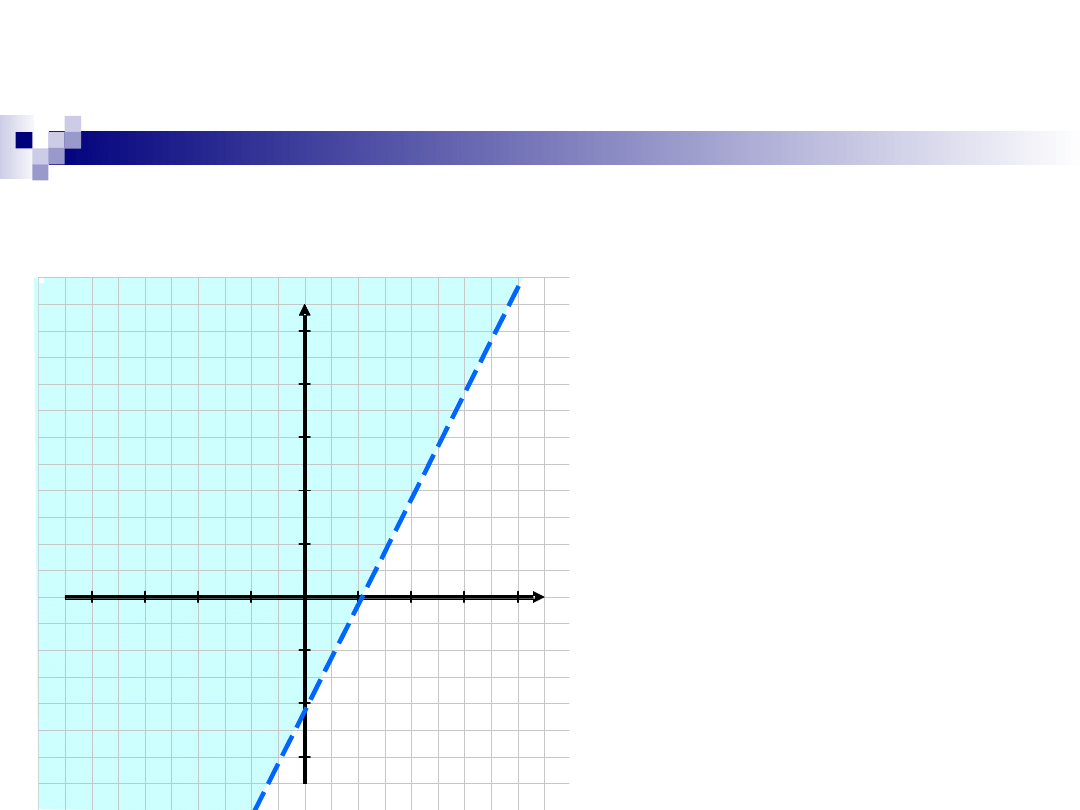
Przykład

Podać interpretację geometryczną dziedziny
funkcji:

2

2

( , )

9

.

z f x y

x

y

=

=

-

-

Wzór ma sens, gdy
liczba
podpierwiastkowa jest
nieujemna, zatem

2

2

2

{( , )

: 9

0}

D

x y

R

x

y

=

�

-

-

�

2

2

9

x

y

+ �

2

2

9

x

y

+

=

D

Slajd nr 11 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

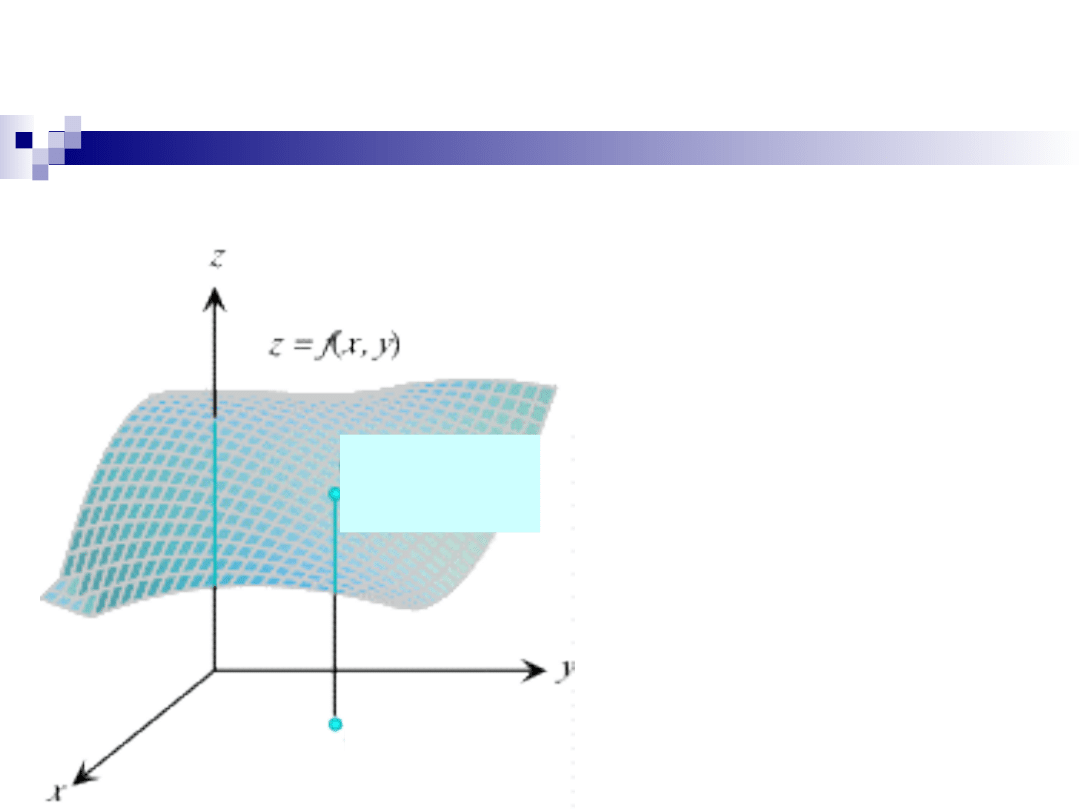
Przykład

Podać interpretację geometryczną dziedziny
funkcji:

( , ) ln(

2

2).

z f x y

y

x

=

=

-

+

Wzór ma sens, gdy
liczba
logarytmowana jest
większa od zera,
zatem

2

{( , )

:

2

2 0}

D

x y

R y

x

=

�

-

+ >

2

2

y

x

> -

-4 -3 -2 -1

1

2

3

4

-3

-2

-1

1

2

3

4

5

x

Y

O

2

2

y

x

= -

D

Slajd nr 12 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Wykres funkcji dwóch
zmiennych

Niech z = f(x,y) będzie funkcją określoną w
zbiorze D.

Podzbiór przestrzeni
postaci:

nazywamy wykresem tej
funkcji.

(x,
y)

(x, y,
f(x,y))

}

)

,

(

,

)

,

(

:

)

,

,

(

{

y

x

f

z

D

y

x

z

y

x

S







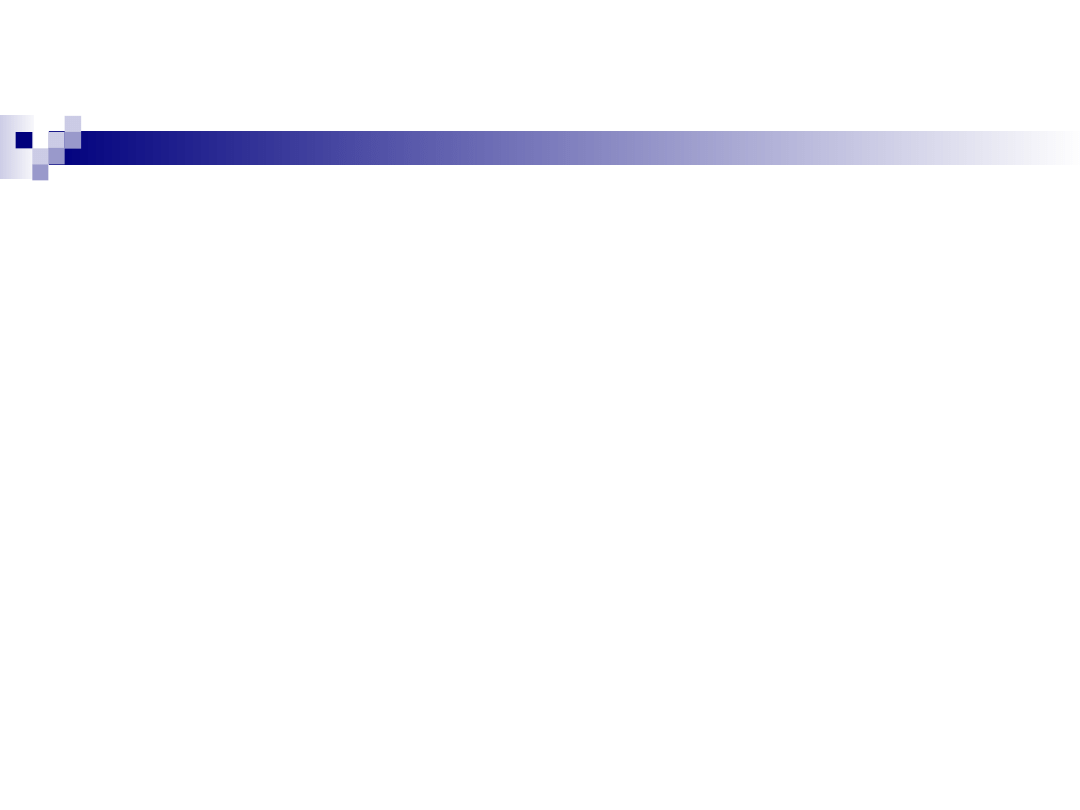
Slajd nr 13 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Wykres funkcji dwóch
zmiennych

Wykres funkcji dwóch zmiennych jest najczęściej
pewną powierzchnią , której rzut na płaszczyznę
XOY jest zbiorem D (w przypadku funkcji
nieujemnej - powierzchnią „rozpiętą” nad zbiorem
D).

Równość z = f(x,y) nazywamy wtedy równaniem tej
powierzchni.

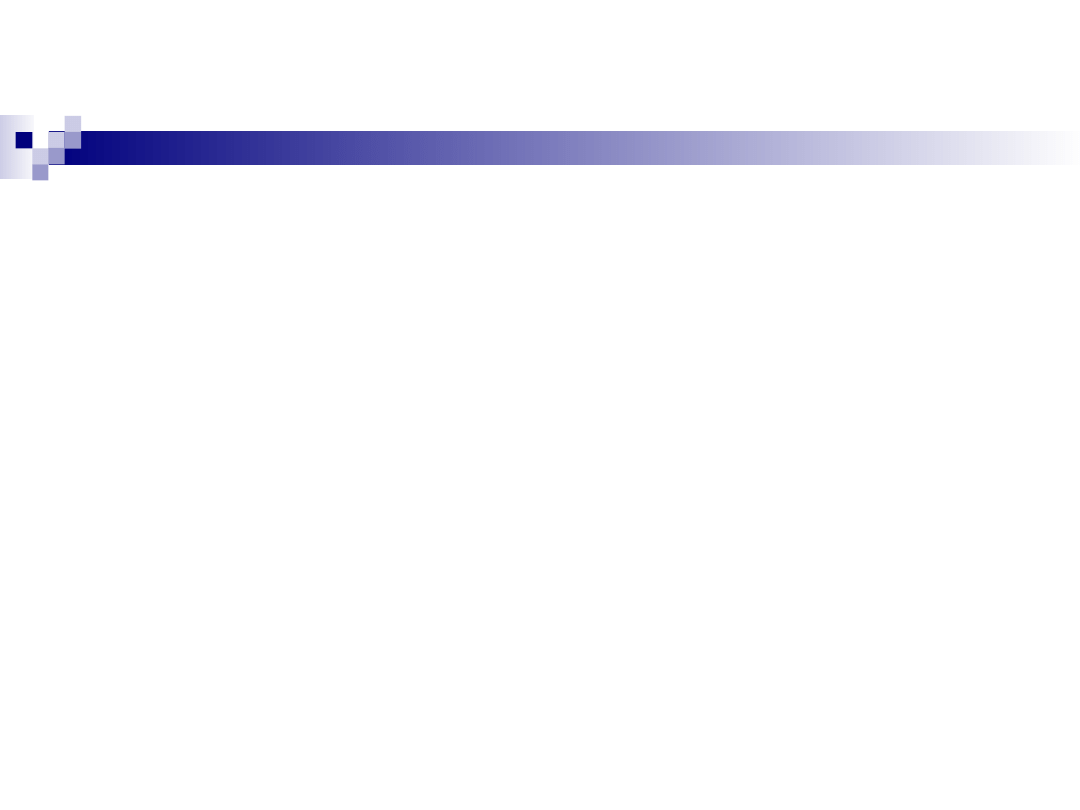
Slajd nr 14 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

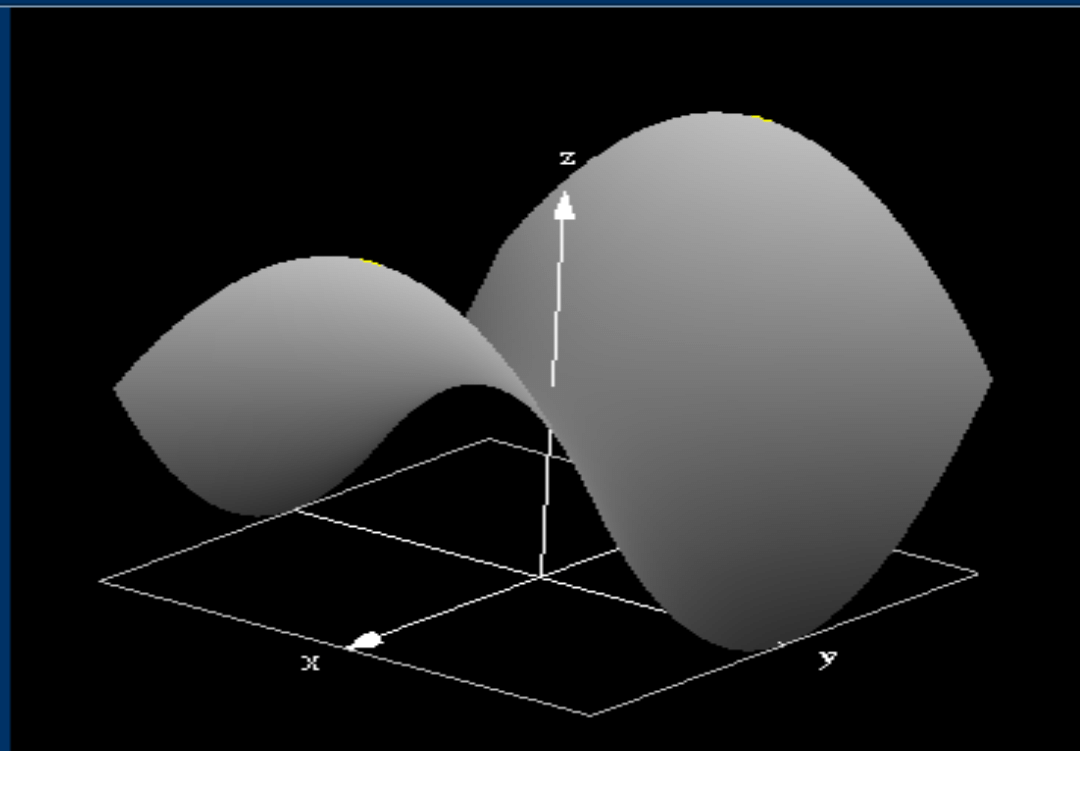
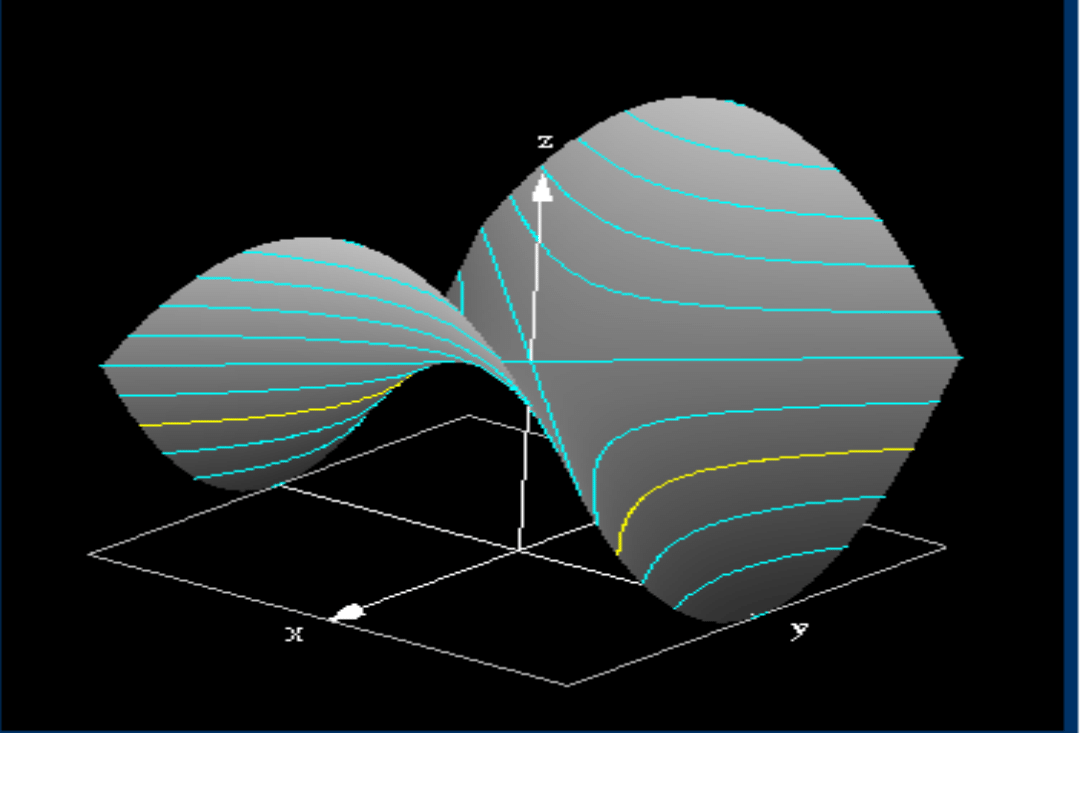
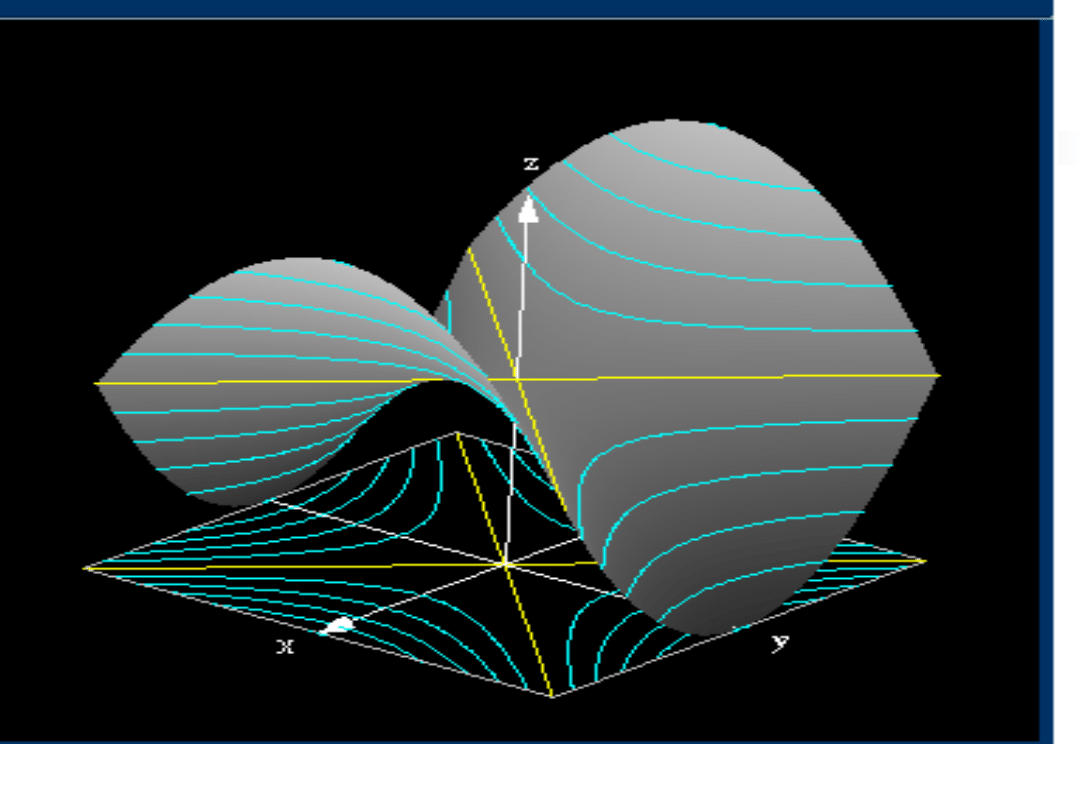
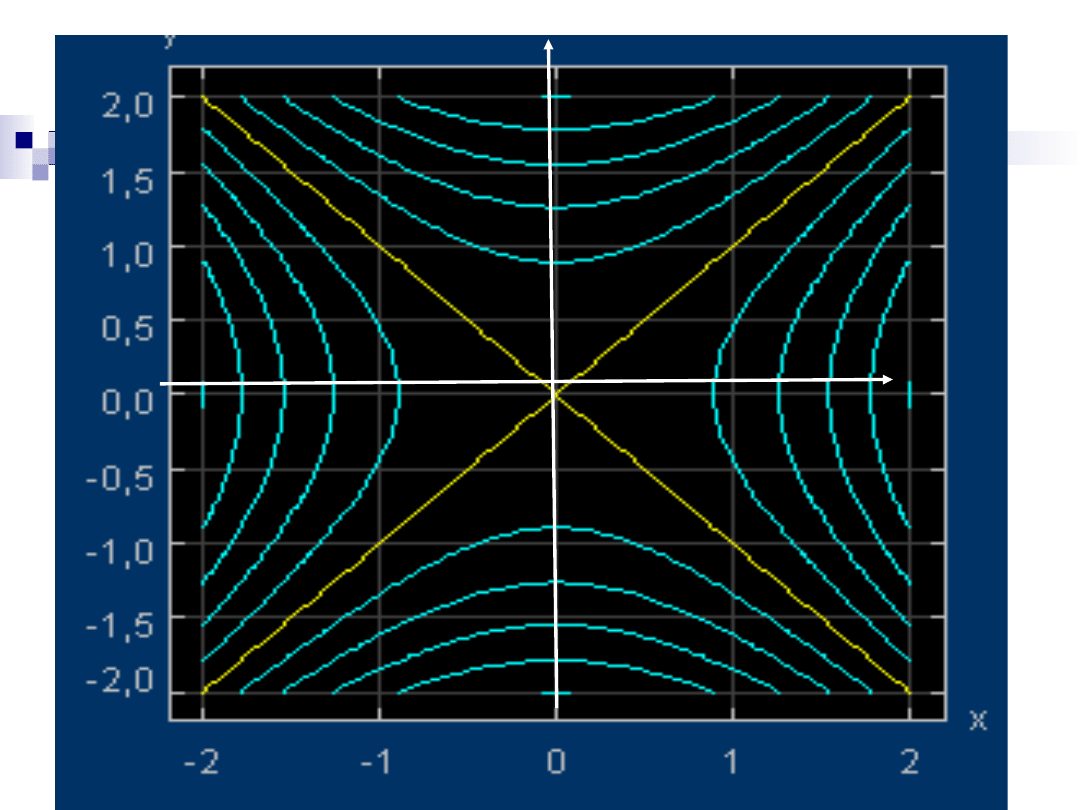
Plan warstwicowy funkcji

Sporządzanie wykresów funkcji dwóch
zmiennych może być bardzo uciążliwe, a
praktyczna korzyść niewielka.

Często zmienność funkcji przedstawia się na
wykresach płaskich, podobnych do map
wycinków Ziemi.

W zbiorze D (dziedzinie funkcji) prowadzi się
linie (tzw. warstwice) łącząc punkty, w których
dana funkcja przyjmuje jednakowe wartości.

Przez naszkicowanie dostatecznie wielu
warstwic powstaje tzw. plan warstwicowy,
który pozwala zorientować się o przebiegu
funkcji.

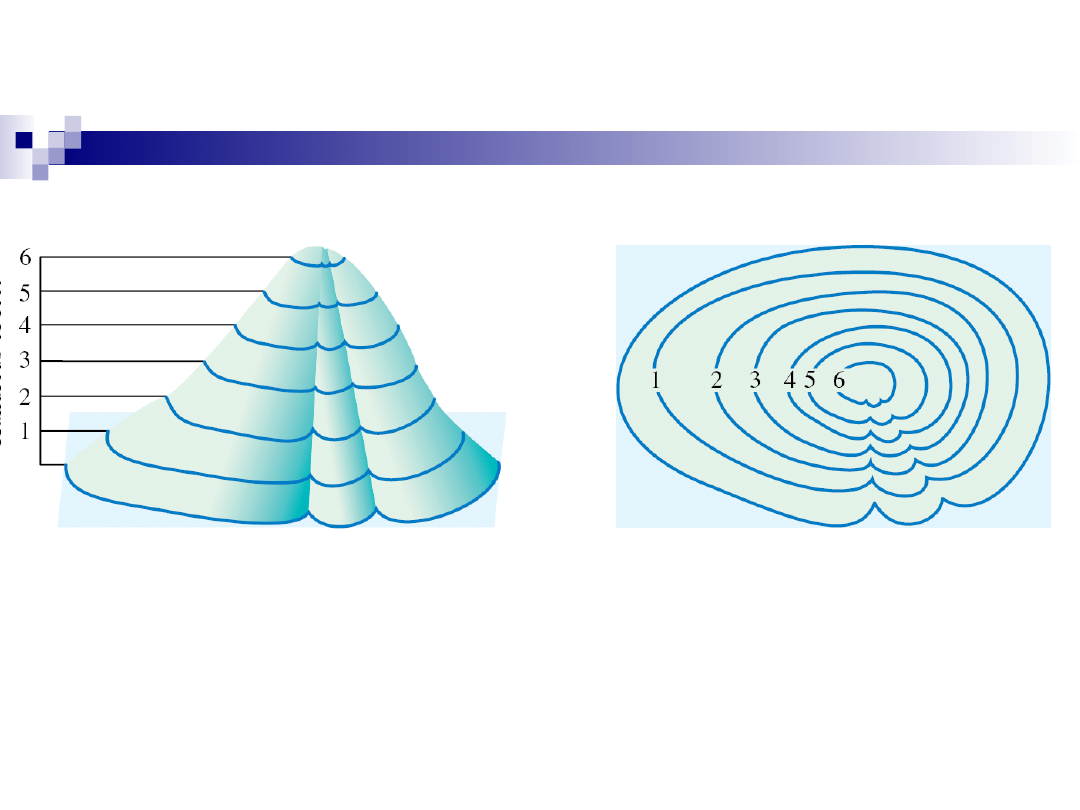
Slajd nr 15 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

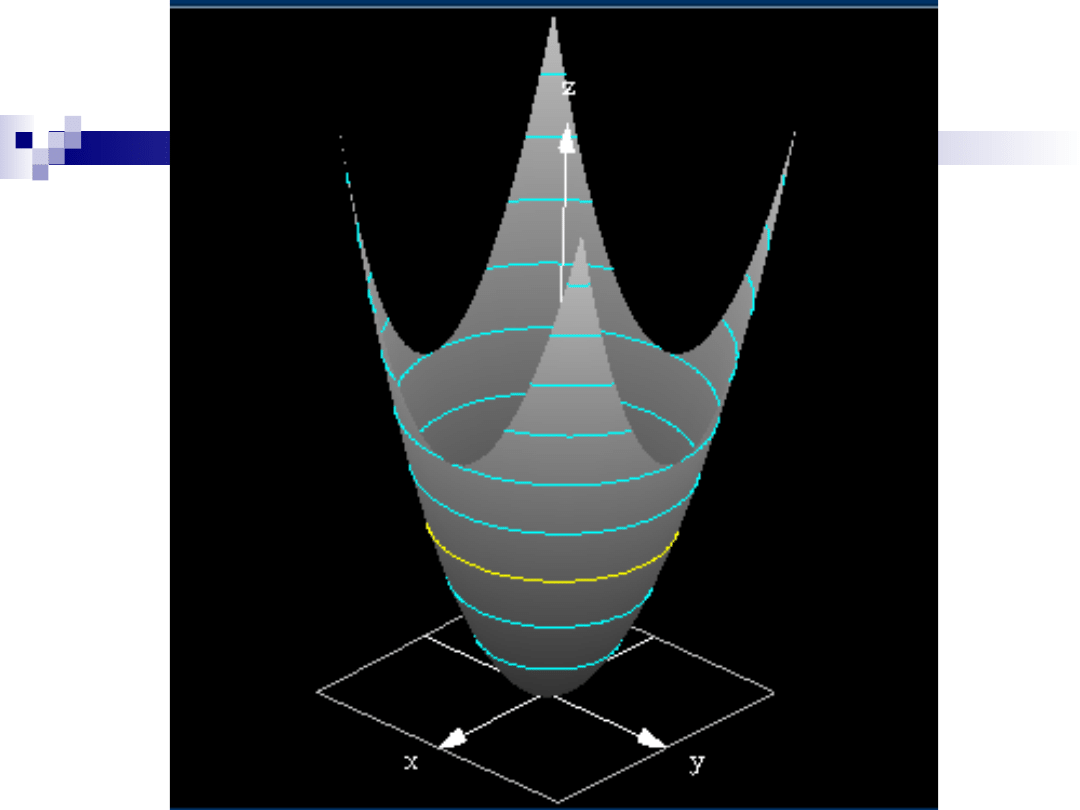
Slajd nr 16 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

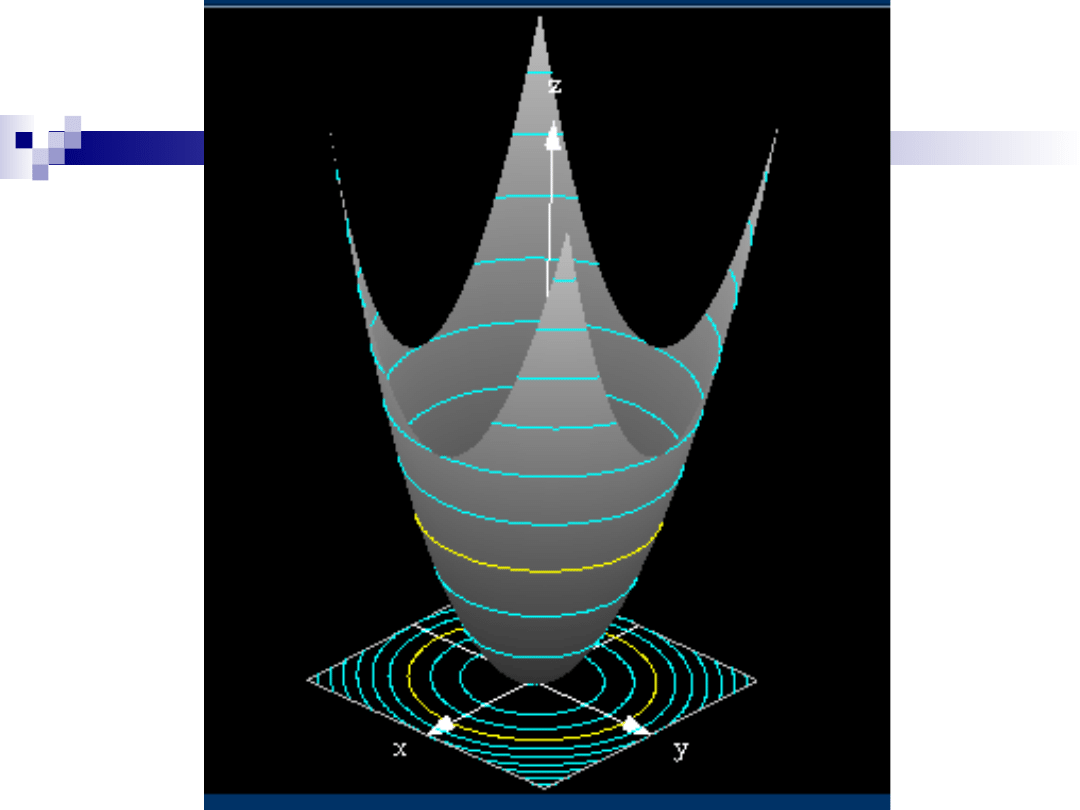
Slajd nr 17 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

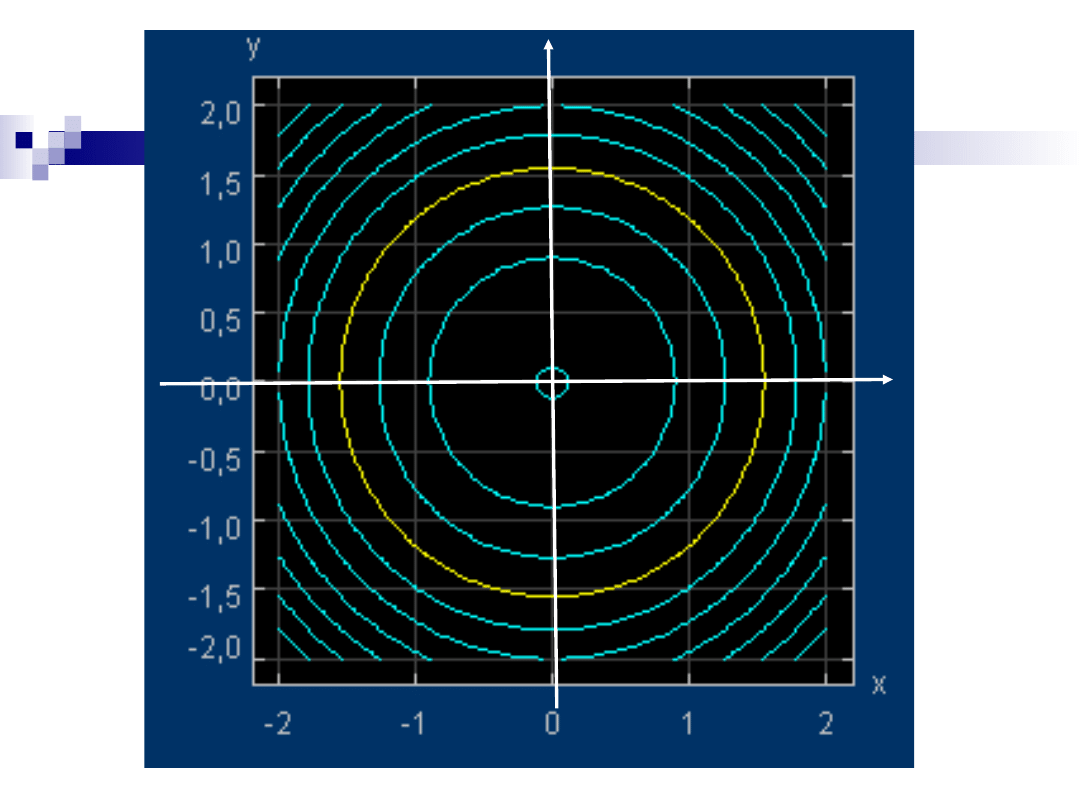
Slajd nr 18 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 19 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 20 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 21 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 22 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 23 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Warstwic

a

Równanie w

płaszczyźnie XOY

Naszkicować plan warstwicowy funkcji:

2

2

( , )

.

z f x y

x

y

=

= +

Dziedziną funkcji jest płaszczyzna. Funkcja przyjmuje
wartości nieujemne.

-3 -2 -1

1

2

3

-3

-2

-1

1

2

3

X

Y

O

z =
0

x

2

+ y

2

= 0

pkt
(0,0)

z =
0

z =
1

x

2

+ y

2

= 1

Okrąg o środku (0,0) i
r = 1

z =
1

z =
4

x

2

+ y

2

= 4

Okrąg o środku (0,0) i
r = 2

z =
4

z =
9

x

2

+ y

2

= 9

Okrąg o środku (0,0) i
r = 3

z =
9

Slajd nr 24 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 25 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Pochodne cząstkowe

Niech z = f(x,y) będzie funkcją określoną w
pewnym otoczeniu U punktu P

0

(x

0

,y

0

).

Przyjmijmy, że zmienna y przyjmuje stałą
wartość y = y

0

.

Wówczas funkcja f(x,y

0

) =



(x) jest funkcją jednej

tylko zmiennej i określona jest w pewnym
przedziale (x

0

–



; x

0

+



).

Jeżeli istnieje skończona granica:

0

0

0

0

0

0

0

0

(

)

( )

(

, )

( , )

lim

lim

,

h

h

x

h

x

f x

h y

f x y

h

h

�

�

F

+ - F

+

-

=

to nazywamy ją pochodną cząstkową funkcji f
w punkcie (x

0

,y

0

) względem zmiennej x

i oznaczamy jednym z symboli:

)

,

(

),

,

(

0

0

/

0

0

y

x

f

y

x

x

f

x





lub krótko:

/

,

.

x

f

f

x

�

�

Slajd nr 26 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Pochodne cząstkowe cd.

Niech z = f(x,y) będzie funkcją określoną w
pewnym otoczeniu U punktu P

0

(x

0

,y

0

).

Przyjmijmy teraz, że zmienna x przyjmuje stałą
wartość x = x

0

.

Wówczas funkcja f(x

0

,y) =



(y) jest funkcją jednej

tylko zmiennej i określona jest w pewnym
przedziale (y

0

–



; y

0

+



).

Jeżeli istnieje skończona granica:

0

0

0

0

0

0

0

0

(

)

( )

( ,

)

( , )

lim

lim

,

h

h

y

h

y

f x y

h

f x y

h

h

�

�

Y

+ - Y

+ -

=

to nazywamy ją pochodną cząstkową funkcji f
w punkcie (x

0

,y

0

) względem zmiennej y

i oznaczamy jednym z symboli:

/

0

0

0

0

( , ),

( , )

y

f

x y

f x y

y

�

�

lub krótko:

/

,

.

y

f

f

y

�

�

Slajd nr 27 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Pochodne cząstkowe – technika
obliczeń

Z przyjętych określeń wynika, że obliczanie
pochodnych cząstkowych funkcji wielu
zmiennych sprowadza się w praktyce do
obliczania pochodnej funkcji jednej zmiennej.

Przy obliczaniu pochodnej względem określonej
zmiennej należy funkcję traktować tak, jak gdyby
zależała ona tylko od tej zmiennej, a pozostałe
zmienne były parametrami.

W trakcie rachunków można stosować
odpowiednie twierdzenia rachunku różniczkowego
funkcji jednej zmiennej.

Slajd nr 28 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

2 3

2

( , ) 3

4

5

f x y

x y

x

y

=

+ +

/

( , )

x

f x y =

Slajd nr 29 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

2

3

2

( , ) 3

4

5

f x y

y

y

x

x

=

+ +

/

( , )

x

f x y =

3

3

2

y

x

� �

1

4

+ �

3

6

4

xy +

0

+ =

Slajd nr 30 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

2 3

2

( , ) 3

4

5

f x y

x y

x

y

=

+ +

/

( , )

y

f x y =

Slajd nr 31 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

2

3

2

( , ) 3

4

5

y

f x y

x

x

y

=

+ +

/

( , )

y

f x y =

2

2

3

3

x

y

�

2

5

y

+ �

0

+

2 2

9

10

x y

y

=

+

Slajd nr 32 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

3

( , )

4

ln

xy

f x y

xe

xy

y y

=

+

+

/

( , )

x

f x y =

Slajd nr 33 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

3

( , )

4

ln

y

x

f x y

e

y

x

x

y y

=

+

+

/

( , )

x

f x y =

1

xy

e

� +

3

4 1 y

��

xy

x e

y

� � +

0

+ =

3

4

xy

xy

e

xye

y

=

+

+

Slajd nr 34 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

3

( , )

4

ln

xy

f x y

xe

xy

y y

=

+

+

/

( , )

y

f x y =

Slajd nr 35 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

3

( , )

4

ln

y

x

y

y

y

f x

xe

x

y

=

+

+

/

( , )

y

f x y =

xy

xe

x

�+

1 lny

� +

2

4 3

x y

� +

1

y

y

� =

2

2

12

ln

1

xy

x e

xy

y

=

+

+

+

Slajd nr 36 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Korzystając ze wzorów podstawowych i reguł
różniczkowania obliczyć pochodne cząstkowe funkcji
względem wszystkich zmiennych:

xz

e

y

x

z

y

x

f





 cos

)

,

,

(

/

( , , )

x

f x y z =

1 cosy

�

+

cos

xz

y ze

-

-

( )

xz

e

z

-

-

=

/

( , , )

y

f x y z =

( sin )

x

y

�-

+

sin

x

y

-

0=

/

( , , )

z

f x y z =

( )

xz

e

x

-

-

=

xz

xe

-

-

0+

Slajd nr 37 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

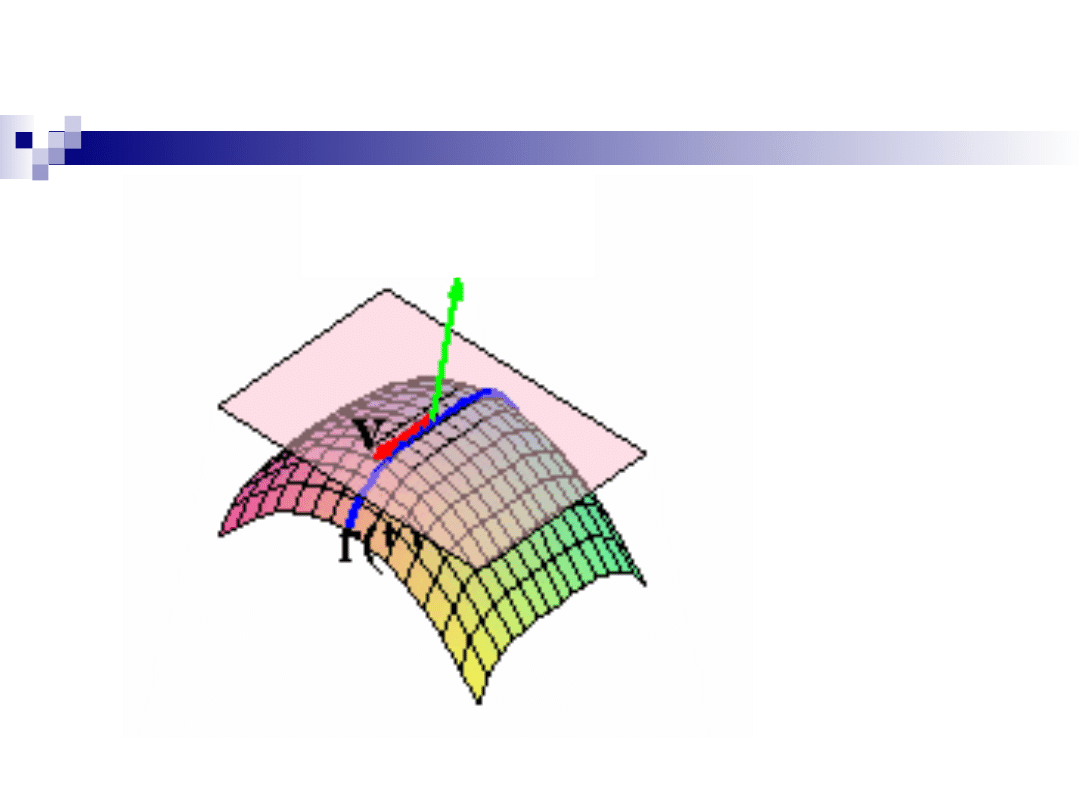
Różniczkowalność funkcji dwóch
zmiennych

Niech z = f(x,y) będzie funkcją określoną w pewnym
otoczeniu U punktu P

0

(x

0

,y

0

).

Jeżeli w tym punkcie istnieją obie pochodne
cząstkowe, które dodatkowo spełniają warunek:

0

0

/

/

0

0

0

0

0

0

0

0

2

2

( , ) ( , )

0

0

( , )

( , )(

)

( , )(

)

( , )

lim

0,

(

)

(

)

x

y

x y

x y

f x y

f x y x x

f x y y y

f x y

x x

y y

�

-

-

-

-

-

=

-

+ -

to funkcję nazywamy różniczkowalną w
punkcie P

0

(x

0

,y

0

).

Slajd nr 38 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Uwagi na temat
różniczkowalności

Granicą ilorazu występującego w definicji
różniczkowalności funkcji w punkcie jest zero oraz
mianownik w tym wyrażeniu dąży do zera.

Jest to możliwe pod warunkiem, że licznik jest
również zbieżny do zera i to znacznie szybciej niż
mianownik.

Oznacza to, że dla punktów (x,y) znajdujących
się blisko punktu (x

0

,y

0

). prawdziwa jest

przybliżona równość:

0

)

,

(

)

)(

,

(

)

)(

,

(

)

,

(

0

0

0

0

0

/

0

0

0

/













y

x

f

y

y

y

x

f

x

x

y

x

f

y

x

f

y

x

lub inaczej

/

/

0

0

0

0

0

0

0

0

( , )

( , )

( , )(

)

( , )(

).

x

y

f x y

f x y

f x y x x

f x y y y

�

+

-

+

-

Slajd nr 39 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Płaszczyzna styczna

/

/

0

0

0

0

0

0

0

0

( , )

( , )

( , )(

)

( , )(

)

x

y

z

f x y

f x y

f x y x x

f x y y y

�

+

-

+

-

1 4 4 4 4 4 4 4 4 4 2 4 4 4 4 4 4 4 4 43

Równani
e

)

)(

,

(

)

)(

,

(

)

,

(

0

0

0

/

0

0

0

/

0

0

y

y

y

x

f

x

x

y

x

f

y

x

f

z

y

x











jest równaniem pewnej płaszczyzny
przechodzącej przez punkt (x

0

,y

0

, f(x

0

,y

0

)), którą

nazywamy płaszczyzną styczną.

Slajd nr 40 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Slajd nr 41 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Napisać równanie płaszczyzny stycznej do
wykresu funkcji

2

2

( , )

f x y

x

y

= +

w punkcie, dla którego x

0

=1,

y

0

= 0.

)

)(

,

(

)

)(

,

(

)

,

(

0

0

0

/

0

0

0

/

0

0

y

y

y

x

f

x

x

y

x

f

y

x

f

z

y

x











2

2

0

0

( , ) 1 0

1

f x y = + =

/

( , ) 2

x

f x y

x

=

/

0

0

( , ) 2

x

f x y =

/

( , ) 2

y

f x y

y

=

/

0

0

( , ) 0

y

f x y =

1 2(

1) 0(

0)

z

x

y

= +

-

+

-

2

1

z

x

= -

Slajd nr 42 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

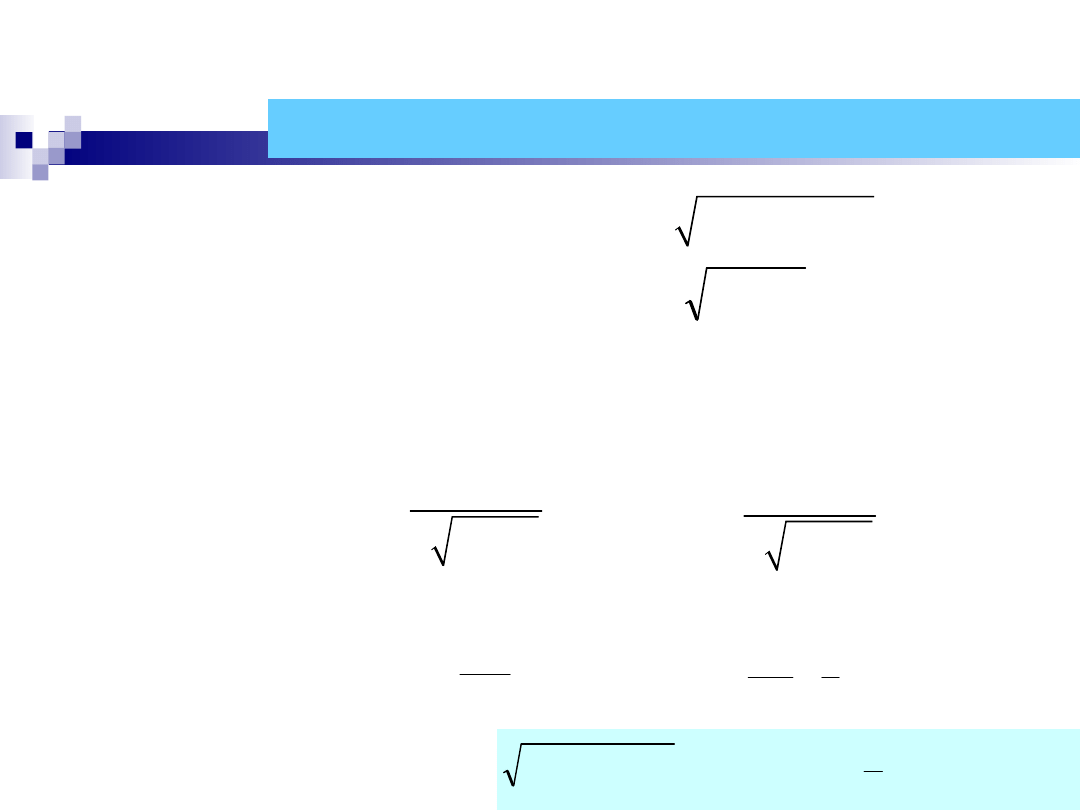
Oznacza to, że za wartość

funkcji w punkcie x

można przyjąć wartość odczytaną z wykresu
odpowiednio dobranej stycznej.

W pobliżu punktu styczności wykres funkcji
i stycznej praktycznie nie różnią się między
sobą.

Slajd nr 43 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Obliczenia przybliżone

Aby obliczyć przybliżoną wartość f(x,y) należy
możliwie blisko punktu (x,y) znaleźć taki punkt
(x

0

, y

0

) aby f (x

0

, y

0

) oraz obie pochodne

cząstkowe w tym punkcie dały się łatwo obliczyć,
a następnie zastosować wzór.

)

)(

,

(

)

)(

,

(

)

,

(

)

,

(

0

0

0

/

0

0

0

/

0

0

y

y

y

x

f

x

x

y

x

f

y

x

f

y

x

f

y

x











Slajd nr 44 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Obliczyć przybliżoną wartość wyrażenia:

3

2,01 0,97.

+

Wyrażenie to jest wartością funkcji

f x y

x

y

( , ) 



3

dla argumentów x = 2,01 i y =
0,97.

)

)(

,

(

)

)(

,

(

)

,

(

)

,

(

0

0

0

/

0

0

0

/

0

0

y

y

y

x

f

x

x

y

x

f

y

x

f

y

x

f

y

x











Pochodnymi cząstkowymi tej funkcji są odpowiednio:

2

/

3

3

( , )

,

2

x

x

f x y

x

y

=

+

Przyjmując x

0

= 2, y

0

= 1 mamy

0

0

( , ) 3,

f x y =

/

0

0

12

( , )

2,

2 3

x

f x y =

=

�

/

0

0

1

1

( , )

2 3 6

y

f x y =

=

�

/

3

1

( , )

.

2

y

f x y

x

y

=

+

Zatem po wstawieniu do
wzoru

201

097 3 2 001

1
6

003 3015

3

,

,

,

( , )

,



  







Slajd nr 45 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Różniczka zupełna

Wyrażenie

/

/

( , )

( , )

x

y

dff

x y dx f x y dy

=

+

nazywamy różniczką zupełną funkcji z =
f(x,y) odpowiadającą przyrostom dx i  dy.

W podobny sposób definiujemy różniczkę
zupełną funkcji wielu zmiennych.

Slajd nr 46 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Obliczyć różniczkę zupełną funkcji

2

2

( , )

ln(

).

f x y

x

x

y

=

+

Poniew
aż

/

2

2

2

2

1

( , ) 1 ln(

)

2

x

f x y

x

y

x

x

x

y

= �

+

+ �

� =

+

2

2

2

2

2

2

ln(

)

,

x

x

y

x

y

+

+

+

/

2

2

1

( , )

2

y

f x y

x

y

x

y

= �

� =

+

2

2

2

,

xy

x

y

+

to

2

2

2

2

2

2

2

2

2

ln(

)

.

x

xy

df

x

y

dx

dy

x

y

x

y

�

�

=

+

+

+

�

�

+

+

�

�

Slajd nr 47 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Gradient funkcji w punkcie

Niech z = f(x,y) będzie funkcją dwóch zmiennych
różniczkowalną w punkcie P

0

(x

0

,y

0

).

Wektor postaci





)

,

(

,

)

,

(

0

0

/

0

0

/

y

x

f

y

x

f

y

x

nazywamy gradientem funkcji w tym
punkcie i oznaczamy symbolem

0

0

grad ( , ).

f x y

�

Slajd nr 48 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Obliczanie gradientu

Wyznaczanie gradientu funkcji dwóch zmiennych
odbywa się według schematu:

)

,

(

y

x

f

z 

[

]

grad ( , )

,

f x y

�

=

pochodna po x

/

( , )

x

f x y

pochodna po y

/

( , )

y

f x y

Slajd nr 49 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Obliczyć w dowolnym punkcie, jeżeli:

f



grad

2

6

( , ) 3

4 .

f x y

x y

y

=

+

[

]

grad ( , )

,

f x y

�

=

pochodna po x

6xy

pochodna po y

2

5

3

24

x

y

+

Slajd nr 50 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Obliczyć w dowolnym punkcie, jeżeli:

f



grad

3

2

( , , ) 6

4

5

.

f x y z

xy

yz

x z

=

+

+

[

]

grad ( , , )

,

,

f x y z

�

=

pochodna po x

6

10

y

xz

+

pochodna po y

3

6

4

x

z

+

pochodna po z

2

2

12

5

yz

x

+

Przykład

Slajd nr 51 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Obliczanie gradientu funkcji w
punkcie

Aby obliczyć

należy po wyznaczeniu gradientu w dowolnym
punkcie przyjąć x = x

0

, y = y

0

.

)

,

(

grad

0

0

y

x

f



Slajd nr 52 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Przykład

Obliczyć , jeżeli:

grad (1, 1)

f

�

-

2

2

2

( , )

.

x

y

f x y

e

+

=

[

]

grad ( , )

,

f x y

�

=

pochodna po x

2

2

2

4

x

y

e

x

+

�

pochodna po y

2

2

2

2

x

y

e

+

�

2 2

2 2

grad (1, 1)

4,

2

f

e

e

�

-

-

�

�

-

=

�

� =

�

�

[

]

4,2

Slajd nr 53 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

Obliczyć , jeżeli:

grad ( 1,1,3)

f

�

-

2

2

( , , )

2

.

f x y z

x

xy z

= +

[

]

grad ( , , )

,

,

f x y z

�

=

pochodna po x

2

2

2

x

y z

+

pochodna po y

4xyz

pochodna po z

2

2xy

Przykład

2

2

grad ( 1,1,3)

2 ( 1) 2 1 3,4 ( 1) 1 3, 2 ( 1) 1

f

�

�

�

-

= �- + � � �- �� �- � =

�

�

[4, 12, 2]

= -

-

Slajd nr 54 / 54

Tomasz Kowalski. Matematyka. Wykład 26: Funkcje

wielu zmiennych

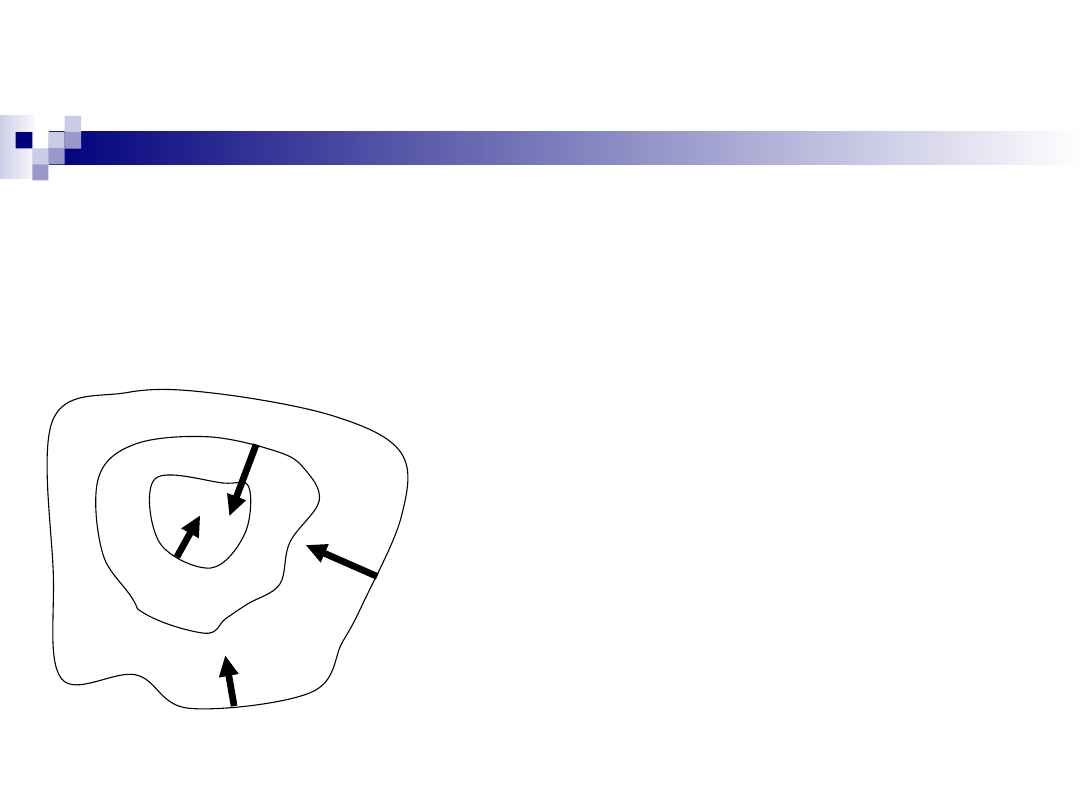
Własności gradientu

1. Jeżeli wektor zaczepić w punkcie

P

0

(x

0

,y

0

) , to jest on prostopadły do warstwicy

przechodzącej przez ten punkt.

)

,

(

grad

0

0

y

x

f



Plan
warstwicowy

2. Gradient pokazuje kierunek

największego wzrostu
funkcji.

z = 0

z = 2

z = 4